Electrokinetics of soft particles

Abstract

Theories of electrokinetics of soft particles, which are particles covered with an ion-penetrable surface layer of polyelectrolytes, are reviewed. Approximate analytic expressions are given, which describe various electrokinetics of soft particles both in dilute and concentrated suspensions, that is, electrophoretic mobility, electrical conductivity, sedimentation velocity and potential, dynamic electrophoretic mobility, colloid vibration potential, and electrophoretic mobility under salt-free condition.

Introduction

The motion of hard particles with no surface structures in a liquid in a steady external electric field, which is called electrophoresis, depends on the particle size, the thickness (1/κ) of the electrical diffuse double layer formed around the charged particles, and the zeta-potential ξ [1–26]. For dilute spherical particles of radius a carrying low ξ, the electrophoretic mobility μ = U/E (where U and E are, respectively, the magnitudes of the particle velocity U and the applied electric field E) is given by either of Smoluchowski’s 1, Hückel’s 2, or Henry’s equation 3, depending on the magnitude of κa, viz.,

$$ \mu = \frac{{\varepsilon _{r} \varepsilon _{o} }} {\eta }\zeta ,\kappa \alpha \gg 1{\left( {Smoluchowski} \right)} $$

(1)

$$ \mu = \frac{{2\varepsilon _{r} \varepsilon _{o} }} {{3\eta }}\zeta ,\kappa a \ll 1{\left( {H{\ddot u} ckel} \right)} $$

(2)

$$ \mu = \frac{{\varepsilon _{r} \varepsilon _{o} }} {\eta }\zeta f{\left( {\kappa a} \right)},\,arbitrary\;\kappa a\quad {\left( {\operatorname{Henry} } \right)} $$

(3)

where κ is the Debye–Hückel parameter, ɛ _r and η are, respectively, the relative permittivity and viscosity of the solution, ɛ _o is the permittivity of a vacuum, and f(κa) is Henry’s function. The following approximate expression for f(κa) has been derived [16] (for cylindrical particles, see [18]):

$$ f{\left( {\kappa a} \right)} = \frac{2} {3}{\left[ {1 + \frac{1} {{2{\left( {1 + \frac{{2.5}} {{\kappa a{\left\{ {1 + 2\exp {\left( { - \kappa a} \right)}} \right\}}}}} \right)}^{3} }}} \right]} $$

(4)

Mobility expressions applicable for particles with higher zeta potentials are given in [8, 10, 12, 21, 24].

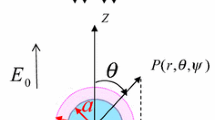
Electrokinetics of soft particles (i.e., hard particles covered with an ion-penetrable surface layer of polyelectrolytes; Fig. 1), however, is quite different from that of hard particles [27–40]. For soft particles, the zeta potential (i.e., the potential at the particle core surface) becomes less important and, for most cases, loses its physical meaning. Instead, the following two potentials play an essential role in electrokinetics of soft particles, that is, the Donnan potential ψ _DON and the potential ψ _o at the boundary between the polyelectrolyte layer and the surrounding electrolyte solution (which we call the surface potential of a soft particle; Fig. 2). We start with the electrophoretic mobility of soft particles. Then, we discuss other types of electrokinetics of soft particles.

Fig. 1

Schematic representation of a soft particle, i.e., a hard particle covered with an ion-penetrable surface layer of polyelectrolytes

Fig. 2

Ion and potential distribution across a surface charge layer of thickness d where x is the coordinate normal to the surface layer. When d ≫ 1/κ, the potential deep inside the surface layer is practically equal to the Donnan potential ψ _DON. The surface potential ψ _o of the soft surface is defined as the potential at the boundary between the surface layer and the surrounding electrolyte solution

Electrophoretic mobility

General mobility expression

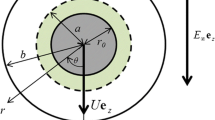
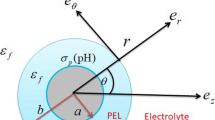
Consider a spherical soft particle moving with a velocity U in a liquid containing a general electrolyte in an applied electric field E (Fig. 3). We assume that the particle core of radius a is coated with an ion-penetrable surface layer of polyelectrolytes of thickness d, and that ionized groups of valence Z are distributed within the polyelectrolyte layer at a uniform density N so that the polyelectrolyte later is uniformly charged at a constant density ρ _fix = ZeN, where e is the elementary electric charge. The polymer-coated particle has thus an inner radius a and an outer radius b ≡ a + d. The origin of the spherical polar coordinate system is held fixed at the center of the particle core. Let the electrolyte be composed of M ionic mobile species of valence z _i , bulk concentration (number density) $n^{\infty }_{i}$, and drag coefficient λ _i (i = 1, 2,..., M). We adopt the model of Debye–Bueche [41, 42] that the polymer segments are regarded as resistance centers distributed uniformly in the polyelectrolyte layer, exerting frictional forces on the liquid flowing in the polyelectrolyte layer.

Fig. 3

A soft particle consisting of the particle core of radius a coated with a polyelectrolyte layer of thickness d. b = a + d

We assume that the liquid velocity u(r) at position r relative to the particle (u(r) → −U as r ≡ ∣r∣→∞) obeys the following Navier–Stokes equations [26, 35, 36]:

$$ \eta \nabla \times \nabla \times u + \nabla p + \rho _{{el}} \nabla \psi = 0, {\kern 1pt} \quad r > b $$

(5)

$$ \eta \nabla \times \nabla \times u + \nu u + \nabla p + \rho _{{el}} \nabla \psi = 0,\quad a < r < b $$

(6)

where p is the pressure, ρ _el(r) is the volume charge density resulting from the mobile charged ionic species, and ψ(r) is the electric potential. The term ν u on the left-hand side of Eq. 6 represents the frictional forces exerted on the liquid flow by the polymer segments in the polyelectrolyte layer, and ν is the frictional coefficient. If it is assumed that each resistance center corresponds to a polymer segment, which in turn is regarded as a sphere of radius a _p, and the polymer segments are distributed at a uniform volume density of N _p in the polyelectrolyte layer, then each polymer segment exerts the Stokes resistance 6πηa _p u on the liquid flow in the polyelectrolyte layer so that:

$$ \nu = 6\pi \eta a_{p} N_{p} $$

(7)

The charge density ρ _el(r) is related to the electric potential ψ(r) by the Poison equations,

$$ \Delta \psi {\left( r \right)} = - \frac{{\rho _{{el}} {\left( r \right)}}} {{\varepsilon _{r} \varepsilon _{o} }},r > b $$

(8)

$$ \Delta \psi {\left( r \right)} = - \frac{{\rho _{{el}} {\left( r \right)} + ZeN}} {{\varepsilon _{r} \varepsilon _{o} }},\quad a < r < b $$

(9)

where the relative permittivity ɛ _r is assumed to take the same value both inside and outside the polyelectrolyte layer.

It can be shown that for a weak applied filed, the electrophoretic mobility μ of a soft particle is given by [40]

$$ \mu = \frac{{b^{2} }} {9}{\int_b^\infty {{\left[ {3{\left( {1 - \frac{{r^{2} }} {{b^{2} }}} \right)} - \frac{{2L_{2} }} {{L_{1} }}{\left( {1 - \frac{{r^{3} }} {{b^{3} }}} \right)}} \right]}} }G{\left( r \right)}dr + \frac{{2L_{3} }} {{3\lambda ^{2} L_{1} }}{\int_a^\infty {{\left( {1 + \frac{{r^{3} }} {{2b^{3} }}} \right)}} }G{\left( r \right)}dr $$

$$ - \frac{2} {{3\lambda ^{2} }}{\int_a^b {\left[ {1 - \frac{{3a}} {{2\lambda ^{2} b^{3} L_{1} }}} \right.{\left\{ {{\left( {L_{3} + L_{4} \lambda r} \right)}\cosh {\left[ {\lambda {\left( {r - a} \right)}} \right]}} \right\}}} } $$

$$\left. {\left. { - {\left( {L_{4} + L_{3} \lambda r} \right)}sinh{\left[ {\lambda {\left( {r - a} \right)}} \right]}} \right\}} \right]G{\left( r \right)}dr$$

(10)

with

$$ L_{1} = {\left( {1 + \frac{{a^{3} }} {{2b^{3} }} + \frac{{3a}} {{2\lambda ^{2} b^{3} }} - \frac{{3a^{2} }} {{2\lambda ^{2} b^{4} }}} \right)}\cosh {\left[ {\lambda {\left( {b - a} \right)}} \right]}p - {\left( {1 - \frac{{3a^{2} }} {{2b^{2} }} + \frac{{a^{3} }} {{2b^{3} }} + \frac{{3a}} {{2\lambda ^{2} b^{3} }}} \right)}\frac{{sinh{\left[ {\lambda {\left( {b - a} \right)}} \right]}}} {{\lambda b}} $$

(11)

$$ L_{2} = {\left( {1 + \frac{{a^{3} }} {{2b^{3} }} + \frac{{3a}} {{2\lambda ^{2} b^{3} }}} \right)}\cosh {\left[ {\lambda {\left( {b - a} \right)}} \right]} + \frac{{3a^{2} }} {{2b^{2} }}\frac{{{\rm{sinh}}{\left[ {\lambda {\left( {b - a} \right)}} \right]}}} {{\lambda b}} - \frac{{3a}} {{2\lambda ^{2} b^{3} }} $$

(12)

$$ L_{3} = \cosh {\left[ {\lambda {\left( {b - a} \right)}} \right]} - \frac{{sinh{\left[ {\lambda {\left( {b - a} \right)}} \right]}}} {{\lambda b}} - \frac{a} {b} $$

(13)

$$ L_{4} = sinh{\left[ {\lambda {\left( {b - a} \right)}} \right]} - \frac{{\cosh {\left[ {\lambda {\left( {b - a} \right)}} \right]}}} {{\lambda b}} + \frac{{\lambda a^{2} }} {{3b}} + \frac{{2\lambda b^{2} }} {{3a}} + \frac{1} {{\lambda b}} $$

(14)

$$ \lambda = {\left( {\nu \mathord{\left/ {\vphantom {\nu \eta }} \right. \kern-\nulldelimiterspace} \eta } \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} $$

(15)

$$ G{\left( r \right)} = - \frac{e} {{\eta r}}\frac{{dy}} {{dr}}{\sum\limits_{i = 1}^M {z^{2}_{i} n^{\infty }_{i} } }e^{{ - z_{i} y}} \phi _{i} $$

(16)

$$ y = \frac{{e\psi ^{{{\left( 0 \right)}}} }} {{kT}} $$

(17)

where ϕ _i (r) is a function relating to the deviation of the electrochemical potential of the ith ionic species due to the applied electric field, ψ ⁽⁰⁾(r) is the equilibrium potential, y is the scaled potential, ρ _e is the Boltzmann constant, T is the absolute temperature, and the reciprocal of λ, i,e., 1/λ, is called the electrophoretic softness.

Analytic approximations

We derive approximate mobility formulas for the simple but important case where the potential is arbitrary but the double layer potential still remains spherically symmetrical in the presence of the applied electric field (the relaxation effect is neglected). Further, we treat the case where the following conditions hold

$$ \kappa a \gg 1,\lambda a \gg 1{\left( {\operatorname{and} \;thus\,\kappa b \gg 1,\lambda b \gg 1} \right)}\operatorname{and} \;\kappa d \gg 1\;\operatorname{and} \;\lambda d \gg 1 $$

(18)

Here,

$$\kappa = {\left( {\frac{1}{{\varepsilon _{r} \varepsilon _{o} kT}}{\sum\limits_{i = 1}^N {z^{2}_{i} e^{2} n^{\infty }_{i} } }} \right)}^{{1/2}} $$

(19)

is the Debye–Hückel parameter of the electrolyte solution. Equation 18 is satisfied for most practical cases. For the case in which the electrolyte is symmetrical with a valence z and bulk concentration n, if κd ≫ 1, then the potential inside the polyelectrolyte layer can be approximated by

$$ \psi ^{{{\left( 0 \right)}}} {\left( r \right)} = \psi _{\rm{DON}} + {\left( {\psi _{o} - \psi _{\rm{DON}} } \right)}e^{{ - \kappa _{m} {\left| {r - b} \right|}}} ,a < r < b $$

(20)

with

$$ \psi _{\rm{DON}} = {\left( {\frac{{kT}} {{ze}}} \right)}\ln {\left[ {\frac{{ZN}} {{2zn}} + {\left\{ {{\left( {\frac{{ZN}} {{2zn}}} \right)}^{2} + 1} \right\}}^{{1/2}} } \right]} $$

(21)

$$ \psi _{o} = \frac{{kT}} {{ze}}{\left( {\ln {\left[ {\frac{{ZN}} {{2zn}} + {\left\{ {{\left( {\frac{{ZN}} {{2zn}}} \right)}^{2} + 1} \right\}}^{{1/2}} } \right]} + \frac{{2zn}} {{ZN}}{\left[ {1 - {\left\{ {{\left( {\frac{{ZN}} {{2zn}}} \right)}^{2} + 1} \right\}}^{{1/2}} } \right]}} \right)} $$

(22)

$$ \kappa _{m} = \kappa {\left[ {1 + {\left( {\frac{{ZN}} {{2zn}}} \right)}^{2} } \right]}^{{1/4}} $$

(23)

where κ _m is the Debye–Hückel parameter in the surface layer that involves the contribution of the fixed-charges ZeN, and ψ _DON and ψ _o = ψ(b) are, respectively, the Donnan potential and the surface potential of the surface charge layer.

For such cases, it can be shown that Eq. 10 yields [35]

$$ \mu = \frac{{\varepsilon _r \varepsilon _0 }}{\eta }\frac{{{{\psi _0 } \mathord{\left/ {\vphantom {{\psi _0 } {\kappa _m }}} \right. \kern-\nulldelimiterspace} {\kappa _m }} + {{\psi _{\text{DON}} } \mathord{\left/ {\vphantom {{\psi _{\text{DON}} } \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}{{{1 \mathord{\left/ {\vphantom {1 {\kappa _m }}} \right. \kern-\nulldelimiterspace} {\kappa _m }} + {1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}f\left( {\frac{d}{a}} \right) + \frac{{\text{Ze}N}}{{\eta \lambda ^2 }} $$

(24)

with

$$ f{\left( {\frac{d} {a}} \right)} = \frac{2} {3}{\left( {1 + \frac{{a^{3} }} {{2b^{3} }}} \right)} = \frac{2} {3}{\left\{ {1 + \frac{1} {{2{\left( {{1 + d} \mathord{\left/ {\vphantom {{1 + d} a}} \right. \kern-\nulldelimiterspace} a} \right)}^{3} }}} \right\}} $$

(25)

In the limit of d ≫ a, in which case f(d/a)→2/3, Eq. 24 reduces to

$$ \mu = \frac{{2\varepsilon _r \varepsilon _0 }}{{3\eta }}\frac{{{{\psi _0 } \mathord{\left/ {\vphantom {{\psi _0 } {\kappa _m }}} \right. \kern-\nulldelimiterspace} {\kappa _m }} + {{\psi _{\text{DON}} } \mathord{\left/ {\vphantom {{\psi _{\text{DON}} } \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}}{{{1 \mathord{\left/ {\vphantom {1 {\kappa _m }}} \right. \kern-\nulldelimiterspace} {\kappa _m }} + {1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} + \frac{{\text{Ze}N}}{{\eta \lambda ^2 }}$$

(26)

For the low-potential case, Eq. 26 further reduces to

$$ \mu = \frac{{ZeN}} {{\eta \lambda ^{2} }}{\left[ {1 + \frac{2} {3}{\left( {\frac{\lambda } {\kappa }} \right)}^{2} {\left( {\frac{{{1 + \lambda } \mathord{\left/ {\vphantom {{1 + \lambda } {2\kappa }}} \right. \kern-\nulldelimiterspace} {2\kappa }}} {{{1 + \lambda } \mathord{\left/ {\vphantom {{1 + \lambda } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }}} \right)}} \right]} $$

(27)

which agrees with Hermans–Fujita’s equation for the electrophoretic mobility of a spherical polyelectrolyte (a soft particle with no particle core) [41].

In the opposite limit of d ≪ a, in which case f(d/a)→1, Eq. 24 reduces to

$$ \mu = \frac{{\varepsilon _{r} \varepsilon _{0} }}{\eta }\frac{{{\psi _{0} } \mathord{\left/ {\vphantom {{\psi _{0} } {\kappa _{m} }}} \right. \kern-\nulldelimiterspace} {\kappa _{m} } + {\psi _{{DON}} } \mathord{\left/ {\vphantom {{\psi _{{DON}} } \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}{{1 \mathord{\left/ {\vphantom {1 {\kappa _{m} }}} \right. \kern-\nulldelimiterspace} {\kappa _{m} } + 1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }} + \frac{{{\text{Ze}}N}}{{\eta \lambda ^{2} }}$$

(28)

which, for low potentials, gives

$$ \mu = \frac{{\operatorname{Ze} N}} {{\eta \lambda ^{2} }}{\left[ {1 + {\left( {\frac{\lambda } {\kappa }} \right)}^{2} {\left( {\frac{{{1 + \lambda } \mathord{\left/ {\vphantom {{1 + \lambda } {2\kappa }}} \right. \kern-\nulldelimiterspace} {2\kappa }}} {{{1 + \lambda } \mathord{\left/ {\vphantom {{1 + \lambda } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }}} \right)}} \right]} $$

(29)

Equation 24 consists of two terms: the first term is a weighted average of the Donnan potential ψ _DON and the surface potential ψ _o. It should be stressed that only the first term is subject to the shielding effects of electrolytes, tending zero as the electrolyte concentration n increases, while the second term does not depend on the electrolyte concentration. In the limit of high electrolyte concentrations, all the potentials vanish, and only the second term of the mobility expression remains, that is, as κ→∞, μ tends to a non-zero limiting value $\mu ^{\infty }$ (Fig. 4), given by

$$ \mu \to \mu ^{\infty } = \frac{{\operatorname{Ze} N}} {{\eta \lambda ^{2} }} $$

(30)

Fig. 4

The electrophoretic mobility μ of a negatively charged particle as a function of electrolyte concentration. The mobility of a soft particle tends to a non-zero value ($\mu ^{\infty }$) in the limit of high electrolyte concentrations, while the mobility of a hard particle tends to zero owing to ionic shielding effects

This is a characteristic of the electrokinetic behavior of soft particles, in contrast to the case of the electrophoretic mobility of hard particles, which should reduce to zero due to the shielding effects, as the mobility expressions for rigid particles do not have $\mu ^{\infty }$. Furthermore, it is to be noted that Eq. 24 does not depend on the potential ψ ⁽⁰⁾(a) at the slipping plane at r = a. This means that the mobility of soft particles is insensitive to the precise position of the slipping plane. In other words, for such cases, the zeta potential loses its meaning. The term $\mu ^{\infty }$ can be interpreted as resulting from the balance between the electric force acting on the fixed-charges (ZeN)E and the frictional force νu, viz., (ZeN)E + νu = 0, from which Eq. 23 follows.

Weakly charged spherical soft particles

If the fixed-charge density ZeN is low, then from Eq. 20, one can derive the following approximate expression for μ without recourse to conditions given by Eq. 18 [40]:

$$ \mu = \frac{{\operatorname{Ze} Nb^{2} f_{0} }} {{2\eta }}\left[ {\frac{{a^{3} }} {{6b}}{\int_b^\infty {\frac{{e^{{ - \kappa {\left( {r - b} \right)}}} }} {{r^{3} }}} }dr - \frac{{a^{3} b}} {2}{\left( {1 - \frac{{2L_{2} }} {{3L_{1} }} + \frac{{2L_{3} }} {{\lambda ^{2} b^{2} L_{1} }}} \right)}{\int_b^\infty {\frac{{e^{{ - \kappa {\left( {r - b} \right)}}} }} {{r^{5} }}} }dr} \right. $$

$$ \left. { - \frac{2} {{3\kappa b}} + \frac{{L_{3} }} {{\lambda ^{2} b^{2} L_{1} }}{\left( {1 + \frac{{a^{3} }} {{2b^{3} }} + \frac{1} {{\kappa b}} + \frac{1} {{\kappa ^{2} b^{2} }}} \right)} + \frac{{2L_{2} }} {{3\kappa bL_{1} }}{\left( {1 + \frac{1} {{\kappa b}}} \right)}} \right] $$

$$ - \frac{{\operatorname{Ze} Na^{2} {\left( {1 + \kappa b} \right)}}} {{4\eta \lambda ^{3} b^{3} {\left( {1 + \kappa a} \right)}}}e^{{ - \kappa {\left( {b - a} \right)}}} \left[ {{\left( {\frac{{L_{3} + L_{4} }} {{L_{1} }}} \right)}{\left\{ {{\left( {1 - \frac{1} {{\kappa a}}} \right)}f_{1} {\left( {\kappa ,\lambda } \right)} + {\left( {1 + \frac{1} {{\kappa a}}} \right)}f_{1} {\left( { - \kappa ,\lambda } \right)}} \right\}}} \right. $$

$$ - \left. {{\left( {\frac{{L_{3} - L_{4} }} {{L_{1} }}} \right)}{\left\{ {{\left( {1 - \frac{1} {{\kappa a}}} \right)}f_{1} {\left( {\kappa , - \lambda } \right)} + {\left( {1 + \frac{1} {{\kappa a}}} \right)}f_{1} {\left( { - \kappa , - \lambda } \right)}} \right\}}} \right] $$

$$ - \frac{{\operatorname{Ze} N{\left( {1 + \kappa b} \right)}}} {{3\eta \lambda ^{2} {\left( {1 + \kappa a} \right)}}}e^{{ - \kappa {\left( {b - a} \right)}}} \left[ {{\left( {1 - \frac{{L_{3} }} {{L_{1} }}} \right)}{\left\{ {{\left( {1 - \frac{1} {{\kappa a}}} \right)}f_{2} {\left( \kappa \right)} + {\left( {1 + \frac{1} {{\kappa a}}} \right)}f_{2} {\left( { - \kappa } \right)}} \right\}}} \right. $$

$$ \left. { - \frac{{L_{3} }} {{L_{1} }}{\left\{ {{\left( {1 - \frac{1} {{\kappa a}}} \right)}f_{3} {\left( \kappa \right)} + {\left( {1 + \frac{1} {{\kappa a}}} \right)}f_{3} {\left( { - \kappa } \right)}} \right\}}} \right] $$

(31)

where

$$ f_{0} = 1 - \frac{1} {{\kappa b}} + \frac{{{\left( {1 - \kappa a} \right)}{\left( {1 + \kappa b} \right)}}} {{{\left( {1 + \kappa a} \right)}\kappa b}}e^{{ - 2\kappa {\left( {b - a} \right)}}} $$

(32)

$$ f_{1} {\left( {\kappa ,\lambda } \right)} = \frac{{\kappa a^{3} }} {2}{\int_a^b {\frac{{e^{{ - {\left( {\kappa + \lambda } \right)}{\left( {r - a} \right)}}} }} {{r^{3} }}} }dr - \frac{{3a^{3} }} {{2\lambda }}{\int_a^b {\frac{{e^{{ - {\left( {\kappa + \lambda } \right)}{\left( {r - a} \right)}}} }} {{r^{5} }}} }dr + \frac{3} {{2\lambda a}} + \frac{\kappa } {{\kappa + \lambda }} - {\left\{ {\frac{1} {{\lambda b}}{\left( {1 + \frac{{a^{3} }} {{2b^{3} }}} \right)} + \frac{\kappa } {{\kappa + \lambda }}} \right\}}e^{{ - {\left( {\kappa + \lambda } \right)}{\left( {b - a} \right)}}} $$

(33)

$$ f_{2} (\kappa ) = \frac{{3a^{4} }} {2}{\int_a^b {\frac{{e^{{ - \kappa (r - a)}} }} {{r^{5} }}} }dr + \frac{a} {b}e^{{ - \kappa (b - a)}} {\left( {1 + \frac{{a^{3} }} {{2b^{3} }}} \right)} - \frac{3} {2} $$

(34)

$$ f_{3} (\kappa ) = \frac{a} {{2b}}e^{{ - \kappa (b - a)}} {\left( {1 + \frac{{a^{3} }} {{2b^{3} }} + \frac{3} {{\kappa b}} + \frac{3} {{\kappa ^{2} b^{2} }}} \right)} - \frac{{3a^{3} }} {{4b^{3} }}{\left( {1 + \frac{2} {{\kappa a}} + \frac{2} {{\kappa ^{2} a^{2} }}} \right)} $$

(35)

In Fig. 5, the results of the calculation of the scaled electrophoretic mobility via Eq. 31 as a function of κa for various vales of a/b at λa = 10 is given, showing how the electrophoretic mobility μ of a soft particle depends on κa, λa, and a/b.

Fig. 5

Scaled electrophoretic mobility μ* = (η/ρ _fix a ²)μ of a soft particle as a function of κa for various values of a/b at λa = 10

Consider various limiting forms of Eq. 31.

• (1) Low electrolyte concentration limit. In the limit κ→0 (Hückel’s limit), Eq. 31 becomes

  $$ \mu = \frac{Q} {{D_{H} }} $$

  (36)

  with

  $$ Q = \frac{4} {3}\pi {\left( {b^{3} - a^{3} } \right)}\rho _{{fix}} $$

  (37)
  $$ D_{H} = 6\pi \eta a{\left[ {\frac{a} {b}{\left( {\frac{{L_{2} }} {{L_{1} }} + \frac{{3L_{3} }} {{2\lambda ^{2} b^{2} L_{1} }}} \right)}} \right]}^{{ - 1}} $$

  (38)

  where Q is the total particle charge, and D _H is the drag coefficient of a soft particle [43]. Note that Eq. 36 can be directly derived from the condition of balance between the electric force and the drag force acting on the particle by using an expression for the drag force acting on a particle covered with an uncharged polymer layer derived by Masliyah et al. [44]. Note also that Eq. 36 corresponds to Hückel’s equation (Eq. 2) for hard spheres.

• (2) High electrolyte concentration limit. In the limit κ→∞, Eq. 31 becomes

  $$ \mu = \frac{{\operatorname{Ze} N}} {{\eta \lambda ^{2} }}{\left( {1 + \frac{{a^{3} }} {{2b^{3} }}} \right)}{\left\{ {\frac{{L_{3} }} {{L_{1} }} - \frac{1} {3} + \frac{{a{\left( {1 - \lambda b} \right)}}} {{4\lambda ^{2} b^{3} }}{\left( {\frac{{L_{3} - L_{4} }} {{L_{1} }}} \right)}e^{{\lambda {\left( {b - a} \right)}}} } \right\}} $$

  (39)

  which is an extension of Eq. 30 to cover the case where Eq. 41 does not hold.

• (3) Spherical polyelectrolyte. In the limit a→0, Eq. 31 tends to

  $$ \mu = \frac{{\operatorname{Ze} N}} {{\eta \lambda ^{2} }}\left[ {1 + \frac{1} {3}{\left( {\frac{\lambda } {\kappa }} \right)}^{2} {\left( {1 + e^{{ - 2\kappa b}} - \frac{{1 - e^{{ - 2\kappa b}} }} {{\kappa b}}} \right)}} \right.\left. { + \frac{1} {3}{\left( {\frac{\lambda } {\kappa }} \right)}^{2} \frac{{{1 + 1} \mathord{\left/ {\vphantom {{1 + 1} {\kappa b}}} \right. \kern-\nulldelimiterspace} {\kappa b}}} {{{\left( {\lambda \mathord{\left/ {\vphantom {\lambda \kappa }} \right. \kern-\nulldelimiterspace} \kappa } \right)}^{2} - 1}}{\left\{ {{\left( {\frac{\lambda } {\kappa }} \right)}\frac{{1 + e^{{ - 2\kappa b}} - {{\left( {1 - e^{{ - 2\kappa b}} } \right)}} \mathord{\left/ {\vphantom {{{\left( {1 - e^{{ - 2\kappa b}} } \right)}} {\kappa b}}} \right. \kern-\nulldelimiterspace} {\kappa b}}} {{{{\left( {1 + e^{{ - 2\lambda b}} } \right)}} \mathord{\left/ {\vphantom {{{\left( {1 + e^{{ - 2\lambda b}} } \right)}} {{\left( {1 - e^{{ - 2\lambda b}} } \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {1 - e^{{ - 2\lambda b}} } \right)}}{ - 1} \mathord{\left/ {\vphantom {{ - 1} {\lambda b}}} \right. \kern-\nulldelimiterspace} {\lambda b}}} - {\left( {1 - e^{{ - 2\kappa b}} } \right)}} \right\}}} \right] $$

  (40)

  For λb ≫ 1 and κb ≫ 1, Eq. 40 reduces to Eq. 27. Equation 40, as well as Eq. 27, is known as Hermans–Fujita formulas [41] for the electrophoretic mobility of spherical polyelectrolytes.

• (4) Plate-like soft particle. In the limit a→∞, Eq. 31 tends to

  $$ \mu = \frac{{ZeN}} {{2\eta \kappa ^{2} }}\left[ {{\left( {1 - e^{{ - 2\kappa d}} } \right)}{\left\{ {1 + \frac{\kappa } {\lambda }{\rm{tanh}}{\left( {\lambda d} \right)}} \right\}}} \right. $$
  $$ \left. { + {\left\{ {\frac{1} {{1 - {\left( {\lambda \mathord{\left/ {\vphantom {\lambda \kappa }} \right. \kern-\nulldelimiterspace} \kappa } \right)}^{2} }}} \right\}}{\left\{ {1 + e^{{ - 2\kappa d}} - \frac{\kappa } {\lambda }{\left( {1 - e^{{ - 2\kappa d}} } \right)}tanh{\left( {\lambda d} \right)} - \frac{{2e^{{ - 2\kappa d}} }} {{cosh{\left( {\lambda d} \right)}}}} \right\}}} \right] $$
  $$ + \frac{{\operatorname{Ze} N}} {{\eta \lambda ^{2} }}{\left( {1 - e^{{ - 2\kappa d}} } \right)}{\left\{ {1 - \frac{1} {{{\rm{cosh}}{\left( {\lambda d} \right)}}}} \right\}} $$

  (41)

  This case corresponds to a plate-like practice covered with a polyelectrolyte layer of thickness d (=b − a).

• (5) Large soft particles. For the case where κa ≫ 1, λa ≫ 1, κ(b − a) ≡ κd ≫ 1, and λ(b − a) ≡ λd ≫ 1, Eq. 41 tends to

  $$ \mu = \frac{{\operatorname{Ze} N}} {{\eta \lambda ^{2} }}{\left[ {1 + \frac{2} {3}{\left( {\frac{\lambda } {\kappa }} \right)}^{2} {\left( {\frac{{{1 + \lambda } \mathord{\left/ {\vphantom {{1 + \lambda } {2\kappa }}} \right. \kern-\nulldelimiterspace} {2\kappa }}} {{{1 + \lambda } \mathord{\left/ {\vphantom {{1 + \lambda } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }}} \right)}{\left( {1 + \frac{{a^{3} }} {{2b^{3} }}} \right)}} \right]} $$

  (42)

  which covers Eqs. 27 and 29 for the corresponding limiting cases.

Concentrated soft particles

For the case of a concentrated suspension of soft particles of volume fraction ϕ, it is shown that on the basis of Kuwabara’s cell model [44], the function f(d/a) in Eq. 24 is replaced by f(d/a, ϕ), which is given by [45]

$$ f{\left( {\frac{d} {a},\phi } \right)} = \frac{2} {3}{\left[ {1 + \frac{1} {2}{\left( {\frac{a} {b}} \right)}^{3} } \right]}{\left( {\frac{{1 - \phi }} {{1 - \phi _{c} }}} \right)} $$

(43)

where ϕ _c is the volume fraction of the particle core only.

Effect of polymer segment distribution

So far, we have assumed that the polyelectrolyte layer coating the particle core is assumed to have a definite thickness with a uniform segment density distribution. Varoqui [46] considered the case where neutral polymers are adsorbed with an exponential segment density distribution. In the following, we extend Varoqui’s theory [46] to the case where adsorbed polymers are charged. We assume that the particle surface can be assumed to be planar. We take an x-axis perpendicular to the surface with its origin 0 at the particle surface so that the region x > 0 corresponds to the solution phase (Fig. 6). Following Varoqui [46], we assume that the polymer segment distribution is an exponential function of the distance x form the particle surface so that the frictional coefficient may be expressed as νexp(−x/d), ν being a constant. Here, d is the average thickness of the polyelectrolyte layer. In other words, the particle surface is covered by a diffuse polyelectrolyte layer with the average thickness d. We assume that the density of fixed charges in the polyelectrolyte layer is proportional to the segment density in the same way as the frictional coefficient so that we can write ρ _fixexp(−x/d). Note that ν and ρ _fix correspond to average values of the friction coefficient and the fixed-charge density within the polyelectrolyte layer.

Fig. 6

Schematic representation of the surface of a particle adsorbed by polyelectrolytes (upper) and the segment density distribution (lower)

The Poisson–Boltzmann equation for the electric potential ψ(x) at position x is

$$ \frac{{d^{2} \psi }} {{dx^{2} }} = - \frac{{\rho _{{el}} {\left( x \right)} + \rho _{{\operatorname{fix} }} e^{{{ - x} \mathord{\left/ {\vphantom {{ - x} d}} \right. \kern-\nulldelimiterspace} d}} }} {{\varepsilon _{r} \varepsilon _{o} }} $$

(44)

The Navier–Stokes equation for the liquid velocity u(x) (flowing parallel to the particle surface) relative to the particle surface is

$$ \eta \frac{{d^{2} u}} {{dx^{2} }} - \gamma e^{{{ - d} \mathord{\left/ {\vphantom {{ - d} x}} \right. \kern-\nulldelimiterspace} x}} u{\left( x \right)} + \rho _{{el}} {\left( x \right)} = 0 $$

(45)

with

$$ \lambda = {\sqrt {\gamma \mathord{\left/ {\vphantom {\gamma \eta }} \right. \kern-\nulldelimiterspace} \eta } } $$

(46)

We treat the case where electric potential ψ(x) is low enough to allow the Debye–Hückel linearization approximation. Then, Eq. 44 is solved to give

$$ \psi {\left( x \right)} = \frac{{\rho _{{fix}} }} {{\varepsilon _{r} \varepsilon _{o} \kappa ^{2} }}\frac{{{\left( {\kappa d} \right)}^{2} e^{{{ - x} \mathord{\left/ {\vphantom {{ - x} d}} \right. \kern-\nulldelimiterspace} d}} - \kappa de^{{ - \kappa x}} }} {{{\left( {\kappa d} \right)}^{2} - 1}} $$

(47)

We thus obtain the following expression for the electrophoretic mobility μ [47]:

$$ \mu = \frac{{\rho _{{fix}} }} {{\eta \lambda ^{2} }}\frac{{{\left( {\kappa d} \right)}^{2} }} {{{\left( {\kappa d} \right)}^{2} - 1}}\left[ {1 - \frac{1} {{I_{0} {\left( {2\lambda d} \right)}}} - \frac{1} {{I_{0} {\left( {2\lambda d} \right)}}}\frac{{{\left\{ {\Gamma {\left( {\kappa d} \right)}} \right\}}^{2} }} {{\kappa d}}\left. {{\sum\limits_{n = 0}^\infty {\frac{{{\left( {\lambda d} \right)}^{{2n + 2}} }} {{{\left\{ {\Gamma {\left( {\kappa d + n + 1} \right)}} \right\}}^{2} }}} }} \right]} \right. $$

(48)

where Γ(z) is the Gamma function.

Further developments

The electrophoretic mobility of cylindrical soft particles is derived in [48] and [49]. The electroosmotic velocity in an array of parallel soft cylinders was discussed in [50]. Dukhin et al. [51] proposed a theory which accounts for the degree of dissociation of charged groups in the polyelectrolyte layer. Duval and coworkers [52–55] proposed a new model of diffuse soft particle which has a charged diffuse polyelectrolyte layer. The diffuse character of the polyelectrolyte layer is defined by a gradual distribution of the density of polymer segments in the interspatial region separating the core from the bulk electrolyte solution. For numerical calculations of the electrophoretic mobility based on more rigorous theories, the readers are referred to studies of Saville [56], Hill et al. [57–60], and Lopez-Garcia et al. [61, 62] as well as Duval and Ohshima [55]. Other studies for effects of non-uniform distribution of the fixed charges and the relative permittivity in the surface layer are discussed in [63–65]. The case where the polyelectrolyte layer is not fully ion-penetrable is considered in [66].

Electrical conductivity

The electrical conductivity K* of a suspension of colloidal particles in an electrolyte solution is different from the conductivity $K^{\infty }$ of the electrolyte solution where $K^{\infty }$ is given by

$$ K^{\infty } = {\sum\limits_{i = 1}^M {{z^{2}_{i} e^{2} n^{\infty }_{i} } \mathord{\left/ {\vphantom {{z^{2}_{i} e^{2} n^{\infty }_{i} } {\lambda _{i} }}} \right. \kern-\nulldelimiterspace} {\lambda _{i} }} } $$

(49)

The difference between $K * - K^{\infty }$ due to the presence of charged particles results from two effects: (1) the decrease in conductivity due to the presence of non-conducting particles and (2) the increase in conductivity due to the surface conductivity of the particles in the double layer region [67, 68, 12]. The conductivity of a colloidal suspension can be derived from the same electrokinetic equations for the electrophoresis problem. Liu and Keh [69] presented a theory of electrical conductivity of a dilute suspension of soft particles. For the low potential and dilute case, it can be shown that K* of a suspension of soft particles can be expressed as

$$ \frac{{K*}}{{K^{\infty } }} = 1 - \phi {\left( {1 - \frac{{a^{3} }}{{b^{3} }}} \right)}{\left( {1 + \frac{{a^{3} }}{{2b^{3} }}} \right)}{\left( {\frac{{e\psi _{{DON}} }}{{kT}}} \right)}\frac{{{\sum\limits_{i = 1}^M {{z^{3}_{i} n^{\infty }_{i} } \mathord{\left/ {\vphantom {{z^{3}_{i} n^{\infty }_{i} } {\lambda _{i} }}} \right. \kern-\nulldelimiterspace} {\lambda _{i} }} }}}{{{\sum\limits_{i = 1}^M {{z^{2}_{i} n^{\infty }_{i} } \mathord{\left/ {\vphantom {{z^{2}_{i} n^{\infty }_{i} } {\lambda _{i} }}} \right. \kern-\nulldelimiterspace} {\lambda _{i} }} }}} $$

(50)

where ϕ is the volume fraction of soft particles. Equation 50 can be extended to cover the concentrated case with the help of a cell model [70]. The result is

$$ \frac{{K^* }}{{K^\infty }} = \frac{{1 - \phi _c }}{{{{1 + \phi _c } \mathord{\left/ {\vphantom {{1 + \phi _c } 2}} \right. \kern-\nulldelimiterspace} 2}}}\left( {1 - \frac{{\phi \left( {{{1 - a^3 } \mathord{\left/ {\vphantom {{1 - a^3 } {b^3 }}} \right. \kern-\nulldelimiterspace} {b^3 }}} \right)\left( {{{1 + a^3 } \mathord{\left/ {\vphantom {{1 + a^3 } {2b^3 }}} \right. \kern-\nulldelimiterspace} {2b^3 }}} \right)}}{{\left( {1 - \phi _c } \right)\left( {{{1 + \phi _c } \mathord{\left/ {\vphantom {{1 + \phi _c } 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}}\left( {\frac{{e\psi _{DON} }}{{kT}}} \right)\frac{{\sum\limits_{i = 1}^M {{{z_i^3 n_i^\infty } \mathord{\left/ {\vphantom {{z_i^3 n_i^\infty } {\lambda _i }}} \right. \kern-\nulldelimiterspace} {\lambda _i }}} }}{{\sum\limits_{i = 1}^M {{{z_i^2 n_i^\infty } \mathord{\left/ {\vphantom {{z_i^2 n_i^\infty } {\lambda _i }}} \right. \kern-\nulldelimiterspace} {\lambda _i }}} }}} \right) $$

(51)

where ϕ _c is the volume fraction of the particle core.

Sedimentation velocity and potential

When charged spherical particles are falling steadily under gravity, the electrical double layer around each particle loses its spherical symmetry because of the fluid motion. This is called the relaxation effect. A microscopic electric field arising from the distortion of the double layer reduces the falling velocity (called the sedimentation velocity) of the particle, and the fields from the individual particles are then superimposed to give rise to a macroscopic field (called the sedimentation field) [71–73]. Keh and Liu [74] presented a theory of sedimentation of a dilute suspension of soft particles. Fundamental electrokinetic equations describing sedimentation phenomena in a suspension of soft particles are closely related to those of electrophoresis, viz.,

$$ \eta \nabla \times \nabla \times u + \nabla p + \rho _{{el}} \nabla \psi - \rho _{o} g + \nu u = 0,\;a < r < b $$

(52)

$$ \eta \nabla \times \nabla \times u + \nabla p + \rho _{{el}} \nabla \psi - \rho _{o} g = 0,\;r > b $$

(53)

where g is the gravity. It can be shown that the following Onsager relation between electrophoretic mobility μ and sedimentation field E _SED holds:

$$ E_{{SED}} = - \frac{{{\left( {\phi _{c} \Delta \rho _{c} + \phi _{s} \Delta \rho _{s} } \right)}}} {{K^{\infty } }}\mu g, $$

(54)

with

$$ \Delta \rho _{c} = \rho _{c} - \rho _{o} $$

(55)

$$ \Delta \rho _{s} = \rho _{s} - \rho _{o} $$

(56)

where ρ _c and ρ _s are the mass densities of the particle core and the polymer segments, ϕ _c is the volume fraction of the particle core, and ϕ _s is the volume fraction of the polymer segments. For the concentrated case, we obtain [75]

$$E_{{\operatorname{SED} }} = - \frac{{{\left( {1 - \phi _{c} } \right)}}}{{{\left( {{1 + \phi _{c} } \mathord{\left/ {\vphantom {{1 + \phi _{c} } 2}} \right. \kern-\nulldelimiterspace} 2} \right)}}}\frac{{{\left( {\phi _{c} \Delta \rho _{c} + \phi _{s} \Delta \rho _{s} } \right)}}}{{K^{\infty } }}\mu g$$

(57)

We thus see that the prefactor

$$ \frac{{1 - \phi _{c} }} {{{1 + \phi _{c} } \mathord{\left/ {\vphantom {{1 + \phi _{c} } 2}} \right. \kern-\nulldelimiterspace} 2}} $$

(58)

is a correction factor for concentrated suspensions.

Dynamic electrophoretic mobility

When a suspension of colloidal particles is in an oscillating electric field, the electrophoretic mobility of the particles depends on the frequency ω of the applied field. The mobility for such cases is called dynamic electrophoretic mobility, which is important particularly because colloid vibration potential (CVP; see next section) and electrokinetic sonic amplitude are proportional to dynamic electrophoretic mobility, as demonstrated by O’Brien [76]. A number of authors proposed theories of dynamic electrophoresis [76–80]. For a spherical soft particle, the following approximate expression for μ(ω) for the dynamic electrophoretic mobility has been derived [81]:

$$ \mu {\left( \omega \right)} = \frac{{2\varepsilon _{r} \varepsilon _{o} }} {{3\eta }}{\left[ {\frac{{1 - i\gamma b}} {{1 - i\gamma b - {\left( {{\gamma ^{2} b^{2} } \mathord{\left/ {\vphantom {{\gamma ^{2} b^{2} } 3}} \right. \kern-\nulldelimiterspace} 3} \right)} - \Gamma }}} \right]}{\left( {1 + \frac{{a^{3} }} {{2b^{3} }}} \right)}{\left[ {\frac{{{\psi _{o} } \mathord{\left/ {\vphantom {{\psi _{o} } {\kappa _{m} }}} \right. \kern-\nulldelimiterspace} {\kappa _{m} }{ + \psi _{{DON}} } \mathord{\left/ {\vphantom {{ + \psi _{{DON}} } \beta }} \right. \kern-\nulldelimiterspace} \beta }} {{1 \mathord{\left/ {\vphantom {1 {\kappa _{m} }}} \right. \kern-\nulldelimiterspace} {\kappa _{m} } + 1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-\nulldelimiterspace} \beta }}} \right]} + {\left[ {\frac{{1 - i\gamma b - {\left( {{\gamma ^{2} b^{2} } \mathord{\left/ {\vphantom {{\gamma ^{2} b^{2} } 3}} \right. \kern-\nulldelimiterspace} 3} \right)}{\left( {{1 - a^{3} } \mathord{\left/ {\vphantom {{1 - a^{3} } {b^{3} }}} \right. \kern-\nulldelimiterspace} {b^{3} }} \right)}}} {{1 - i\gamma b - {\left( {{\gamma ^{2} b^{2} } \mathord{\left/ {\vphantom {{\gamma ^{2} b^{2} } 3}} \right. \kern-\nulldelimiterspace} 3} \right)} - \Gamma }}} \right]}\frac{{\operatorname{Ze} N}} {{\eta \beta ^{2} }} $$

(59)

with

$$ \lambda = {\left( {\nu \mathord{\left/ {\vphantom {\nu \eta }} \right. \kern-\nulldelimiterspace} \eta } \right)}^{{1/2}} $$

(60)

$$ \gamma = {\sqrt {\frac{{i\omega \rho _{o} }} {\eta }} } = {\left( {1 + i} \right)}{\sqrt {\frac{{\omega \rho _{o} }} {{2\eta }}} } $$

(61)

$$ \beta = \lambda {\sqrt {1 - {\left( {\gamma \mathord{\left/ {\vphantom {\gamma \lambda }} \right. \kern-\nulldelimiterspace} \lambda } \right)}^{2} } } $$

(62)

$$ \Gamma = \frac{{\gamma ^{2} {\left( {V_{c} \Delta \rho _{c} + V_{s} \Delta \rho _{s} } \right)}}} {{6\pi b\rho _{o} }} = \frac{{2{\left( {\gamma b} \right)}^{2} {\left( {f_{c} \Delta \rho _{c} + f_{s} \Delta \rho _{s} } \right)}}} {{9\rho _{o} }} $$

(63)

$$ f_{c} = {\left( {\frac{a} {b}} \right)}^{3} $$

(64)

$$ f_{s} = \frac{{V_{s} }} {{{4\pi b^{3} } \mathord{\left/ {\vphantom {{4\pi b^{3} } 3}} \right. \kern-\nulldelimiterspace} 3}} $$

(65)

where V _c is the volume of the particle core, and V _s is the volume of the polymer segments per particle.

Colloid vibration potential

When a sound wave is propagated in an electrolyte solution, the motion of cations and that of anions may differ from each other because of their different masses so that periodic excesses of either cations or anions should be produced at a given point in the solution, generating vibration potentials. This potential is called ion vibration potential (IVP) [82, 83]. A similar electroacoustic phenomenon occurs in a suspension of colloidal particles and is called colloid vibration potential. As colloidal particles are much larger and carry a much greater charge than electrolyte ions, the potential difference in the suspension is caused by the asymmetry of the electrical double layer around each particle rather than the relative motion of cations and anions [84–91]. It must also be noted that in a colloidal suspension in an electrolyte solution, IVP and CVP are both generated simultaneously, and the total vibration potential between two points in the suspension, which is given by the sum of IVP and CVP, is observed. Recently, we have developed a general acoustic theory for a suspension of spherical particles, which accounts for both of CVP and IVP [92, 93].

For a suspension of soft particles in a symmetrical electrolyte of valence z and bulk concentration n, we have [94]

$$ \rm{TVP} = IVP + CVP $$

(66)

where IVP and CVP are given by

$$ IVP = \frac{{\operatorname{zen} }} {{\rho _{o} K^{ * } }}{\left( {\frac{{m_{ + } - \rho _{o} V_{ + } }} {{\lambda _{ + } }} - \frac{{m_{ - } - \rho _{o} V_{ - } }} {{\lambda _{ - } }}} \right)}\Delta P $$

(67)

$$ CVP = \frac{{(\phi _{c} \Delta \rho _{p} + \phi _{s} \Delta \rho _{s} )}} {{\rho _{o} K^{ * } }}\mu {\left( \omega \right)}\Delta P $$

(68)

with

$$ K^{*} = K^{\infty } - i\omega \varepsilon _{r} \varepsilon _{o} $$

(69)

where V ₊ and V ₋ are, respectively, the volumes of a cation and an anion, ΔP is the pressure difference between the two points is, $K^{\infty }$ and K* are, respectively, the usual conductivity and the complex conductivity of the electrolyte solution in the absence of the particles, and μ(ω) is the dynamic electrophoretic mobility of soft particles (Eq. 59). Equation 68 is an Onsager relation between CVP and μ(ω) which takes a similar form for an Onsager relation between sedimentation potential and static electrophoretic mobility (Eq. 54).

Electrophoresis in a salt-free medium

So far, we have treated charged colloidal particle in an electrolyte solution so that the potential distribution around a charged colloidal particle in an electrolyte solution is described by the Poisson–Boltzmann equation (Eqs. 8 and 9). Consider a particle carrying ionized groups on the particle surface in an electrolyte solution. In the suspension, in addition to electrolyte ions, there exist counterions produced by dissociation of the particle surface groups. When we consider a dilute suspension of colloidal particles, the following two assumptions are usually made: (1) the concentration of counterions produced from the surface groups can be neglected as compared with the added electrolyte concentration, and (2) the suspension is assumed to be infinitely dilute so that any effects resulting from the finite particle volume fraction can be neglected. The assumption (1) becomes invalid where the electrolyte concentration is as low as or lower than that of counterions from the particle. The assumption (2) does not hold when the concentration of all ions (electrolyte ions and counterions from the particle) is very low, as, in this case, the potential around each particle becomes quite long-range, and the effects of the finite particle volume fraction become appreciable. Thus, we must consider explicitly the effects of the finite particle volume fraction ϕ even for dilute suspensions (Fig. 7). The most remarkable characteristic of a suspension of colloidal particles in salt-free media is the counter ion condensation effect. Namely, for a highly charged particle, counter ions are condensed in a very thin layer around the particle [95–101]. It can be shown that there is a certain critical value of the particle charge separating two cases, that is, the low-charge case and the high surface charge case. For the low-charge case (case 1), the mobility is proportional to the particle charge and coincides with that of a particle in an electrolyte solution in the limit of very low electrolyte concentrations κ→0 (Hückel’s limit). For the high-charge case (case 2), however, μ becomes essentially constant independent of the particle charge due to the counterion condensation effect (Fig. 8).

Fig. 7

A spherical particle of radius a in a free volume of radius R. (a/R)³ equals the particle volume fraction ϕ

Fig. 8

Approximate dependence of the scaled electrophoretic mobility E _m = (3ηze/2ɛ _r ɛ _o kT)μ upon the scaled total surface charge Q* = (ze/kT)Q/4πɛ _r ɛ _o b (note that Q* is always positive). There is a critical value of Q* (Q _cr* = ln(1/ϕ)) separating the low-charge case and the high-charge case [101]

The results for soft particles carrying charge Q in a salt-free medium containing counterions of valence z only are given below [101].

$$\mu = \frac{Q}{{D_{\operatorname{H} } }}\;{\text{for}}\;\frac{Q}{{4\pi \varepsilon _{r} \varepsilon _{o} b}} \cdot \frac{{ze}}{{kT}} \leqslant \ln {\left( {1 \mathord{\left/ {\vphantom {1 \phi }} \right. \kern-\nulldelimiterspace} \phi } \right)},\;{\left( {\operatorname{low} - charge\;case} \right)}$$

(70)

$$ \mu = \frac{{4\pi \varepsilon _{r} \varepsilon _{o} b}} {{D_{H} }} \cdot \frac{{kT}} {{ze}}\ln {\left( {1 \mathord{\left/ {\vphantom {1 \phi }} \right. \kern-\nulldelimiterspace} \phi } \right)}\;\operatorname{for} \;\frac{Q} {{4\pi \varepsilon _{r} \varepsilon _{o} b}} \cdot \frac{{ze}} {{kT}} > \ln {\left( {1 \mathord{\left/ {\vphantom {1 \phi }} \right. \kern-\nulldelimiterspace} \phi } \right)},\;{\left( {\operatorname{high} - charge\;\operatorname{case} } \right)} $$

(71)

where Q is the total particle charge (Eq. 37), and D _H is the drag coefficient of a soft particle (Eq. 38). Note that Eq. 70 agrees with Eq. 36.

Conclusion

The electrokinetic behaviors of soft particles are different from those of hard particles. The most remarkable difference is that the zeta potential, which plays an essential role in electrokinetics of hard particles, loses its meaning for soft particles. Instead, the Donnan potential is a fundamental quantity determining the electrokinetic behaviors of soft particles. Equation 24, which can be applied for most cases, involves two parameters (ZeN and 1/λ), the latter of which can be considered to characterize the “softness” of the polyelectrolyte layer because in the limit of 1/λ→ 0, the particle becomes a rigid particle. Experimentally, these parameters may be determined from a plot of measured mobility values of a soft particle as a function of electrolyte concentration by a curve-fitting procedure. A number of experimental studies have been carried out to analyze experimental mobility data via Eq. 24 (or Eq. 28) (e.g., [102–112]).