Introduction

Due to widespread applications ranging from basic to applied sciences, specifically for the measurement of electrical properties of the surface of charged colloidal particles, the electrophoretic transport phenomenon is studied by several researchers in the past few decades. It is interesting to note that from the electrophoretic mobility data one can measure the surface ζ-potential or the surface charge carried by the colloidal particle [1]. Early study on this field was addressed by von Smoluchowski [2], and subsequently by Huckel [3] in order to consider two extreme situations where the particle radius is far greater or less than the characteristic electric double layer (EDL) thickness. Later, Henry [4] provided a general description of the problem and derived an explicit expression for the electrophoretic mobility (i.e., electrophoretic velocity per unit field strength) for the entire range of Debye-Huckel parameter. These classical studies are based on weak field and low potential approximation. Subsequently, several authors consider the double layer polarization (DLP) and relaxation effects on the particle electrophoresis for the case when the surface charge is reasonably high and strength of the applied field is moderate to strong [5,6,7,8].

It may be noted that the above mentioned studies have considered the case in which the particle is rigid in nature. However, such a description is no longer valid in the case of bio-particles. There are various types of bio-particles, e.g., virus, bacteria, yeast, humic substances, where the rigid core is surrounded by a fuzzy layer which is made of polymer materials [9, 10]. Such types of colloids are often termed as soft particle. It may be noted that the classical ζ-potential concept losses its meaning in the case of soft particle. For such type of colloids, the rigid core is harboring a surface polymer layer, often termed as a polyelectrolyte layer (PEL), which allows the penetration of mobile ions and fluid flow across it. In addition, the surface PEL bears additional functional group which results in net volumetric charges entrapped within it. On the one hand, the PEL charge enhances the net electrical driving force, and on the other hand, the net opposing drag force is also enhanced due to the presence of monomers across the surface PEL. Therefore, the electrophoretic behavior of soft particle is significantly affected by the physicochemical and hydrodynamic properties of the surface PEL and reasonably differs than that of rigid particle case.

There are of course a huge body of literatures that exist in the study of electrophoresis of soft particle. One of the early work was made by Donath and Voigt [11] to study the electrokinetic theory of soft surfaces. Later, Ohshima and co-researchers studied extensively the electrophoresis of soft particle [12,13,14,15,16,17] based on Debye-Huckel limit and weak electric field assumption. Subsequently, the effects of DLP and relaxation on the electrophoresis of soft particle were considered by several researchers [18,19,20,21,22]. In all the aforementioned studies, the inner core of the undertaken particle is considered to possess a constant surface charge/potential and the outer PEL entraps constant volumetric charge density. However, the inner core’s surface charge as well as volumetric PEL charge may depend strongly on the pH values of the bulk electrolyte. For example, if the inner core is made of SiO2 or TiO2, the surface charge of the inner core depends on the bulk pH [23, 24]. In addition, if the PEL entraps the dissociable functional groups, e.g., such as succinoglycan (pKA = 4.58, pKB = 8.6 [25]), glycine (pKA = 2.35, pKB = 9.78 [26]), glutamine (pKA = 2.17, pKB = 9.13 [27]), to quote a few, the PEL charge depends strongly on the bulk pH. Hence, in order to consider the realistic model for electrophoresis of soft particle, the regulation of charge properties due to the nearby microenvironment needs to be considered.

Zhang et al. [28] studied the electrophoresis of charge-regulated soft particle comprising non conducting charged inner core with constant ζ-potential and is wrapped with pH-regulated charged PEL. Later, several authors (Tseng et al. [29], Yeh et al. [30]) studied the effect of pH-regulated PEL charge on the electrophoresis of soft particle with an uncharged inner core. Recently, Gopmandal et al. [31, 32] studied the electrophoresis of MS2 bactiriophase, modeled via soft particle, by considering the pH-regulated PEL charge. Quite surprisingly, to date, no literature is available on the electrophoresis of soft particle where both surface charges of the inner core as well as PEL charge depend on the bulk pH.

Based on existing knowledge gap, we have provided a comprehensive study on the electrophoresis of a typical soft particle comprising the inner core made of either SiO2 or TiO2 and the PEL bears succinoglycan functional group. For such a particle, the charge properties of the inner core’s surface and outer PEL of the composite particle can be actively tuned by the bulk pH. The mathematical model adopted here is based on the Poisson-Boltzmann equation for the EDL potential and Darcy-Brinkman extended Stokes equation for fluid flow. In order to study the electrophoresis of such type of soft particle, we adopt the Ohshima’s linearization technique [14,15,16,17] under a low potential and weak electric field assumptions. The low potential limit can be achieved for the case when the bulk molar concentration is higher than 1 mM and the molar concentration of the functional group resides along the peripheral PEL is lower than 100 mM [33]. In addition, the weak electric field assumption referring to the applied electric field low enough to create the potential drop across the EDL is lower than the thermal voltage drop [31]. We have highlighted the dependency of various pertinent parameters on the electrophoresis of the undertaken particle, which includes the pH and concentration of bulk electrolyte, physicochemical, and hydrodynamic properties of the PEL and the charge properties of the inner core surface. In addition, we have also identified the parameter range to achieve the zero mobility and reversal in particle mobility.

Mathematical model

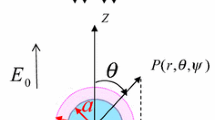
As shown in Fig. 1, we have considered the electrophoresis of soft particle of radius b under the influence of electric field E applied along z-direction. The undertaken particle is composed of charged inner core of radius a and is decorated with ion and fluid penetrable charged PEL of thickness (b − a). For convenience, a spherical polar coordinate system is adopted with origin held fixed at the center of the particle. In this article, we have restricted ourselves with low potential and weak electric field limit. We have also assumed the following assumptions: (i) the system is at steady-state situation and fluid flow is in creeping flow regime and (iii) the PEL is non-deformable. These assumptions are almost certainly valid for the electrokinetics of soft bio- colloids [34,35,36,37]. In addition, the water content of the peripheral PEL is considered to be sufficiently high, so that the dielectric permittivity (εf) and viscosity therein to identify with that in the liquid phase [37,38,39]. In addition, we have treated the case where the particle-fixed charge is low. In such cases, the assumption that the dielectric permittivity and viscosity of the liquid phase are the same as those in the PEL is reasonable [14,15,16,17]. The inner core and the PEL carries zwitterionic functional group that leads to pH-regulated charge density along the particle surface as well within the PEL. For instance, if the inner core is composed of SiO2 or TiO2, the inner core surface possesses pH-dependent surface charge density(σp), given as [40]

$$ \sigma_{p}=-F{N}_{\text{total}}\Big[\frac{K_{\text{A1}}}{K_{\text{B1}}[\text{H}^{+}]_{s}^{2}+[\text{H}^{+}]_{s}+K_{\text{A1}}}-\frac{K_{\text{B1}}[\text{H}^{+}]_{s}^{2}}{K_{\text{B1}}[\text{H}^{+}]_{s}^{2}+[\text{H}^{+}]_{s}+K_{\text{A1}}}\Big] $$
(1)
Fig. 1
figure 1

Schematic representation of electrophoresis of a spherical soft particle which consists of charged inner core of radius a and is decorated with charged PEL of thickness (b − a) under the influence of electric field E. The inner core bears pH-regulated surface charge density σp, and the peripheral PEL bears pH-regulated volumetric charge density ρfix. The dielectric constant of the PEL and electrolyte medium is taken to be same as 𝜖f

Full size image

where Ntotal is the total number of density of the functional groups distributed along the particle surface. Here, [H+]s represents the concentration of H+ ion along the inner core’s surface. Under a low potential limit, the concentration of H+ ion follows the Boltzmann distribution, given as

$$ [\text{H}^{+}]=[\text{H}^{+}]_{0}\exp\left[-\frac{e\psi}{K_{\text{B}}T}\right] $$
(2)

where [H+]0 is the bulk concentration of H+ ion with bulk pH=\(-\log [\text {H}^{+}]_{0}\). Here, ψ is the equilibrium EDL potential; e, KB, and T are the elementary charge, Boltzmann constant and absolute temperature, respectively. It may be noted that the value of [H+] ion on the inner core surface can be obtained from Eq. (2) along r = a. Here, KA1 and KB1 are the equilibrium constants of the acidic and basic charged groups, respectively, and F is the Faraday constant. We have considered that the PEL entraps pH-regulated zwitterionic functional group, e.g., succinoglycan, which results in the volumetric charge density across the peripheral PEL, given as [37]

$$ \rho_{\text{fix}}=-\frac{F{N}_{\text{A2}}}{1+\Big(\frac{[\text{H}^{+}]_{0}}{K_{\text{A2}}}\Big)\exp(-\frac{e\psi} {K_{\text{B}}T})}+\frac{F{N}_{\text{B2}}\Big(\frac{[\text{H}^{+}]_{0}}{K_{\text{B2}}}\Big)\exp(-\frac{\text{e}\psi} {K_{\text{B}}T})}{1+\Big(\frac{[\text{H}^{+}]_{0}}{K_{\text{B2}}}\Big)\exp(-\frac{e\psi}{K_{\text{B}}T})} $$
(3)

Here, NA2, NB2, and KA2 and KB2 are the molar concentration and equilibrium constant of the acidic and basic charged groups, respectively.

The fluid flow within the PEL and electrolyte media is governed by Darcy-Brinkman extended Stokes equation, given as

$$ \eta\nabla^{2}\textbf{u}-\nabla p-\text{e}{\Sigma} z_{j}n_{j}\nabla{\Phi}-D\eta\lambda^{2}\textbf{u} =0 $$
(4)

along with continuity equation for incompressible fluid as follows:

$$ \nabla.\textbf{u}=0 $$
(5)

where u is the fluid velocity. Here, p is the pressure, η is the fluid viscosity, and λ− 1 is the hydrodynamic softness parameter of the surface PEL. The binary parameter D appears in Eq. (4) takes the value 1 within the PEL and D = 0 outside of it. It may be noted that D = 0 represents Stokes equation which govern the fluid flow within the electrolyte media. On the other hand, D = 1, the corresponding equation is known as Darcy-Brinkman equation where the extra term − ηλ2u represents the frictional force due to presence of monomers within the PEL. The term \({-}e {\sum }_{j=1}^{4} z_{j}n_{j}\nabla {\Phi }\) represents the electrokinetic driving force, where zj and nj (j= 1,2,3,4) are the valence and concentration of the mobile ions due to added salt (j= 1,2) and the charged species H+ and OH− (j= 3,4). Here, Φ is the total potential (i.e., sum of equilibrium EDL potential (ψ), applied electric potential, and potential due to polarization of EDL potential due to applied electric field). Under a small potential limit, the concentration of mobile ions at equilibrium follows the Boltzmann distribution, given as

$$ n_{j}=n_{j}^{\infty}\exp\Big[-z_{j}\frac{\text{e}\psi}{K_{B}T}\Big] $$
(6)

where \(n_{j}^{\infty }\) is the bulk ionic concentration of j th species. In our current study, we have considered the added electrolyte as binary symmetric electrolyte with valence z1 = 1 and z2 = − 1 for cation and anion, respectively.

Due to axisymmetry nature of the flow, we may write the velocity field as [41]

$$ \textbf{u}(r,\theta)=\Big(-\frac{2}{r}h(r)\text{E} \cos\theta, \frac{1}{r}\frac{d}{dr}\Big(rh(r)\Big) \text{E} \sin\theta, 0 \Big) $$
(7)

where the electrophoretic mobility (μE) can be obtained from the relation given below

$$ \ \mu_{E}=\frac{U}{E} =\lim_{r\rightarrow\infty}\frac{2h(r)}{r} $$
(8)

Here, \( {E}= \lvert E \rvert \). The governing equation of h(r) is given by [14, 15]

$$ \left. \begin{array}{ll} \mathcal{L}(\mathcal{L}h-\lambda^{2}h)= G(r); & a \le r \le b \\ \mathcal{L}(\mathcal{L}h)= G(r); & r > b \end{array} \right\} $$
(9)

where the term G(r) in the right hand side of Eq. (9) can be written as

$$ G(r)= -\frac{\text{e}}{\eta r}\frac{dy}{dr}\sum\limits_{i=1}^{4}{z^{2}_{i}}n_{i}\exp(-z_{i}y)\phi_{i} $$
(10)

Here, y(r) = ψ(r)/ϕ0 is the scaled EDL potential, scaled by ϕ0 = KBT/e. A detailed discussion on the induced EDL potential is made later in this section. Equation (10) involves ϕi and is governed by

$$ \mathcal{L}\phi_{i} = \frac{dy}{dr}\left( z_{i}\frac{d\phi_{i}}{dr} - \frac{2\lambda_{i}}{\text{e}}\frac{h}{r} \right) $$
(11)

where the operator \({\mathscr{L}}\) is defined as

$$ \mathcal{L}\equiv \frac{d^{2}}{dr^{2}}+\frac{2}{r}\frac{d}{dr}-\frac{2}{r^{2}} $$
(12)

Here, λi is the ionic conductance of i th ionic species. An explicit expression for scaled mobility, scaled by εeϕ0/η, may be derived as follows [14, 15]:

$$ \begin{array}{@{}rcl@{}} \mu_{E} &=& \frac{(\kappa b)^{2}}{9}{\int}_{1}^{\infty}\Big[3(1-r^{2})-\frac{2L_{2}}{L_{1}}(1-r^{3})\Big]\bar{G}(r)dr+ B_{1} {\int}_{\gamma}^{\infty}\Big[(1+\frac{r^{3}}{2})\Big]\bar{G}(r)dr\\ && -B_{2}{\int}_{\gamma}^{1}\Big[1-\frac{3\gamma}{2L_{1}\beta^{2}}\Bigl\{(L_{3}+L_{4}\beta r)\cosh c(r)-(L_{4}+L_{3}\beta r)\sinh c(r)\Bigr\}\Big] \bar{G}(r)dr \end{array} $$
(13)

where c(r) = β(r − γ), β = λb, and α = λa. The values of Li (i = 1,2,3,4) and Bi (i = 1,2) are defined as follows

$$ \left\{ \begin{array}{ll} L_{1}=\Big[1+\frac{\gamma^{3}}{2}+\frac{3\gamma}{2\beta^{2}}-\frac{3\gamma^{2}}{2\beta^{2}}\Big]\cosh(\beta-\alpha)-\Big[1+\frac{\gamma^{3}}{2}+\frac{3\gamma}{2\beta^{2}}-\frac{3\gamma^{2}}{2}\Big]\frac{\sinh(\beta-\alpha)}{\beta} & \\ L_{2}=\Big[1+\frac{\gamma^{3}}{2}+\frac{3\gamma}{2\beta^{2}}\Big]\cosh(\beta-\alpha)+\frac{3\gamma^{2}}{2}\frac{\sinh(\beta-\alpha)}{\beta}-\frac{3\gamma}{2\beta^{2}} & \\ L_{3}= \cosh(\beta-\alpha)-\frac{\sinh(\beta-\alpha)}{\beta}-\gamma & \\ L_{4}= \sinh(\beta-\alpha)-\frac{\cosh(\beta-\alpha)}{\beta}+\frac{\alpha\gamma}{3}+\frac{2\beta}{3\gamma}+\frac{1}{\beta} & \\ B_{1}= \frac{2L_{3}(\kappa b)^{2}}{3L_{1}\beta^{2}} & \\ B_{2}=\frac{2(\kappa b)^{2}}{3\beta^{2}} \end{array} \right. $$
(14)

It may be noted that the mobility expression Eq. (13) involves the term \(\bar {G}(r)\), given as

$$ \bar{G}(r)=-\left[1+\frac{\gamma^{3}}{2r^{3}}\right]\frac{dy}{dr} $$
(15)

where γ = a/b, the scaled inner core radius. Under a low potential limit, the scaled equilibrium EDL potential, y(r) follows from the linearized Poisson-Boltzmann equation, given as

$$ \frac{1}{r^{2}}\frac{d}{dr}\Big(r^{2}\frac{dy}{dr}\Big)=\left\{ \begin{array}{ll} (\kappa b)^{2}y- Q_{fix}(r) & ; \gamma \leq r\leq 1 \\ (\kappa b)^{2}y & : r>1 \end{array} \right. $$
(16)

where κ− 1 is the EDL thickness with \( \kappa =\sqrt { {\sum }_{j=1}^{4} (z_{j}\text {e})^{2}n_{j}^{\infty }/\varepsilon _{f}\text {K}_{\text {B}} \text {T}} \). Here, the bulk ionic concentration \(n_{j}^{\infty }\) is taken to be the scale for concentration of mobile ions. It is interesting to note that unless pH is extremely high or low (i.e., concentration of H+ and OH− is not very large), the concentration \(n_{j}^{\infty }\) is practically equal to the concentration of added electrolyte [42]. The term Qfix(r) appearing in Eq. (16) represents the scaled volumetric charge entrapped within the PEL, given as

$$ Q_{\text{fix}}(r)=\Big[\frac{-Q_{A}}{1+ 10^{\text{pK}_{\text{A2}}-\text{pH}}\exp(-y(r))}+\frac{Q_{B}}{1+ 10^{\text{pH}-\text{pK}_{\text{B2}}}\exp(y(r))}\Big] $$
(17)

where the scaled parameters QA and QB appears in Eq. (17) are the maximum charge densities due to acidic and basic charged group residing along the peripheral PEL, given as

$$ Q_{j}=\frac{FN_{j2}b^{2}}{\varepsilon_{e}\phi_{0}}~~~~({j=A,~B}) $$
(18)

In order to compute y(r), we need to solve Eq. (16) subject to the appropriate boundary conditions defined along the inner core surface (r = γ), PEL-electrolyte interface (r = 1), and along the far-field, given as

$$ \left. \begin{array}{ll} \frac{dy}{dr}|_{r=\gamma} = -\sigma_{p}^{*} & \\ y|_{r=1^{-}} = y|_{r= 1^{+}}& \\ \frac{dy}{dr}|_{r=1^{-}} = \frac{dy}{dr}|_{r= 1^{+}}& \\ y(r)\rightarrow 0~~~~ \text{as}~~r\rightarrow~\infty~& \end{array} \right\} $$
(19)

where \( \sigma _{p}^{*}\) is the scaled surface charge density distributed along the core surface with \(\sigma _{p}^{*}=\sigma _{p}b/\varepsilon _{e}\phi _{0}\), and the dimensional surface charge σp is already defined in Eq. (1).

In order to obtain the scaled equilibrium potential y(r), we employ an iterative numerical method. The discretized form of Eq. (16) is obtained by finite difference method through a second-order central difference scheme. The discretized equation subject to the boundary condition Eq. (19) is solved by using tridiagonal matrix algorithm (TDMA) and an iterative method is employed to obtain the converged value of y(r). The iteration is continued until the absolute difference between two successive iterations is smaller than 10− 6. With known potential, we obtain the electrophoretic mobility by using the Eq. (13). It is interesting to note that the electrophoretic mobility data obtained from Ohishima’s model is recognized by various experimentalist to determine the physicochemical and electrical properties of the bio-particle [43, 44]. In our previous article [32], we have already validated the computed mobility for the charge-regulated soft particle composed of uncharged inner core and charged PEL with the available experimental result. However, no such literature is available for the electrophoresis of bio-particle composed of both pH-regulated inner core and peripheral PEL.

Results and discussion

In this section, we have presented some of the representative results of this rigorous study. The inner core of the undertaken particle is composed of either SiO2 (pKA1 = 7, pKB1 = 2) or TiO2 (pKA1 = 7.8, pKB1 = − 4.95) [23, 40]. In addition, the PEL entraps additional immobile zwitterionic functional groups, such as succinoglycan (pKA2= 4.58, pKB2= 8.6) [25]. The bulk pH of the aqueous medium may vary from 2 to 12. For illustration, we have considered the soft particle of radius b= 15 nm and the inner core radius a is varied from case to case. Unless stated otherwise, the scaled radius of the inner core is taken to be γ(= a/b) = 0.5. The electrolyte concentration is varied from low to high so that the Debye-Huckel parameter κb ranges from 1 to 100 for fixed particle radius b. The softness parameter β ranges from 1 to 100. It may be noted that the above set of parameters are reasonable for wide class of bio-particles [29].

Soft particle with charged inner core coated with uncharged PEL

We first consider the electrophoresis of soft particle composed of charged inner core and uncharged surface PEL. In Fig. 2, we have shown the results for EDL potential with various values of bulk pH (= 2, 4, 6, 8, 10, and 12) with fixed Debye-Huckel parameter κb(= 1). The scaled inner core radius is taken to be γ = 0.5 and is composed of either SiO2 (Fig. 2a) or TiO2 (Fig. 2b). The results are presented here for a fixed value of the total number density of the functional group distributed along the inner core’s surface, i.e., Ntotal = 0.5 × 10− 7mol/m2. A strong dependence of the inner core charge and hence the EDL potential on the bulk pH are evident from Fig. 2. From Fig. 2a, it is clear that the EDL potential remains negative except for pH is close to 2 (see inset figure of Fig. 2a). For higher values of pH, the acidic counterpart of the functional group distributed along the core’s surface dominates and results in negative values of EDL potential. On the other hand, when the inner core is made of TiO2, both the acidic and basic counterpart of the zwitterionic functional group has strong impact on the EDL potential (Fig. 2b). Here, depending on the bulk pH, the surface charge along the inner core of the undertaken particle becomes either positive or negative and it leads to positive or negative values of EDL potential. Hence, the magnitude of EDL potential depends on the nearby microenvironment and material properties of the inner core. The influence of the EDL potential on the particle electrophoresis is shown in the next figures.

Fig. 2
figure 2

The equilibrium potential distribution for a soft particle with charged inner core and uncharged PEL is presented for various values of bulk pH. The results in a and b represent the cases when the inner core is composed of either SiO2 or TiO2, respectively. Other model parameters are κb = 1, Ntotal = 0.5 × 10− 7mol/m2, and γ = 0.5. The inset of Fig. 2a shows the enlarged view of the region 0.6 ≤ r ≤ 1.5

Full size image

In Fig. 3, we have shown the variation of electrophoretic mobility with bulk pH for various values of Debye-Huckel parameter (κb) at a fixed value of Ntotal = 0.5 × 10− 7mol/m2, λb(= 1), and γ(= 0.5). We found a change in sign in electrophoretic mobility depending on the critical choice of pH, which certainly refers to the isoelectric point (IEP). It may be noted that the IEP refers to the critical value of bulk pH at which the net charge entrapped by the particle approaches to zero. In such a case, the acidic and basic counterpart of the zwitterionic functional group balances each other and results in a zero net charge, and hence, the particle mobility vanishes when pH is equal to IEP. In the inset figures in Fig. 3a and b, we have indicated the IEP values of respective functional groups. We found the IEP for the case of SiO2 is 2.5 (see inset figure of Fig. 3a) and IEP = 6.375 when the inner core of the undertaken particle is composed of TiO2 (Fig. 3b). A change in sign in the EDL potential and hence in the mobility values may occur when pH crosses the IEP. The maximum positive (or negative) value in EDL potential and hence the electrophoretic mobility may occur when pH is significantly smaller (or larger) than the IEP. A similar observation has been reported by Chen et al. [23] for electrophoresis of pH-regulated charged rigid colloids. As expected, the concentration of bulk electrolyte plays a significant role in the particle mobility. The magnitude of the particle mobility decreases with the rise in bulk electrolyte concentration (i.e., increase in the Debye-Huckel parameter κb with fixed particle radius). Such a situation is reasonable, since the higher the electrolyte concentration is, the stronger the shielding effect and the counterion condensation effect are, which result in a decrement in net effective charges of the inner core and hence leads to a significant reduction in the magnitude of the particle mobility.

Fig. 3
figure 3

The dependence of electrophoretic mobility on bulk pH is shown when the inner core is composed of either a SiO2 or b TiO2 with fixed Ntotal = 0.5 × 10− 7mol/m2. The other model parameters are κb (= 1,2.5,5,10,25, and 50), λb(= 1) and γ(= 0.5). The horizontal black color line represents the zero mobility, and the vertical black color line represents the isoelectric point (IEP). The inset of Fig. 3a shows the enlarged view of the region around IEP

Full size image
Fig. 4
figure 4

Similar results as in Fig. 2 except for the charged PEL where the peripheral PEL entraps the succinoglycan zwitterionic functional group with NA2 = NB2= 10 mM

Full size image

Soft particle with charged inner core and charged PEL

In this section, we have considered the case when both the inner core and surface PEL of the soft particle bears pH-regulated charges. We have considered the cases when the inner core of the particle is composed of either SiO2 or TiO2 and is coated with charged PEL which entraps the succinoglycan functional group. We have shown the effect of pH-regulated charges on the EDL potential (Fig. 4) and hence on the electrophoretic mobility (Fig. 5). The results are presented here for various values of bulk pH and electrolyte concentration with fixed molar concentration of the zwitterionic functional group entrapped within the surface PEL, i.e., NA2 = NB2= 10 mM and fixed Ntotal = 0.5 × 10− 7mol/m2. In Fig. 4, we have shown the EDL potential at fixed κb(= 1) and for various values of bulk pH and the result of electrophoretic mobility presented in Fig. 5 by varying the bulk pH for various choices of Debye-Huckel parameter κb and for a fixed value of β = 1. It is clear from Fig. 4 that the EDL potential significantly differs from that of the uncharged PEL case as shown in Fig. 2. In addition, a significant difference in the mobility is also observed in the case of charged PEL. This is due to the presence of charged functional group across the peripheral PEL which results in significant change in net charge entrapped by the particle and hence leads to a significant deviation of EDL potential as well as electrophoretic mobility compared to the uncharged case. The increase in κb for fixed particle radius decreases the EDL thickness. Due to strong shielding effect and counterion condensation effect for thin EDL, the net effective charges carried by the particle reduce which leads to a reduction in magnitude of the particle mobility.

Fig. 5
figure 5

Similar results as in Fig. 3 except for the charged PEL where the peripheral PEL entraps the succinoglycan zwitterionic functional group with NA2 = NB2= 10 mM. The horizontal black color line is included to show the zero mobility and mobility reversal. The inset of Fig. 5 shows the enlarged view of the region around zero mobility

Full size image

We observe a change in sign in the electrophoretic mobility as shown in Fig. 5. We define the critical value of bulk pH as the point of zero mobility (PZM), at which the particle mobility attains zero value while bearing a net nonzero charge. We found that the PZM significantly differs from that of the IEP in both the cases, i.e., when the inner core is made of either SiO2 or TiO2. It is reasonable since for IEP the particle’s net charge reduces to zero and leads to zero mobility. On the other hand, the critical choice of bulk pH (i.e., PZM) for which net charge enclosed by the core-shell particle is nonzero but the particle may attain zero mobility. In addition, when bulk pH crosses the PZM, the composite particle switches its propulsion direction, which often termed as mobility reversal. For a number of biopolymers, including humic substances, environmental entities, bacterial cells, etc., being the paradigm of spherical soft particle may bear pH-regulated charges across the inner core’s surface and within the harboring PEL. Besides these, the bio-particle may also be treated as a multilayered soft particle for which the inner is coated with layered distribution of anionic and cationic charges [45] and the heterogeneous and structural distribution of pH-regulated charges may lead to a zero mobility and hence the mobility reversal. In this article, however, we have considered a typical soft particle where the zwitterionic surface charge is distributed along the inner core’s surface and zwitterionic volumetric PEL charge distributed across the harboring PEL. We have highlighted the occurrence of zero mobility for the such a typical particle in Figs. 5, 6, and 7. We found from the inset figures of Fig. 5a and b that the occurrence of PZM depends on bulk electrolyte concentration and the choice of functional groups. In addition, PZM may also depend on the inner core radius, inner core surface charge, as well as PEL charge. We have summarized our findings on PZM and its dependence on the pertinent parameters next in the article.

Fig. 6
figure 6

The dependence of point of zero mobility (PZM) on the Debye-Huckel parameter κb is shown for various values of γ (= 0.25, 0.5, 0.75) and fixed λb = 1, \(N_{\text {total}}=0.5\times 10^{-7} \text {mol}/\text {m}^{2}\), NA2 = NB2= 10 mM. The results are shown here when the inner core comprises either a SiO2 or b TiO2. The corresponding results for critical PEL charge (\(Q_{\text {fix}}^{*}\)) are shown in Fig. 6c and d

Full size image
Fig. 7
figure 7

The dependence of point of zero mobility (PZM) on the total number density of the surface functional groups along the inner core’s surface is shown for various choice of γ (= 0.25,0.5, and 0.75) and NA2 = NB2(= 10mM, 25mM). The results are shown here when the inner core is composed of either a SiO2 or b TiO2. The corresponding results for critical PEL charge (\(Q_{\text {fix}}^{*}\)) are also shown in Fig. 7c and d.

Full size image

In Fig. 6, we have shown the results for PZM as a function of Debye-Huckel parameter (κb). The results are shown here for various choices of inner core radius (γ) with fixed Ntotal = 0.5 × 10− 7mol/m2 and NA2 = NB2= 10 mM. The results are shown here when the inner core of the undertaken particle is either made of SiO2 (Fig. 6a) or TiO2 (Fig. 6b). We observe that the PZM increases with the increase in electrolyte concentration (i.e., Debye-Huckel parameter κb for fixed radius of the composite particle). In order to justify the results for the PZM, we have shown the corresponding results for critical (\(Q_{\text {fix}}^{*}\)) in Fig. 6c and d where (\(Q_{\text {fix}}^{*}\)) is defined as

$$ Q_{\text{fix}}^{*}=\frac{3{\int}_{\gamma}^{1}Q_{\text{fix}}(r)r^{2}dr}{1-\gamma^{3}} $$

It may be noted that such critical is obtained when pH is equal to PZM at which the particle attains the zero mobility. It is clear from Fig. 6c and d that the critical is positive and its value increases with increase in κb at a given inner core radius. Hence, in order to compensate the increasing positive , the effective negative surface charge should increase and it can be achieved for increasing value of bulk pH. As a result, the critical pH to attain the zero mobility increases with rise in concentration of the bulk electrolyte. It is interesting to note that the increase in critical pH within the limit of pH<IEP of the functional group entrapped within the PEL decreases the positive. From Fig. 6a and b, it is clear that with a fixed electrolyte concentration, the PZM increases with the decrease in inner core radius. The effective surface charge along the inner core’s surface decreases with the decrease in inner core radius. Hence, for smaller values of γ, the requirement of net positive to nullify the core’s surface charge is also small, which may be achieved for higher values of critical pH within the limit of pH<IEP of the PEL’s functional group.

Next, in Fig. 7, we have shown the results for critical pH at which the particle attains the zero mobility (i.e., PZM) and its dependence on the core’s surface charge and the molar concentration of the functional group residing along the surface PEL are illustrated. The results are shown here for various choices of core’s radius with a fixed value of composite particle size and fixed electrolyte concentration. We have presented the results for both cases when the inner core is composed of either SiO2 (Fig. 7a) or TiO2 (Fig. 7b), respectively. In addition, we have also shown the corresponding results for the net PEL charge (Fig. 7c and d) when the bulk pH is equal to PZM.

We observed that the PZM decreases with the rise in total number density of the zwitterionic functional group distributed along the core’s surface. On the other hand, the PZM increases with the molar concentration of succinoglycan functional group entrapped with the surface PEL. It is clear from Fig. 7a and b that the PZM is always greater than IEP of the zwitterion distributed along the core’s surface and less than that of the functional group entrapped within the surface PEL. For such a typical value of PZM, a heterogeneity in the charge distribution of the inner core’s surface and the PEL may occur. Here, for the critical value of pH, i.e., PZM leads to a negative surface charge along the core’s surface and the outer PEL becomes positively charged (Fig. 7c and d). The net effective core’s surface charge with negative polarity increases with the rise in Ntotal. In order to compensate the effect of increasing core charge, the requirement of net positive PEL charge should increase and it can be achieved in smaller value of PZM (Fig. 7c and d). On the other hand, higher value of the molar concentration of PEL charge increases the net effective PEL charge (Fig. 7c and d) which requires a higher values of inner core’s surface charge to attain the zero mobility and it can be achieved with higher value of critical pH. In addition, with increasing core’s radius, the effective core charge increases and it is reasonable for zero mobility to have an increase in net PEL charge, which occurs for decreasing PZM.

Conclusions

In this article, we have extended the conventional studies on the electrophoresis of soft particle by considering the effect of pH-regulated charges of both the inner rigid core’s surface and volumetric charge of the peripheral PEL. For illustration, we have considered typical situations where the inner core is made up of either SiO2 or TiO2 and the surface PEL bears succinoglycan, which results in pH-regulated zwitterionic charges. The study of the electrophoresis of such a typical soft particle is closer to reality, and it renders an overall outline of the electrophoretic behavior of a wide class of bio-particle. Under a low potential and weak electric field assumption, we have obtained the electrophoretic mobility of the undertaken soft particle by solving the linearized Poisson-Boltzmann equation, Darcy-Brinkman, and Stokes equation. We observed that the particle mobility is greatly influenced by the bulk pH and concentration of bulk electrolyte. For the composite particle with charged inner core and uncharged PEL, the particle may attain positive, negative, and zero mobility which we have justified via concept of IEP of the functional group distributed along the core’s surface. In addition, we have also presented the results for electrophoresis of the most general situation where both the inner core’s surface and harboring PEL bear the zwitterionic functional group. We have justified the results for electrophoretic mobility by introducing various mechanisms, namely shielding effect and counterion condensation effect. We have also shown the results for the most interesting case, namely the occurrence of zero mobility even when the particle entraps the net nonzero charges. Such a situation often arises for a composite core-shell particle with heterogenous charge distribution, which we have highlighted in a great detail.