1 Introduction

The large-scale atmospheric motion in the middle–high latitudes is mainly characterized by the Rossby wave, which is quasi-horizontal and nondivergent (Rossby 1939; Charney 1947). There exist ridges and troughs as well as high- and low-pressure systems developed by the perturbation of the zonal atmospheric motions, and the centers and strength of the Rossby wave reflect the characteristics of the atmospheric circulation in the corresponding region. In contrast, at low latitudes, the motion is dominated by overturning Hadley and Walker circulations within the meridional and zonal planes, respectively (Hartmann 1994). The Hadley circulation is considered one of the most important circulations affecting the balance of the incoming and outgoing physical quantities of the global atmospheric circulations (Oort and Peixóto 1983; Trenberth and Solomon 1994), whereas the Walker circulation is considered a component of the El Niño Southern Oscillation (ENSO) phenomenon in the tropical ocean and atmosphere (Julian and Chervin 1978; Hosking et al. 2012). The Rossby, Hadley and Walker circulations within the horizontal, meridional and zonal planes, respectively, are the most important global large-scale circulations. Their movements and evolutions can greatly affect the global atmospheric circulation and the thermal and water vapor exchange between the high and low latitudes and between the ocean and continent, and thus impact the formation and evolution of weather and climate (Bowman and Cohen 1997; Diaz and Bradley 2004; Lau and Waliser 2012; England et al. 2014).

The huge importance of the Rossby, Hadley and Walker circulations has motivated numerous studies on their dynamics. For instance, according to the traditional two-dimensional (2D) decomposition of the vortex and divergent circulations in the fluid dynamics, the horizontal velocity components of the Rossby wave at middle–high latitudes can be represented by the stream function when ignoring the influence of the vertical motion. The evolution of the Rossby wave can then be studied and predicted by introducing the stream function into the vorticity equation (Holton 2004). In contrast, the horizontal vortex motion is often neglected in low latitudes since the vertical motion is intense. Based on this assumption, Schwendike et al. (2014, 2015) have proposed a method for the partitioning of the tropical vertical motion into meridional and zonal circulations called the local Hadley circulation and local Walker circulation. Schwendike et al. (2014, 2015) also examined the evolution characteristics of the Hadley and Walker circulations and their connections with ENSO and proved that the method is useful for studying the Hadley and Walker circulations, particularly at the local scale.

The horizontal vortex circulation at middle–high latitudes and the vertical motion at low latitudes are focused, whereas the vertical motion at middle–high latitudes and the horizontal vortex motion at low latitudes are often ignored when analyzing the global large-scale circulations, which leads to two subjects in the modern theory of the atmosphere, i.e., the middle–high-latitude and low-latitude atmospheric dynamics (Holton 2004). Nevertheless, such a division undermines the integrity of the global atmospheric motion, resulting in an insufficient understanding of the interactions between the motions at low latitudes and those at middle–high latitudes (Kiladis and Weickmann 1992; Kiladis and Feldstein 1994; Haarsma and Selten 2012; Farneti et al. 2014) and the interactions between the horizontal and overturning circulations (Held and Phillips 1990; Kiladis 1998; Houze et al. 2000). Furthermore, although the vertical motion is smaller than the horizontal motion in the middle–high latitudes, it plays an important role in the exchange of physical quantities in the meridional and zonal planes. Similarly, the horizontal motion at low latitudes also plays an important role in the evolution of the meridional and zonal overturning circulations. Based on these important features of the global atmospheric circulations, the mathematical definitions of three-pattern circulations, which means the three-dimensional (3D) horizontal, meridional and zonal circulations, are proposed to obtain a unified description of the atmospheric circulation. This is the three-pattern decomposition of global atmospheric circulation (Xu 2001; Hu 2006; Liu et al. 2008; Hu et al. 2015).

The following questions arise: Is the three-pattern decomposition model a simple superposition of the representation method of the horizontal vortex circulation at middle–high latitudes and the local partitioning of the overturning circulation at low latitudes? What are the differences and connections between the representation method of the horizontal vortex circulation at middle–high latitudes, the local partitioning of the overturning circulation in the tropics and the three-pattern decomposition of global atmospheric circulation? What are the advantages of the new proposed three-pattern decomposition model? This study aims to answer these questions.

In Sect. 2, we introduce the representation method of the horizontal vortex circulation at middle–high latitudes and the local partitioning of the overturning circulation in the tropics (Schwendike et al. 2014) and investigate the connections between them. In Sect. 3, we briefly introduce the three-pattern decomposition of global atmospheric circulation and point out that the dynamic theory of velocity fields can be naturally converted into the dynamic theory of large-scale circulations by inserting the three-pattern decomposition model into the primitive equations of the atmosphere. The differences and connections between the three-pattern decomposition model and the methods proposed in Sect. 2 are discussed in Sect. 4. The advantages of the three-pattern decomposition model in representing the local Hadley and Walker circulations are discussed in Sect. 5. Section 6 provides the conclusions of this study.

2 Traditional 2D decomposition

The 3D velocity fields of the atmosphere satisfy the following continuity equation in the pressure coordinates:

$${{\nabla }_{p}}\cdot \vec{V}+\frac{\partial \omega }{\partial p}=0,$$
(1)

where \(\vec{V}(\lambda ,\varphi ,p)=u(\lambda ,\varphi ,p)\vec{i}+v(\lambda ,\varphi ,p)\vec{j}\) is the horizontal velocity, \(\omega (\lambda ,\varphi ,p)\) is the vertical velocity, \(p\) is the atmospheric pressure, \(\varphi\) is the latitude and \(\lambda\) is the longitude. The vectors \(\vec{i}\) and \(\vec{j}\) are the horizontal unit vectors in the spherical \(p\)-coordinate system and \({{\nabla }_{p}}=\frac{1}{a\cos \varphi }\frac{\partial }{\partial \lambda }\vec{i}+\frac{1}{a}\frac{\partial }{\partial \varphi }\vec{j}\) is the gradient operator along a pressure surface. For any given pressure surface, we can decompose the horizontal velocity \(\vec{V}\) into \({{\vec{V}}_{div}}\) and \({{\vec{V}}_{rot}}\) using the traditional 2D decomposition of the vortex and divergent circulations (“Appendix A”),

$$\vec{V}(\lambda ,\varphi ,p)={{\vec{V}}_{div}}(\lambda ,\varphi ,p)+{{\vec{V}}_{rot}}(\lambda ,\varphi ,p),$$
(2)

where \({{\vec{V}}_{div}}\) and \({{\vec{V}}_{rot}}\) represent the divergent (irrotational) part and the vortex (nondivergent) part of the horizontal velocity \(\vec{V}\) along the given pressure surface, respectively. We then have the following two parts of Eq. (1) when we combine Eq. (2) with Eq. (1):

$${{\nabla }_{p}}\cdot {{\vec{V}}_{rot}}=0,$$
(3)
$${{\nabla }_{p}}\cdot {{\vec{V}}_{div}}+\frac{\partial \omega }{\partial p}=0.$$
(4)

Equations (3) and (4) represent the horizontal vortex motion (nondivergent) and vertical motion in the continuity Eq. (1), respectively. Next, we will provide the traditional representation process of the horizontal vortex circulation at middle–high latitudes and the local partitioning of the overturning circulation in the tropics using the continuity Eqs. (1), (3) and (4).

2.1 Horizontal vortex circulation at middle–high latitudes

Since the large-scale atmospheric motion at middle–high latitudes is mainly the vortex Rossby wave, the velocity components of \({{\vec{V}}_{div}}\) and \(\omega\) that induce the vertical motions are always neglected in the traditional studies for the large-scale motion. Applying Eqs. (1) and (2), we can then obtain the horizontal vortex circulation at middle–high latitudes as follows:

$${{\vec{V}}_{rot}}={{u}_{rot}}\vec{i}+{{v}_{rot}}\vec{j},$$
(5)

which satisfies the continuity Eq. (3), i.e.,

$${{\nabla }_{p}}\cdot {{\vec{V}}_{rot}}=\frac{1}{a\cos \varphi }\frac{\partial {{u}_{rot}}}{\partial \lambda }+\frac{1}{a\cos \varphi }\frac{\partial {{v}_{rot}}\cos \varphi }{\partial \varphi }=0.$$
(6)

According to “Appendix A”, for the given vertical vorticity \({{\zeta }_{p}}\) on a given pressure surface, Eq. (6) ensures that \({{\vec{V}}_{rot}}\) can be represented by the stream function \({{\psi }_{R}}\):

$${{u}_{rot}}=-\frac{1}{a}\frac{\partial {{\psi }_{R}}}{\partial \varphi },\quad {{v}_{rot}}=\frac{1}{a\cos \varphi }\frac{\partial {{\psi }_{R}}}{\partial \lambda },$$
(7)

where \({{\psi }_{R}}\) satisfies

$${{\Delta }_{2}}{{\psi }_{R}}={{\zeta }_{p}}.$$
(8)

Equations (7) and (8) indicate that after neglecting the vertical circulations, the large-scale atmospheric motion at middle–high latitudes can be expressed by the stream function \({{\psi }_{R}},\) which is the reason we usually represent the evolution of the Rossby wave at middle–high latitudes using the image of \({{\psi }_{R}}\) and the vorticity equation performed by \({{\psi }_{R}}\).

2.2 Local partitioning of the overturning circulation in the tropics

Similarly, we usually neglect the horizontal vortex circulation \({{\vec{V}}_{rot}}\) and represent the large-scale motion in the low latitudes as the following overturning circulation:

$$\vec{V}={{\vec{V}}_{div}}+\omega \vec{k},$$
(9)

which satisfies the continuity Eq. (4), i.e.,

$${{\nabla }_{p}}\cdot {{\vec{V}}_{div}}+\frac{\partial \omega }{\partial p}=\frac{1}{a\cos \varphi }\frac{\partial {{u}_{div}}}{\partial \lambda }+\frac{1}{a\cos \varphi }\frac{\partial {{v}_{div}}\cos \varphi }{\partial \varphi }+\frac{\partial \omega }{\partial p}=0,$$
(10)

where \(\vec{k}\) is the vertical unit vector in the spherical \(p\)-coordinate system.

Using Eqs. (9) and (10), Schwendike et al. (2014, 2015) defined the zonal overturning circulation \({{\vec{V}}_{\lambda }}\) and the meridional overturning circulation \({{\vec{V}}_{\varphi }}\) in the tropics as

$${{\vec{V}}_{\lambda }}={{u}_{div}}\vec{i}+{{\omega }_{\lambda }}\vec{k},\ {{\vec{V}}_{\varphi }}={{v}_{div}}\vec{j}+{{\omega }_{\varphi }}\vec{k},$$
(11)

which satisfy the following continuity equations:

$$\frac{1}{a\cos \varphi }\frac{\partial {{u}_{div}}}{\partial \lambda }+\frac{\partial {{\omega }_{\lambda }}}{\partial p}=0,$$
(12)
$$\frac{1}{a\cos \varphi }\frac{\partial {{v}_{div}}\cos \varphi }{\partial \varphi }+\frac{\partial {{\omega }_{\varphi }}}{\partial p}=0.$$
(13)

The divergent wind \(({{u}_{div}},{{v}_{div}})\) is denoted by \(({{u}_{\lambda }},{{u}_{\varphi }})\) in the studies by Schwendike et al. (2014, 2015). Equations (12) and (13) ensure that the components \({{u}_{div}}\), \({{\omega }_{\lambda }}\), \({{v}_{div}}\) and \({{\omega }_{\varphi }}\) can be represented by the stream functions \({{\psi }_{\lambda }}\) and \({{\psi }_{\varphi }}\) as follows:

$${{u}_{div}}=-\frac{\partial {{\psi }_{\lambda }}}{\partial p},\ {{\omega }_{\lambda }}=\frac{1}{a\cos \varphi }\frac{\partial {{\psi }_{\lambda }}}{\partial \lambda },$$
(14)
$${{v}_{div}}=-\frac{\partial {{\psi }_{\varphi }}}{\partial p},\ {{\omega }_{\varphi }}=\frac{1}{a\cos \varphi }\frac{\partial {{\psi }_{\varphi }}\cos \varphi }{\partial \varphi }.$$
(15)

Combined with Eqs. (9), (11), (12) and (13), we have

$$\vec{V}={{\vec{V}}_{div}}+\omega \vec{k}={{\vec{V}}_{\lambda }}+{{\vec{V}}_{\varphi }},$$
(16)

which means that \({{\vec{V}}_{\lambda }}\) and \({{\vec{V}}_{\varphi }}\) represent a decomposition of the overturning circulation at low latitudes. Meanwhile, Eqs. (12) and (13) also represent a decomposition of the continuity Eq. (10). Schwendike et al. (2014, 2015) referred to Eq. (16) as the local partitioning of the overturning circulation in the tropics and \({{\vec{V}}_{\lambda }}\) and \({{\vec{V}}_{\varphi }}\) as the local Hadley circulation and local Walker circulation, respectively.

According to Eq. (48) in “Appendix A” and Eqs. (14) and (15), we have

$${{u}_{div}}=-\frac{\partial {{\psi }_{\lambda }}}{\partial p}=\frac{1}{a\cos \varphi }\frac{\partial \chi }{\partial \lambda },\ {{v}_{div}}=-\frac{\partial {{\psi }_{\varphi }}}{\partial p}=\frac{1}{a}\frac{\partial \chi }{\partial \varphi },$$
(17)

where \(\chi\) is the velocity potential function of \({{\vec{V}}_{div}}\), which satisfies the 2D Poisson equation (49) in “Appendix A”. Equation (17) shows that the velocity potential function \(\chi\) determines the stream functions \({{\psi }_{\lambda }}\) and \({{\psi }_{\varphi }}\) and further determines the vertical velocity components \({{\omega }_{\lambda }}\) and \({{\omega }_{\varphi }}\). Thus, when \({{\vec{V}}_{\lambda }}\) and \({{\vec{V}}_{\varphi }}\) are defined as in Eqs. (11), (12) and (13), the overturning circulation in the tropics defined by Eq. (9) is decomposed into the two orthogonal overturning circulations \({{\vec{V}}_{\lambda }}\) and \({{\vec{V}}_{\varphi }}\) by the traditional 2D decomposition process (2).

The decomposition methods in this section show that we usually neglect the effect of the vertical motion when we describe the middle–high-latitude atmospheric motion, and we only keep the vertical circulations when we represent the low-latitude motion, leading to a natural defect that the traditional studies cannot describe the global circulation in a united way. At the same time, since the traditional 2D decomposition leads to \({{\nabla }_{p}}\times {{\vec{V}}_{rot}}={{\zeta }_{p}}\vec{k}\) and \({{\nabla }_{p}}\times {{\vec{V}}_{div}}=0,\) it cannot separate the vertical vorticity induced by the divergent motion from the total vertical vorticity \({{\zeta }_{p}}\). This problem can be resolved using the three-pattern decomposition model.

3 Three-pattern decomposition of global atmospheric circulation

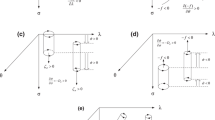
For the convenience of the 3D vorticity vector calculation in right-hand orthogonal coordinates, the spherical \(\sigma\)-coordinate system is introduced in the three-pattern decomposition of global atmospheric circulation (Hu et al. 2015) without loss of generality. Namely, we have

$${u}'=\frac{u}{a},\ {v}'=\frac{v}{a},\ \dot{\sigma }=\frac{\omega }{{{P}_{s}}},\ \sigma =\frac{p}{{{P}_{s}}},$$
(18)

where \(({u}',{v}',\dot{\sigma })\) and \((u,v,\omega )\) denote the three velocity components in the spherical \(\sigma\)-coordinate system and spherical \(p\)-coordinate system, respectively. Here, \({{P}_{s}}\)=1000 hPa denotes the pressure at earth surface and \(\theta\) is the colatitude. Thus, we have

$${\vec{V}}'(\lambda ,\theta ,\sigma )={u}'(\lambda ,\theta ,\sigma )\vec{i}+{v}'(\lambda ,\theta ,\sigma )\vec{j}+\dot{\sigma }(\lambda ,\theta ,\sigma )\vec{k},$$
(19)

which represents the 3D velocity field, and we rewrite the continuity Eq. (1) as follows:

$$\frac{1}{\sin \theta }\frac{\partial {u}'}{\partial \lambda }+\frac{1}{\sin \theta }\frac{\partial (\sin \theta {v}')}{\partial \theta }+\frac{\partial \dot{\sigma }}{\partial \sigma }=0.$$
(20)

We define the global horizontal circulation \({{{\vec{V}}'}_{R}}\) as

$${{{\vec{V}}'}_{R}}(\lambda ,\theta ,\sigma )={{{u}'}_{R}}(\lambda ,\theta ,\sigma )\vec{i}+{{{v}'}_{R}}(\lambda ,\theta ,\sigma )\vec{j},$$
(21)

and the following continuity equation is satisfied:

$$\frac{1}{\sin \theta }\frac{\partial {{{{u}'}}_{R}}}{\partial \lambda }+\frac{1}{\sin \theta }\frac{\partial (\sin \theta {{{{v}'}}_{R}})}{\partial \theta }=0.$$
(22)

Equation (22) is the sufficient condition such that \({{{u}'}_{R}}\) and \({{{v}'}_{R}}\) can be represented by a stream function \(R(\lambda ,\theta ,\sigma )\) as follows (Hu et al. 2015):

$${{{u}'}_{R}}=-\frac{\partial R}{\partial \theta },\ {{{v}'}_{R}}=\frac{1}{\sin \theta }\frac{\partial R}{\partial \lambda }.$$
(23)

Similarly, we define the global meridional circulation \({{{\vec{V}}'}_{H}}\) and zonal circulation \({{{\vec{V}}'}_{W}}\) as

$${{{\vec{V}}'}_{H}}(\lambda ,\theta ,\sigma )={{{v}'}_{H}}(\lambda ,\theta ,\sigma )\vec{j}+{{\dot{\sigma }}_{H}}(\lambda ,\theta ,\sigma )\vec{k},$$
(24)
$${{{\vec{V}}'}_{W}}(\lambda ,\theta ,\sigma )={{{u}'}_{W}}(\lambda ,\theta ,\sigma )\vec{i}+{{\dot{\sigma }}_{W}}(\lambda ,\theta ,\sigma )\vec{k},$$
(25)

and the following continuity equations are satisfied:

$$\frac{1}{\sin \theta }\frac{\partial (\sin \theta {{{{v}'}}_{H}})}{\partial \theta }+\frac{\partial {{{\dot{\sigma }}}_{H}}}{\partial \sigma }=0,$$
(26)
$$\frac{1}{\sin \theta }\frac{\partial {{{{u}'}}_{W}}}{\partial \lambda }+\frac{\partial {{{\dot{\sigma }}}_{W}}}{\partial \sigma }=0.$$
(27)

Equations (26) and (27) allow the components of \({{{\vec{V}}'}_{H}}\) and \({{{\vec{V}}'}_{W}}\) to be represented by the stream functions \(H(\lambda ,\theta ,\sigma )\) and \(W(\lambda ,\theta ,\sigma )\) as follows (Hu et al. 2015):

$${{{v}'}_{H}}=-\frac{\partial H}{\partial \sigma },\ {{\dot{\sigma }}_{H}}=\frac{1}{\sin \theta }\frac{\partial (\sin \theta H)}{\partial \theta },$$
(28)
$${{{u}'}_{W}}=\frac{\partial W}{\partial \sigma },\ {{\dot{\sigma }}_{W}}=-\frac{1}{\sin \theta }\frac{\partial W}{\partial \lambda }.$$
(29)

As noted above, the global atmospheric circulation should include the horizontal and vertical circulation in a unified manner at both middle–high and low latitudes. Thus, we naturally decompose the atmospheric circulation \({\vec{V}}'\) into \({{{\vec{V}}'}_{R}}\), \({{{\vec{V}}'}_{H}}\) and \({{{\vec{V}}'}_{W}}\) from a global perspective:

$${\vec{V}}'={{{\vec{V}}'}_{H}}+{{{\vec{V}}'}_{W}}+{{{\vec{V}}'}_{R}}.$$
(30)

According to Eqs. (23), (28) and (29), the components of Eq. (30) can be written as follows:

$$\left\{ \begin{gathered} u^{\prime} = u^{\prime}_{W} + u^{\prime}_{R} = \frac{{\partial W}}{{\partial \sigma }} - \frac{{\partial R}}{{\partial \theta }}, \hfill \\ v^{\prime} = v^{\prime}_{R} + v^{\prime}_{H} = \frac{1}{{\sin \theta }}\frac{{\partial R}}{{\partial \lambda }} - \frac{{\partial H}}{{\partial \sigma }}, \hfill \\ \dot{\sigma } = \dot{\sigma }_{H} + \dot{\sigma }_{W} = \frac{1}{{\sin \theta }}\frac{{\partial (\sin \theta H)}}{{\partial \theta }} - \frac{1}{{\sin \theta }}\frac{{\partial W}}{{\partial \lambda }}. \hfill \\ \end{gathered} \right.$$
(31)

We refer to Eqs. (30) or (31) as the three-pattern decomposition of the global atmospheric circulation (Hu et al. 2015). In contrast to the traditional 2D decomposition methods described in Sect. 2, Eqs. (22), (26) and (27) cannot ensure the uniqueness of \(H\), \(W\) and \(R\) because \({{{\vec{V}}'}_{H}}\), \({{{\vec{V}}'}_{W}}\) and \({{{\vec{V}}'}_{R}}\) have three spatial dimensions and we need the following restriction condition to select the correct ones (Hu et al. 2015):

$$\frac{1}{\sin \theta }\frac{\partial H}{\partial \lambda }+\frac{1}{\sin \theta }\frac{\partial (W\sin \theta )}{\partial \theta }+\frac{\partial R}{\partial \sigma }=0.$$
(32)

Equation (32) guarantees both the uniqueness of \(H\), \(W\) and \(R\) and the physical rationality of the three-pattern decomposition of the global atmospheric circulation. A more detailed discussion can be found in Theorem 2 in Hu et al. (2015).

Combining Eq. (32) with Eq. (31), we have

$${{\Delta }_{3}}R=\zeta ,$$
(33)
$$\frac{\partial H}{\partial \sigma }=\frac{1}{\sin \theta }\frac{\partial R}{\partial \lambda }-{v}',$$
(34)
$$\frac{\partial W}{\partial \sigma }=\frac{\partial R}{\partial \theta }+{u}',$$
(35)

where \(\zeta =\frac{1}{\sin \theta }\frac{\partial {v}'}{\partial \lambda }-\frac{1}{\sin \theta }\frac{\partial ({u}'\sin \theta )}{\partial \theta }\) represents the vertical vorticity of the entire atmospheric layer and \({{\Delta }_{3}}=\frac{1}{{{\sin }^{2}}\theta }\frac{{{\partial }^{2}}}{\partial {{\lambda }^{2}}}+\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }(\sin \theta \frac{\partial }{\partial \theta })+\frac{{{\partial }^{2}}}{\partial {{\sigma }^{2}}}\) denotes the 3D Laplacian in the spherical \(\sigma\)-coordinate system. We determine the stream functions \(H\), \(W\) and \(R\) and then obtain the three-pattern decomposition of the global atmospheric circulation by solving Eqs. (33), (34) and (35).

The three-pattern decomposition model (31) can be rewritten as an operator equation:

$$\left( \begin{matrix} {{u}'} \\ {{v}'} \\ {\dot{\sigma }} \\\end{matrix} \right)=\left( \begin{matrix} 0 & \frac{\partial }{\partial \sigma } & -\frac{\partial }{\partial \theta } \\ -\frac{\partial }{\partial \sigma } & 0 & \frac{1}{\sin \theta }\frac{\partial }{\partial \lambda } \\ \frac{1}{\sin \theta }\frac{\partial \sin \theta }{\partial \theta } & -\frac{1}{\sin \theta }\frac{\partial }{\partial \lambda } & 0 \\\end{matrix} \right)\left( \begin{matrix} H \\ W \\ R \\\end{matrix} \right).$$
(36)

A new set of dynamical equations of the large-scale circulations \({{{\vec{V}}'}_{R}}\), \({{{\vec{V}}'}_{H}}\) and \({{{\vec{V}}'}_{W}}\) is then established by applying the operator Eq. (36) to the primitive equations of the atmosphere. The new dynamical equations replace the three velocity components \(({u}',{v}',\dot{\sigma })\) in the primitive equations with the three stream functions \((H,W,R)\). They can be used to uncover the mechanisms of the large-scale circulation evolutions through the perspective of the stream functions.

4 Comparison of the three-pattern decomposition and traditional 2D decomposition

Comparing the decomposition methods in Sects. 2 and 3, except for the regional division of the middle–high latitudes and low latitudes, we consider whether the three-pattern decomposition method can be taken as a simple superposition of the representation method of the horizontal vortex circulation at middle–high latitudes and the local partitioning of the overturning circulation in the tropics. This section attempts to answer this question.

4.1 Theoretic comparison: decomposition of the vertical vorticity

The stream function \({{\psi }_{R}}\) of the vortex circulation \({{\vec{V}}_{rot}}\) at middle–high latitudes defined by the traditional 2D decomposition method satisfies the 2D Poisson Eq. (8),

$${{\Delta }_{2}}{{\psi }_{R}}={{\zeta }_{p}}.$$
(37)

However, the stream function \(R\) of the horizontal circulation \({{{\vec{V}}'}_{R}}\) defined by the three-pattern decomposition procedure satisfies the 3D Poisson Eq. (33),

$${{\Delta }_{3}}R={{\Delta }_{2}}R+\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}=\zeta ,$$
(38)

where \({{\zeta }_{p}}\) is the value of the vertical vorticity \(\zeta\) on a given pressure surface. To determine the differences between the two horizontal circulations \({{\vec{V}}_{rot}}\) and \({{{\vec{V}}'}_{R}}\), we have to analyze the physical meaning of each term in Eqs. (37) and (38). First, for Eq. (37), \({{\Delta }_{2}}{{\psi }_{R}}=\frac{1}{a\cos \varphi }\frac{\partial {{v}_{rot}}}{\partial \lambda }-\frac{1}{a\cos \varphi }\frac{\partial {{u}_{rot}}\cos \varphi }{\partial \varphi }={{\zeta }_{p}}\) using Eq. (7), which shows that \({{\Delta }_{2}}{{\psi }_{R}}\) represents the vertical vorticity of \({{\vec{V}}_{rot}}\). Nevertheless, for Eq. (38), \({{\Delta }_{2}}R=\frac{1}{\sin \theta }\frac{\partial {{{{v}'}}_{R}}}{\partial \lambda }-\frac{1}{\sin \theta }\frac{\partial {{{{u}'}}_{R}}\sin \theta }{\partial \theta }\) (represented as \({{\zeta }_{R}}\)) denotes the vertical vorticity of \({{{\vec{V}}'}_{R}}\) using Eq. (23). \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\) represents the vertical vorticity of the divergent motion (represented by \({{{u}'}_{W}}\) and \({{{v}'}_{H}}\)) because it has the following form using Eqs. (22), (28), (29), (31) and (32):

$$\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}=\frac{1}{\sin \theta }\frac{\partial {{{{v}'}}_{H}}}{\partial \lambda }-\frac{1}{\sin \theta }\frac{\partial {{{{u}'}}_{W}}\sin \theta }{\partial \theta },$$
(39)

where

$$\frac{1}{\sin \theta }\frac{\partial {{{{u}'}}_{W}}}{\partial \lambda }+\frac{1}{\sin \theta }\frac{\partial ({{{{v}'}}_{H}}\sin \theta )}{\partial \theta }=\frac{1}{\sin \theta }\frac{\partial {u}'}{\partial \lambda }+\frac{1}{\sin \theta }\frac{\partial ({v}'\sin \theta )}{\partial \theta }=D,$$
(40)

and \(D\) is the divergence field of the original velocities \({u}'\) and \({v}'\). This suggests that \({{\Delta }_{2}}R\) and \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\) decompose the vertical vorticity \(\zeta\) into two parts: one part is caused by the horizontal circulation, whereas the other one is induced by the divergent motion. Furthermore, \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\) can be decomposed to \(\frac{1}{\sin \theta }\frac{\partial {{{{v}'}}_{H}}}{\partial \lambda }\) (represented as \({{\zeta }_{H}}\)) and \(-\frac{1}{\sin \theta }\frac{\partial {{{{u}'}}_{W}}\sin \theta }{\partial \theta }\) (represented as \({{\zeta }_{W}}\)) according to Eq. (39). From definitions (24) and (25), \({{\zeta }_{H}}\) and \({{\zeta }_{W}}\) are the vertical vorticities of the meridional circulation \({{{\vec{V}}'}_{H}}\) and zonal circulation \({{{\vec{V}}'}_{W}}\), respectively. The decomposition of the vertical vorticity (\(\zeta ={{\zeta }_{R}}+{{\zeta }_{H}}+{{\zeta }_{W}}\)) using the three-pattern decomposition model is helpful for studying the interaction mechanisms of the three-pattern circulations through the vorticity equation.

The quantitative differences between the horizontal circulations \({{\vec{V}}_{rot}}\) and \({{{\vec{V}}'}_{R}}\) inevitably cause differences between the overturning circulations \(({{\vec{V}}_{\varphi }},{{\vec{V}}_{\lambda }})\) defined by the local partitioning method of the overturning circulation in the tropics and the overturning circulations \(({{{\vec{V}}'}_{H}},{{{\vec{V}}'}_{W}})\) defined by the three-pattern decomposition method of the global atmospheric circulation. Next, we will focus on this issue.

Since the stream functions \({{\psi }_{\varphi }}\) and \({{\psi }_{\lambda }}\) of the overturning circulations \({{\vec{V}}_{\varphi }}\) and \({{\vec{V}}_{\lambda }}\) satisfy Eqs. (14) and (15), we have

$${{\psi }_{\varphi }}=-\int_{0}^{p}{{{v}_{div}}dp}\ or\ {{\psi }_{\varphi }}=\frac{a}{\cos \varphi }\int_{-\frac{\pi }{2}}^{\varphi }{{{\omega }_{\varphi }}\cos \varphi d\varphi },$$
(41)
$${{\psi }_{\lambda }}=-\int_{0}^{p}{{{u}_{div}}dp}\ or\ {{\psi }_{\lambda }}=a\int_{0}^{\lambda }{{{\omega }_{\lambda }}\cos \varphi d}\lambda ,$$
(42)

which shows that \({{\vec{V}}_{\lambda }}\) and \({{\vec{V}}_{\varphi }}\) are completely determined by the divergent winds \({{u}_{div}}\) and \({{v}_{div}}\) (\({{u}_{div}}\) and \({{v}_{div}}\) are irrotational with zero vertical vorticity) on the given pressure surfaces. We then obtain

$$[{{\psi }_{\varphi }}]=-\int_{0}^{p}{[{{v}_{div}}]dp},\ \langle {{\psi }_{\lambda }}\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}=-\int_{0}^{p}{\langle{{u}_{div}}\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}dp},$$
(43)

where ‘[]’ represents the global zonal average andand ‘\(<\text{ }>_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}\) ’ denotes the meridional average of 5 degrees of the northern and southern latitudes. Referring to “Appendix B”, \([{{\psi }_{\varphi }}]\) and \(<{{\psi }_{\lambda }}>_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}\) are the same as the traditional mass stream functions \({{\psi }_{H}}\) and \({{\psi }_{W}}\) (see “Appendix B”) of the Hadley and Walker circulations except for multiple constants.

However, if we rewrite the partial differential Eqs. (34) and (35) using Eq. (23) as

$$H=\int_{1}^{\sigma }{\left(\frac{1}{\sin \theta }\frac{\partial R}{\partial \lambda }-{v}'\right)d\sigma =}\int_{1}^{\sigma }{({{{{v}'}}_{R}}-{v}')d\sigma =}-\int_{1}^{\sigma }{{{{{v}'}}_{H}}d\sigma },$$
(44)
$$W=\int_{1}^{\sigma }{\left( \frac{\partial R}{\partial \theta }+{u}' \right)d\sigma =}\int_{1}^{\sigma }{(-{{{{u}'}}_{R}}+{u}')d\sigma =}\int_{1}^{\sigma }{{{{{u}'}}_{W}}d\sigma },$$
(45)

then the stream functions \(H\) and \(W\) of the vertical circulations \({{{\vec{V}}'}_{H}}\) and \({{{\vec{V}}'}_{W}}\) are determined by the divergent motions \({{{v}'}_{H}}\) and \({{{u}'}_{W}}\). Different from \({{u}_{div}}\) and \({{v}_{div}}\), \({{{u}'}_{W}}\) and \({{{v}'}_{H}}\) are rotational with the vertical vorticity \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\). The stream functions \((H,W)\) are not equal to \(({{\psi }_{\varphi }},{{\psi }_{\lambda }})\), and \(([H],<W>_{{{5}^{\circ }}S}^{{{5}^{\circ }}N})\) are different from \(({{\psi }_{H}},{{\psi }_{W}})\) for the differences in the divergent winds \(({{u}_{div}},{{v}_{div}})\) and \(({{{u}'}_{W}},{{{v}'}_{H}})\).

The differences between the stream functions \(({{\psi }_{\varphi }},{{\psi }_{\lambda }})\) and \((H,W)\) correspond to the differences between the overturning circulations \(({{\vec{V}}_{\varphi }},{{\vec{V}}_{\lambda }})\) and \(({{{\vec{V}}'}_{H}},{{{\vec{V}}'}_{W}})\). The circulations \({{{\vec{V}}'}_{H}}\) and \({{{\vec{V}}'}_{W}}\) have vertical vorticities (\({{\zeta }_{H}}\) and \({{\zeta }_{W}}\)) caused by the divergent motions \({{{v}'}_{H}}\) and \({{{u}'}_{W}}\), but \({{\vec{V}}_{\varphi }}\) and \({{\vec{V}}_{\lambda }}\) have zero vertical vorticities. Thus, the different definitions of the horizontal circulations \({{\vec{V}}_{rot}}\) and \({{{\vec{V}}'}_{R}}\) induce the differences between the local partitioning of the overturning circulation in the tropics and the three-pattern decomposition of the global atmospheric circulation.

Furthermore, if we let \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}=0\), then \({{{\vec{V}}'}_{R}}\) must be equal to \({{\vec{V}}_{rot}}\). The overturning circulations \({{{\vec{V}}'}_{W}}\) and \({{{\vec{V}}'}_{H}}\) are also equal to \({{\vec{V}}_{\lambda }}\) and \({{\vec{V}}_{\varphi }}\), and the three-pattern decomposition model reduces to the traditional 2D decomposition method. Thus, the three-pattern decomposition of the global atmospheric circulation can be considered a generalization of the traditional 2D decomposition methods.

4.2 Climate characteristics of the decomposed vertical vorticities

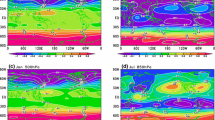
To verify the above-mentioned theoretical analysis, we calculate \(H\), \(W\) and \(R\) using Eqs. (33)–(35) and the ERA-Interim reanalysis with a horizontal resolution of \({{2.5}^{\circ}}\times {{2.5}^{\circ}}\) for the period from 1979 to 2013. We then determine the six velocity components of circulations \({{{\vec{V}}'}_{R}}\), \({{{\vec{V}}'}_{H}}\) and \({{{\vec{V}}'}_{W}}\) using Eqs. (23), (28) and (29). The climatological mean of the vertical vorticities derived from Eqs. (37), (38) and (39) in boreal winter (DJF) at 850 hPa (the first row), 500 hPa (the second row), 200 hPa (the third row) and the vertical mean surface (the fourth row) are shown in Fig. 1. The first and second columns of Fig. 1 represent \({{\Delta }_{2}}R\) and \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\), respectively, the third column provides the sum of \({{\Delta }_{2}}R\) and \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\), and the fourth column provides the vertical vorticity \(\zeta\) calculated by the horizontal wind from the ERA-Interim reanalysis.

A comparison of the four columns in Fig. 1 shows that the actual vertical vorticity \(\zeta\) (the fourth column) is nearly identical to \({{\Delta }_{2}}R+\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\) (the third column), which means that \(\zeta\) is decomposed into two parts, where one is caused by the vortex motion (\({{{u}'}_{R}}\) and \({{{v}'}_{R}}\), the first column) and the other one is caused by the divergent motion (\({{{u}'}_{W}}\) and \({{{v}'}_{H}}\), the second column). The component \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\) caused by the divergent motion cannot be ignored at 850 hPa (Fig. 1b) and 200 hPa (Fig. 1j). However, it equals approximately zero at 500 hPa (Fig. 1f) and the vertical mean surface (Fig. 1n). This behavior corresponds to the classic theory that the motion at 500 hPa is quasi-horizontal and nondivergent and can be used to represent the mean state of the entire atmospheric layer. The vertical vorticity \(\zeta\) and its decomposed components in boreal summer (JJA) share the same characteristics in winter (see Fig. S1), and the results based on the NCEP1 and NCEP2 data are similar to that derived from the ERA-Interim data (not shown), which indicates the robustness of the results shown in Fig. 1.

Fig. 1
figure 1

a Climatological mean of \({{\Delta }_{2}}R\) at 850 hPa from the ERA-Interim reanalysis (1979–2013) for DJF. b–d same as a, but for \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\), \({{\Delta }_{2}}R+\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\) and \(\zeta\), respectively. e–h, i–l and m–p same as a–d, but for 500, 200 hPa and the vertical mean surface, respectively. The unit of the vertical vorticities is 1.0 × 10−6 s−1

Full size image

In general, the traditional 2D decomposition methods cannot separate the vertical vorticity of the divergent motions from the total vertical vorticity [comparing Eq. (37) with Eq. (38)] because they always need to limit the motions along a pressure surface and then decompose the horizontal velocity into \({{\vec{V}}_{div}}\) (irrotational) and \({{\vec{V}}_{rot}}\) (nondivergent). The vortex circulation \({{\vec{V}}_{rot}}\) has the total value of the vertical vorticity \(\zeta\) on a given pressure surface (denoted by \({{\zeta }_{p}}\)). However, the three-pattern decomposition method quantitatively decomposes the actual vertical vorticity \(\zeta\) into \({{\Delta }_{2}}R\) and \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\), where \({{\Delta }_{2}}R\) denotes the vertical vorticity of the horizontal motion and \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\) represents the effect of the entire layer of divergent motions on \(\zeta\). The climate characteristics of \({{\Delta }_{2}}R\) and \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\) reveal the rationality of the decomposition of the vertical vorticity (Fig. 1). Thus, the three-pattern decomposition method is not the simple superposition of the representation method of the horizontal vortex circulation at middle–high latitudes and the local partitioning of the overturning circulation in the tropics. Instead, it is a new 3D decomposition of the global atmospheric circulation.

4.3 Comparison of the three-pattern circulations and the traditional circulations

In this section, for convenience and to distinguish from the traditional methods, we call the Rossby, Hadley and Walker circulations derived from the three-pattern decomposition model the Horizontal, Meridional and Zonal circulations. We will compare the climate characteristics of the two sets of large-scale circulations.

Because the stream functions \([{{\psi }_{\varphi }}]\) and \(\langle{{\psi }_{\lambda }}\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}\) and the traditional mass stream functions \({{\psi }_{H}}\) and \({{\psi }_{W}}\) are identical except for a difference in factors, we compare the traditional stream functions (\({{\psi }_{R}}\), \({{\psi }_{H}}\) and \({{\psi }_{W}}\)) with the stream functions (\(R\), \([H]\) and \(\langle W \rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}\)) defined by the three-pattern decomposition model.

4.3.1 Horizontal circulations

The climatological means of the Horizontal circulation and Rossby circulation and the difference between them in winter are shown in Fig. 2. A comparison of the first two columns in Fig. 2 shows that the Horizontal and Rossby circulations are generally similar. They share the same characteristics at 500 hPa and the vertical mean surface, whereas the differences are apparent at 850 and 200 hPa, which shows that the Horizontal circulation captures the main characteristics of the Rossby circulation.

The third column in Fig. 2 indicates that the differences between the two circulations are mainly presented as the differences in the zonal wind, compared to the meridional wind (also see Figs. S2 and S3). Specifically, the main differences between the two circulations appear as the west wind at 850 hPa and the east wind at 200 hPa. The difference at 500 hPa mainly occurs at low latitudes, except for an anticyclone over eastern Asia to western North America at mid–high latitudes. However, the magnitudes of the differences at 500 hPa and the vertical mean surface are considerably smaller than those at 850 and 200 hPa (Note the reference vector in the top right corner of Fig. 2c, f, i, l).

The above characteristics are correspond to the theoretical analysis in Sect. 4.1 that the spatial distribution of \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\) is the main cause of the difference between the Horizontal and Rossby circulations. \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\) at 500 hPa and the vertical mean surface is nearly zero and smaller than that at 200 and 850 hPa, which causes more apparent differences between the Horizontal and Rossby circulations at 850 and 200 hPa than that at 500 hPa.

Fig. 2
figure 2

a Climatological mean of the Horizontal circulation represented by the stream function \(R\) (shaded) and the streamlines at 850 hPa for DJF (1979–2013). b Same as a, but for the Rossby circulation represented by the stream function \({{\psi }_{R}}\) and related streamlines. c The difference between Horizontal and Rossby circulations represented by the vectors at 850 hPa. Only the regions where the statistical significance is above the 95% confidence level are plotted. d–f, g–i and j–l Same as a–c, but for 500, 200 hPa and the vertical mean surface, respectively. The unit of \(R\) is 1.0 × 10−6 s−1 and the unit of \({{\psi }_{R}}\) is 1.0 × 108 m2 s−1

Full size image

In addition, the vertical shear of the horizontal winds is usually used to represent the baroclinicity of the atmosphere. Because the magnitude of \({{u}_{200hPa}}-{{u}_{850hPa}}\) is larger than \({{v}_{200hPa}}-{{v}_{850hPa}}\) (compare Figs. S2 and S3), the baroclinicity of the Horizontal and Rossby circulations can be mainly represented by the zonal wind. According to the third column of Fig. 2 and Figs. S2 and S3, we find that the baroclinicity of the Horizontal circulation defined by three-pattern decomposition model is smaller than that of the Rossby circulations. The three-pattern decomposition model attributes more baroclinicity of atmosphere to the Zonal and Meridional circulations, compared with the traditonal ones. The results in summer share the same characteristics in winter (see Figs. S4–S6).

4.3.2 Vertical circulations

According to Eqs. (31), (44) and (45), the difference between the Horizontal circulation \(({{{u}'}_{R}},{{{v}'}_{R}})\) and the Rossby circulation \(({{u}_{rot}},{{v}_{rot}})\) will cause differences in the zonal winds of the Zonal and Walker circulations and differences in the meridional winds of the Meridional and Hadley circulations (see Figs. S7 and S8), leading to differences between the Zonal and Walker circulations and differences between the Meridional and Hadley circulations (Figs. 3, 4).

The spatial patterns of \({{\psi }_{H}}\) and \([H]\) are nearly identical. There are three meridional cells in both the northern and southern hemispheres, which are the Hadley, Ferrel and polar cells (Fig. 3a, b). In the northern hemisphere winter, the Hadley circulation in the northern hemisphere is the strongest, moving upward at the equator and southern tropical areas and downward at the northern subtropical latitudes. However, it is weak in the southern hemisphere, covering only a small region (Fig. 3a, b). The difference between the Meridional and Hadley circulations illustrates that the Meridional circulation is generally stronger than the Hadley circulation and that the anomalous circulation has a system south shift compared to the mean state of the Meridional and Hadley circulation (Fig. 3). However, the magnitude of the difference is small compared to the mean state of the two meridional circulations (Note the reference vector in the top right corner of Fig. 3).

For both \({{\psi }_{W}}\) and \(\left\langle W \right\rangle _{{5^{ \circ } S}}^{{5^{ \circ } N}}\), the tropical zonal circulation contains three main components: the Indian Ocean circulation, the Pacific Walker circulation and the Atlantic Ocean circulation (Fig. 4a, b). However, the vertical motion of the Zonal circulation \({{{\vec{V}}'}_{W}}\) is more intense than that of the circulation \({{\vec{V}}_{\lambda }}\) (Fig. 4a, b). The difference between \({{\psi }_{W}}\) and \(\left\langle W \right\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}\) (Fig. 4c) is more notable than that between \({{\psi }_{H}}\) and \([H]\) (Fig. 3c), which corresponds to the difference in the zonal and meridional winds (Figs. S7 and S8).

According to the theoretical analysis in Sect. 4.1, the main cause for the above differences is that the vertical circulations \({{{\vec{V}}'}_{W}}\) and \({{{\vec{V}}'}_{H}}\) have vertical vorticities (\({{\zeta }_{W}}\) and \({{\zeta }_{H}}\)), whereas the overturning circulations \({{\vec{V}}_{\lambda }}\) and \({{\vec{V}}_{\varphi }}\) have zero ones. Meanwhile, the meridional average of \({{\zeta }_{W}}\) over 5 degrees of northern and southern latitudes is considerably larger than the global zonal average of \({{\zeta }_{H}}\) (Fig. S9), which leads to the notable difference between \({{\psi }_{W}}\) and \(\left\langle W \right\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}\) or \({{\vec{V}}_{\lambda }}\) and \({{{\vec{V}}'}_{W}}\) (Fig. 4c). Similarly, because the regional zonal average of \({{\zeta }_{H}}\) is non-zero, the vertical vorticity \({{\zeta }_{H}}\) of the meridional circulation \({{{\vec{V}}'}_{H}}\) has an important influence on the local Hadley circulation (Figs. S10 and S11). Thus, the contributions of the vertical vorticities \({{\zeta }_{W}}\) and \({{\zeta }_{H}}\) should not be neglected when studying the regional overturning circulations. The results in summer (see Figs. S9, S10 and S12–S16) share the same characteristics as those in winter.

Fig. 3
figure 3

a Climatological mean of the global zonal averaged Meridional circulation for DJF (1979–2013). \(\left[ {{\omega }_{H}} \right]\) is shaded, \(\left[ H \right]\) is in contour and the vectors represent the wind \((\left[ {{v}_{H}} \right],\left[ {{\omega }_{H}} \right])\). b Same as a, but for the Hadley circulation. \(\left[ {{\omega }_{\varphi }} \right]\) is shaded, \(\left[ {{\psi }_{H}} \right]\) is in contour and the vectors represent the wind \((\left[ {{v}_{div}} \right],\left[ {{\omega }_{\varphi }} \right])\). c Difference between the Meridional and Hadley circulations represented by the vectors and the vertical wind (shaded). Only the regions where the statistical significance is above the 95% confidence level are plotted. The vertical winds in vector are scaled by a factor of −150. The unit of \(H\) is 1.0 × 10−6 s−1 and the unit of \({{\psi }_{H}}\) is 1.0 × 109 kg s−1

Full size image
Fig. 4
figure 4

a Climatological mean of the Zonal circulation averaged between 5°S and 5°N for DJF (1979–2013). \(\langle{{\omega }_{W}}\rangle_{5{}^\circ S}^{5{}^\circ N}\) is shaded, \(\left\langle W \right\rangle_{5{}^\circ S}^{5{}^\circ N}\)is in contour and the vectors represent the wind \(\left(\langle{{u}_{W}}\rangle_{5{}^\circ S}^{5{}^\circ N},\langle{{\omega }_{W}}\rangle_{5{}^\circ S}^{5{}^\circ N}\right)\). b Same as a, but for the Walker circulation. \(\langle{{\omega }_{\lambda }}\rangle_{5{}^\circ S}^{5{}^\circ N}\) is shaded, \(\langle{{\psi }_{W}}\rangle_{5{}^\circ S}^{5{}^\circ N}\) is in contour and the vectors represent the wind \(\left(\langle{{u}_{div}}\rangle_{5{}^\circ S}^{5{}^\circ N},\langle{{\omega }_{\lambda }}\rangle_{5{}^\circ S}^{5{}^\circ N}\right)\). c Difference between the Zonal and Walker circulations represented by the vectors and the vertical wind (shaded). Only the regions where the statistical significance is above the 95% confidence level are plotted. The vertical winds in vector are scaled by a factor of −150. The unit of \(W\) is 1.0 × 10−6 s−1 and the unit of \({{\psi }_{W}}\) is 1.0 × 109 kg s−1

Full size image

5 Advantages in representing the local Hadley and Walker circulations

Referring to the studies by Schwendike et al. (2014, 2015), the meridional and zonal components of the vertical velocity are useful for quantitatively studying the local Hadley and Walker circulations. According to Eqs. (18) and (31), the three-pattern decomposition model can decompose the vertical velocity \(\omega ={{P}_{s}}\dot{\sigma }\) into meridional component \({{\omega }_{H}}={{P}_{s}}{{\dot{\sigma }}_{H}}\) and zonal component \({{\omega }_{W}}={{P}_{s}}{{\dot{\sigma }}_{W}}\). In this section, we introduce the advantages of the three-pattern decomposition method in representing the local Hadley and Walker circulations.

Figures 5 and 6 show the climate characteristics of the global (regional) zonal mean of the meridional circulation and the global (regional) meridional mean of the zonal circulation in winter from 1979 to 2013, respectively. In the case of the global zonal average, though \([\omega ]=[{{\omega }_{W}}]+[{{\omega }_{H}}],\) the vertical velocity of zonal circulation is zero, which means that \([{{\omega }_{W}}]=0\), the contribution of the zonal circulation vanishes and \([\omega ]\) contains only \([{{\omega }_{H}}]\) (Fig. 5a, b). Thus, it is appropriate to use \([\omega ]\) to represent the Hadley circulation in the previous studies. Similarly, in the case of the global meridional average (denoted by ‘< >’), though \(\left\langle \omega \right\rangle = \left\langle {\omega _{W} } \right\rangle + \left\langle {\omega _{H} } \right\rangle\), the vertical velocity of the meridional circulation is zero, which means that \(\left\langle {\omega _{H} } \right\rangle = 0\) and the contribution of the meridional circulation vanishes (Fig. 5c, d).

However, the traditional definition of the Walker circulation is often restricted to the tropical Pacific region, and \(\left\langle \omega \right\rangle _{{5^{ \circ } S}}^{{5^{ \circ } N}}\) is used to represent the Walker circulation. In this case, \(\left\langle \omega \right\rangle _{{5^{ \circ } S}}^{{5^{ \circ } N}} = \left\langle {\omega _{H} } \right\rangle _{{5^{ \circ } S}}^{{5^{ \circ } N}} + \left\langle {\omega _{W} } \right\rangle _{{5^{ \circ } S}}^{{5^{ \circ } N}}\) but \(\left\langle {\omega _{H} } \right\rangle _{{5^{ \circ } S}}^{{5^{ \circ } N}} \ne 0\), which means that the contribution of the meridional circulation is included in the vertical velocity of the Walker circulation (Fig. 6d–f). The effect of \(\left\langle {\omega _{H} } \right\rangle _{{5^{ \circ } S}}^{{5^{ \circ } N}}\) on \(\left\langle \omega \right\rangle _{{5^{ \circ } S}}^{{5^{ \circ } N}}\) over the tropical region is notable (Fig. 6f). Thus, it is not accurate to use \(\left\langle\omega \right\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}\) to represent the Walker circulation because \(\left\langle\omega \right\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}\) includes the vertical velocity \(\left\langle{{\omega }_{H}}\right\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}\) of the local Hadley circulation. Similarly, it is not accurate to use \([\omega ]_{{{\lambda }_{1}}}^{{{\lambda }_{2}}}\) to represent the local Hadley circulation for the contribution of the local Walker circulation (Fig. 6a–c). Here, ‘\([\text{ }]_{{{\lambda }_{1}}}^{{{\lambda }_{2}}}\)’ represents the zonal average over the longitudes \({{\lambda }_{1}}\) to \({{\lambda }_{2}}\). Thus, \([{{\omega }_{H}}]_{{{\lambda }_{1}}}^{{{\lambda }_{2}}}\) and \(\left\langle{{\omega }_{W}}\right\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}\) should be used instead of \([\omega ]_{{{\lambda }_{1}}}^{{{\lambda }_{2}}}\) and \(\left\langle\omega \right\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}\) to represent the local Hadley and Walker circulations. The results in summer (see Figs. S17 and S18) exhibit the same characteristics as in winter.

Fig. 5
figure 5

a Climatological mean zonal mean of the meridional circulation for DJF (1979–2013). The vertical velocity \([{{\omega }_{H}}]\) is shaded and the vectors represent the wind \(([{{v}_{H}}],[{{\omega }_{H}}]).\) b Same as a, but for \([\omega ]\) and \(([{{v}_{H}}],[\omega ])\). c Same as a, but for the meridional mean of the zonal circulation. \(\left\langle{{\omega }_{W}}\right\rangle\) is shaded and the vectors represent the wind \((\left\langle{{u}_{W}}\right\rangle,\left\langle{{\omega }_{W}}\right\rangle)\). d Same as c, but for \(\left\langle\omega \right\rangle\) and \((\left\langle{{u}_{W}}\right\rangle,\left\langle\omega \right\rangle)\). The vertical winds in vector are scaled by a factor of −100 for a and b, and −300 for c and d

Full size image
Fig. 6
figure 6

a Climatological mean of the regional meridional circulation for DJF (1979–2013). The vertical velocity \([{{\omega }_{H}}]_{{{60}^{\circ }}E}^{{{140}^{\circ }}E}\) is shaded and the vectors represent the wind \(([{{v}_{H}}]_{{{60}^{\circ }}E}^{{{140}^{\circ }}E},[{{\omega }_{H}}]_{{{60}^{\circ }}E}^{{{140}^{\circ }}E})\). b Same as a, but for \([\omega ]_{{{60}^{\circ }}E}^{{{140}^{\circ }}E}\) and \(([{{v}_{H}}]_{{{60}^{\circ }}E}^{{{140}^{\circ }}E},[\omega ]_{{{60}^{\circ }}E}^{{{140}^{\circ }}E})\). c The vertical velocity \([{{\omega }_{W}}]_{{{60}^{\circ }}E}^{{{140}^{\circ }}E}\) is shaded. d Same as a, but for the meridional mean of the regional zonal circulation. \(\left\langle{{\omega }_{W}}\right\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}\) is shaded and the vectors represent the wind \((\left\langle{{u}_{W}}\right\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N},\left\langle{{\omega }_{W}}\right\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N})\). e Same as d, but for \(\left\langle\omega \right\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}\) and \((\left\langle{{u}_{W}}\right\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N},\langle \omega \rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N})\). f The vertical velocity \(\left\langle{{\omega }_{H}}\right\rangle_{{{5}^{\circ }}S}^{{{5}^{\circ }}N}\) is shaded. The vertical winds in vector are scaled by a factor of −120

Full size image

6 Summary

The main purpose of this study is to analyze the essential differences and connections between the three-pattern decomposition of the global atmospheric circulation, the representation method of the horizontal vortex circulation in the middle–high latitudes and the local partitioning of the overturning circulation in the tropics. We conclude that the latter two available methods are based on the traditional 2D decomposition of the vortex and divergent circulations in the fluid dynamics. The three-pattern decomposition model is not a simple superposition of the representation methods of the horizontal vortex circulation at middle–high latitudes and the overturning circulations in the tropics. Instead, it is a new 3D decomposition method of the global atmospheric circulation.

Because the traditional 2D decomposition methods must restrict the motions on a pressure surface through the 2D Poisson Eq. (37), they decompose the horizontal velocity into divergent wind \({{\vec{V}}_{div}}\) (irrotational) and vortex wind \({{\vec{V}}_{rot}}\) (nondivergent) such that \({{\vec{V}}_{rot}}\) has the total value of the vertical vorticity \(\zeta\) on the given pressure surface. The traditional 2D decomposition methods cannot separate the contributions of the divergent motions from the total vertical vorticity \(\zeta\). However, through the 3D Poisson Eq. (38), the three-pattern decomposition method can quantitatively decompose the vertical vorticity \(\zeta\) into two components: \({{\Delta }_{2}}R\) and \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\), where \({{\Delta }_{2}}R\) denotes the vertical vorticity of the horizontal circulation \({{{\vec{V}}'}_{R}}\) and \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\) is the vertical vorticity of the divergent motions \({{{u}'}_{W}}\) and \({{{v}'}_{H}}\). \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\) is the main cause of the differences between the three-pattern circulations and traditional circulations.

The effect of \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\) cannot be ignored at 850 and 200 hPa. However, it equals approximately zero at 500 hPa and the vertical mean surface. This corresponds to the classic theory that the motion at 500 hPa is quasi-horizontal and nondivergent and can be used to represent the mean state of the entire atmospheric layer. The three-pattern decomposition model reduces to the traditional 2D decomposition procedure when \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}=0\). This emphasizes that the three-pattern decomposition of the global atmospheric circulation can be considered a generalization of the representation method of the horizontal vortex circulation at middle–high latitudes and the local partitioning of the overturning circulation in the tropics.

The comparison of the climate characteristics of the traditional mass stream functions and the stream functions derived from the three-pattern decomposition model shows that the spatial patterns of the three-pattern circulations are similar to that of the traditional circulations. The differences between the horizontal and Rossby circulations are mainly presented as the differences in the zonal wind, especially the differences in the west wind at 850 hPa and the east wind at 200 hPa. However, because the effect of \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\) is weakened by the global zonal mean process, the meridional circulation is nearly equal to Hadley circulation except a system south shift of the anomalous circulation. Since the differences in the zonal winds are significant than that in the meridional winds, the zonal and Walker circulations in the tropics have more notable differences than the global zonal mean meridional circulation and Hadley circulation.

Like the studies of Schwendike et al. (2014, 2015), the three-pattern decomposition model can also effectively separate the vertical velocities of the meridional and zonal circulations from the total vertical velocity. Compared with the zonal or meridional mean of the total velocities, the three-pattern decomposition model more accurately represents the regional vertical circulations, particularly the local Hadley and Walker circulations.

The vertical vorticitiy \(\frac{{{\partial }^{2}}R}{\partial {{\sigma }^{2}}}\) caused by the divergent motions can also be decomposed into the vertical vorticitiy \({{\zeta }_{H}}\) of the meridional circulation \({{{\vec{V}}'}_{H}}\) and the vertical vorticitiy \({{\zeta }_{W}}\) of the zonal circulation \({{{\vec{V}}'}_{W}}\), then the three-pattern decomposition model actually decomposes the vertical vorticity \(\zeta\) into three components: \(\zeta ={{\zeta }_{R}}+{{\zeta }_{H}}+{{\zeta }_{W}}\). The vertical vorticitiy decomposition is useful for quantitatively studying the effects of the horizontal circulation \({{{\vec{V}}'}_{R}}\), meridional circulation \({{{\vec{V}}'}_{H}}\) and zonal circulation \({{{\vec{V}}'}_{W}}\) on the evolution of the vertical vorticity \(\zeta\). In the future, we will fit the three components \({{\zeta }_{R}}\), \({{\zeta }_{H}}\) and \({{\zeta }_{W}}\) into the vertical vorticity equation to analyze the source terms that change the circulations \({{{\vec{V}}'}_{R}}\), \({{{\vec{V}}'}_{H}}\) and \({{{\vec{V}}'}_{W}}\) and to study the interaction mechanisms of these large-scale circulations.