A Bayesian statistical model for deriving the predictive distribution of hydroclimatic variables

Abstract

Recent publications have provided evidence that hydrological processes exhibit a scaling behaviour, also known as the Hurst phenomenon. An appropriate way to model this behaviour is to use the Hurst-Kolmogorov stochastic process. The Hurst-Kolmogorov process entails high autocorrelations even for large lags, as well as high variability even at climatic scales. A problem that, thus, arises is how to incorporate the observed past hydroclimatic data in deriving the predictive distribution of hydroclimatic processes at climatic time scales. Here with the use of Bayesian techniques we create a framework to solve the aforementioned problem. We assume that there is no prior information for the parameters of the process and use a non-informative prior distribution. We apply this method with real-world data to derive the posterior distribution of the parameters and the posterior predictive distribution of various 30-year moving average climatic variables. The marginal distributions we examine are the normal and the truncated normal (for nonnegative variables). We also compare the results with two alternative models, one that assumes independence in time and one with Markovian dependence, and the results are dramatically different. The conclusion is that this framework is appropriate for the prediction of future hydroclimatic variables conditional on the observations.

1 Introduction

A lot of work has been done in predicting the future of hydroclimatic processes using Bayesian statistics. Berliner et al. (2000) applied a Markov model to a low-order dynamical system of tropical Pacific SST, using a hierarchical Bayesian dynamical modelling, which led to realistic error bounds on forecasts. Duan et al. (2007) illustrated how the Bayesian model averaging (BMA) scheme can be used to generate probabilistic hydrologic predictions from several competing individual predictions. Kumar and Maity (2008) used two different Bayesian dynamic modelling approaches, namely a constant model and a dynamic regression model (DRM) to forecast the volume of the Devil’s lake. Maity and Kumar (2006) used a Bayesian dynamic linear model to predict the monthly Indian summer monsoon rainfall. Bakker and Hurk (2012) used a Bayesian model to predict multi-year geostrophic winds.

On the other hand, climate models (i.e. general circulation models—GCMs) give deterministic projections of future hydroclimatic processes for some hypothesized scenarios e.g. for the increase of CO₂ concentration, etc. However, the uncertainty of these projections whose sources may be attributed to insufficient current understanding of climatic mechanisms, to inevitable weaknesses of numerical climatic and hydrologic models to represent processes and scales of interest, to complexity of processes and to unpredictability of causes (Koutsoyiannis et al. 2007), is not estimated by these models. Consequently, it is impossible to estimate whether any observed changes reflect the natural variability of the climatic processes or should be attributed to external forcings. Additionally, using deterministic projections and thus neglecting the uncertainty in future hydroclimatic conditions, may result in underestimation of possible range of the future hydroclimatic variation.

Koutsoyiannis et al. (2007) have done some work on the uncertainty assessment of future hydroclimatic predictions. They propose a stochastic framework for future climatic uncertainty, where climate is expressed by the 30-year time average of a natural process exhibiting a scaling behaviour, also known as the Hurst phenomenon or Hurst-Kolmogorov (HK) behaviour (Hurst 1951; Koutsoyiannis et al. 2008). To this end, they combine analytical and Monte Carlo methods to determine uncertainty limits and they apply the framework developed to temperature, rainfall and runoff data from a catchment in Greece, for which measurements are available for about a century.

In the study by Koutsoyiannis et al. (2007), the climatic variability and the influence of parameter uncertainty are studied separately. As a result, a hydroclimatic prediction needs two confidence coefficients to be defined, one referring to the uncertainty of the climatic evolution and one to the uncertainty of model parameters. In this paper we unify the study of the two uncertainties so that a climatic prediction needs only one confidence coefficient to be defined. To this end, we solve the problem of climatic predictions of natural processes using Bayesian statistics, instead of the stochastic framework developed by Koutsoyiannis et al. (2007). For physical consistency with natural processes such as rainfall and runoff, whose values are nonnegative, we also examine the case where truncation of the negative part of the distributions is applied. No prior information for the parameters of processes is assumed, so that the prior distribution is non-informative. The posterior joint distribution is derived from a mixture for the case where truncation is not applied and a Gibbs sampler for the case where truncation is applied. We derive the posterior predictive distribution (Gelman et al. 2004, p. 8) of the process in closed form given the posterior distribution of the parameters. We simulate a sample from the posterior predictive distribution and use it to make inference about the future evolution of the averaged process. We apply this procedure using the same data as in Koutsoyiannis et al. (2007), and specifically runoff (Case 1 or C1), rainfall (C2) and temperature (C3) data from catchments in Greece and temperature data from Berlin (C4, C6 with the last 90 years excluded from the dataset); in addition we used temperature data from Vienna (C5, C7 with the last 90 years excluded from the dataset). For the rainfall and runoff data we use truncated distributions.

As per the temporal dependence of the processes, three alternative assumptions are made: (a) independence in time; (b) Markovian dependence modelled by first-order autoregressive [AR(1)] process; and (c) HK dependence (see Markonis and Koutsoyiannis 2013, for a justification of the latter). In the last section we compare the results of the three models. Additional results such as the posterior distributions of the parameters and the asymptotic behaviour of the predictive distribution are also given.

While this paper uses the same case studies as those in Koutsoyiannis et al. (2007), the results of the two papers are not directly comparable to each other. Here we give posterior predictive distributions of the climatic variables, whereas Koutsoyiannis et al. (2007) give confidence limits for specified quantiles of climatic variables. The posterior predictive distribution of the variables given here is exactly what we call climatic prediction, whereas we could say that the confidence limits of the quantiles, given by Koutsoyiannis et al. (2007), are intermediate or indirect results. The Bayesian methodology applied here aims at (stochastic) prediction (Robert 2007, p. 7) and is direct, while its disadvantage compared to Koutsoyiannis et al. (2007) framework is the much heavier computational burden.

2 Definition of AR(1) and HK process

We use the Dutch convention for notation, according to which random variables and stochastic processes are underlined (Hemelrijk 1966). We assume that {x _t }, t = 1, 2,… is a normal stationary stochastic process with mean μ := E[x _t ], standard deviation $\sigma \;:= \sqrt {{\text{Var}}[\underline{x} _{{t}}]}$, autocovariance function γ _k := Cov[x _t , x _{t + k} ] and autocorrelation function (ACF) ρ _k := Corr[x _t , x _{t + k} ] = γ _k /γ ₀ (k = 0, ±1, ±2,…) and that there is a record of n observations x _n  = (x ₁… x _n )^T. Each observation x _t represents a realization of a random variable x _t , so that x _n is a realization of the vector of random variables x _n  = (x ₁…x _n )^T.

We assume that {a _t } is a zero mean normal white noise process (WN), i.e. a sequence of independent random variables from a normal distribution with mean E[a _t ] = 0 and variance Var[a _t ] = $\sigma_{a}^{2}$. In the following discussion {a _t } is always referred to as WN. The following equation defines the first-order autoregressive process AR(1).

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{{t}} - \mu = \varphi_{ 1} \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{{{{t}} - 1}} - \mu } \right) \, + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{{t}} ,\quad \, \left| {\varphi_{ 1} } \right| \, < { 1} $$

(1)

The ACF of the AR(1) is (Wei 2006, p. 34)

$$ \rho_{k} = \varphi_{1}^{k} ,\quad k = \, 0,{ 1}, \ldots $$

(2)

Let κ be a positive integer that represents a timescale larger than 1, the original time scale of the process x _t . The averaged stochastic process on that timescale is denoted as

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{t}^{(\kappa )} := (1/\kappa )\sum\limits_{l = (t - 1)\kappa + 1}^{t\kappa } {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_l} $$

(3)

The notation implies that a superscript (1) could be omitted, i.e. $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{t}^{(1)} \equiv \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{t}$. Now we consider the following equation that defines the Hurst-Kolmogorov stochastic process (HKp). (Koutsoyiannis 2003)

$$ (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} _{i}^{(\kappa )} - \mu ) {\mathop = \limits ^{\text d}} \left( {\frac{\kappa }{\lambda }} \right)^{H - 1} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{j}^{(\lambda )} - \mu ),\quad 0 < H < 1,\quad i,j = 1,2, \ldots {\text{ and}}\;\kappa ,\lambda \ge 1 $$

(4)

where H is the Hurst parameter.

The ACF of the HKp is (Koutsoyiannis 2003)

$$ \rho_{k} = \, \left| {k + { 1}} \right|^{ 2H} /{ 2 } + \, \left| {k - 1} \right|^{ 2H} /{ 2} - \left| k \right|^{ 2H} ,\quad k = \, 0,{ 1}, \ldots $$

(5)

and does not depend on averaging time scale κ.

3 Posterior distribution of the parameters of a stationary normal stochastic process

The distribution of the variable x _n  = (x ₁…x _n )^T is

$$ f\left( {\varvec{x}_{n} |\varvec{\theta}} \right) \, = \, \left( {2{{\uppi}}} \right)^{ - n/2} \left| {\sigma^{2} \varvec{R}_{n} } \right|^{ - 1/2} \exp [\left( { - 1/2\sigma^{2} } \right) \, \left( {\varvec{x}_{n} - \mu \varvec{e}_{n} } \right)^{\rm T} \varvec{R}_{n}^{ - 1} \left( {\varvec{x}_{n} - \mu \varvec{e}_{n} } \right)] $$

(6)

where R _n is the autocorrelation matrix with elements r _ij  = ρ _|i−j|, i,j = 1,2,…,n and e _n  = (1 1…1)^T is a vector with n elements. Details on the distributions used thereafter are given in Appendix 1. The autocorrelation ρ _|i−j| is assumed to be function of a parameter (scalar or vector) φ, so that θ := (μ, σ ², φ) is the parameter vector of the process. We note that if x _n is white noise then ρ ₀ = 1 and ρ _k  = 0, k = 1, 2,…; if it is AR(1) then ρ _k is given by (2) if it is HKp then ρ _k is given by (5).

We assume that φ is uniformly distributed a priori. We set as prior distribution for θ the non-informative distribution (see also Robert 2007, example 3.5.6)

$$ \pi \left(\varvec{\theta}\right) \propto 1/\sigma^{2} $$

(7)

(notice that we generally use the symbol π for probability density functions of parameters).

The posterior distribution of the parameters does not have a closed form. However it can be calculated from a mixture based on conditional distributions. Specifically, it is shown (see Appendix 2) that

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}} {\mu} |\sigma^{2} ,\varvec{\varphi },\varvec{x}_{n} \sim N\left[ {(\varvec{x}_{n}^{\text{T}} \varvec{R} _{n}^{ - 1} \varvec{e}_{n} )/(\varvec{e}_{n}^{\text{T}} \varvec{R} _{n}^{ - 1} \varvec{e}_{n} ),\sigma^{2} /(\varvec{e}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} )} \right] $$

(8)

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}} {\sigma}^{ 2} |\varvec{\varphi },\varvec{x}_{n} \sim {\text{Inv-gamma}}\left\{ {\left( {n - 1} \right)/ 2, \, \left[ {\varvec{e}_{n}^{\text{T}} \varvec{ R}_{n}^{ - 1} \varvec{e}_{n} \varvec{x}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{x}_{n} - \left( {\varvec{x}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} } \right)^{ 2} } \right]/\left( { 2\;\varvec{e} _{n}^{\text{T}} \varvec{R} _{n}^{ - 1} \varvec{e}_{n} } \right)} \right\} $$

(9)

$$ \pi (\varvec{\varphi }|\varvec{x}_{n} ) \propto \left| {\varvec{R}_{n} } \right|^{ - 1/ 2} \left[ {\varvec{e}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} \varvec{x}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{x}_{n} - (\varvec{x} _{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} )^{ 2} } \right]^{ - (n - 1)/ 2} \left( {\varvec{e}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} } \right)^{n/ 2- 1} $$

(10)

As real world problems often impose upper or lower bounds on the variables x _t , we assume that the distribution of x _n is two-sided truncated by bounds a and b, i.e.,

$$ f\left( {\varvec{x}_{n} |\varvec{\theta}} \right) \propto { \exp }[\left( { - 1/ 2\sigma^{ 2} } \right) \, \left( {\varvec{x}_{n} - \mu \varvec{e}_{n} } \right)^{\rm T} \varvec{R}_{n}^{ - 1} \left( {\varvec{x}_{n} - \mu \varvec{e}_{n} } \right)]{\text{ I}}_{{[a,b]^{n} }} \left( {x_{ 1} , \ldots ,x_{n} } \right) $$

(11)

where I denotes the indicator function, so that ${\text{I}}_{{[a,b]^{n} }}$ (x ₁,…,x _n ) = 1 if x _n ∈ [a, b]ⁿ and 0 otherwise.

We assume that the truncation set of μ is [a, b], a, b ∈ R∪{−∞,∞}. The following Gibbs sampler is used to obtain a posterior sample from θ = (μ, σ ², φ) (see Appendix 2).

$$ \pi (\mu |\sigma^{ 2} ,\varvec{\varphi },\varvec{x}_{n} ) \propto { \exp }\left\{ { - \left[ {\mu - \left( {\varvec{x} _{n}^{\text{T}} \varvec{R} _{n}^{ - 1} \varvec{e}_{n} } \right)/\left( {\varvec{e}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} } \right)} \right]^{ 2} /\left( { 2\sigma^{ 2} /\varvec{e}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} } \right)} \right\}{\text{ I}}_{[a,b]} (\mu ) $$

(12)

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }^{ 2} |\mu ,\varvec{\varphi },\varvec{x}_{n} \sim {\text{Inv-gamma}}\left\{ {n/ 2, \, \left( {\varvec{x}_{n} - \mu \varvec{e}_{n} } \right)^{\text{T}} \varvec{R}_{n}^{-1} \left( {x_{n} - \mu \varvec{e}_{n} } \right)/ 2} \right\} $$

(13)

$$ \pi \left( {\varvec{\varphi }|\mu ,{\sigma^2} ,\varvec{x}_{n} } \right) \propto \left| {\varvec{R}_{n} } \right|^{ - 1/ 2} { \exp }\left[ { - (\varvec{x}_{n} - \mu \varvec{e}_{n} )^{\text{T}} \varvec{R}_{n}^{ - 1} (x_{n} - \mu \varvec{e}_{n} )/ 2\sigma^{ 2} } \right] $$

(14)

4 Posterior predictive distributions

As we stated in the Introduction, we seek to make an inference about the future evolution of a process given observations of its past. To this end, in this section we derive the posterior predictive distributions of x _n+1,n+m |x _n for the cases of the white noise, the AR(1) and the HKp, where x _n+1,n+m := (x _n+1,…,x _n+m )^T.

4.1 White noise

We assume that x _t , t = 1, 2,… is white noise, with f(x _t |μ,σ ²) = (2πσ ²)^−1/2 exp[− (x _t  − μ)²/(2σ ²)]. A non-informative prior distribution for θ = (μ,σ ²) is π(θ) ∝ 1/σ ². The posterior distributions of the parameters are given by (Gelman et al. 2004, p. 75–77)

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu } |\varvec{x}_{n} \sim {\text{ t}}_{n - 1} \left( {\bar{x}_{n} ,s_{n}^{2} /(n - 1)} \right) $$

(15)

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma }^{ 2} |\varvec{x}_{n} \sim {\text{ Inv-gamma}}\left( {(n - 1)/ 2,n \, s_{n}^{2} /{ 2}} \right) $$

(16)

Notice that (15) and (16) are derived from (8), (9), (10) for R _n  = I _n (the former after integrating out σ ²). The posterior predictive distribution is

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{t} |\varvec{x}_{n} \sim t_{n - 1} (\bar{x}_{n} ,\left( {(n + 1)/(n - 1)} \right)s_{n}^{2} ),\quad t = n + 1,n + 2, \ldots $$

(17)

where x _n+1, x _n+2,… are mutually independent,

$$ \bar{x}_{n} := \sum\limits_{i = 1}^{n} {x_i/n} $$

(18)

$$ s_{n}^{2} := \sum\limits_{i = 1}^{n} {(x_i - \bar{x}_n)}^{2} /n $$

(19)

are the maximum likelihood estimates of μ and σ ² respectively and t _v (μ,σ ²) is the Student’s distribution with v degrees of freedom.

4.2 AR(1) and HKp

When there is dependence among the elements of x _n+m , the posterior predictive distribution of x _n+1,n+m given θ and x _n is (Eaton 1983, p. 116, 117)

$$ f\left( {\varvec{x}_{n + 1,n + m} |\varvec{\theta},\varvec{x}_{n} } \right) \, = \, \left( {2\pi \sigma^{2} } \right)^{ - m/2} \left| {\varvec{R}_{m|n} } \right|^{ - 1/2} \exp \left[ {\left( { - 1/2\sigma^{2} } \right) \, \left( {\varvec{x}_{n + 1,n + m} -\varvec{\mu}_{m|n} } \right)^{\text{T}} \varvec{R}_{m|n}^{ - 1} \left( {\varvec{x}_{n + 1,n + m} -\varvec{\mu}_{m|n} } \right)} \right] $$

(20)

where μ _m|n and R _m|n are given by:

$$ \varvec{\mu}_{m|n} = \mu \varvec{e}_{m} + \varvec{R}_{{\left[ {\left( {n + 1} \right):\left( {n + m} \right)} \right] \, [ 1:n]}} \varvec{R}_{n}^{ - 1} \left( {\varvec{x}_{n} - \mu \varvec{e}_{n} } \right) $$

(21)

$$ \varvec{R}_{m|n} = \varvec{R}_{{\left[ {\left( {n + 1} \right):\left( {n + m} \right)} \right] \, \left[ {\left( {n + 1} \right):(n + m)} \right]}} - {\varvec{R}^{\text T}_{{\left[ {1:n} \right]\left[ {\left( {n + 1} \right):\left( {n + m} \right)} \right]}}} \varvec{R}_{n}^{ - 1} \varvec{R}_{{\left[ { 1:n} \right]\left[ {\left( {n + 1} \right):(n + m)} \right]}} $$

(22)

where R _{[k:l] [m:n]} is the submatrix of R which contains the elements r _ij , k ≤ i ≤ l, m ≤ j ≤ n, whereas the notation R _{[1:n] [1:n]} with identical subscripts [1:n] can be simplified to R _n as defined above. The elements of the correlation matrices R _n and R _m+n are obtained from (2) for the case of the AR(1) and from (5) for the case of HKp. In the implementation of the AR(1) model we assume that all three parameters μ, σ, φ ₁ are unknown. For the HKp we examine two cases: (a) all three parameters μ, σ, H, are unknown, and (b) μ, σ, are unknown but H is considered to be known and equal to its maximum likelihood estimate (Tyralis and Koutsoyiannis 2011).

In the case that all three parameters of the AR(1) or HKp are unknown, we obtain a simulated sample of θ from (8), (9), (10) and use this sample to simulate μ _m|n and R _m|n from (21) and (22) and generate a sample of x _n+1,n+m from (20). In the case where H is considered as known, we obtain a simulated sample of θ = (μ, σ ²) from (8), (9) and use this sample to simulate μ _m|n and R _m|n from (21) and (22) and generate a sample of x _n+1,n+m from (20).

4.3 Asymptotic behaviour of AR(1) and HKp

In most applications, it is useful to know the ultimate confidence regions as prediction horizon tends to infinity. This is expressed by the distribution of x _n+m+1,n+m+l := (x _n+m+1,…,x _n+m+l ) as m → ∞, conditional on x _n . For given θ this distribution is:

$$ f\left( {\varvec{x}_{n + m + 1,n + m + l} |\varvec{\theta},\varvec{x}_{n} } \right) \, = \, \left( { 2\pi \sigma^{ 2} } \right)^{-l/ 2} \left| {\varvec{R}_{l|n} } \right|^{ - 1/ 2} { \exp }\left[ {\left( { - 1/ 2\sigma^{ 2} } \right)\left( {\varvec{x}_{n + m + 1,n + m + l} -\varvec{\mu}_{l|n} } \right)^{\text{T}} \varvec{R}_{l|n}^{ - 1} \left( {\varvec{x}_{n + m + 1,n + m + l} -\varvec{\mu}_{l|n} } \right)} \right] $$

(23)

where μ _l|n and R _l|n are given by:

$$ \varvec{\mu}_{l|n} = \mu \varvec{e}_{l} + \varvec{R}_{{\left[ {\left( {n + m + 1} \right):\left( {n + m + l} \right)} \right] \, [ 1:n]}} \varvec{R}_{n}^{ - 1} \left( {\varvec{x}_{n} - \mu \varvec{e}_{n} } \right) $$

(24)

$$ \varvec{R}_{l|n} = \varvec{R}_{{\left[ {\left( {n + m + 1} \right):\left( {n + m + l} \right)} \right] \, \left[ {\left( {n + m + 1} \right):(n + m + l)} \right]}} - \varvec{R}_{{\left[ {1:n} \right]\left[ {\left( {n + m + 1} \right):(n + m + l)} \right]}}^{\text{T}} \varvec{R} _{n}^{ - 1} \varvec{R}_{{\left[ { 1:n} \right] \, \left[ {\left( {n + m + 1} \right):(n + m + l)} \right]}} $$

(25)

We observe that, as m → ∞, R _{[1:n] [(n+m+1):(n+m+l)]} and R _{[(n+m+1):(n+m+l)] [1:n]} become zero matrices and R _{[(n+m+1):(n+m+l)] [(n+m+1):(n+m+l)]} = R _l . This implies that:

$$ \varvec{\mu}_{l|n} = \mu \varvec{e}_{l} $$

(26)

$$ \varvec{R}_{l|n} = \varvec{R}_{l} $$

(27)

where R _l is again obtained from (2) for the case of the AR(1) and from (5) for the case of HKp.

Accordingly, the application can proceed as follows. We obtain a simulated sample of θ from (8), (9), (10) and use this sample to simulate μ _l|n and R _l|n from (26) and (27) and generate a sample of x _n+m+1,n+m+l from (23) for a large m.

4.4 Truncated white noise, AR(1) and HKp

To examine real world problems which often impose upper or lower bounds on the variables x _t , we assume that the distribution of x _n is two-sided truncated, and is given by (11). We obtain a posterior sample of θ using the Gibbs sampler defined by (12), (13), (14). When φ is known, we obtain a posterior sample of (μ,σ ²) using the Gibbs sampler defined by (12) and (13). Then x _m |θ follows a truncated normal multivariate distribution and according to Horrace (2005) the conditional multivariate distributions of x _n+1,n+m |θ,x _n are again truncated normal. As a result (20) still holds after slight modifications and (21), (22) are valid. The posterior predictive distribution of x _n+1,n+m |θ,x _n is then a multivariate truncated normal distribution:

$$ f\left( {\varvec{x}_{n + 1,n + m} |\varvec{\theta},\varvec{x}_{n} } \right) \propto { \exp }\left[ {\left( { - 1/ 2\sigma^{ 2} } \right) \, \left( {\varvec{x}_{n + 1,n + m} -\varvec{\mu}_{m|n} } \right)^{\text{T}} \varvec{R}_{m| n}^{ - 1} \left( {\varvec{x}_{n + 1,n + m} -\varvec{\mu}_{m|n} } \right)} \right]{\text{ I}}_{{ [ {{a,b]}}^{{m}} }} \left( {\varvec{x}_{n + 1,n + m} } \right) $$

(28)

Now for the case of white noise, (15), (16) and (17) are not valid. But from (21), (22) and for ρ ₀ = 1 and ρ _k  = 0, k = 1, 2,…, we obtain that μ _m|n  = μ e _m and R _m|n  = R _m .

When looking for the asymptotic behaviour of the process, (23) still holds after slight modifications, according to Horrace (2005). As a result, the distribution of x _n+m+1,n+m+l |θ,x _n is truncated multivariate normal, while (26) and (27) remain valid:

$$ f\left( {\varvec{x}_{n + m + 1,n + m + l} |\varvec{\theta},\varvec{x}_{n} } \right) \propto { \exp }\left[ {\left( { - 1/ 2\sigma^{ 2} } \right)\left( {\varvec{x}_{n + m + 1,n + m + l} -\varvec{\mu}_{l|n} } \right)^{\text{T}} \varvec{R}_{l|n}^{ - 1} \left( {\varvec{x}_{n + m + 1,n + m + l} -\varvec{\mu}_{l|n} } \right)} \right]{\text{ I}}_{{ [ {{a,b]}}^{l} }} \left( {\varvec{x}_{n + m + 1,n + m + l} } \right) $$

(29)

4.5 Asymptotic convergence of MCMC

To simulate from (10) we use a random walk Metropolis–Hastings algorithm with a normal instrumental (or proposal) distribution (Robert and Casella 2004, p. 271). We implement the algorithm using the function MCMCmetrop1R of the R package ‘MCMCpack’ (Martin et al. 2011). The variable ‘burnin’ in this package is given the value 0, whereas the other variables keep their default values.

There are a lot of methods to decide whether convergence can be assumed to hold for the generated sample (see Gamerman and Lopes 2006, p. 157–169; Robert and Casella 2004, p. 272–276). We use the methods of Heidelberger and Welch (1983) and Raftery and Lewis (1992). These methods are described by Smith (2007), whose notation we use here. We use the R package ‘coda’ (Plummer et al. 2011) to implement these methods. We assume that we have obtained a sample ψ ₁, ψ ₂…, of a scalar variable φ using the MCMC algorithm.

The diagnostic of Heidelberger’s method provides an estimate of the number of samples that should be discarded as a burn-in sequence and a formal test for non-convergence. The null hypothesis of convergence to a stationary chain is based on Brownian bridge theory and uses the Cramer-von-Mises test statistic $\int_{0}^{1} {B_{n} (t)^{2} dt}$, where

$$ B_{n} \left( t \right) = \left( {T_{{\left\lfloor {nt} \right\rfloor }} - \left\lfloor {nt} \right\rfloor \bar{\psi }} \right)/\sqrt {nS(0)} $$

(30)

$$ T_{k} = \sum\limits_{j = 1}^{k} {\psi_{j} } ,\quad k = { 1},{ 2}, \ldots {\text{ and}}\;T_{0} = \, 0 $$

(31)

where $\left\lfloor x \right\rfloor$ denotes the floor of x (the greatest integer not greater than x) and S(0) is the spectral density evaluated at frequency zero. In calculating the test statistic, the spectral density is estimated from the second half of the original chain. If the null hypothesis is rejected, then the first 0.1n of the samples are discarded and the test is reapplied to the resulting chain. This process is repeated until the test is either non-significant or 50 % of the samples have been discarded, at which point the chain is declared to be non-stationary. For more details see Smith (2007).

The methods of Raftery and Lewis are designed to estimate the number of MCMC samples needed when quantiles are the posterior summaries of interest. Their diagnostic is applicable for the univariate analysis of a single parameter and chain. For instance, let us consider the estimation of the following posterior probability of a model parameter θ:

$$ P\left( {f\left( \theta \right) \, < a|\varvec{x}} \right) \, = q $$

(32)

where x denotes the observed data. Raftery and Lewis sought to determine the number of MCMC samples to generate and the number of samples to discard in order to estimate q to within ±r with probability s. In practice, users specify the values of q, r and s to be used in applying the diagnostic (For more details see Smith 2007).

To simulate from (14) we use an accept-reject algorithm (Robert and Casella 2004, p. 51–53) with a uniform instrumental density. Simulation from (12) and (13) is trivial. We assess the convergence of the chain simulated from (12), (13), (14) using the method of Gelman and Rubin (1992; see also Gelman 1996; Gamerman and Lopes 2006, p. 166–168). An indicator of convergence is formed by the estimator of a potential scale reduction (PSR) that is always larger than 1. Convergence can be evaluated by the proximity of PSR to 1. Gelman (1996) suggested accepting convergence when the value of PSR is below 1.2.

5 Case studies

In this section we apply the methodology developed in the previous sections to five historical datasets; three of them obtained from the Boeoticos Kephisos River basin, one from Berlin and one from Vienna. The choice of these datasets was dictated by the fact that they have been also studied in other works with similar objectives, i.e. Koutsoyiannis et al. (2007) and Koutsoyiannis (2011), so that the interested reader can make some comparisons. We present the results of the application of the methodology to the aforementioned datasets.

5.1 Historical datasets

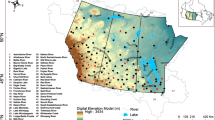
The first case study is performed on an important catchment in Greece, which is part of the water supply system of Athens and has a history, as regards hydraulic infrastructure and management that extends backward at least 3,500 years. This is the closed (i.e. without outlet to the sea) basin of the Boeoticos Kephisos River (Fig. 1), with an area of 1,955.6 km², mostly formed over a karstic subsurface. Owing to its importance for irrigation and water supply, data availability for the catchment extends for about 100 years (the longest dataset in Greece) and modelling attempts with good performance have already been carried out on the hydrosystem (Rozos et al. 2004).

Fig. 1

The Boeoticos Kephisos River basin

The long-term dataset for the basin extends from 1908 to 2003 and comprises a flow record at the river outlet at the Karditsa station (C1), rainfall observations in the raingage Aliartos (C2) and a temperature record at the same station (C3); the station locations are shown in Fig. 1. Further details on the construction of these datasets are given by Koutsoyiannis et al. (2007). The relatively long records have already made it possible to identify the scaling behaviour of rainfall and runoff in this basin (Koutsoyiannis 2003), and make the catchment ideal for a case study of uncertainty assessment.

The two other datasets which we use are the mean annual temperature record of Berlin/Templehof and Vienna, two of the longest series of instrumental meteorological observations. For further details on the Berlin mean annual temperature dataset see Koutsoyiannis et al. (2007) and for the Vienna mean annual temperature dataset see Koutsoyiannis (2011). We examine two cases. In the first case we assume that the update of the prior information is done (C4, C5), using the whole dataset. In the second case the update is done excluding the last 90 years of the datasets (C6, C7).

5.2 Application of the method

We classified the data into three classes, the first containing the data from the Boeoticos Kephisos River basin (C1–C3), the second containing the data from Berlin and Vienna (C4, C6) and the third containing again the data from Berlin and Vienna (C5, C7) but excluding the last 90 years. In the third case the posterior results were compared to the actual 90 last years.

First we calculated the maximum likelihood estimates of the parameters for all the examined cases (WN, AR(1), HKp). The results are given in Tables 1, 2. Truncated models were used for C1 and C2 datasets due to the relatively high estimated σ which otherwise would result in negative values. Instead, when we examined the temperature datasets (C3–C7), simulated values near the absolute zero never appeared, indicating a good behaviour of the non-truncated model.

Table 1 Summarized results and maximum likelihood estimates for the cases of WN, AR(1) and HKp at Boeoticos Kephisos River basin

Table 2 Summarized results and maximum likelihood estimates for the cases of WN, AR(1) and HKp at Berlin and Vienna

The procedure for the temperature datasets is described below. We used (15) and (16) to generate a posterior sample from μ and σ ² for the WN case. To simulate from (10) for the φ ₁ and H posterior distribution of the AR(1) and HK cases correspondingly, we used a random walk Metropolis–Hastings algorithm. We simulated a single chain with 3,000,000 MCMC samples. The Metropolis acceptance rates are given in Table 3. To decide whether convergence has been achieved, we used the Heidelberger and Welch method (1983). We tested four cases, the first case containing all the 3,000,000 samples, the second containing the last 2,000,000 samples and so forth. The results are presented in Tables 4, 5, from where we conclude that stationary chain hypothesis holds in every case. We also used the methods of Raftery and Lewis (1992), to estimate the number of MCMC samples needed when quantiles are the posterior summaries of interest. The minimum number of samples and the burn-in period for the simulation is given in Tables 6, 7, where q = 0.025, 0.500, 0.975 are the quantiles to be estimated, r = 0.005 is the desired margin of error of the estimate and s = 0.95 is the probability of obtaining an estimate in the interval (q − r, q + r). We decided to use the last 2,000,000 samples of the chains, to obtain the histograms of the posterior distributions of the parameters φ ₁ and H. The simulation of μ, σ ² from (8) and (9) is then trivial. Summarized results for the parameters of the AR(1) and HK cases respectively are shown in Tables 8, 9.

Table 3 Metropolis acceptance rate for the MCMC simulation of φ ₁ and H, respectively, at Boeoticos Kephisos River basin

Table 4 Heidelberger and Welch test, for significance level 0.05, at Boeoticos Kephisos River basin

Table 5 Heidelberger and Welch test, for significance level 0.05, at Berlin and Vienna

Table 6 Raftery and Lewis test for the case of Boeoticos Kephisos River basin

Table 7 Raftery and Lewis test for the cases of Berlin and Vienna

Table 8 Summary results for the parameters of the AR(1) and HK cases at Boeoticos Kephisos River basin

Table 9 Summary results for the parameters of the AR(1) and HK cases respectively at Berlin and Vienna

From the simulated samples we obtained the posterior probability plots of μ, σ, Η, φ ₁ for the AR(1) and HK cases (Figs. 2, 3). The last 100,000 simulated samples of the parameters, described in the previous paragraph were used to obtain samples from the required posterior predictive probabilities. The samples from the posterior predictive probability of x _t |x _n , t = n + 1, n + 2,…, n + 90 were used to obtain samples for the variable of interest $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{t}^{(30)}$ given by (33).

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{t}^{(30)} := \, \left( { 1/ 30} \right)\left( {\sum\limits_{l = t - 29}^{n} {x_{l} } + \sum\limits_{l = n + 1}^{t} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{l} } \right),\quad t = n + 1, \ldots ,n + 2 9\;{\text{and}}\;\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{t}^{(30)} := \left( { 1/ 30} \right)\sum\limits_{l = t - 29}^{t} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{l} ,\quad t = n + 30,n + 3 1, \ldots \, $$

(33)

Fig. 2

Posterior probability distributions of μ, σ, φ1, Η for the cases of AR(1) and HK processes for: a Runoff of Boeoticos Kephisos. b Rainfall at Aliartos. c Temperature at Aliartos

Fig. 3

Posterior probability distributions of μ, σ, φ1, Η for the cases of AR(1) and HK processes, for the temperature at: a Berlin/Tempelhof with parameters are estimated from years 1756–2009. b Vienna with parameters estimated from years 1775–2009. c Berlin/Tempelhof with parameters estimated from years 1756–1919. d Vienna with parameters estimated from years 1775–1919

We examined the cases of WN, AR(1), asymptotic behaviour of AR(1), HK where H is considered to be known and has the value of the maximum likelihood estimate, HK when H is not known, and its asymptotic behaviour. Figures 4, 5a, b show the 0.025, 0.500 and 0.975 quantiles of the posterior predictive distributions of x _t ⁽³⁰⁾|x _n , t = n + 1, n + 2,···, n + 90.

Fig. 4

Historical climate and confidence regions of future climate (for 1 − a = 0.95 and climatic time scale of 30 years) for (upper) runoff of Boeoticos Kephisos, (middle) rainfall at Aliartos, and (lower) temperature at Aliartos

Fig. 5

Historical climate and confidence regions of future climate (for 1 − a = 0.95 and climatic time scale of 30 years) for: a (upper) temperature at Berlin, and (lower) temperature at Vienna. b (upper) temperature at Berlin/Tempelhof after the year 1920 and (lower) temperature at Vienna after the year 1920

The procedure for C1 and C2 is described below. We simulated from (12), (13) and (14) to obtain a posterior sample from μ, σ ² and φ for all cases. We simulated 10 chains with each one having 300,000 MCMC samples. To decide whether convergence has been achieved, we used the Gelman and Rubin (1992) rule. In all cases PSR ≈ 1 which shows that the chains converged to the target distribution. We decided to use the last 200,000 samples of each chain, to obtain the histograms of the posterior distributions of the parameters φ ₁ and H. Summarized results for the parameters of the AR(1) and HK cases respectively are shown in Table 8.

From the simulated samples we obtained the posterior probability plots of μ, σ, Η, φ ₁ for the AR(1) and HK cases (Fig. 2a, b). The last 10,000 simulated samples of the parameters of each chain, described in the previous paragraph are used to obtain samples from the required posterior predictive probabilities. The samples from the posterior predictive probability of x _t |x _n , t = n + 1, n + 2,…, n + 90 are used to obtain samples for the variable of interest $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{t}^{(30)}$ given by (33). We examined the cases of WN, AR(1), asymptotic behaviour of AR(1), HK where H is considered to be known and has the value of the maximum likelihood estimate, HK with unknown H and its asymptotic behaviour. Figure 4 shows the 0.025, 0.500 and 0.975 quantiles of the posterior predictive distributions of x _t ⁽³⁰⁾|x _n , t = n + 1, n + 2,…, n + 90.

5.3 Results

A first important result of the proposed framework is that it provides good estimates of the model parameters without introducing any assumptions (i.e., using non-informative priors). While common statistical methods give point estimates of parameters, the Bayesian framework provides also interval estimates based on their posterior distributions. The estimated values of μ are given in Table 10. It turns out that irrespective of the method used (MLE or posterior medians) they are almost equal. When examining temperatures, HKp resulted in the largest $\hat{\mu }$ and AR(1) in the second largest. In C4 and C6, $\hat{\mu }$ was larger than in C5 and C7 respectively. From the density diagrams of the posterior distributions (Figs. 2, 3) it seems that the posterior distribution of μ is wider when HKp is used. The posterior distribution of σ is also wider on the right (see the values of the 0.975 quantiles in Tables 8, 9) for the HKp. However the estimated values of σ are almost equal for the three used models (Tables 1, 2). The estimated φ ₁ and H are given in Tables 1, 2. Their estimated values for C5 are considerably higher compared to C7, but their posterior distributions are narrower (Table 9), probably because of the bigger sample size in the former case. Their posterior distributions are also narrower for C4 compared to C6.

Table 10 Estimates of μ using various methods

The second result of the framework is the predictive distribution of the future evolution of the process of interest. The posterior predictive 0.95-confidence regions for the 30-year moving averages are given in Figs. 4, 5a, b. For C1 the confidence region is not symmetric with respect to the estimated mean, owing to the lower truncation bound alongside with the relatively big $\hat{\sigma }$. In contrast, there is a symmetry for C2 owing to the relatively small $\hat{\sigma }$, which justifies our decision to use models without truncation in those cases where $\hat{\sigma }$ is even smaller (compared to mean). For all cases, the widest confidence regions correspond to the HKp (due to the existence of persistence), followed by the AR(1), while the narrowest confidence regions appear for the WN. Of course the confidence regions for unknown H are wider than in the case where H was considered to be known and equal to its maximum likelihood estimate. In C5 and C7 the HKp seems to be the best model, because it captures better than the others the observed values of the climate variable for the last 90 years based on the observed values of the previous years. In C7 it seems that the HKp did not capture the increase of temperature in last decades. But when we examine the full dataset (C5), the behaviour in last 90 years does not appear extraordinary. For the asymptotic values in the HKp, the 0.95-confidence region ranges at intervals of the order of 150 mm (C1), 220 mm (C2), 1.6 °C (C3), 1.9 °C (C4), 1.4 °C (C5) for the 30-year moving average. The corresponding values for the case of the WN of the order of 50 mm (C1), 75 mm (C2), 0.5 °C (C3), 0.6 °C (C4), 0.6 °C (C5) are considerably smaller compared to the case of the HKp.

6 Summary

We developed a Bayesian statistical methodology to make hydroclimatic prognosis in terms of estimating future confidence regions on the basis of a stationary normal stochastic process. We applied this methodology to five cases, namely the runoff (C1), the rainfall (C2) and the temperature (C3) at Boeoticos Kephisos river basin in Greece, as well as the temperature at Berlin (C4, C6) and the temperature at Vienna (C5, C7). The Bayesian statistical model consisted of a stationary normal process (or truncated stationary normal process for the runoff and rainfall cases) with a non-informative prior distribution. Three kinds of stationary normal processes were examined, namely WN, AR(1) and HKp. We derived the posterior distributions of the parameters of the models, the posterior predictive distributions of the variables of the process and the posterior predictive distribution of the 30-year moving average which was the climatic variable of interest. The methodology can also be applied to other structures of the ACF.

A first important conclusion is that for all the examined cases and for all the examined processes their estimated means are almost equal as expected. However the posterior distributions of the means are wider when using the HKp, due to the persistence of the process, and even wider when all parameters of the process are assumed to be unknown. This results in wider confidence regions for future climatic variables of the processes. Moreover the confidence regions of truncated future variables are asymmetric. This asymmetry depends on the variance of the examined process. However the posterior distributions of the means of all processes were less asymmetric.

Another important conclusion is that the use of short-range dependence stochastic processes is not suitable to model geophysical processes, because they underestimate uncertainty. However stationary persistent stochastic processes are suitable to achieve this purpose. In the examined cases they performed well and were able to explain the fluctuations of the process.

One may claim that, when climate is to be predicted, an assumption of stationarity is not an appropriate one as currently several climate models project a changing future climate. Nonetheless, an assessment of future climate variability and uncertainty based on the stationarity hypothesis is a necessary step in establishing a stochastic method, whose generalization at a second step would enable incorporating nonstationary components. In addition, without knowing the variability under stationary conditions, it would not be possible to quantify the credibility of climate models and even their usefulness. Work on the generalization of the methodology to incorporate deterministic predictions by climate models is under way and its results will be reported in due course.

Appendices

Appendix 1: Standard probability distributions

For easy reference, the details of the distribution functions used in this paper are summarized in Table 11

Table 11 Distributions used in the Bayesian framework

Appendix 2: Mathematical proofs

In Appendix 2 the proofs of (8), (9), (10), (12), (13), (14) are given. It is easily shown that

$$ (\varvec{x}_{n} - \mu \varvec{e}_{n} )^{\text{T}} \varvec{R}_{n}^{ - 1} (\varvec{x}_{n} - \mu \varvec{e}_{n} ) \, = \varvec{e}_{n}^{\text{T}} \varvec{R} _{n}^{ - 1} \varvec{e}_{n} \mu^{ 2} - 2\varvec{x}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} \mu + \varvec{x}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{x}_{n} $$

(34)

After completing the squares the above expression becomes:

$$ \begin{aligned} \varvec{e}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} \mu^{2} - 2\varvec{x}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} \mu + \varvec{x}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{x}_{n} &= \varvec{e}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} \left[ {\mu - \left( {\varvec{x}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} } \right) \, / \, \left( {\varvec{e}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} } \right)} \right]^{2} \hfill \\ &\quad \varvec{ + } \left[ {\varvec{e}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} \varvec{x}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{x}_{n} - \left( {\varvec{x}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} } \right)^{2} } \right]/\left( {\varvec{e}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} } \right) \hfill \\ \end{aligned} $$

(35)

From (6) and (7) we obtain the following:

$$ \pi \left(\varvec{\theta}\right)f\left( {\varvec{x}_{n} |\varvec{\theta}} \right) \propto \sigma^{{ - \left( {n + 2} \right)}} \left| {\varvec{R}_{n} } \right|^{ - 1/ 2} { \exp }\left[ {\left( { - 1/ 2\sigma^{ 2} } \right) \, \left( {\varvec{x}_{n} - \mu \varvec{e}_{n} } \right)^{\text{T}} \varvec{R }_{n}^{ - 1} \left( {\varvec{x}_{n} - \mu \varvec{e}_{n} } \right)} \right] $$

(36)

From (34), (35) and (36) we obtain (8). After integration of (36) we obtain (37) which proves (9):

$$ \pi \left( {\sigma^{ 2} |\varvec{\varphi },\varvec{x}_{n} } \right) \propto \left( {\sigma^{ 2} } \right)^{{ - \left( {n + 1} \right)/ 2}} \left| {\varvec{R}_{n} } \right|^{ - 1/ 2} { \exp }\left[ {\left( { - 1/ 2\sigma^{ 2} } \right)\left[ {\varvec{e}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} \varvec{x}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{x}_{n} - \left( {\varvec{x}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} } \right)^{ 2} } \right]/\left( {\varvec{e}_{n}^{\text{T}} \varvec{R}_{n}^{ - 1} \varvec{e}_{n} } \right)} \right] $$

(37)

After integration of (36) we obtain (38), which proves (10) after integration:

$$ \pi \left( {\varvec{\varphi }|\varvec{x}_{n} } \right) \propto \iint \sigma^{{ - \left( {n + 2} \right)}} \left| {\varvec{R}_{n} } \right|^{ - 1/ 2} { \exp }\left[ {\left( { - 1/ 2\sigma^{ 2} } \right) \, \left( {x_{n} - \mu \varvec{e}_{n} } \right)^{\text{T}} \varvec{R}_{n}^{ - 1} \left( {x_{n} - \mu \varvec{e}_{n} } \right)} \right]{\text{ d}}\mu {\text{d}}\sigma^{ 2} $$

(38)

See also Falconer and Fernadez (2007) for some results.Now for the case where truncation is applied we obtain from (7) and (11):

$$ \pi \left(\varvec{\theta}\right)f\left( {\varvec{x}_{n} |\varvec{\theta}} \right) \propto \sigma^{{ - \left( {n + 2} \right)}} \left| {\varvec{R}_{n} } \right|^{ - 1/ 2} { \exp }\left[ {\left( { - 1/ 2\sigma^{ 2} } \right) \, \left( {\varvec{x}_{n} - \mu \varvec{e}_{n} } \right)^{\text{T}} \varvec{R}_{n}^{ - 1} \left( {\varvec{x}_{n} - \mu \varvec{e}_{n} } \right)} \right]{\text{ I}}_{{ [ {{a,b]}}^{{n}} }} \left( {x_{ 1} , \ldots ,x_{n} } \right) $$

(39)

Conditional on μ ∈ [a, b], a, b ∈ R∪{− ∞,∞} the derivation of (12), (13) and (14) from (39) is then trivial.