Application of regularised optimal fingerprinting to attribution. Part I: method, properties and idealised analysis

Abstract

Optimal fingerprinting has been the most widely used method for climate change detection and attribution over the last decade. The implementation of optimal fingerprinting often involves projecting onto k leading empirical orthogonal functions in order to decrease the dimension of the data and improve the estimate of internal climate variability. However, results may be sensitive to k, and the choice of k remains at least partly arbitrary. One alternative, known as regularised optimal fingerprinting (ROF), has been recently proposed for detection. This is an extension of the optimal fingerprinting detection method, which avoids the projection step. Here, we first extend ROF to the attribution problem. This is done using both ordinary and total least square approaches. Internal variability is estimated from long control simulations. The residual consistency test is also adapted to this new method. We then show, via Monte Carlo simulations, that ROF is more accurate than the standard method, in a mean squared error sense. This result holds for both ordinary and total least square statistical models, whatever the chosen truncation k. Finally, ROF is applied to global near-surface temperatures in a perfect model framework. Improvements provided by this new method are illustrated by a detailed comparison with the results from the standard method. Our results support the conclusion that ROF provides a much more objective and somewhat more accurate implementation of optimal fingerprinting in detection and attribution studies.

1 Introduction

Optimal fingerprinting is currently the most widely used method for climate change detection and attribution. In particular, the last two assessment reports by the Intergovernment Panel on Climate Change (IPCC 2001, 2007) highlighted results from several studies based on this method.

Optimal fingerprinting involves assessing the contribution of external forcings via the estimation of so-called scaling factors, in a linear regression model (Hasselmann 1997; Allen and Tett 1999). Scaling factors correspond to a regression coefficient that should be applied to the amplitude of the simulated response to a forcing in order to best fit the observations. In terms of scaling factors, detection may be carried out by performing a statistical test to assess whether their values are consistent (no detection) or not consistent (detection) with zero. Attribution additionally requires the observed response to be consistent with the expected response to a combination of external forcings, and inconsistent with alternative, physically plausible explanations. In terms of scaling factors, this means that they have to be consistent with unity, and that the scaling factor associated with some particular forcing is significantly non-zero, even if the response to others forcings has been underestimated or overestimated. Within such a framework, the main statistical issue concerns the estimation of the scaling factors, together with their confidence intervals.

Estimation and confidence interval computation are well-known in linear regression models, even when the residuals are not white noise. Nevertheless, the case of regression models for climate change studies has rather special characteristics, in particular because of the typically high dimension of climate datasets. Its high dimension makes the covariance matrix of the internal climate variability very hard to evaluate. It is thus customary to reduce the dimension of the random vector involved in the statistical analysis. In particular, this issue arises at the global scale, where the spatial or spatio-temporal size of climate datasets is very large and needs to be decreased. The dimension reduction is achieved partly via data pre-processing (e.g. computation of decadal mean, filtering out of smaller spatial scales, etc). Such a treatment is based on the assumption that the signal-to-noise ratio is higher on large scales (Stott and Tett 1998). But the dimension reduction obtained by the pre-processing is usually insufficient, and some additional treatment is required (see e.g. Stott et al. 2006; Zhang et al. 2007).

The most popular method for reducing this dimension is to project data onto the leading EOFs of internal climate variability (e.g. Hegerl et al. 1996; Allen and Tett 1999, and many others). This option, however, involves specific issues related to the choice of the number of retained EOFs (the truncation). On the one hand, results of the algorithm in terms of scaling factor estimates and their confidence intervals are usually at least partly sensitive to this choice. The presentation of the results must then involve a discussion regarding the sensitivity of the results to the truncation. This is usually done by assessing the robustness of the results over quite a wide range of truncations (e.g. Stott et al. 2006). On the other hand, from a statistical point of view, there are no optimality results regarding the use of EOF projections.

One alternative to EOF projection was introduced in Ribes et al. (2009) and involves the use of a regularised estimate of the covariance matrix of the internal climate variability. This version, called regularised optimal fingerprinting (ROF), uses a specific estimate of the covariance matrix instead of decreasing the dimension via a projection on EOFs. So far, this version of optimal fingerprinting has been introduced for detection alone, and has only been applied to a temperature dataset covering France.

The first aim of this paper is to extend ROF to the attribution problem. This extension is done for both the ordinary least squares (Allen and Tett 1999, hereafter AT99) and the total least squares statistical models (Allen and Stott 2003, hereafter AS03). The treatment of internal climate variability is thoroughly revised relative to that implemented by Ribes et al. (2009). The internal climate variability is estimated from control simulations here, as in the approach used by AT99 and AS03. The novelty regarding the implementation of the fingerprinting method also comes from a modification of the residual consistency test (AT99 and AS03). The test procedure is revisited in order to make it suitable for large-dimension datasets.

The second objective of this paper is to discuss the properties and the efficiency of ROF with respect to the EOF projection version (or pseudo inverse version) of optimal fingerprinting. In particular, regarding global mean temperatures, Monte Carlo simulations are used to show that ROF is more accurate than EOF projection, whatever the truncation chosen.

The third purpose of this paper is to provide a first illustration of the capabilities of ROF in the analysis of the recent (1901–2010) evolution of global near-surface mean temperatures. This is done in a perfect model framework, that is to say by applying ROF to historical simulations from the CNRM-CM5 model and using the same model to evaluate the response pattern to each forcing. Such an idealised framework ensures the validity of the assumption that the model is able to reproduce the spatio-temporal pattern of response to each forcing accurately. It also allows a comparison between ROF and the commonly used EOF projection based on realistic data. This comparison illustrates the attractiveness of ROF in the analysis of global mean temperature.

The data and its pre-processing are presented in Sect. 2. In Sect. 3, we introduce ROF for attribution, together with the other version of the optimal fingerprinting attribution methodology considered in this study. The results of the application of these methods to idealised Monte Carlo simulations and to pseudo-observations from CNRM-CM5 are then discussed in Sect. 4. The application of ROF to real observations, using estimated responses to forcings and estimates of internal variability from CMIP5 (Coupled Model Intercomparison Project version 5) models, will be discussed in Part II.

2 Data and pre-processing

Because this work is devoted to a perfect model framework, we focus on simulated global near-surface annual mean temperatures. These data come from two different sources. First, several ensembles of simulations from the CNRM-CM5 model are used to perform the perfect model framework analysis. Second, a much wider ensemble of simulations from both CMIP3 and CMIP5 are used to estimate the internal climate variability.

2.1 Pseudo-observations and forced response patterns

Pseudo-observations and forced response pattern estimates are derived from simulations performed with CNRM-CM5. The CNRM-CM5 model is the atmosphere-ocean general circulation model (AOGCM) designed at CNRM and CERFACS to participate in CMIP5. A complete, detailed description of this model can be found in the reference paper by Voldoire et al. (2011).

We used the global temperatures from historical simulations (HIST, 10 members) as pseudo-observations. These are transient climate change simulations covering the period from 1850 to 2012, which include historical variations of all external forcings. Specifically, we take the following external forcings into account: anthropogenic variations of greenhouse gas concentrations (GHG), anthropogenic variations of aerosol concentrations (AER), and variations of natural forcing (NAT), which includes variations of aerosol concentrations due to volcanic eruptions and changes in solar activity. Note that, strictly speaking, historical forcings are imposed only over the 1850–2005 period. The extension to 2006–2012 involves atmospheric greenhouse gas and aerosols concentrations from the RCP8.5 scenario and repetition of solar cycle 23, with no volcanic eruption over the period. The use of the 10 members from the HIST ensemble allows a virtual analysis of global temperatures to be reproduced 10 times.

Standard detection and attribution analysis also requires the use of climate model simulations to provide estimates of the expected response pattern of the climate system to each external forcing taken into consideration. Here, we consider two combinations of external forcings (ANT and NAT) or, alternatively, three clusters of external forcings (GHG, AER and NAT). In order to evaluate the response pattern to each cluster of forcings, three ensembles of transient climate change simulations covering the 1850–2012 period are used, each with an “individual” forcing: simulations with historical anthropogenic forcings only (ANT, 10 members), including changes in greenhouse gas concentrations and anthropogenic aerosol emissions; simulations with historical greenhouse gas concentrations (GHG, 6 members); and simulations with natural forcings only (NAT, 6 members). Note that no simulations were available with the AER forcing alone. In consequence, the contribution from the AER forcing was indirectly estimated by the method, based on the difference between ANT and GHG contributions, assuming the additivity of the responses to different forcings (see Sect. 3). This means that AER refers to all anthropogenic forcings except GHG. The same assumptions as in the HIST ensemble are made over the 2006–2012 period with regard to forcings. Note that ANT, GHG and NAT ensembles are used to provide estimates of the expected response to the corresponding forcings; consequently, we use only the ensemble mean.

2.2 Internal climate variability

An estimate of internal climate variability is required in detection and attribution analysis, for both optimal estimation of the scaling factors and uncertainty analysis. Estimates of internal variability are usually based on climate simulations, which may be control simulations (i.e. in the present case, simulations with no variations in external forcings), or ensembles of simulations with the same prescribed external forcings. In the latter case, m − 1 independent realisations of pure internal variability may be obtained by subtracting the ensemble mean from each member (assuming again additivity of the responses) and rescaling the result by a factor $\sqrt{\frac{m}{m-1}}$, where m denotes the number of members in the ensemble. Note that estimation of internal variability usually means estimation of the covariance matrix of a spatio-temporal climate-vector, the dimension of this matrix potentially being high.

We choose to use a multi-model estimate of internal climate variability, derived from a large ensemble of climate models and simulations. This multi-model estimate is subject to lower sampling variability and better represents the effects of model uncertainty on the estimate of internal variability than individual model estimates. We then simultaneously consider control simulations from the CMIP3 and CMIP5 archives, and ensembles of historical simulations (including simulations with individual sets of forcings) from the CMIP5 archive. All control simulations longer than 220  years (i.e. twice the length of our study period) and all ensembles (at least 2 members) are used. The overall drift of control simulations is removed by subtracting a linear trend over the full period. Details of the simulations and ensembles involved are given in "Appendix 1". We then implicitly assume that this multi-model internal variability estimate is reliable.

2.3 Data pre-processing

This paper aims to illustrate the results provided by ROF at the global scale; therefore, the pre-processing applied to the data is as similar as possible to that used in previous studies, in particular Stott et al. (2006, hereafter S06) and Tett et al. (2002). The main period studied in this paper is 1901–2010. In line with S06, we focus on the period after 1900, and add the past decade to the period they considered. Note, for instance, that Gillett et al. (2012) recently chose to focus on a longer period from 1851 to 2010.

In order to base our analysis on pseudo-observations as close as possible to real observations, the spatio-temporal missing data mask from real observations is first applied to simulated data, at the monthly time-step. The median HadCRUT4 dataset (Morice et al. 2012) is used to provide this observational mask. In the case of historical simulations, the same 110-year period is selected and processed. In the case of pre-industrial simulations, several 110-year periods (see below) are selected and treated.

Data are then processed as follows. Annual anomalies are computed from monthly ones if at least 8 months are available; otherwise, the data are considered missing. In the case of simulated data, monthly anomalies are computed with respect to the same period as observations, i.e. the 1961–1990 period. Decadal anomalies are then computed where at least 5 years are available; otherwise, the data are again considered missing. A 110-year period thus provides 11 time steps. The temporal mean over these 11 time steps is then subtracted in order to focus only on temporal anomalies. Next, the spatial dimension is reduced via projection on spherical harmonics. Prior to the computation of spectral coefficients, missing data are set to 0, and the data are interpolated onto a gaussian grid with a conservative method. The obtained spectral coefficients are then weighted by $1/\sqrt{2l+1}$, where l denotes the total wave number, in order to give each spatial scale equal weight (following Stott and Tett, 1998). The highest resolution used in this paper corresponds to a T4-truncation, i.e. removing spatial scales below 5,000 km. In such a case, one global field results in 25 non-zero real coefficients, and a 110-year period thus finally results in a vector of size 275, which is used in the statistical analysis. Note that other spherical harmonic truncations are also used in Sect. 4.2.2, in order to discuss the sensitivity of the result to this choice (in particular truncation T0 to analyse the global mean only, and truncations T1 and T2).

Note that some choices within the pre-processing step are potentially non-optimal (e.g. the computation of spectral coefficients considering missing data as 0) but applying the same treatment to all data, including those from control simulations, implies that the whole statistical analysis is performed in an internally consistent manner.

3 Method

3.1 Classical optimal fingerprinting

The standard statistical model behind the optimal fingerprint (OF) method was introduced by Hasselmann (1979), (1997); Hegerl et al. (1997); Allen and Tett (1999, hereafter AT99) and then Allen and Stott (2003, hereafter AS03), and has been very widely used since then. Here we review the main features of both the statistical model and the usual inference technique before introducing the specifics of ROF.

Standard optimal fingerprinting is based on the generalised linear regression model

$$ y = \sum_{i=1}^{l} \beta_{i} x_{i} + \varepsilon $$

(1)

where y are the observations, x _i is the climate response to the ith external forcing considered, β _i is an unknown scaling factor and $\varepsilon$ denotes the internal climate variability. y, x _i , and $\varepsilon$ consist of spatio-temporal vectors. The basic principle behind this statistical model is to estimate the amplitude of the response to each external forcing from the observations via the estimation of the scaling factors β _i . $\varepsilon$ is assumed to be a Gaussian random variable, and we write $C=\hbox {Cov}(\varepsilon)$. Note that this regression model assumes that the response to several external forcings is additive (see e.g. Gillett et al. 2004).

Two assumptions have been made regarding the vectors x _i . In the so-called Ordinary Least Square approach (OLS, see AT99), the vectors x _i are assumed to be perfectly known from climate model simulations. In the so-called Total Least Square approach (TLS, see AS03), the vectors x _i are unknown and the information provided by the ensemble mean of climate model simulations is only $\widetilde{x}_{i}$, with

$$\widetilde{x}_i = x_i + \varepsilon_{x_i}, $$

(2)

where $\varepsilon_{x_{i}}$ denotes a random term representing the internal climate variability within the climate model simulation (or ensemble mean). In the TLS approach considered here, it is assumed that the random terms $\varepsilon$ and $\varepsilon_{x_{i}}$ are Gaussian and have the same covariance structure, because they represent the same internal variability (i.e. $\hbox{Cov}(\varepsilon_{x_{i}}) = \frac{1}{n} \hbox{Cov}(\varepsilon)$, where n denotes the size of the ensemble of simulations used to compute $\widetilde{x}_{i}$). In both cases, the underlying assumption is that climate models accurately reproduce the shape of the response to an external forcing (both in terms of space and time) but are potentially inaccurate at reproducing the amplitude of that change (potentially due to some missing feedback).

The statistical treatment of each approach is presented in detail in the corresponding papers, AT99 for OLS, and AS03 for TLS. This treatment includes the estimation of the internal variability covariance matrix C, the computation of the optimal estimate of β, the uncertainty analysis on β and the implementation of a residual consistency test. Optimal estimation and uncertainty analysis both require the matrix C to be known, but in practice it must be estimated. Hegerl et al. (1997), AT99 and AS03 suggest computing two independent estimates of the matrix $C: \widehat{C}_{1}$ and $\widehat{C}_{2}$. For the estimation procedure to be optimal, the first estimate $\widehat{C}_{1}$ is used for prewhitening the data. The second estimate $\widehat{C}_{2}$ is used for the uncertainty analysis on the estimated scaling factors $\widehat{\beta}$. $\widehat{C}_{1}$ and $\widehat{C}_{2}$ are respectively based on a sample of y-like vectors Z ₁ and Z ₂ (respectively of size n ₁ and n ₂), corresponding to random internal variability realisations.

Note that among other technical details, we used the method proposed by Tett et al. (1999) (see in particular, supplementary material, Sec. 9), to derive scaling factors of GHG, AER and NAT, when the only available response patterns are GHG, ANT and NAT. This technique involves fitting the linear regression model to the available response patterns as a first step. This provides estimates of β _GHG , β _ANT and β _NAT . Then, in a second step, the desired scaling factors (here GHG, AER and NAT) are derived from the first ones, based on the linear additivity assumption (some additional details are referred to in "Appendix 2").

3.2 EOF projection

One specific feature of the statistical models mentioned above, in the case of climate studies, is the high dimension of the datasets typically involved. Even after the pre-processing described in Sect. 2.3, which strongly decreases both the temporal and spatial dimensions of the data, the size of the resulting y-vector is 275. The dimension of the matrix C is then 275 × 275. The computation of an accurate estimate $\widehat{C}$ would need to be based on a sample Z containing 10³–10⁴ realisations. If Z is too small, the efficiency of the full OF algorithm may be reduced due to imprecise prewhitening, resulting in a deteriorated optimisation. In such a case, the eigenspectrum is distort, with low-order eigenvalues overestimated, high-order eigenvalues underestimated, and eigenvalues above the rank of $\widehat{C}$ set to 0. This phenomenon was discussed by AT99, specifically in regard to the underestimation of the lowest eigenvalues of $\widehat{C}_{1}$. In practice, samples Z of size 10³–10⁴ are unreachable: typically, long control simulations cover 10³ years and provide less than 10 non-overlapping 110-year segments. Therefore, the use of the large ensemble of simulations described in Sect. 2.2 does not provide much more data than two samples Z with a size of about 10².

The EOF projection version (or pseudo-inverse version) of OF then proposes the truncation of the estimate $\widehat{C}_{1}$ to the k leading EOFs, thus reducing the size of y to k. This focuses on the leading modes of variability, which are usually assumed to represent large-scale signals, and allows optimal statistics to be performed within a reduced space of dimension k. However, some disadvantages can also be highlighted. These are partly discussed in Ribes et al. (2009, hereafter R09), and are only recalled briefly here. First, no optimality results are known when such a projection is applied. Even if the OF algorithm maximises the signal-to-noise ratio in a given subspace (following Hasselmann 1993), the projection on the leading EOFs is equivalent to selecting the directions that maximise the noise, which is not necessarily favourable to an increase of the signal-to-noise ratio. In consequence, the choice of the value of k is not easy from a statistical point of view. Secondly, the results are usually somewhat sensitive to the value of k. The use of such a projection then requires a careful sensitivity analysis. For instance, Stott et al. (2006) have highlighted a range of values of k over which the results are stable but the selected values of k are different for the three climate models considered (see Fig. 4 in S06). The difficulty implied by the choice of k seems to increase when we deal with other applications, for example at the regional scale (e.g. Ribes et al. 2009), or with variables other than temperature (e.g. Terray et al. 2011), and is not always discussed. Note that this difficulty regarding the choice of k was also discussed by Allen et al. (2006), who pointed out this additional degree of freedom of the analysis, and the danger of focusing misleadingly on false-positive detections.

3.3 Regularised optimal fingerprinting

Regularised optimal fingerprinting (ROF) was introduced in R09. We review the main concept here and refer the reader to R09 for a complete presentation. More importantly, we introduce the specifics of the present study with respect to R09, in order to extend ROF to the attribution problem. In particular, these concern the treatment of the internal climate variability and the residual consistency test (which is discussed in Sect. 3.4).

The basic idea behind ROF is to derive, from a sample Z, a regularised estimate $\widehat{C}_{I}$ of C. Regularisation means here that $\widehat{C}_{I}$ has the form $\lambda \widehat{C} + \rho I$, where λ and ρ are real coefficients while I denotes the identity matrix. Regularisation with the identity matrix, which is proposed here, avoids the underestimation of the lowest eigenvalues, that occurs in $\widehat{C}$. It also provides a type of interpolation between the exact optimal fingerprint solution (i.e. the generalised least-square estimate, which involves the true matrix C), and the unoptimised fingerprint (i.e. the classical least square solution, which involves the identity matrix). Ledoit and Wolf (2004) have provided estimators for the coefficients λ and ρ, and have shown the resulting estimate $\widehat{C}_{I}$ of C (thereafter, the LW estimate) to be more accurate than the empirical estimate $\widehat{C}$ with respect to the mean square error.

It is important to note that other regularisation methods (e.g. based on a matrix other than the identity matrix, other estimation techniques, etc) could potentially also be used. Ledoit and Wolf (2004) noted themselves that the identity matrix, which is used here to regularise, may be considered a bayesian prior on the matrix C. This prior, however, ignores some physical knowledge: for instance, the magnitude of the variability (which tends to be higher over land and at high latitudes) and known features of spatial dependencies. So the use of another prior could be of interest. Similarly, the method of estimating λ and ρ could potentially be improved. The LW estimate, however, has the advantage of providing a simple regularisation method. This estimate overestimates the smallest eigenvalues of C (which are more difficult to estimate accurately). This may be seen as an additional advantage, as it prevents an excess of weight being given to small scales (defined as high order EOFs), which occurs with the sample covariance matrix as a result of unrealistically low high-order eigenvalues (see e.g. AT99). Finally, ROF, as presented in this paper (as in R09), provides one way to use regularisation in optimal fingerprinting. Alternatives could be of interest, but to our knowledge, no results on optimality are currently available.

Unlike in R09, we estimate internal climate variability based on two independent estimates of C, both derived from control simulations (following AT99 and AS03). In such a case, regularisation is used for the first estimate, then denoted $\widehat{C}_{I_1}$, which is used for optimisation (or equivalently, for prewhitening), i.e. for computing the optimal estimate of β. The projection on the first leading EOFs is thus not required. The second estimate used in uncertainty analysis may be regularised or not, which deserves some comments.

The formulas used in uncertainty analysis [formula (14) in AT99 for OLS, formulas (36,37) in AS03 for TLS] are only precisely valid in the case where $\widehat{C}_{2}$ follows a Wishart distribution, i.e. without regularisation. For the sake of simplicity, we prefer not to use a regularised estimate $\widehat{C}_{2}$ here, following AT99 and AS03, in order to use exactly the same approach for uncertainty analysis. The use of a regularised $\widehat{C}_{2}$ (say $\widehat{C}_{I_{2}}$), although potentially attractive, would require the distributions given in the formulas mentioned above (which are Fisher distributions in both cases) to be completely re-derived, which is well-beyond the scope of this paper. Note that the TLS formula in AS03 was given under the assumption of a high signal-to-noise ratio. A detailed assessment of the appropriate signal to noise range is potentially of interest, but is also beyond the scope of this paper.

We emphasize that, under the same assumptions, the use of a regularised $\widehat{C}_{I_{1}}$ together with a classical empirical estimate $\widehat{C}_{2}$ leaves the full algorithm virtually unchanged. Some small technical changes appear however, compared to previous studies, in the preparation of the sample Z ₁ used for computing $\widehat{C}_{I_{1}}$.

First, in a 110-year diagnosis, it is quite common to concatenate spatio-temporal vectors corresponding to overlapping periods, e.g. from the same control simulation, into Z ₁ (see e.g. AS03). This slightly increases the accuracy of the resulting estimate. In such a case, the columns of Z ₁ are not independent and the estimation of a number of equivalent degrees of freedom is required. In the case of ROF, the LW estimate is designed for independent realisations. If some dependency occurs between the realisations in Z ₁, the coefficients λ and ρ are no longer optimally estimated, and the accuracy of the estimate $\widehat{C}_{I_{1}}$ is decreased. Consequently, we use non-overlapping periods in Z ₁ here, and compute the LW estimate assuming these realisations to be independent. Note that the case of Z ₂ is different, and that $\widehat{C}_{2}$ may be computed from dependent realisations, provided that its sampling distribution is correctly taken into account in the uncertainty analysis. For the sake of simplicity in the present application, both samples Z ₁ and Z ₂ consist of non-overlapping periods, which are assumed to be independent. We also choose to construct two samples of the same size (i.e. n ₁ = n ₂), with the data provided by each CGCM split between both samples.

Second, the LW estimate is designed for a full-ranked covariance matrix, because regularisation with the identity matrix implies that the regularised matrix estimate is always full-ranked. In the pre-processing described above, the computation of anomalies with respect to the mean over the full period means that this condition is broken. More precisely, for a 110-year period, the dimension of y would be 275 in truncation T4, but the rank of its covariance matrix is 250 (computation of anomalies is equivalent to removing one time-step, i.e. 25 coefficients). So the statistical analysis will be performed within a subspace of dimension 250 in order for the covariance matrix to be full-ranked. The technique used to achieve this dimension reduction is found to have a very small impact on the results.

Finally, the full implementation of ROF for both OLS and TLS statistical models is provided on-line as described in "Appendix 2".

3.4 Residual consistency test

A residual consistency test was introduced by AT99 to check that the estimated residuals in statistical model (1) or (1–2) are consistent with the assumed internal climate variability. Indeed, as the covariance matrix of internal variability is assumed to be known in these statistical models, it is important to check whether the inferred residuals are consistent with it; i.e., that they are a typical realisation of such variability. If this test is passed, the overall statistical model can be considered suitable. If this test is rejected, then at least one assumption should be revised. Rejection may occur if, e.g., the estimated internal variability is too low, the expected response patterns are not correct, etc.

Here, we propose to adapt the residual consistency test introduced by AT99 and AS03, in order to make it more suitable in the context of ROF. The proposed modification primarily involves the estimation of the null-distribution of this hypothesis test. This modification is done with $\widehat{C}_{1}$ regularised and $\widehat{C}_{2}$ unregularised. The potential benefit of using two regularised estimates (e.g. in terms of the power of the statistical test), or other variations, is not assessed here but would impact the estimation of the null-distribution presented below.

3.4.1 OLS case

The first residual consistency test for optimal fingerprinting was introduced by AT99 in the context of the OLS statistical model. Two formulas were provided to implement the test, corresponding to whether the estimation uncertainty on $\widehat{C}_{2}$ was accounted for [formula (20) in AT99], or not [formula (18) in AT99].

A careful analysis of formula (20) from AT99, and numerical simulations, show that this formula is suitable in the case where n ₂ ≫ n, where n denotes the dimension of y. This formula seems less appropriate in other cases, however. Some evidence supporting this conclusion is provided in "Appendix 3". This discrepancy with AT99 is important because n is much closer to n ₂ with ROF. Even cases where n > n ₂ are encountered in many optimal fingerprinting studies. Strictly speaking, the distribution of the residual consistency test variable is theoretically not known with ROF. For instance, the use of the LW estimate for prewhitening, instead of the exact covariance matrix C, means that even formula (18) from AT99 is not perfectly satisfied (see "Appendix 3").

Because parametric formulas are not known, we propose to evaluate the null distribution $\mathcal{D}$ of the statistical variable used by AT99 via Monte Carlo simulations. The Monte Carlo algorithm consists of reproducing the whole procedure, and requires y, Z ₁ and Z ₂ to be simulated. The input parameters required for implementing such a Monte Carlo simulation are X (i.e. the expected response to external forcings) and C. A difficulty arises here because the true value of C is not known (the situation is different for X, as X is assumed to be known in the OLS approach). The resulting distribution $\mathcal{D}$ may depend on the initial value chosen for C. An illustration of the results from such a simulation is provided in "Appendix 3". It suggests that the discrepancies between these formulas are substantial, and the use of one instead of another may have a strong impact on the result of the residual consistency test. It also suggests that the sensitivity of the simulated null-distribution to the value of C used is weak.

3.4.2 TLS case

Similarly to what was done in AT99, the residual consistency test was extended to the TLS statistical model by AS03. Inference under the TLS statistical model is based on the singular value decomposition of the concatenated matrix M = [Y, X], which is an n × (l + 1) matrix. Let λ _i be the sorted singular values of M, and u _i the corresponding singular (l + 1)-vectors. Two formulas were proposed by AS03. First, if the estimation uncertainty on $\widehat{C}_{2}$ is not taken into account [formula (26) in AS03], the residual consistency test is based on λ ² _min  = λ ² _l+1 . Second, if the estimation uncertainty on $\widehat{C}_{2}$ is taken into account [formula (35) in AS03], the residual consistency test is based on a corrected singular value $\widehat{\lambda}_{l+1}^{2}$ (see formula (34) in AS03). AS03 used the notation $\widehat{\lambda}_{min}^{2}$, which is potentially ambiguous here because $\widehat{\lambda}_{min}^{2}$ (i.e. the smallest $\widehat{\lambda}_{i}^{2}$) does not necessarily correspond to $\widehat{\lambda}_{l+1}^{2}$ (i.e. the corrected singular value corresponding to the last singular vector u _l+1 of M). We based our computations on $\widehat{\lambda}_{l+1}^{2}$.

Demonstrations of these formulas were not provided by AS03. However, based on numerical simulations, it seems that the assumption of a high signal-to-noise ratio is still required here. It is also fairly clear that, similarly to the OLS case (cf "Appendix 3"), the use of an estimated covariance matrix $\widehat{C}_{1}$ for prewhitening (or optimisation) is not accounted for in this null distribution.

This is why we propose, in line with the OLS case, to evaluate the null distribution of the residual consistency test via Monte Carlo simulations based on $\widehat{\lambda}_{l+1}^{2}$ in order to apply this test with ROF. Here again, the Monte Carlo procedure has two input parameters: C and X, where X denotes the true (i.e. noise-free) version of the simulated $\widetilde{X}$ [cf Eq. (2)]. The resulting null distribution depends on these two parameters. Unlike the OLS case, however, additional numerical simulations (not shown) suggest that the value used for C may have a substantial impact on the estimated null-distribution. Note that the value used for X is found to have less impact. This uncertainty regarding the null-distribution, and thus on the p value of the test, requires the analysis of the test result to be done very carefully.

An illustration of the results from such simulations is provided in "Appendix 4", in realistic cases. Some differences appear between the parametric formulas by AS03 and the Monte Carlo distribution in these cases, as the dimensionality increases. Note however that smaller discrepancies are found when the high signal-to-noise ratio assumption is more clearly satisfied. Unlike the OLS case, however, the use of parametric formulas appears to be too conservative in the TLS case. The values of $\widehat{\lambda}_{l+1}^{2}$ provided by the Monte Carlo simulations are smaller than expected under the parametric distributions (whether the χ² or the Fisher distribution is considered). So, the use of parametric formulas in these cases would result in too frequent acceptance of the null hypothesis. In particular, H ₀ may be accepted, while the test variable is well outside its null distribution.

Then, the same Monte Carlo procedure was used with EOF projection for some values of the truncation k, in order to allow a direct comparison with the ROF results (see e.g. Sect. 4.2.2). An illustration of the results from these simulations is also provided in "Appendix 4". The same type of discrepancies as in ROF are found with the AS03 distribution. As these discrepancies are related to the dimensionality, they increase with the truncation k.

In the following (Sect. 4), the p value of the residual consistency test is estimated from the null-distribution as simulated by MC simulations performed with input parameters C and X as follows: C is the covariance matrix as estimated by the LW estimate from the full sample of control segments Z, and X is the expected response as simulated by the CNRM-CM5 model. It must be noted that, based on other MC simulations performed with other and realistic values for C, the null-distribution seems to be conservative (meaning that the p values are overestimated). Further results shown in Part II are consistent with this conclusion.

4 Results

Two types of results are presented in order to compare ROF to the use of EOF projection. We first assess the accuracy of each approach based on numerical idealised Monte Carlo simulations. We then apply both methods to data from historical simulations performed with the CNRM-CM5 model. Most of these results are analyses of the respective contributions of two (ANT + NAT) or three (GHG + AER + NAT) external forcings on simulated global annual mean temperature over the 1901–2010 period.

4.1 Monte Carlo simulations

Idealised Monte Carlo simulations are first implemented in order to evaluate the accuracy of each method. The accuracy metric is the mean square error of the scaling factor estimates. We use the following simulation protocol.

We first select some realistic parameters C, X and β. C is estimated from the whole set of simulations mentioned above for estimating internal climate variability (see Sect. 2.2). Two climate change patterns x _i , respectively associated with all anthropogenic (ANT) and natural forcings (NAT), are computed from ensembles from the CNRM-CM5 model. Note that x _i is here a vector of dimension p = 275, while C is a p × p matrix. Finally, the “true” scaling factors used in numerical simulations are 1 for both forcings.

Second, given these fixed parameters, Monte Carlo simulations are performed in order to provide virtual data for the optimal fingerprint methods, i.e. y, Z ₁ and, in the TLS case, $\widetilde{X}$. y is simulated following statistical model (1), with a random term $\varepsilon$. Z ₁ consists of random vectors with covariance C. In the OLS case, the parameters x _i are assumed to be known and therefore are directly available for the estimation procedure. In the TLS case, $\widetilde{x}_i$ are simulated following Eq. (2), with a random term $\varepsilon_{x_i}$. The covariance of $\varepsilon_{x_i}$ is C divided by the virtual number of model simulations used to evaluate x (see Sect. 3.1), fixed at 10 and 6, respectively, for the ANT and NAT forcings (similarly to what was actually available from CNRM-CM5 ensembles). Note that the simulation of virtual sets Z ₂ is not required here because the methods are evaluated with respect to the mean square error of the scaling factor estimates, so the uncertainty analysis on $\widehat{\beta}$ is not required.

Third, both versions of the optimal fingerprint algorithm (i.e. ROF and EOF projection) are applied to the virtual data y, X (or $\widetilde{X}$) and Z ₁, in order to estimate the scaling factors β. The estimated values are then compared to those used in the simulations, namely 1. This allows us to compute the estimation error of the whole algorithm.

Results from 8 simulations are presented in Fig. 1. Simulations were carried out for both the OLS and the TLS statistical model, and for different assumptions regarding the number of independent realisations available in the sample Z ₁, namely n ₁ = 30, n ₁ = 75, n ₁ = 150, or n ₁ = 300. Note that the case n ₁ = 150 is the most realistic (i.e. the closest to the application presented in Sect. 4.2). The two versions of the optimal fingerprint method are compared in each case. The perfect case where the matrix C is known is also represented in order to illustrate the accuracy of the “perfectly optimised” OF estimate. The set Z ₁, only used for estimating C, is then useless, so the results do not depend on n ₁. In each case, the mean square error of the β estimate is computed from N = 10000 simulations. It should be noted that, similarly to the real case, the truncation parameter k cannot be higher than 250. This is due to the fact that, as mentioned above, the rank of C is 250. Consequently, the ranks of Z ₁ and $\widehat{C}_{1}$ cannot be higher than 250 either. In the cases where n ₁ < 250, the rank of $\widehat{C}_{1}$ is n ₁, and k cannot exceed n ₁.

Fig. 1

Mean square error of the β-estimate, as evaluated from Monte Carlo simulations for ROF (red), EOF projection (blue) and the idealised case where the matrix C is known (black), as a function of the truncation k. Simulations were made for both OLS and TLS statistical models, and under different assumptions regarding the size of the sample Z ₁ (n ₁ = 30, 75, 150, 300)

This figure shows that ROF is more accurate than EOF projection in all cases considered. This result is relatively strong, because it occurs whatever the selected value of k selected. It is also robust to the choice of the OLS or TLS statistical model, at least over a broad range of values for the parameter n ₁. This result shows that in addition to being simpler (because it avoids the difficult choice of the parameter k), ROF should be preferred because it allows a more accurate estimation of β.

Additional valuable information comes from the illustration that the accuracy of EOF projection is higher when k ranges from a few tens to, say, two hundred (if n ₁ = 300). This provides some additional justification for the choice of k made by S06. It should also be noted that such Monte Carlo simulations could be potentially valuable in providing a criterion for selecting a value of the truncation parameter k. Here, the criterion is the mean square error of the corresponding estimator. An alternative, sometimes used in previous studies, is to use the residual consistency test when selecting k. This option was discussed first by AT99, which showed that the consistency test failed when the values of the truncation parameter k were increased. This phenomenon was partly explained by a defect in the estimation procedure, as follows. C is commonly estimated by using the empirical estimate computed from a typically small sample Z ₁. This is the reason why the lowest eigenvalues of the covariance matrix are underestimated. Such an underestimation may explain why residuals are not consistent with the assumed internal variability if k is too large; i.e., if some underestimated eigenvalues are taken into account. Our Monte Carlo simulations even allow us to go one step further. If the smallest eigenvalues are underestimated, the prewhitening used for optimisation in the scaling factor estimation would be deteriorated. It can then be expected that the mean square error of the scaling factors estimate will also be deteriorated (i.e. increased). The results shown in Fig. 1 indicate that this does occur (with the mean square error increasing with truncation), but mainly for high truncation levels (typically k > 100 in the case where n ₁ = 150). It suggests that the impact of underestimating the smallest eigenvalues in $\widehat{C}_1$ is relatively low for smaller values of k. In the case of ROF, the use of a regularised estimate alleviates this problem because the smallest eigenvalues are no longer underestimated.

Figure 1 also shows that the accuracy of the β estimate is higher in the case of the OLS statistical model. This is expected because the noise $\varepsilon_{x_{i}}$ is added in the TLS case, increasing the uncertainty. Note, however, that in the real world, the OLS approach is applied while the response pattern really is contaminated with noise. In such a case, the OLS estimate of β, based on $\widetilde{x}$ instead of x, is less accurate than the TLS estimate (not shown). Finally, Fig. 1 illustrates how the accuracy of both versions increases with the parameter n ₁: both curves are closer to the black straight line when n ₁ increases. This is expected, too, because the higher n ₁, the more accurate the estimate $\widehat{C}_{1}$ of C, and thus $\widehat{\beta}$.

Note that these results are qualitatively similar to the power study illustrated in R09. The novelty lies in the illustration of the accuracy of ROF in the case of attribution, the use of initial values C and X corresponding to the global scale, and the illustration on both OLS and TLS statistical models, and for several values of n ₁.

4.2 Application to historical simulations

The second step in comparing the two versions involves the application to historical simulations performed with the CNRM-CM5 climate model.

This application is based on the ensembles of simulations performed with the CNRM-CM5 model, and on the set of control simulations taken from CMIP archives. Such an application is partly idealised, because data from the same model (but not from the same ensemble of simulations) are used as pseudo-observations, and as expected responses to each forcing. The TLS statistical model takes into account the uncertainty in the estimate of the expected response to forcings, whereas the OLS statistical model does not, so this section focuses on the TLS approach. TLS has also been the most widely used method over the last decade. In addition to presenting results from ROF, this section provides a comparison with EOF projection in terms of scaling factor estimates.

4.2.1 Individual comparisons

Figure 2 illustrates the results obtained from one historical simulation (HISTr1) with a 2-forcing analysis (ANT + NAT), based on T4 spherical harmonics in both cases. It appears from this example that the results from ROF are very consistent with those obtained by applying EOF projection. This is particularly true in the case of the ANT forcing, where the results obtained by using EOF projection are only very slightly sensitive to the choice of truncation. This is also mainly true in the case of the NAT forcing, where the best estimate and the confidence interval from ROF are very close to the one provided by EOF projection over a wide range of values of k (e.g. from k ≃ 10 to k ≃ 120 here). Note that the comparison is only presented for one historical simulation but the results are qualitatively very similar for the other simulations.

Fig. 2

Scaling factor best-estimates and their 90 % confidence intervals, as estimated from the CNRM-CM5 historical simulation HISTr1 over the 1901–2010 period, in a 2-forcing analysis. Results are shown under the TLS statistical model, based on T4 spherical harmonics, for ROF (left) and for EOF projection (right), as a function of the truncation k

Figure 3 illustrates the same kind of results in the case of a 3-forcing analysis (GHG + AER + NAT), still based on T4 spherical harmonics. Some agreement is also found between the two versions, and the results from ROF are close to the results provided by EOF projection at some truncation levels. However, this particular case provides an illustration of how the results from EOF projection may be sensitive to the choice of k. For instance, confidence intervals for β_GHG or β_AER, as estimated at different truncations k, are virtually disjoint (e.g. 35 < k < 45 vs 90 < k < 110). The conclusion with respect to detection (i.e. acceptance of β = 0), or attribution (i.e. acceptance of β = 1) also depends on k. Due to this sensitivity of the results from EOF projection, the agreement between the two versions occurs at different truncation levels for the three external forcings considered.

Fig. 3

Scaling factor best-estimates and their 90 % confidence intervals, as estimated from the CNRM-CM5 historical simulation HISTr1 over the 1901–2010 period, in a 3-forcing analysis. Results are shown under the TLS statistical model, based on T4 spherical harmonics, for ROF (left) and for EOF projection (right), as a function of the truncation k

In Figs. 2 and 3, it is worth noting that the confidence intervals from ROF are somewhat smaller than the ones provided by EOF projection. This occurs in particular over the range of truncations providing results similar to ROF. This result, which is consistent with a more accurate estimate in terms of the mean square error, will be more clearly illustrated in Fig. 5.

4.2.2 Overall results

Figures 4 and 5 show the results obtained when applying ROF and EOF projection to each of the 10 members of the HIST ensemble. The results from ROF are illustrated for projections onto spherical harmonics from the largest to smaller scales (T0, T1, T2 and T4 spherical harmonics). The use of T0, T1 or T2 spherical harmonics may be regarded as a way of reducing the spatial dimension of the data with respect to the T4 case. T0 means that only the global average is considered (spatial dimension equals one) over 11 decades, so the size of y is 11. In truncation T1 (resp. T2, T4), the spatial dimension taken into account is 4 (resp. 9, 25), resulting in a vector y of size 44 (resp. 99, 275). The results from EOF projection are shown only for two truncations (k = 15 and k = 30). These levels have been used in a recent study by Gillett et al. (2012), and are representative of the truncation levels typically used in previous studies (e.g. S06). The results are shown both in terms of scaling factors (best estimates and confidence intervals) and, in the case of ROF, the p value from the residual consistency test.

Fig. 4

Results of the attribution analysis applied to global temperatures from each simulation in the HIST ensemble (10 members) over the 1901–2010 period, in a 2-forcing (ANT + NAT) analysis. The figure shows: results from ROF, with several choices on the number of spherical harmonics used (T0, T1, T2 or T4 spherical harmonics), and from EOF projection, based on T4 spherical harmonics, for two choices of the number of EOFs retained (k = 15 or k = 30). Results are presented, in each case, both in terms of the scaling factor best estimates and their 90 % confidence intervals (left), and in terms of the p value from the residual consistency test (RCT, right). All these results were obtained by with the TLS algorithm

Fig. 5

Same as in Fig. 4, in the case of a 3-forcing analysis (GHG + AER + NAT)

First, the results obtained by applying ROF to T4 spherical harmonics deserve some comment. Note that these results correspond to the ones shown in Figs. 2 and 3 (still for ROF).

The 2-forcing analysis (Fig. 4, case ROF, T4) shows that the results obtained from different simulations are very consistent with one another, and confidence intervals are relatively small. For both forcings, the estimated scaling factors are consistent with the expected value, 1. Best estimates are distributed slightly above or slightly below this value, so no clear bias appears. Confidence intervals include unity in most cases, which indicates some consistency between the historical simulation analysed and the expected responses involved. Detection (i.e. rejection of β = 0) occurs for each simulation and each forcing. Note that this is not necessarily expected, and shows that the signal-to-noise ratios from the CNRM-CM5 model are high enough to allow detection of each external forcing. Note, too, that the scaling factors estimated by ROF for the NAT forcing are more sensitive to the simulation, and that the confidence intervals are larger, which is consistent with a lower signal-to-noise ratio than for the ANT forcing.

The 3-forcing analysis (Fig. 5, case ROF, T4) also illustrates the accuracy of ROF. Best estimates are still distributed around unity. The estimated confidence intervals are still consistent with 1, but inconsistent with 0, for virtually each forcing and each simulation. The biggest difference between the 2-forcing and the 3-forcing analyses lies in the size of the confidence intervals estimated. The uncertainty on the scaling factors from both GHG and AER forcings is much larger than that associated with the ANT forcing in the 2-forcing analysis. This provides a useful illustration of how uncertainty increases as the number of external forcings considered increases in such an analysis. Note, however, that this phenomenon may also be partly explained by the size of the ensembles used for estimating the response to each forcing (e.g. 6 for GHG versus 10 for ANT) and by some compensation between the GHG and AER forcings (e.g. warming vs cooling, with rather similar temporal shapes), making the sum of the two (i.e. the response to ANT) more constrained than each component (i.e. GHG or AER). Conversely, the best estimates and confidence intervals for the NAT forcing are virtually identical to those obtained in the 2-forcing analysis (i.e. results in both cases are virtually the same for each simulation).

For both the 2-forcing and 3-forcing analyses, the results of the residual consistency test (RCT) may be regarded as somewhat unexpected. In all cases, the p value is high, indicating that the test was passed. Nevertheless, the p values obtained are actually too high, and do not appear to follow a uniform distribution on [0,1] as expected under H ₀. This phenomenon is discussed further below.

Secondly, the comparison of the results from ROF under different filtering of the data (spatial dimension) allows us to discuss the benefits of taking a relatively high spatial dimension into account. In a 2-forcing analysis, the impact of increasing the spatial dimension is rather low in terms of best estimates and confidence intervals. In particular, the scaling factor estimates are only slightly more constrained with a high spatial dimension (i.e. the typical size of the confidence intervals is somewhat reduced; this is clearer in the case of the NAT forcing). This is fairly consistent with a primarily global response to the ANT and NAT forcings. In a 3-forcing analysis, the conclusion is clearer, as the size of the confidence intervals is more substantially reduced when the dimension increases. This reduction is particularly clear when the results with T0-truncation are compared with those for T4-truncation (e.g. the size of the β _AER confidence intervals is reduced by about a factor of 2), but some reduction also occurs with T1 or T2 spherical harmonics. This is also clearer in the case of the GHG and AER forcings, which makes sense physically, because the geographical patterns of response help distinguish AER from GHG.

The results from the residual consistency test are much more dependent on the choice of the spatial dimension, both under 2-forcing and 3-forcing analyses. With T0 spherical harmonics, the p values from the RCT are scattered nearly as expected (i.e. roughly consistent with the H ₀ uniform distribution). There is, however, a slight tendency towards smaller p values than expected (e.g. 3 out of 10 cases under the 10 % threshold). This may be due to a variability of the decadal global mean temperature in the CNRM-CM5 model being slightly higher than that simulated on average by CMIP models (a precise computation indicates that the variance is 25 % higher in CNRM-CM5). With other resolutions, the p values are closer to 1 and, as the resolution increases, higher than expected. For instance, there are no p values lower than 0.5 at T2 or T4 resolutions. This suggests that the null distribution of the RCT, which is used to compute the p value, is not suitably estimated. Several explanations may be involved here. Primarily, as mentioned in Sect. 3.4, the null-distribution used here was derived from Monte Carlo simulations, which are somewhat sensitive to the value of the input parameters used, in particular the covariance matrix C. MC simulations based on alternative, plausible values of C (e.g. other estimates than the LW estimate), may provide null-distributions in better agreement with the values found in this perfect model framework. However, as the true value of C remains unknown, we choose to continue to use the LW estimate to simulate the null-distribution, as it has been shown to be well-conditioned for large-dimensional covariance matrices. Therefore, the results from the RCT must be interpreted carefully. Finally, note that other potential explanations of this phenomenon may also be involved. For instance, the spatio-temporal variability from CNRM-CM5 taken as a whole (i.e. not only the variability of the global mean) could be lower than the assumed CMIP variability.

Third, the comparison between ROF and EOF projection is illustrative. The most important comment stems from the comparison of the results from the two approaches under the 3-forcing analysis. In that case, the best estimates as computed by EOF projection are significantly more dispersed than those of ROF (case T4), and the confidence intervals obtained with EOF projection appear to be significantly larger. This occurs for both k = 15 and k = 30. This is very consistent with the results from the Monte Carlo idealised experiments, essentially showing that the EOF projection estimate is less accurate with respect to the mean-square error. Although both techniques are based on T4 spherical harmonics, the reduction of the spatial dimension involved in EOF projection (projection onto k EOFs) leads to the loss of some of the spatial information that discriminates between forcings. This results in a less accurate estimation.

The comparison of EOF projection with the results obtained with ROF under different pre-processings is also interesting. A first comment concerns the size of the confidence intervals computed, which appears closer to that obtained for ROF with T0 or T1 spherical harmonics (clearer under 3-forcing analysis). A second comment concerns the results obtained from each individual historical simulation. In both cases, the results from EOF projection appear to be very close to the results obtained with ROF using only the global average (i.e. T0), or T1 spherical harmonics. This occurs in terms of both best estimate and confidence interval. This also occurs, in particular in the case k = 15, in terms of the p value from the RCT. This suggests that, with such a treatment, the spatial shape of each pattern constrains the scaling factor estimate very little. The similarity, if any, is higher than with the results obtained with ROF based on T4 spherical harmonics. Again, this suggests that the spatial information is rather weakly involved.

5 Conclusions

The Regularised Optimal Fingerprinting (ROF) version of the optimal fingerprinting algorithm is relevant to the attribution problem, under both the OLS and the TLS statistical models. The implementation described here is very close to those presented in AT99 or AS03, and leaves the majority of their algorithms unchanged. In particular, ROF may be applied with a treatment of internal climate variability based on the computation of two independent estimates from a set of long control simulations (or equivalent), as was done in AT99 and AS03. The main difference with other versions of the optimal fingerprinting method then lies in the use of a regularised estimate of the internal variability covariance matrix for optimisation (or, equivalently, for prewhitening). Another important difference comes from the implementation of the residual consistency test, where a more accurate estimation of the null-distribution is proposed.

ROF avoids the difficult and partly arbitrary choice of a truncation k, which is required in EOF projection. In this respect, ROF helps to make the implementation of optimal fingerprinting more objective. However, some arbitrary choices are still required with ROF in the pre-processing step. In particular, the problem of choosing an appropriate degree of spatial and temporal filtering remains.

The accuracy of ROF is higher than that of EOF projection in all the cases considered in this paper. Accuracy is understood here with respect to the mean square error of the scaling factor estimates. This result was shown to hold for both the OLS and TLS statistical models, for all possible EOF truncations, and for several assumptions regarding the number of independent realisations available from control simulations. This supports the conclusion that ROF is also a little more efficient than previous implementations.

The application of ROF to idealised data (namely historical simulations from a CGCM) reinforces these conclusions. First, it provides a realistic illustration of the benefits of avoiding the choice of the EOF truncation k. Second, it shows that the results in terms of the accuracy of the scaling factor estimation are improved with ROF when the dimension of the data is not reduced a priori. In particular, the results provided by the ROF method based on T4 spherical harmonics are more accurate than those provided by EOF projection at the same spatial resolution. The results provided by ROF based on a T4 spatial resolution are also more accurate than those obtained with the same method at lower spatial resolutions (e.g. global mean only).

ROF then allows us to deal more objectively and a little more efficiently with the typically high dimensions of climate datasets. All applications illustrated in this paper were, however, carried out after an initial large reduction of the dimension via pre-processing (both in space and time). This first step of the study remains partly arbitrary and appears difficult to overcome from a statistical point of view. In this respect, the development of a wholly objective version of the optimal fingerprinting algorithm, which would be able to pre-process the data optimally by itself, remains a challenge.

Finally, we have focused only on an idealised analysis here, as the main goal of this paper is to provide a first illustration of the capabilities of ROF for analysing global changes with respect to attribution. The application of this new method to real observations is addressed in Ribes and Terray (2013), based on the ensembles of simulations recently provided by CMIP5. Another potentially attractive extension of this work, still in the methodological area, would be to extend ROF to the recently developed error in variables method (EIV, see Huntingford et al. 2006), designed for multi-model attribution studies.

Appendices

Appendix 1: Simulations used for evaluating internal variability

We list here the simulations used to estimate the internal climate variability. The control simulations with pre-industrial conditions are presented in Table 1 (CMIP3 models), and in Table 2 (CMIP5 models). The name of the global coupled model is given together with the length of the simulation, and the number of non-overlapping 110-year segments obtained. The CMIP5 ensembles of simulations used are listed in Table 3, with the name of the model, a subjective name of the ensemble (basically which external forcings were imposed), and the number of simulations, which is also the number of independent realisations provided by the ensemble.

Table 1 List of CMIP3 control simulations used for evaluating the internal climate variability

Table 2 List of CMIP5 control simulations used for evaluating the internal climate variability

Table 3 List of CMIP5 ensembles of simulations used to estimate the internal climate variability

Appendix 2: On-line scripts

The main scripts used in this paper are available on-line via the CNRM-GAME website at the following URL: http://www.cnrm-game.fr/spip.php?article23&lang=en. The routines are written for Scilab, which is a free open-source software package for numerical computation, similar to MatLab. The package allows ROF to be applied in both OLS and TLS statistical models.

The purpose of this package is similar to that of the Optimal Detection Package (ODP), maintained by Dáithí Stone, available at (http://web.csag.uct.ac.za/daithi/idl_lib/detect/idl_lib.html) and written for IDL software. We should point out that the ODP probably includes more options and permits the use of a wider range of statistical analyses introduced over the last 15 years. The interest of our package lies in the implementation of ROF and also in its availability in free, open-source software. Note that our routines were developed independently of the ODP.

At present, two differences have been noted between ODP and our package, both with the TLS statistical model. The first involves the possibility of computing 1-dimensional confidence intervals that have some bounds but that include an infinite slope. The second concerns the uncertainty analysis in TLS. This treatment is described in AS03 and involves the computation of revised singular values $\hat{\lambda}_{i}$ of the matrix Z (following the notation of AS03). We used the formula mentioned in AS03 (formula (34)), i.e.

$$ \hat{\lambda}_i^2 = \frac{u_i^T Z Z^T u_i}{\frac{1}{\mu} u_i^T P \hat{\Upupsilon}_2 \hat{\Upupsilon}_2^T P^T u_i}. $$

(3)

The formula implemented within the current version of ODP can be written as

$$ \hat{\lambda}_{i}^{2} = \frac{u_{i}^{T} Z Z^{T} u_{i}}{\frac{1}{\mu} (u_{i}^{\#2})^{T} (P \hat{\Upupsilon}_{2})^{\#2} {\bf 1}_{n_{2}}}, $$

(4)

where A ^#2 denotes the matrix with entries (a ² _ij ) _i,j if A = (a _ij ) _i,j , and where ${\bf 1}_{n_{2}}$ is a vector of dimension n ₂, with ${\bf 1}_{n_{2}}=(1, \dots, 1)^{T}$.

Appendix 3: Consistency check within the OLS approach

Here we discuss Equation (20) of AT99, used to construct a residual consistency test. Both the statistical model and the consistency check are first recalled briefly in order to introduce the notation.

The OLS statistical model may be seen as the classical regression model:

$$ Y = X \beta + \varepsilon, $$

(5)

where $\hbox{Cov}(\varepsilon) = C$ is assumed to be known. The optimal estimate of β can then be written as the generalised least-square estimate:

$$\widehat{\beta} = (X' C^{-1} X)^{-1} X' C^{-1} Y. $$

(6)

After having estimated β, the residual term $\varepsilon$ can be estimated by

$$ \widehat{\varepsilon} = Y - X \widehat{\beta}, $$

(7)

and then we have

$$ \widehat{\varepsilon}' C^{-1} \widehat{\varepsilon} \sim \chi^2(n-l), $$

(8)

where l = rank(X).

The last equation can be used to assess whether the estimated residuals $\widehat{\varepsilon}$ are consistent with the covariance matrix C. In particular, if the estimated residuals are greater than expected, the quantity $\widehat{\varepsilon}' C^{-1} \widehat{\varepsilon}$ may be outside the range of values expected in (8) (e.g. higher than the 95 % quantile of the χ²(n − l) distribution). This allows a residual consistency test based on Eq. (8) (Allen and Tett 1999) to be introduced.

As noted by AT99 themselves, the covariance matrix C is usually not known, and is estimated from control integration. This estimation procedure means that C is only approximately known. Let us now consider that climate models simulate the real climate perfectly, and that the covariance matrix that would be provided by an infinitely-long control integration is the true one. With these assumptions, the covariance matrices $\widehat{C}_{1}$ and $\widehat{C}_{2}$ used respectively for computing the generalised least-square estimate and for uncertainty analysis, satisfy

$$ \widehat{C}_1 \sim \frac{1}{n_1} W(n_1,C), $$

(9)

$$ \widehat{C}_2 \sim \frac{1}{n_2} W(n_2,C), $$

(10)

where W denotes the Wishart distribution and n ₁ and n ₂ are the number of independent realisations used as a basis for estimating $\widehat{C}_{1}$ and $\widehat{C}_{2}$.

Due to the uncertainty in (9, 10), $\widehat{C}_{1} \neq C$, and (8) no longer holds. The discussion in Sect. 4 of AT99 deals with the case where:

• the exact generalised least-square estimate is used, i.e. $\widehat{C}_{1} = C$ (or equivalently, no error arises from the use of an imperfect prewhitening),

• the consistency test is based on imperfectly estimated covariance matrix $\widehat{C}_{2}$, i.e. $\widehat{C}_{2} \sim \frac{1}{n_{2}} W(n_{2},C)$.

With these assumptions, it can be shown that

$$ \widehat{\varepsilon}' \widehat{C}_{2}^{-1} \widehat{\varepsilon} = \frac{\widehat{\varepsilon}' \widehat{C}_{2}^{-1} \widehat{\varepsilon}}{\widehat{\varepsilon}' C^{-1} \widehat{\varepsilon}} \,\,\, \widehat{\varepsilon}' C^{-1} \widehat{\varepsilon}, $$

(11)

$$ \sim n_{2} \,\, \frac{1}{\chi^{2}(n_{2}-n+1)} \,\, \chi^{2}(n-l), $$

(12)

$$ \sim \frac{n_2 (n-l)}{n_2-n+1} \,\, F(n-l,n_2-n+1) $$

(13)

The formula provided in AT99 using the same assumptions was somewhat different:

$$ \widehat{\varepsilon}' \widehat{C}_2^{-1} \widehat{\varepsilon}\,\sim\,(n-l) F(n-l,n_2). $$

(14)

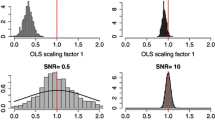
Both formulas are consistent, however, in the case where n ₂ ≫ n. AT99 focused on the EOF projection approach, so the size n of Y was actually the EOF truncation k (i.e. n = k), which was rather small. Therefore, this assumption was more reasonable.

The discrepancies between the three parametric distributions mentioned above [respectively Eqs. (8), (13) and (14)], and the $\mathcal{D}$-distribution as evaluated from Monte Carlo simulations (see Sect. 3.4), are illustrated in Fig. 6. The Monte Carlo simulations are performed with input parameters C and X corresponding to real-case estimated values, at T0 and T2 resolutions: C is the covariance matrix as estimated by the LW estimate from the full sample of control segments Z, and X is the expected responses as simulated by the CNRM-CM5 model (in a 2-forcing analysis, so that l = 2).

Fig. 6

H ₀ distribution of the residual consistency test in OLS analysis, as evaluated from different formulas and under different assumptions: the χ² distribution (blue), the Fisher distribution used in AT99 (red), the corrected Fisher distribution given in Eq. (13) (green), and the distribution derived from Monte Carlo simulations (black histogram)

As expected, the discrepancies between $\mathcal{D}$ and the parametric formulas used by AT99 tend to be reduced when n is much smaller than n ₂ (left-hand side). They become much larger when n is close to n ₂ (right-hand side). In such a case, the distributions have virtually disjoint supports, so the use of one instead of the other would result in very different conclusions. Conversely, the distribution defined by Eq. (13) appears to be relatively suitable in these cases with ROF. This close agreement between the results from the MC simulations and formula (13), where the value of C doesn’t appear, suggests that the null-distribution is not very sensitive to the initial value of C in the MC algorithm.

Finally, it may be noted that the distribution $\mathcal{D}$ is still well defined in the case where n > n ₁, because the regularised estimate $\widehat{C}_{1}$ is always invertible. The case where n > n ₂ is more problematic, because $\widehat{C}_{2}$ is then not invertible. A $\mathcal{D}$-distribution may, however, be computed via Monte Carlo simulations by using the pseudo-inverse of $\widehat{C}_{2}$. In such a case, however, the revisited parametric formula provided by Eq. (13) cannot be used, because n ₂ − n − 1 is negative. This is the reason why results at T4 resolution are not shown in Fig. 6.

Appendix 4: Consistency check within the TLS approach

The discrepancies between the two parametric distributions proposed by AS03 and the null-distribution as evaluated from Monte Carlo simulations when ROF is used, are illustrated in Fig. 7. The Monte Carlo simulations are performed with input parameters C and X corresponding to real-case estimated values, at T0, T2 and T4 resolutions: C is the covariance matrix as estimated by the LW estimate from the full sample of control segments Z, X is the expected responses as simulated by the CNRM-CM5 model (in a 2-forcing analysis, so that l = 2).

Fig. 7

H ₀ distribution of the residual consistency test in TLS analysis for ROF, as evaluated from different formulas and under different assumptions: the χ² distribution used by AS03 (blue), the Fisher distribution used by AS03 (red), and the distribution derived from Monte Carlo simulations (black histogram)

The corresponding results for EOF projection are shown in Fig. 8. The Monte Carlo simulations are then performed with the same input parameters C and X as in Fig. 7 at T4 resolution. Then, the pre-whitening applied in the Monte Carlo algorithm is based on EOF projection instead of involving the LW estimate. Results are shown for several values of the EOF truncation k, corresponding to those used in Part II.

Fig. 8

H ₀ distribution of the residual consistency test in TLS analysis for EOF projection, as evaluated from different formulas and under different assumptions: the χ² distribution used by AS03 (blue), the Fisher distribution used by AS03 (red), and the distribution derived from Monte Carlo simulations (black histogram)