Estimating signal amplitudes in optimal fingerprinting, part I: theory

Abstract

There is increasingly clear evidence that human influence has contributed substantially to the large-scale climatic changes that have occurred over the past few decades. Attention is now turning to the physical implications of the emerging anthropogenic signal. Of particular interest is the question of whether current climate models may be over- or under-estimating the amplitude of the climate system's response to external forcing, including anthropogenic. Evidence of a significant error in a model-simulated response amplitude would indicate the existence of amplifying or damping mechanisms that are inadequately represented in the model. The range of uncertainty in the factor by which we can scale model-simulated changes while remaining consistent with observed change provides an estimate of uncertainty in model-based predictions. With any model that displays a realistic level of internal variability, the problem of estimating this factor is complicated by the fact that it represents a ratio between two incompletely known quantities: both observed and simulated responses are subject to sampling uncertainty, primarily due to internal chaotic variability. Sampling uncertainty in the simulated response can be reduced, but not eliminated, through ensemble simulations. Accurate estimation of these scaling factors requires a modification of the standard "optimal fingerprinting" algorithm for climate change detection, drawing on the conventional "total least squares" approach discussed in the statistical literature. Code for both variants of optimal fingerprinting can be found on http://www.climateprediction.net/detection.

1 Introduction

This study describes a variant of the regression-based technique of climate change detection and attribution that is generally known as "optimal fingerprinting" (see, e.g. Hasselmann 1979, 1993, 1997; Bell 1986; North et al. 1995; Leroy 1998; Allen and Tett 1999). The fingerprinting approach is to define a pattern of response to external climate forcing using a climate model and then to estimate the amplitude of that pattern, or signal, in the observed climate record. If the hypothesis of zero pattern-amplitude can be rejected with confidence, then that signal is said to be detected.

The standard approach to optimal fingerprinting assumes that the model-simulated response-pattern is known exactly, that is, it is not subject to sampling uncertainty. By sampling uncertainty, we mean the variability in the model-simulated response which would be observed if the simulation (or ensemble of simulations) were repeated with an identical model and forcing and different initial conditions. A more general definition of sampling uncertainty would encompass how the response-pattern might vary were we to use a different but equally plausible model or forcing series. The generalisation of the algorithm described here to encompass these wider sources of uncertainty (which are also much more difficult to quantify) is still in progress: the key problem here is obtaining meaningful statistics of variability resulting from systematic inter-model differences given the small number of full-scale climate models currently available (although see Allen 1999; Stainforth et al. 2002; Allen and Ingram 2002).

Early applications using atmosphere–ocean general circulation models (A-OGCMs) in optimal fingerprinting ensured that the assumption of zero sampling uncertainty was satisfied by using response-patterns derived from simulations of mid-twenty first century climate change (e.g. Hegerl et al. 1996, 1997). By that time, the signal-to-noise is so high that sampling uncertainty in the response-pattern can be safely neglected. The main limitation of this approach is that it confines the analysis to spatial patterns of trends: twenty first century information cannot be used to determine the temporal evolution of the climate response to external forcing over the past few decades. This excludes information on the differing time-histories of different components of anthropogenic climate change and, even more importantly, excludes direct consideration of naturally-forced signals (even if the information were available, the model response to twenty first century solar forcing is not relevant to its twentieth century response).

Direct comparison of noisy A-OGCM or AGCM simulations and the observed record can proceed through correlation-based approaches, as in Barnett and Schlesinger (1987); Santer et al. (1993, 1996); Tett et al. (1996), and Folland et al. (1998). The difficulty here, again, lies in physical interpretation. Even if the correlation between modelled and observed changes is very high, this does not provide any information on whether the model-simulated amplitude of the change is accurate.

The simplest results to interpret are those based on a direct comparison of "like with like": A-OGCM simulations of twentieth century climate change compared directly with the corresponding period in the observed record, exploiting both pattern and amplitude information in the model-data comparison (Allen and Tett 1999; Tett et al. 1999; Stott et al. 2001; Allen et al. 2001). To date, such studies have used ensembles to reduce sampling uncertainty in model-simulated responses and have not attempted to account for this uncertainty explicitly in their analyses. The problem, of course, is that even with the four-member ensembles used in the studies mentioned, sampling uncertainty is still far from negligible, particularly in weak signal-to-noise situations such as the analysis of the response to solar forcing. With more advanced models (Röckner et al. 1999), even four-member ensembles may be unfeasible.

We describe a revised approach to optimal fingerprinting that provides unbiased estimates of pattern-amplitudes and amplitude uncertainties when model-simulated response-patterns are subject to a finite level of noise. The algorithm is applicable even in the case where the model is subject to the same level of noise as the observations, as is the case (assuming model-simulated variability is realistic) in a single-member ensemble simulation. Uncertainties will typically be quite large in this situation, for obvious reasons: if the signal is poorly known in the first place, the uncertainty in its amplitude in a noisy observed record is even larger.

Accounting for this noise is particularly important if pattern-amplitudes are to be subject to a physical interpretation, such as addressing the question of whether the A-OGCM is over- or under-estimating the response to a particular forcing agent. Standard estimates are subject to a known bias towards zero and may therefore give a misleading impression of a weaker response in the real world than that simulated by the models, even if the models are perfectly accurate. The extent of this bias in typical climate change detection problems, and the extent to which we can eliminate it, is assessed in an accompanying study: Stott et al. (2003).

Estimated upper bounds are particularly severely affected. This should be intuitively clear from the following considerations: in estimating a pattern amplitude, we are estimating the ratio between the amplitude of the observed and the model-simulated response. The presence of noise in the denominator means that the underlying noise-free model-simulated response (that which we would obtain from a hypothetical infinite ensemble) could be smaller than the response simulated in this particular experiment. If the uncertainty is large enough that this unknown noise-free response could approach zero, then the ratio between the noise-free model-simulated response and the observed response could be very high, even infinite.

This point is illustrated in Fig. 1, which shows hypothetical estimation results based on a single observable quantity (global mean temperature trend, for example) that is subject to unit variance noise due to Gaussian internal climate variability. We assume that the model-simulated variability in this quantity is realistic and a four-member ensemble is available to simulate the response to external forcing, so the variance of the simulation is one quarter that of the observations. Suppose we find an observed trend of two units and an ensemble-mean model-simulated trend of one unit. The distribution of noise-free, underlying trends in the real world consistent with this observation is shown as the solid line in the upper panel, while the distribution of noise-free model trends (those that we would obtain given a hypothetical infinite ensemble) consistent with this four-member ensemble mean is shown as the dashed line. The question is, given only this single observation and this four-member ensemble simulation, by how much can we conclude that the model is over- or under-estimating the underlying noise-free response, and with what range of uncertainty?

Fig. 1.

a: distributions of underlying, noise-free trends in the real world (solid line) and a hypothetical climate model (dashed line) that are consistent with an observed trend of two units, a four-member (ℓ = 4) ensemble mean trend of one unit and known unit variance in both modelled and observed trends. b, dashed line: estimated distribution of ratios of real-world versus model-simulated trends implied by conventional optimal fingerprinting (obtained simply by taking the model-simulated trend as given and accounting only for variance in the observations). b, dotted line: the same but, including the 1 + 1/ℓ correction for finite ensemble size (see text). b, solid line: true distribution of ratios obtained from random samples from the two distributions shown in the a

The answer provided by standard optimal fingerprinting, neglecting uncertainty in the model simulation altogether, is shown as the dashed line in the lower panel. This is obtained simply by dividing the distribution of trends consistent with that observed by the mean trend obtained in this particular ensemble. This is an example of a regression problem in which the observations comprise only a single observable quantity, the trend: in this trivial case, the standard regression solution is to divide the observed trend and its estimated standard deviation by the model-simulated trend, which is unity in this example.

The correct answer for the distribution of ratios of observed/model-simulated responses consistent with these results is shown as the solid line in the lower panel, obtained simply by computing the distribution of ratios from samples drawn at random from the two distributions shown in the upper panel (the distribution of the ratio of two normally-distributed quantities is known as a Cauchy distribution). The median (50^th percentile) of this distribution is close to two, which is the estimate based on standard regression. In this case, only a small fraction of underlying noise-free model-simulated trends consistent with this ensemble simulation are negative and, provided the distribution of the denominator does not straddle zero, the median of the ratio of two symmetrically distributed quantities will be close to the ratio of their medians. The true underlying distribution, however, falls off less rapidly than the standard regression-based estimate as we move to percentiles higher than the 50^th. Hence any estimate of uncertainty in the ratio of observed/model-simulated signal amplitudes that is based on standard regression will tend to underestimate the likelihood of high ratios. Points in this "fat tail" at the high end of the distribution correspond to the model understating the true observed response by a substantial margin, which is clearly an outcome whose likelihood we would like to pin down. Quantifying these likelihoods, or inferring the correct distribution of observed/model-simulated signal amplitudes from a single observation and ensemble simulation, in the more general case of multiple observable quantities, is the purpose of the algorithm provided in this study.

Several authors using the standard regression-based approach, aware of the presence of noise in their model-simulated signals, attempted to correct for its impact by scaling the estimated variance of their regression-based estimates by 1 + 1/ℓ, where ℓ is the ensemble size (Allen and Tett 1999; Tett et al. 1999; Stott et al. 2000). The impact of this correction is shown by the dotted line in the lower panel. As noted by those authors, this correction is only asymptotically valid in the limit of high signal-to-noise, which is not the case here. Both standard and "corrected" variants of optimal fingerprinting suggest a very low probability that the true response in the "real world" exceeds 4.5 times the "true" (noise-free, infinite ensemble) model response, whereas a significant fraction of the true distribution of observed/model-simulated trend ratios lies above this threshold.

Before proceeding to details, we would like to stress that, although the algorithm described later allows the bias due to sampling uncertainty in model-simulated responses to be quantified and eliminated, it is not a substitute for reducing this uncertainty directly through the use of larger ensembles. The size of ensemble required to pin down the response to an external forcing agent accurately depends, of course, on the signal-to-noise ratio as in Wehner (2000). For strong signals, such as the response to greenhouse gases in the large-scale surface temperature record over the past few decades (Tett et al. 1999; Stott et al. 2000), a 3- to 4-member ensemble may be enough, but for weaker signals such as the response to solar forcing, larger ensembles are likely to be required. In the drive for higher-resolution models, it should not be forgotten that single-member ensembles are of relatively little value in the analysis of observed climate change, so a compromise will always be required between model resolution and ensemble size.

One way of avoiding the use of large ensembles while still relying on the standard optimal fingerprinting algorithm for model-data comparison would be to use a noise-free model, such as an energy balance model, to simulate the response-patterns (e.g. Stevens and North 1996; Wigley et al. 1997; North and Stevens 1998; Knutti et al. 2002). Unless, however, the spatio-temporal pattern of response simulated by the EBM can be assumed to be accurate (which seems implausible, since so many important processes are omitted from these models), the advantage is illusory. In a straightforward detection problem (assessing whether the amplitude of a particular pattern is significantly different from zero), inaccuracies in the model-simulated pattern are of secondary importance because, although they may reduce the power of the algorithm, they are unlikely to lead to a false-positive result. If, on the other hand, pattern-amplitudes are to be interpreted physically (e.g. Allen et al. 2000; North and Wu (2001), inaccuracies in model-simluated responses become very important. A low estimated amplitude of an incorrectly specified greenhouse response pattern does not necessarily mean that the true greenhouse response in the real world is small: it may simply mean that the algorithm was looking in the wrong direction. An even more fundamental problem is that EBMs are no longer the primary tools for detailed climate change prediction, so the information that a particular EBM is over- or under-estimating the response to a particular forcing agent is of limited practical value unless it can be related to predictions of more detailed models.

2 Optimal fingerprinting as linear regression

2.1 Estimation procedure

We begin by summarising the standard linear regression algorithm as applied to the detection of climate change in order to introduce notation and make the link between total least squares and the standard approach. The standard detection model assuming noise-free model-simulated response-patterns is as follows:

$$ {\bf y} = \sum\limits_{i = 1}^m {{\bf x}_i \beta _i + \user2{\upsilon } = {\bf X}\user2{\beta } + \user2{\upsilon }} $$

(1)

where y is the rank-n vector of observations, the m columns of X are the model-simulated response-patterns, x _i , the elements of β, β _i , are the unknown pattern-amplitudes to be estimated and ν is the climate noise in the observations. We will use unadorned suffixes, such as x _i or β _i , to distiguish between different matrices, vectors and scalars, and suffixes outside square brackets to identify elements within matrices and vectors. Hence [X] _ij denotes the j ^th element of the i ^th column of the matrix X, and [x _i ] _j denotes the j ^th element of the vector x _i .

The climate noise covariance,

$$ {\bf C}_N \equiv \user1{{\cal E}}\left( {\user2{\upsilon \upsilon }^T } \right), $$

(2)

where ℰ denotes the expectation operator, is generally unknown and must be estimated from a control run of a climate model. Because the noise is generally far from white, or C _N ≠ σ ² I, unweighted least squares regression gives highly inefficient estimators for β and strongly biased estimates of the errors in β. The solution is to introduce a "pre-whitening" operator, P, defined such that

$$ \user1{{\cal E}}\left( {{\bf P}\user2{\upsilon \upsilon }^T {\bf P}^T } \right) = {\bf I}_\kappa , $$

(3)

where I _κ is the rank-κ unit matrix. Note that κ, the rank of P, may be much smaller than n, the rank of y, in general, a full-rank pre-whitening operator (which would render the noise variance equal on all spatio-temporal scales) will not be available because small-scale noise variance is either unknown or expected to be poorly simulated by the climate model.

Because P υ is independent, identically distributed (i.i.d.) "white noise", the best (lowest-variance) linear unbiased estimator of β, $\user2{\tilde \beta }$ is given by minimisation of the merit function

$$ r^2 \left( {\user2{\tilde \beta }} \right) \equiv \left( {{\bf PX}\user2{\tilde \beta } - {\bf Py}} \right)^T \left( {{\bf PX}\user2{\tilde \beta } - {\bf Py}} \right) \equiv \user2{\tilde \upsilon }^T {\bf P}^T {\bf P}\user2{\tilde \upsilon } $$

(4)

with respect to $\user2{\tilde \beta }$ . At the minimum,

$$ \user2{\tilde \beta } = \left( {{\bf X}^T {\bf P}^T {\bf PX}} \right)^{ - 1} {\bf X}^T {\bf P}^T {\bf Py} \equiv {\bf F}^T {\bf y}, $$

(5)

where the rows of F are the "distinguishing fingerprints" (Allen and Tett 1999) and

$$ r_{\min }^2 \sim \chi _{\kappa - m}^2 . $$

(6)

If we ignore uncertainty in the estimate of the noise variance, discussed later, $\user2{\tilde \beta }$ is normally distributed with mean β and variance

$$ \matrix{ {{\rm V}\left( {\user2{\tilde \beta }} \right)} & \equiv & {\user1{{\cal E}}\left( {\user2{\tilde \beta } - \user2{\beta }} \right)\left( {\user2{\tilde \beta } - \user2{\beta }} \right)^T } \cr {} & = & {\left( {{\bf X}^T {\bf P}^T {\bf PX}} \right)^{ - 1} .} \cr } $$

(7, 8)

Equivalently,

$$ \matrix{ {\left( {\user2{\tilde \beta } - \user2{\beta }} \right)^T \left( {{\bf X}^T {\bf P}^T {\bf PX}} \right)\left( {\user2{\tilde \beta } - \user2{\beta }} \right)} \hfill & = \hfill & {\Delta r^2 \left( \user2{\beta } \right) \equiv r^2 \left( \user2{\beta } \right) - r_{\min }^2 } \hfill \cr {} \hfill & \sim \hfill & {\chi _{\min }^2 .} \hfill \cr } $$

(9, 10)

To map a desired confidence region, therefore, we determine the critical value of the appropriate distribution (e.g. $\chi _m^2 \left( {0.05} \right)$) and plot the surface of values of β for which Δr ²(β) is equal to that critical value. In the absence of any additional information on the likely values of β, we can then expect (at this confidence level) the vector of true coefficient values to lie within this region.

Many applications require an estimate of uncertainty in individual signal amplitudes, or in specific combinations of signals, rather than the joint uncertainty in all components of $\user2{\tilde \beta }$. For example, to quantify uncertainty in the trend in global mean temperature over a particular period, we introduce a vector c, where c _i is the corresponding trend in the model simulation which provides the i ^th column of X. The vector $\user2{\tilde \beta }$ represents the combination of model-simulated signals which best reproduces the observations, so the best-guess trend over this period is simply $\tilde \phi = {\bf c}^T \user2{\tilde \beta }$ . The variance in $\tilde \phi$ is provided by ${\rm V}\left( {\tilde \phi } \right) = {\bf c}^T {\rm V}\left( {\user2{\tilde \beta }} \right){\bf c}$ . To determine a confidence interval, we find the values of φ for which

$$ {{\left( {\phi - \tilde \phi } \right)^2 } \over {{\bf c}^T {\rm V}\left( {\user2{\tilde \beta }} \right){\bf c}}} = \chi _1^2 \left( {0.05} \right). $$

(11)

If φ depends on the i ^th signal only (e.g. only one of the signals displays a trend), then the denominator of the LHS of Eq. (11) is proportional to the corresponding diagonal element of ${\rm V}\left( {\user2{\tilde \beta }} \right)$ , or the variance in $\tilde \beta _i$ : $\left[ {{\rm V}\left( {\user2{\tilde \beta }} \right)} \right]_{i,i} = {\rm V}\left( {\tilde \beta _i } \right)$ .

It will prove helpful to note that an equivalent method of computing confidence intervals in individual signals or signal-combinations is to map the surface of values β ₁ for which $\Delta r^2 \left( {\user2{\beta }_1 } \right) = \chi _1^2 \left( {0.05} \right)$. We then compute φ ₁=c ^T β ₁ for all points on this surface, and the limits on the confidence interval are given by the maximum and minimum values of the φ ₁. This is exactly equivalent to Eq. (11) when ${\rm V}\left( {\user2{\tilde \beta }} \right)$ is available (Press et al. 1992), but proves useful when it is not.

2.2 Accounting for uncertainty in the estimated noise variance

Ignoring uncertainty in the estimated noise properties simplifies the analysis but can lead to "artificial skill" (systematic bias towards underestimation of uncertainties) in a climate change detection context (Bell 1986). The simplest way to deal with this problem is to base the uncertainty analysis on a set of ν noise realisations, ${\bf \hat \Upsilon }_2$ , which are statistically independent of the noise realisations, ${\bf \hat \Upsilon }_1$ , used to estimate P. The ν columns of ${\bf \hat \Upsilon }_2$ correspond to y-like vectors of pure noise ("pseudo-observations") drawn, for example, from ν statistically independent segments of a control integration of a climate model. If adjacent columns of ${\bf \hat \Upsilon }_2$ are not statistically independent, the degrees of freedom of covariance estimated based on this noise realisation, ν ₂ , will be less than the number of columns, ν. If these pseudo-observations are drawn from a control integration of a climate model, it is standard practice to use overlapping segments in order to maximise the number that can be extracted from a limited length integration. In this case, ν ₂ is approximately equal to 1.5 times the number of non-overlapping segments in the control (Allen and Smith 1996).

The standard fingerprinting algorithm is linear, so ${\rm V}\left( {\user2{\tilde \beta }} \right)$ does not depend on the actual amplitude of the signal in the observations, y. An estimate of ${\rm V}\left( {\user2{\tilde \beta }} \right)$ can therefore be obtained by applying the same operator, F ^T, that was used to extract $\user2{\tilde \beta }$ from y to the columns of ${\bf \hat \Upsilon }_2$ and estimating the variance of the result:

$$ {\rm \hat V}\left( {\tilde \beta } \right) \equiv {{{\bf F}^T {\bf \hat \Upsilon }_2 {\bf \hat \Upsilon }_2^T {\bf F}} \over {\nu _2 }} $$

(12)

Taking into account the sampling uncertainty in ${\bf \hat \Upsilon }_2$ gives

$$ \left( {\tilde \beta - \beta } \right)^T {\rm \hat V}\left( {\tilde \beta } \right)^{ - 1} \left( {\tilde \beta - \beta } \right) \sim mF_{m,\nu _2 } , $$

(13)

which can be used in place of Eq. (10) to provide confidence intervals on $\user2{\tilde \beta }$ .

We also have, to a reasonably good approximation, that

$$ \hat r_{\min }^2 = \sum\limits_{i = 1}^\kappa {{{\left( {{\bf P}\user2{\tilde \upsilon \tilde \upsilon }^T {\bf P}^T } \right)_{i,i} } \over {{1 \over {\nu _2 }}\left( {{\bf P\hat \Upsilon }_2^T {\bf P}^T } \right)_{i,i} }} \sim \left( {\kappa - m} \right)F_{\kappa - m,\nu _2 .} } $$

(14)

This provides the F-test for residual consistency proposed in Allen and Tett (1999), ignoring the off-diagonal elements of ${\bf P\hat \Upsilon }_2 {\bf \hat \Upsilon }_2^T {\bf P}^T$ . Since ${\bf C}_{N_2 }$ as defined in Allen and Tett (1999), is non-invertible, there is potential ambiguity as to which pseudo-inverse should be used. The algorithm detailed here gives reasonably unbiased results and is the one used in Allen and Tett (1999), Tett et al. (1999) and Stott et al. (2001).

It should be stressed that Eq. (14) is only approximately valid, since the LHS actually represents the sum of (κ–m)$F_{1,\nu _2 }$ -distributed quantities rather than an F-distributed quantity itself, we are grateful to Simon Tett for drawing this point to our attention. Defining its distribution is complicated by the fact that, in typical climate applications, the individual terms in this sum are not mutually independent, for the following reason. The denominator represents an estimate of the power in the direction defined by the i ^th column of P in the model control, ${\bf \hat \Upsilon }_2$ . A control segment which, by chance, contains more power than the long-term average in direction i is also likely to contain excess power in direction j. In this respect, coupled climate models (and also, presumably, the climate system itself) differ from a typical Markov random field in that a relatively small number of processes with global impact, such as El Niño or fluctuations in the thermohaline circulation, are responsible for the bulk of the variability in simulated variability from epoch to epoch: quiet epochs tend to be quiet everywhere, active epochs active everywhere. This is a difficult hypothesis to test, since these "epochs" correspond to multi-century segments of model control integrations, and we typically only have a very small number of such segments available for any individual model.

Equation (14) is only strictly valid if the correlation in fluctuations in variability in different modes is complete, which might be expected if only one process, such as the model thermohaline circulation, was causing some epochs to be more active than others. As these correlations fall, the expected value of $\hat r_{\min }^2$ falls, introducing a liberal bias into the Allen and Tett (1999), test for residual consistency. Differences are of the same order as the differences arising from uncertainty in the degrees of freedom of the control, ν ₂, so we believe this is an acceptable approximation provided Eq. (14) is simply being used as a post-hoc check for internal consistency and not an integral part of the analysis (Allen and Tett 1999). The fact that the test is subject to a liberal bias serves to emphasise, however, that results in which the test is passed only marginally should be viewed with caution.

Uncertainty intervals in individual signals or signal-combinations are given by replacing Eq. (11) with

$$ {{\left( {\phi - \tilde \phi } \right)^2 } \over {{\bf c}^T {\bf \hat V}\left( {\user2{\tilde \beta }} \right){\bf c}}} = F_{1,\nu _2 } \left( {0.05} \right). $$

(15)

Note that, because $t_{\nu _2 }$ (0.025) = $\sqrt {F_{1,\nu _2 } \left( {0.05} \right)}$ , this corresponds to the same critical value of the two-tailed t-distribution (or the one-tailed distribution at confidence level P/2).

3 Noise in model-simulated response-patterns

We now consider the impact of noise in X as well as in y. In place of the simple statistical model (1), we have:

$$ {\bf y} = \sum\limits_{i = 1}^m {\left( {{\bf x}_i - {\bf \upsilon }_i } \right)\beta _i + {\bf \upsilon }_0 ,} $$

(16)

where x _i is the i ^th model-simulated response-pattern, estimated from a finite ensemble and therefore contaminated with sampling noise υ _i , and υ ₀ is the noise in the observations. We reiterate that the only contributor to the υ _i we consider here is the sampling uncertainty due to the use of a small ensemble of simulations to obtain the response-pattern.

A simple case in which X has only a single column is shown in Fig. 2. The "true", uncontaminated, elements of y ^true ≡ y – υ ₀ and x ^true ≡ x ₁ – υ ₁, are plotted as the crosses, while the observable quantities y and x ₁ are shown as squares. The noise contamination contains both horizontal and vertical components, shown by the thin arrow. Ordinary least squares minimised the vertical distance between the scatter of points and the best fit line, shown by the thick arrow in the left panel.

Fig. 2.

a: application of ordinary least squares regression to a system in which both "model" (plotted in the horizontal) and "observations" (plotted in the vertical) are contaminated with equal levels of noise. "True" values (normally unobservable, except this is a synthetic example, and uncontaminated with any noise) are plotted as crosses along the dotted line; noise-contaminated "observations" and "simulation" are plotted as squares, with the thin arrow showing the orientation of the noise vector in one case; best-fit line and reconstructed observations are shown as the diamonds, with heavy arrow showing the hypothetical noise that is minimised in the OLS algorithm. The best estimate is biased towards zero under OLS and, in this example, the 5–95% confidence interval, shown by the dashed lines, does not include the correct slope. b: application of total least squares regression to the same example. TLS minimises the perpendicular distance from the best-fit line, shown by the heavy arrow, not the vertical distance minimised by OLS. The bias towards zero slope is removed, and the 5–95% confidence interval on the slope now includes the correct value

Having recognised that optimal fingerprinting is simply a variant of linear regression (e.g. Leroy 1998; Allen and Tett 1999), the solution to the problem of noise in both "independent" (predictor) and "dependent" (predictand) variables (being the response-patterns and observations respectively) is readily available (Adcock 1878; Deming 1943; van Huffel and Vanderwaal 1994). Several approaches have been proposed, the differences between which are likely to be much less important than the impact of neglecting response-pattern noise altogether. The total least squares (TLS) algorithm discussed in this study minimises the distance perpendicular to the best-fit line, shown by the thick arrow in the right panel. In this particular example, the 5–95% confidence interval on the slope of the best-fit line includes the correct value only if the TLS algorithm is used: clearly, it is possible to select a synthetic example to force this to be the case, yet if the example is regenerated many times, OLS is indeed found to be subject to a bias towards zero slope which is resolved by the use of TLS.

Among alternatives to TLS, Press et al. (1992), present the "iterated weighted least squares" (IWLS) solution of Jeffreys (1980), reviewed in Lybanon (1984). In the simple case of a straight-line fit (m = 1) and equal and uncorrelated noise in all elements of y and x, the IWLS and TLS solutions are identical, with the only difference being that TLS is a single-step rather than an iterated algorithm. TLS is, however, much simpler to generalise to the multi-signal case (m > 1), not discussed in Press et al. (1992). Ripley and Thompson (1987), discuss biases in the IWLS solution in the situation where the noise variance increases monotonically with signal amplitude. This might be the case in a climate change detection problem, despite the use of a pre-whitening operator which, in principle, assigns equal noise variance to all input variables. The pre-whitening operator is based on a control simulation of a climate model, and because of non-linearities in the real climate system which may not be adequately represented in the model (e.g. Palmer 1999), model-simulated variance may be underestimated in precisely the patterns in which the signal amplitude is large. We therefore follow Ripley and Thompson's (1987) approach, based on maximum likelihood fitting of a functional relationship (MLFR), which is closely related to Adcock's (1878) original solution. We use the name total least squares, following van Huffel and Vanderwaal (1994), since this seems an intuitive way of describing the algorithm.

Since the bias in OLS estimates due to noise in the independent variables can be quantified with a straightforward Monte Carlo simulation (see Fig. 1), a third option would be to use OLS and then correct both estimates and estimated errors to account for this noise systematically, rather than with the ad hoc variance correction used by Allen and Tett (1999). Tett et al. (1999), and Stott et al. (2000). Like IWLS, this approach should, in a single-signal case, give identical results to TLS, and this has, indeed, been verified by Professor David Ritson (personal communication). An implicit algorithm based on Monte Carlo simulation, is, however, more cumbersome to generalise to the multi-signal case. In summary, there are various ways of dealing with the presence of noise in model-simulated response patterns: differences between the different approaches, correctly implemented, are likely to be much less important than neglecting this noise altogether or simply relying on ad hoc corrections. In the general multi-signal case with correlated noise, we believe a full implementation of any valid alternative ends up being as or more complicated than TLS.

3.1 The total least squares algorithm

Having confined ourselves to sampling uncertainty due to finite ensemble size, and assuming model-simulated variability is consistent with that in the real world, we can assume that the noise has the same autocorrelation structure in y as in every column of X. Under these circumstances, the same pre-whitening operator, P, may be applied to all variables. Note that this assumption will only be valid if the dominant source of noise is internal climate variability which is correctly simulated by the model used to generate the columns of X. We should not a priori expect noise due to model error or observation error to share the autocorrelation structure of climate variability, so if either of these is a significant contributor then a more complex treatment is called for which we will pursue elsewhere. If the expected noise variance in X is different from that in y, for example, if ensemble means have been used to reduce noise in model-simulated response-patterns, individual columns of X can simply be scaled up to make the expected noise variance in each the same as that in y, and the same scaling factor(s) applied to the final parameter estimates. For simplicity, we will ignore these scaling factors in the following, so the following discussion applies directly to the case of single-member ensembles.

Given that there is the same noise in each column of X as expected in y, we have

$$ \user1{{\cal E}}\left( {{\bf P}\upsilon _1 \upsilon _i^T {\bf P}^T } \right) = {\bf I}_\kappa $$

(17)

and

$$ \user1{{\cal E}}\left( {{\bf P}\upsilon _0 \upsilon _0^T {\bf P}^T } \right) = {\bf I}_\kappa . $$

(18)

If m′ ≡ m + 1, we define the m′ × κ matrix

$$ {\bf Z} \equiv \left[ {{\bf PX},\;{\bf Py}} \right] $$

(19)

as the observed (pre-whitened but still noise-contaminated) values of X and y.

Our basic linear model asserts that there exists a Z ^true whose columns are linearly related, that is

$$ {\bf Z}^{{\rm true}} {\bf v} = \left( {{\bf Z} - \Upsilon } \right){\bf v} = {\bf 0}, $$

(20)

where v is a rank-m′ vector of coefficients, and Υ is an m′ × κ matrix representing the true (pre-whitened) noise contamination in the m′ variables. If the noise is normally distributed to begin with, then as a result of the prewhitening operator, P, all the elements of Υ are normally distributed with unit variance, so the maximum likelihood estimator of v, ${\bf \tilde v}$ , is given by maximising

$$ L = {\rm constant} - {1 \over 2}{\rm tr}\left( {{\bf \tilde \Upsilon }^T {\bf \tilde \Upsilon }} \right), $$

(21)

where ${\bf \tilde \Upsilon } = {\bf Z} - {\bf \tilde Z}$ and ${\bf \tilde Z\tilde v} = {\bf 0}$ . The rows of ${\bf \tilde \Upsilon }$ are uncorrelated with ${\bf \tilde v}$ , so maximising L is equivalent to minimising the revised merit function

$$ s^2 \left( {{\bf \tilde v}} \right) = {\bf \tilde v}^T {\bf \tilde \Upsilon }^T {\bf \tilde \Upsilon \tilde v}. $$

(22)

We require a constraint to avoid the trivial solution ${\bf \tilde v} = {\bf 0}$ Since all columns of Z are subject to noise of equal amplitude, this constraint should not discriminate between them, so we use the standard normalisation, ${\bf \tilde v}^T {\bf \tilde v} = 1$ Imposing the constraint $\left[ {{\bf \tilde v}} \right]_{m'} = - 1$ (i.e. only constraining the coefficient on y) and minimising s ² gives the standard regression model (1).

Incorporating this constraint into our merit function gives

$$ s^2 \left( {{\bf \tilde v}} \right) = {\bf \tilde v}^T {\bf Z}^T {\bf Z\tilde v} + \lambda ^2 \left( {1 - {\bf \tilde v}^T {\bf \tilde v}} \right) $$

(23)

where λ ² is a Lagrange multiplier. In geometric terms, minimising s ² is equivalent to finding the m-dimensional plane in an m′-dimensional space which minimises the sum squared perpendicular distance from the plane to the κ points defined by the rows of Z: the Adcock (1878), solution.

Differentiation of Eq. (23) with respect to ${\bf \tilde v}$ gives an eigen-equation defining the stationary points of s ² at which

$$ {1 \over 2}{{\partial \left( {s^2 } \right)} \over {\partial \left( {{\bf \tilde v}} \right)}} = {\bf Z}^T {\bf Z\tilde v} - \lambda ^2 {\bf \tilde v} = {\bf 0}, $$

(24)

and the curvature matrix

$$ {1 \over 2}{{\partial \left( {s^2 } \right)} \over {\partial \left( {{\bf \tilde v}} \right)}} = {\bf Z}^T {\bf Z} - \lambda ^2 {\bf I}. $$

(25)

The solution which minimises s ² is $\lambda ^2 = \lambda _{\min }^2$, the smallest eigenvalue of Z ^T Z, and ${\bf \tilde v}$ being the corresponding eigenvector (the vector normal to the best-fit m-dimensional plane). In a practical implementation, we simply take the singular value decomposition (SVD) Z = UΛV ^T so, after sorting, ${\bf \tilde v} = {\bf v}_{m'}$

The m′^th element of the solution vector corresponds to the best-fit scaling parameter on the observations, y. Since we are looking for a model to reproduce the observations themselves, not some scaled version thereof, we translate these coefficients into more familiar pattern-amplitudes by taking the ratios $\tilde \beta _i = \left[ {{\bf \tilde v}} \right]_i /\left[ {{\bf \tilde v}} \right]_{m'}$. At the minimum,

$$ s_{\min }^2 = \lambda _{\min }^2 \sim \chi _{\kappa - m}^2 , $$

(26)

provided κ ≫ m and neglecting, for now, uncertainty in the noise estimate. This provides an approximate check on residual consistency analogous to that which we use in standard regression. The detailed small-sample properties of $s_{\min }^2$ when κ ≃ m require a discussion in terms of Wishart matrices, which we will not attempt here.

Uncertainty analysis of the $\user2{\tilde \beta }$ is somewhat more complicated. If the diagonal matrix Λ ² contains the ranked eigenvalues of Z ^T Z, and the columns of V contain the corresponding eigenvectors, v _i , we can rewrite Eq. (25) as

$$ {1 \over 2}{{\partial ^2 \left( {s^2 } \right)} \over {\partial \left( {{\bf \tilde v}} \right)^2 }} = {\bf V}\left( {{\bf \Lambda }^2 - \lambda _{\min }^2 } \right){\bf V}^T . $$

(27)

Note the relationship between Eq. (27) and the perturbation analysis of North et al. (1982): like them, we are analysing the stability of an eigen-decomposition. It is tempting to treat the pseudo-inverse of Eq. (27) as a standard covariance matrix on ${\bf \tilde v}$ and this is indeed a reasonable approximation in the limit of high signal-to-noise. Because of the non-linearity introduced by the normalisation constraint on ${\bf \tilde v}$ however, the merit function s ² is not quadratic, so more realistic confidence intervals are obtained by explicitly mapping surfaces v where $\Delta s^2 \left( {\bf v} \right) = s^2 \left( {\bf v} \right) - s_{\min }^2$ has some constant value. As in the standard model,

$$ \matrix{ {\Delta s^2 \left( {\bf v} \right)} \hfill & = \hfill & {\Delta ^T {\bf V}\left( {{\bf \Lambda }^2 - \lambda _{\min }^2 {\bf I}} \right){\bf V}^T {\bf v}} \hfill \cr {} \hfill & \sim \hfill & {\chi _{\min }^2 ,} \hfill \cr } $$

(28, 29)

so having selected a confidence level, we compute the corresponding critical values of the $\Delta s^2 \left( {\bf v} \right) = s^2 \left( {\bf v} \right) - s_{\min }^2$ distribution and map the vectors v for which Δs ²(v) is equal to this critical value.

In a practical implementation, this mapping is achieved by first defining a set of points on an m-sphere of radius $\chi _m^2$ , where $s_{crit}^2$ is the critical value of the $\chi _m^2$ (or $mF_{m,\nu _2 }$ distribution – see next sub-section):

$$ \sum\limits_{i = 1}^m {a_i^2 = \Delta s_{{\bf crit}}^2 .} $$

(30)

For each of these points, we compute

$$ b_i = {{a_i } \over {\sqrt {\lambda _i^2 - \lambda _{\min }^2 } }}. $$

(31)

If the b _i provide the weights on eigenvectors 1 – m in V used to generate v, then Eq. (28) is automatically satisfied. The weight on v _m′ is provided by the normalisation constraint,

$$ \sum\limits_{i = 1}^{m'} {b_i^2 = 1} . $$

(32)

If $\Delta s_{{\rm crit}}^2$ is too large, then b _m′ will be zero or imaginary, and the confidence region will be unbounded in this direction. This means that the v are unconstrained (at this confidence level) to rotations through 360° in some plane.

In order to express these uncertainties in terms of familiar pattern-amplitudes, we need to take ratios β _i = [v] _i /[v] _m′ , giving confidence regions which may differ markedly from ellipsoidal. To compute confidence intervals on individual signals or signal-combinations, we compute surfaces β ₁ for which Δs ²(v) is equal to the appropriate critical value of the $\chi _1^2$ distribution, and simply take the maximum and minimum values of φ ₁ = c ^T β ₁ as before. Note that certain signal-combinations can be well constrained by the observations even if the full m-dimensional confidence interval is open-ended.

3.2 Uncertainty in noise variance under total least squares

If we take into account noise in all variables, the estimation algorithm becomes non-linear, so we cannot simply compute a series of $\user2{\tilde \beta }$ -like estimates from a set of independent realisations of pure climate noise (referred to earlier as the columns of ${\bf \hat \Upsilon }_2$ ) and use the resulting distribution to provide a confidence interval. Instead, we note that each $\lambda _i^2$ represents the signal-to-noise ratio in the corresponding pair of singular vectors of Z:

$$ \lambda _i^2 = {{{\bf u}_i^T {\bf ZZ}^T {\bf u}_i } \over {{1 \over \mu }{\bf u}_i^T {\bf P\hat \Upsilon }_1 {\bf \hat \Upsilon }_1^T {\bf P}^T {\bf u}_i }}, $$

(33)

where the denominator is identical to unity if the μ columns of ${\bf \hat \Upsilon }_1$ have been used to derive the pre-whitening operator, P. Relying on these λ for the uncertainty analysis may be misleading if ${\bf \hat \Upsilon }_1 {\bf \hat \Upsilon }_1^T$ is rank-deficient, as will generally be the case because only relatively short control segments of model-simulated variability are available. Poorly sampled state-space directions will automatically be given high weight by the pre-whitening operator, since by construction ${\bf P\hat \Upsilon }_1 {\bf \hat \Upsilon }_1^T {\bf P}^T = \mu {\bf I}$ This artificially inflates the differences between eigenvalues and reduces estimated uncertainties.

The solution, as in the linear case, is simply to replace ${\bf \hat \Upsilon }_1$ with ${\bf \hat \Upsilon }_2$ in Eq. (33), giving

$$ \hat \lambda _i^2 = {{{\bf u}_i^T {\bf ZZ}^T {\bf u}_i } \over {{1 \over {\nu _2 }}{\bf u}_i^T {\bf P\hat \Upsilon }_2 {\bf \hat \Upsilon }_2^T {\bf P}^T {\bf u}_i }}. $$

(34)

Because ${\bf \hat \Upsilon }_2$ is independent of P, if P is artificially inflating variance in a particular state-space direction, the same bias will be apply to both numerator and denominator in Eq. (34), whereas in Eq. (33) it only applied to the numerator. The estimates, ${\bf \tilde v}$ and $\user2{\tilde \beta }$ are unaffected, but $s_{\min }^2$ is replaced by $\hat s_{\min }^2$ in the uncertainty analysis, as follows: the check for residual consistency, Eq. (26), becomes

$$ \hat s_{\min }^2 = \hat \lambda _{\min }^2 \sim \left( {\kappa - m} \right)F_{\left( {\kappa - m} \right),\nu _2 } , $$

(35)

and Eq. (29) becomes

$$ \matrix{ {\Delta \hat s^{\rm 2} \left( {\bf v} \right)} \hfill & \equiv \hfill & {{\bf v}^T {\bf V}\left( {{\bf \hat \Lambda }^2 - \hat \lambda _{\min }^2 {\bf I}} \right){\bf V}^T {\bf v}} \hfill \cr {} \hfill & \sim \hfill & {mF_{m,\nu _2 } .} \hfill \cr } $$

(36, 37)

3.3 Properties of TLS estimators and the problem of open-ended confidence intervals

In the simplest case in which there is an equal level of noise in model and observations (i.e. assuming an ensemble of size one: and, as noted, an ensemble of size n can be transformed into this case by pre- and post-multiplying the model-simulated signals by $n^{{1 \over 2}}$ and $n^{ - {1 \over 2}}$ respectively), TLS estimates of the angle of slope of the line relating model and observations are symmetrically distributed about the correct value. If we were to perform the estimation procedure many times, the average angle of slope would converge to the correct one. In conventional regression analysis, however, results are normally quoted in terms of the tangent of this slope (the familiar scaling parameter β), or the ratio between observed and model-simulated signal amplitudes. Because the tangent operator is non-linear, if we express TLS results in terms of familiar scaling parameters, their behaviour can appear unfamiliar. For example, with exactly the same level of correlation between model and observations, the TLS-based uncertainty interval on the angle of orientation of the line relating could be either –5° to 50° or 40° to 95°. Expressed in terms of scaling parameters, β, the latter interval includes infinity: what does this mean?

In interpreting coefficients derived from standard regression, we are accustomed to see these coefficients decline to zero as the amplitude of the signal in the observations goes to zero. With noise in both observations and model-simulated patterns, there is no reason for the vector $\user2{\tilde \beta }$ to prefer one orientiation over any other as the signal amplitude in both model and observations goes to zero, because model and observations are equivalent. The orientation the line relating model and observations thus becomes arbitrary, and the ratios $\tilde \beta _i = \left[ {{\bf \tilde v}} \right]_i /\left[ {{\bf \tilde v}} \right]_{m'}$ can take any value. The physical interpretation of a near-infinite "pattern-amplitude" requires some thought. What it means is that, because we are allowing for the presence of noise in the model-simulated patterns, it may be the case that the true response-pattern (the pattern which we would obtain if we were to run an infinite ensemble) may be close to zero everywhere. Supposing that this pattern has a finite amplitude in the observations, this means we would have to multiply this near-zero pattern by an arbitrarily large number to get a reasonable fit.

At higher signal-to-noise levels, the main impact of adopting TLS estimators in place of the standard approach will generally be to increase the best-guess pattern amplitudes and also to increase, possibly substantially, the estimated upper bounds on parameter uncertainty ranges. Lower bounds (which are crucial for claims of detection) may either increase or decrease depending on the confidence level specified. The question will doubtless arise as to whether the additional precision of these revised estimators justifies these additional complications of interpretation. In view of the fact that we know that any response-patterns obtained from small ensembles are subject to sampling uncertainty, there should be no question that we should satisfy ourselves what the impact of this uncertainty is within an unbiased estimation framework. Whenever these revised estimators give qualitatively different results from the traditional approach, we have two options: either we use the revised approach in policy advice, accepting the additional complexity that this entails; or we increase the size of the ensembles we use to estimate the response-patterns until differences between the two approaches are negligible. While the latter option is clearly preferable in principle, the cost of running very large ensembles to pin down weak signals may dictate otherwise.

3.4 Reconstructing noise-reduced observations and signals

Under OLS, reconstructing the noise-reduced observations and signals scaled by best-fit scaling parameters is straightforward: we simply compute ${\bf \tilde y} = {\bf X}\user2{\tilde \beta }$ Under TLS, the problem is only slightly more complicated. Assuming, as before, equal noise in observations and signals, we project both onto the plane orthogonal to ${\bf \tilde v}$ , thus:

$$ {\bf \tilde Z} = {\bf Z} - {\bf Z\tilde v\tilde v}^T . $$

(38)

This provides a "best-fit" reconstruction of both observations and signals: note that the presence of noise in X now means that the true (noise-free) model-predicted response-patterns must be estimated along with the noise-free observations.

Noise-reduced observations and model-simulated signals associated with the v on a particular confidence surface are computed identically to ${\bf \tilde Z}$ This gives a set of possible observation-signal combinations that are consistent with the statistical model at a given confidence level. If we desire an uncertainty range on a single quantity, such as the trend attributable to a particular signal, then we require the v corresponding to univariate confidence intervals (i.e. those on the surface where $\Delta \hat s^2 \left( {\bf v} \right) = F_{1,\nu _2 }$ For the joint distribution of two trends, we require bivariate intervals and so on. Note that reconstructions of noise-reduced observations and model-simulated signals will, in general, be much better behaved than the corresponding regression coefficients: if a particular v corresponds to the model-simulated signal having zero amplitude while the observed signal has a finite amplitude, the corresponding β _i will be infinite, but the reconstructed noise-reduced observed and model-simulated signals will all be finite.

4 Example: application to climate change in a simple chaotic system

We now demonstrate the estimation algorithms described in this paper to a numerical model of climate change in a non-linear system proposed by Palmer (1999), based on the Lorenz (1963), model of low-order deterministic chaos. The governing equations are very familiar,

$$ \matrix{ {{{dX} \over {dt}}} \hfill & = \hfill & { - \sigma X + \sigma Y + f_0 \cos \theta } \hfill \cr {{{dY} \over {dt}}} \hfill & = \hfill & { - XZ + rX - y + f_0 \sin \theta } \hfill \cr {{{dZ} \over {dt}}} \hfill & = \hfill & {xy - bZ,} \hfill \cr } $$

(39)

where X, Y and Z are the prognostic variables while σ, r and b are adjustable parameters, set here to put us squarely in the "chaotic" regime (10, 28 and 8/3 respectively). The final terms on the RHS of the first two equations represent an imposed external forcing in the horizontal (X, Y) plane, with amplitude f ₀ and direction θ.

We use output from this model to generate both "climate change signals" and "climate noise", rather than simply adding pre-defined signals to the more usual linear stochastic ("red noise": e.g. Hasselmann 1976) model of internal variability for the following reason. The estimation theory described is based on the assumption that the climate variability can be thought of as a linear stochastic process which is independent of externally forced signals of climate change. Hence, if the statistical model is correctly specified, validating our estimation procedure against the output of such a linear process (which we have, of course, done) is simply a check for coding accuracy, not a fundamental test of the theory.

Palmer (1999), observed that climate change in a non-linear system could also be thought of as a change in the occupancy statistics of certain preferred "weather regimes" in response to external forcing, and argued that this might cause problems for the linear analysis techniques used for climate change detection. It is therefore of interest to test out our estimation procedures on precisely the system Palmer (1999), proposed.

We do this by imposing a forcing as shown in the Eq.-set (39) whose magnitude, f ₀, increases linearly over time, representing the effect of, for example, a 1% per year increase in greenhouse gas levels. The principal impact of the forcing is to increase the fraction of time the system spends in one of its two basins of attraction. This is shown in Fig. 3. The left hand panel displays an estimate of the attractor probability density function, or PDF, of the unforced system (f ₀ = 0). The two lobes of the "Lorenz butterfly" are clearly evident, and are of equal size, since the unforced attractor is symmetric.

Fig. 3.

a: estimate of the attractor probability density function (PDF) of the unforced Lorenz (1963), system. The plot shows a two-dimensional histogram of the location of "one-Lorenz-day" time-averaged values of the (X, Y) variables obtained from a long integration. b: PDF after imposing a steady forcing in the (X, Y) plane in the direction shown by the arrow, following Palmer (1999)

It is important to stress that the appearence of the PDF is sensitive to the averaging period represented by individual points making up the histogram. In Fig. 3, this is one "Lorenz-day" which is comparable to the time scale of exponential error growth in this system. The only component of the climate system that has been unambiguously shown to display exponential error growth is the mid-latitude atmosphere. For example, despite years of research, the jury remains out whether the El Niño phenomenon is best represented by chaotic or damped linear stochastic dynamics on seasonal to interannual time scales (Jin et al. 1994; Penland and Sardeshmukh 1995). In climate change detection studies, we are typically working with diagnostics based on averages over time-periods several orders of magnitude longer than the atmospheric error growth time. A better model of the climate change detection problem, therefore, is to work with long time-averages of the Lorenz (1963), system, as shown in Fig. 4. The impact of the Central Limit Theorem is immediately apparent, with the distribution of 500-day averaged values of the Lorenz variables being much closer to Gaussian and displaying none of the bi-modal behaviour shown in Fig. 3. Studies reporting non-Gaussian or multi-modal behaviour in the climate system have generally been based on relatively high time-resolution data (monthly or daily averages: e.g. Corti et al. 1999; Gillett et al. 2001). Failure to detect multi-modal behaviour on longer time scales is generally attributed to the lack of sufficiently long data records, but it is equally reasonable (and arguably more conservative) to assume that the statistics of internal climate variability do in fact converge to Gaussian if we average over multi-year time scales.

Fig. 4a, b.

As Fig. 3, but based on 500-Lorenz-day averaged data, to show the impact of time-averaging on the distributional properties of variability generated by a chaotic system: a simple consequence of the Central Limit Theorem

If we impose a steady forcing in the direction shown by the arrows in Figs. 3 and 4 (θ=140°) and repeat the integration, the size (average rate of occupancy) of the upper right lobe in Fig. 3 increases while that of the lower left lobe diminishes. Although it is not particularly evident from Fig. 3, the location of the maxima is also displaced slightly in the direction of the forcing (i.e. above the line X=Y). This latter component of the response is more evident in the histograms of 500-day averages (Fig. 4), which shows that the centre of gravity of the system has moved into the upper right quadrant but has also moved slightly above the X=Y line.

The point made by Palmer (1999), was that the sign of the response in the X direction can (as in the case shown here) be opposite to that of the forcing. Some early climate change detection studies (e.g. Santer et al. 1996) used patterns of forcing in place of model-simulated responses as signals to be looked for in the observed record. If the real climate system is conforming to this non-linear "paradigm," these studies might well have been looking in the wrong direction, although it should be stressed that there is no a priori reason to expect this problem to result in an excessive number of false-positive detection claims. Likewise, other studies have used signals derived from equilibrium climate change experiments or simulations of twentyfirst century climate change (e.g. Hegerl et al. 1996). In a non-linear system, the direction (pattern) of response can depend on the amplitude of the forcing. For example, in the system shown here, as we increase f ₀ the centre of gravity of the whole attractor moves further into the upper right quadrant but does not move much further off the X=Y line. Hence a signal derived from a strong-forcing experiment might prove inappropriate to the relatively weak forcings observed over the twentieth century. Again, this problem would be more likely to result in failure to detect a climate change than in a false-positive result.

Recognising these problems, more recent climate change detection studies (Tett et al. 1996, 1999; Allen and Tett 1999; Stott et al. 2001) have compared simulations of the twentieth century, with as realistic forcing amplitudes as possible, directly with observations. This approach entails costs: ensemble simulations are required, and quantitative comparison of models with observations requires the more complex total least squares analysis procedure detailed here. The great advantage, however, is that there is no a priori reason to suppose that the presence of non-linearity per se will result in the model-simulated response-pattern pointing in the wrong direction, provided the same non-linearities are represented in the climate model as are operating in the real world (and the objective of the exercise is to establish whether or not this is the case). Moreover, in using the Palmer (1999), example, we aim to show in this paper that there is also no reason to suppose that the linear analysis techniques used in climate change detection are rendered inapplicable simply because the underlying system is non-linear.

The key constraint is that the forcing amplitude must be small enough that the characteristics of internal variability on the time scales of interest do not change as a result of the imposition of external forcing. This is illustrated in Figs. 3 and 4. Variability in "daily" averaged data (Fig. 3) does change as a result of the forcing: the distribution becomes more skewed towards the upper right quadrant. Gillett et al. (2001), see tentative evidence of similar behaviour in daily averages of certain diagnostics of atmospheric circulation over the past few decades. Yet the characteristics of variability in "annually" (500-Lorenz-day) averaged data (Fig. 4) are unchanged. There is no contradiction here, nor is it simply a question of insufficient sampling on the 500-day time scale. A system can be non-Gaussian on short time scales and Gaussian on much longer timescales simply by the operation of the Central Limit Theorem. Evidence of interesting non-linear behaviour, such as multi-modality, threshold or saturation effects, on short time scales therefore does not necessarily imply that behaviour should depart significantly from linearity on longer time scales. While difficult to confirm in the real world, modelling studies to date (e.g. Timmermann et al. 1999; Fyfe et al. 1999; Collins 2000) suggest that much larger forcing amplitudes than have been observed over the twentieth century are required to have a significant impact on internal variability on interannual to decadal time scales.

In the context of our idealised system, we impose a reasonably strong forcing amplitude: increasing f ₀ linearly over a 2500 Lorenz-day period to about half that required to cause the attractor to collapse altogether. The response is shown in the left-hand panel of Fig. 5, which displays the time-evolution of the of 500-day averages of the Lorenz variables over this 2500-day period averaging based on a 4-member ensemble. This may be thought of as the motion of the centre of gravity of the attractor shown in Fig. 4. The 1000-day fluctuations in the lines are partly attributable to sampling noise, and would be different in another ensemble, but the overall response is consistent: Y increases first, so the centroid moves upwards away from the X axis in Fig. 4. X and Y then increase together as the forcing strengthens, meaning the centroid moves out into the upper right quadrant following the line X=Y.

Fig. 5.

a: response of three variables in model (39) to a linear increase in forcing f ₀ from 0 to 5 units, with θ=140°, showing an initial increase in Y (upward movement on the previous plot) followed by a simultaneous increase in X and Y, with no change in Z. b: optimised climate change fingerprint after multiplying this signal (the spatio-temporal pattern of response shown on the left, arranged as a single column-vector y, by the inverse noise covariance estimated from a long control integration of the unforced model

Mimicking the experimental design of, e.g. Tett et al. (1999), we generate:

• 1. A time-history of pseudo-observations of all three Lorenz variables using the model described by Eq. (39) and a linear increase in forcing

• 2. A spatio-temporal response pattern using ensemble simulations with the identical model and forcing history, varying initial conditions between ensemble members

• 3. A simulation of internal variability using a long, unforced, "control" integration of the model

Hence, comparing these response patterns with the pseudo-observations, we should find the pattern-amplitudes, β to be consistent with unity, since the model-simulated response is correct.

We use this "perfect model" set-up to focus on the statistical techniques used for model-data comparison. With such an idealised system, there is less point in exploring the impact of systematic model errors since this would be specific to the problem considered. First, we show the impact of pre-whitening, or "optimisation", which is used in both TLS and OLS algorithms. The right hand panel in Fig. 5 shows what Hasselmann (1993), refers to as the "optimised fingerprint" of this particular climate change, or F (which has only a single column, because we have only one candidate response-pattern) in Eq. (5). In the OLS algorithm, this is simply the pattern by which we need to multiply the raw data to obtain the best (lowest variance) linear unbiased estimator of the response amplitude, $\tilde \beta$ (the scaling on the model-simulated signal required to reproduce the observations). There is no such simple interpretation in the TLS case, because all the analysis is done in terms of pre-whitened variables, but the principle is the same.

What is striking about the optimised fingerprint in this case is that it points in a direction almost orthogonal to the original signal: the fingerprint is increasing linearly in a direction orthogonal to the X=Y line (X decreases while Y increases in the right panel of Fig. 5), while the signal primarily consists of a movement along the X=Y line (both X and Y are positive by day 2500 in the left panel). The reason is simple: most of the noise in this system is along the X=Y line, since this is the way the PDF is oriented in Fig. 4. Hence the component of the response that best distinguishes it from internal variability is the small displacement away from the X=Y line, even though the largest single component of the response is along the X=Y line. In this particular example, the fingerprint happens to point in the direction of the forcing, but this is largely a coincidence: for different values of θ, it can be engineered to point elsewhere.

When pseudo-observations are projected onto the raw climate change signal, we find that no response can be detected to this forcing at, for example, the P = 0.05 level in the vast majority of cases regardless of the ensemble size used to estimate the signal. This supports the point made by Palmer (1999), that responses oriented in the preferred directions of the noise "attractor" may be difficult to detect. However, if we project pseudo-observations onto the optimised fingerprint, the response can almost always be detected at a high significance level. This demonstrates the power of the optimisation algorithm in enhancing signal-to-noise, and also provides a test-bed to the OLS and TLS algorithms described in this study.

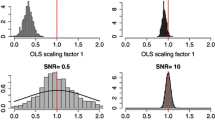
Since this is a perfect model set-up, we focus on the hypothesis $\user1{{\cal H}}_0 \left( {\beta = 1} \right)$ . Testing at the P = 0.05 level (one-tailed), we should find $\user1{{\cal H}}_0$ rejected with β significantly greater than unity (the ensemble simulation underestimating the "observed" response) or β significantly less than unity (simulation overestimating observed) in approximately 5% of cases respectively, if the statistical analysis techniques are working perfectly. What we actually find is shown in Fig. 6. With 500-day averaged data (left panel) and small (one- to four-member) ensembles there is a systematic bias towards OLS underestimating the observed response amplitude. That is, OLS is found to indicate β significantly less than unity in up to 21% of cases (solid line), while indicating β significantly greater than unity in as few as 0.5% of cases (dashed line). Results with TLS (dash-dot and dash-triple-dot lines) are not subject to this low bias, although for small ensembles TLS appears to be slightly over-conservative in both directions, with somewhat fewer than the nominal 5% of cases being found to be both too high and too low. Both algorithms converge on the correct (5%) rejection rate for very large (64-member) ensembles.

Fig. 6a, b.

Fractions of cases in which $\user1{{\cal H}}_0 \left( {\beta = 1} \right)$ is rejected in a "perfect model" study in which the true value of β is known to be unity. Ideally, rejection rates should equal the nominal significance level of 0.05, shown by the dotted line in both panels. The a shows results based on 500-day averaged data, the b results based on 50-day averages. The solid (dashed) lines show the percentage of cases in which OLS significantly under- (over-)estimates the observed response amplitude, falsely indicating the model response is significantly higher (lower) than observed response when it is, in fact, correct. The dash-dot (dash-triple-dot) lines show the corresponding statistics for TLS. Note the strong bias in OLS results towards indicating that the observed response is lower than the model-simulated response with small ensemble sizes

Differences between the two algorithms are more marked if we consider 50-day averaged data, in which the signal-to-noise level is lower and the underlying PDF is further from Gaussian. Results are shown in the right hand panel of Fig. 6. For single-member ensembles, OLS suggests that the model is significantly over-estimating the observed response in over 50% of cases. Given the implications for future climate change if models are indeed found to be overestimating the observed response, introducing this level of error simply through the adoption of an inadequate statistical model is clearly unacceptable. TLS results display no such systematic bias, although there is a tendency for the algorithm to be liberal (underestimate uncertainty ranges) with small ensembles, with rather more than the nominal 5% of cases being rejected.

Our reasons for demonstrating the algorithms described in this paper on the Palmer (1999), variant of the Lorenz (1963), system were three-fold. First, we wanted to demonstrate the advantages in accuracy of the TLS algorithm in a case which was clearly not expressly designed to "show it off" but which was, nevertheless, sufficiently idealised for large ensemble tests to be performed. Second, we wished to motivate the experimental design of the more up-to-date climate change detection and attribution studies that are based on ensemble simulations of the twentieth century with approximately realistic forcing amplitudes rather than signals obtained from idealised forcing scenarios or idealised models. This approach has its price, both in the cost of running the ensembles and in the additional complexity of interpreting results, and we wished to demonstrate in the context of an idealised system that this price is worth paying. Third, and more generally, we wanted to show that the linear statistical models (1) and (16) are applicable to the analysis of externally forced changes even in highly non-linear systems and not simply the linear stochastic processes on which the supporting theory is based. The requirement is simply that the noise distribution is approximately Gaussian on the time scales of interest in the detection problem and that the forcing amplitude is small enough not to affect it. It does not matter whether the noise has been generated by a stochastic or deterministic chaotic process, nor whether it can be distinguished from Gaussian if sampled on shorter time scales.

5 Summary

We have described a variant on the standard "optimal fingerprinting" approach to climate change detection and attribution that explicitly takes into account sampling uncertainty in AOGCM-simulated responses to external forcing that have been derived from small initial-condition ensembles. The analysis procedure, known as total least squares (TLS), is drawn from the standard statistics literature with some adaptation to the climate change detection and attribution problem. The principal advantage over the standard ordinary least squares (OLS) approach, which neglects uncertainty in model-simulated response-patterns, is that it eliminates a systematic bias towards underestimating the relative magnitude of the observed versus model-simulated response that is evident in OLS results.

The conclusion that current models are systematically over-predicting observed climate change would have considerable implications for the future, so we clearly need to minimise the chance of drawing this conclusion incorrectly through the application of an inadequate statistical model. We cannot eliminate this chance completely, and the problem of error in model-simulated response-patterns due to systematic errors in forcing or response remains, but the problem of sampling error due to the use of small ensembles is clearly identifiable and can be largely eliminated through the application of the TLS algorithm. Given sufficient resources, the problem can also be eliminated through the use of OLS in conjunction with much larger ensembles: the size of ensemble required for results from the two algorithms to converge clearly depends on the specific application and signal-to-noise level. These issues are explored in the context of AOGCM simulations of twentieth century climate change in a companion paper by Stott et al. (2003).

We demonstrated the advantages in accuracy of the TLS algorithm with an analysis of externally-forced "climate change" in the Palmer (1999), variant of the Lorenz (1963), model of deterministic aperiodic flow. Use of this model also allowed us to show that linear analysis procedures are applicable to highly non-linear systems under certain circumstances. Provided we are dealing with time-averages taken over periods sufficiently long that the noise distribution is approximately Gaussian, and forcing amplitudes sufficiently small that they do not have a detectable impact on the noise characteristics, it does not matter whether the noise has been generated by a linear stochastic process or deterministic chaos: the same procedures apply. While not wishing to down-play the potential importance of non-linearity in the climate change detection and attribution problem, it is important to demonstrate that essentially linear analysis techniques can be applied to the output of non-linear chaotic systems and give coherent and accurate results.