1 Introduction

Energetic quantities represent essential aspects of the behaviour of the atmosphere. Long-term climatological values characterize basic balances and budgets of the climate system while the variations in these quantities give information on the natural variability of energetic quantities. Since the terms in the energy cycle involve the first and second order climate statistics (means, variances and covariances) of the basic prognostic variables they are also basic in this sense. The physically motivated intercomparison of these quantities offers a “second order” avenue of insight into model behaviour. Data from 12 AGCMs participating in AMIP2 are analyzed and intercompared in terms of energy cycle quantities and results are compared with estimates based on NCEP and ERA reanalysis products. The ability of the models and of the “ensemble model” to reproduce the energy cycle and its variations is analyzed and processes which are associated with distortions in the energy cycles of models are tentatively identified.

1.1 AMIP

The first Atmospheric Model Intercomparison Project (AMIP1) was initiated in 1990 with the endorsement of the Working Group on Numerical Experimentation (WGNE) of the World Climate Research Programme and under the guidance of the WGNE AMIP1 Panel (L. Gates, G. J. Boer and L. Bengtsson). The Program for Climate Model Diagnostics and Intercomparison (PCMDI) located at the Lawrence Livermore National Laboratory (LLNL) collected, stored and distributed the AMIP1 data to participants in diagnostic subprojects.

The intent of AMIP1, as listed on the PCMDI website (http://www-pcmdi.llnl.gov/projects/amip/NEWS/overview.php) was to devise a standard experimental protocol for global atmospheric general circulation models (AGCMs) to encourage diagnosis, evaluation, intercomparison, documentation and data access. Virtually the entire international climate modelling community has participated in this project since its inception in 1990. A summary of AMIP1 results can be found in Gates et al. (1992, 1999) and on the PCMDI website. AMIP2 is a second phase of AMIP with an expanded set of data and with newer versions of AGCMs.

The AMIP experiments are straightforward. AGCMs are integrated for the period from 1979 to 1995 with observationally based sea surface temperature and sea-ice distributions supplied as boundary conditions. An extensive suite of data is saved for diagnostic research. The website http://www-pcmdi.llnl.gov/projects/amip/index.php describes the current state of AMIP2 and its data and analysis protocols as well as listing some of the reports and papers that have resulted.

1.2 Model intercomparison

In a general context, model intercomparison attempts to answer a range of questions including how well models can reproduce current climate, if models correctly incorporate known “climate mechanisms”, how well models are able to reproduce perturbed climates and, the original impetus for intercomparison, how models may be improved.

Several categories of model intercomparison may be recognized (Boer 2000a). They include intercomparisons which concentrate on the morphology of the simulated climate and resemblances to or differences from that observed, intercomparison of climate budgets, balances and cycles, and intercomparison of specific processes such as, for instance, the Madden–Julien oscillations simulated in the models. The morphology of climate includes the spatial distribution and structure of means, variances, and covariances (and possibly other statistics) of basic climate parameters. Some of the earliest intercomparisons considered only zonally averaged values of mean sea level pressure and precipitation (Gates 1987). These were followed by intercomparisons which added a number of basic zonally averaged cross-sections such as those of temperature and wind (e.g. Boer et al. 1992). With the advent of AMIP, the number of variables collected, analyzed, and intercompared made a quantum jump and all types of intercomparison studies were undertaken facilitated by the larger data set retained for AMIP2.

The study and intercomparison of budgets, balances, and cycles in the real system and in climate models deals with the source, transport, transformation, and sinks of quantities in the atmosphere. These include budgets of the water substance (the hydrological cycle), angular momentum and, in particular as investigated here, of energy in various forms. Because the governing equations are quadratically non-linear, the climatological budget equations necessarily involve second order statistics of the prognostic variables. Thus, to study these budgets, climatological data beyond basic means are required and, at least partially for this reason, budgets studies of these kinds have not been prominent in model intercomparisons. AMIP2 with its more comprehensive data set includes many (but not all) of the second order statistics that arise in the budget equations and so facilitates the kind of analysis and intercomparison we undertake here.

The nature of our analysis is motivated by a number of general principles which posit that analysis/intercomparison should proceed by reducing the dimensionality of the data by averaging/integrating the data in a progressive way (time, zonal, vertical, global), by treating dominant quantities and budget equations (amounts, fluxes/transports, source/sinks) using a hierarchy of statistics (means, variances, covariances, higher order statistics) and by avoiding excessively local measures (i.e. regions of strong gradients, particular levels, points, small regions or short time intervals). The number of quantities should be kept manageable, the diagnostics should be robust in the sense that they are not strongly dependent on small changes or differences and diagnostic quantities should be known from observations and/or conservation principles.

The energy cycle involves basic physical processes in the atmosphere as characterized by the amounts and distributions of available potential and kinetic energies together with the generation of, conversions between, and sinks thereof. The overall strength of the energy cycle gives the “rate of working” of the climate system as thermodynamic energy is converted into kinentic energy which is ultimately dissipated into heat. Basic first and second order climate statistics arise naturally when averaging the governing equations and have physical meanings. Several levels of comparison are possible under different levels of averaging and integration.

2 Climate statistics

The first and second order climate statistics that arise under time and zonal averaging and the notation used are shown in the first three rows of Table 1. The raw data which are used to calculate these statistics are 6 or 12 hourly model and reanalysis values. Mean and transient statistics are calculated on a monthly average basis from these data. Energy budget quantities are subsequently calculated from these monthly statistics and there are 17 years of monthly values of each term for each model. The notation used for area averaging as well as for ensemble averaging across the collection of models is also given in Table 1.

Table 1 Notation and statistics under averaging
Full size table

Terms involving deviations from time averages are termed “transient eddy” components and those involving deviations from zonal and time averages are termed “standing eddy” components. For many purposes the standing and transient eddy components are combined \([\overline{X \nu}]=[\overline{X}] [\overline{\nu}]+[\overline{X}^{*} \overline{\nu}^{*}]+[\overline{X^{\prime}\nu^{\prime}}]=[\overline{X}] [\overline{\nu}]+[\overline{X_{E}\nu_{E}}]\) into a single eddy component. These first and second order statistics are intimately connected with the form of the atmospheric equations and arise upon averaging as indicated by averaging the prototype atmospheric equation

$$\frac{\partial X}{\partial t}+{\user2{V}} \cdot \nabla X+ \omega \frac{\partial X}{\partial p}=\frac{\partial X}{\partial t}+\nabla \cdot X {\user2{V}}+\frac{\partial}{\partial p}X \omega=S$$
(1)

which adopts its simplest lowest order form when pressure is used as the vertical coordinate. Under time averaging (1) becomes

$$\frac{\partial}{\partial t}\overline{X}+\overline{{\user2{V}}} \cdot \nabla \overline{X}+ \overline{\omega}\frac{\partial}{\partial p}\overline{X}= \overline{S}-\left(\nabla \cdot \overline{X^{\prime}{\user2{V}}^{\prime}}+\frac{\partial}{\partial p}\overline{X^{\prime}\omega^{\prime}}\right)$$
(2)

where covariances arise as well as means and have the physical meaning of eddy fluxes. Similarly, under time and zonal averaging (1) becomes

$$\frac{\partial}{\partial t}[\overline{X}]+\frac{[\overline{\nu}]}{{\hbox{acos}}\,\varphi} \frac{\partial}{\partial \varphi}[\overline{X}]+[\overline{\omega}] \frac{\partial}{\partial p}[\overline{X}]=[\overline{S}]-\left(\frac{1}{{\hbox{acos}}\, \varphi} \frac{\partial}{\partial \varphi}[\overline{X_{E}\nu_{E}}] \hbox{cos}\,\varphi+\frac{\partial}{\partial p}[\overline{X_{E}\omega_{E}}]\right)$$
(3)

Energy budget equations are essentially equations for variances and are obtained by manipulating equations of this kind. For instance, the equation for \(\overline{X}^{2}\) is obtained by multiplying (2) by \(\overline{X},\) time averaging, and rearranging terms while the equation for \(\overline{X^{\prime2}},\) is obtained by multiplying (1) by \(X^{\prime}\) and averaging and rearranging terms. The equation for the transient plus standing eddy variance \(\overline{X_{E}^{2}}\) is likewise obtained under zonal and time averaging.

2.1 Energy cycle equations

The energy cycle equations (Lorenz 1955, see also Peixoto and Oort, 1992 for example) give the relationships between different forms of available and potential energy and are listed in the Appendix. The simplest representation is the “2-component” energy cycle

$$\begin{aligned}\frac{\partial A}{\partial t}&=-C(A, K)+G\\ \frac{\partial K}{\partial t}&=C(A, K)-D\\\end{aligned}$$
(4)

where A is the amount of available potential energy, G its generation rate and C its conversion rate to kinetic energy K which is dissipated at a rate D. We consider also the “4-component” energy cycle

$$\begin{aligned} \frac{\partial A_{Z}}{\partial t}=-C(A_{Z},K_{Z})- C(A_{Z},A_{E})+G_{Z}\\ \frac{\partial A_{E}}{\partial t}=-C(A_{E},K_{E})+C(A_{Z},A_{E})+G_{E}\\ \frac{\partial K_{Z}}{\partial t}=C(A_{Z},K_{Z})-C(K_{Z},K_{E})-D_{Z}\\ \frac{\partial K_{E}}{\partial t}=C(A_{E},K_{E})- C(K_{Z},K_{E})-D_{E}\\ \end{aligned}$$
(5)

where A Z , A E and K Z , K E are the amounts of zonal and eddy available potential and kinetic energy. The conversion rates between the various forms of energy are indicated by the C terms while G Z , G E and D Z , D E represent generation of zonal and eddy forms of A and dissipation of K. The expression of each of the terms in (4, 5) in terms of the mean, variance and covariance statistics in Table 1 is given in the Appendix. The terms in (4, 5) are in the form of integrals over the mass of the atmosphere and we consider also the distribution of their integrands in what follows.

The 2-component and 4-component versions of the energy cycle are diagrammed in Fig. 1. The terms in the boxes give the amount of available potential and kinetic energy in the atmosphere while the arrows indicate the generation, conversion and dissipation of various energy components. A 6-component version of the energy cycle, which treats stationary and transient eddy components separately, is not considered here because certain statistics are unavailable.

Fig. 1
figure 1

Representations of the energy cycle. The upper panel indicates the basic climatological “2-component” energy cycle in which available potential energy (A) is generated (G), converted (C) to kinetic energy (K) and subsequently dissipated (D). Here G =  C =  D is the “rate of working” of the atmosphere as it converts thermodynamic energy into kinetic energy which is subsequently dissipated. The lower panel indicates the further decomposition of the energy terms into mean zonal and eddy components

Full size image

The AMIP2 data set is not complete in the covariance terms that arise in the energy cycle equations and terms involving the transient transport components \(\overline{\omega^{\prime}{\user2{V}}^{\prime}},\) and \(\overline{u^{\prime}T^{\prime}}\) are missing as are most of the components for the generation G and dissipation D terms. These latter terms are obtained here as residuals assuming the budget is in near balance. The missing terms involving ω are small so omitting them is relatively unimportant in the overall budget. However, the lack of the zonal transport of heat by the transient eddies, means that the conversion term C(A S ,A T ) between stationary and transient available potential energy is not available for use in a 6-component energy cycle diagram. Combining the standing and transient eddy components into an overall “eddy” component results in a 4-component budget and combining the zonal and eddy components results in the 2- component energy budget.

Heuristically in the 4-component diagram, A Z and A E are generated by “heating where it is warm and cooling where it is cold”. That is by generating meridional temperature gradients in the north-south in the case of G Z . Baroclinic processes associated with down-gradient heat transport act to weaken these temperature gradients and convert A Z to A E which is, in turn, converted to K E as “warm air rises and cool air sinks”. Barotropic processes convert K E into K Z and both components suffer loses via dissipation. The overall working of the atmosphere as a heat engine is measured by the A to K conversion rate.

2.2 Integrals and integrands

The energy cycle components in (4) are in the form of integrals over the mass of the atmosphere. Monthly values of A and K and their zonal and eddy components, generation and dissipation rates G, D and the conversions C are all calculated and retained. As well as values for each model, two multi-model representations of the budgets are calculated. The “ensemble model” energetic quantities, labelled MBUD in the diagrams are simple ensemble averages of energy budget terms such as {A Z } and so on. A second multi-model version is labelled MMOD and is obtained by first averaging the mean fields and the transient statistics before calculating energy budget quantities. The Appendix describes the differences in these terms in more detail. The MBUD “ensemble model” approach is straightforward and is preferred.

These two ways of calculating multi-model statistics are the same when only mean fields are considered and Lambert and Boer (2001) show that the ensemble average model is generally the “best” model in terms of the spatial distributions of climatological mean quantities, at least when goodness is measured by the usual second order measures (mean square difference, correlation, ratio of variances). We are interested if this holds true also for the higher order terms arising in the energy cycle.

As well as considering the mass-integrated energy budget quantities we also consider and intercompare the structures of their integrands. Thus for kinetic energy,

$$K=K_{Z}+K_{E}=\int k_{Z}(\varphi, p) dm+\int k_{E}(\varphi, p) dm$$
(6)

where the integrands k Z and k E are functions of latitude and pressure.

3 Data

The AMIP2 period is from 1979 to 1995. The quantities considered are the first and second order atmospheric statistics entering into the integrands of the components of A and K and for the conversions C between them. These include monthly means and standing and transient eddy covariances of the basic prognostic variables for the atmosphere for each month of the 17 years of AMIP2. The NCEP/NCAR reanalysis (Kalney et al. 1996) and the ERA40 reanalysis (Uppala et al. 2005) provide observation-based estimates which are compared with the results from the 12 atmospheric models listed in Table 2 and with the “ensemble mean model”. Most comparisons are with NCEP reanalysis results which have been available for some time in contrast to the more recent ERA reanalysis. There are modest differences in the energetic budget from the two analyses and some indication of this is also given in what follows. Although the models vary in their native resolution, data are analyzed on a common 128 ×  64 gaussian grid and on 17 pressure levels in the vertical. Data difficulties prevent the inclusion of results from several modelling centres.

Table 2 Model and reanalysis data; gg and ll indicate gaussian and lat/long grid, respectively
Full size table

4 Results

A bewildering array of statistics are possible for the many terms in the energy budget, including their seasonal and temporal variation and the spatial distribution of their integrands. We confine ourselves to a modest set of statistics beginning with those most heavily averaged and integrated in space and time and expanding from there.

4.1 Statistics of the energy budget terms

The analysis is in terms of the 17 year sequence of monthly values of the integrands and integrals of the energy budget quantities A, K, G, D, C and their components. The further decomposition

$$X=\int x (\varphi, p, t) dm= X_{m}+X_{a}+X_{d}=\int ({x}_{m}+x_{a}+x_{d}) dm$$
(7)

is into, respectively, the climatological mean X m (the 17 year annual average) of the monthly values, the climatological annual cycle (CAC) X a , and X d the deviations from the CAC.

The climatological mean X m and annual cycle X a of an energy budget term are considered to be forced deterministic quantities which should agree, to good approximation, with the reanalysis-based quantities. The variability term X d will contain a component forced by the imposed SST boundary conditions, which should be common to the model simulations, but will also include internally generated natural variability which is not expected to agree among the model simulations.

4.2 Climatological mean values

We deal here with the climatological mean quantities in (7). The observation-based energy budget quantity X m is compared to the individual model values Y m and to multi-model means. The model values can be further decomposed into ensemble means and the deviations therefrom as Y m  = {Y m } + Y # m whence \(\sum^{2}={\{(Y_{m}-\{Y_{m}\})}^{2}\}=\{Y_{m}^{\#2}\}\) is the ensemble variance. The intermodel correlation between different energetic quantities is defined as \(R_{YZ}=\{Y_{m}^{\#}Z_{m}^{\#}\}/\sum_{Y}\sum_{Z}.\)

Figure 2 shows the available potential energy A, kinetic energy K and the conversion between them C for the 17 year average climatological 2-component energy diagram. Values from the reanalyses, from the AMIP2 data for each of the models, and for the multi-model quantities are given. In equilibrium, G =  C =  D, that is, the rate of generation of available potential energy is equal to the rate of conversion from available potential to kinetic which is, in turn, equal to the rate of dissipation of kinetic energy. The middle panel in the figure gives the basic “rate of working” of the atmosphere. Most models, including the multi-model cases, exhibit a basic “rate of working” which is higher than the than the estimate calculated from the NCEP reanalysis. The estimate from the ERA reanalysis is larger than that from the NCEP reanalysis although most model values are on the high side of this estimate as well Similarly, the amount of available potential energy A is generally larger than the estimates from the reanalyses. By contrast, the modelled kinetic energy K, while also tending to be larger than the reanalyses values, nevertheless displays a number of models with lower values. It is clear by inspection that the dissipation rate is not proportional to the total amount of kinetic energy in the models since high (low) values of K in the lower panel are not obviously associated with high (low) values of D. Overall, the energy cycle of most models is somewhat too vigorous. Models generate too much A, convert it to K and dissipate it at too rapid a rate. Which processes in the models might be responsible for this aspect of their behaviour is of considerable interest.

Fig. 2
figure 2

Terms in the climatological annual mean 2-component energy cycle from NCEP and ERA reanalysis data, for each of the AMIP2 models, and for the multi-model measures. The conversion rate C is calculated from the data and, in equilibrium, G =  D =  C. Standard units for energy amounts (A, K) are 105 Jm−2 and for generation/conversion/dissipation terms are Wm−2

Full size image

Table 3 gives some statistics for the collection of models including the ensemble mean denoted as {Y} and the ensemble standard deviation ∑ Y . The coefficient of variation (cofv) ∑ Y /{Y} relates the scatter across the models to the magnitude of the ensemble mean. In general, if the cofv is small the variation of the quantity in question is correspondingly unimportant compared to its mean value. If the cofv is large, on the other hand, either the variability is important compared to the mean or the mean itself is small. In particular from Table 3 and Fig. 2 for the very basic climatological 2-component energy cycle, we see that the models tend to have too strong an energy cycle where A, K and G =  C =  D are larger than the average of the two observation-based values by 13, 3 and 17%, respectively.

Table 3 Statistics for climatological mean energy cycle terms
Full size table

The idea of calculating inter-model correlations in Table 3 is to see if there is any consistency in the differences among models that might cast light on the mechanisms involved. The table shows that differences in G =  C =  D from model to model are associated with the corresponding differences of A with a correlation coefficient of 0.68. This suggests that the models’ generally too strong generation G results in too strong values of A which in turn is associated with strong values of conversion C to kinetic energy. However, the variations from model to model of K don’t correlate particularly well with C or equivalently with the dissipation D since the correlation coefficient is only 0.17.

Figure 3 further decomposes the energy cycle into its zonal and eddy components. The results are arranged as in the 4-component energy diagram of Fig. 1. The generation and dissipation terms are obtained as residuals. This decomposition separates out the energetic quantities associated with zonally and time averaged structures and the deviations from the time and zonal mean state termed the eddies. Table 4 gives the same statistics as Table 3 but now for the 12 terms in the 4-component energy diagram. Figure 4 (upper panel) compares the multi-model average of the budget terms with the values from the NCEP and ERA reanalyses and also gives the percentage difference from the average of the observationally based values (i.e. from the reanalysis ensemble mean, albeit an average over only two values). As noted previously, the modelled energy cycle is too strong on average in the models. Terms range from about 2 to 22 percent larger than the observation-based average with the exception of K E and D Z which are 9 and 8% smaller, respectively. The cofv of the C(A Z ,K Z ) term is very large (i.e. the term itself is small and variable from model to model) so is generally not part of these considerations.

Fig. 3
figure 3

Terms in the annual average climatological 4-component energy cycle from NCEP and ERA reanalysis data, for each of the AMIP2 models, and for the multi-model measures. The results are arranged as in the lower panel of Fig. 1. The generation (G) and dissipation (D) terms are obtained as residuals. Standard units of 105 Jm−2 and Wm−2

Full size image
Fig. 4
figure 4

The upper panel gives model ensemble mean quantities for the climatological 4-component energy budget compared to the values based on the NCEP and ERA reanalyses. The percentage difference is calculated with respect to the average of the two observational-based estimates. Standard units of 105 Jm−2 and Wm−2. The lower panel gives inter-model correlations of the adjacent terms in the energy cycle diagram (connected by straight arrows) as well as correlations between non-adjacent quantities which exceed 0.70 and hence account for at least 50% of the intermodal variance (connected by curved arrows). The C(A Z ,K Z ) correlations are not shown because of the smallness of that term

Full size image
Table 4 Observation-based and ensemble averaged climatological mean energy terms. X m indicates the observation-based estimates, {Y m } the model ensemble mean, ∑ y the intermodel ensemble standard deviation, ∑ y /{Y m } the coefficient of variation and R the intermodel correlation.
Full size table

The correlation diagram in Fig. 4 (lower panel) is an attempt to indicate how the different terms in the energy cycle vary among models. If models with high values of G Z also have high values of A Z then the G Z , A Z correlation will be high and this kind of relationship can potentially give some information as to which processes in the models control the strength of the energy cycle. In the lower panel of Fig. 4, the intermodel correlations are given for all “adjacent” terms in the energy budget connected by straight arrows and, in addition, correlations of greater than 0.70 (accounting for at least 50% of the intermodel variation) between non-adjacent terms are shown by curved arrows.

The eye is immediately drawn to the strong correlative connection between D E , the dissipation of eddy kinetic energy, and terms involving the eddy available potential energy A E in models. Thus when D E is larger or smaller, all the energy budget terms involving A E tend to be larger or smaller also. Although A E and K E are connected in a like manner, the connection of other terms with K E is not as robust. D E is too large by about 22% compared to the average of the observation-based values, K E is too small by 9% and the conversion C(A E ,K E ) is too large by about 20%.

The suspicion is that excessive eddy dissipation in models may be implicated in the too weak K E and potentially in the too strong energy cycle. This might be termed the “eddy dissipation pull” hypothesis in that excessive eddy dissipation weakens K E which “pulls” more energy from A E while A E is maintained against this pull by excessive eddy generation G E as well as excessive conversion from A Z and excessive G Z . This reasoning suggests that decreasing D E in models would result in a weakening of the energy cycle and suggests that more attention be given to those physical processes that control D E in models.

Negative correlations are few in the lower panel of Fig. 4 and those that appear involve the connection between D Z and both K E and K Z . Models with higher values of D Z have lower values of K Z and K E and vice versa. It is certainly plausible that more dissipation means less kinetic energy (negative correlation) just as more generation correlates with greater available potential energy (positive correlation) as is seen in the diagram. For the kinetic energy side of the diagram, an increase in D Z might be expected to reduce K Z which would also be in the right direction. However, larger D Z is associated with smaller K E in current models which is in the wrong direction and would have to be counteracted by other changes. The “dissipation pull” view would recommend a modest increase in zonal dissipation D Z in models leading to reduced K Z as well as a marked decrease in eddy dissipation D E bolstering K E and reducing the pull from the available potential energy side of the budget.

A similar “generation push” argument can be made where too large values of G Z are linked by energy flow and by correlation with too large amounts of A Z and conversion of A Z to A E (where it is subsequently converted to K E at too great a rate). This suggests in turn that moderating G Z could help reduce the excessive vigor of the modelled energy cycle.

4.3 The variance of energetic quantities

The basic energy cycle quantities are heavily averaged by being integrated over the mass of the atmosphere. For this reason the temporal variations of the terms in the integrated energy budget are comparatively small. From (7) the temporal variance of the 17 years of monthly values of an energetic quantity X may be expressed as

$$\sigma_{X}^{2}= \sigma^{2}_{{X_{a}}} + \sigma ^{2}_{{X_{d} }} $$
(8)

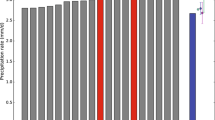
The climatological annual cycle is deterministic while the variation about the CAC is largely internally generated non-deterministic natural variability. The observation-based variability is represented by the standard deviations σ X , the coefficient of variation σ X /X m , and the fraction of variance accounted for by the CAC is \(\sigma_{X_{a}}^{2}/\sigma_{X}^{2}.\) The corresponding ensemble mean model quantities are \(\hat{\sigma}_{Y}=\sqrt{\{\sigma_{Y}^{2}\}},\hat{\sigma}_{Y}/\{Y_{m}\},\) and \(\{\sigma_{Y_{d}}^{2}\}/\{\sigma_{Y}^{2}\}.\) The ratio of the modelled to observed variance \(\{\sigma_{Y}^{2}\}/\sigma_{X}^{2}\) is plotted in Fig. 5. Table 5 gives results for the basic quantities A, G = C = D and K.

Fig. 5
figure 5

The variability of the energy budget quantities A, G =  C =  D, and K compared to the NCEP observation-based value represented by the variance ratio σ 2 Y /σ 2 X where the numerator is the model value. The first red bar is the observations so the value is 1 and the remaining bars apply to the individual models and to the multi-model measure

Full size image
Table 5 The temporal standard deviation of the observation-based NCEP reanalysis σ X and model ensemble mean \(\hat{\sigma}_{Y}=\sqrt{\{\sigma^{2}_{Y}\}}\) energy budget quantities A and K (105 Jm −2) and of G =  C =  D (Wm −2) together with the ratio of net model ensemble variance to the reanalysis value \(\{\sigma_{Y}^{2}\}/\sigma_{X}^{2}\) and of the fraction of the variance accounted for by the climatological annual cycle \(\{\sigma_{X_{a}}^{2}\}/\sigma_{X}^{2}, \{\sigma_{Y_{a}}^{2}\}/\{\sigma_{Y}\}^{2}.\) Finally, the coefficients of variation \(\sigma_{X}/X_{m}, \hat{\sigma}_{Y}/\{Y_{m}\}\) show that the variation of the quantities is small compared to the mean
Full size table

It is apparent from Table 5 that the temporal variability of these quantities is small compared to the mean values as indicated by the values of the cofv in the last two columns which are less than 10%. Of this variability, 80–90% is accounted for by the climatological annual cycle for A and K and about 50% for G = C = D for the observation-based NCEP values while for the models, the CAC accounts for slightly less of the variance for K and somewhat more for G = C = D. Figure 5 indicates that the temporal variance of the models, dominated largely by the CAC, is generally smaller than the observation-based value although a number of models have values which are as large or larger. The ensemble mean variability is generally more consistently in agreement with the observationally based estimate than any particular model. This is the result, however of rather divergent variance estimates across the models.

For completeness, Table 6 gives similar information for the 12 quantities in the 4-component energy cycle. The terms in Table 6 can be considered in groups of four, the first four columns are the energy amounts, the second four the conversion rates between them, and the last four columns are the generation and dissipation rates obtained as residuals. For the energy amounts, the average model variance is greater than the observationally based NCEP value for the zonal components and less for the eddy components. Most of the variance is associated with the CAC and the variability is small compared to the mean for all but K E .

Table 6 The temporal standard deviations of the observation-based NCEP reanalysis σ X and model ensemble mean \(\hat{\sigma}_{Y}=\sqrt{\{\sigma^{2}_{Y}\}}\) energy budget quantities together with the ratio of model ensemble variance to that observed \(\{\sigma_{Y}^{2}\}/\sigma_{X}^{2},\) the fraction of the variance accounted for by the climatological annual cycle \(\{\sigma_{X_{a}}^{2}\}/\sigma_{X}^{2}, \{\sigma_{Y_{a}}^{2}\}/\{\sigma_{Y}\}^{2}\) and the coefficients of variation \(\sigma_{X}/X_{m}, \hat{\sigma}_{Y}/\{Y_{m}\}.\) Units for A, K are (105 Jm−2) and for G, C, D (Wm−2)
Full size table

For the conversions in the next four columns, the annual cycle is not quite so dominant in the variability and the average model variability is less than that of the observational-based values with the notable exception of the conversion between K E and K Z which exhibits more variability and a stronger annual cycle. Finally, the generation and dissipation terms in the last four columns are residuals and should not be given too much credence. The model based variability is again generally smaller with the notable exception of G E for which the cofv is also comparatively high.

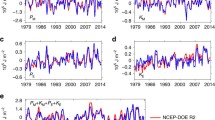
Figure 6 plots the CACs for these quantities (which typically dominate the temporal variance). The black line in Fig. 6 is based on the NCEP reanalysis, the red lines are the multi-model quantities and the remaining lines are for the individual models. The plots give a sense of the behaviour and scatter of these quantities. Since these are global quantities the seasonal cycle is not as strong as it would be if the hemispheres were considered separately. There is general agreement among the models and the observed annual cycle of energetic quantities (correlations are generally high for instance) with the exception of the model dissipation terms which tend to be out of phase with the observationally based quantities. As in Fig. 4, the D E term stands out.

Fig. 6
figure 6

The climatological annual cycles of the terms in the 4-component energy cycle. The black curve is the observation-based NCEP estimate, the red curves are the multi-model measures and the remaining curves are the values of the individual models. According to Tables 5 and 6, the climatological annual cycle accounts for a large percentage of the variance of the quantities but the variability is small compared to the mean value as measured by the coefficient of variation. Standard units of 105 Jm−2 and Wm−2

Full size image

4.4 Integrands

The energy cycle quantities treated in previous sections are mass integrals over the atmosphere X = ∫ x(φ, p)dm. The integrands x(φ, p) are functions of latitude and pressure and, as shown in the Appendix, involve means, variances and covariances among the primary variables. Energetic quantities thus contain information on the non-linearities that characterize the atmosphere. We are interested in the ability of the models to reproduce these statistics and the location and nature of the differences with their observation-based estimates.

Tables 7 and 8 give the temporal standard deviations \({\tilde{\sigma}}_{x}\) of the integrand of the observation-based NCEP energy budget quantities calculated from \({\tilde{\sigma}}_{x}=\sqrt{\int \sigma_{x}^{2}dm}.\) The corresponding model based values integrands y(φ, p) provide the multi-model ensemble mean standard deviation from \({\tilde{\sigma}}_{y}=\sqrt{\int \{\sigma_{y}^{2}\}dm}.\) The ratio of variances and the fraction of the variance accounted for by the climatological annual cycle are also given. These quantities may be compared with the variability of the integrated quantities in Tables 5 and 6. In both cases, the climatological annual cycles account for a large fraction of the temporal variance and the standard deviations are small compared to the mean. For this reason, the main comparison is between the climatological means of the energetic quantities.

Table 7 The temporal variability σ x of the integrands x(φ, p) of energy budget quantities provide the standard deviations \({\tilde{\sigma}}_{x}=\sqrt{\int \sigma_{x}^{2}dm}\) from observation-based NCEP reanalysis
Full size table
Table 8 As Table 7 but for the terms in the 4-component energy cycle
Full size table

4.4.1 Climatological means

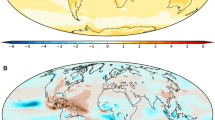
Figure 7 displays the climatological means of the integrands of the energy quantities A Z , A E , K Z and K E and Fig. 8 the integrands of the conversions C(A Z ,A E ), C(A E ,K E ), C(K E ,K Z ) and C(A Z ,K Z ). Since generation and dissipation are inferred as residuals they are not shown. The cross-sections are shown in pairs. The observationally based NCEP integrand x m (φ, p) is contoured in the left panels and the multi-model ensemble mean {y m } is contoured in the right panel. The difference between them, d = {y m } − x m , is indicated by shading in the left panels. The intermodel standard deviation ∑ y is indicated by shading in the right panels.

Fig. 7
figure 7

Integrands of the climatological mean energy quantities A Z , A E , K Z and K E as pairs of cross-sections. The the NCEP observationally based quantity is contoured in the left panels and the ensemble mean model quantity is contoured in the right panels. The difference between them is shaded in the left panels and the ensemble standard deviation among model results is shaded in the right panels. Units are 104 JKg −1

Full size image
Fig. 8
figure 8

As for Fig. 7 but for the integrands of the conversions C(A Z ,A E ), C(A E ,K E ), C(K E ,K Z ) and C(A Z ,K Z ) between the energetic quantities. Units are 0.1 Wkg−1

Full size image

Reanalysis and model values of the various quantities entering the integrands are given everywhere on pressure surfaces even when these pressure surfaces are pierced by topography. These “underground” interpolated values are provided so that the fields are simply connected and easier to plot and view. However, these values should not enter budget calculations and are excluded using the formalism of Boer (1982) as indicated by the equations in the Appendix. The values of the integrands are, therefore, zero under Antarctica and are reduced at other latitudes where part of the pressure surface is “underground”. This treatment of the fields near topography contributes to the structure there and is noticeable, for instance, just above Antarctica. Finally, in presenting these integrands it is important to remember that terms representing transports within the atmosphere but which integrate to zero are not included since they do not contribute to the final integrated values.

The integrand of A Z in the uppermost pair of panels involves the square of the deviation of the temperature from its meridional mean scaled by a stability parameter (A2). It is apparent that the average model value is generally larger than the observationally based quantity with the largest differences in the poleward upper troposphere. This is the energetic signature of the classical (e.g. Boer et al. 1992, 2000b, Gates 1987, 1999 etc.) systematic model error where temperatures are too cold in these regions. This temperature error contributes to the excessive A Z shown by the models in Figs. 3 and 4. The intermodel standard deviation of this quantity is also comparatively large with largest values at poleward locations generally coincident with the largest values of the integrand.

The quantity d/∑ y is implicit in the information given in the panels (the ratio of the shaded difference d in the left panel to the shaded quantity ∑ y in the right panel) but is not plotted explicitly. The value of d/∑ y gives an indication of the “systematic” nature of the difference between {y m } and x m in the sense that larger values imply that the model values are, on average, systematically and statistically different from the reanalysis-based values.

The integrand of A E in the second row of panels is determined by the spatial and temporal variance of the temperature field (A2). There are maxima in the lower and the upper extratropical troposphere. The values are modestly larger than reanalysis-based values in much of the troposphere as is the integrated value in Fig. 4. The exception is in the upper troposphere/lower stratosphere especially in the Northern Hemisphere where temperature variability is weaker on average in models. This presumably is a consequence of the lack of suitable sudden warmings in some models. The intermodel standard deviation is comparatively large and found also in the upper troposphere in conjunction with the large value of the integrand of A Z .

The top panel of Fig. 8 gives the integrand of the conversion C(A Z ,A E ) between these two forms of available potential energy. According to (A5) the conversion is a consequence of the downgradient transport of heat by the eddies expressed as a function of the covariances between temperature and velocities and the gradient of the zonal temperature structure. There are two maximum in this term as well and the average model value is larger than that of the observationally based estimate. The intermodel scatter largely mirrors the pattern of the field itself.

The second set of panels in Fig. 8 displays the conversion of A E to K E calculated in (A4) from the covariance between eddy (pressure) vertical motion and temperature and characterized as the rising of warm and sinking of cool air associated with the conversion of potential plus internal energy into the kinetic energy of the eddies. Here there is a single maximum in the extratropical mid to upper troposphere and once again the conversion rate is too strong, on average, in the models compared to the reanalysis value, although the broad structure of the term is certainly reasonable.

In brief, the available potential energy side of the energy cycle in Figs. 4, 7 and 8 indicate that models, on average, exhibit excessive values of A Z , A E , the conversion C(A Z ,A E ) between them and the subsequent conversion C(A E ,K E ) to eddy kinetic energy. The available potential energy side of the energy cycle is too vigorous with average model values of the quantities exceeding the observationally based average by from 2 to 22% according to Fig. 4. Excessive A Z is a associated with the traditional error of too cold poleward upper tropospheric temperatures in models and with a too large conversion rates to A E and thence to K E . Although causation is not direct, the presumption that the flow of energy implies also the flow of causation is bolstered by the intermodel correlations of the terms in the bottom panel of Fig. 4. Thus models with large values of A Z preferentially have large values of C(A Z ,A E ) with a correlation of 0.81 and so on among other terms. One conclusion is that correcting the excessive pole to equator meridional temperature gradient in models should moderate this too vigorous side of the energy cycle.

Despite the excessive conversion of A E to K E the K E itself is deficient mainly in the Northern Hemisphere extratropics according in Fig. 7 and overall in Fig. 4. According to Fig. 4 there are two aspects of this, an excessive rate of dissipation of K E as well too large a conversion rate from K E to K Z . However, the barotropic conversion C(K E ,K Z ), the integrand of which is shown in the third pair of panels in Fig. 8, is, overall, only about a fifth of the rate of the conversion of energy from A E into K E . The observation-based and model-based patterns are very similar and, according to (A6) represent the eddy transport of momentum against the gradient of zonal angular momentum. The main reason for the deficiency in K E is plausibly an excessive rate of its dissipation in the models. This impression is bolstered by the correlation results in Fig. 4 which were discussed also in Section 4.2. Here the implication is that excessive eddy dissipation drains the away the eddy kinetic energy and, to the extent that “dissipation pull” operates, serves to also drain away A E and support the excessive flow of A Z to A E to K E .

The zonal temperature structure, via geostrophy and the thermal wind equation, implies also that the zonal wind structure, and thus K Z , is too strong as shown in Fig. 7. In the Southern Hemisphere at least, the maximum of K Z is also displaced equatorward. K Z is apparently too strong both because of excess conversion from K E and also because of too little dissipation (Fig. 4). The upshot is that decreased eddy and increased zonal dissipation should help correct the modelled kinetic energy component of the budget.

Finally, the integrand of the conversion between K Z and A Z is plotted in the bottom most pair of panels in Fig. 8. The pattern is one of alternating positive and negative regions but the integrated result in Fig. 4 and Table 4 is small and uncertain as to sign so doesn’t play an important role in the overall energy cycle of the system.

4.4.2 BLT diagrams

Figures 7 and 8 give cross-sections of the integrands of the main terms in the energy cycle. Despite the differences, noted in detail in the previous section, the distribution of the integrands of budget quantities in latitude and pressure are reasonably similar to the observation-based distributions. This can be quantified using the so-called BLT diagram (Boer and Lambert 2001) which is a variant of the Taylor diagram (Taylor 2001). These diagrams compare variances, mean square differences and correlations of the individual model distributions of the integrands discussed in Figs. 7 and 8.

The integrands are written as x =  < x > +  x + where 〈x〉 is the meridional average and is a function of pressure but not of latitude. Because of the broad agreement of the modelled and analysis-based integrands in Figs. 7 and 8, a somewhat more stringent comparison is between the deviations x +,y + from the meridional average. The interest is in how well the models capture the variation about the strong vertical structure. The statistics considered are variances, mean square differences, and correlations calculated as

$$\begin{aligned} \tilde{\sigma}_{x+}^{2}&=g^{-1}\int \langle x^{+2}\rangle dp, \quad {\tilde{\sigma}}_{y+}^{2}=g^{-1}\int \langle y^{+2}\rangle dp\\ d^{2}&=g^{-1}\int \langle {(y^{+}-x^{+})}^{2} \rangle dp\\ r&=\frac{g^{-1}\int \langle y^{+}x^{+}\rangle dp}{\tilde{\sigma}_{x+}\; {\tilde{\sigma}}_{y+}} \end{aligned}$$
(9)

where the observation-based reference x is taken as the average of the NCEP and ERA40 reanalysis values. The BLT diagram plots \(d^{2}/\tilde{\sigma}_{x+}^{2}, \tilde{\sigma}_{y+}^{2}/\tilde{\sigma}_{x+}^{2}\) and r. These statistics are displayed in Fig. 9 for each model, for the multi-model values (in red) and for the NCEP and ERA40 values themselves (in purple). The generation and dissipation terms, available only as residuals, are not considered. Energy amounts are shown in the upper four panels and the conversions between them in the lower four panels.

Fig. 9
figure 9

BLT diagrams comparing the spatial distributions of the average of the NCEP and ERA observation-based integrands of the energetic quantities with individual model results in terms of mean square differences, correlation, and the ratio of variances as discussed in the text. Multi-model results are labelled in red and the NCEP and ERA values, as compared to their average, in purple

Full size image

Figure 9 gives some indication of the agreement between the reanalysis based estimates as compared to their mean as well as the agreement of the individual and multi-model values with this reference. Viewed in this way, the reanalysis based distributions show some divergence although typically less than any of the models. Figure 9 indicates that the details of the spatial distribution (in the sense of x +,y +) of the integrands of A Z , A E , K Z , K E , which depend on variances of temperatures and velocities, are relatively well simulated compared to the reanalysis-based values. Correlations are typically better than 0.9 and means square differences modest. The integrands of A Z and K Z in models typically show more structure than in the observation-based terms \((\tilde{\sigma}_{y+}^{2}/\tilde{\sigma}_{x+}^{2} > 1)\) while the reverse is true for K E . The mean model and mean budget values are consistently the best or among the best in these comparisons supporting the “ensemble model” argument discussed further below.

The integrands of the main conversions C(A Z ,A E ), C(A E ,K E ), C(K E ,K Z ) depend on the covariances between temperatures and velocities and on the gradients of the zonal mean structures. They are less well simulated than the variance based energy amounts. Here the ensemble mean model and budget versions are typically best in the comparisons. These results indicate that second order covariance terms are less well simulated in models than are means and variances and that their distribution deserves additional attention.

5 The “ensemble mean” model

The results of this study provide additional evidence that the “ensemble mean” model is the “best” model when compared to observation-based quantities. Based on the results of an intercomparison of the mean fields simulated in the CMIP project, Boer and Lambert (2001) showed that basic observation-based climatological mean quantities (such as temperature, precipitation, mean sea level pressure etc.) were in better accord with the ensemble mean model values than were those of any individual model. This agreement was measured by several second order statistics and not only by mean square error which might benefit from the smoothing implied by ensemble averaging.

The virtue of the ensemble mean model for the simulation of higher order climatological statistics and derived quantities is also apparent in the results obtained here. The integrands of energetic terms depend on second order variances and covariances for which the virtues of ensemble averaging might not be obvious. However, the approach where the budget quantities themselves are ensemble averaged (MBUD in the diagrams) has a clear advantage in Fig. 9 and in other results. The closely aligned approach, where the statistics themselves are ensemble averaged before the energetic quantities are calculated (MMOD in the diagrams) is also better than most individual models but generally not quite as good as the ensemble mean result.

Both the current and previous results lend support to the “mean” model or, perhaps better, the “ensemble” model approach. An analogy is made (e.g. Boer 2003) between the “sensitivity to initial conditions” that limits the skill of deterministic forecasts and the “sensitivity to numerics and parameterizations” in climate models which limits the skill of climate simulations. Ensemble methods can help overcome the barrier that such a sensitivity implies as indicated by the results obtained here and elsewhere.

The basis of the ensemble approach for climate considers AMIP, CMIP or other collection of model results as a sample from the population of models “produced with current knowledge”, that is, by reasonable researchers using reasonable approaches and embodying the current levels of resolution, numerics and physical parameterization. The ensemble, therefore, is expected to provide a better estimation of the “population” parameters (i.e. of the parameters of the real climate system) than is a single sample (model). Population estimates are obtained by pooling the climate statistics from individual models.

In its extreme expression the “ensemble model” approach abandons the idea of a “best” or “perfect” climate model arguing that the sensitive dependence on numerics and parameterizations results in a sort of climate model chaos and a “simulation barrier” analogous to the “predictability barrier” of weather forecasting. One therefore deals with the collection of climate model results in a probabilistic framework using ensemble approaches to average out noise and error to improve simulations for means and also, as here, for higher moments and other statistics, replacing the deterministic with a probabilistic view of climate modelling.

6 Summary

The energy cycle characterizes basic aspects of the physical behaviour of the climate system. Terms in the energy cycle involve first and second order climate statistics (means, variances and covariances) and the intercomparison of energetic quantities offers physically motivated “second order” insight into model and system behaviour. The components of the energy cycle from 12 atmospheric climate models participating in the AMIP2 intercomparison project are calculated and intercompared. In addition to individual model energetic terms, multi-model “ensemble average” energetic terms are calculated and intercompared. The modelled energetic quantities are compared with those calculated from NCEP and ERA40 reanalyses for the same period.

The basic 4-component energy cycle is evaluated involving the generation (G Z ,G E ) of zonal and eddy forms of available potential energy (A Z ,A E ) and their conversion to kinetic energy (K Z ,K E ) and subsequent dissipation (D Z ,D E ). This flow of energy gives the basic “rate of working” of the atmospheric climate system operating as a heat engine. Amounts and distributions of zonal and eddy available potential and kinetic energies depend on the variance in space and time of the temperature and velocity fields. Conversions between the various forms of energy depend on eddy covariances between velocities and temperatures and on the zonal structures of temperature and velocities in the atmosphere. Since generation and dissipation terms are not directly available from AMIP data, their values are inferred as budget residuals.

In general, the models simulate a somewhat too vigorous energy cycle with too strong generation and excessive amounts of zonal available potential energy which is seen in the common and systematic model error of too cold upper tropospheric temperatures at high latitudes. The conversion of A Z to A E and its generation G E are both generally too strong and the amount of A E is too large compared to reanalysis-based estimates. The conversion from A E to K E is also too strong but simulated K E , by contrast, tends to be too weak in the face of somewhat too strong conversion to K Z and rather too large dissipation D E . Finally, K Z is also too large. The overall rate of working of the model atmospheres is, on average, about 17% more vigorous than the average of the reanalysis-based estimates.

These results, together with an attempt to connect differences in individual model values of the energetic quantities with each other in order to infer something of the mechanisms involved, suggests that the excessive generation G Z and amount of A Z are important drivers of the overactive energy cycle through “generation push”. However, excessive dissipation D E of K E is also potentially implicated through “dissipation pull”.

The energetic quantities are integrals over the mass of the atmosphere and their temporal variation, dominated by the annual cycle, is small compared to their mean values as measured by the coefficient of variation. For this reason most attention is given to the climatological distributions themselves. The distributions of the integrands of the terms, representing the distributions of both first and second order climate statistics in the model atmosphere, agree quite well in a qualitative sense, with those based on NCEP data although a number of characteristic deficiencies are apparent. The vertical structures of the integrands of energetic quantities is reasonably well captured with the remaining structure captured less well. Comparison of the structure of the model and reanalysis-based integrands, after removing the vertical structures, is undertaken in terms of mean square error, spatial correlation, and the ratio of variances.

One of the more striking results is that the ensemble model result is consistently the best or among the best in these comparisons supporting the “ensemble model” approach not only for 1st order climate quantities as in Boer and Lambert (2001) but also for higher order climate quantities as investigated here. These and other results suggest that the “sensitive dependence on numerics and parameterizations” in climate models limits the accuracy with which the climate can be simulated. If the individual model results can be considered to be a reasonably random sample from the population of reasonable models reflecting current knowledge of the climate system, it is plausible to use the ensemble approach to simulating current and future climates.