Degree Conditions for Graphs to Have Spanning Trees with Few Branch Vertices and Leaves

Abstract

A leaf of a tree is a vertex of degree one and a branch vertex of a tree is a vertex of degree strictly greater than two. This paper shows two degree conditions for graphs to have spanning trees with total bounded number of branch vertices and leaves. Moreover, the sharpness of our results is shown.

1 Introduction

We consider finite undirected graphs without loops or multiple edges. Let G be a graph with vertex set V(G) and edge set E(G). The order of G is denoted by |G|. For a vertex $x\in V(G)$, we denote the degree of x in G by $\text {deg}_G(x)$ and the set of vertices adjacent to x in G by $N_{G}(x)$. For two vertices $x,y\in V(G)$, $\mathrm {dist}_{G}(x,y)$ denotes the distance between x and y in G. For a subset $S\subset V(G)$, we write $N_{G}(S)=\cup _{x\in S}N_{G}(x)$.

A leaf of a tree is a vertex of degree one and a branch vertex of a tree is a vertex of degree strictly greater than two. For a tree T, let

$$\begin{aligned} L(T)&=\{x\in V(T) \mid x\ \text {is a leaf of}\ T\}\ \text {and} \\ B(T)&=\{x\in V(T) \mid x\ \text {is a branch vertex of}\ T\}. \end{aligned}$$

For two vertices x and y of T, $P_T(x, y)$ denotes the unique path in T connecting x and y. Given a tree T with oreder at least two, we often regard T as a rooted tree in which all the edges are directed away from a specified vertex of T and such a specified vertex of T is called a root of T. Let T be a rooted tree with root r. For a vertex subset $X \subseteq V(T){\setminus } \{r\}$, $X^{-}$ denotes the set of vertices adjacent to a vertex of X and $v^{-} \in V(T)$ denotes the vertex adjacent to v. For a vertex subset $Y \subseteq V(T) {\setminus } L(T)$, $Y^{+}$ denotes the set of vertices adjacent from a vertex of Y.

A tree having at most k leaves is called a k-ended tree, where $k \ge 2$ is an integer.

2 Main Results and Related Topics

We prove the following theorem, which gives a degree condition for a graph to have a spanning tree with bounded total number of branch vertices and leaves.

Theorem 1

Let $k\ge 2$ be an integer. Suppose that a connected graph G satisfies

$$\begin{aligned} \max \{\deg _{G}(x),\deg _{G}(y)\}\ge \dfrac{|G|-k+1}{2} \end{aligned}$$

for every two nonadjacent vertices $x,y\in V(G)$. Then G has a spanning tree T with $|L(T)|+|B(T)|\le k+1$.

The lower bound of the degree condition in Theorem 1 is sharp as shown in Sect. 4. One might conjecture that the sentence “for every two nonadjacent vertices” in Theorem 1 can be replaced by “for every two vertices $x,y\in V(G)$ with $\mathrm {dist}_{G}(x,y)=2$”, which is so-called a Fan-type degree condition.

The following problem assumes a weaker degree condition than Theorem 1.

Problem 2

Let $k\ge 2$ be an integer. Let G be a connected graph. Suppose that G satisfies

$$\begin{aligned} \max \{\deg _{G}(x),\deg _{G}(y)\}\ge \dfrac{|G|-k+1}{2} \end{aligned}$$

for every two vertices $x,y\in V(G)$ with $\mathrm {dist}_{G}(x,y)=2$. Does G have a spanning tree T with $|L(T)|+|B(T)|\le k+1$?

The answer of Problem 2 is in the negative and the counterexample for Problem 2 is shown in Sect. 6. When we restrict ourselves to 2-connected graphs, we also obtain the following result, which contains a Fan-type degree condition.

Theorem 3

Let $k\ge 2$ be an integer. Let G be a 2-connected graph. Suppose that

$$\begin{aligned} \max \{\deg _{G}(x),\deg _{G}(y)\}\ge \dfrac{|G|-k+1}{2} \end{aligned}$$

for every two vertices $x,y\in V(G)$ with $\mathrm {dist}_{G}(x,y)=2$. Then G has a spanning tree T with $|L(T)|+|B(T)|\le k+1$.

The following two results motivate our results. Theorem 4 gives an Ore-typecondition for a graph to have a spanning k-ended tree.

Theorem 4

(Broersma and Tuinstra [1]) Let $k\ge 2$ be an integer and let G be a connected graph. If G satisfies $\deg _{G}(x)+\deg _{G}(y)\ge |G|-k+1$ for every two nonadjacent vertices $x,y\in V(G)$, then G has a spanning k-ended tree.

The following theorem is stronger than Theorem 4 although it assumes the same condition as Theorem 4.

Theorem 5

(Nikoghosyan [2], Saito and Sano [3]) Let $k\ge 2$ be an integer. If aconnected graph G satisfies $\deg _{G}(x)+\deg _{G}(y)\ge |G|-k+1$ for every twononadjacent vertices $x,y\in V(G)$, then G has a spanning tree T with $|L(T)|+|B(T)|\le k+1$.

3 Preliminary Lemmas

We prove the following lemmas which are used in the proof of Theorems 1 and 3.

Lemma 1

Let G be a connected graph and let T be a spanning tree of G such that $|L(T)|+|B(T)|$ is minimal. If $B(T) \ne \emptyset$, then L(T) is an independent set of G.

Proof

Suppose that there exist two vertices $u,v\in L(T)$ with $uv\in E(G)$. Then $T+uv$ contains a unique cycle C. By $B(T)\ne \emptyset$, C has a branch vertex w. For $x\in N_{T}(w)\cap V(C)$, $T^{\prime }:=T+uv-wx$ is a spanning tree of G such that $L(T^{\prime })\subseteq (L(T){\setminus }\{u,v\})\cup \{x\}$ and $B(T^{\prime }) \subseteq B(T)$. This contradicts the minimality of $|L(T)|+|B(T)|$. $\square$

Lemma 2

Let G be a connected graph and let T be a spanning tree of G such that $|L(T)|+|B(T)|$ is minimal. Suppose that $B(T) \ne \emptyset$ and for any leaf x of T, T is regarded as a rooted spanning tree of G with the root x.

Then the following two statements hold:

• (i) $N_{G}(x)^{-} \cap N_{G}(y)=\emptyset$ for each $y \in L(T){\setminus }\{x\}$ and

• (ii) $N_{G}(x)^{-} \cap B(T)=\emptyset$.

Proof

(i) Suppose that there exists $y \in L(T) {\setminus }\{x\}$ such that $N_{G}(x)^{-} \cap N_{G}(y) \ne \emptyset$. Since T is a spanning tree of G such that $\deg _T(x)=\deg _T(y)=1$ and $B(T)\ne \emptyset$, $P_{T}(x, y)$ contains a branch vertex v. For $u \in N_{G}(x)^{-} \cap N_{G}(y)$, $T+u^{+}x+uy-u^{+}u$ contains a unique cycle C. For $w \in N_{T}(v) \cap V(C)$, $T^{\prime }:=T+u^{+}x+uy-u^{+}u-vw$ is a spanning tree of G with $L(T^{\prime }) \subseteq (L(T)\cup \{w\}) {\setminus } \{x,y\}$ and $B(T^{\prime }) \subseteq B(T)$. This contradicts the minimality of $|L(T)|+|B(T)|$. Hence $N_{G}(x)^{-} \cap N_{G}(y)=\emptyset$ for each $y \in L(T){\setminus }\{x\}$.

(ii) If there exists a vertex $z \in N_{G}(x)^{-} \cap B(T)$, then $T^{\prime }:=T+xz^{+}-z^{+}z$ is a spanning tree of G with $L(T^{\prime })=L(T){\setminus }\{x\}$ and $B(T^{\prime }) \subseteq B(T)$. This is a contradiction. Consequently, $N_{G}(x)^{-} \cap B(T)=\emptyset$. $\square$

Let T be a tree with $B(T)\ne \emptyset$. For all pairs $x \in L(T)$ and $y \in B(T)$ such that $(V(P_{T}(x,y)){\setminus }\{y\}) \cap B(T)=\emptyset$, we delete $V(P_{T}(x,y)){\setminus }\{y\}$ from T. Let $T^{\prime }$ be the resulting graph. Then $T^{\prime }$ is a tree and $L(T^{\prime }) \subseteq B(T)$. We say that a leaf of $T^{\prime }$ is a peripheral branch vertex of T. By the definition of $T'$, we obtain the following fact.

Fact 1

Let T be a tree and let v be a peripheral branch vertex of T. Then the number of leaves x in T satisfying $(V(P_{T}(x,v)){\setminus }\{v\}) \cap B(T)=\emptyset$ equals $\deg _{T}(v)-1$.

Lemma 3

Let G be a connected graph having no Hamiltonian path. Choose a spanning tree T of G such that

• (T1) $|L(T)|+|B(T)|$ is as small as possible and

• (T2) $\min \{\deg _{T}(x) :\$x$\ \text {is a peripheral branch vertex of}\ T\}$ is as small as possible, subject to (T1).

Let y be a peripheral branch vertex of T such that $\deg _{T}(y)$ is minimal and let z be a leaf of T such that $(V(P_{T}(y,z)){\setminus }\{y\}) \cap B(T)=\emptyset$. Then $N_{G}(z) \cap (B(T){\setminus }\{y\})=\emptyset$.

Proof

Suppose that there exists a vertex $w \in N_{G}(z) \cap (B(T){\setminus }\{y\})$. We regard T as a rooted tree with the root z. Then $T^{\prime }:=T+wz-yy^{-}$ is a spanning tree of G with $L(T^{\prime })=(L(T){\setminus }\{z\})\cup \{y^{-}\}$. If $\deg _{T}(y)=3$, then $B(T^{\prime })=B(T){\setminus }\{y\}$ and $|L(T^{\prime })|=|L(T)|$, which is a contradiction to (T1). If $\deg _{T}(y) \ge 4$, then y is a peripheral branch vertex of $T^{\prime }$ with $\deg _{T^{\prime }}(y)<\deg _{T}(y)$, which is a contradiction to (T2). $\square$

4 Sharpness of Theorem 1

In Theorem 1, we cannot replace the lower bound $(|G|-k+1)/2$ in the degree condition by $(|G|-k)/2$, which is shown in the following example. Let t be a positive integer and let $k\ge 2$ be an integer. Consider the complete bipartite graph G with partite sets A and B such that $|A|=t$ and $|B|=t+k$. Then $|G|=2t+k$ and $\max \{\deg _{G}(x),\deg _{G}(y)\}\ge t= (|G|-k)/2$ for every two nonadjacent vertices $x,y\in V(G)$. Suppose that G has a spanning tree T with $|L(T)|+|B(T)|\le k+1$. If $|L(T)| \le k$, then $|E(T)|\ge |B\cap L(T)|+2|B{\setminus }(B\cap L(T))| =2|B|-|B\cap L(T)| \ge k+2t=|G|$. This is a contradiction. If $|L(T)| \ge k+1$, then $|L(T)|+|B(T)|\ge k+2$ because T has at least one branch vertex. Hence G has no spanning tree T with $|L(T)|+|B(T)|\le k+1$.

5 Proof of Theorem 1

Suppose that a graph G satisfies all the conditions of Theorem 1, but has no desired spanning tree. Choose a spanning tree T of G so that

• (T1) $|L(T)|+|B(T)|$ is as small as possible and

• (T2) $\min \{\deg _{T}(x) :\, x\ \text {is a peripheral branch vertex of}\ T\}$ is as small as possible, subject to (T1).

If $|L(T)|=2$, then T is a Hamiltonian path of G, which satisfies $|L(T)|+|B(T)|=2<k+1$, a contradiction. Hence we may assume that $|L(T)|\ge 3$ and $|B(T)|\ge 1$. By Lemma 1 and the assumption of Theorem 1, the number of leaves in T having the degree at least $(|G|-k+1)/2$ in G is at least $|L(T)|-1$, i.e.,

$$\begin{aligned} |\{v \in L(T) : \deg _{G}(v) \ge (|G|-k+1)/2\}|\ge |L(T)|-1 \ge 2. \end{aligned}$$

(1)

We divide the proof into two cases according to the value of |B(T)|.

Case 1

$|B(T)|=1$.

By (1), we can choose two distinct vertices $x, y \in L(T)$ which satisfy $\deg _{G}(x)\ge (|G|-k+1)/2$ and $\deg _{G}(y) \ge (|G|-k+1)/2$. We regard T as a rooted tree with the root x. By Lemma 1, $N_{G}(y) \cap L(T)=\emptyset$. By Lemmas 2(i) and (ii), $N_{G}(x)^{-} \cap N_{G}(y)=\emptyset$ and $|N_{G}(x)^{-}|=|N_{G}(x)|$. Hence we obtain

$$\begin{aligned} \deg _G(x)+\deg _G(y)=|N_{G}(x)^{-}|+|N_{G}(y)| \le |G|-|L(T)|+|\{x\}|. \end{aligned}$$

On the other hand, $\deg _G(x)+\deg _G(y) \ge |G|-k+1$ by the hypothesis of this theorem. Conbining two inequalities above, we obtain $|L(T)| \le k$ and hence $|L(T)|+|B(T)|\le k+1$. This is a contradiction. This completes the proof of Case 1.

Case 2

$|B(T)| \ge 2$.

Choose a peripheral branch vertex $b_{1}$ of T such that $\deg _{T}(b_{1})$ is as small as possible. By Fact 1, there exist two leaves $x_{1}$ and $x_{2}$ of T such that $(V(P_{T}(b_{1},x_{i})){\setminus }\{b_{1}\})\cap B(T)=\emptyset$ for each $i=1,2$. By $|B(T)| \ge 2$, there exists a peripheral branch vertex $b_{2}$ of T with $b_{2} \ne b_{1}$. Fact 1 implies that there exist two leaves $x_{3}$ and $x_{4}$ of T such that $(V(P_{T}(b_{2},x_{i})){\setminus }\{b_{2}\})\cap B(T)=\emptyset$ for each $i=3,4$. By (1), without loss of generality, we may assume that $\deg _{G}(x_{i}) \ge (|G|-k+1)/2$ for each $i=1,3$. Note that $x_{1} \ne x_{3}$. We regard T as a rooted tree with root $x_{3}$. By Lemma 1, $N_{G}(x_{1}) \cap L(T)=\emptyset$. By Lemmas 2(i) and (ii), $N_{G}(x_{1}) \cap N_{G}(x_{3})^{-}=\emptyset$ and $|N_{G}(x_{3})^{-}|=|N_{G}(x_{3})|$. By Lemma 2(ii) and Lemma 3, $N_{G}(x_{3})^{-} \cap B(T)=\emptyset$ and $N_{G}(x_{1}) \cap (B(T){\setminus }\{b_{1}\})=\emptyset$. Hence

$$\begin{aligned} |N_{G}(x_{1})|+|N_{G}(x_{3})|&=|N_{G}(x_{1})|+|N_{G}(x_{3})^{-}| \\&\le |T|-(|L(T)|-|\{x_{3}\}|+|B(T)|-|\{b_{1}\}|) \\&=|G|-(|L(T)|+|B(T)|)+2. \end{aligned}$$

On the other hand, $|N_{G}(x_{1})|+|N_{G}(x_{3})|=\deg _{G}(x_{1})+\deg _{G}(x_{3}) \ge |G|-k+1$. Consequently, $|L(T)|+|B(T)| \le k+1$. This is a contradiction. This completes the proof of Case 2. Hence Theorem 1 is proved. $\square$

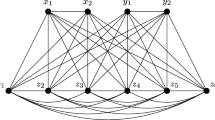
6 Counterexample of Problem 2

For two integers k and t such that $k\ge 2$ and $t\ge k+1$, denote by $K_t$ a complete graph of order t and denote by $P_{i}=a_{i}b_{i}$ a path of order two for each $i=1,\ldots ,k+1$.

We define a graph G of order $t+2k+2$ as follows:

$$\begin{aligned} V(G)&= V(K_t) \cup \left( \bigcup _{i=1}^{k+1} V(P_{i})\right) ~~\text{ and } \\ E(G)&=E(K_t) \cup \left( \bigcup _{i=1}^{k+1} \{xa_{i} : x \in V(K_{t})\}\right) \cup \left( \bigcup _{i=1}^{k+1}E(P_{i})\right) . \end{aligned}$$

Then, by $t\ge k+1$, $\max \{\deg _{G}(x),\deg _{G}(y)\}\ge t+1=|G|-2k-1\ge (|G|-k+1)/2$ for every two vertices $x,y\in V(G)$ with $\mathrm {dist}_{G}(x,y)=2$. Since all the vertices in $\{b_{1},b_{2},\ldots ,b_{k+1}\}$ are leaves for each spanning tree T of G, we obtain $|L(T)|\ge k+1 \ge 3$ and thus $|L(T)|+|B(T)|\ge k+2$. Therefore the answer for Problem 2 is in the negative.

7 Proof of Theorem 3

Suppose that a graph G satisfies all the conditions of Theorem 3, but has no desired spanning tree. Let $S=\{v \in V(T) : \deg _{G}(v) \ge (|G|-k+1)/2\}$. Choose a spanning tree T of G such that

• (T1) $|L(T)|+|B(T)|$ is as small as possible and

• (T2) $|S \cap L(T)|$ is as large as possible subject to (T1).

If $|L(T)|=2$, then T is a Hamiltonian path, which satisfies $|L(T)|+|B(T)|=2<k+1$, a contradiction. Hence we consider the case when $|L(T)|\ge 3$ and $|B(T)|\ge 1$.

Claim 1

For any leaf x of T, $\deg _{G}(x) \ge (|G|-k+1)/2$.

Proof

Suppose that $\deg _{G}(x)<(|G|-k+1)/2$ for some leaf x of T. Choose a vertex $w \in N_{G}(x)$ such that $|P_{T}(x,w)|$ is as large as possible. Write $P_{T}(x,w)=v_{1}v_{2} \ldots v_{m}$ with $v_{1}=x$ and $v_{m}=w$. Note that $m \ge 3$ because G is 2-connected and $\deg _T(x)=1$. We regard T as a rooted tree with root $v_{1}$.

Subclaim 1.1

$\{v_{2},v_{3},\ldots ,v_{m}\} \subseteq N_{G}(v_{1})$.

Proof

Suppose that $v_{1}v_{i-1} \notin E(G)$ for some i with $v_{1}v_{i} \in E(G)$. Then $\mathrm {dist}_{G}(v_{1},v_{i-1})=2$. It follows from the degree condition of this theorem that $\deg _{G}(v_{i-1}) \ge (|G|-k+1)/2$. Since $v_{i-1} \notin B(T)$ by Lemma 2(ii), $T^{\prime }:=T+v_{1}v_{i}-v_{i}v_{i-1}$ is a spanning tree of G with $L(T^{\prime })=(L(T){\setminus }\{x_{1}\})\cup \{v_{i-1}\}$, $B(T^{\prime })=B(T)$, and $|S \cap L(T^{\prime })| >|S \cap L(T)|$. This contradicts the choice (T2). Hence $v_{1}v_{i-1} \in E(G)$ for all i with $v_{1}v_{i} \in E(G)$. By $v_1v_m \in E(G)$, this subclaim holds. $\square$

By Lemma 2(ii) and Subclaim 1.1, $\{v_{1},v_{2},\ldots ,v_{m-1}\} \cap B(T)=\emptyset$.

Subclaim 1.2

$\deg _{G}(v_i) < (|G|-k+1)/2$ for any $v_i$ with $i=1,2,\ldots ,m-1$.

Proof

If $\deg _{G}(v_i) \ge (|G|-k+1)/2$ for some $v_i$ with $i=2,\ldots ,m-1$, then $T+v_1v_{i+1}-v_iv_{i+1}$ contradicts the choice (T2). Hence Subclaim 1.2 is proved. $\square$

We denote by $\mathcal {T}$ the set of spanning trees $T_{i}$ for $1 \le i \le m-1$ such that $L(T_{i})= (L(T){\setminus }\{x\})\cup \{v_{i}\}$, $B(T_{i})=B(T)$ and $\max \{|P_{T_{i}}(v_{i}, u)| : u \in N_G(v_{i}) \}$ is as large as possible. Note that each $T_{i}$ satisfies (T1) and (T2). Choose $T_{k} \in \mathcal {T}$ so that

• (T3) $\max \{|P_{T_{k}}(v_{k}, u)| : u \in N_G(v_{k}) \}$ is as large as possible.

Then $v_{k} \in L(T_{k})$ by the choice of $T_{k}$ and $\deg _{G}(v_k) < (|G|-k+1)/2$ by (T2). Hence the role of $v_{k}$ in $T_{k}$ is similar to that of $v_{1}$ in T. Therefore, without loss of generality, we may assume $k=1$. Then $|P_{T_1}(v_1, u)|$ is maximal.

Subclaim 1.3

$N_{G}(v_{i}) \subseteq \{v_{1},v_{2},\ldots ,v_{m}\}$ for each $i=1,2,\ldots ,m-1$.

Proof

By the definitions of $v_1=x$ and u, the subclaim holds for $i=1$. Suppose that $v_i$ is adjacent to $u' \in V(G) {\setminus } \{v_{1},v_{2},\ldots ,v_{m}\}$ for some $i=2,\ldots ,m-1$. By Subclaim 1.1, $v_{1}v_{i+1} \in E(G)$ and let $T^{\prime } :=T_{1}+v_{1}v_{i+1}-v_{i}v_{i+1}$. Then $|P_{T^{\prime }}(v_{i},u')| > m=|P_{T_1}(v_1, u)|$, this implies that there exists the tree $T_{i} \in \mathcal {T}$ such that $\max \{|P_{T_{i}}(v_{i},u)| : u\in N_{G}(v_{i})\}>\max \{|P_{T_{1}}(v_{1},u)| : u\in N_{G}(v_{1})\}$. This contradicts the choice (T3). $\square$

By Subclaim 1.3, $v_{m}$ is a cut-vertex of G, which contradicts the condition that G is 2-connected. Consequenlty, Claim 1 is proved. $\square$

Take any peripheral branch vertex b of T and put $\deg _{T}(b)=p$. By Fact 1, T contains $p-1$ leaves $x_{1},\ldots ,x_{p-1}$ such that $V(P_{T}(x_{i},b))\cap (B(T){\setminus }\{b\})=\emptyset$ for each $i=1, \ldots , p-1$. Note that $p-1=\deg _{T}(b)-1\ge 2$ because b is a branch vertex of T.

Claim 2

$N_{G}(x_{i}) \cap (B(T){\setminus }\{b\})\ne \emptyset$ for each $i=1,\ldots ,p-1$.

Proof

Suppose that $N_{G}(x_{i}) \cap (B(T){\setminus }\{b\})=\emptyset$ for some $i=1,\ldots ,p-1$. Without loss of generality, we may assume that $i=1$. We regard T as a rooted tree with root $x_{2}$. By Lemma 2(ii), we obtain $N_{G}(x_{2})^{-} \cap B(T)=\emptyset$ and hence $|N_{G}(x_{2})|=|N_{G}(x_{2})^{-}|$. Moreover, $N_{G}(x_{1}) \cap N_{G}(x_{2})^{-}=\emptyset$ by Lemma 2(i) and $N_{G}(x_{1}) \cap L(T)=\emptyset$ by Lemma 1. Consequently

$$\begin{aligned} |N_{G}(x_{1})|+|N_{G}(x_{2})|&=|N_{G}(x_{1})|+|N_{G}(x_{2})^{-}| \\&\le |T|-(|L(T)|-|\{x_{2}\}|+|B(T)|-|\{b\}|) \\&\le |G|-k. \end{aligned}$$

On the other hand, $|N_{G}(x_{1})|+|N_{G}(x_{2})|=\deg _{G}(x_{1})+\deg _{G}(x_{2}) \ge |G|-k+1$ by Claim 1. This is a contradiction. $\square$

For each $i=1,2,\ldots , p-2$, let $y_{i} \in N_{T}(b) \cap V(P_{T}(b,x_{i}))$ and let $b_{i}\in N_{G}(x_{i}) \cap (B(T){\setminus }\{b\})$. Then $T^{\prime }:=T+x_{1}b_{1}+\cdots +x_{p-2}b_{p-2}-by_{1}-\cdots -by_{p-2}$ is a spanning tree of G with $L(T^{\prime }) \subseteq L(T){\setminus }\{x_{1},\ldots ,x_{p-2}\} \cup \{y_{1},\ldots ,y_{p-2}\}$ and $B(T^{\prime }) \subseteq B(T){\setminus }\{b\}$. This is a contradiction to (T1). Therefore the proof of Theorem 3 is completed. $\square$