Chorded Cycles

Abstract

A chord is an edge between two vertices of a cycle that is not an edge on the cycle. If a cycle has at least one chord, then the cycle is called a chorded cycle, and if a cycle has at least two chords, then the cycle is called a doubly chorded cycle. The minimum degree and the minimum degree-sum conditions are given for a graph to contain vertex-disjoint chorded (doubly chorded) cycles containing specified elements of the graph, i.e., specified vertices, specified edges as cycle-edges, specified paths, or specified edges as chords. Furthermore, the minimum degree condition is given for a graph to be partitioned into chorded cycles containing specified edges as cycle-edges.

1 Introduction

We only consider finite simple graphs. In this paper, “disjoint” means “vertex-disjoint.” The study of cycles and systems of disjoint cycles in graphs is well established. Recently, there have been numerous papers considering cycles with additional properties, i.e., cycles containing a specific set of vertices, cycles containing a specific set of edges, or cycles containing a set of disjoint paths (see the survey [7]). Let G be a graph, and let C be a cycle in G. A chord is an edge between two vertices of C that is not an edge of C. If C has at least one chord, then it is called a chorded cycle, and if C has at least two chords, then it is called a doubly chorded cycle. Another natural additional property for cycles is that of containing at least one chord or at least some integer t chords. The study of chorded cycles has been increasing (see for example [1, 5, 8, 9]). In this paper, we extend several well-known results on disjoint cycles containing specified elements such as edges or vertices to similar results on disjoint chorded (doubly chorded) cycles containing these elements.

For $u\in V(G)$, the set of neighbors of u in G is denoted $N_G(u)$, and $\deg _G(u)=|N_G(u)|$ is the degree of u in G. Let H be a subgraph of G, and let S be a subset of V(G). For $u\in V(G)-V(H)$, we denote the neighborhood of u in H as $N_H(u)=N_G(u)\cap V(H)$ and $\deg _H(u)=|N_H(u)|$. For $u\in V(G)-S$, $N_S(u)=N_G(u)\cap S$. Furthermore, $N_G(S)=\cup _{w\in S}N_G(w)$ and $N_H(S)=N_G(S)\cap V(H)$. Let A, B be subgraphs of G. Then $N_G(A)=N_G(V(A))$ and $N_B(A)=N_G(A)\cap V(B)$. Let $G-H$ denote the subgraph of G induced by $V(G)-V(H)$, and let $G-S$ denote the subgraph of G induced by $V(G)-S$. If $S=\{u\}$, then we write $G-u$ for $G-S$. For graphs $G_1, G_2$, and $G_3$, $G_1\cup G_2$ denotes the union of $G_1$ and $G_2$, $G_1+G_2$ denotes the join of $G_1$ and $G_2$, and $G_1+G_2+G_3=(G_1\cup G_3)+G_2$. For distinct $x, y\in V(G)$, $G+xy$ denotes the graph obtained from G by adding the edge xy ($G+xy=G$, if $xy\in E(G)$). Similarly, if $xy\in E(G)$, then $G-xy$ denotes the graph obtained from G by removing the edge xy. For $e\in E(G)$, V(e) denotes the set of both end-vertices of e. Let C be a cycle with a given orientation, and let $x, y\in V(C)$. Then, according to the orientation, $x^+$ denotes the first successor of x on C, and $x \overrightarrow{C} y$ denotes the subpath on C from x to y. For $\{u_1, u_2, \ldots , u_k\}\subseteq V(G)$, let $\deg _H(u_1, u_2,\ldots , u_k) =\sum _{i=1}^k \deg _H(u_i)$. If $H=G$, then we denote $\deg _G(u_1, u_2,\ldots , u_k)=\deg _H(u_1, u_2, \ldots , u_k)$. The minimum degree of G is denoted by $\delta (G)$. For a non-complete graph G, let

$$\begin{aligned} \sigma _2 (G) = ~\text{ min }~ \{\deg _G(u )+\deg _G(v )~|~ u, v\in V(G), u\ne v, uv\not \in E(G) \}, \end{aligned}$$

and $\sigma _2(G)=\infty$ when G is a complete graph. A cycle of length l is called an l-cycle. The complement of G is denoted $\overline{G}$. For terminology and notation not defined here, see [6].

First, we note the following result on disjoint cycles containing specified vertices.

Theorem 1

[4] Let G be a graph of order $n\ge 6k-3$ for an integer $k\ge 1$. If

$$\begin{aligned} \delta (G)\ge \frac{n}{2}, \end{aligned}$$

then for any k distinct vertices $v_1, \ldots , v_k$ in G, there exist k disjoint cycles $C_1, \ldots , C_k$ such that $v_i\in V(C_i)$ and $3\le |V(C_i)|\le 5$ for all $1\le i\le k$.

We also note a similar result on disjoint cycles containing specified edges.

Theorem 2

[3] Let G be a graph of order n, and for $2\le k\le n/4$, let $e_1, \ldots , e_k$ be any k independent edges in G. Suppose that

$$\begin{aligned} \delta (G)\ge \frac{n}{2}+k-1. \end{aligned}$$

Then there exist k disjoint cycles $C_1, \ldots , C_k$ such that $e_i\in E(C_i)$ and $3\le |V(C_i)|\le 4$ for all $1\le i\le k$. Furthermore, G contains k disjoint cycles $C_1', \dots , C_k'$ such that $e_i\in E(C_i')$ for all $1\le i\le k$ and $V(G)=\bigcup _{i=1}^k V(C_i')$.

Note that when $k=1$, a packing result in Theorem 2 holds under the same minimum degree condition. (See [3] for more details).

In this paper, we extend Theorems 1 and 2 to disjoint chorded (doubly chorded) cycles for a graph of sufficiently large order with respect to k. In addition, we show when k disjoint chorded cycles containing specified edges can be extended to span the entire vertex set of a graph. We also consider the question of when k independent edges can be chords for k disjoint cycles, one per cycle.

2 Results

First, we extend Theorem 1 to k disjoint chorded cycles for a graph of sufficiently large order with respect to k. A vertex of a graph G with n vertices is r -pancyclic if it is contained in an l-cycle for every $r\le l\le n$, and G is vertex r -pancyclic if every vertex in G is r-pancyclic. The following theorem will be useful in our proof.

Theorem 3

[11] Let G be a graph of order $n \ge 4$ with $\sigma _2 (G) \ge n$. Then G is vertex 4-pancyclic unless n is even and $G = K_{n/2, n/2}$.

Theorem 4

Let G be a graph of order $n\ge 16k-5$ for an integer $k\ge 1$. If

$$\begin{aligned} \delta (G)\ge \frac{n}{2}, \end{aligned}$$

then for any k distinct vertices $v_1, \ldots , v_k$ in G, there exist k disjoint chorded cycles $C_1, \ldots , C_k$ such that $v_i\in V(C_i)$ and $4\le |V(C_i)|\le 6$ for all $1\le i\le k$.

Proof

Suppose that $k = 1$, then $n \ge 11$. If n is even and $G = K_{n/2, n/2}$, then we can find a chorded 6-cycle containing $v_1$. Hence, G is vertex 4-pancyclic by Theorem 3. Now consider a 5-cycle $C = w_1, w_2, w_3, w_4, w_5, w_1$, where $w_1 = v_1$. If C is a chorded cycle, then the theorem holds for $k=1$. Thus, we may assume that C is not a chorded cycle, and then $w_1w_3, w_2w_4 \notin E(G)$. We claim that $|N_G(w_1)\cap N_G(w_3)|\ge 2$. Suppose that $|N_G(w_1)\cap N_G(w_3)|\le 1$. Then $\deg _G(w_1)+\deg _G(w_3)\le (n-2)+1=n-1<n$, a contradiction to the degree condition. Thus the claim holds. Similarly, $|N_G(w_2)\cap N_G(w_4)|\ge 2$. Let x (resp. y) be a common neighbor of $w_1$ and $w_3$ (resp. $w_2$ and $w_4$) in $V(G)-V(C)$. If $x=y$, then $x, w_3, w_4, w_5, w_1, x$ is a 5-cycle containing $v_1=w_1$ and $xw_4$ as a chord. If $x\ne y$, then $x, w_3, w_4, y, w_2, w_1, x$ is a 6-cycle containing $v_1=w_1$ and $w_2w_3$ as a chord. This completes the case where $k=1$. Hence we may assume that $k\ge 2$.

Suppose that the theorem does not hold. Let G be an edge-maximal counterexample. Since a complete graph of order at least 4k contains the desired k disjoint chorded cycles, we may assume that G is not complete. Let x and y be nonadjacent vertices in G, and define $G'=G+xy$. Then $G'$ is not a counterexample by the edge-maximality of G. Hence $G'$ contains the desired k disjoint chorded cycles $C_1, \ldots , C_k$. Without loss of generality, we may assume that $xy\not \in \cup _{i=1}^{k-1}E(C_i)$, that is, G contains $k-1$ disjoint chorded cycles $C_1, \ldots , C_{k-1}$ such that $v_i\in V(C_i)$, $4\le |V(C_i)|\le 6$ for all $1\le i\le k-1$, and $v_k\not \in \cup _{i=1}^{k-1}V(C_i)$. We choose $C_1, \ldots , C_{k-1}$ such that

$$\begin{aligned} \displaystyle \sum _{i=1}^{k-1}|V(C_i)| \text { is a minimum.} \end{aligned}$$

(1)

Let ${\mathscr {C}}=\cup _{i=1}^{k-1}C_i$ and let $H=G-{\mathscr {C}}$. Then since $k\ge 2$ and $|V({\mathscr {C}})|\le 6(k-1)$,

$$\begin{aligned} |V(H)|&=|V(G)|-|V({\mathscr {C}})|\\&\ge n-6(k-1)\\&\ge (16k-5)-6k+6 \\&=10k+1\\&\ge 21. \end{aligned}$$

Claim 1. For any $x\in V(H)$, $\deg _{C_i}(x)\le 4$ for all $1 \le i \le k-1$.

Proof

Suppose that $\deg _{C_i}(x)\ge 5$ for some $x\in V(H)$ and some $1\le i\le k-1$. We consider the following cases. In each case, we find a chorded cycle $C_i'$ containing the specified vertex either $v_i$ or $v_k$ such that $|V(C_i')|<|V(C_i)|$, contradicting (1).

Case 1 $|V(C_i)|=5$.

Let $C_i=w_1, w_2, w_3, w_4, w_5, w_1$. Without loss of generality, we may assume that $v_i=w_1$. In this case, x must be adjacent to all of the vertices in $C_i$. If $x\ne v_k$, then $x, w_5, w_1, w_2, x$ is a 4-cycle containing $v_i$ and $xw_1$ as a chord. If $x=v_k$, then $x, w_2, w_3, w_4, x$ is a 4-cycle containing $v_k$ and $xw_3$ as a chord.

Case 2 $|V(C_i)|=6$.

Let $C_i=w_1, w_2, w_3, w_4, w_5, w_6, w_1$. Without loss of generality, we may assume that x is adjacent to all of the vertices in $\{w_1, w_2, w_3, w_4, w_5\}$. First suppose that $x\ne v_k$. If $v_i\in \{w_1, w_2, w_3, w_4\}$, then $x, w_1, w_2, w_3, w_4, x$ is a 5-cycle containing $v_i$ and $xw_2$ as a chord. If $v_i\in \{w_5, w_6\}$, then $x, w_5, w_6, w_1, w_2, x$ is a 5-cycle containing $v_i$ and $xw_1$ as a chord. Now suppose that $x=v_k$. If $v_i\in \{w_1, w_2, w_6\},$ then $x, w_3, w_4, w_5, x$ is a 4-cycle containing $v_k$ and not containing $v_i$, with $xw_4$ as a chord. If $v_i=w_3$, then $x, w_4, w_5, w_6, w_1, x$ is a 5-cycle containing $v_k$ and not containing $v_i$, with $xw_5$ as a chord. If $v_i\in \{w_4, w_5\}$, then $x, w_1, w_2, w_3,x$ is a 4-cycle containing $v_k$ and not containing $v_i$, with $xw_2$ as a chord.

This completes the proof of the claim. $\square$

Now, $\delta (G)\ge n/2\ge (16k-5)/2=8k-5/2$, and $\deg _{{\mathscr {C}}}(v_k)\le 4(k-1)$ by Claim 1. Then $\deg _H(v_k)\ge 8k-5/2-4(k-1)=4k+3/2\ge 19/2$, since $k\ge 2$. Let $U=\{u_1, u_2, u_3\}\subset N_H(v_k)$. For any $u\in V(H)$, $\deg _{{\mathscr {C}}}(u)\le 4(k-1)$ by Claim 1. Thus,

$$\begin{aligned} \deg _H(u)\ge \delta (G)-4(k-1). \end{aligned}$$

(2)

Case 1 There exist two distinct vertices $u, u'\in U$ such that $N_{H-v_k}(u)\cap N_{H-v_k}(u')=\emptyset$.

Without loss of generality, we may assume that $u=u_1$ and $u'=u_2$. The vertices $u_1$ and $u_1$ may be adjacent in G, and there exists at most one edge among $u_1$, $u_2$, and $u_3$, otherwise there exists a chorded 4-cycle containing $v_k$ in H. Also, $|N_{H-(U\cup \{v_k\})}(u_i)\cap N_H(v_k)|\le 1$ for all $i\in \{1, 2\}$. By (2),

$$\begin{aligned} |V(H)|&\ge \deg _H(v_k)+1+(\deg _H(u_1)-3)+(\deg _H(u_2)-3)\\&=\deg _H(v_k)+\deg _H(u_1)+\deg _H(u_2)-5\\&\ge 3(\delta (G)-4(k-1))-5\\&=3\delta (G)-12k+7. \end{aligned}$$

Then

$$\begin{aligned} n&=|V(H)|+|V({\mathscr {C}})|\\&\ge 3\delta (G)-12k+7+4(k-1)\\&=3\delta (G)-8k+3\\&\ge 3\left( \frac{n}{2}\right) -8k+3\\ \Longrightarrow n&\le 16k-6, \text { a contradiction.} \end{aligned}$$

Case 2 There exist at least two pairs $(u, u')$ and $(u', u'')$ for pairwise distinct $u, u', u''\in U$ such that $x\in N_{H-v_k}(u)\cap N_{H-v_k}(u')$, $y\in N_{H-v_k}(u')\cap N_{H-v_k}(u'')$, and $x\ne y$.

Without loss of generality, we may assume that $u=u_1$, $u'=u_2$, and $u''=u_3$, that is, $x\in N_{H-v_k}(u_1)\cap N_{H-v_k}(u_2)$, $y\in N_{h-v_k}(u_2)\cap N_{H-v_k}(u_3)$, and $x\ne y$. Then $v_k, u_1, x, u_2, y, u_3, v_k$ is a 6-cycle containing $v_k$ and $v_ku_2$ as a chord.

Case 3 The vertices $u_1, u_2$, and $u_3$ all have exactly one common neighbor in $H-v_k$.

There exist no edges among $u_1, u_2$, and $u_3$, otherwise there is a chorded 4-cycle containing $v_k$ in H. Also, $|N_{H-(U\cup \{v_k\})}(u_i)\cap N_H(v_k)|\le 1$ for all $i\in \{1, 2, 3\}$, similar to Case 1. By (2),

$$\begin{aligned} |V(H)|&\ge \deg _H(v_k)+1+(\deg _H(u_1)-2)+(\deg _H(u_2)-3)+(\deg _H(u_3)-3)\\&=\deg _H(v_k)+\deg _H(u_1)+\deg _H(u_2)+\deg _H(u_3)-7\\&\ge 4(\delta (G)-4(k-1))-7\\&= 4\delta (G)-16k+9. \end{aligned}$$

Then

$$\begin{aligned} n&=|V(H)|+|V({\mathscr {C}})|\\&\ge 4\delta (G)-16k+9+4(k-1)=4\delta (G)-12k+5\\&\ge 4\left( \frac{n}{2}\right) -12k+5=2n-12k+5.\\ \Longrightarrow n&\le 12k-5, \text { a contradiction.} \end{aligned}$$

This completes the proof of the theorem. $\square$

Next, we extend the packing result in Theorem 2 to disjoint doubly chorded cycles for a graph of sufficiently large order with respect to k. In order to prove the extension, we will use the following lemma.

Lemma 1

Let G be a graph of order $n \ge 18k - 3$ for an integer $k\ge 1$ with

$$\begin{aligned} \delta (G)\ge \frac{n}{2}+k-1. \end{aligned}$$

Suppose that $D\subseteq V(G)$ with $3\le |D|\le 6k-1$. Then for any $X\subseteq D$ with $|X|=3$, some pair of vertices in X have a common neighbor in $H=G-D$.

Proof

Let $X=\{u_1, u_2, u_3\}$. Suppose that no two vertices in X have a common neighbor in H. Then

$$\begin{aligned} 3\left( \frac{n}{2}+k-1-(|D|-1)\right)&\le 3(\delta (G)-(|D|-1|))\\&\le \deg _H(u_1, u_2, u_3) \\&\le n-|D|.\\ \Longrightarrow n&\le 4|D|-6k\le 4(6k-1)-6k\\&=18k-4, \text { a contradiction.} \end{aligned}$$

$\square$

Theorem 5

Let G be a graph of order $n\ge 18k-3$ for an integer $k\ge 1$. If

$$\begin{aligned} \delta (G)\ge \frac{n}{2}+k-1, \end{aligned}$$

then for any k independent edges $e_1, \ldots , e_k$ in G, there exist k disjoint doubly chorded cycles $D_1, \ldots , D_k$ such that $e_i$ is a cycle-edge of $D_i$ and $4\le |V(D_i)|\le 6$ for all $1\le i\le k$.

Remark

The minimum degree condition is sharp in the following sense. Let $H=K_{n/2-k+1}+K_{2k-2}+K_{n/2-k+1}$, (n is even). Consider the graph G obtained from H by adding an edge e between two $K_{n/2-k+1}$’s. Take $k-1$ independent edges in $K_{2k-2}$ and e as the specified k independent edges. Then $\delta (G)=(n/2-k+1-1)+(2k-2)=n/2+k-2$. However, there is no doubly chorded cycle containing e as a cycle-edge without the vertices in $K_{2k-2}$.

Proof

By Theorem 2, G contains k disjoint cycles $C_1, \ldots , C_k$ such that $3\le |V(C_i)|\le 4$ and $e_i\in E(C_i)$ for all $1\le i\le k$. Let ${\mathscr {C}}=\cup _{i=1}^kC_i$ and let $H=G-{\mathscr {C}}$. Since $|V({\mathscr {C}})|\le 4k$, we have $|V(H)|\ge (18k-3)-4k=14k-3$. By applying Lemma 1 to each $C_i$, we extend each $C_i$ to a doubly chorded cycle. We consider the following cases.

Case 1 $C_i$ is a 3-cycle.

Let $C_i=u_1, u_2, u_3, u_1$ and let $e_i=u_1u_2$. By Lemma 1, some pair of vertices in $\{u_1, u_2, u_3\}$ must have a common neighbor in H, say $x_1$. We consider the following two pairs: $(u_1, u_2)$ and $(u_2, u_3)$. Note that $(u_1, u_3)$ is equivalent to $(u_2, u_3)$ by symmetry.

Subcase 1.1 $(u_1, u_2)$.

Consider the set $X=\{x_1, u_2, u_3\}$. By Lemma 1, some pair of vertices in X must have a common neighbor in $H-x_1$, say $x_2$. We consider the following two pairs: $(x_1, u_2)$ and $(x_1, u_3)$. Note that $(u_2, u_3)$ is equivalent to $(x_1, u_2)$ by symmetry.

First suppose that $(x_1, u_2)$. Then, since there are no doubly chorded cycles containing $e_i$ as a cycle-edge, consider the set $X'=\{u_1, x_1, x_2\}$. By Lemma 1, some pair of vertices in $X'$ must have a common neighbor in $H'=H-\{x_1, x_2\}$, say $x_3$. If $x_3\in N_{H'}(u_1)\cap N_{H'}(x_1)$, then $u_1, x_3, x_1, x_2, u_2, u_1$ is a 5-cycle containing $e_i$ as a cycle-edge and $u_1x_1$ and $u_2x_1$ as chords. If $x_3\in N_{H'}(x_1)\cap N_{H'}(x_2)$, then $u_1, x_1, x_3, x_2, u_2, u_1$ is a 5-cycle containing $e_i$ as a cycle-edge and $u_2x_1$ and $x_1x_2$ as chords. If $x_3\in N_{H'}(u_1)\cap N_{H'}(x_2)$, then $u_1, x_3, x_2, x_1, u_2, u_1$ is a 5-cycle containing $e_i$ as a cycle-edge and $u_1x_1$ and $u_2x_2$ as chords.

Next suppose that $(x_1, u_3)$. Then $u_1, u_2, x_1, x_2, u_3, u_1$ is a 5-cycle containing $e_i$ as a cycle-edge and $u_1x_1$ and $u_2u_3$ as chords.

Subcase 1.2 $(u_2, u_3)$.

Consider the set $X=\{u_1, u_3, x_1\}$. By Lemma 1, some pair of vertices in X must have a common neighbor in $H'=H-x_1$, say $x_2$. If $x_2\in N_{H'}(u_1)\cap N_{H'}(u_3)$, then $u_1, u_2, x_1, u_3, x_2, u_1$ is a 5-cycle containing $e_i$ as a cycle-edge and $u_1u_3$ and $u_2u_3$ as chords. If $x_2\in N_{H'}(u_1)\cap N_{H'}(x_1)$, then $u_1, u_2, u_3, x_1, x_2, u_1$ is a 5-cycle containing $e_i$ as a cycle-edge and $u_1u_3$ and $u_2x_1$ as chords. If $x_2\in N_{H'}(u_3)\cap N_{H'}(x_1)$, then $u_1, u_2, x_1, x_2, u_3, u_1$ is a 5-cycle containing $e_i$ as a cycle-edge and $u_2u_3$ and $u_3x_1$ as chords.

Case 2 $C_i$ is a 4-cycle.

Let $C_i=u_1, u_2, u_3, u_4, u_1$ and without loss of generality, let $e_i=u_1 u_2$. If $C_i$ has a chord, then this is Case 1. Hence we may assume that $C_i$ has no chords. Consider the set $X=\{u_2, u_3, u_4\}$. By Lemma 1, some pair of vertices in X must have a common neighbor in H, say $x_1$. Let $H'=H-x_1$. We consider the following three pairs: $(u_2, u_3)$, $(u_3, u_4)$, and $(u_2, u_4)$.

Subcase 2.1 $(u_2, u_3)$.

Since there are no doubly chorded cycles, consider the set $X'=\{x_1, u_3, u_4\}$. By Lemma 1, some pair of vertices in $X'$ must have a common neighbor in $H'$, say $x_2$. If $x_2\in N_{H'}(x_1)\cap N_{H'}(u_3)$, then $u_1, u_2, x_1,x_2, u_3, u_4, u_1$ is a 6-cycle containing $e_i$ as a cycle-edge and $u_2u_3$ and $u_3x_1$ as chords. If $x_2\in N_{H'}(u_3)\cap N_{H'}(u_4)$, then $u_1, u_2, x_1, u_3, x_2, u_4, u_1$ is a 6-cycle containing $e_i$ as a cycle-edge and $u_2u_3$ and $u_3u_4$ as chords. If $x_2\in N_{H'}(x_1)\cap N_{H'}(u_4)$, then $u_1, u_2, u_3, x_1, x_2, u_4, u_1$ is a 6-cycle containing $e_i$ as a cycle-edge and $u_2x_1$ and $u_3u_4$ as chords.

Subcase 2.2 $(u_3, u_4).$

Since there are no doubly chorded cycles, consider the set $X'=\{u_2, u_3, x_1\}$. By Lemma 1, some pair of vertices in $X'$ must have a common neighbor in $H'$, say $x_2$. If $x_2\in N_{H'}(u_2)\cap N_{H'}(u_3)$, then $u_1, u_2, x_2, u_3, x_1, u_4, u_1$ is a 6-cycle containing $e_i$ as a cycle-edge and $u_2u_3$ and $u_3u_4$ as chords. If $x_2\in N_{H'}(u_3)\cap N_{H'}(x_1)$, then $u_1, u_2, u_3, x_2, x_1, u_4, u_1$ is a 6-cycle containing $e_i$ as a cycle-edge and $u_3u_4$ and $u_3x_1$ as chords. If $x_2\in N_{H'}(u_2)\cap N_{H'}(x_1)$, then $u_1, u_2, x_2, x_1, u_3, u_4, u_1$ is a 6-cycle containing $e_i$ as a cycle-edge and $u_2u_3$ and $u_4x_1$ as chords.

Subcase 2.3 $(u_2, u_4).$

Since there are no doubly chorded cycles, consider the set $X'=\{u_2, u_3, x_1\}$. By Lemma 1, some pair of vertices in $X'$ must have a common neighbor in $H'$, say $x_2$. If $x_2\in N_{H'}(u_2)\cap N_{H'}(u_3)$ or $x_2\in N_{H'}(u_2)\cap N_{H'}(x_1)$, then we have a doubly chorded 6-cycle containing $e_i$ as a cycle-edge by the arguments used in Subcase 2.1. If $x_2\in N_{H'}(u_3)\cap N_{H'}(x_1)$, then $u_1, u_2, x_1,x_2, u_3, u_4, u_1$ is a 6-cycle containing $e_i$ as a cycle-edge and $u_2u_3$ and $u_4x_1$ as chords.

By applying Lemma 1 repeatedly to each $C_i$, we have the desired system of disjoint doubly chorded cycles. This completes the proof of the theorem. $\square$

Next, we extend Theorem 5 to disjoint doubly chorded cycles containing specified paths. Given k independent paths $P_1, \ldots , P_k$, where $P_i$ has order $r_i\ge 2$ for all $1\le i\le k$, let $r=\sum _{i=1}^kr_i$. Then the number of interior vertices in the path system is $r-2k$.

Theorem 6

Let G be a graph of order $n\ge 16k+r-3$ for an integer $k\ge 1$ with

$$\begin{aligned} \delta (G)\ge \frac{n}{2}+r-k-1, \end{aligned}$$

and let $P_1, \ldots , P_k$ be any k independent paths in G. Then there exist k disjoint doubly chorded cycles $D_1, \ldots , D_k$ such that $D_i$ contains $P_i$ as a path along the cycle and $r_i+2\le |V(D_i)|\le r_i+4$ for all $1\le i\le k$.

Proof

Consider the graph $G'$ obtained by replacing each path $P_{i}$ in G by an edge $e_i$. Then

$$\begin{aligned} |V(G')|=n-(r-2k)\ge (16k+r-3)-r+2k=18k-3, \end{aligned}$$

and

$$\begin{aligned} \delta (G')\ge \delta (G) - (r-2k) \ge \left( \frac{n}{2}+r-k-1\right) -r+2k =\frac{n}{2}+k-1. \end{aligned}$$

Then by Theorem 5, there exist k disjoint doubly chorded cycles $D_1, \ldots , D_k$ in $G'$ such that $e_i$ is a cycle-edge in $D_i$ and $4\le |V(D_i)| \le 6$ for all $1\le i\le k$. Now replace the edge $e_i$ by the path $P_{i}$ for all $1\le i\le k$, that is, insert the interior vertices of each $P_i$ back into $G'$ to form the original graph G. For all $1\le i\le k$, let $D_i'$ be the doubly chorded cycle obtained from $D_i$ by the addition of the interior vertices of $P_i$. Then $D_i'$ contains $P_i$ as a path on the cycle, and $r_i+2=4+(r_i-2)\le |V(D_i')|\le 6+(r_i-2)=r_i+4$ for all $1\le i\le k$. $\square$

Next, we prove the following theorem which shows the existence of disjoint chorded cycles containing specified edges as cycle-edges and spanning the entire vertex set of a graph. In order to prove the theorem, we need the following lemma.

Lemma 2

[3] Let $P=u_1, u_2, \ldots , u_q$ be a path, and A, B be subsets of V(P) such that $|A|+|B|>q$. Then there exists a number h with $1\le h < q$ such that either $u_h\in A$ and $u_{h+1}\in B$ or $u_h\in B$ and $u_{h+1}\in A$, unless q is odd and $A=B=\{u_1, u_3, \ldots , u_q\}$.

Theorem 7

Let G a graph of order $n\ge 4k$ for an integer $k\ge 1$ with

$$\begin{aligned} \delta (G)\ge \frac{n+k}{2}, \end{aligned}$$

and let $e_1, \ldots , e_k$ be any k independent edges in G. Suppose that G contains k disjoint chorded cycles $C_1, \ldots , C_k$ such that $e_i$ is a cycle-edge of $C_i$ for all $1\le i \le k$. Then there exist k disjoint chorded cycles $C_1', \ldots , C_k'$ such that $e_i$ is a cycle-edge of $C_i'$ for all $1\le i\le k$ and $V(G)=\cup _{i=1}^kV(C_i')$.

Remark

Since a chorded cycle must have at least four vertices, $n\ge 4k$ is necessary. The minimum degree condition is also sharp in the following sense. Let $G= K_{p+k-1}+\overline{K}_p$, with $n\ge 5k+1$, $p=(n-k+1)/2\ge 2k+1$, and $n\not \equiv k~(\text {mod } 2)$. Take k independent edges in $K_{p+k-1}$. Then $\delta (G)=(n+k-1)/2$, and G contains k disjoint chorded cycles containing the specified edges as cycle-edges. However, the chorded cycle system cannot be extended to span V(G). To see this, contract the k specified edges to k vertices. Now if a spanning chorded cycle system existed, then we could replace each contracted vertex by its original specified edge to give the desired spanning chorded cycle system. However, the contracted $K_{p+k-1}$ graph has $(n+k-1)/2 -k=(n-k-1)/2$ vertices, while the $\overline{K}_p$ graph has $(n-k+1)/2$ vertices. Hence, the disjoint chorded cycles cannot span V(G).

Proof

We choose k disjoint chorded cycles $C_1, \ldots , C_k$ such that $e_i$ is a cycle-edge of $C_i$ for all $1\le i\le k$, and

$$\begin{aligned} \sum _{i=1}^k |V(C_i)| \quad \text { is as large as possible.} \end{aligned}$$

(3)

For all $1\le i\le k$, let $P_i=C_i-e_i$ and let ${{\mathscr {P}}}=\cup _{i=1}^kP_i$. Note that $|V(P_i)|=|V(C_i)|\ge 4$ since $C_i$ is a chorded cycle for all $1\le i\le k$. Let $W=\cup _{i=1}^kV(P_i)$. We may assume that $V(G)\ne W$, otherwise the theorem holds.

Claim 1. For any $x\in V(G)-W$, $\deg _{P_i}(x)\le (|V(P_i)|+1)/2$ for all $1\le i\le k$.

Proof

Let each $C_i$ be a chorded cycle with a given orientation. Suppose that $u, u^+\in N_{C_i}(x)$ with $uu^+\ne e_i$ for some $1\le i\le k$. Then there exists a longer cycle containing $e_i$ as a cycle-edge and $uu^+$ as a chord, contradicting (3). Hence $|V(P_i)|\ge 2\deg _{P_i}(x)-1$, and therefore the claim holds. $\square$

Claim 2. The number of components in $G-W$ is exactly one.

Proof

Suppose that the claim does not hold. Let $H_1$ and $H_2$ be distinct components of $G-W$. By Claim 1, for any $x\in V(G)-W$,

$$\begin{aligned} \deg _{{{\mathscr {P}}}}(x)&\le \frac{|{V({\mathscr {P}}})|+k}{2}. \end{aligned}$$

(4)

Consider $x_1\in V(H_1)$ and $x_2\in V(H_2)$. By the minimum degree condition and (4), we have

$$\begin{aligned} |V(G)|&\ge |V(H_1)|+|V(H_2)|+|V({\mathscr {P}})|\\&\ge (\deg _G(x_1)-\deg _{{\mathscr {P}}}(x_1)+1)+(\deg _G(x_2)-\deg _{{\mathscr {P}}}(x_2)+1)+|V({\mathscr {P}})|\\&\ge 2\left( \frac{n+k}{2}-\frac{|V({{\mathscr {P}}})|+k}{2}+1\right) +|V({\mathscr {P}})|\\&= n+k-|V({{\mathscr {P}}})|-k+2+|V({{\mathscr {P}}})|\\&=n+2>n, \quad \text {a contradiction.} \end{aligned}$$

$\square$

Now, let H be the component of $G-W$.

Claim 3. $|V(H)|\ge 3$.

Proof

Suppose that the claim does not hold, that is, $|V(H)|\le 2$. First, suppose that $|V(H)|=1$ and let $V(H)=\{x\}$. By Claim 2, $n=|V({\mathscr {P}})|+|V(H)|=|V(P_1)|+\cdots + |V(P_k)|+1$. Therefore, we have

$$\begin{aligned} \deg _{{\mathscr {P}}}(x)=\deg _G(x)&\ge \frac{n+k}{2}\\&=\frac{(|V(P_1)|+\cdots +|V(P_k)|+1)+k}{2}\\&=\frac{(|V(P_1)|+1)+\cdots +(|V(P_k)|+1)+1}{2}. \end{aligned}$$

Hence by Claim 1, there must exist two neighbors of x that are adjacent on $P_i$ for some $1\le i\le k$. Then there exists a longer chorded cycle containing $e_i$ as a cycle-edge, contradicting (3).

Next, suppose that $|V(H)|=2$ and let $V(H)=\{x_1, x_2\}$. By Claim 2, $n=|V({\mathscr {P}})|+|V(H)|=|V(P_1)|+\cdots + |V(P_k)|+2$. For $x\in \{x_1, x_2\}$, we have

$$\begin{aligned} \deg _{{\mathscr {P}}}(x)=\deg _G(x)-1&\ge \frac{n+k}{2}-1=\frac{n+k-2}{2}\\&=\frac{(|V(P_1)|+\cdots +|V(P_k)|+2)+k-2}{2}\\&=\frac{|V(P_1)|+\cdots +|V(P_k)|+k}{2}\\&=\frac{(|V(P_1)|+1)+\cdots +(|V(P_k)|+1)}{2}. \end{aligned}$$

Hence, by Claim 1, $\deg _{P_i}(x)=(|V(P_i)|+1)/2$ for all $1\le i\le k$. Consider $i=1$, and let $P_1=u_1, u_2,\ldots , u_r$ and $e_1=u_1 u_r$. Then by Lemma 2, r is odd and $N_{P_1}(x_1)=N_{P_1}(x_2)=\{u_1, u_3, \dots , u_r\}$. Thus $u_1, x_1, x_2, u_3, u_4, \dots , u_r, u_1$ is a longer cycle containing $e_1$ as a cycle-edge and $u_1x_2$ as a chord, contradicting (3). Therefore, the claim holds. $\square$

Claim 4. H contains a Hamiltonian cycle.

Proof

For all $x\in V(H)$, we have

$$\begin{aligned} \deg _H(x)=\deg _G(x)-\deg _{{\mathscr {P}}}(x)&\ge \frac{n+k}{2}- \frac{|V({{\mathscr {P}}})|+k}{2}\nonumber \\&=\frac{n-|V({{\mathscr {P}}})|}{2}\nonumber \\&=\frac{|V(H)|}{2} \end{aligned}$$

Thus the claim holds by Dirac’s theorem [2]. $\square$

Claim 5. If $|V(H)|\ge 4$, then $\deg _H(x)\ge 3$ for all $x\in V(H)$.

Proof

From the proof of Claim 4, $\deg _H(x)\ge |V(H)|/2$, for all $x\in V(H)$. If $|V(H)|\ge 5$, then the claim holds. Hence we only need to consider the case where $|V(H)|= 4$. In this case, we may assume that there exist two distinct vertices $x_1, x_2\in V(H)$ such that $\deg _H(x_1)=\deg _H(x_2)=2$, otherwise the claim holds. By Claim 2, $n=|V({{\mathscr {P}}})|+|V(H)|=|V(P_1)|+\cdots +|V(P_k)|+4$. Then for all $x\in \{x_1,x_2\}$,

$$\begin{aligned} \deg _{{\mathscr {P}}}(x)&=\deg _G(x)-\deg _H(x)\\&\ge \frac{n+k}{2}-2=\frac{n+k-4}{2}\\&=\frac{(|V(P_1)|+\cdots +|V(P_k)|+4)+k-4}{2}\\&=\frac{|V(P_1)|+\cdots +|V(P_k)|+k}{2}\\&=\frac{(|V(P_1)|+1)+\cdots +(|V(P_k)|+1)}{2}. \end{aligned}$$

By Claim 1, equality holds in the above inequality. Consider $i=1$ and let $P_1=u_1, u_2, \dots , u_r$ and $e_1=u_1u_r$. Let $x_1P^*x_2$ be a path from $x_1$ to $x_2$ in H. Then $u_1, x_1P^*x_2, u_3, u_4, \dots , u_r, u_1$ is a longer cycle containing $e_1$ as a cycle-edge and $u_1x_2$ as a chord, contradicting (3). $\square$

Since $\delta (G)\ge (n+k)/2$, G is $(k+1)$-connected. Then $|N_{{\mathscr {P}}}(H)|\ge k+1$.

Claim 6. There exist two independent edges between H and $P_i$ for some $1\le i\le k$.

Proof

We consider the following two cases. Note that $|V(H)|\ge 3$ by Claim 3.

Case 1 $|V(H)|\ge k+1$.

Since G is $(k+1)$-connected, we have $|N_H({\mathscr {P}})|\ge k+1$. Then we may assume that $|N_H({\mathscr {P}})|=k+1.$ If there are $k+1$ independent edges between H and ${\mathscr {P}}$, then the claim holds. Hence we may assume that there are not $k+1$ such edges. By Hall’s Theorem [10], there exists some $S\subseteq N_H({\mathscr {P}})$ such that $|N_{{\mathscr {P}}}(S)|<|S|$. Then $(N_H({\mathscr {P}})-S)\cup N_{{\mathscr {P}}}(S)$ is a vertex-cut of cardinality at most k, a contradiction of the connectivity of G.

Case 2 $3\le |V(H)|\le k$.

Let $V(H)=\{x_1, x_2, \ldots , x_t\}$ for $3\le t\le k$. Since G is $(k+1)$-connected, $N_H({\mathscr {P}})=V(H)$. Now, we may assume that $|N_{{\mathscr {P}}}(H)|=k+1$. Then there exists some $x\in V(H)$ such that $|N_{P_i}(x)|\ge 2$ for some $1\le i\le k$, say $x=x_1$ and $i=1$, otherwise the claim holds. If $N_{P_1}(x_i)\ne \emptyset$ for some $2\le i\le t$, then the claim also holds. Hence $N_{P_1}(x_i)=\emptyset$ for all $2\le i\le t$, and then $N_{{\mathscr {P}}-P_1}(x_i)\ne \emptyset$ for all $2\le i\le t$. Since $|\cup _{i=2}^tN_{{\mathscr {P}}-P_1}(x_i)|\le k-1$, $\{x_1\}\cup (\cup _{i=2}^tN_{{\mathscr {P}}-P_1}(x_i))$ is a vertex-cut of cardinality at most k, a contradiction of the connectivity of G. $\square$

By Claim 6, without loss of generality, we may assume that there are two independent edges between H and $P_1$. Let $P_1=u_1, u_2, \ldots , u_r$ and $e_1=u_1 u_r$. In addition, let $xu_s, x'u_t\in E(G)$ for distinct $x, x'\in V(H)$ and $s<t$. We choose $u_s, u_t$ so that $t-s$ is minimized. Then $t-s\ge 2$ by (3). Let $P=u_1, u_2, \ldots , u_s$, $Q=u_t, u_{t+1}, \ldots , u_r$, and $W'=W-\{u_i|s<i<t\}$. Now, we have

$$\begin{aligned} \deg _G(x, u_{s+1})\ge 2\delta (G)&\ge n+k. \end{aligned}$$

(5)

By the minimality of $t-s$, $N_{G-W'}(x)\subseteq V(H)-\{x\}$ and $N_{G-W'}(u_{s+1}) \subseteq V(G)-W'-V(H)-\{u_{s+1}\}$. Then it follows from (5) that

$$\begin{aligned} \deg _{W'}(x, u_{s+1}) \ge (n+k)-(n-|W'|-2)=|W'|+k+2. \end{aligned}$$

Similarly, $\deg _{W'}(x', u_{t-1})\ge |W'|+k+2$. Combining these two inequalities, we obtain

$$\begin{aligned} \deg _{W'}(x, x', u_{s+1}, u_{t-1})&\ge 2(|W'|+k+2). \end{aligned}$$

(6)

On the other hand, by Claim 1, it follows that for $R\in \{P, Q, P_2, \ldots , P_k\}$,

$$\begin{aligned} \deg _R(x, x')\le 2\left( \frac{|V(R)|+1}{2}\right) =|V(R)|+1. \end{aligned}$$

(7)

Now, let $xP^*x'$ be a path from x to $x'$ in H. If $u_{s+1}u_h, u_{t-1}u_{h+1}\in E(G)$ for some $1\le h< s$, then $u_1, \ldots , u_h, u_{s+1}, \ldots , u_{t-1}, u_{h+1}, \ldots , u_s, xP^*x',$ $u_t, \ldots , u_r, u_1$ is a longer cycle containing $e_1$ as a cycle-edge and $u_hu_{h+1}$ as a chord, contradicting (3). If $u_{s+1}u_{h+1}, u_{t-1} u_h\in E(G)$ for some $1\le h<s$, then again there exists a longer chorded cycle containing $e_1$ as a cycle-edge, contradicting (3). Thus, by Lemma 2, $\deg _{P}(u_{s+1}, u_{t-1})\le |V(P)|+1$ and similarly, $\deg _Q(u_{s+1}, u_{t-1})\le |V(Q)|+1$.

Next, let $P_i=u_1',\dots , u_{r'}'$ with $e_i=u_1'u_{r'}'$ for all $2\le i\le k$. By Claim 4, H contains a Hamiltonian cycle, say C, with a given orientation. If $|V(H)|\ge 4$, then a chord of C is incident to x, by Claim 5. Let xy (possibly $y=x'$) be such a chord. Then $y\in V(x\overrightarrow{C}x')$ or $y\in V(x'\overrightarrow{C}x)$. Without loss of generality, we may assume that $y\in V(x\overrightarrow{C}x')$. If $|V(H)|=3$, without loss of generality, we may assume that $x\overrightarrow{C}x'$ is a path of length two in C. Then note that $xx'\in E(C)$.

If $u_{s+1}u_{h}', u_{t-1}u_{h+1}'\in E(G)$ for some $1\le h<r'$, then there exist two disjoint chorded cycles with specified edges as cycle-edges as follows: $u_1, \dots , u_s, x\overrightarrow{C}x', u_t,\ldots , u_r, u_1$ is a chorded cycle containing $e_1$ as a cycle-edge, and $u_1', \ldots , u_h', u_{s+1}, \ldots , u_{t-1}, u_{h+1}', \ldots , u_{r'}', u_1'$ is a cycle containing $e_i$ as a cycle-edge and $u_h'u_{h+1}'$ as a chord, contradicting (3). If $u_{s+1}u_{h+1}', u_{t-1}u_{h}'\in E(G)$ for some $1\le h<r'$, then again there exist two disjoint chorded cycles with specified edges as cycle-edges, contradicting (3).

By the above observations and Lemma 2, for all $2\le i\le k$, we obtain

$$\begin{aligned} \deg _{P_i} (u_{s+1}, u_{t-1})\le |V(P_i)|+1. \end{aligned}$$

Consequently, for $R\in \{P, Q, P_2, \ldots , P_k\}$,

$$\begin{aligned} \deg _R(u_{s+1}, u_{t-1})\le |V(R)|+1. \end{aligned}$$

(8)

It follows from (7) and (8) that

$$\begin{aligned} \sum _{R\in \{P, Q, P_2, \ldots , P_k\}} \deg _R(x, x', u_{s+1}, u_{t-1})\le 2(|W'|+k+1). \end{aligned}$$

(9)

Since

$$\begin{aligned} \deg _{W'}(x, x', u_{s+1}, u_{t-1})= \sum _{R\in \{P, Q, P_2, \ldots , P_k\}}\deg _R(x, x', u_{s+1}, u_{t-1}), \end{aligned}$$

by (6) and (9),

$$\begin{aligned} 2(|W'|+k+2)&\le 2(|W'|+k+1)\\ |W'|+k+2&\le |W'|+k+1, \text { a contradiction.} \end{aligned}$$

This completes the proof of the theorem. $\square$

By Theorem 7, we have the following corollaries.

Corollary 8

Let G be a graph of order $n\ge 4k$ for an integer $k\ge 1$ with $\delta (G)\ge (n+k)/2.$ Suppose that G contains k disjoint chorded cycles $C_1, \ldots , C_k$. Then there exists k disjoint chorded cycles $C_1', \ldots , C_k'$ in G such that $V(G)=\cup _{i=1}^kV(C_i')$.

Corollary 9

Let G be a graph of order $n\ge 4k$ for an integer $k\ge 1$ with $\delta (G)\ge (n+k)/2.$ Let $v_1, \ldots , v_k$ be any k distinct vertices in G. Suppose that G contains k disjoint chorded cycles $C_1, \dots , C_k$ such that $v_i\in V(C_i)$ for all $1\le i\le k$. Then there exist k disjoint chorded cycles $C_1', \ldots , C_k'$ such that $v_i\in V(C_i')$ for all $1\le i\le k$, and $V(G)=\cup _{i=1}^kV(C_i')$.

Proof

Let $e_i=v_i w_i$ be a cycle-edge of $C_i$, for all $1\le i\le k$. We apply Theorem 7 to extend the chorded cycle system, keeping $e_i$ as a cycle-edge. Hence the corollary holds. $\square$

By Theorems 5 and 7, we also have the following theorem, similar to Theorem 2.

Theorem 10

Let G be a graph of order $n\ge 18k-3$ for an integer $k\ge 2$, and let $e_1, e_2, \ldots , e_k$ be any k independent edges in G. Suppose that $\delta (G)\ge n/2+k-1$. Then G contains k disjoint doubly chorded cycles $D_1, D_2, \ldots , D_k$ such that $e_i$ is a cycle-edge of $D_i$ and $4\le |V(D_i)|\le 6$ for all $1\le i\le k$. Furthermore, there exist k disjoint chorded cycles $C_1, C_2, \ldots , C_k$ such that $e_i$ is a cycle-edge of $C_i$ for all $1\le i\le k$, and $V(G)=\cup _{i=1}^kV(C_i)$.

Finally, we prove the following theorem which shows the existence of disjoint chorded cycles containing specified edges as chords.

Theorem 11

Let G be a graph of order $n\ge 6k+1$ for an integer $k\ge 2$. If

$$\begin{aligned} \sigma _2(G)\ge n+3k-2 \text { and }~\delta (G)\ge 6k-3, \end{aligned}$$

then for any k independent edges $e_1, e_2, \ldots , e_k$ in G, there exist k disjoint cycles $C_1, C_2, \ldots , C_k$ such that $e_i$ is a chord of $C_i$ and $4\le |V(C_i)|\le 6$ for all $1\le i\le k$.

Here, we make the following conjecture.

Conjecture 1

Let G be a graph of order $n\ge 6k$ for an integer $k\ge 1$. If

$$\begin{aligned} \sigma _2(G)\ge n+3k-2, \end{aligned}$$

then for any k independent edges $e_1, \ldots , e_k$, there exist k disjoint cycles $C_1, \ldots , C_k$ such that $e_i$ is a chord of $C_i$ and $4\le |V(C_i)|\le 6$ for all $1\le i\le k$.

Remark

The degree-sum condition is sharp in the following sense. Let $H=K_{2k}+K_{2k-1}+K_{n-4k+1}$. Consider k independent edges $e_1, e_2, \ldots , e_k$ in $K_{2k}$, and say $e_i=x_iy_i$ for all $1\le i\le k$. Now, consider a graph G obtained from H where, for all $1\le i\le k$, $y_i$ is adjacent to every vertex in $K_{n-4k+1}$. Since $x_iz\not \in E(G)$ for any $z\in V(K_{n-4k+1})$, we have

$$\begin{aligned} \sigma _2(G)&=\deg _G(x_i)+\deg _G(z)\\&=(2k-1+2k-1)+(n-4k+2k-1+k)\\&=n+3k-3. \end{aligned}$$

For any $e_i$ to be a chord of a cycle requires at least two neighbors in $K_{2k-1}$. Hence, there are not k disjoint chorded cycles in G containing the specified edges as chords.

Before proving Theorem 11, we first prove the following lemma and the following theorem, which is the extension of Theorem 11 to the case where $k=1$.

Lemma 3

Let G be a graph of order $n\ge 4$ with $\sigma _2(G)\ge n$. Then any edge $e\in E(G)$ lies either on a 3-cycle or a 4-cycle.

Proof

Let $e=uu'\in E(G)$. If e lies on a 3-cycle, then the lemma holds. Hence, we may assume that e does not exist on any 3-cycle. Since $\sigma _2(G)\ge n$, G is 2-connected. Without loss of generality, we may assume that $ux\in E(G)$ for $x\in V(G)-\{u, u'\}$. Then $u'x\not \in E(G)$, otherwise e lies on a 3-cycle. By the degree-sum condition, $\deg _G(u')+\deg _G(x)\ge n$ and therefore $|N_G(u')\cap N_G(x)|\ge 2$. Let $y\in N_G(u')\cap N_G(x)$ for $y\in V(G)-\{u, u', x\}$. Then e lies on the 4-cycle $u, x, y, u', u$.

$\square$

Theorem 12

Let G be a graph of order $n\ge 6$ with $\sigma _2(G)\ge n+1$. Then for any $e\in E(G)$, there exists a cycle C such that e is a chord of C and $4\le |V(C)|\le 6$.

Remark

In Theorem 12, 6-cycles are necessary. Consider the graph G of order n which is obtained from $K_{n-2}$ and an edge $e=xy$ such that x is adjacent to exactly two vertices in $K_{n-2}$ and y is adjacent to every vertex in $V(G)-N_G(x)$. Then for $z\in V(G)-(N_G(x)\cup \{x\})$, $\sigma _2(G)= \deg _G(x)+\deg _G(z)=3+(n-2)=n+1$, and the shortest cycle to have e as a chord in G is a 6-cycle.

Proof

Let e be any edge in the graph G. By Lemma 3, e lies on either a 3-cycle or a 4-cycle. Note that the degree-sum condition implies that G is 3-connected and $\delta (G)\ge 3$. We consider the following two cases.

Case 1 The edge e lies on a 3-cycle, say $C=u_1, u_2, u_3, u_1$.

Let $e=u_1u_2$. Letting $R=G-\{u_1, u_2, u_3\}$, we know $u_1, u_2,$ and $u_3$ must each have at least one neighbor in R, say $u_1', u_2'$, and $u_3'$ respectively. If $u_1'=u_2'$ then $u_1',u_2,u_3,u_1,u_1'$ is a 4-cycle containing e as a chord. Next suppose that $u_1'\ne u_2'$. If $u_1'u_2'\in E(G)$, then $u_1',u_2',u_2, u_3,u_1, u_1'$ is a 5-cycle containing e as a chord. Now if $u_1'u_2'\not \in E(G)$, then $u_1'$ and $u_2'$ must share some neighbor $w\in R$. Then $u_1',w,u_2', u_2, u_3, u_1, u_1'$ is a 6-cycle containing e as a chord.

Case 2 The edge e lies on a 4-cycle, $C=u_1, u_2, u_3, u_4, u_1$.

Let $e=u_1u_2$ and note that C does not have a chord, otherwise e lies on a 3-cycle and we may refer back to Case 1. From the degree condition, the nonadjacent vertices $u_2$ and $u_4$ have at least three common neighbors, therefore there exists a vertex $w\ne u_1$ or $u_3$ that is adjacent to both $u_2$ and $u_4$. Similarly, there is a vertex $w'\ne u_2$ or $u_4$ that is adjacent to both $u_1$ and $u_3$. If $w=w'$ then $w, u_2, u_3, u_4, u_1, w$ is a 5-cycle containing e as a chord. Otherwise, $w, u_4, u_1, w', u_3, u_2, w$ is a 6-cycle containing e as a chord.

This completes the proof of the theorem. $\square$

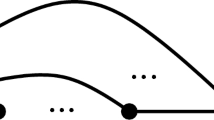
Proof (of Theorem 11) Suppose that the theorem does not hold. Let G be an edge-maximal counterexample. Since a complete graph of order at least 4k contains the desired k disjoint chorded cycles, we may assume that G is not complete. Let $uv\not \in E(G)$ for distinct $u, v\in V(G)$, and define $G'=G+uv$. Then $G'$ is not a counterexample by the edge-maximality of G, and thus $G'$ contains k disjoint chorded cycles $C_1, \ldots , C_k$ such that $e_i$ is a chord of $C_i$ and $4\le |V(C_i)|\le 6$ for all $1\le i\le k$. Without loss of generality, we may assume that $uv\not \in \cup _{i=1}^{k-1}E(C_i)$, that is, G contains $k-1$ disjoint cycles $C_1, C_2, \ldots , C_{k-1}$ such that $e_i$ is a chord of $C_i$ and $4\le |V(C_i)|\le 6$ for all $1\le i\le k-1$. Note that there exist two distinct types of chorded 6-cycles which are shown in Fig. 1. Let $C_i=u_1, u_2, \ldots , u_p, u_1$ for $1\le i\le k-1$ and $4\le p\le 6$, and let ${\mathscr {C}}=\cup _{i=1}^{k-1}C_i$. Note that in $G-{\mathscr {C}}$, there exists a 3, 4, or 5-cycle, say C, containing $e_k$ as an edge with an adjacency to a vertex in $R=G-{\mathscr {C}}-C$ from at least one end-vertex of $e_k$. Let $C=w_1, w_2, \ldots , w_q, w_1$ for $3\le q\le 5$, and let $e_k=w_1w_2$. $\square$

Fig. 1

The two types of chorded 6-cycles

We choose ${\mathscr {C}}$ such that

• 1. $\sum _{i=1}^{k-1}|V(C_i)|$ is a minimum.

• 2. Subject to (1), |V(C)| is a minimum.

• 3. Subject to (1) and (2), the number of Type II chorded 6-cycles is a maximum.

Without loss of generality, we may assume that $w_1x\in E(G)$ for $x\in V(R)$. By condition (2), $|N_C(w_2)|=2$. Since $\delta (G)\ge 6k-3$ and $|N_{{\mathscr {C}}}(w_2)|\le 6(k-1)$, we have $|N_{G-{\mathscr {C}}}(w_2)|\ge 6k-3-6(k-1)=3$. Hence $N_R(w_2)\ne \emptyset$, and let $y\in N_R(w_2)$. If $y=x$, then $G-{\mathscr {C}}$ contains a cycle $C'$ such that $e_k$ is a chord of $C'$ and $4\le |V(C')|\le 6$, a contradiction. Hence we may assume that $y\ne x$. Note that $|V(R)|=|V(G-{\mathscr {C}}-C)|\ge 6k+1-6(k-1)-5=2$. For the nonadjacent pairs of vertices $(w_1, y)$ and $(w_2, x)$, we first consider the adjacencies from these pairs to the cycles in ${\mathscr {C}}$.

Claim 1. Let $1\le i\le k-1.$ Then the following statements hold.

• (i) $\deg _{C_i}(w_1, w_2, x, y)\le 14$ for any chorded 4-cycle $C_i$,

• (ii) $\deg _{C_i}(w_1, w_2, x, y)\le 16$ for any chorded 5-cycle $C_i$, and

• (iii) $\deg _{C_i}(w_1, w_2, x, y)\le 18$ for any chorded 6-cycle $C_i$.

Proof

For $1\le i\le k-1$, let $M=N_{C_i}(w_1)\cap N_{C_i}(w_2)$ and $Z=V(C_i)-V(e_i)$. Note that if $C_i$ is a chorded p-cycle for $p\in \{4, 5\}$, then without loss of generality, we may assume that $e_i=u_1u_3$ and if $C_i$ is a chorded 6-cycle, then we may assume that either $e_i=u_1 u_3$ (Type I) or $e_i=u_1u_4$ (Type II). We consider the following cases. $\square$

Case 1 C is a 3-cycle.

Subcase 1.1 $C_i$ is a chorded 4-cycle.

Suppose that $M\cap Z\ne \emptyset$. By symmetry, we may assume that $u_4\in M\cap Z$, that is, $w_1u_4, w_2 u_4\in E(G)$. Then $w_1, u_4, w_2, w_3, w_1$ is a 4-cycle containing $e_k$ as a chord. We claim that $|N_{V(e_i)}(v)|\le 1$ for all $v\in \{x, y\}$. If $|N_{V(e_i)}(v)|=2$ for some $v\in \{x, y\}$, say $v=x$, then $u_1, x, u_3, u_2, u_1$ is a 4-cycle containing $e_i$ as a chord, and we have the two desired cycles containing the specified edges as chords. Hence the claim holds. Then $\deg _{C_i}(w_1, w_2)\le 8$ and $\deg _{C_i}(x, y)\le 6$. If $M\cap Z =\emptyset$, then $\deg _{C_i}(w_1, w_2)\le 6$ and $\deg _{C_i}(x, y)\le 8$. Therefore, in both cases, we have $\deg _{C_i}(w_1, w_2, x, y)\le 14$.

Subcase 1.2 $C_i$ is a chorded 5-cycle.

If $M\cap Z\ne \emptyset$, then there exists a 4-cycle containing $e_k$ as a chord, contradicting condition (1). Hence $M\cap Z=\emptyset$ and thus, $\deg _{C_i}(w_1, w_2)\le 7$. If $|N_{V(e_i)}(v)|=2$ for some $v\in \{x, y\}$, similarly, (1) is contradicted. Hence $|N_{V(e_i)}(v)|\le 1$ for all $v\in \{x, y\}$, and then $\deg _{C_i}(x,y)\le 8$. Therefore, we have $\deg _{C_i}(w_1, w_2, x, y)\le 15<16$.

Subcase 1.3 $C_i$ is a chorded 6-cycle.

Since $M\cap Z=\emptyset$, $\deg _{C_i}(w_1, w_2)\le 8$. Also, $|N_{V(e_i)}(v)|\le 1$ for all $v\in \{x, y\}$, otherwise there is a 4-cycle or 5-cycle (depending on the type of chorded 6-cycle, $C_i$) containing $e_i$ as a chord, contradicting (1). Hence, $\deg _{C_i}(x, y)\le 10$. Therefore, we have $\deg _{C_i}(w_1, w_2, x, y)\le 18$.

Case 2 C is a 4-cycle.

Subcase 2.1 $C_i$ is a chorded 4-cycle.

If $\deg _{C_i}(v)\le 3$ for all $v\in \{x, y\}$ then claim (i) holds. Hence, without loss of generality, we may assume that $\deg _{C_i}(x)=4$. Then $M\cap Z=\emptyset$, otherwise we have the two desired cycles containing the specified edges as chords. Hence $\deg _{C_i}(w_1, w_2)\le 6$. Noting that $\deg _{C_i}(x, y)\le 8$, we have $\deg _{C_i}(w_1, w_2, x, y)\le 14$.

Subcase 2.2 $C_i$ is a chorded 5-cycle.

If $M\cap \{u_4, u_5\}\ne \emptyset$, then there exists a 5-cycle containing $e_k$ as a chord and $e_i$ is left on a 3-cycle, contradicting (2). Hence $M\cap \{u_4, u_5\}=\emptyset$, and then $\deg _{C_i}(w_1, w_2)\le 8$. Since $|N_{V(e_i)}(v)|\le 1$ for all $v\in \{x, y\}$, $\deg _{C_i}(x, y)\le 8$. Therefore, we have $\deg _{C_i}(w_1, w_2, x, y)\le 16$.

Subcase 2.3 $C_i$ is a chorded 6-cycle.

If $M\cap Z\ne \emptyset$, then there exists a 5-cycle containing $e_k$ as a chord, contradicting (1). Hence $M\cap Z=\emptyset$, thus $\deg _{C_i}(w_1, w_2)\le 8$. Since $|N_{V(e_i)}(v)|\le 1$ for all $v\in \{x, y\}$, $\deg _{C_i}(x, y)\le 10$. Therefore, we have $\deg _{C_i}(w_1, w_2, x, y)\le 18$.

Case 3 C is a 5-cycle.

Subcase 3.1 $C_i$ is a chorded 4-cycle.

By the same arguments as Subcase 1.1, we have $\deg _{C_i}(w_1, w_2, x, y)\le 14$.

Subcase 3.2 $C_i$ is a chorded 5-cycle.

Since $|N_{V(e_i)}(v)|\le 1$ for all $v\in \{x, y\}$, we have $\deg _{C_i}(x)\le 4$ and $\deg _{C_i}(y)\le 4$. If $\deg _{C_i}(x)\le 3$ and $\deg _{C_i}(y)\le 3$, then claim (ii) holds. First we may suppose that $\deg _{C_i}(x)=4$ and $\deg _{C_i}(y)\le 3$ by symmetry. Let $N_{C_i}(x)=\{u_2, u_3, u_4, u_5\}$. Then $x, u_5, u_1, u_2, u_3, x$ is a 5-cycle containing $e_i$ as a chord. If $u_4\in M$, then $w_1, u_4, w_2, w_3, w_4, w_5, w_1$ is a 6-cycle containing $e_k$ as a chord, and we have the two desired cycles containing the specified edges as chords. Hence $u_4\not \in M$, thus $\deg _{C_i}(w_1, w_2)\le 9$. Therefore, we have $\deg _{C_i}(w_1, w_2, x, y)\le 16$.

Next, suppose that $\deg _{C_i}(x)=\deg _{C_i}(y)=4$. Under this assumption we must consider two cases. First assume that $N_{V(e_i)}(x)\cap N_{V(e_i)}(y)=\emptyset$. Then either $u_4$ or $u_5$ can be replaced by x (resp. y) depending on the adjacencies from x (resp. y) to $C_i$, and there exists a 5-cycle containing $e_i$ as a chord. If $M\cap \{u_4, u_5\}\ne \emptyset$, then there exists a 6-cycle containing $e_k$ as a chord, and we have the two desired cycles with the specified edges as chords. Hence $M\cap \{u_4, u_5\}=\emptyset$, and $\deg _{C_i}(w_1, w_2)\le 8$. Therefore, we have $\deg _{C_i}(w_1, w_2, x, y)\le 16$. Now assume that $N_{V(e_i)}(x)\cap N_{V(e_i)}(y)\ne \emptyset$. Without loss of generality, we may assume that $u_1\in N_{V(e_i)}(x)\cap N_{V(e_i)}(y)$. Then $x, u_1, u_2, u_3, u_4, x$ is a 5-cycle containing $e_i$ as a chord. If $u_5\in M$ then there exists a 6-cycle containing $e_k$ as a chord, and we have the desired two cycles containing the specified edges as chords. If $vu_5\not \in E(G)$ for all $v\in \{w_1, w_2\}$, then $\deg _{C_i}(w_1, w_2)\le 8$, and $\deg _{C_i}(w_1, w_2, x, y)\le 16$. Hence, without loss of generality, we may assume that $w_1u_5\in E(G)$ and $w_2u_5\not \in E(G)$. If $u_4\in M$, then $w_1, u_5, y, w_2, u_4, w_1$ is a 5-cycle containing $e_k$ as a chord, and $e_i$ is left on a 3-cycle, contradicting (2). Hence, at most one vertex in $\{w_1,w_2\}$ is adjacent to $u_4$. Then $\deg _{C_i}(w_1, w_2)\le 8$, and therefore, $\deg _{C_i}(w_1, w_2, x, y)\le 16$.

Subcase 3.3 $C_i$ is a chorded 6-cycle.

First suppose that $C_i$ is a Type I chorded 6-cycle. If $M\cap \{u_4, u_5, u_6\}\ne \emptyset$, then there exists a 6-cycle containing $e_k$ as a chord, and $e_i$ is left on a 3-cycle, contradicting (2). Hence $M\cap \{u_4, u_5, u_6\}=\emptyset$, thus $\deg _{C_i}(w_1, w_2)\le 9$. Also, $|N_{V(e_i)}(v)|\le 1$ for all $v\in \{x, y\}$. If $\deg _{C_i}(x, y)\le 9$, then claim (iii) holds. So we may assume that $\deg _{C_i}(x, y)\ge 10$. Now, we consider two cases. First, suppose that $N_{V(e_i)}(x)\cap N_{V(e_i)}(y)=\emptyset$. Without loss of generality, we may assume that $xu_1\in E(G)$ and $yu_3\in E(G)$. Then $u_1, x, u_2, u_3, y, u_6, u_1$ is a 6-cycle containing $e_i$ as a chord. This cycle is a Type II chorded 6-cycle, which contradicts (3). Next, suppose that $N_{V(e_i)}(x)\cap N_{V(e_i)}(y)\ne \emptyset$. Without loss of generality, we may assume that $u_1\in N_{V(e_i)}(x)\cap N_{V(e_i)}(y)$. Then $u_1, y, u_2, u_3, u_4, x, u_1$ is a Type II 6-cycle containing $e_i$ as a chord, contradicting (3).

Next, suppose that $C_i$ is a Type II chorded 6-cycle. If $M\cap \{u_2, u_3, u_5, u_6\}\ne \emptyset$, then there exists a chorded 6-cycle containing $e_k$ as a chord, and $e_i$ is left on a 4-cycle, contradicting (2). Hence $\deg _{C_i}(w_1, w_2)\le 8$. Also, $|N_{V(e_i)}(v)|\le 1$ for all $v\in \{x, y\}$. Hence $\deg _{C_i}(x, y)\le 10$. Therefore, we have $\deg _{C_i}(w_1, w_2, x, y)\le 18$.

This completes the proof of Claim 1. $\square$

Recall that C is a q-cycle for $3\le q\le 5$ containing $e_k$ as a cycle-edge.

Claim 2. $\deg _R(w_1, w_2, x, y)\le 2|V(R)|-2.$

Proof

Note that $N_R(w_1)\cap N_R(w_2)=\emptyset$, otherwise $G-{\mathscr {C}}$ contains a $q'$-cycle for some $4\le q'\le 6$ (depending on |V(C)|) containing $e_k$ as a chord, a contradiction. Hence $|N_R(w_1)\cup N_R(w_2)|=|N_R(w_1)|+|N_R(w_2)|$. Suppose that there exists an edge between $N_R(w_1)$ and $N_R(w_2)$. If C is a 3-cycle (resp. 4-cycle), then $G-{\mathscr {C}}$ contains a 5-cycle (resp. 6-cycle) containing $e_k$ as a chord, a contradiction. If C is a 5-cycle, then $G-{\mathscr {C}}$ contains a 4-cycle with $e_k$ as a cycle-edge, contradicting (2). Hence, there are no edges between $N_R(w_1)$ and $N_R(w_2)$, thus $|N_R(x)|\le |V(R)|-1-|N_R(w_2)|$ and $|N_R(y)|\le |V(R)|-1-|N_R(w_1)|$. Therefore, we have

$$\begin{aligned} \deg _R(w_1, w_2, x, y)\le & {} |N_R(w_1)|+|N_R(w_2)|+(|V(R)|-1-|N_R(w_2)|)\\&+\,(|V(R)|-1-|N_R(w_1)|)\\= & {} 2|V(R)|-2 \end{aligned}$$

This completes the proof of Claim 2. $\square$

Claim 3. $\deg _C(w_1, w_2, x, y)\le 2q+2$.

Proof

By (2), $\deg _C(w_1)=2$ and $\deg _C(w_2)=2$. Since $N_R(w_1) \cap N_R(w_2)=\emptyset$, $\deg _C(x)\le q-1$ and $\deg _C(y)\le q-1$. Hence, $\deg _C(w_1, w_2, x, y)\le 2+2+2(q-1)=2q+2$. $\square$

Suppose that there are r chorded 4-cycles, s chorded 5-cycles, and t chorded 6-cycles in ${\mathscr {C}}$. Then by Claims 1, 2, and 3, we have

$$\begin{aligned} 2(n+3k-2)\le 2\sigma _2(G)&\le \deg _G(w_1, w_2, x, y)\\&\le (14r+16s+18t)+2(|V(R)|-2)+(2q+2)\\&=14r+16s+18t+ 2(n-4r-5s-6t-q)+2q\\&= 2n+6(r+s+t)\\&=2n+6(k-1)\\ \Longrightarrow n+3k-2&\le n+3k-3, \text { a contradiction.} \end{aligned}$$

This completes the proof of the theorem. $\square$

Corollary 13

Let G be a graph of order $n\ge 9k-5$ for an integer $k\ge 2$. If

$$\begin{aligned} \delta (G)\ge \frac{n+3k-2}{2}, \end{aligned}$$

then for any k independent edges $e_1, e_2, \ldots , e_k$, there exist k disjoint cycles $C_1, C_2, \ldots , C_k$ such that $e_i$ is a chord of $C_i$ and $4\le |V(C_i)|\le 6$ for all $1\le i\le k$.