Total generalized variation-based Retinex image decomposition

Abstract

Human visual system (HVS) can perceive color under varying illumination conditions, and Retinex theory is precisely aimed to simulate and explain how the HVS perceives reflectance regardless of different illumination conditions. In this paper, we introduce a reflectance and illumination decomposition model for the Retinex problem via total generalized variation regularization and $H^{1}$ decomposition. The total generalized variation regularization ameliorates the staircasing artifacts that appear in the reflectance component of existing total variation-based models and $H^{1}$ norm guarantees smoother illumination. We analyze the existence and uniqueness of the proposed model and employ an alternating minimization scheme based on split Bregman iteration. We present numerous numerical experiments on both grayscale and color images to make comparisons with several state-of-the-art methods and demonstrate that our method is comparable both quantitatively and qualitatively.

1 Introduction

Retinex theory is originally proposed by Land and McCann [34] to deal with compensation for illumination effects in images, whose idea is to simulate how human visual system (HVS) automatically perceives color under varying illumination conditions. An important feature of HSV is our visual system tends to see the same color in a given image regardless of the light. The primary goal of Retinex theory is to decompose a given image I into two components, reflectance R and illumination L, such that

$$\begin{aligned} {I}(x) = {R}(x)\times {L}(x), \end{aligned}$$

(1)

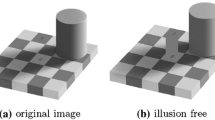
at each pixel $x \in \Omega$ where $\Omega \subset {\mathbb {R}}^{2}$ is the image domain. Equation (1) exactly explains why region A of Fig. 1a is visually darker than region B, while they have the same intensity value just shown in Fig. 1b. This is because, by Retinex theory, they are in different illumination conditions. Actually, the region B is in the shadow of the green cylinder so that the illumination of the region A is stronger than that of the region B, i.e., ${L}(A) > {L}(B)$; thus, the reflectance of the region A is smaller than that of the region B, i.e., ${R}(A) < {R}(B)$.

To simulate the HVS, we need to recover the reflectance R and illumination L from a given image I accurately, and it is a mathematically ill-posed problem since both parts are unknown. Numerous techniques have been developed to implement the Retinex theory in the past 40 years and a first step taken by most algorithms is the conversion to the logarithmic domain by $i = \log (I), r = \log (R), l = \log (L)$, and thereby, $i = r + l$. For example, path-based algorithm [10, 30, 31, 34, 45, 55] was proposed with the path geometry of piecewise linear, double spirals and Brownian paths. However, these path-based methods contain a lot of parameters, and they have high computational complexity. The recursive algorithms [13, 47] extend the path-based algorithms and replace the path computation by a recursive matrix calculation which highly improves the computational efficiency, but the result strongly depends on the number of iterations. The center/surround algorithms [24, 25] assume the illumination component changes smoothly and the reflectance component is computed by subtracting a blurred version of the input image, but these methods need too many parameters. Later on, the idea of path following is formulated into PDE-based models [1, 21, 49, 50] and variational models [28, 38, 42, 43, 51, 72]. The former recovers the reflectance component by solving a Poisson equation with the assumption that the illumination is relative small, and the latter utilizes different regularizations on reflectance and illumination due to their different properties, such as total variation (TV) is introduced to ensure getting piecewise constant reflectance. But it loses too much details of the reflectance component, especially for the high-contrast regions. Recently, deep learning-based image processing methods have been proposed in the Retinex-based image decomposition field [39, 53, 60, 61, 70]. As there is no ground truth of the reflectance and illumination, making difficult to generating and annotating dataset of natural images, these methods train their networks either on synthetic dataset, real-world dataset with sparse annotations or image pairs/sequences, and perform not well on real-world data.

In this paper, we consider a decomposition model in the variational framework to recover R and L simultaneously. In particular, we propose to use total generalized variation (TGV) as a regularization term of the reflectance component to capture more details, which has been successfully applied in image restoration [27, 29, 63], and extract smoother illumination component with ${H}^{1}$ norm. We develop a rather simple, efficient optimization algorithm based on split Bregman iteration, and the keys to our method are recovering richly detailed reflectance and small smooth illumination alternately. We denote our method as TGVH1 reflectance and illumination decomposition model. Compared to the state-of-the-art methods [14, 28, 38, 42, 51], we can achieve a more detail-preserved reflectance and smoother illumination and increase the contrast precisely.

Fig. 1

Adelsons checker shadow illusion. a Original image. b Illusion free image

The rest of the paper is organized as follows. In Sect. 2, we review several different Retinex algorithms. In Sect. 3, we present the proposed model including theoretical analysis about the existence and uniqueness of the solution. In Sect. 4, we introduce an alternating optimization based on split Bregman iteration to solve the proposed model. In Sect. 5, we present the numerical experiments on visual illusion images, synthetic images, natural color images, medical images and shadowed color images and make comparison with several existing methods. Finally, the conclusion and future work are discussed in Sect. 6.

2 Related work

Generally, image decomposition algorithms can be classified into two categories: intrinsic image decomposition [44] and Retinex-based image decomposition [22]. The former focuses on recovering reflectance close to ground truth as far as possible but losing objects’s shape, while the latter aims to restore the reflectance with good shape and visual realism. Here, we mainly work on and review Retinex-based methods. For the past few decades, many interpretations, implementations and improvements of the Retinex algorithm have been studied and basically classified into four categories (see [22, 28, 36, 50] for details): path-based algorithms, recursive algorithms, center/surround algorithms, formulas-based algorithms and supervised deep learning-based algorithms. These seemingly different algorithms are actually very similar since they are all based on the assumption that the illumination component is spatially smooth.

Path-based algorithms The key idea of path-based algorithms was the lightness of each pixel depending on the multiplication of ratios along random walks. Land’s original works [30,31,32, 34] used piecewise linear paths and laid out a time-consuming algorithm. Later, Marini and Rizzi [45] implemented the original Retinex algorithm using Brownian motion to approximate each path and greatly improved the effectiveness of the Retinex algorithm. Provenzi et al. [56] presented a detailed mathematical analysis of the original Retinex algorithm to describe the behavior of the algorithm. Base on this work, Provenzi et al. [57] proposed a “random spray Retinex” in which paths were replaced by 2-D pixel sprays, and achieved faster performances than the path-wise one.

Recursive algorithms As a variant of path-based algorithms, recursive algorithms replaced the path computation by a recursive matrix comparison where the comparison between pixels could be calculated simultaneously. Frankle–McCann Retinex [13] used single pixel comparisons with variable separations where a single pixel eventually averages different products from all other pixels data. McCann99 Retinex [47] created a multiresolution pyramid from the input by averaging image, and pixel comparisons and lightness estimates are in an alternate progress from high level to low level until the pyramids bottom level. Both implementations were presented in [15], and the parameter determinations were discussed in [9].

Center/surround algorithms The center/surround approach was first proposed by [33] and later improved by Jobson et al. [24] with an easy implementation and better result. Single-scale Retinex (SSR) [25] and multiscale Retinex (MSR) [58] were the representative algorithms of the center/surround approach, and both were based on the idea that lightness values could be computed by subtracting a blurred version of the input image from the original image. Because of their simplicity and effectiveness, many improved algorithms [7, 8, 23, 54, 68] were proposed. For example, the multiscale Retinex with color restoration (MSRCR) [59] was an improvement in the MSR while there were halo artifacts near strong edges.

Formulas-based algorithms Formulas-based algorithms were proposed to translate the Retinex principles into a physical model solving by a set of equations or an optimization problem. Poisson equation-type Retinex algorithms were developed by solving a Poisson equation under the assumptions that reflectance was a piecewise constant and illumination was spatially smooth [34]. Horn [21] applied the Laplacian to get $\Delta {i} = \Delta {r} + \Delta {l}$ and then used a threshold function clipping the finite parts to get a Poisson equation, namely

$$\begin{aligned} \Delta {r}(x) =\tau {(\Delta {i})}, \end{aligned}$$

(2)

where the threshold function is defined by

$$\begin{aligned} \tau (x)=\left\{ \begin{aligned} x&\mathrm{if}\,\,\left| x\right| > t\\ 0&\mathrm{otherwise} \end{aligned} \right. \end{aligned}$$

(3)

The Poisson equation (2) was solved by an iterative scheme of a low-pass filter. Blake [1] introduced an improvement in Horn’s method, extracting the discontinuities from the image gradient magnitude instead of the Laplacian with better boundary conditions. Funt et al. [16] improved Horn’s method by applying a new curl-correction technique at the thresholded locations. Additional algorithmic improvements [49, 50] by Morel constructed a very tight connection with Horn’s and Blake’s method and yielded an exact and fast implementation using only two fast Fourier transforms.

By the same assumption with Poisson equation-type Retinex algorithms, variational Retinex algorithms have been applied to image decomposition in the past 2 decades. Let $\Omega \subset {\mathbb {R}}^{d}$ be a bounded open domain with a compact Lipschitz boundary, the primary variational model was proposed by Kimmel [28], only focusing on the penalty functional of the illumination component l, and the followed $H^{1}+L^{2}$ model is

$$\begin{aligned} \begin{aligned}&\hat{l} =\arg \min _{l}\int _{\Omega }\left\{ \left| \nabla {l}\right| ^{2} + \alpha (l-i)^{2} + \beta \left| \nabla (l-i)\right| ^{2}\right\} \mathrm{d}x,\\&\ \ \ \ \ \ \ \mathrm {s.t.} \ \ \ l\ge i, \ <\nabla l, \mathbf {n}> =0 \ \ \mathrm{on} \ \ \partial \Omega \end{aligned} \end{aligned}$$

(4)

which was a quadratic programming problem solved by the project normalized steepest descent method. Ma and Osher [43] proposed total variation (TV) model to recover piecewise constant reflectance component r, namely

$$\begin{aligned} \hat{r} =\arg \min _{r}\int _{\Omega }\left( t\left| \nabla {r}\right| + \frac{1}{2} \left| \nabla r - \nabla i\right| ^{2}\right) \mathrm{d}x, \end{aligned}$$

(5)

where parameter $t > 0$. Afterward, Ma [42] improved a $L_{1}$-based model on reflectance r, which reads

$$\begin{aligned} \hat{r} =\arg \min _{r}\int _{\Omega }\left| \nabla {r} - \delta _{t}(\nabla i)\right| \mathrm{d}x, \end{aligned}$$

(6)

where $\delta _{t}(\nabla i)$ was gradient threshold function with respect to t. Both models were solved effectively by Bregman iteration, but the penalization on the magnitude of image gradient caused the loss of reflection’s details and contrast. The same was to optimize reflectance r, Zosso et al. [72] extended the TV-based models to a unified nonlocal formulation of the reflectance, and Li et al. [37] applied an adaptive perceptually inspired variational model to adjust the uneven intensity distribution.

Several decomposition models have been developed by considering both reflectance r and illumination l simultaneously. For instance, Ng and Wang [51] added an $L^{2}$ fidelity term and some constraints in the proposed energy functional, namely

$$\begin{aligned} \min _{\begin{array}{c} r\le 0,\\ l \ge i \end{array}}\int _{\Omega }\left\{ \left| \nabla {r}\right| + \frac{\alpha }{2}\left| \nabla l\right| ^{2} + \frac{\beta }{2}(i-r-l)^{2} + \frac{\mu }{2}l^{2}\right\} \mathrm{d}x, \end{aligned}$$

(7)

where the constraint $r \le 0$ corresponded to the assumption $0< R < 1$. Recently, decomposition models combined various kinds of techniques upon r or l with formulation (7) aiming to estimate the reflectance with more details. For example, Chang et al. [5] used sparse and redundant representations of the reflectance component replacing of the TV term. Similarly, Wang et al. [67, 69] used nonlocal bounded variation (NLBV) and variational model with barrier functionals upon the reflectance, respectively. Liang and Zhang [38] adopted higher-order total variation $L^{1}$(HoTVL1) on the illumination component. Wang et al. [64] constructed a variational Bayesian model with Gibbs distributions for both reflectance and illumination and the gamma distributions for the model’s parameters. In addition, a weighted variational model was proposed in [14] to eliminate impact of log-transform and a variational model with hybrid hyper-Laplacian priors was presented in [6]. Guo et al. [20] and Gao et al. [17] only estimate illumination with structure priors. Gu et al. [19] integrate ASR to represent image large-scale structures and SSR to represent image fine-scale textures.

Supervised deep learning-based algorithms With the rapid development of deep neural network, supervised deep learning-based algorithms have been proposed in the low-light image enhancement. Lore et al. [39] use stacked-sparse denoising autoencoder to learn adaptively enhance and denoise from synthetically darkened and noise-added training data. Shen et al. [60] analyze the property of MSR algorithm in the sense of convolutional neural network (CNN) and proposed MSR-net to enhance the low-light image trained on synthetically high quality and low-light images pairs. Park [53] combine the stacked and convolutional autoencoders on illumination and reflectance, respectively, also trained on synthetic high-contrast and low-light images. However, those synthetic data are quite different from the real world data, so those methods cannot generalize well to real-world images. To overcome above difficulties, Wei et al. [70] adopt a deep end-to-end Retinex-Net including a Decom-Net and an Enhance-Net, learning without ground truth decompositions under the key constraints that the consistent reflectance is shared by paired low/normal-light images and Shi [62] proposed a generative adversarial network (GAN).

3 TGV + $H^{1}$ decomposition model

In this section, we first review the TGV regularization in Sect. 3.1 and Hilbert space $H^{1}$, then formulate the optimization for reflectance and illumination decomposition in Sect. 3.3 and show existence and uniqueness of solution for the above problem in Sect. 3.4.

3.1 Background of total generalized variation

The total generalized variation (TGV) was proposed by Bredies et al. [2], as a generalization of the infimal convolution of TV and second-order TV regularizers [4] is written as follows:

$$\begin{aligned} \begin{aligned} \mathrm {TGV}_{\varvec{\alpha }}^{k}(u) =&\sup _{\nu } \Bigg \{ \int _{\Omega }u\mathrm {div}^{k}(\nu )\mathrm{d}x \ | \ \nu \in {\mathcal {C}}_{c}^{k}(\Omega ,\mathrm {Sym}^{k}({\mathbb {R}}^{d})),\\&\Vert \mathrm {div}^{j}(\nu )\Vert _{\infty } \le \alpha _{j},\quad j = 0,\ldots ,k-1 \Bigg \}, \end{aligned} \end{aligned}$$

(8)

where $\varvec{\alpha } =(\alpha _{0},\alpha _{1},\ldots ,\alpha _{k-1})$ is fixed positive vector, $\mathrm {Sym}^{k}({\mathbb {R}}^{d})$ denotes the space of symmetric k-tensors on ${\mathbb {R}}^{d}$ as $\mathrm {Sym}^{k}({\mathbb {R}}^{d}) = \{ \xi :{\mathbb {R}}^{d} \times \cdots \times {\mathbb {R}}^{d}|\; \xi \, is\, k-linear\, and\, symmetric\},$ and ${\mathcal {C}}_{c}^{k}(\Omega ,\mathrm {Sym}^{k}({\mathbb {R}}^{d}))$ is the space of compactly supported symmetric tensor fields. Especially, it is equivalent to the TV regularizer when $k = 1,\; \alpha _{0} =1$.

It has been shown in [2] that $\mathrm {TGV}_{\varvec{\alpha }}^{k}$ can be interpreted as a k-fold infimal convolution by employing the Fenchel–Rockafellar duality formula, as follows:

$$\begin{aligned} \mathrm {TGV}_{\varvec{\alpha }}^{k}(u) = \inf _{u_{j}} \sum _{j=1}^{k}\varvec{\alpha }_{k-j}\int _{\Omega }|{\mathcal {E}}(u_{j-1})-u_{j}|\;\mathrm{d}x, \end{aligned}$$

(9)

where $u_{0}=u, u_{k}=0, u_{j}\in {\mathcal {C}}_{c}^{k-j}(\Omega ,\mathrm {Sym}^{j}({\mathbb {R}}^{d}))$ for $j=1,\ldots ,k$, and ${\mathcal {E}}$ represents the distributional symmetrized derivative, i.e., ${\mathcal {E}}(u_{j-1})=\frac{\nabla u_{j-1} + (\nabla u_{j-1})^{T}}{2}$. Thus, $\mathrm {TGV}_{\varvec{\alpha }}^{k}$ automatically balances the first to the kth derivatives of u among themselves and reduces the staircasing effects of the TV. Similar to the definition of the bounded variation space (BV) on a non-empty open set $\Omega \subset {\mathbb {R}}^{d}$ in [52], the space of functions of bounded generalized variation of order k with $\varvec{\alpha }$ is defined on $\Omega$ in [2] is a Banach space, as follows:

$$\begin{aligned} \mathrm {BGV}_{\varvec{\alpha }}^{k}(\Omega ) = \left\{ u \in L^{1}(\Omega )|\mathrm {TGV}_{\varvec{\alpha }}^{k}<\infty \right\} , \end{aligned}$$

(10)

equipped with the norm $\Vert u\Vert _{\mathrm {BGV}_{\varvec{\alpha }}^{k}} = \Vert u\Vert _{1}+\mathrm {TGV}_{\varvec{\alpha }}^{k}(u)$. For instance, when $k = 2, \mathrm {TGV}_{\varvec{\alpha }}^{2}$ involves the $l_{1}$-norm of ${\mathcal {E}}(u_{0})-u_{1}=\nabla u -u_{1}$ and ${\mathcal {E}}(u_{1})$ via the Radon norm.

In this work, we particularly utilize the second-order $\mathrm {TGV}$ denoted by $\mathrm {TGV}_{\varvec{\alpha }}^{2}$ and corresponding Banach space $\mathrm {BGV}_{\varvec{\alpha }}^{2}(\Omega )$ and their mainly analytical properties [2, 3] to obtain the existence and uniqueness of the solutions of our proposed model in the last subsection of this part.

3.2 Background of Hilbert Space $H^{1}$

We first present some preliminaries for Sobolev spaces proposed in [26, 46]. Let $\Omega$ be an open subset of ${\mathbb {R}}^{n}$ with Lipschitz boundary, the Sobolev space $W^{k,p}(\Omega )$ consists of functions $u \in L^{p}(\Omega )$ such that for every multi-index $\mathbf {\alpha }$ with $|{\alpha }| \le k$, the weak derivative $D^{{\alpha }}u$ (same with the classical derivative $\nabla ^{\mathbf {\alpha }}u$ for smooth function) exists and $D^{{\alpha }}u \in L^{p}(\Omega )$. Thus,

$$\begin{aligned} W^{k,p}(\Omega ) = \{u \in L^{p}(\Omega ):D^{{\alpha }}u \in L^{p}(\Omega ), |\mathbf {\alpha }| \le k\}, \end{aligned}$$

equipped with the norm

$$\begin{aligned} \Vert u\Vert _{W^{k,p}(\Omega )} = \left( \sum _{|{\alpha }| \le k}\int _{\Omega }|D^{{\alpha }}u|^{p} \mathrm{d}x\right) ^{\frac{1}{p}},\quad 1\le p < \infty . \end{aligned}$$

It is important to emphasize that the Sobolev space $W^{k,p}(\Omega )$ is a Banach space. In particular, $H^{k}(\Omega )=W^{k,2}(\Omega )$ is a Hilbert space with the inner product,

$$\begin{aligned}<u,v>_{H^{k}(\Omega )} = \sum _{|{\alpha }| \le k} <D^{{\alpha }}u,D^{{\alpha }}v>_{L^{2}(\Omega )}, \end{aligned}$$

and the norm $\Vert u\Vert _{{H^{k}}(\Omega )} = <u,u>^{\frac{1}{2}}$. Here, we mainly focus on the $H^{1}(\Omega )$ and summarize some definitions and main properties in $H^{1}(\Omega )$ and write the $\Vert u\Vert _{2} = \Vert u\Vert _{L^{2}(\Omega )}$ and $\Vert u\Vert _{1} = \Vert u\Vert _{H^{1}(\Omega )} = (\Vert u\Vert ^{2}_{2} + \Vert \nabla u\Vert ^{2}_{2})^{\frac{1}{2}}$ as a convenience.

(Lower semicontinuity) If the sequence $\{u_{k}\}_{k\in {\mathbb {N}}}$ satisfies $u_{k} \rightarrow u$ and $\nabla u_{k} \rightarrow \nabla u$, then $\Vert u\Vert _{1} \le \liminf \nolimits _{k\rightarrow \infty }\Vert u_{k}\Vert _{1}$. In particular, for $\liminf \nolimits _{k\rightarrow \infty }\Vert u_{k}\Vert _{1} < \infty$, then $u \in H^{1}(\Omega )$.

(Compactness) Suppose $\{u_{k}\}_{k}$ is bounded in $H^{1}(\Omega )$, then there exists a subsequence $\{u_{k_{j}}\}_{j \in {\mathbb {N}}}$ and $u \in H^{1}(\Omega )$ such that $u_{k_{j}} \rightarrow u$ and $\nabla u_{k_{j}} \rightarrow \nabla u$ as $k \rightarrow \infty$.

(Embedding) If $\Omega$ has a Lipschitz boundary and it is connected and $u \in H^{1}(\Omega )$, then it can be shown that there exists positive constant C such that $\Vert u\Vert _{1} \le C\Vert \nabla u\Vert _{2}$.

3.3 Proposed model

Here, we present $\mathrm {TGV_{\varvec{\alpha }}^{2}}+ H^{1}$ variational model for reflectance and illumination decomposition, recovering the reflectance component with more details by $\mathrm {TGV_{\varvec{\alpha }}^{2}}$ and the spatially smooth illumination component penalized by $H^{1}$ norm. We also consider this problem on the logarithmic domain like most variational methods, and the energy function E(r, l) is defined as follows

$$\begin{aligned} \mathrm {TGV_{\varvec{\alpha }}^{2}}(r) + \int _{\Omega }\left\{ \frac{c_{1}}{2}|\nabla {l}|^{2}+\frac{c_{2}}{2}(i-l-r)^{2}+ \frac{c_{3}}{2}l^{2}\right\} \mathrm{d}x, \end{aligned}$$

(11)

Since the number of unknowns is twice the number of equations, we further consider constraints ${\mathcal {B}}_{r}$ and ${\mathcal {B}}_{l}$ on both r and l, aiming to recover the best contrast of the inputs. So the associated minimization problem is given as follows

$$\begin{aligned} (r^{*},l^{*}) = \mathop {{{\,\mathrm{argmin}\,}}}\limits _{(r,l)\in \Lambda \bigcap {\mathcal {B}}_{r} \times {\mathcal {B}}_{l}} E(r,l) \end{aligned}$$

(12)

where $\Lambda = \{(r,l)|(r,l)\in \mathrm {BGV}_{\varvec{\alpha }}^{2}(\Omega )\times H^{1}(\Omega )$}. $c_{1}, c_{2}$ and $c_{3}$ are positive parameters, the term $\int _{\Omega }(i-l-r)^{2}\mathrm{d}x$ is used for the fidelity and $\int _{\Omega }l^{2}\mathrm{d}x$ is the guarantee of the theory proof. Numerically, $c_{3}$ is set very small. $\mathrm {TGV}_{\varvec{\alpha }}^{2}(r)$ is minimized over all gradients of the deformation field ${\mathbf {p}}=(p_{1},p_{2})$ on image space $\Omega$, which reads

$$\begin{aligned} \inf _{{\mathbf {p}} \in {\mathcal {C}}_{c}^{2}(\Omega ,{\mathbb {R}}^{2})}\alpha _{1}\int _{\Omega }|\nabla {r} - {\mathbf {p}}|\;\mathrm{d}x + \alpha _{0}\int _{\Omega }|{\mathcal {E}}({\mathbf {p}})|\;\mathrm{d}x, \end{aligned}$$

(13)

where $\alpha _{0}$ and $\alpha _{1}$ are positive parameters balancing between the first- and the second-order derivative of r.

Remark 1

Here, we show the effect of constraints ${\mathcal {B}}_{r}$ and ${\mathcal {B}}_{l}$ we used on improving the contrast of estimated reflectance. Figure 2 shows a contrast comparison on different constraints by computing the intensity difference between A and B denoted as D(A, B). (a) shows the input gray image with the same intensity of A and B, (b) takes ${\mathcal {B}}_{r} =(-\infty , 0]$ and ${\mathcal {B}}_{l} =[i,\infty )$ similar with Ng and Wang [51] and (c) takes ${\mathcal {B}}_{r} =(0, 255]$ and ${\mathcal {B}}_{l} =[-255,0)$. It can be noticed that constraints in (c) can help to improve the contrast significantly.

Fig. 2

Contrast comparison with different constraints. a shows the input gray image with the intensity of masked A and B 140, $D(A,B) = 0$; b shows the result of ${\mathcal {B}}_{r} =(-\infty , 0]$ and ${\mathcal {B}}_{l} =[i,\infty )$ with the intensity of masked A 73 and B 159, $D(A,B) = 86$; and c shows the result of ${\mathcal {B}}_{r} =(0, 255]$ and ${\mathcal {B}}_{l} =[-255,0)$ with the intensity of masked A 25 and B 250, $D(A,B) = 225$

3.4 Existence and uniqueness of solution

We give a general existence and uniqueness result for solution of the above minimization problem.

Theorem 1

Suppose $i \in L^{\infty }(\Omega )$ and $c_{1}, c_{2}, c_{3} >0$, then problem (12) has a unique solution pair $(r^{*},l^{*})\in \mathrm {BGV}_{\varvec{\alpha }}^{2}(\Omega )\times H^{1}(\Omega )$.

Proof

For any $(r,l) \in \Lambda$, the objective functional of (12) is proper and nonnegative (by the property of $\mathrm {BGV}_{\varvec{\alpha }}^{2}(\Omega )$), i.e., E(r, l) is bounded below. Specifically, it is easy to see that the functional is the correct setting since any constant r and l will yield a finite energy. Hence, we can choose a minimizing sequence $\{r^{k}, l^{k}\}_{k\in {\mathbb {N}}} \subset \Lambda$ for the problem (12), and there exists a constant $M > 0$ such that

$$\begin{aligned} E(r^{k},l^{k}) \le M. \end{aligned}$$

This yields that

$$\begin{aligned}&\Vert \nabla {l^{k}}\Vert ^{2}_{2}<M,\ \ \Vert l^{k}\Vert ^{2}_{2} < M, \end{aligned}$$

(14)

$$\begin{aligned}&\mathrm {TGV}_{\varvec{\alpha }}^{2}(r^{k})<M,\ \ \Vert i-r^{k}-l^{k}\Vert ^{2}_{2} < M, \end{aligned}$$

(15)

$$\begin{aligned}&r^{k} \in {\mathcal {B}}_{r},\ \ l^{k} \in {\mathcal {B}}_{l}, \end{aligned}$$

(16)

for $\forall k\in {\mathbb {N}}$. $\{l^{k}\}$ is uniformly bounded in $H^{1}(\Omega )$ by the bounded conditions (14). With the compact embedding of $H^{1}(\Omega )$ in $L^{2}(\Omega )$, it is easy to deduce that $\{l^{k}\}_{k\in {\mathbb {N}}}$ converges (up to a subsequence) in $H^{1}(\Omega )$ to $l^{*}$. As a consequence of the lower semicontinuity for $H^{1}(\Omega )$ norm, we obtain

$$\begin{aligned} \frac{c_{1}}{2}\Vert \nabla {l^{*}}\Vert ^{2}_{2} + \frac{c_{3}}{2}\Vert l^{*}\Vert ^{2}_{2} \le \mathop {\lim \inf }\limits _{k\rightarrow \infty } \left( \frac{c_{1}}{2}\Vert \nabla {l^{k}}\Vert ^{2}_{2} + \frac{c_{3}}{2}\Vert l^{k}\Vert ^{2}_{2}\right) . \end{aligned}$$

(17)

For $\{r^{k}\}$, we can get

$$\begin{aligned} \Vert r^{k}\Vert _{2}^{2} = \Vert r^{k} + l^{k} - i + i - l^{k}\Vert ^{2}_{2} \le \Vert r^{k} + l^{k} - i\Vert ^{2} + \Vert i - l^{k}\Vert ^{2}_{2} < M. \end{aligned}$$

As $i \in L^{\infty }(\Omega )$ and $\{l^{k}\}$ is uniformly bounded in $L^{2}(\Omega ), \{r^{k}\}$ is also uniformly bounded in $L^{2}(\Omega )$. By the boundedness of $\Lambda , \{r^{k}\}$ is bounded in $L^{1}(\Omega )$ and bounded in $\mathrm {BGV}_{\varvec{\alpha }}^{2}(\Omega )$ by the boundedness of $\mathrm {TGV}_{\varvec{\alpha }}^{2}(r^{k})$ in (15) and the lower semicontinuity. Similar with $\{l^{k}\}$, we can derive that $\{r^{k}\}_{k \in {\mathbb {N}}}$ converges (up to a subsequence) in $\mathrm {BGV}_{\varvec{\alpha }}^{2}(\Omega )$ to $r^{*} \in \mathrm {BGV}_{\varvec{\alpha }}^{2}(\Omega )$. By the lower semicontinuity of $\mathrm {BGV}_{\varvec{\alpha }}^{2}(\Omega )$ norm, we obtain

$$\begin{aligned} \mathrm {TGV}_{\varvec{\alpha }}^{2}(r^{*}) \le \mathop {\lim \inf }\limits _{k\rightarrow \infty } \mathrm {TGV}_{\varvec{\alpha }}^{2}(r^{k}). \end{aligned}$$

(18)

Since $l^{k} + r^{k} \rightharpoonup l^{*} + r^{*}$ in $L^{2}(\Omega )$ and recalling the lower semicontinuity for the $L^{2}(\Omega )$ norm, we also obtain

$$\begin{aligned} \frac{c_{2}}{2}\Vert i - r^{*} - l^{*}\Vert ^{2}_{2} \le \mathop {\lim \inf }\limits _{k\rightarrow \infty } \frac{c_{2}}{2}\Vert i - r^{k} - l^{k}\Vert ^{2}_{2}. \end{aligned}$$

(19)

From the above inequations (17),  (18) and  (19), we have

$$\begin{aligned} \min _{(r,l)\in \Lambda } E(r,l) = \mathop {\lim \inf }\limits _{k\rightarrow \infty } E(r^{k},l^{k}) \ge E(r^{*},l^{*}). \end{aligned}$$

Since the functional (11) is convex (by the convexity of $\mathrm {TGV}_{\varvec{\alpha }}^{2}$) and the constraint sets ${\mathcal {B}}_{r}$ and ${\mathcal {B}}_{l}$ are closed, the minima can be attained at $(r^{*},l^{*})$. Uniqueness is straightforward with the strict convexity of E(r, l) with respect to (r, l). This completes the proof. $\square$

4 Algorithm

In this section, we present the algorithm for solving the problem (12). Note that the two unknowns r and l are coupled in (12), and our idea is to use the alternating minimization scheme based on split Bregman iteration to fully decouple the subproblems for r and l, which yields a simple iteration procedure. The details of our algorithm are described in Algorithm 1.

4.1 Optimizing r of $\mathrm {(P1)}$

To solve the minimization subproblem containing a TGV term in $\mathrm {(P1)}$, we adopt the fast split Bregman method [11, 12, 18, 40]. More precisely, we introduce auxiliary variables $({\mathbf {w}},{\mathbf {v}};{\mathbf {b}},{\mathbf {d}})$ and penalty parameters $(\theta _{0},\theta _{1})$, transforming $\mathrm {(P1)}$ into the following form:

$$\begin{aligned} \begin{aligned} \max _{{\mathbf {b}},{\mathbf {d}}}\min _{\begin{array}{c} r\in {\mathcal {B}}_{r},\\ {\mathbf {p}},{\mathbf {w}},{\mathbf {v}} \end{array}} \bigg \{&E_{1}(r,{\mathbf {p}},{\mathbf {w}},{\mathbf {v}};{\mathbf {b}},{\mathbf {d}}) =\frac{c_{2}}{2}\int _{\Omega }(i-r-l^{k})^{2}\,\mathrm{d}x\\&+\int _{\Omega }\left( \alpha _{1}|{\mathbf {w}}| + \frac{\theta _{1}}{2}({\mathbf {w}} - \nabla {r} + {\mathbf {p}} - {\mathbf {b}})^{2}\right) \,\mathrm{d}x\\&+\int _{\Omega }\left( \alpha _{0}|{\mathbf {v}}| + \frac{\theta _{0}}{2}({\mathbf {v}} - {\mathcal {E}}({\mathbf {p}}) - {\mathbf {d}})^{2}\right) \,\mathrm{d}x \bigg \}. \end{aligned} \end{aligned}$$

(20)

We discrete the energy (20) on each pixel (details can be found in “Appendix”) and break down (P1) into five steps. In the following, we will give a brief statement on solving each step.

Update of $r^{t+1}$ To recover $r^{t+1}$, we take the partial derivative of the energy (20) with respect to r, which leads to the following Euler equation:

$$\begin{aligned} c_{2} r - \theta _{1} \Delta {r} = c_{2}(i - l^{k}) - \theta _{1} \mathrm{div}({\mathbf {w}}^{t} + {\mathbf {p}}^{t} - {\mathbf {b}}^{t}), \end{aligned}$$

(21)

The solution of this linear PDE is given by discrete Fourier transform ${\mathcal {F}}$, which namely

$$\begin{aligned} r^{t+\frac{1}{2}} = {\mathfrak {R}}\Bigg ({\mathcal {F}}^{-1}\Bigg (\frac{{\mathcal {F}}(G_r)}{{\xi }_{r}}\Bigg )\Bigg ), \end{aligned}$$

(22)

where ${\mathcal {F}}(G_r)$ and ${\xi }_{r}$ are derived in “Appendix”. Then, we apply the projection method to $r^{t+\frac{1}{2}}$, thus $r^{t+1} = {\mathcal {P}}_{{\mathcal {B}}_{r}}(r^{t+\frac{1}{2}})$.

Update of ${\mathbf {p}}^{t+1}$ Similar with $r^{t+1}$, we derive the Euler equation with respect to ${\mathbf {p}}^{t}=(p_{1}^{t},p_{2}^{t})$. For each $p_{1}^{t}$ and $p_{2}^{t}$, there are two discrete formulations as follows:

$$\begin{aligned}&\left( \theta _{1} - \theta _{0}\partial _{x}^{+}\partial _{x}^{-} - \frac{\theta _{0}}{2}\partial _{y}^{+}\partial _{y}^{-}\right) p_{1}^{t+1} - \frac{\theta _{0}}{2}\partial {y}^{+}\partial {x}^{-}p_{2}^{t+1} = h_{1},\nonumber \\ \end{aligned}$$

(23)

$$\begin{aligned}&\left( \theta _{1} - \frac{\theta _{0}}{2}\partial _{x}^{+}\partial _{x}^{-} - \theta _{0}\partial _{y}^{+}\partial _{y}^{-}\right) p_{2}^{t+1} - \frac{\theta _{0}}{2}\partial {y}^{+}\partial {x}^{-}p_{1}^{t+1} = h_{2}.\nonumber \\ \end{aligned}$$

(24)

where the differential operators in (23) and (24) can be found in “Appendix” and

$$\begin{aligned} h_{1}= & {} \theta _{1}(\partial _{x}^{+} r^{t+1} + {b}_{1}^{t} - {w}_{1}^{t})- \theta _{0}\partial _{x}^{+}({v}_{11}^{t} - {d}_{11}^{t})\\&- \theta _{0}\partial _{y}^{+}({v}_{3}^{t}-{d}_{3}^{t}),\\ h_{2}= & {} \theta _{1}(\partial _{y}^{+} r^{t+1} + {b}_{2}^{t} - {w}_{2}^{t})- \theta _{0}\partial _{y}^{+}({v}_{22}^{t} - {d}_{22}^{t})\\&- \theta _{0}\partial _{x}^{+}({v}_{3}^{t}-{d}_{3}^{t}), \end{aligned}$$

By applying the discrete Fourier transform ${\mathcal {F}}$ to both sides of (23) and (24), we get the following linear system

$$\begin{aligned} \begin{pmatrix} a_{11}&{}a_{12}\\ a_{21}&{}a_{22} \end{pmatrix} \begin{pmatrix} {\mathcal {F}}(p_{1}^{t+1})\\ {\mathcal {F}}(p_{2}^{t+1}) \end{pmatrix}= \begin{pmatrix} {\mathcal {F}}(h_{1})\\ {\mathcal {F}}(h_{2}) \end{pmatrix}, \end{aligned}$$

(25)

and easily obtain the analytical solution of $p_{1}^{t+1}$ and $p_{2}^{t+1}$ with discrete inverse Fourier transform ${\mathcal {F}}^{-1}$.

Update of ${\mathbf {w}}^{t+1}$ and ${\mathbf {v}}^{t+1}$ The subproblems for ${\mathbf {w}}$ and ${\mathbf {v}}$ in (20) have closed form solutions using shrink operator as follows:

$$\begin{aligned} {\mathbf {w}}^{t+1}= & {} \mathrm{shrink}\left( \nabla r^{t+1} - {\mathbf {p}}^{t+1} + {\mathbf {b}}^{t},\frac{c_{1}}{\theta _{1}}\right) , \end{aligned}$$

(26)

$$\begin{aligned} {\mathbf {v}}^{t+1}= & {} \mathrm{shrink}\left( {\mathcal {E}}({\mathbf {p}}^{t+1}) + {\mathbf {d}}^{t},\frac{c_{2}}{\theta _{0}}\right) , \end{aligned}$$

(27)

where the shrink operator is defined as

$$\begin{aligned} \mathrm{shrink}(s,t) = \frac{s}{|s|_{1}}\max (|s|_{1}-t,0). \end{aligned}$$

Update of ${\mathbf {b}}$ and ${\mathbf {d}}$ To enforce ${\mathbf {w}} = \nabla {r} - {\mathbf {p}}$ and ${\mathbf {v}} = {\mathcal {E}}({\mathbf {p}})$, both Bregman iterative parameters ${\mathbf {b}}^{t+1}$ and ${\mathbf {d}}^{t+1}$ are updated as follows:

$$\begin{aligned} \begin{aligned}&{\mathbf {b}}^{t+1} = {\mathbf {b}}^{t} + \nabla {r^{t+1}} - {\mathbf {p}}^{t+1} - {\mathbf {w}}^{t+1},\\&{\mathbf {d}}^{t+1} = {\mathbf {d}}^{t} + {\mathcal {E}}({\mathbf {p}}) - {\mathbf {v}}. \end{aligned} \end{aligned}$$

(28)

Finally, the split Bregman algorithm for r subproblem (20) is summarized in Algorithm 2.

4.2 Optimizing l of $\mathrm {(P2)}$

The subproblem of $\mathrm {(P2)}$ is rather simple since it is a quadratic optimization under the closed constraint ${\mathcal {B}}_{l}$. First, Euler equation is derived with respect to l as follows:

$$\begin{aligned} -c_{1} \Delta {l} + (c_{2} + c_{3})l = c_{2}(i - r^{k+1}), \end{aligned}$$

(29)

then solved efficiently by discrete Fourier transform ${\mathcal {F}}$ under the periodic boundary condition, which namely

$$\begin{aligned} l^{k+\frac{1}{2}} = {\mathfrak {R}}\Bigg ({\mathcal {F}}^{-1}\Bigg (\frac{{\mathcal {F}}(G_l)}{{\xi }_{l}}\Bigg )\Bigg ), \end{aligned}$$

where ${\mathcal {F}}(G_l)$ and ${\xi }_{l}$ are derived in “Appendix”. Finally, we apply the projection method to $l^{k+\frac{1}{2}}$, thus $l^{k+1} = {\mathcal {P}}_{{\mathcal {B}}_{l}}(l^{k+1})$.

The final estimated reflectance and illumination are obtained by $R = \exp (r)$ and $L = \exp {(l)}$, respectively. In the next section, the experimental results are presented to show the effectiveness of the proposed algorithm.

5 Experimental results and comparison

In this section, we compare the performance of our proposed model with several variational Retinex methods including VF [28], L1 [42], TVM [51], HoTVL1 [38] and WVM [14], the state-of-the-art HDR tone mapping method [19] and supervised deep learning-based method [70] and consider the decomposition problem on several classic test images including synthetic examples, natural images with low contrast or non-uniform lighting and medical images. All experiments are executed with MATLAB R2011b on a windows 7 platform with an Intel Corei7 at 3.2 GHz and 8 GB RAM.

For all tests, the recovered r of the VF method is obtained via $i-l$ since the reflection function of VF is not considered, and the recovered l of the L1 method is obtained via $i-r$. For fair comparison, the parameters are set to be optimal according to their papers. In our algorithm, we fixed $c_{3} = 1e^{-8}, \alpha _0 = 1, \alpha _1 = 0.5, \theta _0 = \theta _1 = 5$ and the stopping parameters $\epsilon _{1} = \epsilon _{2} = 5e^{-4}$. We use the HSV Retinex model for color images with constraint sets ${\mathcal {B}}_{r} = {\mathcal {B}}_{l} =[\log (1e^{-10}),0]$ and omit the logarithm and exponent process for gray images just as suggested in [50].

5.1 Synthetic images

We start with two different synthetic examples, shown in Figs. 3 and 4, respectively. In Fig. 3, we get the darker color image by changing luminance of the ground truth. In Fig. 4, we make a piecewise constant gray image r and a piecewise smooth gray image l, then get the simulated image i by summation of them, namely $i=r+l$.

Fig. 3

Synthetic example 1. a Ground truth. b Input darker image

Fig. 4

Synthetic example 2. a Synthetic reflectance image r; b synthetic illumination/shadow image l and c composed image $i = r + l$

Fig. 5

Decomposition comparison of synthetic example 1. First row: estimated reflectance images by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively. Second row: the spatial distribution of S-CIELAB errors between the ground truth and estimated reflectance components by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively. Third row: the histogram distribution of S-CIELAB errors between the ground truth and estimated reflectance components by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively. Numbers in bracket denote the maximum, average of the S-CIELAB and the proportion of pixels whose S-CIELAB error are $>10$ units, respectively

The decomposition results are shown in Figs. 5 and 6, respectively. To measure the accuracy of the estimated r, the S-CIELAB color metric [71] is adopted by drawing spatial locations and histogram distribution of errors. The first and second row in Fig. 5 shows the estimated reflectance and illumination results of different methods, respectively. The third row in Fig. 5 marks the pixels whose S-CIELAB errors between the ground truth and estimated reflectance of different methods are $>10$ units, and the last row shows the histogram distribution of S-CIELAB errors between the ground truth and the estimated reflectance of different methods. As can be seen from the spatial locations of the errors, the green area of our result is smaller than those of other five methods. From the histogram distribution of errors, it indicates our result achieves the lowest maximum and average S-CIELAB error in agreement with our empirical assessment. This example demonstrates that our proposed model can recover more accurate result in dealing with darker image. From Fig. 6, we can observe that TGVH1, L1 and HoTVL1 produce the better visual results than other methods, where the estimated r and l better approximate the ground truth in some properties. Intuitively, VF, WVM and TVM either take the illumination information as details of reflectance or lose many sharp features of reflectance, such as the edges of rectangles shown in Fig. 6.

Fig. 6

Decomposition comparison of synthetic example 2. First row: estimated reflectance images by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively. Second row: estimated illumination images by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively

Fig. 7

Natural images

For these two examples, we both set $c_{1} = c_{2} = 20$, and the constraint sets for the second example are ${\mathcal {B}}_{r} = {\mathcal {B}}_{l} =[0,255]$.

5.2 Natural image color correction

To demonstrate the performance of our proposed model on natural image color correction, three tests are done on natural images in Fig. 7, and the comparison results of different methods are presented in Figs. 8, 9 and 10.

Fig. 8

Decomposition comparison of natural example 1. First row: estimated reflectance images by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively. Second row: estimated illumination images by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively

Fig. 9

Decomposition comparison of natural example 2. First row: estimated reflectance images by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively. Second row: estimated illumination images by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively

Fig. 10

Decomposition comparison of natural example 3. First row: estimated reflectance images by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively. Second row: estimated illumination images by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively

In these three figures, we show the comparisons of different methods both on reflectance and illumination. One can observe that details of the high-contrast parts are more improved by using our proposed algorithm than other methods. The improved details include the wrinkle on the man’s face in Fig. 8, the tree leaves and the radiators behind flower leaves in Fig. 9, and the plants and characters in Fig. 10. The corresponding zoomed parts are shown with enlargements in red rectangles. Note that the TVM method always gives overenhanced reflectance with less details and adds the details to recovered illumination. L1 and HoTVL1 suffer from the loss of reflectance details and contrast due to the penalization on the magnitude of image gradient. As VF does not consider reflectance directly, so the $i-l$ always performs poorly, especially for low-contrast color images. WVM can estimate reflectance with finer details due to the modification of the weight in log-transform domain, but it is failed for some low-contrast color images, shown in Fig. 10. However, TGVH1 can successfully reveal reflectance with many details in shadows and illumination with smooth property, increasing the contrast simultaneously.

In addition, since the ground truth of the reflectance image is unknown, we utilize the natural image quality evaluator (NIQE) [48] to evaluate the results of different methods. A lower NIQE value represents a higher image quality and the best results are boldfaced, as shown in Table 1. It demonstrates that our method achieves a lower average than other methods, consistent with our empirical assessment that our method outputs the highest quality of reflectance images.

For the first two examples, we both set $c_{1} = c_{2} = 50$, and $c_{1} = c_{2} = 1$ for the third example.

5.3 Medical image bias field correction

Medical images such as MRI are always corrupted by bias fields due to non-uniform illuminations, so the correction of the bias field by removing the light effect caused by illumination is important for clinical diagnosis. Here, we test three brain MRI images in Fig. 11 and apply different models to recover a detail-preserved reflectance shown in Fig. 12. For fair comparison, we replace L1 by the smoothed L1 method [42] to recover many subtle details followed [42]. In the original MRI images (see in Fig. 11), there is apparent bias field effect at the neck area we hardly observe. In Fig. 12, from left to right are the results of six methods where tissues and vessels are significantly improved. It is obvious that the HoTVL1 method gets the piecewise constant results where some small details are lost, and the WVM method introduces some noises, especially in the black background.

Table 1 NIQE values of Figs. 8, 9 and  10

Fig. 11

Medical examples

Fig. 12

Comparison of Medical image bias field correction. First row: the results of view 1 by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively. Second row: the results of view 2 by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively. Third row: the results of view 3 by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively

Other methods produce good bias field corrections, especially for the details near the lower neck area and the edge of the MRI slice are significantly visible by TGVH1 with the suppression of noises in the background.

For these two examples, we both set $c_{1} = c_{2} = 0.5$, and the constraint sets for the these examples are all set to ${\mathcal {B}}_{r} = {\mathcal {B}}_{l}=[-255,0]$.

5.4 Shadow removal of color images

The final explanatory example is the removal of shadowed color images. Figure 13 gives two color images with different kinds of shadow, and the comparison results of different methods are shown in Figs. 14 and 15. Note that the L1 method can eliminate shadow effectively, but always recovers reflectance with big color difference, mainly due to the the value of one pixel fixed in solving a Poisson equation for the sake of a unique solution. VF, TVM and WVM can perform better for images with milder shadows, but fail to remove the adequate shadows shown in Fig. 15. The HoTVL1 and TGVH1 method can give visually accurate results where the shadow effect can be partially removed. Moreover, TGVH1 can simulate the shadows spread all over the whole image, including the shadow area of two signboards in Wall image.

Fig. 13

Color images for shadow removal

Fig. 14

Comparison of shadow removal on Text image. First row: estimated reflectance images by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively. Second row: estimated illumination images by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively

Fig. 15

Comparison of shadow removal on Wall image. First row: estimated reflectance images by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively. Second row: estimated illumination images by VF, L1, TVM, HoTVL1, WVM and proposed method, respectively

For the first example, we set $c_{1} = c_{2} = 50$, and $c_{1} = 0.1, c_{2} = 5$ for the second example.

5.5 Comparison with HDR tone mapping method

We compare our method with the state-of-the-art HDR tone mapping method JCAS [19] aimed to reproduce a low dynamic range (LDR) image with fine details and colors of the HDR counterpart. The source code is obtained from the original authors, and parameters are set following the paper. Figure 16 shows visual comparison on two natural images. It is easy to see that JCAS can recover most of the details in the HDR image, but the results are too overexposed and blurry, while our method generates higher quality reflectance with more details and faithful colors benefited from the edge-preserving property of TGV regularization.

5.6 Comparison with supervised deep learning-based method

We also compare our proposed method with Retinex-Net [70], which is the most state-of-the-art supervised deep learning-based method for low-light image enhancement built on Retinex theory, on real-scene images from public DICM [35] dataset collected 69 images with commercial digital cameras. We get all Retinex-Net’s results with the trained model provided by author. Figure 17 shows visual comparison on two natural images. As shown in each result, our method estimates the reflectance with more details without overexposure, especially for the objects buried in dark lightness, which benefits from the edge-preserving property of TGV regularization. In addition, our method is succeeded in suppressing noise in dark areas, while Retinex-Net contains so many noises. In other words, our proposed method outperforms Retinex-Net.

Fig. 16

Comparison with JCAS [19]

Fig. 17

Comparison with Retinex-Net [70]

We also evaluate the reflectance component of our method quantitatively on real-scene images from public DICM [35], Fusion [65], LIME [20], MEF [41] and NPE [66]. Table 2 shows the corresponding average NIQE values of the five datasets and demonstrates that our method has the lower NIQE value on natural images than Retinex-Net, which indicates that our model estimates the reflectance with high quality.

Table 2 Average NIQE values on several public datasets

5.7 Convergence

Since our energy function is locally convex with respect to r and l, it is effective to apply alternating minimization scheme to decrease the energy monotonically. However, it should be mentioned that it is difficult to prove the convergence of Algorithm 1 because of the bound box constraints on r and l. Furthermore, in real computations, we do not employ many inner loop iterations of Algorithm 2 and in the numerical tests, we set the max iterations as 5. Figure 18 shows the change of $\epsilon _{r}, \epsilon _{l}$ with the number of iterations on a $512\times 512$ image. From the error curve, it is clear that both errors drop severely during the optimization and asymptotically goes toward 0 with increasing number of iterations.

Fig. 18

Change of $\epsilon _{r}$ and $\epsilon _{l}$ with the number of iterations on a $512\times 512$ image

5.8 Parameters impact

We do some tests about the parameters impact on the proposed model (Eq. (12)). $c_{1}$ and $c_{2}$ are related to the regularization of illumination, and we found the algorithm is relatively stable when they are equal for most examples in our tests and the example is done with $c_{1} = c_{2} =50$ shown in Fig. 8. To test the impact of different parameters, respectively, we set both parameters to 1 and 5 to compare. As can be seen in Fig. 19, details of estimated reflectance are fuzzed since the penalty of illumination decreases as $c_{1}$ and $c_{2}$ decreases, leading to the estimated illumination with more details while reflectance with poor details. Conversely, we can get a detail-preserved reflectance and smooth illumination.

Fig. 19

Examples of parameters impact. First row: estimated reflectance images. Second row: estimated illumination images

5.9 Computational time

As an important factor of an algorithm, computational time of different methods is compared. Among the methods, the VF method is the fastest and the L1 method is the second since they both consider only one variable. The TVM and WVM methods are the third and fourth where both r and l are considered. HoTVL1 and our method both are time- consuming mainly because the former involves the second-order TV regularization and the latter involves TGV regularization. Specifically, our algorithm is a two-step alternating minimization scheme including r and l update, and the most time-consuming part is the r update which consists of three subproblems. For example, in Fig. 10 with image size $713\times 357$, it takes 7.6 s for the VF method, 9.5 s for the L1 method with 112 iterations, 71.3 s for the TVM method with 175 iterations, 466.5 s for the WVM method with 249 iterations, 920.1 s for the HoTVL1 method with 5342 iterations and 890.2 s for our method with 477 iterations. Since the experiments are performed by unoptimized MATLAB implementation, the computational time can be improved by C programming or trying other algorithms.

6 Conclusion

In this paper, we have presented a reflectance and illumination decomposition model for the Retinex problem via total generalized variation regularization and $H^{1}$ decomposition, which nicely separates the smoother global illumination from richly detailed reflectance. We proved the existence and uniqueness of the minimizers for the proposed model and provided an alternating minimization algorithm based on split Bregman iteration to handle the convex optimization under some constraints. Compared with state-of-the-art methods, the proposed algorithm performed effectively to capture more detailed structures or features of the reflectance and extract HVS preferable illumination for both inhomogeneous background removal and color shadow correction.

In the future, we hope to consider the decomposition problem on some low-quality images, such as severe noised, blurred images in low-light conditions. How to extend these techniques to the digital images of wall paintings which are captured in the dark conditions will also be a future work.

Appendix

In this appendix, we introduce detailed discretization of first-order and second-order differential operators using finite difference scheme.

The first-order forward and backward difference schemes are first given. Let $\Omega \rightarrow {\mathbb {R}}^{M\times N}$ denote the two-dimensional grayscale image space with size M and N. The coordinates x and y are oriented along columns and rows, respectively. So the first-order forward differences of u at point (i, j) along x and y directions are, respectively,

$$\begin{aligned} \partial _{x}^{+} u_{i,j}=\left\{ \begin{array}{ll} u_{i,j+1} - u_{i,j}&{} \mathrm{if} \ 1\le i \le M, 1 \le j < N,\\ u_{i,1} - u_{i,j}&{} \mathrm{if} \ 1 \le i \le M, j= N. \end{array}\right. \end{aligned}$$

$$\begin{aligned} \partial _{y}^{+}u_{i,j}=\left\{ \begin{array}{ll} u_{i+1,j} - u_{i,j}&{} \mathrm{if} \ 1\le i < M, 1 \le j \le N,\\ u_{1,j} - u_{i,j}&{} \mathrm{if} \ i = M, 1 \le j \le N. \end{array}\right. \end{aligned}$$

The first-order backward differences are, respectively,

$$\begin{aligned} \partial _{x}^{-} u_{i,j}=\left\{ \begin{array}{ll} u_{i,j} - u_{i,j-1}&{} \mathrm{if} \ 1\le i \le M, 1 < j \le N,\\ u_{i,j} - u_{i,N}&{} \mathrm{if} \ 1 \le i \le M, j= 1. \end{array}\right. \end{aligned}$$

$$\begin{aligned}\partial _{y}^{-} u_{i,j}=\left\{ \begin{array}{ll} u_{i,j} - u_{i-1,j}&{} \mathrm{if} \ 1< i \le M, 1 \le j \le N,\\ u_{i,j} - u_{M,j}&{} \mathrm{if} \ i = 1, 1\le j \le N. \end{array}\right. \end{aligned}$$

And the discrete second-order derivatives $\partial _{x}^{-}\partial _{x}^{+}u, \partial _{x}^{+}\partial _{x}^{-}u, \partial _{y}^{-}\partial _{y}^{+}u$ and $\partial _{y}^{+}\partial _{y}^{-}u$ at point (i, j) can be written by the corresponding compositions of the discrete first-order derivative, as follows

$$\begin{aligned} \begin{aligned} \partial _{x}^{+}\partial _{x}^{-} u_{i,j}&=\left\{ \begin{array}{ll} u_{i,N} - 2u_{i,j} + u_{i,j+1}&{} \mathrm{if} \ 1\le i\le M, j = 1,\\ u_{i,j-1} - 2u_{i,j} + u_{i,j+1}&{} \mathrm{if} \ 1\le i\le M, 1< j< N,\\ u_{i,j-1} - 2u_{i,j} + u_{i,1}&{} \mathrm{if} \ 1 \le i\le M, j = N. \end{array}\right. \\&=\partial _{x}^{-}\partial _{x}^{+} u_{i,j} \\ \partial _{y}^{+}\partial _{y}^{-} u_{i,j}&=\left\{ \begin{array}{ll} u_{M,j} - 2u_{i,j} + u_{i+1,j}&{} \mathrm{if} \ i = 1, 1\le j\le N,\\ u_{i-1,j} - 2u_{i,j} + u_{i+1,j}&{} \mathrm{if} \ 1< i< M, 1 \le j \le N,\\ u_{i-1,j} - 2u_{i,j} + u_{1,j}&{} \mathrm{if} \ i = M, 1 \le j\le N. \end{array}\right. \\&=\partial _{y}^{-}\partial _{y}^{+} u_{i,j} \end{aligned} \end{aligned}$$

Thus, the gradient, symmetrized derivative, divergence and Laplace can be discretized as follows, respectively:

$$\begin{aligned} \nabla u = \left( \partial _{x}^{+}u, \partial _{y}^{+}u \right) , \end{aligned}$$

(30)

$$\begin{aligned} {\mathcal {E}}({\mathbf {p}}) = \begin{pmatrix} \partial _{x}^{-} p_{1}&{}\frac{\partial _{y}^{-}p_{1} + \partial _{x}^{-}p_{2}}{2}\\ \frac{\partial _{y}^{-}p_{1} + \partial _{x}^{-}p_{2}}{2}&{} \partial _{y}^{-}p_{2}, \end{pmatrix} \end{aligned}$$

(31)

$$\begin{aligned} \mathrm {div}({\mathbf {p}}) = \partial _{x}^{-}p_{1} + \partial _{y}^{-}p_{2}, \end{aligned}$$

(32)

$$\begin{aligned} \Delta u_{i,j} = \mathrm {div}(\partial {u_{i,j}})=\partial _{x}^{-}\partial _{x}^{+}u_{i,j} + \partial _{y}^{-}\partial _{y}^{+}u_{i,j}. \end{aligned}$$

(33)

So the ${\mathcal {F}}(G_r)$ and ${\xi }_{r}$ in Eq. (22) can be written as

$$\begin{aligned} \begin{aligned} {\mathcal {F}}(G_r)&= \beta {\mathcal {F}}(i-l^{k}) - \theta _{1}{\mathcal {F}}\{\partial _{x}^{-}({w}_{1i,j}-b_{1i,j}) \\&\quad + \partial _{y}^{-}(w_{2i,j}-b_{2i,j})\}. \end{aligned} \end{aligned}$$

(34)

and

$$\begin{aligned} \begin{aligned} {\xi }_{r}&= \beta - \theta _{1}{\mathcal {F}}(\partial _{x}^{-}\partial _{x}^{+} + \partial _{y}^{-}\partial _{y}^{+}),\\&=\beta - 2\theta _{1}\left( \cos {\frac{2\pi n}{N} + \cos {\frac{2\pi m}{M}}}-2\right) . \end{aligned} \end{aligned}$$

(35)