1 Introduction

The development of new approaches and technologies in computer vision, also called artificial vision, can improve or complement human vision in several areas. Applications of computer vision are numerous, including recognition, object localization, 3D reconstruction, mobile robotics, and medical imaging. The reasons for using computer vision are the possibilities offered by computer science: speed of processing a large volume of information, reliability, and availability. What is of interest to us in this work is the use of computer vision for three-dimensional perception of the environment, also called 3D vision. The input data to be treated are images taken by cameras from different views. A 3D vision system is designed to extract the information of a three-dimensional nature; this requires the calibration of the cameras. The parameters of the cameras can be estimated by two major methods: calibration and self-calibration. In this paper, we are interested in the self-calibration methods that can calibrate the cameras without any prior knowledge about the scene. The standard process of most of these methods is to search for equations according to intrinsic parameters and the invariants in the images, whose aim generally is to solve a nonlinear equation system. The algorithm used to solve this system requires two steps, initialization and optimization of a cost function. Self-calibration of the cameras is the main step to obtain three-dimensional coordinates of points from matches between pairs of images. Several methods of camera self-calibration with constant intrinsic parameters [1–8] and those with varying intrinsic parameters [9–20] are treated in this area.

Problems in the field of camera self-calibration are usually related to the constraints of the camera self-calibration system (the number of images used, the characteristics of the cameras, and the type of scene). These constraints limit the majority of the methods described in the literature and entail many difficulties; for example, self-calibration with a large number of images provides more equations, and its resolution becomes more complicated and requires powerful algorithms, and, finally, the execution time to optimize the solution increases. The methods developed by the use of cameras with constant intrinsic parameters are limited in cases where cameras having varying intrinsic parameters are used. Moreover, the planar scenes rarely exist in nature, which shows the importance of using 3D scenes.

A new approach will be discussed in this paper. It is an approach of camera self-calibration having the varying intrinsic parameters by the use of an unknown three-dimensional scene. After the detection of control points in the images by the Susan approach [24] and the matching of these points in each pair of images by the correlation measure NCC [28], the fundamental matrix can be estimated from eight matches by the Ransac algorithm [22]. This matrix is used with the projection of two points of the 3D scene in images taken by different views in order to formulate linear equations. Solving these equations allows the estimation of the projection matrices. The determination of a relationship between the two points of the 3D scene and their projections in the planes of the images i and j and the relationships between the images of the absolute conic allow the formulation of a nonlinear cost function. The minimization of this function by the Levenberg–Marquart algorithm [23] allows the estimation of the intrinsic parameters of the cameras used.

This new approach has several advantages: the use of any camera (with varying intrinsic parameters), two images only are sufficient to estimate the cameras’ intrinsic parameters, and the use of an unknown 3D scene (more common in nature). These advantages allow us, on the one hand, to solve some problems mentioned in the previous paragraph and related to the self-calibration system and, on the other hand, to work freely in the domain of self-calibration with fewer constraints.

The remainder of this paper is organized as follows. The second part explains the related work. The third part presents the camera model. Camera self-calibration is explained in the fourth part. The experiment results are discussed in the fifth part, and the conclusions are presented in the sixth part.

2 Related work

This section presents a summary of some methods of cameras self-calibration. It starts with methods based on constant intrinsic parameters, and, in the third paragraph of this section, it moves to methods based on the varying intrinsic parameters. Several approaches have been discussed in the literature on constant parameters. A theoretical and practical method is presented in [1]; it is based on the projection of two circular points of an unknown planar scene in different images and the use of homographies between the images (at least five images) to estimate the unknown intrinsic parameters of cameras. The use of the Kruppa equations in [2] allows the estimation of the cameras’ parameters. These equations are obtained from information contained in the images taken by a camera, without any knowledge about its movement and the structure of the 3D scene used. The minimization of the nonlinear cost function [3] allows the estimation of the camera parameters. This function is formulated from a particular movement of the camera, “a translation and a small rotation,” and the estimation of the homography of the plane at infinity. The use of vanishing line is the main idea discussed in [4]. The solving of three linear equations formulated from the circles and their respective center allows determining the vanishing line. The camera’s intrinsic parameters are estimated from the theory of these lines and the circular points. A simple method is discussed in [5]. It is based on the calculation of the fundamental matrix (estimated from the matches between pairs of images) and the proposal of some constraints (the pixels are square, and principal point is in the image center) to estimate the focal length of two cameras. A method in [6] uses an unknown planar scene and parallelogram for camera self-calibration. The projection matrices are determined from the projection of the parallelogram vertices on the three images used. They are used with the relationship between the images of the absolute conic and the homographies between image pairs to formulate a nonlinear cost function. The resolution of this function allows estimating the camera’s intrinsic parameters. In [7], a new method is based on geometric constraints to estimate the intrinsic and extrinsic parameters of the camera. The use of geometric constraints on the first image provides the initial solution, and the minimization between the scene points and their projections in the image planes by exploiting geometric constraints on the two images allows optimizing the initial solution. The main idea presented in [8] is based on the use of an equilateral triangle. The projection of the triangle vertices in the planes of the three images allows obtaining the projections matrices. The resolution of a nonlinear cost function, which is formulated from homography matrices, projections, and the relationship between the images of the absolute conic, allows obtaining the intrinsic camera parameters.

Each method presented in the previous paragraph is based on a new idea, which is different from the ideas developed by other methods, but each method has specific advantages and disadvantages. For example, one of the disadvantages of the method presented in [1, 6], and [8] is the use of a planar scene. Moreover, the method [1] requires at least five images to calibrate the camera used. The weak point of the method [3] is the use of a simple rotation of the camera instead of using arbitrary rotations. Among the drawbacks of the method [5], there is the proposal of some constraints on the self-calibration system (the pixels are square, and the principal points are at the center of the images). In addition to that, all the methods presented in the previous paragraph are based on the self-calibration of camera with constant parameters. These methods are limited in cases where cameras having varying parameters are used.

This section presents some methods of camera self-calibration with varying intrinsic parameters. A theoretical and practical method is presented in [9]; it is based on the recovery of metric reconstruction from a set of images taken by cameras, and the absence of the skew factor is sufficient to estimate the intrinsic parameters of different cameras. The camera’s intrinsic parameters are estimated in [10] by simplifying the Kruppa equations by the singular value decomposition of the fundamental matrices and uncertainty related to these matrices. A method of camera self-calibration with varying and unknown focal length (other parameters are considered known) is treated in [11]. It is based on the complete derivation of critical motion sequences to estimate the focal lengths of different cameras. A new method of camera self-calibration with varying focal length is discussed in [12]. The intrinsic camera parameters and those related to the observed Euclidean structure are estimated from an image sequence of an object whose Euclidean structure is unknown, by solving a nonlinear cost function, but the initialization step of the focal length leads to some problems. To solve these problems, a new formulation of the cost function independently from the focal length is proposed. The use of a constant movement between images taken from different views of an object rotating around a single axis is the main idea discussed in [13]. A nonlinear cost function is defined from the relationship between the projection matrices and fundamental matrices (determined from the matched points), and its minimization provides the camera parameters. The idea discussed in [14] is based on the transformation of the image of the absolute dual quadric to get the camera parameters. The solution obtained from the estimation of elements of the dual absolute quadric is very sensitive to noise because these elements have a large difference of magnitude. To solve this problem, the authors propose a transformation to obtain the same magnitude for all these elements, and they show that the solution becomes more stable by this transformation. A new self-calibration method based on the relative distance is presented in [15]. A nonlinear cost function is defined from invariant relative distance and homography matrix (which transforms the projective reconstruction to the metric reconstruction), whose elements depend on the intrinsic camera parameters. Its minimization provides the camera parameters and the 3D structure of the scene. The idea discussed in [16] is based on the quasi-affine reconstruction; the camera intrinsic parameters are estimated after this reconstruction, which is performed from the homography matrix of the plane at infinity, and constraints on the image of the absolute conic. In [17], a method with a positive tri-prism is based on circular points. The coordinates of these points are determined from the properties of the positive tri-prism, and after determining the coordinates of the circular points in the images and the vanishing points of the tri-prism corners, the intrinsic camera parameters can be estimated linearly. A new multistage approach of low complexity is presented in [18]. The intrinsic camera parameters are obtained by deriving an optimization function, which is expressed according to these parameters, and the refinement of the estimated parameters is realized by a multistage algorithm. A method based on a circle is presented in [19]. The camera parameters are estimated from the use of at least four images. The projection of two points of the planar scene in different images allows estimating the four projection matrices. To obtain a nonlinear cost function, these matrices are exploited with the images of the absolute conic and homographies. The minimization of this function allows the estimation of the intrinsic parameters of the cameras used.

The advantage of the methods presented in the previous paragraph is the use of cameras characterized by varying parameters (the use of any cameras). However, each method has specific disadvantages. For example, in [9] the authors propose the absence of skew factor (=0). The authors of [11] assume that the principal point, the scale factor, and the skew factor are known. The method of [13] is based on a constant movement (and not a random one) of cameras when taking images. Therefore, it is limited in cases of any movement. The authors of the article [16] use some constraints on the image of the absolute conic. The method [18] requires at least four images to estimate the camera parameters.

A detailed study up to 2003 on methods of camera self-calibration with constant and varying intrinsic parameters is presented in [20].

3 Camera model

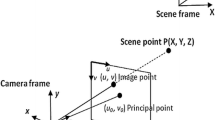
Figure 1 shows the pinhole model used in this work. This model projects the scene in the image planes; a 3×4 matrix characterizes this model; for the camera i, it is defined by M i (R i t i ) with a 3×4 matrix (R i t i ) containing extrinsic parameters R i , the rotation matrix, and t i , the translation vector of camera in space; M i  is a 3×3 matrix containing the intrinsic parameters and is expressed as follows:

$$ M_{i} = \left( \begin{array}{c@{\quad}c@{\quad}c} f_{i} & s_{i} & x_{0 i} \\ 0 & \varepsilon_{i} f_{i} & y_{0 i} \\ 0 & 0 & 1 \end{array} \right), $$
(1)

where f i is the focal length, ε i is the scale factor, s i is the skew factor, and (x 0i ,y 0i ) represent the coordinates of the principal point in the images.

Fig. 1
figure 1

Pinhole camera model

Full size image

The passage of the scene reference to the camera reference (Fig. 1) is made by the 3×4 matrix (R i t i ), and the passage of the camera reference to the image reference (Fig. 1) is performed by the 3×3 matrix M i . A point k of the image is the projection of a point K of the 3D scene. This projection is conducted by the following formula: k∼M i (R i t i )K, where ∼ indicates equality up to multiplication by a nonzero scale factor. (x y 1)T and (X Y Z 1)T are the homogeneous coordinates of the points k and K, respectively.

4 Camera self-calibration

4.1 Detection and matching of control points

Control points in the images can be detected by several methods [24–27]. This article uses the Susan algorithm [24].

The matching of control points is an important step to calibrate the cameras used. Several studies [28–30] are developed in this area. This approach uses the mapping by Normalized Cross Correlation NCC [28].

4.2 Estimation of the projection matrices

Let K 1 and K 2 denote the two points on the 3D scene. Considering a plane π that contains these two points, let us denote the Euclidean reference by \(\mathcal{R}(O\ X\ Y\ Z)\) such that the center O of the reference coincides with the midpoint of segment [K 1 K 2] and Z⊥π. The homogeneous coordinates of the two points K 1 and K 2 (Fig. 2) in the reference \(\mathcal{R}(O\ X\ Y)\) are given as follows:

$$K_{1} = (r\cos\emptyset, r\sin\emptyset, 1)^{T}\quad \mbox{and } $$
$$K_{2} = (-r\cos\emptyset, -r\sin\emptyset, 1)^{T} $$

where r=K 1 K 2/2, and ∅ is the angle between the line (K 1 K 2) and the x-axis (X).

Fig. 2
figure 2

The projection of the two points K 1 and K 2 in the planes of images i and j

Full size image

Considering two homographies H i and H j that can project the plane π in images i and j, therefore, the projection of the two points K 1 and K 2 can be given by the following expressions:

$$ k_{im} \sim H_{i} K_{m}, $$
(2)
$$ k_{jm} \sim H_{j} K_{m}, $$
(3)

where m=1,2 and k im ,k jm , respectively, represent the points in the images i and j that are the projections of the two vertices K 1 and K 2 of the 3D scene, and H n (n=i,j) represent the homography matrices that are expressed as follows:

$$ H_{n} \sim M_{n} R_{n} \left( \begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & \\ 0 & 1 & R_{n}^{T} t_{n} \\ 0 & 0 & \end{array} \right), \quad n=i,j. $$
(4)

Expressions (2) and (3) can be written as follows:

$$ k_{im} \sim H_{i} E K_{m} ', $$
(5)
$$ k_{jm} \sim H_{j} E K_{m} ', $$
(6)

where \(E= \left( \begin{array}{c@{\quad}c@{\quad}c} r\cos\emptyset& 0 & 0 \\ 0 & r\sin\emptyset& 0 \\ 0 & 0 & 1 \end{array} \right)\) and

$$K_{m} ' = \left( \begin{array}{c} q \\ q\ \\ 1 \end{array} \right) \quad \left\{ \begin{array}{l} m=1\quad \Leftrightarrow \quad q=1 \\ m=2\quad \Leftrightarrow \quad q=-1 \end{array} \right\}. $$

Let us represent the projection matrices by

$$ P_{n} \sim H_{n} E, \quad n=i, j, $$
(7)

where P i and P j represent the projection matrices of the two points \(K_{1} '\) and \(K_{2} '\) in images i and j (Fig. 2).

Formula (7) gives:

$$ P_{j} \sim H_{ij} P_{i}, $$
(8)

where

$$ H_{ij} \sim H_{j} H_{i}^{-1}; $$
(9)

H ij is the homography between the images i and j.

Expressions (5), (6), and (7) give:

$$ k_{im} \sim P_{i} K_{m} ', $$
(10)
$$ k_{jm} \sim P_{j} K_{m} '. $$
(11)

In addition, expressions (8) and (11) yield the following formula:

$$ k_{jm} \sim H_{ij} P_{i} K_{m} ', $$
(12)

and expression (12) leads to

$$ e_{j} ' k_{jm} \sim e_{j} ' H_{ij} P_{i} K_{m} '. $$
(13)

Knowing that \(F_{ij} \sim e_{j} ' H_{ij}\), where F ij is the fundamental matrix between the images i and j, it is estimated from eight matches between these images by the Ransac algorithm [22],

$$e_{j} ' = \left( \begin{array}{c@{\quad}c@{\quad}c} 0 & - e_{j3} & e_{j2} \\ e_{j3} & 0 & -e_{j1} \\ -e_{j2} & e_{j1} & 0 \end{array} \right) \quad\mbox{and} $$

e j =(e j1 e j2 e j3)T is the epipole of the image j, which is estimated from the fundamental matrix by the formula \(F_{ij}^{T} e_{j} =0\).

Therefore,

$$ e_{j} ' k_{jm} \sim F_{ij} P_{i} K_{m} '. $$
(14)

Expression (10) gives

$$ k_{i1} \sim P_{i} K_{1} ' $$
(15)

and

$$ k_{i2} \sim P_{i} K_{2} '. $$
(16)

Therefore, the latter two relations give four equations with eight unknowns, which are the P i elements.

Expression (14) gives:

$$ e_{j} ' k_{j1} \sim F_{ij} P_{i} K_{1} ' $$
(17)

and

$$ e_{j} ' k_{j2} \sim F_{ij} P_{i} K_{2} '. $$
(18)

Therefore, each of expressions (17) and (18) gives two equations with eight unknowns that are the P i elements.

Expressions (15), (16), (17), and (18) give eight equations with eight unknowns that are the P i elements (each of these expressions gives two equations with eight unknowns that are the P i elements).

So, the P i parameters can be estimated from these eight equations with eight unknowns.

Expression (8) gives

$$ e_{j} ' P_{j} \sim e_{j} ' H_{ij} P_{i}. $$
(19)

Therefore,

$$ e_{j} ' P_{j} \sim F_{ij} P_{i}. $$
(20)

The above expression gives eight equations with eight unknowns which are the P j elements. Therefore, the P j parameters can be estimated from these eight equations with eight unknowns.

4.3 Self-calibration equations

A nonlinear cost function will be defined in the main part of this work from the determination of the relationships between the images of the absolute conic (ω i and ω j ) and from the relationships between two points (K 1,K 2) of the 3D scene and their projections (k i1,k i2) and (k j1,k j2) in the planes of the images i and j, respectively. The different relationships are based on some techniques of projective geometry. The defined cost function will be minimized by the Levenberg-Marquart algorithm [23] to estimate the ω i and ω j elements and, finally, by the intrinsic parameters of the cameras used.

Expression (10) gives

$$ \lambda_{im} k_{im} = P_{i} K_{m} ', $$
(21)

where

$$P_{i} = \left( \begin{array}{c@{\quad}c@{\quad}c} P_{i11} & P_{i12} & P_{i13} \\ P_{i21} & P_{i22} & P_{i23} \\ P_{i31} & P_{i32} & P_{i33} \end{array} \right), \qquad k_{im} = \left( \begin{array}{l} x_{im} \\ y_{im} \\ 1 \end{array} \right), $$

and

$$\lambda_{im} =q P_{i31} +q P_{i32} + P_{i33}. $$

λ im is a nonzero scale factor that is used to switch from expression (10) to expression (21) (the transition between equality with a scale factor ∼ to precise equality =). The value of λ im is determined from expression (21).

Therefore, formula (21) leads to

$$ \lambda_{im} k_{im} ' = P_{i} K_{m}^{''}, $$
(22)

where

$$k_{im} ' = \left( \begin{array}{c@{\quad}c@{\quad}c} x_{im} & \frac{P_{i12}}{\lambda_{im}} & \frac{P_{i13}}{\lambda_{im}} \\ y_{im} & \frac{P_{i22}}{\lambda_{im}} & \frac{P_{i23}}{\lambda_{im}} \\ 1 & \frac{P_{i32}}{\lambda_{im}} & \frac{P_{i33}}{\lambda_{im}} \end{array} \right), \qquad K_{m}^{''} = \left( \begin{array}{c@{\quad}c@{\quad}c} q & 0 & 0 \\ q & 1 & 0 \\ 1 & 0 & 1 \end{array} \right). $$

Expression (22) gives

$$ P_{i} \sim k_{im} ' K_{m}^{''-1} $$
(23)

and the same for P j :

$$ P_{j} \sim k_{jm} ' K_{m}^{''-1}. $$
(24)

Expressions (4) and (7) give

$$ P_{n} \sim M_{n} R_{n} \left( \begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & \\ 0 & 1 & R_{n}^{T} t_{n} \\ 0 & 0 & \end{array} \right) E, \quad n=i,j. $$
(25)

The previous formula leads to

$$ M_{n}^{-1} P_{n} \sim R_{n} \left( \begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & \\ 0 & 1 & R_{n}^{T} t_{n} \\ 0 & 0 & \end{array} \right) E, \quad n=i,j. $$
(26)

Formula (26) gives

$$ P_{i}^{T} \omega_{i} P_{i} \sim \left( \begin{array}{c@{\quad}c} E^{'T} E ' & E^{'T} R_{i}^{T} t_{i} \\ t_{i}^{T} R_{i} E ' & t_{i}^{T} t_{i} \end{array} \right), $$
(27)

where \(\omega_{i} = ( M_{i} M_{i}^{T} )^{-1}\) is the image of the absolute conic, and

$$ E ' = \left( \begin{array}{c@{\quad}c} r\cos\emptyset& 0 \\ 0 & r\sin\emptyset \\ 0 & 0 \end{array} \right), $$
(28)

and the same for P j :

$$ P_{j}^{T} \omega_{j} P_{j} \sim \left( \begin{array}{c@{\quad}c} E^{'T} E ' & E^{'T} R_{j}^{T} t_{j} \\ t_{j}^{T} R_{j} E ' & t_{j}^{T} t_{j} \end{array} \right). $$
(29)

Expressions (23) and (27) give

$$ \begin{aligned}[b] &\bigl(k_{im} ' K_{m}^{''-1} \bigr)^{T} \omega_{i} \bigl(k_{im} ' K_{m}^{''-1} \bigr) \\ &\quad \sim\left( \begin{array}{c@{\quad}c} E^{'T} E ' & E^{'T} R_{i}^{T} t_{i} \\ t_{i}^{T} R_{i} E ' & t_{i}^{T} t_{i} \end{array} \right). \end{aligned} $$
(30)

The previous expression gives

$$ \begin{aligned}[b] &\bigl(k_{i1} ' K_{1}^{''-1} \bigr)^{T} \omega_{i} \bigl(k_{i1} ' K_{1}^{''-1} \bigr) \\ & \quad \sim \left( \begin{array}{c@{\quad}c} E^{'T} E ' & E^{'T} R_{i}^{T} t_{i} \\ t_{i}^{T} R_{i} E ' & t_{i}^{T} t_{i} \end{array} \right), \end{aligned} $$
(31)

And:

$$ \begin{aligned}[b] &\bigl(k_{i2} ' K_{2}^{''-1} \bigr)^{T} \omega_{i} \bigl(k_{i2} ' K_{2}^{''-1} \bigr) \\ &\quad \sim \left( \begin{array}{c@{\quad}c} E^{'T} E ' & E^{'T} R_{i}^{T} t_{i} \\ t_{i}^{T} R_{i} E ' & t_{i}^{T} t_{i} \end{array} \right) \end{aligned} $$
(32)

The expressions (31) and (32) give:

$$ \begin{aligned}[b] &\bigl(k_{i1} ' K_{1}^{''-1} \bigr)^{T} \omega_{i} \bigl(k_{i1} ' K_{1}^{''-1} \bigr) \\ &\quad \sim \bigl(k_{i2} ' K_{2}^{''-1} \bigr)^{T} \omega_{i} \bigl(k_{i2} ' K_{2}^{''-1} \bigr) \end{aligned} $$
(33)

Let

$$C= \left( \begin{array}{c@{\quad}c@{\quad}c} c_{11i} & c_{12i} & c_{13i} \\ c_{12i} & c_{22i} & c_{23i} \\ c_{13i} & c_{23i} & c_{33i} \end{array} \right) $$

denotes the matrix corresponding to \((k_{i1} ' K_{1}^{''-1} )^{T} \omega_{i} (k_{i1} ' K_{1}^{''-1} )\) and

$$D= \left( \begin{array}{c@{\quad}c@{\quad}c} d_{11i} & d_{12i} & d_{13i} \\ d_{12i} & d_{22i} & d_{23i} \\ d_{13i} & d_{23i} & d_{33i} \end{array} \right) $$

denotes the matrix corresponding to \((k_{i2} ' K_{2}^{''-1} )^{T} \omega_{i} (k_{i2} ' K_{2}^{''-1} )\).

Therefore, the formula (33) gives:

$$ \left\{ \begin{aligned} &c_{12i} =0, \qquad d_{12i} =0, \qquad\frac{d_{11i}}{d_{13i}} = \frac{c_{11i}}{c_{13i}} \\ &\frac{d_{13i}}{d_{22i}} = \frac{c_{13i}}{c_{22i}}, \qquad\frac{d_{22i}}{d_{23i}} = \frac{c_{22i}}{c_{23i}}, \qquad\frac{d_{23i}}{d_{33i}} = \frac{c_{23i}}{c_{33i}} \end{aligned} \right. $$
(34)

The previous expression gives:

$$ \left\{ \begin{aligned} &c_{12i} =0 \\ &d_{12i} =0 \\ &d_{11i} c_{13i} - c_{11i} d_{13i} =0 \\ &d_{13i} c_{22i} - c_{13i} d_{22i} =0 \\ &d_{22i} c_{23i} - c_{22i} d_{23i} =0 \\ &d_{23i} c_{33i} - c_{23i} d_{33i} =0 \end{aligned} \right. $$
(35)

The expressions (24) and (29) give:

$$ \begin{aligned}[b] &\bigl(k_{jm} ' K_{m}^{''-1} \bigr)^{T} \omega_{j} \bigl(k_{jm} ' K_{m}^{''-1} \bigr) \\ &\quad\sim \left( \begin{array}{c@{\quad}c} E^{'T} E ' & E^{'T} R_{j}^{T} t_{j} \\ t_{j}^{T} R_{j} E ' & t_{j}^{T} t_{j} \end{array} \right) \end{aligned} $$
(36)

The previous expression gives:

$$ \begin{aligned}[b] &\bigl(k_{j1} ' K_{1}^{''-1} \bigr)^{T} \omega_{j} \bigl(k_{j1} ' K_{1}^{''-1} \bigr) \\ &\quad\sim \left( \begin{array}{c@{\quad}c} E^{'T} E ' & E^{'T} R_{j}^{T} t_{j} \\ t_{j}^{T} R_{j} E ' & t_{j}^{T} t_{j} \end{array} \right), \end{aligned} $$
(37)

and

$$ \begin{aligned}[b] &\bigl(k_{j2} ' K_{2}^{''-1} \bigr)^{T} \omega_{j} \bigl(k_{j2} ' K_{2}^{''-1} \bigr) \\ &\quad \sim \left( \begin{array}{c@{\quad}c} E^{'T} E ' & E^{'T} R_{j}^{T} t_{j} \\ t_{j}^{T} R_{j} E ' & t_{j}^{T} t_{j} \end{array} \right). \end{aligned} $$
(38)

Expression (28) gives

$$ E^{'T} E ' = \left( \begin{array}{c@{\quad}c} r^{2} \cos^{2} \emptyset& 0 \\ 0 & r^{2} \sin^{2} \emptyset \end{array} \right). $$
(39)

Let

$$A= \left( \begin{array}{c@{\quad}c@{\quad}c} a_{11j} & a_{12j} & a_{13j} \\ a_{12j} & a_{22j} & a_{23j} \\ a_{13j} & a_{23j} & a_{33j} \end{array} \right) $$

denote the matrix corresponding to \((k_{j1} ' K_{1}^{''-1} )^{T} \omega_{j} (k_{j1} ' K_{1}^{''-1} )\).

Therefore, from formulas (37) and (39) we have

$$ a_{12j} =0. $$
(40)

Let

$$B= \left( \begin{array}{c@{\quad}c@{\quad}c} b_{11j} & b_{12j} & b_{13j} \\ b_{12j} & b_{22j} & b_{23j} \\ b_{13j} & b_{23j} & b_{33j} \end{array} \right) $$

denote the matrix corresponding to \((k_{j2} ' K_{2}^{''-1} )^{T} \omega_{j} (k_{j2} ' K_{2}^{''-1} )\).

Then, from the expressions (38) and (39) we get

$$ b_{12j} =0. $$
(41)

Equations (37) and (38) give

$$ \begin{aligned}[b] &\bigl(k_{j1} ' K_{1}^{''-1} \bigr)^{T} \omega_{j} \bigl(k_{j1} ' K_{1}^{''-1} \bigr) \\ &\quad{}\sim\bigl(k_{j2} ' K_{2}^{''-1} \bigr)^{T} \omega_{j} \bigl(k_{j2} ' K_{2}^{''-1} \bigr). \end{aligned} $$
(42)

The previous expression gives

$$ \left\{ \begin{aligned} &\frac{b_{11j}}{b_{13j}} = \frac{a_{11j}}{a_{13j}}, \qquad \frac{b_{13j}}{b_{22j}} = \frac{a_{13j}}{a_{22j}}, \\ &\frac{b_{22j}}{b_{23j}} = \frac{a_{22j}}{a_{23j}}, \qquad\frac{b_{23j}}{b_{33j}} = \frac{a_{23j}}{a_{33j}}. \end{aligned} \right. $$
(43)

Therefore, formulas (40), (41), and (43) give

$$ \left\{ \begin{aligned} &a_{12j} =0, \\ &b_{12j} =0, \\ &b_{11j} a_{13j} - a_{11j} b_{13j} =0, \\ &b_{13j} a_{22j} - a_{13j} b_{22j} =0, \\ &b_{22j} a_{23j} - a_{22j} b_{23j} =0, \\ &b_{23j} a_{33j} - a_{23j} b_{33j} =0. \end{aligned} \right. $$
(44)

Expressions (31) and (37) show that the first line and columns of the matrices \((k_{i1} ' K_{1}^{''-1} )^{T} \omega_{i} (k_{i1} ' K_{1}^{''-1} )\) and \((k_{j1} ' K_{1}^{''-1} )^{T} \omega_{j} (k_{j1} ' K_{1}^{''-1} )\) are identical, which gives

$$ \ \frac{c_{11i}}{c_{22i}} = \frac{a_{11 j}}{a_{22 j}}. $$
(45)

Therefore,

$$ c_{11i} a_{22j} - a_{11j} c_{22i} =0. $$
(46)

Expressions (32) and (38) show that the first line and columns of the matrices \((k_{i2} ' K_{2}^{''-1} )^{T} \omega_{i} (k_{i2} ' K_{2}^{''-1} )\) and \((k_{j2} ' K_{2}^{''-1} )^{T} \omega_{j} (k_{j2} ' K_{2}^{''-1} )\) are identical, which gives

$$ \ \frac{d_{11i}}{d_{22i}} = \frac{b_{11 j}}{b_{22 j}}. $$
(47)

Therefore,

$$ d_{11i} b_{22j} - b_{11j} d_{22i} =0. $$
(48)

Expressions (35), (44), (46), and (48) give a system of fourteen equations with ten unknowns that are expressed as follows:

$$ \left\{ \begin{aligned} &c_{12i} =0, \\ &d_{12i} =0, \\ &d_{11i} c_{13i} - c_{11i} d_{13i} =0, \\ &d_{13i} c_{22i} - c_{13i} d_{22i} =0, \\ &d_{22i} c_{23i} - c_{22i} d_{23i} =0, \\ &d_{23i} c_{33i} - c_{23i} d_{33i} =0, \\ &a_{12j} =0, \\ &b_{12j} =0, \\ &b_{11j} a_{13j} - a_{11j} b_{13j} =0, \\ &b_{13j} a_{22j} - a_{13j} b_{22j} =0, \\ &b_{22j} a_{23j} - a_{22j} b_{23j} =0, \\ &b_{23j} a_{33j} - a_{23j} b_{33j} =0, \\ &c_{11i} a_{22j} - a_{11j} c_{22i} =0, \\ &d_{11i} b_{22j} - b_{11j} d_{22i} =0. \end{aligned} \right. $$
(49)

The following nonlinear cost function will be minimized to solve the previous nonlinear equations:

$$ \begin{aligned}[b] &\min_{\omega i, j} \sum_{i=1}^{n-1} \sum_{j=i+1}^{n} \bigl( \Delta_{i}^{2} + \varGamma_{i}^{2} + \alpha_{i}^{2} + \beta_{i}^{2} + \gamma_{i}^{2} +\theta_{i}^{2} + \vartheta_{j}^{2} \\ &\quad{} + \zeta_{j}^{2} + \eta _{j}^{2} + \varphi_{j}^{2} +\rho_{j}^{2} + \psi_{j}^{2} + \chi_{ij}^{2} + \delta_{ij}^{2} \bigr), \end{aligned} $$
(50)

where Δ i =c 12i , Γ i =d 12i , α i =d 11i c 13i −c 11i d 13i ,

$$\beta_{i} = d_{13i} c_{22i} - c_{13i} d_{22i}, $$
$$\gamma_{i} = d_{22i} c_{23i} - c_{22i} d_{23i}, $$
$$\theta_{i} = d_{23i} c_{33i} - c_{23i} d_{33i}, \qquad \vartheta_{j} = a_{12j}, $$
$$\zeta_{j} = b_{12j}, \qquad \eta_{j} = b_{11j} a_{13j} - a_{11j} b_{13j}, $$
$$\varphi_{j} = b_{13j} a_{22j} - a_{13j} b_{22j}, $$
$$\rho_{j} = b_{22j} a_{23j} - a_{22j} b_{23j}, $$
$$\psi_{j} = b_{23j} a_{33j} - a_{23j} b_{33j}, $$
$$\chi_{ij} = c_{11i} a_{22j} - a_{11j} c_{22i}, $$
$$\delta_{ij} = d_{11i} b_{22j} - b_{11j} d_{22i}, $$

and n is the number of images.

The cost function (50) is minimized by using the algorithm in [23]. This algorithm requires an initialization step; therefore, the camera parameters are initialized as follows. Pixels are square; thus, ε i =ε j =1, s i =s j =0, the principal point is in the image center; therefore, x 0i =y 0i =x 0j =y 0j =256 (because the images used are of size 512×512), and focal lengths f i and f j are obtained by solving the system of equations (49) after the replacement of the parameters x 0i ,y 0i ,ε i,,s i ,x 0j ,y 0j ,ε j ,s j in this system.

5 Experiment results

5.1 Simulations

In this section, a sequence of twelve 512×512 images of a checkerboard pattern is simulated to test the performance and robustness of the present approach. After the detection of control points by the Susan algorithm [24], the matches between each pair of images are determined by the correlation function NCC [28]. The pattern is projected in images taken from different views with Gaussian noise of standard deviation σ, which is added to all image pixels. The projection of the pattern points in the image planes allows formulating the linear equations, and the solution of these equations gives the projection matrices. The determination of a relationship between the two points of the pattern and their projections in the images i and j and the relationships between images of the absolute conic can define a nonlinear cost function. The minimization of this function by the Levenberg–Marquart algorithm [23] allows estimating the intrinsic parameters of the cameras used.

Figure 3, given below, shows the relative errors on x 0 according to the number of images by the present method, the methods of Zhang [21], Wang [31], Jiang [16], and Triggs [1].

Fig. 3
figure 3

The relative errors of x 0 according to the number of images

Full size image

Figure 4, presented below, shows the relative errors on y 0 according to the number of images by the five methods.

Fig. 4
figure 4

The relative errors of y 0 according to the number of images

Full size image

Figure 5, presented below, shows the relative errors on f according to the number of images by the five methods.

Fig. 5
figure 5

The relative errors of f according to the number of images

Full size image

Figure 6, presented below, shows the relative errors of ε according to the number of images by the five methods.

Fig. 6
figure 6

The relative errors of ε according to the number of images

Full size image

Figure 7, presented below, shows, in the present method, the relative errors on the coordinates of the principal point, focal length, scale factor, and skew factor, according to the Gaussian noises∖sigma (standard deviation).

Fig. 7
figure 7

The relative errors of x 0,y 0,f,ε, and s according to Gaussian noises∖sigma (standard deviation)

Full size image

Figure 8, presented below, shows the execution time according to the number of images by the five methods.

Fig. 8
figure 8

The execution time according to the number of images

Full size image

A simple reading of Figs. 3, 4, 5, and 6 shows that the relative errors of the coordinates of the principal point, focal length, and scale factor calculated by the present method decrease almost linearly if the number of images is between two and six; they decrease slowly if the number of images is between six and eight; and they become almost stable if the number of images exceeds eight. Therefore, if the number of images increases, the relative errors decrease, which means that this method gives higher precision. But the mathematical calculations become somewhat complex, and, in practice, the execution time of the program becomes high because the increase in image number implies the increase of parameter number to be estimated, which implies the increase of the equation number, and which finally shows the increase of execution time. It is clearly seen in Fig. 8 because this figure shows that when the number of images increases, the execution time of the different methods increases, and finally it shows the effect of the use of a large image number.

A Gaussian noise with a standard deviation of 1 pixel (so that σ≤5 pixels) is added to all image pixels to show the performance and robustness of the present method. After calculating errors of the coordinates of the principal point, focal length, scale factor, skew factor, and their presentations (Fig. 7) according to noise, it may be concluded that the errors increase slowly if 0<σ≤3 pixels, but these errors increase quickly if σ exceeds three pixels. This shows that noise has little effect on this method if σ≤3 pixels; on the other hand, it has more influence if σ>3 pixels.

In order to show the performance and robustness of the algorithms presented in this paper, the simulation results are compared to those obtained by several efficient methods of Zhang [21], Wang [31], Jiang [16], and Triggs [1]. After reading the results obtained by these different methods (Figs. 3, 4, 5, and 6), it appears that the relative errors corresponding to the intrinsic parameters estimated by the present method are lower than those obtained by Triggs and Jiang, and they are closer to those calculated by Zhang and Wang. This shows that the present approach gives satisfactory results compared to the method presented by Triggs and Jiang, and it gives similar results to those obtained by the methods of Zhang and Wang. Furthermore, the method of Wang requires at least six images, and the method of Triggs requires at least five images to calibrate the camera. However, two images are sufficient to calibrate the cameras used by the present method.

5.2 Real data

This section deals with the experiment results of the different algorithms (Susan, NCC, Ransac, Levenberg–Marquardt, etc.) implemented by the Java object-oriented programming language. These experiments were conducted on eight 512×512 images of an unknown three-dimensional scene, taken by a CCD camera having varying intrinsic parameters. Two images (among eight) are shown in Fig. 9. The control points and the matches (obtained by the Ransac algorithm) between these two images are shown respectively in Figs. 10 and 11, and the intrinsic parameters estimated by three methods (the present method, Wang’s [31], and Jiang’s [16]) are shown in Table 1 below.

Fig. 9
figure 9

Two images of an unknown 3D scene

Full size image
Fig. 10
figure 10

The control points are shown in red in the two images

Full size image
Fig. 11
figure 11

The matches are shown and numbered in red in the two images

Full size image
Table 1 The results of the intrinsic camera parameters estimated by the three methods
Full size table

Figure 10 bellow shows the control points obtained by the Susan algorithm in the two images. 691 control points were detected in the first image, and 694 control points were detected in the second image.

The control points detected by de Susan algorithm are matched between two images by the correlation function NCC. The result obtained contains false matches. To eliminate them, the authors of this paper regularized all the matches by the Ransac algorithm. Figure 11 bellow shows the 132 matches obtained by this algorithm.

After comparing the results on the synthetic data, the results of the present approach on real data (the two images shown in Fig. 8 and the six other images) are compared to those obtained by Wang [31] and Jiang [16] on the same data. The reading and the analysis of the intrinsic camera parameters presented in Table 1 and those estimated in the four other images show that the results of the present approach are similar to those obtained by Wang, and they are a little different from those obtained by Jiang. Furthermore, the present approach is also compared with two other methods of Zhang [21] and Triggs [1]. The results of the present approach are almost identical to those obtained by Zhang, and they are a little different from those obtained by Triggs. Therefore, this approach provides a robust performance, and it is very close to the other well-established methods. In addition, this method has several advantages: the use of any camera, two images are sufficient to estimate the intrinsic camera parameters, and the use of an unknown 3D scene.

6 Conclusions

In this paper, a robust method of camera self-calibration by an unknown three-dimensional scene is presented. This new method is based on the determination of a relationship between two points in the 3D scene and their projections in the planes of the images i and j and between the relationships between the images of the absolute conic. These relationships give a nonlinear cost function, and the minimization of this function provides the intrinsic parameters of the cameras used. The positive points that characterize this approach are diverse. Among these, there are the use of any camera (with varying intrinsic parameters), a 3D scene, and sufficiency of two points of the scene and two images to achieve the camera’s self-calibration procedure. The robustness of this method in terms of simplicity, accuracy, stability, and convergence is shown by the results of the experiments and the simulations conducted.