1 Introduction

Fractures in geological porous media usually occur at different length scales with very complex geometry and treated as lower dimensional objects within the porous matrix. In addition to the complex geometry of the fracture network, high contrast in the physical properties and the scale discrepancy between the fractures and the matrix formation result in significant challenges for flow simulation. Therefore, it is very important to develop efficient numerical solution strategies for fractured formations.

Lots of models have been proposed in the literature for simulating fluid flow in fractured reservoirs. Among them, the most widely used approach is discrete fracture modeling (DFM), in which the fractures are represented explicitly as low-dimensional objects embedded within the matrix formation [1,2,3,4]. The complex geometry of the discrete fracture network is captured accurately using unstructured grid. The grid is generated with the constraint that the fracture segments lie at the interface of matrix elements. Although DFM approach is considered one of the most accurate methods to describe fluid flow through fractured porous media; however, its application at the field scale leads to large, heterogeneous, and anisotropic linear systems that exceeds the computational capability of available reservoir simulators. These important challenges motivate the need for development of efficient multiscale methods for flow simulation in heterogeneous fractured porous media.

Multiscale methods have been developed to provide a computationally efficient numerical solution for multiphase flow in large-scale heterogeneous porous media [5,6,7,8]. In the multiscale methods, the reduction in computational cost is achieved by dividing the global fine-scale problem into a set of smaller local problems which are solved separately. The approximate fine-scale solution is then constructed by assembling the solutions of small-size local problems. Among the proposed multiscale methods, the mixed multiscale finite-element (MMSFE) [9] and the multiscale finite volume (MSFV) [6, 10,11,12] methods provide locally conservative velocity fields, which is a crucial property for accurately solving the transport equations.

The first implementation of MSFV method in fractured porous media was developed for two-dimensional problems using a hierarchical fracture modeling approach, in which there exists one fracture basis function per network to add only one additional degree of freedom per connected fracture network in the matrix system [13]. The proposed method was efficient for highly conductive fractures. However, for test cases with high-pressure gradients inside fractures, further improvement is required. Later, a multiscale approach was developed for 2D reservoirs which coarse nodes are assigned at fracture intersections and dual coarse edges coincide with the fractures [14]. This method did not allow for independent coarse grids for fracture and matrix domains. An algebraic multiscale method with embedded discrete fractures (F-AMS) was developed on structured grids [15]. The F-AMS relies on primal and dual coarse grids for both the matrix and fracture networks to construct the multiscale prolongation and restriction operators. Afterward, a multiscale restricted smoothed basis method for fractured media (F-MsRSB) was developed [16] on unstructured grids in which basis functions for matrix and fractures are constructed by restricted smoothing. This method employs an embedded fracture modeling approach, in which the matrix and fractures are represented on independent grids. The first multiscale finite volume method for discrete fracture modeling on fully unstructured grids was developed in [17]. In this method, to enable error reduction, a convergent iterative strategy is extended, where MS-DFM is employed along with a fine-scale smoother to resolve low- and high-frequency modes in the error.

Although promising progress has been made in recent years [18,19,20], the literature is lacking a multiscale method which allows for flexible unstructured coarse grids inside the matrix and fractured networks. It is well known that multiscale methods suffer from non-monotonicity at highly heterogeneous permeability fields, resulting in numerical spurious oscillations in the pressure field. Note that none of previous methods allow reducing errors by adapting the coarse grid geometry to follow the fracture and matrix permeability features. Recently, an unstructured grid adaptation technique for multiscale finite volume method have been introduced for highly heterogeneous, but non- fractured, porous media [21].

The purpose of this paper is to develop an efficient method for generating multiscale unstructured grids that are tailored to the characteristics of heterogeneous fractured porous media. To this end, the MSFV method for the discrete fracture modeling approach is employed with adaptive unstructured coarse grids, such that the coarse grid geometries are optimized based on local variations of permeability in both matrix and fracture networks. Given two independent partitions of the fine-scale cells into primal coarse cells for the matrix and fractures, adaptive dual coarse grids are constructed based on local changes in permeability in each domain (matrix and fracture networks). Permeability-adapted coarse grids notably modify basis functions for challenging problems which is here shown to improve the monotonicity behavior of the MSFV method.

The accuracy of the proposed method is assessed through several challenging test cases including highly heterogeneous permeability field in both fractures and matrix domain. Numerical results show that the proposed method for generating flexible and adaptive unstructured coarse grids significantly improves the accuracy of the MSFV method for multiphase flow simulation in highly heterogeneous fractured porous media.

The paper is structured as follows. First, the DFM fine-scale discrete system is explained in Sect. 2. Then, algebraic description of the MSFV method for DFM is described in Sect. 3, along with adaptive unstructured grid generation technique. Numerical results are presented in Sect. 4. Finally, the paper is concluded in Sect. 5.

2 Discrete fracture modeling approach

The pressure equation for incompressible flow in fractured porous media, using Darcy's law, can be written as

$$-\nabla \bullet \left(\lambda \bullet \nabla p\right)=q,$$
(1)

where \(p\), \(\lambda\), and \(q\) represent pressure, mobility, and source term, respectively. This equation is solved for matrix and fracture pressures, \({p}^{m}\) and \({p}^{f}\), using discrete fracture modeling approach in which fractures are represented as low-dimensional objects embedded at the interfaces of matrix cells (Fig. 1).

Fig. 1
figure 1

Matrix and fracture cells in discrete fracture model

Full size image

The control volume finite-difference method is applied with two-point flux approximation based on the cell-center pressures for evaluation of the face fluxes

$${u}_{ij}={T}_{ij}\left({p}_{i}-{p}_{j}\right),$$
(2)

where \({p}_{i}\) and \({p}_{j}\) are the pressures in the neighboring cells and \({T}_{ij}\) is the face transmissibility, and is computed by the harmonic average of the half transmissibilities corresponding to the adjacent cells

$${T}_{ij}=\frac{{\alpha }_{i}{\alpha }_{j}}{{\alpha }_{i}+{\alpha }_{j}}.$$
(3)

The half transmissibility of cell \(i\) is defined as [1]

$${\alpha }_{i}=\frac{{A}_{i}{k}_{i}}{{D}_{i}}{\mathbf{n}}_{i}\bullet {\mathbf{f}}_{i}.$$
(4)

Here, \({A}_{i}\) is the face area, \({k}_{i}\) is the permeability assigned to the cell \(i\), \({D}_{i}\) is the distance from cell center to the face centroid, \({\mathbf{n}}_{i}\) is unit normal vector of the face, and \({\mathbf{f}}_{i}\) is the unit vector along the direction of the line joining the cell center to the face centroid.

Fracture cells are lower dimensional in the geometric grid, expanded by the aperture size in the computational domain. Therefore, the transmissibility between matrix and fracture cells can also be obtained by the general transmissibility formula in Eq. (3).

Small control volumes at fracture intersections adversely impact numerical stability. As shown in Fig. 2, the well-known star-delta transformation is used to eliminate intermediate cells at fracture intersections [1]. Then, the transmissibility between fracture cells with n connections can be calculated as

Fig. 2
figure 2

Star-delta transformation for transmissibility calculation

Full size image
$${T}_{ij}=\frac{{\alpha }_{i}{\alpha }_{j}}{{\sum }_{k=1}^{n}{\alpha }_{k}}.$$
(5)

The discretized form of the Eq. (1) for matrix and fractures is finally obtained as

$$\left[\begin{array}{cc}{A}^{mm}& {A}^{mf}\\ {A}^{fm}& {A}^{ff}\end{array}\right]\left[\begin{array}{c}{p}^{m}\\ {p}^{f}\end{array}\right]=\left[\begin{array}{c}{q}^{m}\\ {q}^{f}\end{array}\right],$$
(6)

where super-indices \(m\) and \(f\) are intended for the matrix and the fracture, respectively. The diagonal blocks indicate the matrix–matrix and fracture-fracture transmissibilities and off-diagonal blocks indicate matrix-fracture transmissibilities.

Solving the system of Eq. (6) for large-scale heterogeneous formations with complex fracture network is quite challenging. It is therefore of interest to develop more efficient solution strategies such as multiscale methods. In this paper, the multiscale finite volume method is applied with permeability-adapted unstructured grids to provide an efficient and accurate approximation of the flow in highly heterogeneous fractured porous media.

3 MSFV method for DFM with adaptive unstructured grids

The MSFV method aims to efficiently compute an approximate fine-scale solution while reducing the number of degrees of freedom. The method relies on a set of numerically computed functions which are local solutions of the flow problem computed on a coarse grid. Superposition of the local solutions is used to construct a coarse-scale system, which is computationally inexpensive to solve. The approximate fine-scale solution is then reconstructed based on the coarse-scale solution. In this section, first algebraic multiscale finite volume formulation extended for discrete fracture modeling is described. Then, efficient algorithms for generating adaptive unstructured coarse grids are presented.

3.1 MSFV formulation for fractured media

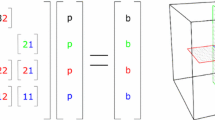
The multiscale finite volume method to approximate the solution of Eq. (6) employs a prolongation operator \(\mathbf{P}\) that maps the solution from coarse scale to fine scale. The approximate fine-scale solution \({p}_{ms}\) is obtained from the coarse-scale solution \({p}_{c}\) as

$$p\approx {p}_{ms}=\mathbf{P}{p}_{c},$$
(7)

where prolongation operator \(\mathbf{P}\) is constructed from locally computed basis functions. Note that \({p}_{ms}\) contains multiscale pressure approximations for the matrix and fractures at fine-scale,\({ p}_{ms}={\left[\begin{array}{cc}{p}_{ms}^{m}& {p}_{ms}^{f}\end{array}\right]}^{T}\), and \({p}_{c}\) contains coarse pressure solution for the matrix and fractures, \({p}_{c}={\left[\begin{array}{cc}{p}_{c}^{m}& {p}_{c}^{f}\end{array}\right]}^{T}\) [16]. To compute \({p}_{c}\), the following coarse-scale system is constructed and solved

$$\underbrace {{\left( {{\mathbf{R}}A{\mathbf{P}}} \right)p_{c} }}_{{A_{c} }} = \underbrace {{{\mathbf{R}}q}}_{{q_{c} }},$$
(8)

where \(\mathbf{R}\) is the restriction operator which maps the fine-scale system to the coarse scale, and can be obtained based on a finite volume scheme as integration over the coarse control volumes

$$\mathbf{R}\left(i,j\right)=\left\{\begin{array}{c}1, \mathrm{if fine cell} j \mathrm{belongs to coarse cell} i \\ 0,\mathrm{ otherwise}\end{array}.\right.$$
(9)

The prolongation operator \(\mathbf{P}\) is a matrix constructed by the basis function values, Φ, which are computed by solving localized flow problems on a dual coarse grid. The dual coarse grid is constructed in each domain (matrix and fracture) based on the wirebasket ordering [22, 23]. For 2D problem, the dual coarse grid divides the fine-scale matrix cells into three categories (interior, edge, and vertex) and the fine-scale fracture cells into two categories (edge and vertex). Vertices are the coarse grid nodes, the edge cells are the boundaries of the dual cells, and internal cells are those that lie inside dual coarse cells. To compute basis functions, first, the reduced problems along dual coarse cell boundaries (edge cells) are solved subject to Dirichlet condition at the coarse nodes. Then, the solutions of the reduced problems at the boundaries are used as Dirichlet condition for the interior cells of local problems.

The basis functions obtained from the above procedure are assembled in the columns of the prolongation operator \(\mathbf{P}\), with the column size of \({N}_{c}\) and the row size of \({N}_{f}\), where \({N}_{c}=\left({N}_{cm}+{N}_{cf}\right)\) and \({N}_{f}=\left({N}_{fm}+{N}_{ff}\right)\) are the total number of coarse and fine cells (including both matrix and fractures), respectively [14]. The prolongation operator can be written as

$$\mathbf{P}=\left[\begin{array}{c}{\mathbf{P}}^{m}\\ {\mathbf{P}}^{f}\end{array}\right]=\left[\begin{array}{cc}{\mathbf{P}}^{mm}& {\mathbf{P}}^{mf}\\ {\mathbf{P}}^{fm}& {\mathbf{P}}^{ff}\end{array}\right],$$
(10)

where the sub-block \({\mathbf{P}}^{m}\) which corresponds to the matrix fine cells defined as

$${\mathbf{P}}^{m}=\left[\begin{array}{ccc}\vdots & \cdots & \vdots \\ {\Phi }_{1}^{mm}& \cdots & {\Phi }_{{N}_{cm}}^{mm}\\ \vdots & \cdots & \vdots \end{array}\left|\begin{array}{ccc}\vdots & \cdots & \vdots \\ {\Phi }_{1}^{mf}& \cdots & {\Phi }_{{N}_{cf}}^{mf}\\ \vdots & \cdots & \vdots \end{array}\right.\right],$$
(11)

and the prolongation operator for fracture fine cells can be written as

$${\mathbf{P}}^{f}=\left[\begin{array}{ccc}\vdots & \cdots & \vdots \\ {\Phi }_{1}^{fm}& \cdots & {\Phi }_{{N}_{cm}}^{fm}\\ \vdots & \cdots & \vdots \end{array}\left|\begin{array}{ccc}\vdots & \cdots & \vdots \\ {\Phi }_{1}^{ff}& \cdots & {\Phi }_{{N}_{cf}}^{ff}\\ \vdots & \cdots & \vdots \end{array}\right.\right].$$
(12)

Here, \({\Phi }^{mm}\) and \({\Phi }^{mf}\) represent matrix–matrix and matrix-fracture coupling. Similarly, \({\Phi }^{ff}\) and \({\Phi }^{fm}\) represent fracture–fracture and fracture–matrix coupling.

Note that the prolongation operator described in Eq. (10) considers the two-way coupling between matrix and fractures that leads to more accurate solution. However, it can result in much denser prolongation operator and hence additional computational cost. In this paper, the effect of matrix coarse pressure in the fracture pressure interpolation is eliminated (\({\mathbf{P}}^{fm}=0\)), resulting in a sparser prolongation operator. Therefore, the fracture basis functions \({\Phi }^{ff}\) are computed subject to no-flow conditions at their connections with the matrix domain. Then, the multiscale pressure for the fractures at fine scale is obtained from the coarse-scale solution \(({p}_{c}^{f})\) via superposition of the computed fracture basis functions \(({\Phi }^{ff})\), that is

$${p}_{ms}^{f}=\sum_{i=1}^{{N}_{cf}}{\Phi }_{i}^{ff}{p}_{c,i}^{f}.$$
(13)

Since the present approach considers one-way coupling between matrix and fractures, the effect of matrix–fracture transmissibility \({(A}^{mf})\) is taken into account. Once fracture basis functions computed, the obtained values imposed as Dirichlet boundary conditions while solving \({\Phi }^{mf}\) basis functions. To account for the matrix basis functions \({\Phi }^{mm}\), \({\Phi }^{fm}=0\) is used as Dirichlet boundary conditions. This leads to the following multiscale superposition expression in the matrix domain:

$${p}_{ms}^{m}=\sum_{i=1}^{{N}_{cm}}{\Phi }_{i}^{mm}{p}_{c,i}^{m}+\sum_{i=1}^{{N}_{cf}}{\Phi }_{i}^{mf}{p}_{c,i}^{f}.$$
(14)

Illustration of fracture and matrix basis functions is presented in the following subsection, after describing adaptive unstructured coarse grid generation algorithms.

3.2 Adaptive unstructured coarse grids for DFM

The MSFV method employs two sets of overlapping coarse grids. The first one is the primal coarse grid where conservative coarse-scale system is constructed (restriction operator construction), and the second one is the dual coarse grid over which the basis functions are computed (prolongation operator construction). Implementation of MSFV method on unstructured grids requires more sophisticated strategies to construct primal and dual coarse grids. Although a limited amount of literature extended the MSFV on unstructured grids [17, 24, 25], they however have restrictions on intelligent generation of coarse grids which allows error reduction and quality improvement. It is known that multiscale methods are sensitive to heterogeneity contrasts. Previous studies shown that an iterative procedure is required to reduce error for highly heterogeneous porous media [26, 27]. Moreover, the high contrast in the physical properties of fractures and their complex geometries add more computational challenges. This motivated to develop an efficient method to construct adaptive unstructured coarse grids inside matrix and fracture domains, such that the accuracy of MSFV method can be significantly improved for flow simulation in highly heterogeneous fractured porous media. The following paragraphs describe the proposed procedure for construction of primal and dual coarse grids in a fracture porous media.

The primal coarse grid represents a coarse partitioning of the fine-scale grid which is constructed for the matrix and fracture domains independently. In this work, a grid partitioning method based on a multilevel tabu search algorithm is used to construct unstructured primal coarse grid [28]. The algorithm employs the equivalent graph of the unstructured grid in which vertices and edges of the graph refer to grid elements and their connectivity, respectively. The aim is to divide the set of vertices of the graph into a given number of partitions, such that each partition contains the same number of vertices and also the number of edges with endpoints in different partitions (cutting edges) is minimized.

The multilevel graph partitioning framework is used to handle large-scale graphs. In this framework, the original graph is recursively coarsened into a smaller graph by clustering vertices (coarsening phase). The next step is to partition the coarsest graph (initial partitioning phase). This step is followed by uncoarsening back to the original graph successively (uncoarsening phase). At each step of uncoarsening, tabu search algorithm is employed to improve the partitioning. Tabu search is a local search strategy with a flexible memory which uses a tabu list to prevent cycling and getting stuck in local optimum.

Given an initial partitioning of the graph into \(k\) subsets \(\left\{{S}_{1},{S}_{2},\dots ,{S}_{k}\right\}\). At each iteration of the algorithm, the subset with the maximum vertex weight is selected. Then, the vertex with the maximum gain is chosen for migration to the preferred subset (the subset with the highest gain vertex). The gain \(g(v,n)\) of vertex \(v\) for migration to the neighboring subset \({S}_{n}\) is defined as

$$g\left(v,n\right)=ED{\left[v\right]}_{n}-ID\left[v\right],$$
(15)

where \(ED{\left[v\right]}_{n}\) is the sum of common edge weights between vertex \(v\) and its neighboring vertices located in the subset \({S}_{n}\), and \(ID\left[v\right]\) is the sum of common edge weights between vertex v and its neighboring vertices in the same subset. To further explain the gain concept, a sample graph is illustrated in Fig. 3 which is partitioned into four subsets. The highlighted vertex in partition 2 has one internal neighbor and two external neighbors in partition 3. Therefore, the gain of moving this vertex to partition 3 is one. After moving each vertex, the gain of the vertex and its neighbors are updated. Also, information of the immigrated vertex is stored in the tabu list to avoid solution cycling. The algorithm continues until stopping criteria are met. The general scheme of the grid partitioning algorithm is presented in Alg. 1. More detailed explanations can be found in [29].

Fig. 3
figure 3

An example graph that is partitioned into four subsets. Highlighted vertex in partition 2 can move to partition 3 with the gain value of 1

Full size image
figure a

Figure 4 shows an example of primal coarse grids constructed by the proposed algorithm for the matrix and fractures domains. The fine-scale grid contains 10180 matrix and 196 fracture cells and the coarse-scale grid contains 10 matrix and 4 fracture primal coarse cells.

Fig. 4
figure 4

Primal coarse grids for (a) matrix domain and (b) fracture networks

Full size image

The dual coarse grid is constructed by connecting the coarse nodes which are defined corresponding to each of the primal coarse cells. By connecting the coarse nodes belonging to adjacent primal coarse cells, dual edge cells are generated. Fine-scale cells that are located inside dual coarse cells are considered as interior cells. Given that in DFM approach, fractures are considered as low-dimensional objects within the matrix domain, dual coarse cells in fracture domain do not include interior cells. Hence, fracture fine-scale cells are classified into coarse node and edge cells (for 2D problem). Figure 5 depicts dual coarse grids in matrix and fracture domains corresponding to the partitioning of Fig. 4.

Fig. 5
figure 5

Dual coarse grids defined on matrix (left) and fracture (right) domains

Full size image

Previous studies have used grid connectivity data and geometrical information to construct dual coarse grids in fractured porous media, and therefore, there is no ability to optimize coarse grid geometry to reduce errors and improve multiscale solution results. In this work, dual coarse grids in fracture and matrix domains are constructed based on physical properties that significantly improve the accuracy of MSFV method. The proposed algorithm is described as follows.

The proposed algorithm to construct dual coarse grid employs the equivalent graph of fine-scale unstructured grid. Therefore, this algorithm is applicable for any grid-type element as well as 3D problems. The first step in generation of dual coarse grid is to specify the coarse node inside each primal coarse cell. In the standard methods, the fine cell whose centroid is closest to the mean centroid of all cells in the primal coarse block is chosen as the coarse node. Previous research shows that the placement of coarse nodes in a low-permeability region causes non-physical oscillations. Therefore, the placement of coarse nodes in low-permeability region should be avoided, while standard methods have no control to move coarse node based on permeability field. On the other hand, since the fracture–matrix transmissibilities \({(A}^{fm})\) are not taken into account when constructing basis functions, if the matrix coarse node interface coincides with a fracture element or located close to it, the corresponding primal coarse cell is poorly influence by the matrix basis function. Figure 6 shows a comparison of matrix basis function for the case that matrix coarse node coincides with the fracture element (Fig. 6a) and the case that matrix coarse node is located away from the fracture element (Fig. 6b).

Fig. 6
figure 6

Comparison of matrix basis function for two matrix coarse node positions: (a) matrix coarse node coincides with the fracture element and (b) matrix coarse node is located away from the fracture element

Full size image

In the proposed algorithm, first, the mean centroid of all cells within the primal coarse block is calculated. Then, the fine cell closest to the mean centroid is chosen and its permeability value is checked. Also, a specific set of its neighbors is chosen and their permeability values are checked, as well. If the selected cell or one of its neighbors is located in a low-permeability region, it will be removed from the list of candidate cells. Then, the algorithm searches for the next fine cell that is closer to the mean centroid. This process continues until the closest cell to the mean centroid with acceptable permeability value is identified. Another criterion to be considered in fractured porous media is that fracture elements should not be placed at the matrix coarse node interface and its neighbors interface as well (due to one-way coupling between matrix and fractures). The set of neighbors is selected based on the number of neighbors layers considered around the coarse node. The number of neighbor layers for each coarse node is chosen based on the required accuracy and also, physical and geometrical limitations. The number of fine cells, permeability distribution, and the map of fractures inside each primal coarse block restrict the number of layers of neighbors. For example, for a primal coarse block with high density of fractures and high contrast in local permeability (the most challenging case), the number of neighbors is limited to satisfy both criteria, although these limited neighboring cells also have a significant effect on improving the solution. A coarse node with its three layers of neighbors in an equivalent graph is illustrated in Fig. 7.

Fig. 7
figure 7

Three layers of neighbors for a coarse node in an equivalent graph

Full size image

It should be noted that the location of coarse node in heterogeneous fracture media has a great impact on the accuracy of multiscale solution. To demonstrate the effect of coarse node location on the fracture basis function distribution, a heterogeneous fracture network is illustrated in Fig. 8. The position of coarse nodes based on standard method (geometric center) corresponding to six primal coarse cells is shown in Fig. 9a. As can be seen, coarse node 3 and coarse node 4 are located in low-permeability region. The fracture basis function resulting from coarse node 3 and coarse node 4 is shown in Fig. 9c, e, respectively. Note that fracture basis functions are restricted in low-permeability region. The position of coarse nodes 3 and 4 based on criteria described above is depicted in Fig. 9b. It can be observed that they are no longer located in low-permeability region, and therefore, their resulting fracture basis functions (Fig. 9d, f) are better distributed. Note that the fracture aperture is magnified for clarity.

Fig. 8
figure 8

A fracture network with heterogeneous permeability field

Full size image
Fig. 9
figure 9

Primal coarse cells and their corresponding coarse nodes for fracture network constructed based on (a) standard method (geometric center) and (b) adaptation rules. The fracture basis function resulting from coarse node 3 and coarse node 4 using standard and adapted grids (c–f)

Full size image

As the coarse nodes are identified, the next step is to specify the edge cells (dual coarse cell boundaries). Since reduced dimensional boundary conditions are imposed at dual cell boundaries (localization assumption [6]), the transmissibilities in direction normal to the boundaries (from edge to interior cells) are neglected, which is the source of error in the MSFV approximation. If there exist strong permeability contrasts along edge cells, the reduced problem boundary conditions lead to significant errors. To reduce the localization error in heterogeneous porous media, there should be no strong permeability contrast along edge cells. The presented algorithm identifies the edge cells based on local changes in permeability field.

The path of edge cells (dual cell boundaries) is constructed for each pair of neighboring primal coarse cells. To this end, first, for each vertex of the equivalent graph, the permeability value of the fine-scale cell corresponding to the vertex is defined. Then, a high threshold and a low threshold are considered for permeability and the vertices whose permeability values do not lie in threshold range are removed from the graph. To determine the path of edge cell between two neighboring coarse node, one of them is considered as the origin and the other as the target. Then, the distance between each two vertices \(i\) and \(j\) in the graph is calculated and assigned to the edges of the graph, \(T(i,j)\). Also, the distance of each vertex \(i\) to the origin is stored in its label, \(D(i)\), which initialize with infinity at first. All vertices of the graph marked as unvisited. The iteration starts by choosing the origin as the current vertex and the distance to it is set to zero. For the current vertex, the distances to all of its unvisited neighbors are calculated. This is done by determining the sum of the distance between an unvisited neighbor \(j\) and the value of the current vertex \((D\left(i\right)+T(i,j))\) and comparing to the current assigned value, \(D(j)\). If the newly calculated distance is less than the unvisited neighbor's current value, the neighbor is relabeled with the smaller one (\(D(j)\)=\(D\left(i\right)+T(i,j)\)). After updating the distances to each neighboring vertex, the current vertex is marked as visited and a neighbor with minimal distance (lowest label value) is selected as the current vertex. Also, the previous current vertex is considered as the current vertex's parents. Vertices which marked as visited are labeled with edge cells. The process continues until the target vertex is marked as visited. The path of edge cells is determined by following the vertex's parents from the target vertex up to the origin vertex. The process is summarized in Alg. 2.

figure b

For the primal coarse blocks coincide with the domain boundaries, the fine cell closest to the mean centroid of the boundary cells is considered as the target. Then, the described algorithm is implemented to construct additional edge cell paths that touch the boundary.

The proposed algorithm considers the conditions, such that the crossing of edge cell paths is avoided completely, and overlapping of edge cell paths is avoided as much as possible. After determining the path of edge cells between two neighboring coarse cells, the fine cells as second-layer and third-layer neighbors of edge cells are removed from the list of candidate fine cells to determine other edge cell paths. In this way, edge cell paths will not cross with each other. In unstructured grids, given that the number of neighboring primal coarse cells is greater than the number of coarse node interfaces, overlapping the paths around the coarse node is inevitable. Therefore, the fine cells around the coarse node are always considered as the candidate cells to determine edge cell paths.

Another important issue is that some of edge cells intersected by fracture elements are not influenced by any matrix coarse node basis functions. Especially for the case that all the edge cell paths of a dual coarse block are not influenced by matrix coarse nodes that results in basis functions have zero values in this area. It is clear that it is not possible to prevent intersection of fracture elements with the path of edge cells. However, in some cases which the path of edge cells intersected by fractures borders, edge cell paths can be moved away from fracture elements. This is applied in the presented algorithm by removing fine cells coincide with fracture borders from the list of candidate cells to determine edge cell paths. Figure 10 illustrates the sum of three matrix coarse node basis function for the case that all the edge cell paths of corresponding dual coarse block intersected by fractures that lead to zero-value basis functions in this area (Fig. 10a). The resulting basis functions after moving the path of edge cells are shown in Fig. 10b.

Fig. 10
figure 10

Comparison of the sum of three matrix coarse node basis functions for the case that (a) edge cell paths intersected by fracture elements, (b) edge cell paths moved away from fracture elements

Full size image

Finally, the interior cells are identified. All cells that do not belong to the edge and node (and face for 3D case) categories are obviously interior cells. However, to compute basis functions locally, the interior cells should be ordered according to the dual coarse blocks. A flood-fill algorithm is implemented to classify the interior cells based on dual coarse blocks. For each dual coarse block, the mean centroid of its coarse nodes is computed. Then, a fine cell that is closest to this point is identified and labeled as an interior cell of the dual block. All neighbors of this interior cell, which is not already categorized as edge cell, are labeled as the interior cells of the dual block. The neighbors to these interior cells are similarly checked until all the fine cells that belong to the dual coarse block are identified.

4 Numerical results

The aim of this section is to investigate the performance of the extended MSFV method with the proposed algorithms for challenging cases. Three test cases are considered: (1) a 2D reservoir with homogeneous permeability field for matrix and heterogeneous permeability field for fracture network, (2) a 2D reservoir with heterogeneous permeability field for matrix and homogeneous permeability field for fracture network, and (3) a 2D reservoir with heterogeneous permeability field for matrix and heterogeneous permeability field for fracture network. The reason for choosing these cases is that the MSFV method using standard coarse grids fails to predict their fine-scale solution accurately and efficiency of optimized unstructured coarse grids for these challenging problems is investigated. The MSFV solutions are compared with the fine-scale reference solutions computed by a fine-scale solver based on the preconditioned conjugate-gradient method.

4.1 Homogeneous matrix and heterogeneous fracture network

A 2D reservoir model in an 18 × 9 m2 domain is considered. The fracture network of this test case is depicted in Fig. 11. The matrix domain is homogeneous and is assigned \({k}_{m}=1\), while the fracture network is heterogeneous (Fig. 12). Dirichlet boundary conditions are applied on the left and right boundaries with normalized pressures of \({P}_{l}=1\) and \({P}_{r}=0\), respectively, and no-flow boundary conditions are specified on the top and bottom boundaries. The fine-scale grid contains 10,244 matrix and 352 fracture cells and the coarse-scale grid contains 12 matrix and 7 fracture primal coarse cells. Figures 13 and 14 present the primal and dual coarse grids in matrix and fracture domains, respectively, that are generated based on standard method in which only geometrical information is considered.

Fig. 11
figure 11

Illustration of the fracture network in a homogeneous matrix rock

Full size image
Fig. 12
figure 12

Fracture permeability

Full size image
Fig. 13
figure 13

Primal and dual coarse grids for the matrix domain generated by the standard method (only geometrical information is considered)

Full size image
Fig. 14
figure 14

Primal and dual coarse grids for the fracture network generated by standard method (only geometrical information is considered)

Full size image

The pressure contour plots obtained by the fine-scale and MSFV method in both of the matrix and the fracture domains are depicted in Fig. 15a, b, respectively. Here, the MSFV approximation based on standard coarse grids contains non-physical peaks. As can be seen in Fig. 14b, coarse node 1 and coarse node 5 in the fracture network are located in a low-permeability region. Also, some of the matrix coarse nodes are located close to the fracture elements (Fig. 13b). As a result, fracture and matrix basis functions are not computed properly. The discrete L2-norm of the pressure error is \({e}_{p}=0.46\).

Fig. 15
figure 15

Comparison of pressure contour plots obtained by the (a) fine-scale solution and (b) MSFV with standard grids and (c) MSFV with adapted coarse grids

Full size image

An adapted dual coarse grid in the matrix domain based on the proposed algorithm is illustrated in Fig. 16. As can be seen, matrix coarse nodes are located away from the fracture elements. Figure 17 shows the adapted dual coarse grid in the fracture domain. Dual coarse nodes 1 and 5 are moved to a higher permeability region. Figure 15c presents the MSFV solution using adapted coarse grids. The pressure error is \({e}_{p}=5.65\times {10}^{-2}\). It is clear that the MSFV method using adapted coarse grids in the matrix and fracture domain accurately captures the fine-scale reference solution. Figure 18 presents a comparison of the basis function of fracture critical coarse node 5 in the matrix domain for the case that the fracture coarse node position is specified based on the standard coarse grid (Fig. 18a) and adapted coarse grid (Fig. 18b). As can be seen, the placement of fracture coarse node in low-permeability region results in restricted basis functions in the matrix domain.

Fig. 16
figure 16

Comparison of the standard and adapted dual grids for the matrix domain (standard and adapted)

Full size image
Fig. 17
figure 17

Adapted dual coarse grid for fracture network

Full size image
Fig. 18
figure 18

The basis function of fracture coarse node 5 in the matrix domain, \({\Phi }_{5}^{mf}\), calculated based on (a) standard coarse grid and (b) adapted coarse grid

Full size image

4.2 Heterogeneous matrix and homogeneous fracture network

As the second test case, a channelized permeability field with high contrast is considered in the matrix domain. Figure 19 depicts the matrix permeability field that is extracted from the SPE10 bottom layer [30]. The fracture domain is homogeneous (\({k}_{f}=10000\)). The fine-scale grid and boundary conditions are the same as in case 4.1. The coarse-scale grid contains 12 matrix and 7 fracture primal coarse cells. Figures 20, 21, and 23a present the standard primal and dual coarse grids in the matrix and fracture domains, respectively, that are generated based on geometrical data.

Fig. 19
figure 19

Natural logarithm of matrix permeability field sampled from bottom layer of the Tarbet formation in the SPE10 dataset

Full size image
Fig. 20
figure 20

Primal coarse grid for the matrix domain generated using geometrical information

Full size image
Fig. 21
figure 21

Primal and dual coarse grids for the fracture network generated using geometrical data

Full size image

As can be seen in Fig. 23a, some of matrix coarse nodes lie in low-permeability regions. Also, strong permeability contrasts exist along some of matrix edge cell paths (dual coarse cell boundaries). Furthermore, some of the matrix coarse nodes are located close to the fracture elements. The pressure contour plots obtained by the fine-scale and MSFV method are illustrated in Figs. 22 and 23b, respectively. Similar to the previous test case, the MSFV approximation based on standard coarse grids fails to correctly capture the fine-scale reference solution (\({e}_{p}=0.52\)).

Fig. 22
figure 22

Fine-scale reference solution

Full size image
Fig. 23
figure 23

Comparison of the matrix dual coarse grid and the resulting pressure field for the standard and adaptive methods

Full size image

Figure 23c shows the dual coarse grid in the matrix domain adapted based on local changes in fine-scale permeability field. As can be seen in the figure, the matrix coarse nodes are no longer located in low-permeability regions. They are also located away from the fracture elements. Also, high permeability contrasts along edge cells are prevented as much as possible. The MSFV method using adapted coarse grids predicts the pressure solution with relative error \({e}_{p}=7.31\times {10}^{-2}\). The pressure contour plot obtained by the MSFV method is shown in Fig. 23d. The result shows that the pressure solution obtained by the MSFV method with adaptive coarse grids is in good agreement with those of fine-scale reference solution.

4.3 Heterogeneous matrix and heterogeneous fracture network

Finally, the performance of the presented algorithms is investigated for the most challenging test case, in which both matrix and fracture domains are heterogeneous. The matrix permeability field is the same as case 4.2, and the permeability of fracture network is considered as in case 4.1. The fine-scale grid and boundary conditions are same to the two previous cases. Also, the standard primal and dual coarse grids in the matrix and fracture domains are the same as Figs. 20, 21 and 23a. The pressure solution obtained by the fine-scale reference method and MSFV method based on standard coarse grids are depicted in Figs. 24 and 25a, respectively. It is clear that the MSFV solution based on standard coarse grids fails to capture the fine-scale reference solution for the reasons mentioned earlier: placement of matrix coarse nodes in low-permeability regions or close to fracture elements, strong permeability contrast along matrix edge cell paths, and placement of fracture coarse nodes in low-permeability regions. All these cases result in poor calculation of basis functions.

Fig. 24
figure 24

Fine-scale reference solution

Full size image
Fig. 25
figure 25

MSFV pressure solution with (a) standard grids and (b) adapted coarse grids

Full size image

The fine-scale reference solution can be recovered by adapting the coarse geometry based on local changes in permeability field in both matrix and fracture domains. The adapted dual coarse grid in the matrix domain is shown in Fig. 23c, and Fig. 26 depicts the adapted dual coarse grid in the fracture domain. The MSFV method using adapted coarse grids in the matrix and fracture domains predicts the pressure solution with relative error \({e}_{p}=6.29\times {10}^{-2}\) (Fig. 25b) which is in good agreement with the fine-scale reference solution. Figure 27 presents a comparison of the matrix basis function for the case that the coarse node position is specified based on the standard coarse grid (Fig. 27a) and adapted coarse grid (Fig. 27b). As can be seen, in the case where the matrix basis function is calculated based on the standard coarse grid, some of the edge cell paths are not influenced by the corresponding coarse node, while they are influenced by matrix coarse nodes in the adapted coarse grid. Furthermore, the basis function of the fracture coarse node 4 in the matrix domain for the case that the fracture coarse node position is specified based on the standard coarse grid and adapted coarse grid is shown in Figs. 28a, b, respectively. In the case that the fracture coarse node is located in a low-permeability region (standard coarse grid), the matrix domain is not influenced properly by the fracture basis function.

Fig. 26
figure 26

Adapted dual coarse grid in fracture domain

Full size image
Fig. 27
figure 27

Basis function of a matrix coarse node calculated based on (a) standard coarse grid and (b) adapted coarse grid

Full size image
Fig. 28
figure 28

The basis function of fracture coarse node 4 in the matrix domain,\({\Phi }_{4}^{mf}\), calculated based on (a) standard fracture coarse grid and (b) adapted fracture coarse grid

Full size image

5 Conclusion

In this paper, the dual-coarse-grid-based multiscale finite volume method for discrete fracture modeling on unstructured grids was developed. Efficient algorithms for generating adaptive multiscale unstructured grids were devised for accurate flow simulation through highly heterogeneous fractured porous media. Flexible unstructured coarse grids are constructed based on permeability features in both matrix and fracture networks. Permeability-adapted coarse grids can significantly modify basis functions for challenging problems, and as a result, the monotonicity behavior of the MSFV method is improved. The accuracy of the proposed algorithms for fractured porous media was assessed for several challenging test cases with highly heterogeneous permeability field in both fractures and matrix domain. Numerical results demonstrate that optimizing unstructured coarse grids based on characteristics of heterogeneous fractured porous media considerably reduced the MSFV errors induced by strong permeability contrasts in matrix and fracture networks. The proposed algorithms for generation of primal coarse grid and adaptive dual coarse grid are extensible to three-dimensional grids. The multilevel tabu search algorithm which is used to generate primal coarse grid employs the equivalent graph of unstructured grids. Adaptive dual coarse grid is generated based on Dijkstra’s routing algorithm which also employs the equivalent graph of fine-scale grid. Therefore, these algorithms are not affected by grid-type elements and grid dimensions. A more detailed discussion on the three-dimensional realistic models will be addressed in future research. Finally, it is concluded that the extended MSFV method with adapted unstructured coarse grids is an efficient and accurate approach for flow simulation in heterogeneous fractured porous media.