1 Introduction

During the past decades, various dynamic condensation techniques have been developed to create reduced-order models (ROMs) that have dynamic characteristics closely matching those of the full-order finite element (FE) model. This attractive possibility has led to the investigation of the applicability of ROMs in both the industry and academia. The application fields of dynamic condensation methods can be found in Refs [1,2,3,4,5]. In the field of structural health monitoring, the ROMs are fundamental for FE model updating [6, 7], optimal sensor placement [8, 9], and damage identification [4, 10, 11].

The strategy of dynamic condensation is to retain some degree-of-freedoms (DOFs) (called masters) and remove a much larger set of DOFs (called slaves), then to solve the eigenproblem of the ROM. The pivot task of dynamic condensation techniques is to generate a coordinate transformation matrix between the master set and the slave set, which can also be employed to expand measured data. Guyan’s method [12] is recognized as the most popular and longstanding condensation technique already embedded in commercial FE analysis software like ANSYS. Due to the complete neglect of inertia terms associated with the slave DOFs, Guyan’s method does not give a good approximation for high-order frequency modes. Kidder [13] and Miller [14] attempted to improve Guyan’s method by including the inertia effect. However, the approximate solution of the two schemes depended on the selection of an appropriate initial eigenvalue. Suarez and Singh [15] improved Guyan’s method by using an iterative process to update the transformation matrix. By adding the influence of the first-order inertia terms, O’Callahan [16] proposed an improved reduced system (IRS) method that yields better results than Guyan’s method. Friswell et al. [17] introduced an iterated IRS (IIRS) method that is an improvement of the original IRS. In their study, an iterative scheme was adopted to calculate the transformation matrix, and the convergence property of the IIRS method was also proved in [18]. Subsequently, some improvements to the IIRS method were made to accelerate its convergence property [19, 20]. In Ref. [20], the iterative order reduction (IOR) method can be considered as an improvement of the IIRS method where the transformation matrix is calculated by a more efficient iterative scheme. Yang [21] presented the Neumann series expansion-based model reduction (NSEMR) method that includes the first-order and second-order inertia items for deriving the dynamic condensation formula. Although a variety of dynamic condensation techniques have been constantly developed in the literature, the above-described methods have been widely used and accepted by the academic community.

In the field of structural damage identification, it is not practical and even impossible to measure the modal information of the monitored structure of all DOFs due to restrictions of practical measurement conditions and budget. In other words, the mode shape information of the damaged structure in real applications is spatially-incomplete with reference to the lower order modes. The spatially-incomplete measurement problem can be solved by either expanding the measured data to include the unmeasured parts or by reducing the size of the full FE model to the measured DOFs. In this regard, the dynamic condensation approach has been recognized as a more practical alternative to address the issue [22, 23]. Various research works have been done on the subject of structural damage identification using dynamic condensation techniques [9, 10, 22, 24,25,26,27,28,29,30,31,32,33]. It is worth noting that one of the most interesting findings required is to explore the comparative ability of various dynamic condensation techniques in the field. This comparative study can help researchers to choose an appropriate condensation technique for their specific problems.

In recent years, the damage identification approach based on FE model updating methods combined with dynamic condensation techniques has aroused the interest of many researchers. In the approach, a powerful global optimizer is used to update the FE model of the target structure, and then a dynamic condensation technique is adopted to condensate the FE model so that the size of the calculated data set closely matches the measured data set. The goal of the FE model updating process is to track the damage ratio of all elements in the target structure so that the discrepancy between the measured and simulated modal data becomes minimum. Selecting an efficient optimization solver as well as an appropriate condensation technique is a key issue in this approach. Several combinations of the two kinds of methods have been reported in the literature. For example, Kourehli et al. [34] presented a damage detection and estimation method for beam and 2D frame structures by utilizing the pattern search algorithm and Guyan’s method. Hosseinzadeh et al. [27] proposed a damage identification method based on democratic particle swarm optimization (DPSO) algorithm and Neumann series expansion-based first-order model reduction (NSEMR-I) method to detect and quantify damage in 2D truss and frame structures. Dinh-Cong et al. [31] introduced a combination of teaching–learning-based optimization (TLBO) algorithm and IRS method for damage identification in 2D frame structures. In the work of Hosseinzadeh et al. [35], a structural damage detection strategy was explored based on a hybrid optimizer (particle swarm optimization with colonial competitive algorithm) and Neumann series expansion-based second-order model reduction (NSEMR-II) method. More recently, Dinh-Cong et al. [9] proposed an effective approach for damage localization and quantification in the laminated beam and composite plate structures by using Jaya algorithm and IIRS method. For damage assessment of 2D truss, frame, and plate structures, Dinh-Cong et al. [11] suggested a combination of lightning attachment procedure optimization (LAPO) algorithm and IIRS method. Based on the brief literature survey, it is found that the aforementioned studies utilized stochastic search algorithms which usually require a high computational cost to converge to the actual global optimum. One of the ways to remedy this drawback is to create a hybrid stochastic/deterministic search algorithm, which will be considered in this current research. Besides, it is worthwhile to highlight that there is not any investigation on the performance of the approach for damage identification in structures made of functionally graded materials (FGM) or functionally graded carbon nanotube-reinforced composite (FG-CNTRC) materials, which are briefly described in the following paragraph.

FGM classified as a class of advanced heterogeneous composites are usually made of two or more components with material properties varied through non-uniform distribution of the predetermined direction. To date, FGM has found extensive applications in many engineering fields such as aerospace, military, mechanics, civil engineering, etc. Inspired by the concept of FGM, carbon nanotubes (CNT) or Carbon Nanotube-reinforced magneto-electro-elastic (CNTMEE) has come up with functionally graded distributions. Due to their typical properties, many investigations [36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51] have mainly focused on mechanical behaviors and performance of structures using these materials, which support engineers for the accurate design and analysis. But in the field of structural damage identification, there are very limited studies on damage diagnosis of FGM and FG-CNTRC structures.

Considering the above-mentioned research gaps, this article for the first time attempts to conduct a comparative study of various dynamic condensation techniques applied to multi-damage identification of FGM and FG-CNTRC plates. The major contributions of this research work are summarized as follows:

  • Investigating the capability of six typical dynamic condensation techniques, including Guyan’s method, Kidder’s method, NSEMR-II, IRS, IIRS, and IOR, to solve the eigenproblem for special composite plate structures made of FGM or FG-CNTRC materials.

  • Dealing with the spatially-incomplete measurement challenge by utilizing the dynamic condensation techniques and examining their implementation in the field of structural damage identification.

  • Proposing a hybrid global–local optimization strategy that combines Manta Ray Foraging Optimization (MRFO) algorithm [52] and Sequential Quadratic Programming (SQP) algorithm [53] which has not yet been tested for structural damage localization and quantification problems.

  • Exploring an effective and efficient optimization solver based on the hybrid MRFO–SQP algorithm combined with the IOR technique to localize and quantify multi-damage in the special composite plate structures using the first few incomplete modes with noise pollution.

The layout of this article is organized as follows. After the introduction, we briefly present the formulation of all the six dynamic condensation techniques in Sect. 2. In Sect. 3, the foundation of the optimization-based damage detection problem is first described, and then the hybrid MRFO–SQP algorithm is provided. In Sect. 4, we evaluate the performance of the condensation techniques for estimating the dynamic behavior of the monitored composite plate structures (a FGM plate and a FG-CNTRC plate) and discuss their implementation for multi-damage identification in these structures. Finally, several overall conclusions are withdrawn in Sect. 5.

2 Dynamic condensation techniques

In this section, the basic formulations of six commonly used condensation techniques will be reviewed. The six techniques are Guyan’s method, Kidder’s method, Neumann series expansion-based second-order model reduction (NSEMR-II) method, improved reduced system (IRS) method, iterated IRS (IIRS) method and iterative order reduction (IOR) method. It should be noted that throughout this section, subscripts ‘G’, “Kidder”, “NSEMR-II”, “IRS”, “IIRS” and “IOR” represent the items of Guyan’s method, Kidder’s method, NSEMR-II method, IRS method, IIRS method, and IOR method, respectively.

2.1 Guyan’s method

For a structural FE model with N DOFs, the free undamped vibration equation for the structural system can be described in the partitioned matrix equation as

$$\overbrace {{\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{kk} } & {{\mathbf{K}}_{kr} } \\ {{\mathbf{K}}_{rk} } & {{\mathbf{K}}_{rr} } \\ \end{array} } \right]}}^{{\mathbf{K}}}\overbrace {{\left\{ {\begin{array}{*{20}c} {\Phi_{k} } \\ {\Phi_{r} } \\ \end{array} } \right\}}}^{\Phi } = \lambda_{{}}^{{}} \overbrace {{\left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{kk} } & {{\mathbf{M}}_{kr} } \\ {{\mathbf{M}}_{rk} } & {{\mathbf{M}}_{rr} } \\ \end{array} } \right]}}^{{\mathbf{M}}}\overbrace {{\left\{ {\begin{array}{*{20}c} {\Phi_{k} } \\ {\Phi_{r} } \\ \end{array} } \right\}}}^{\Phi }$$
(1)

where \(\Phi\) and \(\lambda\) denote the eigenvectors and eigenvalues of the full-order FE model; K and M are, respectively, the global stiffness and mass matrices with the dimension of \((N \times N)\); the subscripts k and r, henceforth, denote the number of kept and reduced DOFs, and k + r = N.

From the second set of Eq. (1), the following relationship between the kept and reduced DOFs can be expressed as

$$\Phi_{r} = \left( {{\mathbf{K}}_{rr}^{{}} - \lambda_{{}}^{{}} {\mathbf{M}}_{rr} } \right)^{ - 1} \left( {\lambda_{{}}^{{}} {\mathbf{M}}_{rk} - {\mathbf{K}}_{rk}^{{}} } \right)\Phi_{k}$$
(2)

Using Neumann series expansion, the inverse of \(\left( {{\mathbf{K}}_{rr}^{{}} - \lambda_{{}}^{{}} {\mathbf{M}}_{rr} } \right)\) is approximately calculated as

$$\begin{aligned} \left( {{\mathbf{K}}_{rr}^{{}} - \lambda_{{}}^{{}} {\mathbf{M}}_{rr} } \right)^{ - 1} =& {\mathbf{K}}_{rr}^{ - 1} + \lambda_{{}}^{{}} {\mathbf{K}}_{rr}^{ - 1} {\mathbf{M}}_{rr} {\mathbf{K}}_{rr}^{ - 1} \\ &+ \lambda_{{}}^{2} {\mathbf{K}}_{rr}^{ - 1} {\mathbf{M}}_{rr} {\mathbf{K}}_{rr}^{ - 1} {\mathbf{M}}_{rr} {\mathbf{K}}_{rr}^{ - 1} + O(\lambda_{{}}^{3} ) + ... \end{aligned}$$
(3)

The commonly used Guyan reduction [12] neglects all the inertia terms of \(\lambda\) in Eq. (3), leading to

$$\left\{ {\begin{array}{*{20}c} {\Phi_{k} } \\ {\Phi_{r} } \\ \end{array} } \right\}\,\, = \left[ {\begin{array}{*{20}c} {\mathbf{I}} \\ { - {\mathbf{K}}_{rr}^{ - 1} \,{\mathbf{K}}_{rk} } \\ \end{array} } \right] = {\mathbf{T}}_{G} \Phi_{k}$$
(4)

in which \({\mathbf{T}}_{G}\) was named as Guyan’s transformation matrix between kept and reduced coordinates.

By substituting Eq. (4) into Eq. (1), per multiplication by \({\mathbf{T}}_{G}\), one can obtain a reduced eigenvalue problem as

$$\left( {{\mathbf{K}}_{R,G} \,\, + \lambda_{R,G}^{{}} {\mathbf{M}}_{R,G} } \right)\Phi_{R,G} = {\mathbf{0}}$$
(5)

where \(\lambda_{R,G}^{{}}\) and \(\Phi_{R,G}\) are, respectively, the approximated eigenvalue and approximated eigenvectors obtained by Guyan’s method. The reduced mass matrix \({\mathbf{M}}_{R,G}\) and stiffness matrix \({\mathbf{K}}_{R,G}\) are, respectively, given by

$${\mathbf{M}}_{R,G} = {\mathbf{T}}_{G}^{T} {\mathbf{MT}}_{G}^{{}} \,\,,\,\,\,\,\,{\mathbf{K}}_{R,G} \,\,\, = {\mathbf{T}}_{G}^{T} {\mathbf{KT}}_{G}^{{}}$$
(6)

There is no doubt that Guyan’s method is simple and cost-effective, and this has made its continued popularity in the industry. Nevertheless, the method does not give a good approximation for high-order eigenvalues owing to neglecting the inertia terms.

2.2 Kidder’s method

According to Ref. [13], Kidder improved Guyan’s method by only omitting the higher-order terms of \(\lambda\). Once two terms of the expansion in Eq. (3) are retained, Eq. (2) can be simplified to

$$\Phi_{r} = \left( {{\mathbf{K}}_{rr}^{ - 1} + \lambda_{{}}^{{}} {\mathbf{K}}_{rr}^{ - 1} {\mathbf{M}}_{rr} {\mathbf{K}}_{rr}^{ - 1} } \right)\left( {\lambda_{{}}^{{}} {\mathbf{M}}_{rk} - {\mathbf{K}}_{rk}^{{}} } \right)\Phi_{k}$$
(7)

As a consequence, a transformation matrix for Kidder’s method is approximated as

$$\left\{ {\begin{array}{*{20}c} {\Phi_{k} } \\ {\Phi_{r} } \\ \end{array} } \right\}\,\, = \left[ {\begin{array}{*{20}c} {\mathbf{I}} \\ {\left( {{\mathbf{K}}_{rr}^{ - 1} + \lambda_{{}}^{{}} {\mathbf{K}}_{rr}^{ - 1} {\mathbf{M}}_{rr} {\mathbf{K}}_{rr}^{ - 1} } \right)\left( {\lambda_{{}}^{{}} {\mathbf{M}}_{rk} - {\mathbf{K}}_{rk}^{{}} } \right)} \\ \end{array} } \right] = {\mathbf{T}}_{Kidder} \Phi_{k}$$
(8)

Accordingly, the reduced mass matrix \({\mathbf{M}}_{R,\,Kidder}\) and stiffness matrix \({\mathbf{K}}_{R,\,Kidder}\) in the Kidder’s method are obtained by

$${\mathbf{M}}_{R,\,Kidder} = {\mathbf{T}}_{Kidder}^{T} {\mathbf{MT}}_{Kidder}^{{}} \,\,,\,\,\,\,\,{\mathbf{K}}_{R,Kidder} \,\,\, = {\mathbf{T}}_{Kidder}^{T} {\mathbf{KT}}_{Kidder}^{{}}$$
(9)

It is apparent that Kidder’s method is more accurate than Guyan’s method when it retains the first-order term of the series in Eq. (3). However, Kidder’s method depends on the selection of an appropriate initial eigenvalue, which means that its high accuracy is preserved at a specific frequency and is far away from the initially selected eigenvalue.

2.3 Neumann series expansion-based second-order model reduction method

To consider the influence of inertia terms, Yang [21] presented the Neumann series expansion-based second-order model reduction (NSEMR-II) method that includes the first-order and second-order inertia items for deriving the condensation formula. The NSEMR-II method is briefly presented as follows:

With considering the terms \(\lambda \,\,\,and\,\,\,\lambda^{2}\) in Eq. (3), Eq. (2) becomes as

$$\begin{aligned} \Phi_{r} = &\left( {{\mathbf{K}}_{rr}^{ - 1} + \lambda_{{}}^{{}} {\mathbf{K}}_{rr}^{ - 1} {\mathbf{M}}_{rr} {\mathbf{K}}_{rr}^{ - 1} + \lambda_{{}}^{2} {\mathbf{K}}_{rr}^{ - 1} {\mathbf{M}}_{rr} {\mathbf{K}}_{rr}^{ - 1} {\mathbf{M}}_{rr} {\mathbf{K}}_{rr}^{ - 1} } \right)\\ &\left( {\lambda_{{}}^{{}} {\mathbf{M}}_{rk} - {\mathbf{K}}_{rk}^{{}} } \right)\Phi_{k} \end{aligned}$$
(10)

In structural FE analysis, the mass matrix is generally diagonalized because of utilizing lumped-mass idealization. This leads to \({\mathbf{M}}_{kr} = {\mathbf{M}}_{rk} = {\mathbf{0}}\). After doing some mathematical manipulation, the condensed stiffness matrix (\({\mathbf{K}}_{R,NSEMR - II}^{{}}\)) and condensed mass matrix (\({\mathbf{M}}_{R,NSEMR - II}\)) in the NSEMR-II method can be expressed as [21]

$$\begin{gathered} {\mathbf{K}}_{R,NSEMR - II}^{{}} \,\,\, = {\mathbf{T}}_{NSEMR}^{T} \,{\mathbf{K}}\,{\mathbf{T}}_{NSEMR}^{{}} \hfill \\ {\mathbf{M}}_{R,NSEMR - II} = {\mathbf{T}}_{NSEMR}^{T} \,{\mathbf{M}}\,{\mathbf{T}}_{NSEMR}^{{}} \hfill \\ \end{gathered}$$
(11)

where the transformation matrix \({\mathbf{T}}_{NSEMR}^{{}}\) of the NSEMR-II method is

$${\mathbf{T}}_{NSEMR} = \left[ {\begin{array}{*{20}c} {\mathbf{I}} \\ { - [{\mathbf{B}}_{1} + {\mathbf{K}}_{rr}^{ - 1} {\mathbf{M}}({\mathbf{A}}_{1} {\mathbf{A}}_{4} + {\mathbf{A}}_{1} {\mathbf{A}}_{5} )]^{ - 1} \,\,[{\mathbf{B}}_{1} + {\mathbf{K}}_{rr}^{ - 1} {\mathbf{M}}({\mathbf{A}}_{1} {\mathbf{A}}_{2} + {\mathbf{A}}_{1} {\mathbf{A}}_{3} )]} \\ \end{array} } \right]$$
(12)

with the following notations:

$$\begin{gathered} {\mathbf{A}}_{1} = {\mathbf{K}}_{rr}^{ - 1} {\mathbf{M}}_{rr} {\mathbf{K}}_{rr}^{ - 1} {\mathbf{K}}_{rk} {\mathbf{M}}_{kk}^{ - 1} \hfill \\ {\mathbf{A}}_{2} = {\mathbf{K}}_{kk} {\mathbf{M}}_{kk}^{ - 1} {\mathbf{K}}_{kk} \hfill \\ {\mathbf{A}}_{3} = {\mathbf{K}}_{kr} {\mathbf{M}}_{rr}^{ - 1} {\mathbf{K}}_{rk} \hfill \\ {\mathbf{A}}_{4} = {\mathbf{K}}_{kk} {\mathbf{M}}_{kk}^{ - 1} {\mathbf{K}}_{kr} \hfill \\ {\mathbf{A}}_{5} = {\mathbf{K}}_{kr} {\mathbf{M}}_{rr}^{ - 1} {\mathbf{K}}_{rr} \hfill \\ {\mathbf{B}}_{1}^{{}} = {\mathbf{I}} + {\mathbf{A}}_{1} {\mathbf{K}}_{kr} \hfill \\ {\mathbf{B}}_{2}^{{}} = {\mathbf{K}}_{rr}^{ - 1} {\mathbf{K}}_{rk} + {\mathbf{A}}_{1} {\mathbf{K}}_{kk} \hfill \\ \end{gathered}$$
(13)

2.4 Improved reduced system method

To produce a better approximation at the lower vibrating modes, O’Callahan [16] improved Guyan’s method through an improved reduced system (IRS) method which includes the inertia terms as pseudo-static forces. The method begins with Eq. (7) that can be rewritten as

$$\Phi_{r} = - {\mathbf{K}}_{rr}^{ - 1} {\mathbf{K}}_{rk}^{{}} \Phi_{k} + {\mathbf{K}}_{rr}^{ - 1} \left( {{\mathbf{M}}_{rk} \Phi_{k} + {\mathbf{M}}_{rr} \Phi_{k} } \right)\lambda_{{}}^{{}}$$
(14)

Then, by assuming a transformation matrix \({\mathbf{t}}\) between \(\Phi_{r}\) and \(\Phi_{k}\), one has

$$\Phi_{r} = {\mathbf{t}}\Phi_{k}$$
(15)

Accordingly, the substitution of Eqs. (15) into (14) and rearranging it yields

$${\mathbf{t}} = - {\mathbf{K}}_{rr}^{ - 1} {\mathbf{K}}_{rk}^{{}} + {\mathbf{K}}_{rr}^{ - 1} \left( {{\mathbf{M}}_{rk} + {\mathbf{M}}_{rr} {\mathbf{t}}} \right)\Phi_{k} \lambda_{{}}^{{}} \Phi_{k}^{ - 1}$$
(16)

For constructing the transformation matrix, the IRS method predicts the lowest k modes from Eq. (5) in Guyan’s method, which can be rewritten in the form of

$$\Phi_{k} \lambda_{{_{k} }}^{{}} \Phi_{k}^{ - 1} = {\mathbf{M}}_{R,G}^{ - 1} {\mathbf{K}}_{R,G}$$
(17)

Additionally, for the sake of simplification, the implicit function \({\mathbf{t}}\) in the right-hand side of Eq. (16) is replaced by \({\mathbf{t}}_{R,G}\)(\({\mathbf{t}}_{R,G} = - {\mathbf{K}}_{rr}^{ - 1} {\mathbf{K}}_{rk}^{{}} )\) in Guyan’s method. Eq. (16) is therefore expressed as

$${\mathbf{t}}_{IRS} = {\mathbf{t}}_{G} + {\mathbf{K}}_{rr}^{ - 1} \left( {{\mathbf{M}}_{rk} + {\mathbf{M}}_{rr} {\mathbf{t}}_{G} } \right){\mathbf{M}}_{R,G}^{ - 1} {\mathbf{K}}_{R,G}$$
(18)

Correspondingly, the transformation matrix for the IRS method becomes

$$\left\{ {\begin{array}{*{20}c} {\Phi_{m} } \\ {\Phi_{s} } \\ \end{array} } \right\} = \underbrace {{\left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{m} } \\ {{\mathbf{t}}_{IRS} } \\ \end{array} } \right]}}_{{{\mathbf{T}}_{IRS} }}\Phi_{m} = {\mathbf{T}}_{IRS} \Phi_{m}$$
(19)

From Eq. (19), we can get the reduced stiffness matrix \({\mathbf{K}}_{R,IRS}\) and reduced mass matrix \({\mathbf{M}}_{R,IRS}\) as

$$\begin{gathered} {\mathbf{K}}_{R,IRS} \,\,\, = {\mathbf{T}}_{IRS}^{T} {\mathbf{KT}}_{IRS}^{{}} \hfill \\ {\mathbf{M}}_{R,IRS} = {\mathbf{T}}_{IRS}^{T} {\mathbf{MT}}_{IRS}^{{}} \hfill \\ \end{gathered}$$
(20)

2.5 Iterated IRS method

To further enhance the accuracy of the IRS method, Friswell et al. [17] proposed an iterated IRS (IIRS) method and then proved its convergence in Ref. [18]. In their study, \({\mathbf{t}}_{IRS}\) in Eq. (18) is updated through an iterative process. Its iterative form is given as

$${\mathbf{t}}_{{_{IIRS} }}^{(n)} = {\mathbf{t}}_{G} + {\mathbf{K}}_{rr}^{ - 1} \left( {{\mathbf{M}}_{rk} + {\mathbf{M}}_{rr} {\mathbf{t}}_{{_{IIRS} }}^{(n - 1)} } \right)\left( {{\mathbf{M}}_{R,IIRS}^{n - 1} } \right)^{ - 1} {\mathbf{K}}_{R,IIRS}^{n - 1}$$
(21)

where

$${\mathbf{T}}_{{_{IIRS} }}^{(n)} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{m} } \\ {{\mathbf{t}}_{{_{IIRS} }}^{(n)} } \\ \end{array} } \right]$$
(22)
$$\begin{gathered} {\mathbf{K}}_{R,IIRS}^{(n)} \,\,\, = \left( {{\mathbf{T}}_{{_{IIRS} }}^{(n)} } \right)^{T} {\mathbf{KT}}_{{_{IIRS} }}^{(n)} \hfill \\ {\mathbf{M}}_{R,IIRS}^{(n)} = \left( {{\mathbf{T}}_{{_{IIRS} }}^{(n)} } \right)^{T} {\mathbf{MT}}_{{_{IIRS} }}^{(n)} \hfill \\ \end{gathered}$$
(23)

In Eqs. (21)–(23), the superscript ‘n’ denotes the nth iteration. Note that when n = 1, it is equivalent to Guyan’s method; and when n = 2, it turns out to be the IRS method.

2.6 Iterative order reduction method

As an effort to include all the inertia terms in Eq. (2), Xia and Lin [20] developed an iterative order reduction (IOR) method utilizing iterative forms of transformation and mass matrices which can converge faster than the Subspace Iteration method. The IOR method begins from Eq. (16) that is rewritten in the form

$${\mathbf{t}} = \underbrace {{ - {\mathbf{K}}_{rr}^{ - 1} {\mathbf{K}}_{rk}^{{}} }}_{{{\mathbf{t}}_{G} }} + \underbrace {{{\mathbf{K}}_{rr}^{ - 1} \left( {{\mathbf{M}}_{rk} + {\mathbf{M}}_{rr} {\mathbf{t}}} \right)\Phi_{k} \lambda_{{}}^{{}} \Phi_{k}^{ - 1} }}_{{{\mathbf{t}}_{d} }} = {\mathbf{t}}_{G} + {\mathbf{t}}_{d}$$
(24)

where the component \({\mathbf{t}}_{d}\) of the transformation matrix can be rewritten as

$${\mathbf{t}}_{d} = {\mathbf{K}}_{rr}^{ - 1} \left( {{\mathbf{M}}_{rk} + {\mathbf{M}}_{rr} {\mathbf{t}}} \right)\Phi_{k} \lambda_{{}}^{{}} \Phi_{k}^{ - 1} = {\mathbf{K}}_{rr}^{ - 1} \left( {{\mathbf{M}}_{rk} + {\mathbf{M}}_{rr} {\mathbf{t}}_{G} + {\mathbf{M}}_{rr} {\mathbf{t}}_{d} } \right)\Phi_{k} \lambda_{{}}^{{}} \Phi_{k}^{ - 1}$$
(25)

For the reduced system, the condensed stiffness and mass matrices are formed as

$$\begin{gathered} {\mathbf{K}}_{R} \,\,\, = {\mathbf{T}}_{{}}^{T} {\mathbf{KT}}_{{}}^{{}} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{k} } & {{\mathbf{t}}^{T} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{kk} } & {{\mathbf{K}}_{kr} } \\ {{\mathbf{K}}_{rs}^{{}} } & {{\mathbf{K}}_{rr} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{k} } \\ {\mathbf{t}} \\ \end{array} } \right] = {\mathbf{K}}_{kk} + {\mathbf{K}}_{kr} {\mathbf{t}} + {\mathbf{t}}^{T} \left( {{\mathbf{K}}_{rk}^{{}} + {\mathbf{K}}_{rr}^{{}} {\mathbf{t}}} \right) \hfill \\ {\mathbf{M}}_{R} = {\mathbf{T}}_{{}}^{T} {\mathbf{MT}}_{{}}^{{}} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{k} } & {{\mathbf{t}}^{T} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{kk} } & {{\mathbf{M}}_{kr} } \\ {{\mathbf{M}}_{rk}^{{}} } & {{\mathbf{M}}_{rr} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{k} } \\ {\mathbf{t}} \\ \end{array} } \right] = {\mathbf{M}}_{kk} + {\mathbf{M}}_{kr} {\mathbf{t}} + {\mathbf{t}}^{T} \left( {{\mathbf{M}}_{rk}^{{}} + {\mathbf{M}}_{rr}^{{}} {\mathbf{t}}} \right) \hfill \\ \end{gathered}$$
(26)

The reduced eigenvalue problem can be written in the form:

$$\begin{gathered} {\mathbf{K}}_{R} - \lambda_{{}}^{{}} {\mathbf{M}}_{R} = {\mathbf{K}}_{kk} + {\mathbf{K}}_{kr} \left( {{\mathbf{t}}_{G} + {\mathbf{t}}_{d} } \right) + \left( {{\mathbf{t}}_{G} + {\mathbf{t}}_{d} } \right)^{T} \left[ {{\mathbf{K}}_{rk}^{{}} + {\mathbf{K}}_{rr}^{{}} \left( {{\mathbf{t}}_{G} + {\mathbf{t}}_{d} } \right)} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \lambda_{{}}^{{}} \left[ {{\mathbf{M}}_{kk} + {\mathbf{M}}_{kr} \left( {{\mathbf{t}}_{G} + {\mathbf{t}}_{d} } \right) + \left( {{\mathbf{t}}_{G} + {\mathbf{t}}_{d} } \right)^{T} \left[ {{\mathbf{M}}_{rk}^{{}} + {\mathbf{M}}_{rr}^{{}} \left( {{\mathbf{t}}_{G} + {\mathbf{t}}_{d} } \right)} \right]} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \,{\mathbf{K}}_{R,G} - \lambda_{{}}^{{}} {\mathbf{M}}_{d} \hfill \\ \end{gathered}$$
(27)

where

$$\begin{gathered} {\mathbf{K}}_{R,G} = {\mathbf{K}}_{kk} + {\mathbf{K}}_{kr} {\mathbf{t}}_{G} \hfill \\ {\mathbf{M}}_{d} = {\mathbf{M}}_{kk} + {\mathbf{M}}_{kr} \left( {{\mathbf{t}}_{G} + {\mathbf{t}}_{d} } \right) + {\mathbf{t}}_{G}^{T} \left[ {{\mathbf{M}}_{rk}^{{}} + {\mathbf{M}}_{rr}^{{}} \left( {{\mathbf{t}}_{G} + {\mathbf{t}}_{d} } \right)} \right] = {\mathbf{M}}_{kk} + {\mathbf{M}}_{kr} \left( {\mathbf{t}} \right) + {\mathbf{t}}_{G}^{T} \left[ {{\mathbf{M}}_{rk}^{{}} + {\mathbf{M}}_{rr}^{{}} \left( {\mathbf{t}} \right)} \right] \hfill \\ \end{gathered}$$
(28)

Note that in Eq. (28), \({\mathbf{K}}_{R,G}\) is the reduced stiffness matrix of Guyan’s method. From Eq. (27), we can obtain the following form of a reduced eigenequation

$$\Phi_{k} \lambda_{{_{k} }}^{{}} \Phi_{k}^{ - 1} = {\mathbf{M}}_{d}^{ - 1} {\mathbf{K}}_{R,G}$$
(29)

Substituting Eq. (29) into Eq. (25), the transformation matrix of IOR method is expressed as

$${\mathbf{t}}_{IOR} = {\mathbf{t}}_{G} + {\mathbf{K}}_{rr}^{ - 1} ({\mathbf{M}}_{rk} + {\mathbf{M}}_{rr} {\mathbf{t}}_{G} + {\mathbf{M}}_{rr} {\mathbf{t}}_{d} ){\mathbf{M}}_{d}^{ - 1} {\mathbf{K}}_{R,G}$$
(30)

As can be seen in Eq. (30), \({\mathbf{K}}_{R,G}\) and \({\mathbf{t}}_{G}\) are constant, whereas \({\mathbf{M}}_{d}^{{}}\) and \({\mathbf{t}}_{d}\) need repeated calculations for updating of \({\mathbf{t}}_{IOR}\). The transformation matrix \({\mathbf{t}}_{IOR}\) is estimated by the following iterative process:

  • In the 1st iteration, the transformation matrix \({\mathbf{t}}_{IOR}^{(1)}\) and mass matrix \({\mathbf{M}}_{d}^{(1)}\) are

    $${\mathbf{t}}_{IOR}^{(1)} = {\mathbf{t}}_{G}$$
    (31)
    $${\mathbf{M}}_{d}^{(1)} = {\mathbf{M}}_{kk} + {\mathbf{M}}_{kr} {\mathbf{t}}_{G} + {\mathbf{t}}_{G}^{T} {\mathbf{M}}_{rk}^{{}} + {\mathbf{t}}_{G}^{T} {\mathbf{M}}_{rr}^{{}} {\mathbf{t}}_{G}$$
    (32)

  • In the kth iteration (k = 2, 3, …), the mass matrix \({\mathbf{M}}_{d}^{(k)}\) and transformation matrix \({\mathbf{t}}_{IOR}^{(k)}\) are

    $${\mathbf{M}}_{d}^{(k)} = \left[ {{\mathbf{M}}_{kk} + {\mathbf{M}}_{kr} {\mathbf{t}}^{(k)} } \right] + {\mathbf{t}}_{G}^{T} \left[ {{\mathbf{M}}_{rk}^{{}} + {\mathbf{M}}_{rr}^{{}} {\mathbf{t}}^{(k)} } \right]$$
    (33)
    $${\mathbf{t}}_{IOR}^{(k)} = {\mathbf{t}}_{G} + {\mathbf{K}}_{rr}^{ - 1} ({\mathbf{M}}_{rk}^{{}} + {\mathbf{M}}_{rr} {\mathbf{t}}^{(k - 1)} )\left( {{\mathbf{M}}_{d}^{(k - 1)} } \right)^{ - 1} {\mathbf{K}}_{R,G}$$
    (34)

Correspondingly, once the transformation matrix \({\mathbf{t}}_{IOR}^{(k)}\) is available, we can obtain the condensed stiffness matrix \({\mathbf{K}}_{R,IOR}^{(k)}\) and mass matrix \({\mathbf{M}}_{R,IOR}^{(k)}\) of the IOR method as shown in Eq. (26). The iterative process will be stopped at a given iteration needed to attain the accurate requirement.

3 Optimization-based damage detection of special composite plates

Optimization-based damage detection can be treated as an inverse optimization problem solved by using a powerful optimization algorithm. The optimization algorithm aims to minimize an objective function that represents the difference between the predicted and measured responses of monitored structures. The structural parameters (i.e. density, stiffness, and geometric dimensions) of the FE model assumed to be damaged are considered as the design variables of the optimization problem. To obtain the optimal solution to the problem, this study proposes a hybrid Manta Ray Foraging Optimization—Sequential Quadratic Programming (MRFO-SQP) algorithm. The detailed descriptions of the optimization problem and the hybrid MRFO-SQP algorithm are introduced in the following subsections.

3.1 Problem statement

The optimization-based damage detection method needs to be associated with an appropriate objective function based on modal characteristics with respect to the structural parameters. In this research, an effective combination of the model flexibility-based residual and Modal Assurance Criterion (MAC)-based residual proposed by Dinh-Cong et al. [54, 55] is adopted to express the distinction between the measured and simulated modal parameters. The combined objective function is defined as follows

$$\begin{gathered} {\text{Minimize}}:\,\,\,\,Obj{(}{\mathbf{x}}{)} = w_{1} \frac{1}{sc}\sum\limits_{n = 1}^{sc} {F_{n} {(}{\mathbf{x}}{)} + w_{2} \frac{1}{nmod}\sum\limits_{k = 1}^{nmod} {\left( {1 - \sqrt {MAC_{k} \left( {\mathbf{x}} \right)} } \right)} } \hfill \\ {\text{subject to:}}\left\{ {\begin{array}{*{20}c} {\left( {{\mathbf{K}} - \lambda {\mathbf{M}}} \right)\Phi = {\mathbf{0}}} \\ {0 \le {\mathbf{x}} \le 1\,,\,\,\,\left( {{\mathbf{x}} = x_{1} ,x_{2} ,...,x_{e} } \right)} \\ \end{array} } \right. \hfill \\ \end{gathered}$$
(35)

where w1 and w2 are the weighting factors to residuals; sc is the total number of columns of the flexible. matrix; nmod denotes the number of considered mode shapes; \(x_{e}\) represents the damage ratio of the eth elements; \(F_{n} {(}{\mathbf{x}}{)}\) and \(MAC_{k} \left( {\mathbf{x}} \right)\) are the two residuals calculated by

$$F_{n} {(}{\mathbf{x}}{)} = \left( {\frac{{\left\| {{\mathbf{F}}_{n}^{d} - {\mathbf{F}}_{n}^{{}} \left( {\mathbf{x}} \right)} \right\|_{Fro} }}{{\left\| {{\mathbf{F}}_{n}^{d} } \right\|_{Fro} }}} \right)^{2}$$
(36)
$$MAC_{k} \left( {\mathbf{x}} \right) = \frac{{\left| {\left( {{{\varvec{\Phi}}}_{k}^{d} } \right)^{T} {{\varvec{\Phi}}}_{k}^{{}} \left( {\mathbf{x}} \right)} \right|^{2} }}{{\left( {\left( {{{\varvec{\Phi}}}_{k}^{d} } \right)^{T} {{\varvec{\Phi}}}_{k}^{d} } \right)\left( {\left( {{{\varvec{\Phi}}}_{k}^{{}} \left( {\mathbf{x}} \right)} \right)^{T} {{\varvec{\Phi}}}_{k}^{{}} \left( {\mathbf{x}} \right)} \right)}}$$
(37)

in which \({\mathbf{F}}_{n}^{d}\) and \({\mathbf{F}}_{n}^{{}} \left( {\mathbf{x}} \right)\) are the nth column of the flexible matrices of the damaged and simulated structures, respectively; \(\left\| {\, \bullet \,} \right\|_{Fro}\) denotes the Frobenius norm of a matrix; \({{\varvec{\Phi}}}_{k}^{d}\) and \({{\varvec{\Phi}}}_{k}^{{}} \left( {\mathbf{x}} \right)\) are the kth mode shape vectors of the damaged and simulated structures, respectively.

3.2 The hybrid Manta Ray foraging optimization—sequential quadratic programming (MRFO-SQP) algorithm

For solving Eq. (35), a hybrid global–local optimization strategy composed of a Manta Ray Foraging Optimization (MRFO) algorithm followed by a Sequential Quadratic Programming (SQP) algorithm is proposed. The MRFO algorithm considered as the deterministic counterpart of the strategy is utilized for global exploration, while the SQP algorithm is used for the local searching process. Both the two algorithms are explained in brief in the next two subsections.

3.2.1 Manta ray foraging optimization algorithm

Manta Ray Foraging Optimization algorithm (MRFO) is a novel bio-inspired based meta-heuristic optimizer developed by Zhao et al. [52] in 2019. The MRFO algorithm mimics the food searching strategies of manta rays that include chaining, cyclone, and somersault in the ocean. The superior performance of MRFO over other optimization algorithms for solving different benchmark and engineering optimization problems have been investigated in Refs. [52, 56].

Similar to other meta-heuristic optimizers, the MRFO algorithm starts up with an initial population (\(X_{i,j}\)) that is randomly generated in the search domain as

$$X_{i,j} = X_{j}^{l} + rand * \left( {X_{j}^{u} - X_{j}^{l} } \right){, }\,\left( {i = 1,2,...,Np; \, \,j = 1,2,...,D} \right)$$
(38)

In Eq. (38), Np is the population size of manta rays and D is the number of design variables (the total number of elements of monitored structure). Each individual in the population set corresponds to a possible candidate solution for the optimization problem. From the initial population set, the best solution (\(X_{best,j}\)) is identified. After that, the updating process for the population in each generation is performed by chain foraging, cyclone foraging, and somersault foraging operators. The mathematical models of three foraging operators are briefly described as follows.

  • Chain foraging

Based on the best position \(X_{best,j} (t)\) and the position of the (i-1) current individual at the tth iteration (\(X_{i - 1,j} (t)\)), the position of manta rays at the (t + 1)th iteration is updated as

$$X_{i,j} (t + 1) = \left\{ {\begin{array}{*{20}c} {X_{i,j} (t) + rand\left[ {X_{best,j} (t) - X_{i,j} (t)} \right] + \alpha \left[ {X_{best,j} (t) - X_{i,j} (t)} \right],\,\,\,\,(i = 1;\,\,\,j = 1,\,2,...,D)} \\ {X_{i,j} (t) + rand\left[ {X_{i - 1,j} (t) - X_{i,j} (t)} \right] + \alpha \left[ {X_{best,j} (t) - X_{i,j} (t)} \right],\,\,\,\,(i = 2,3,...,Np;\,\,\,j = 1,\,2,...,D)} \\ \end{array} } \right.$$
(39)

where \(\alpha\), a weight coefficient, is chosen according to a random vector (\(r,\,\,r \in [0,\,\,1]\)) as

$$\alpha = 2r\sqrt {\left| {\log (r)} \right|}$$
(40)

  • Cyclone foraging

In this operator scheme, if \(\left( {{\raise0.7ex\hbox{$t$} \!\mathord{\left/ {\vphantom {t {T_{max} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${T_{max} }$}} < rand} \right)\)(where \(T_{max}\) is the total number of iterations), the current best position is selected as the reference point for updating their old positions. This can be expressed by the following equation

$$X_{i,j} (t + 1) = \left\{ {\begin{array}{*{20}c} {X_{best,j} (t) + r\left[ {X_{best,j} (t) - X_{i,j} (t)} \right] + \beta \left[ {X_{best,j} (t) - X_{i,j} (t)} \right],\,\,\,\,(i = 1;\,\,\,j = 1,\,2,...,D)} \\ {X_{best,j} (t) + r\left[ {X_{i - 1,j} (t) - X_{i,j} (t)} \right] + \beta \left[ {X_{best,j} (t) - X_{i,j} (t)} \right],\,\,\,\,(i = 2,3,...,Np;\,\,\,j = 1,\,2,...,D)} \\ \end{array} } \right.$$
(41)

where \(\beta\) is the weight coefficient that is defined as

$$\beta = 2e^{{r_{\,1} \frac{T - t + 1}{t}}} \sin (2\pi r_{\,1} )$$
(42)

with \(r_{\,1}\) is the random number within the range of [0,1]. Otherwise, each individual is updated to a new position that is far from the current best position, which aims to improve the exploration of the search space

$$X_{i,j} (t + 1) = \left\{ {\begin{array}{*{20}c} {X_{rand} + r\left[ {X_{rand} - X_{i,j} (t)} \right] + \beta \left[ {X_{rand} - X_{i,j} (t)} \right],\,\,\,\,(i = 1;\,\,\,j = 1,\,2,...,D)} \\ {X_{rand} + r\left[ {X_{i - 1,j} (t) - X_{i,j} (t)} \right] + \beta \left[ {X_{i - 1,j} (t) - X_{i,j} (t)} \right],,\,\,\,\,(i = 2,3,...,Np;\,\,\,j = 1,\,2,...,D)} \\ \end{array} } \right.$$
(43)

in which \(X_{rand}\), a randomly generated position can be represented by

$$X_{rand} = X_{j}^{l} + r\left( {X_{j}^{u} - X_{j}^{l} } \right){, }\,\left( {i = 1,2,...,Np; \, \,j = 1,2,...,D} \right)$$
(44)

  • Somersault foraging

At last, each individual is updated to an arbitrary new location located between the current location and its symmetrical location around the best location, which helps it approximate gradually to the optimal one. The mathematical formula of this operator is presented as

$$X_{i,j} (t + 1) = X_{i,j} (t) + SF\left[ {r_{\,2} X_{best,j} (t) - r_{\,3} X_{i,j} (t)} \right],\,\,\,\,(i = 2,3,...,Np;\,\,\,j = 1,\,2,...,D)$$
(45)

where \(r_{\,2}\) and \(r_{\,3}\) are two random numbers in [0, 1] and SF, the somersault factor, is set to be 2 in Ref. [52].

It should be noted that the updated solution in each operator is accepted if its fitness function is better than the old one. The MRFO algorithm will iterate the course of three foraging operators until the termination criterion is satisfied. As a summary, a flowchart of the MRFO algorithm is depicted in Fig. 1.

Fig. 1
figure 1

The flowchart of MRFO algorithm

Full size image

The MRFO algorithm having the ability in searching a large solution space is established based on the probability search operators, which may result in the inefficiency of local search. Accordingly, its combination with another deterministic algorithm will give better quality solutions and higher performance.

3.2.2 Sequential quadratic programming

The SQP search algorithm is regarded as one of the best non-linear programming methods for solving mathematical optimization problems having different inequality and equality constraints [53]. First, in the search algorithm, the Hessian matrix of the Lagrangian function using quasi-Newton method is approximately calculated in each iteration. Afterward, the approximate calculation is employed to generate a quadratic programming (QP) sub-problem. Finally, the solution QP sub-problem is utilized to form the search direction for linear search and the target function calculation is calculated. As a summary, Fig. 2 presents the flowchart of the SQP search algorithm.

Fig. 2
figure 2

The brief flowchart of SQP search algorithm

Full size image

Similar to other gradient-based optimization methods, a weakness of the SQP algorithm is the trend to be stuck in local optimal regions. The reason is that it depends on a suitable starting point in searching for the optimal result. For highly nonlinear problems with a large number of design variables, selecting that kind of point is highly difficult and risky. Therefore, the SQP algorithm is not utilized alone in this research work.

3.2.3 The hybrid MRFO-SQP algorithm

With regard to the utilization of the advantage of MRFO and SQP algorithms for minimizing the combined objective function (Eq. (35)), they are combined to form a hybrid global–local algorithm. Firstly, the MRFO algorithm is executed for global exploration to get a global near-optimal solution. Then, the optimal solution is set as the starting point of the SQP algorithm which is used as a local search to fine-tune the search space explored by the MRFO. In this way, the optimal results obtained from the hybrid MRFO- SQP algorithm is expected to give high-quality solutions and low computational time.

The practical steps of the hybrid MRFO-SQP algorithm can be summarized as follows:

(1) Set initial parameters for the MRFO optimization algorithm, and then run this algorithm until the given number of iterations is reached.

(2) Consider the best solution obtained from the MRFO as a starting point for the SQP search algorithm.

(3) Run the SQP to find the optimal solution to the damage identification problem.

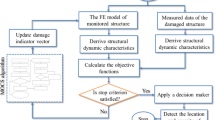
To better explain the above process, the flowchart of the hybrid MRFO-SQP algorithm to solve damage identification problems is depicted in Fig. 3. It should be mentioned here that in this kind of hybrid optimization algorithm, other gradient-based optimization schemes may also be used and tested.

Fig. 3
figure 3

The flowchart of the hybrid MRFO-SQP algorithm to solve damage identification problems considered in this study

Full size image

4 Numerical examples

The six typical dynamic condensation techniques (Guyan’s method, Kidder’s method, NSEMR-II, IRS, IIRS and IOR) and the proposed damage identification approach were presented in the previous sections. This section investigates the applicability of the condensation techniques for multi-damage identification of FGM and FG-CNTRC plates by simulating different damage scenarios. Damage characteristics of the plate structures are represented by a local reduction of the stiffness of selected members. To simulate realistic conditions, the artificial random noise is added to the simulated experimental data using the following equation

$${{data}}_{{}}^{{\,{{noise}}}} = {{data}}\left( {1 + (2{{rand}} - 1)\eta } \right)$$
(46)

where \({{data}}_{{}}^{{\,{{noise}}}}\) are the components of the eigenvectors or eigenvalues matrices contaminated by noise; and \(\eta\) is the level of the additive noise. While the natural frequencies are polluted by 1% noise, the spatially-incomplete mode shapes by 8% noise.

It is noted that for both the IIRS and IOR techniques, five iterations are needed to obtain the eigensolutions for the plate structures. Moreover, considering the random nature of noise, 10 independent runs are performed for each damage detection problem, and the average results of the runs will be reported as the final result in graphical forms. The parameter settings used in the MRFO algorithm are adopted as follows: Np is set to 30; \(T_{{{\text{max}}}}\) is set to 10 for the FGM plate and 15 for the FG-CNTRC plate; SF is set to 2. While the SQP search algorithm is implemented using MatLab optimization toolbox. Matlab program is used in all numerical computations executed on a PC (Intel® Core (TM) i7-6700, 3.40 GHz CPU, 16 GB RAM).

4.1 A FGM plate

In the first example, we consider a cantilevered FGM plate made of a mixture of aluminum (Al) (as metal) and alumina (Al2O3) (as ceramic) [57], the material properties vary continuously in the plate thickness direction in accordance with a power-law distribution as

$$\begin{gathered} E(z) = \left( {E_{c} - E_{m} } \right)V_{f} (z) + E_{m} \hfill \\ \rho (z) = \left( {\rho_{c} - \rho_{m} } \right)V_{f} (z) + \rho_{m} \hfill \\ \end{gathered}$$
(47)

where the subscripts “c” and “m” denote the ceramic and metal constituents; \(V_{f}\) is the volume fraction of the constituents that is calculated based on the power-law index n as follows

$$V_{f} (z) = \left( {{\raise0.7ex\hbox{$z$} \!\mathord{\left/ {\vphantom {z h}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$h$}} + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)^{n}$$
(48)

The mechanical properties of the constituent materials (Al and Al2O3) used in the FGM plate are tabulated in Table 1. The FGM plate dimensions are given as width b = 1 m, length a = 1 m, and uniform thickness h = 0.1 m, as shown in Fig. 4. The FE model of the FGM structure is discretized into 64 quadrilateral Reissner–Mindlin plate elements, resulting in 81 nodes and 405 DOFs.

Table 1 Material properties of the used FGM components
Full size table
Fig. 4
figure 4

a The FGM plate model and (b) its two-dimensional node and element numbering

Full size image

To investigate the performance of the six dynamic condensation techniques applied to multi-damage identification, four various hypothetical damage scenarios are created for the FGM plate. A detailed description of these damage scenarios is listed in Table 2. The first twelve modal frequencies (f1–f12) of the FGM structure of intact and damaged states are presented in Fig. 5. It can be seen in the figure that the variation of the natural frequencies between intact and damaged states is very small. For studying the problem of spatially-incomplete measurement data, a set of sensors are placed at 16 locations (nodes 13, 15, 18, 27, 29, 32, 35, 39, 47, 51, 53, 58, 64, 69, 75, and 80) on the FGM plate to assemble the first few eigenvalues and partial mode shapes. The positions of the measurement points are marked with red dots, as depicted in Fig. 4b.

Table 2 Four damage scenarios of the FGM plate
Full size table
Fig. 5
figure 5

The first twelve natural frequencies of the FGM plate of undamaged and damaged states

Full size image

4.1.1 Dynamic condensation techniques for the solution of eigenproblem

We utilized the six dynamic condensation techniques to create reduced-order models (ROMs) for the calculation of dynamic analysis. In the ROMs, the kept DOFs are selected by the DOFs corresponded to the 16 installed sensor locations, whereas the remaining DOFs are considered as the reduced DOFs. As a result, the full-order FE model with 405 DOFs is reduced to just 80 DOFs (20% of the total DOFs).

For comparison purposes, the eigensolutions of the intact plate structure are calculated by the six dynamic condensation techniques and the full-order FE model. The percentage of relative error between each ROM and the full-order FE model is calculated as

$${\text{er}}(\% ) = \left| {\frac{{\lambda_{{{\text{Full}}}} - \lambda_{{{\text{ROM}}}} }}{{\lambda_{{{\text{Full}}}} }}} \right| \times 100$$
(49)

where \(\lambda_{Full}\) and \(\lambda_{ROM}\) are the natural frequencies of the full-order FE model and ROM, respectively. Herein, the results from the full-order FE model are regarded as the exact target solution.

The relative errors of the first twelve natural frequencies obtained by various ROMs are exhibited in Table 3. It is apparent from the table that for the twelve target frequencies, the IOR has very good agreement with the full-order FE model with a maximum error of 4.00E−11%, whereas the Guyan, Kidder, NSEMR-II, IRS and IIRS yield maximum errors of 1.25E+01%, 2.70E−02%, 9.10E−02%, 1.70E−03% and 1.32E−04%, respectively. In other words, the IOR technique provides the best results among the six techniques. Compared with the IOR technique, the IIRS and IRS technique can be regarded as the second-best and the third-best, and Guyan’s method is the worst.

Table 3 The relative errors of the first twelve natural frequencies obtained by various reduced-order models compared with the full-order FE model
Full size table

Further comparison of the six ROMs is ascertained based on the Modal Assurance Criterion (MAC) [58]. This criterion is used to compare the eigenvectors of each ROM and the full-order FE model. It is expected that the diagonal MAC-values will equal unity and the off-diagonal MAC-values will equal to zero, which means a perfect eigenvector-correlation. Figure 6 depicts the MAC values of the first twelve modes obtained by the six condensation techniques for the FGM plate structure. As can be seen in the figure, only the Guyan’s method cannot identify the 7th mode shape. Whereas for the other methods, all the diagonal elements of the MAC matrix are very close to 1 and off-diagonal MAC-values are very near to zeros with the exception of a few high values. Overall, it can be noticed that ROMs including Kidder’s method, NSEMR-II, IRS, IIRS and IOR are able to represent the first twelve mode shapes of the full-order FE model.

Fig. 6
figure 6

The MAC values of the first twelve modes obtained by different dynamic condensation techniques for the FGM plate: (a) Guyan; (b) Kidder; (c) NSEMR-II; (d) IRS; (e) IIRS; (f) IOR

Full size image

4.1.2 Dynamic condensation techniques for damage identification

In this subsection, a comparative study is carried out to evaluate the performance of the six dynamic condensation techniques in the proposed damage identification approach when the incompleteness condition is considered. It should be noted that the spatially-incomplete measurement data of only the first five vibration modes are available for calculating the cost function (Eq. (35)). The measurement data with noise-free environment and noise contamination are both examined for damage identification of the FGM plate.

Figures 7, 8, 9, 10 present the comparison results of the six dynamic condensation techniques in the damage identification approach for scenario A to D of the FGM plate under the noise-free and noise conditions. It is observed that for all considered damage scenarios, the damage identification approach using Guyan’s method or Kidder’s method cannot localize the assumed damages accurately due to having many false identifications. Whereas the dynamic condensation techniques like NSEMR-II and IRS can provide better damage identification results than both the Guyan’s method and Kidder’s method, although they produce a few false alarms in the damage localization for scenarios A and C. It is also found that the IIRS and IOR can be considered as the best choice to achieve the desired damage localization results.

Fig. 7
figure 7

Comparison of damage identification results for scenario A of the FGM plate using different dynamic condensation techniques: (a) Noise-free; (b) Noise

Full size image
Fig. 8
figure 8

Comparison of damage identification results for scenario B of the FGM plate using six different dynamic condensation techniques: (a) Noise-free; (b) Noise

Full size image
Fig. 9
figure 9

Comparison of damage identification results for scenario C of the FGM plate using six different dynamic condensation techniques: (a) Noise-free; (b) Noise

Full size image
Fig. 10
figure 10

Comparison of damage identification results for scenario D of the FGM plate using six different dynamic condensation techniques: (a) Noise-free; (b) Noise

Full size image

Further, Fig. 11 shows the mean error for damage quantification of each damage scenario with and without noise contamination. The results in the figure demonstrate that using the IOR technique yields a good estimation for the actual damage severities with the smallest error. Thus, the performance, in terms of accuracy, of the proposed damage identification approach based on the hybrid MRFO-SQP algorithm combined with the IOR technique for damage localization and quantitation of the FGM plate structure is revealed.

Fig. 11
figure 11

Mean error of damage severity estimation for each damage scenario of the FGM structure using six different dynamic condensation techniques: (a) Noise-free; (b) Noise

Full size image

Last but not least, the performance of the suggested MRFO-SQP algorithm in term of solution accuracy and computational time is compared with those of the other three meta-heuristic algorithms including the cuckoo search (CS) algorithm [59], artificial ecosystem-based optimization (AEO) algorithm [60] and MRFO algorithm [52]. To do so, the common parameter settings (i.e., population size (Np) = 30, stop criterion = 10–6 and the maximum number of generations = 1000) used for each optimization algorithm are the same, meanwhile, the remaining control parameters of the CS, AEO, and MRFO are taken from [59, 60] and [52], respectively. Here, damage scenario D with noise-corrupted measurements is again used for the aim of the comparison. To deal with the spatially-incomplete measurement data, only the IOR technique is adopted in this investigation.

Figure 12 shows damage identification results for the damage scenario D of the FGM plate using four different optimization algorithms. One can easily observe from the figure that the MRFO and hybrid MRFO–SQP algorithms seem to be the best option for finding the real damaged sites in the structure, the AEO algorithm is the second best and the CS algorithm is the worst. For further investigation, the error and elapsed time comparisons of the four optimization algorithms for damage identification are provided in Figs. 13a, b, respectively. As can be seen in the figures, the hybrid MRFO–SQP algorithm can estimate the actual damage severities with more accuracy and lower computational time compared with the three others. In comparison with the original MRFO algorithm, the computational time of the hybrid MRFO–SQP algorithm is significantly reduced about 4 times for this case. Thus, this investigation indicates the reason for the selection of the hybrid MRFO–SQP algorithm in the damage detection process instead of the others.

Fig. 12
figure 12

Damage identification results for scenario D of the FGM plate using four different optimization algorithms

Full size image
Fig. 13
figure 13

Error and elapsed time comparisons of four optimization algorithms for damage scenario D of the FGM structure

Full size image

4.2 A FG-CNTRC plate

The second example is a functionally graded carbon nanotube-reinforced composite (FG-CNTRC) plate structure [61] with length a = 1 m, width b = 1 m, and thickness h = 0.1 m, as shown in Fig. 14. The material properties of the FG-CNTRC plate is a mixture of armchair (10,10) single-walled carbon nanotubes (SWCNTs) (fiber) and isotropic matrix (polymer), which can be defined according to the extended rule of mixture as [61]

$$\begin{gathered} E_{11} (z) = \eta_{1} V_{{{\text{CNT}}}} (z)E_{11}^{{{\text{CNT}}}} + V_{m} (z)E^{m} \hfill \\ \frac{{\eta_{2} }}{{E_{22} (z)}} = \frac{{V_{{{\text{CNT}}}} (z)}}{{E_{22}^{{{\text{CNT}}}} }} + \frac{{V_{m} (z)}}{{E^{m} }} \hfill \\ \frac{{\eta_{3} }}{{G_{12} (z)}} = \frac{{V_{{{\text{CNT}}}} (z)}}{{G_{12}^{{{\text{CNT}}}} }} + \frac{{V_{m} (z)}}{{G^{m} }} \hfill \\ \end{gathered}$$
(50)

where \(G^{m}\) and \(E^{m}\) represent the shear and Young modulus of the isotropic matrix; \(G_{12}^{CNT}\),\(E_{11}^{{{\text{CNT}}}}\) and \(E_{22}^{{{\text{CNT}}}}\) are the shear and Young modulus of the carbon nanotubes (CNTs); \(\eta_{1}\), \(\eta_{2}\) and \(\eta_{3}\) are the CNT efficiency parameters for considering the scale-dependent material properties; \(V_{m} (z)\) and \(V_{CNT} (z)\) are, respectively, the volume fractions of the matrix and the SWCNTs, which are related by \(V_{m} (z) + V_{{{\text{CNT}}}} (z) = 1\). In the plate structure, the material properties of the isotropic matrix [62] are assumed to be \(E^{m} = 2.1\) (GPa), \(\rho^{m} = 1.15\) (g/cm3), and \(\nu^{m} = 0.34\) at room temperature 3000 K. The material properties of the SWCNT considered by Zhang and Shen [63] are taken as follows: \(E_{11}^{{{\text{CNT}}}} = {5}{\text{.6466}}\) (TPa), \(E_{22}^{{{\text{CNT}}}} = {7}{\text{.08}}\) (TPa), \(G_{12}^{{{\text{CNT}}}} = {1}{\text{.9445}}\) (TPa), \(\rho^{{{\text{CNT}}}} = 1.4\) (g/cm3), and \(\nu^{CNT} = 0.175\). The distribution of the CNTs along the thickness direction is given as: \(V_{{{\text{CNT}}}} (z) = 2\left( {{\raise0.7ex\hbox{${2\left| z \right|}$} \!\mathord{\left/ {\vphantom {{2\left| z \right|} h}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$h$}}} \right)V_{{_{{{\text{CNT}}}} }}^{*}\). As reported in Ref. [62], when \(V_{{_{{{\text{CNT}}}} }}^{*} = 0.14\), \(\eta_{{_{1} }}^{{}} = 0.149\) and \(\eta_{{_{2} }}^{{}} = \eta_{{_{3} }}^{{}} = 1.381\). The FE model of the FG-CNTRC plate is discretized into 81 quadrilaterals Reissner–Mindlin plate elements, resulting in 100 nodes and 500 DOFs.

Four various hypothetical damage scenarios on the FG-CNTRC plate model are considered to investigate the performance of the six dynamic condensation techniques applied to multi-damage identification. The damaged locations and corresponding severities for the considered damage scenarios are provided in Table 4. Figure 15 shows the first twelve modal frequencies (f1 to f12) of the FG-CNTRC structure of intact and damaged states. As can be seen from the figure, there is not a significant change in the natural frequencies before and after the occurrence of damages. For studying the spatially-incomplete measurement problem, only the 80 DOFs at 16 nodes (nodes 12, 14, 17, 25, 26, 29, 46, 49, 62, 63, 65, 67, 73, 77, 83, and 89) are measured and collected via installed sensors. The measurement point locations are marked by red dots, as shown in Fig. 14b.

Table 4 Four damage scenarios of the FG-CNTRC plate
Full size table
Fig. 14
figure 14

a The FG-CNTRC plate model and (b) its two-dimensional node and element numbering.

Full size image
Fig. 15
figure 15

The first twelve natural frequencies of undamaged and damaged states of the FG-CNTRC plate

Full size image

4.2.1 Dynamic condensation techniques for the solution of eigenproblem

The accuracy of the six dynamic condensation techniques in the calculation of the eigenvalues and eigenvectors for the undamaged FG-CNTRC plate structure is first investigated. Here, the selected 80 DOFs are the master DOFs of the condensation techniques. Table 5 reports the relative errors of the first twelve natural frequencies obtained by the six ROMs compared with the full-order FE model. According to the table, the relative errors obtained by the IOR method are much smaller than those obtained by the other methods. Specifically, for the target natural frequencies, the largest observed errors of the Guyan, Kidder, NSEMR-II, IRS, IIRS, and IOR are 4.72E+01, 1.97E+01, 4.90E−01, 2.88E−01, 6.99E−02, and 1.00E−07, respectively. Thus, the ROM based on the IOR is the best, providing very accurate frequency solutions with reference to the full-order FE model.

Table 5 The relative errors of the first twelve natural frequencies obtained by various reduced models compared with the full-order FE model
Full size table

Further, the MAC criterion is utilized for checking the correlation of the eigenvectors between each ROM and the full-order FE model. The MAC values of the first twelve modes obtained by the six condensation techniques for the FG-CNTRC plate structure are reported in Fig. 16. One can find from the figure that for Guyan’s method and Kidder’s method, a few-mode shapes (modes 1 and 2) are well identified. While for the other methods like NSEMR-II, IRS, IIRS, and IOR, all the twelve target modes are well identified with off-diagonal values close to zero and diagonal values close to 1. It is hence concluded that both the Guyan’s method and Kidder’s method yield a really poor eigenvector-correlation; on the contrary, the NSEMR-II, IRS, IIRS, and IOR are capable of providing a good eigenvector-correlation.

Fig. 16
figure 16

The MAC values of the first twelve modes obtained by different dynamic condensation techniques for the FG-CNTRC plate: (a) Guyan; (b) Kidder; (c) NSEMR-II; (d) IRS; (e) IIRS; (f) IOR

Full size image

4.2.2 Dynamic condensation techniques for damage identification

In this subsection, a comparative study is performed among the six dynamic condensation techniques to find out the best technique for damage identification of the FG-CNTRC plate structure. Herein, it is assumed that the spatially-incomplete measurement data of only the first five vibration modes is utilized for minimizing the cost function (Eq. (35)). The four hypothetical damage scenarios with noise-free environment and noise-polluted measurements are examined.

Figure 17 presents the comparison results of the six dynamic condensation techniques in the damage identification approach for the four scenarios of the FG-CNTRC plate under the noise-free condition. It is obviously seen from the figure that the damage identification process using the IOR technique yields good predictions for both the locations and magnitudes of multi-damages in the FG-CNTRC plate structure. Meanwhile, the performance of using the other five condensation techniques (Guyan, Kidder, NSEMR-II, IRS, and IIRS) is very poor as they are unable to predict the real damaged sites for all considered scenarios. Therefore, it can be stated that among all the tested techniques, only the IOR technique is suitable for addressing the damage identification problem of the plate structure. Due to this reason, only the IOR technique is adopted for the process of damage identification with noise-polluted measurements.

Fig. 17
figure 17

Comparison of damage identification results of the FG-CNTRC plate using different dynamic condensation techniques under noise-free condition: (a) Scenario A; Scenario B; Scenario C; Scenario D

Full size image

Figure 18 shows damage identification results for four considered scenarios of the FG-CNTRC plate using the IOR technique under the noise condition. As indicated in the figure, the damage identification approach based on the hybrid MRFO–SQP algorithm combined with the IOR technique provides good predictions of both the locations and magnitudes of multi-damages in the case of noise-polluted measurements. Accordingly, this combination (MRFO–SQP algorithm and IOR technique) has demonstrated the best damage identification performance also for the FG-CNTRC plate.

Fig. 18
figure 18

Damage identification results of the FG-CNTRC plate using IOR technique under noise condition: (a) Scenario A; (b) Scenario B; (c) Scenario C; (d) Scenario D

Full size image

To further examine the robustness of the damage identification approach under different noise conditions, the last damage scenario is designed and higher noise levels, i.e. 12% and 15% on mode shapes are included. According to Fig. 19a, the average identified percentages of undamaged elements becomes slightly worse with the increase of the noise level, although the real damaged elements are still justified perfectly. According to Fig. 19b, when the noise level is increased, the relative error between actual and estimated damage elements is decreased accordingly. Also, the standard deviation of the damage identification results becomes larger with adding the noise levels, as shown in Fig. 20. However, the proposed approach can till yield satisfactory results for structural damage locations and quantification under different noise levels, which exhibits strong resistance to measurement noise influence.

Fig. 19
figure 19

The damage identification results and the relative errors of the proposed approach for damage scenario D of the FG-CNTRC structure under various noise levels

Full size image
Fig. 20
figure 20

The standard deviation of the damage identification results for scenario D of the FG-CNTRC structure under various noise levels

Full size image

5 Conclusion

This article aims at exploring the comparative capability of various dynamic condensation techniques used in the realm of damage localization and quantification of composite plate structures made of functionally graded materials (FGM) and functionally graded carbon nanotube-reinforced composite (FG-CNTRC) materials. To this end, six commonly used dynamic condensation techniques such as Guyan’s method, Kidder’s method, NSEMR-II, IRS, IIRS and IOR are firstly reviewed, and their performance for reduced Eigen and optimization-damage identification problems are then evaluated by using a FGM plate and a FG-CNTRC plate. For solving the optimization-damage identification problem of the plate structures, Manta Ray Foraging Optimization (MRFO) and Sequential Quadratic Programming (SQP) algorithms are combined to form a hybrid global–local (MRFO-SQP) optimization strategy. In the proposed strategy, the MRFO algorithm considered as the deterministic counterpart is utilized for global exploration and the SQP algorithm is employed for the local searching process. Based on the results and discussions presented in the above section, the salient points of the research work are summarized as follows:

  1. (1)

    For reduced Eigen problem, the IOR technique can create a reduced-order model of the considered structure that has dynamic characteristics closely matching with the full-order finite element (FE) model. The relative errors of eigenvalues obtained by the IOR technique are much smaller than those obtained by the other five techniques like Guyan’s method, Kidder’s method, NSEMR-II, IRS and IIRS. As a result, the eigensolutions of the structures with high accuracy are achieved by using the best dynamic condensation technique, IOR.

  2. (2)

    For damage identification problem of the plate structures, the IOR technique has good performance in structural damage localization and quantification with the highest accuracy. Whereas the other five techniques are unable to identify the damages in the FG-CNTRC plate.

  3. (3)

    Among all the tested optimization algorithms (CS, AEO, MRFO, and MRFO–SQP algorithms), the MRFO–SQP algorithm shows the best performance in terms of both accuracy and computational cost.

  4. (4)

    The proposed damage identification approach based on the hybrid MRFO–SQP algorithm combined with the IOR technique provides good predictions for both the locations and magnitudes of multi-damages in the FGM and FG-CNTRC plate structures using the first few incomplete modes with noise-polluted measurements. Further, the application of this damage identification approach can be extended to other kinds of engineering structures.