1 Introduction

In the recent past years, a new horizon is presented by many researchers for using reinforcement materials because of that the materials provide a marvelous performance for different applicable complex structures [1,2,3,4,5,6,7,8,9]. One of the most well-known of these reinforcements is graphene nanoplatelets (GPLs) composite, which solved the mentioned demand [10]. With the aid of an experimental research, Rafiee et al. [11] presented that using a little amount of GPLs in an epoxy basement could provide an impressive thermos mechanical properties compared with other reinforcements.

According to the mentioned applications, in the field of dynamic and static responses of the GPLRC structures, Hajilak et al. [12] provided a researcher about vibration and buckling behavior of the GPLRC shell reinforced with GPLs. They modeled a mathematical formulation by using modified strain gradient for considering size effects. Al-Furjan et al. [13] investigated the dynamic responses of the GPLRC disk with finite element and numerical models. They showed that as the amount of GPLs in an epoxy basement increases, the system's dynamic behavior could improve. Ebrahimi et al. [14] investigated wave responses of a GPLRC shell by considering imperfection or porosity and thermal environment. They showed that increasing the impacts of porosity and thermal environment could decrease the GPLs reinforced shell's stability. Habibi et al. [15] modeled an smart GPLs reinforced shell for investigation of wave propagation responses with the aid of strain radiant theory. They showed that due to increasing GPLs, the phase velocity and frequency of the mentioned system increase. In addition, the thermally affected GPLRC shell's static and dynamic stability are investigated by Safarpour et al. [16]. They presented the best pattern of GPLRC for having the highest frequency in the structure that is affected by a nonlinear thermal site and a foundation. By employing the differential quadrature method, Halpin–Tsai model, higher-order shear deformation, and proelasticity theories, Al-Furjan et al. [17] presented bending, static stability, and stress responses of a GPLs reinforced disk. Pourjabari et al. [18] presented a comprehensive study about free and forced vibration responses of the GPLs reinforced shell with the aid of modified strain gradient theory to consider the size effects. They reported three value for length scale parameters of the modified strain gradient theory. By using a semi numerical method Safarpour et al. [19] investigated the frequency responses of a GPLRC disk. Their results show that viscoelastic properties have an impressive impact on the system's dynamics and the mentioned issue was more considerable at the higher value of GPLs weight fraction. Ebrahimi et al. [20] did research about the effects of GPLs patterns and porosity on the critical thermal loading and dynamic stability with the aid of modified couple stress theory for considering size effects. They showed that when the symmetric GPLs patterns are employed the structure could be able to encounter with the higher critical thermal loading. Habibi et al. [21] presented frequency of the smart GPLRC rotary nanoshell by using differential quadrature method, Halpin–Tsai model, and first-order shear deformation theory. They showed that the critical rotary speed of the smart structure could improve due to increasing the value of GPLs. Using the finite element method, Tam et al. [22] presented a research about nonlinear bending behaviors of a cracked GPLRC beam. they prove that when the crack depth and temperature of the environment increase, the strength of the structure decreases but this issue become negligible due to increasing GPLs weight fraction. Li et al. [23] showed bending responses of the GPLs reinforced plate with the aid of 2D approach and energy method. Liu et al. [24] studied the effects of six kinds of GPLs patterns on the linear free vibration and stress responses of the composite spherical shell based on 3D elasticity theory. Also, this material can be used in advanced structures and systems [25, 26]. A frequency up-conversion mechanism was suggested by Onsorynezhad et al. [27] to improve the performance of the piezoelectric energy harvester, and the mechanical and electrical behaviors of the energy harvester were analytically investigated. The frequency response results showed that the frequency up-conversion mechanism has significantly improved the energy harvester's performance.

Furthermore, Wave responses, static and dynamic stability of different applicable complex and simple structures are investigated in many researches [28,29,30,31,32,33,34,35,36,37,38,39,40] with numerical and experimental methods. Based on the mentioned literature review, this is the first research to present bending responses of hybrid laminated nanocomposite reinforced axisymmetric circular/annular plates within the framework of non-polynomial under mechanical loading and various type of initially stresses via the three-dimensional elasticity theory. The current structure is on the Pasternak type of elastic foundation and torsional interaction. The state-space approach along with differential quadrature method is studied to present the bending characteristics of the current structure by considering various boundary conditions. For predicting the material properties of the bulk, role of mixture and Halpin–Tsai equations are studied. For modeling the circular plate, a singular point is studied. Finally, a parametric study is done to investigate the impacts of various types of distribution of laminated layers, stacking sequence on the stress/strain information of the HLNRACP/ HLNRAAP.

2 Mathematical modeling

In this research HLNRACP reinforced by various distribution GPLs is presented. Based on the Halpin–Tsai model, have [41]

$$\overline{E} = \,\frac{{1 + V_{{{\text{GPL}}}} \eta_{{\text{W}}} \xi_{{\text{W}}} \,}}{{1 - V_{{{\text{GPL}}}} \eta_{{\text{W}}} }}\, \times \frac{{\,5E_{{\text{M}}} }}{8} + \frac{{1 + \eta_{{\text{L}}} V_{{{\text{GPL}}}} \xi_{{\text{L}}} \,}}{{1 - V_{{{\text{GPL}}}} \eta_{{\text{L}}} }}\, \times \,\frac{{3E_{{\text{M}}} }}{8},$$
(1)

where \(\xi_{{\text{L}}} = 2\frac{{L_{{{\text{GPL}}}} }}{{t_{{{\text{GPL}}}} }},\;\xi_{{\text{W}}} = 2\frac{{W_{{{\text{GPL}}}} }}{{t_{{{\text{GPL}}}} }},\;V_{{{\text{GPL}}}}^{*} = \frac{{\Lambda_{{{\text{GPL}}}} }}{{\Lambda_{{{\text{GPL}}}} + \left( {\frac{{\rho_{{{\text{GPL}}}} }}{{\rho_{{\text{M}}} }}} \right)\left( {1 - \Lambda_{{{\text{GPL}}}} } \right)}},\;\eta_{{\text{W}}} = \frac{{\left( {\frac{{E_{{{\text{GPL}}}} }}{{E_{{\text{M}}} }}} \right) - 1}}{{\left( {\frac{{E_{{{\text{GPL}}}} }}{{E_{{\text{M}}} }}} \right) + \xi_{{\text{W}}} }}\) and \(\eta_{{\text{L}}} = \frac{{\left( {\frac{{E_{{{\text{GPL}}}} }}{{E_{{\text{M}}} }}} \right) - 1}}{{\left( {\frac{{E_{{{\text{GPL}}}} }}{{E_{{\text{M}}} }}} \right) + \xi_{{\text{L}}} }}.\)

Based on the following expression, the \(\stackrel{-}{v}\) of the composite is as follows [42]

$$\overline{\nu } = \nu_{{\text{M}}} \left( {1 - V_{{{\text{GPL}}}} } \right) + V_{{{\text{GPL}}}} \nu_{{{\text{GPL}}}}.$$
(2)

For effective shear module have:

$${\overline{\text{G}}} = \frac{{E_{{\text{C}}} }}{{2\left( {1 + \nu_{{\text{C}}} } \right)}}.$$
(3)

FG and uniform distribution of the laminated layers are formulated as below [41]

$$V_{{{\text{GPL}}}} = 4 \times \frac{1}{{\left( {V_{{{\text{GPL}}}}^{*} } \right)^{ - 1} }} \times \left| {z_{j} } \right| \times {\text{h}}^{ - 1} \, \,\,\,\,\,{\text{FG-X}}$$
(4a)
$$V_{{{\text{GPL}}}} = 2 \times \frac{1}{{\left( {V_{{{\text{GPL}}}}^{*} } \right)^{ - 1} }} \times \left( {1 - 2 \times \left| {z_{j} } \right| \times {\text{h}}^{ - 1} } \right) \, \,\,\,\,\,{\text{FG-O}}$$
(4b)
$$V_{{{\text{GPL}}}} = \frac{1}{{\left( {V_{{{\text{GPL}}}}^{*} } \right)^{ - 1} }} \times \left( {1 - 2 \times \left| {z_{j} } \right| \times {\text{h}}^{ - 1} } \right){\text{ FG-A}}$$
(4c)
$$V_{{{\text{GPL}}}} = \frac{1}{{\left( {V_{{{\text{GPL}}}}^{*} } \right)^{ - 1} }} \times \left( {1 + {\text{h}}^{ - 1} \times 2 \times \left| {z_{j} } \right|} \right){\text{ FG-V}}$$
(4d)
$$V_{GPL} = \frac{1}{{\left( {V_{GPL}^{*} } \right)^{ - 1} }}\,\,\,\,\,\,\,\,\,\,{\text{ FG-UD}}$$
(4e)

Here, \(z_{j} = \left( {\frac{1}{2} + \frac{1}{2n} - \frac{j}{n}} \right)h,\quad j = 1,2,3, \ldots ,n\).

2.1 Governing equations of the current structure

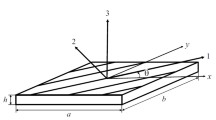
Figure 1 shows the geometry and coordinate of the current structure. 3D governing differential equation of motion by neglecting of body forces are [43,44,45,46,47,48]

$$\sigma_{r,r} + \tau_{rz,z} + r^{ - 1} \tau_{r\theta ,\theta } - r^{ - 1} \left( {\sigma_{\theta } + \sigma_{r} } \right) + \sigma_{0} r^{ - 2} \left( {2u_{\theta ,\theta } + u_{r} - u_{r,\theta \theta } } \right) = 0$$
(5a)
$$\tau_{r\theta ,r} + r^{ - 1} \tau_{\theta z,\theta } + \sigma_{z,z} + 2r^{ - 1} \tau_{r\theta } + \sigma_{0} r^{ - 2} \left( {u_{\theta } - u_{\theta ,\theta \theta } - 2u_{r,\theta } } \right) = 0$$
(5b)
$$\tau_{rz,r} + r^{ - 1} \tau_{\theta z,\theta } + \sigma_{z,z} + r^{ - 1} \tau_{rz} - \sigma_{0} r^{ - 2} u_{z,\theta \theta } = 0$$
(5c)
Fig. 1
figure 1

Geometry and coordinate of the HLNRACP/ HLNRAAP

Full size image

where bigger and smaller value of \(\sigma_{0}\) than zero means the compressive stress, and tensile stress, respectively. Stress–strain relations [49,50,51] of HLNRACP/ HLNRAAP reinforced by GPLs can be presented as follows:

$$\left\{ {\begin{array}{*{20}c} {\sigma_{RR} } \\ {\sigma_{\theta \theta } } \\ {\sigma_{zz} } \\ {\tau_{z\theta } } \\ {\tau_{rz} } \\ {\tau_{r\theta } } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\overline{\mathbb{Q}}_{11} } & {\overline{\mathbb{Q}}_{12} } & {\overline{\mathbb{Q}}_{13} } & 0 & 0 & 0 \\ {\overline{\mathbb{Q}}_{12} } & {\overline{\mathbb{Q}}_{22} } & {\overline{\mathbb{Q}}_{23} } & 0 & 0 & 0 \\ {\overline{Q}_{13} } & {\overline{\mathbb{Q}}_{23} } & {\overline{\mathbb{Q}}_{33} } & 0 & 0 & 0 \\ {} & {} & {} & {\overline{\mathbb{Q}}_{44} } & 0 & 0 \\ {} & {{\text{sym}}.} & {} & 0 & {\overline{\mathbb{Q}}_{55} } & 0 \\ {} & {} & {} & 0 & 0 & {\overline{\mathbb{Q}}_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{RR} } \\ {\varepsilon_{\theta \theta } } \\ {\varepsilon_{zz} } \\ {\gamma_{z\theta } } \\ {\gamma_{rz} } \\ {\gamma_{r\theta } } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {\gamma P} \\ {\gamma P} \\ {\gamma P} \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\},$$
(6)

where the used parameters in Eq. (6) are presented in Refs. [52,53,54,55,56,57,58,59,60,61]. The strains of the HLNRACP/ HLNRAAP reinforced by GPLs can be given as [62]:

$$\varepsilon_{r} = u_{r,r} , \, \varepsilon_{\theta } = r^{ - 1} \left( {u_{r} + u_{\theta ,\theta } } \right){, }\varepsilon_{z} = u_{z,z} ,$$
(7)
$$\gamma_{r\theta } = u_{\theta ,r} + r^{ - 1} u_{r,\theta } - r^{ - 1} u_{\theta } ,\,\,\,\,\,\,\gamma_{rz} = u_{r,z} + u_{z,r} ,\,\,\,\gamma_{\theta z} = r^{ - 1} u_{z,\theta } + u_{\theta ,z}$$
(8)

The other parameter in the Eq. (6) are as below:

$$P = \frac{{\left( {\psi - \left( {\varepsilon_{rr} + \varepsilon_{\theta \theta } + \varepsilon_{zz} } \right)\gamma } \right)}}{{K^{ - 1} }}$$
(9a)
$$K = - \left( {k - k_{u} } \right)\gamma^{ - 2}$$
(9b)
$$k_{u} = \left[ {1 - \frac{{k_{f} \gamma^{2} }}{{\left( {\phi - \gamma } \right)\left( {1 - \gamma } \right)k_{f} + k_{f} \phi }}} \right]k$$
(9c)

In the Eq. (9a), parameter \(\psi = 0\) for un-drained conditions of fluid leads to:

$$P = - K\varepsilon \gamma = - K\left( {\varepsilon_{rr} + \varepsilon_{\theta \theta } + \varepsilon_{zz} } \right)\gamma ,$$
(10)

Now by substituting Eq. (10) into Eq. (6) gives

$$\sigma_{rr} = \overline{\mathbb{Q}}_{13}^{*} u_{z,z} + r^{ - 1} \overline{\mathbb{Q}}_{12}^{*} (u_{r} + u_{\theta ,\theta } ) + \overline{\mathbb{Q}}_{11}^{*} u_{r,r}$$
(11a)
$$\sigma_{\theta \theta } = \overline{\mathbb{Q}}_{23}^{*} u_{z,z} + \overline{\mathbb{Q}}_{12}^{*} u_{r,r} + r^{ - 1} \overline{\mathbb{Q}}_{22}^{*} (u_{\theta ,\theta } + u_{r} )$$
(11b)
$$\sigma_{zz} = \overline{\mathbb{Q}}_{33}^{*} u_{z,z} + r^{ - 1} \overline{\mathbb{Q}}_{23}^{*} (u_{r} + u_{\theta ,\theta } ) + \overline{\mathbb{Q}}_{13}^{*} u_{r,r}$$
(11c)
$$\tau_{\theta z} = \overline{\mathbb{Q}}_{44} \left( {r^{ - 1} u_{z,\theta } + u_{\theta ,z} } \right)$$
(11d)
$$\tau_{rz} = \overline{\mathbb{Q}}_{55} \left( {u_{z,r} + u_{r,z} } \right)$$
(11e)
$$\tau_{r\theta } = \overline{\mathbb{Q}}_{66} \left( {r^{ - 1} u_{r,\theta } - r^{ - 1} u_{\theta } + u_{\theta ,r} } \right),$$
(11f)

where

$$\overline{\mathbb{Q}}_{11}^{*} = \frac{K}{{\gamma^{ - 2} }} + \overline{\mathbb{Q}}_{11}$$
(12a)
$$\overline{\mathbb{Q}}_{12}^{*} = \frac{K}{{\gamma^{ - 2} }} + \overline{\mathbb{Q}}_{12}$$
(12b)
$$\overline{\mathbb{Q}}_{13}^{*} = \frac{K}{{\gamma^{ - 2} }} + \overline{\mathbb{Q}}_{13}$$
(12c)
$$\overline{\mathbb{Q}}_{22}^{*} = \frac{K}{{\gamma^{ - 2} }} + \overline{\mathbb{Q}}_{22}$$
(12d)
$$\overline{\mathbb{Q}}_{23}^{*} = \frac{K}{{\gamma^{ - 2} }} + \overline{\mathbb{Q}}_{23}$$
(12e)
$$\overline{\mathbb{Q}}_{33}^{*} = \frac{K}{{\gamma^{ - 2} }} + \overline{\mathbb{Q}}_{33} .$$
(12f)

Using Eqs. (5a–c) and (11a–f):

$$\frac{{\partial u_{r} }}{\partial z} = - u_{z,r} + \frac{{\tau_{rz} }}{{\overline{\mathbb{Q}}_{55} }}$$
(13a)
$$\frac{{\partial u_{\theta } }}{\partial z} = - \frac{{u_{z,\theta } }}{r} + \frac{{\tau_{z\theta } }}{{\overline{\mathbb{Q}}_{44} }}$$
(13b)
$$\frac{{\partial u_{z} }}{\partial z} = - \frac{{\overline{\mathbb{Q}}_{13}^{*} }}{{\overline{\mathbb{Q}}_{33}^{*} }}u_{r,r} - r^{ - 1} \frac{{\overline{\mathbb{Q}}_{23}^{*} }}{{\overline{\mathbb{Q}}_{33}^{*} }}u_{r} - r^{ - 1} \frac{{\overline{\mathbb{Q}}_{23}^{*} }}{{\overline{\mathbb{Q}}_{33}^{*} }}u_{\theta ,\theta } + \frac{{\sigma_{z} }}{{\overline{\mathbb{Q}}_{33}^{*} }}$$
(13c)
$$\frac{{\partial \sigma_{z} }}{\partial z} = r^{ - 2} \sigma_{0} u_{z,\theta \theta } - \tau_{rz,r} - r^{ - 1} \tau_{rz} + r^{ - 1} \tau_{z\theta ,\theta }$$
(13d)
$$\begin{aligned} \frac{{\partial \tau_{rz} }}{\partial z} & = - \left( {\overline{\mathbb{Q}}_{11}^{*} - \frac{{\overline{\mathbb{Q}}_{13}^{*2} }}{{\overline{\mathbb{Q}}_{33}^{*} }}} \right)u_{r,rr} + r^{ - 2} \sigma_{0} \left( {u_{r,\theta \theta } - 2u_{\theta ,\theta } - u_{r} } \right)\, - r^{ - 1} \left( {\overline{\mathbb{Q}}_{11}^{*} - \frac{{\overline{\mathbb{Q}}_{13}^{*2} }}{{\overline{\mathbb{Q}}_{33}^{*} }}} \right)u_{r,r} - r^{ - 2} \overline{\mathbb{Q}}_{66} u_{r,\theta \theta } \\ & - \frac{{\overline{\mathbb{Q}}_{13}^{*} }}{{\overline{\mathbb{Q}}_{33}^{*} }}\sigma_{z,r} - \left( {\frac{{\overline{\mathbb{Q}}_{13}^{*} - \overline{\mathbb{Q}}_{23}^{*} }}{{\overline{\mathbb{Q}}_{33}^{*} }}} \right)\sigma_{z} - r^{ - 2} \left( {\frac{{\overline{\mathbb{Q}}_{12}^{*} \overline{\mathbb{Q}}_{33}^{*} + \overline{\mathbb{Q}}_{23}^{*2} - \overline{\mathbb{Q}}_{13}^{*} \overline{\mathbb{Q}}_{23}^{*} - \overline{\mathbb{Q}}_{22}^{*} \overline{\mathbb{Q}}_{33}^{*} }}{{\overline{\mathbb{Q}}_{33}^{*} }}} \right)u_{r} \\ & - r^{ - 1} \left( {\overline{\mathbb{Q}}_{12}^{*} + \overline{\mathbb{Q}}_{66} - \frac{{\overline{\mathbb{Q}}_{13}^{*} \overline{\mathbb{Q}}_{23}^{*} }}{{\overline{\mathbb{Q}}_{33}^{*} }}} \right)u_{\theta ,r\theta } - r^{ - 2} \left( {\frac{{\overline{\mathbb{Q}}_{12}^{*} \overline{\mathbb{Q}}_{33}^{*} + \overline{\mathbb{Q}}_{23}^{*2} - \overline{\mathbb{Q}}_{13}^{*} \overline{\mathbb{Q}}_{23}^{*} - \overline{\mathbb{Q}}_{22}^{*} \overline{\mathbb{Q}}_{33}^{*} }}{{\overline{\mathbb{Q}}_{33}^{*} }}} \right)u_{\theta ,\theta } \\ \end{aligned}$$
(13e)
$$\begin{aligned} \frac{{\partial \tau_{\theta z} }}{\partial z} & = - r^{ - 1} \left( {\overline{\mathbb{Q}}_{12}^{*} + \overline{\mathbb{Q}}_{66} - \frac{{\overline{\mathbb{Q}}_{13}^{*} \overline{\mathbb{Q}}_{23}^{*} }}{{\overline{\mathbb{Q}}_{33}^{*} }}} \right)u_{r,r\theta } - r^{ - 2} \left( {\overline{\mathbb{Q}}_{22}^{*} + 2\overline{\mathbb{Q}}_{66} - \frac{{\overline{\mathbb{Q}}_{23}^{*2} }}{{\overline{\mathbb{Q}}_{33}^{*} }}} \right)u_{r,\theta } \\ & - \overline{\mathbb{Q}}_{66} u_{\theta ,rr} - \frac{{\overline{\mathbb{Q}}_{66} }}{r}u_{\theta ,r} - r^{ - 2} \left( {\overline{\mathbb{Q}}_{22}^{*} - \frac{{\overline{\mathbb{Q}}_{23}^{*2} }}{{\overline{\mathbb{Q}}_{33}^{*} }}} \right)u_{\theta ,\theta \theta } \\ & + 2r^{ - 2} \overline{\mathbb{Q}}_{66} u_{\theta } + r^{ - 2} \sigma_{0} \left( {2u_{r,\theta } + u_{\theta ,\theta \theta } - u_{\theta } } \right) - r^{ - 1} \frac{{\overline{\mathbb{Q}}_{23}^{*} }}{{\overline{\mathbb{Q}}_{33}^{*} }}\sigma_{z,\theta } . \\ \end{aligned}$$
(13f)

The form of matrix of Eqs. (13a–f) can be written as:

$$\frac{{{\text{d}}\delta }}{{{\text{d}}z}} = G\delta ,$$
(14)

where \(\delta = \{ u_{r} \,u_{\theta } \,\,u_{z} \,\sigma_{z} \,\tau_{rz} \,\,\tau_{\theta z} \}^{{\text{T}}}\).

And the relations for different boundary conditions can be formulated as follows:

$${\text{Simply}}:\sigma_{r} = u_{z} = u_{\theta } = 0\quad {\text{Clamped}}:u_{z} = u_{r} = u_{\theta } = 0.$$
(15)

Also, for a circular plate at r = 0:

$$u_{z,r} = u_{r} = 0\,\,\,\,\,r = 0$$
(16)

3 Applying linear and torsional elastic foundation

The Winkler–Pasternak foundations for HLNRACP/ HLNRAAP reinforced by GPLs can be formulated as:

$$\chi = - r^{ - 1} \left( {ru_{z,r} k_{p} \left( {r,\theta ,z} \right)} \right)_{,r} - r^{ - 2} \left( {u_{z,\theta } k_{p} \left( {r,\theta ,z} \right)} \right)_{.r} + k_{w} \left( {r,\theta ,z} \right)u_{z}$$
(17)

The used parameters in Eq. (17) can be given as:

$$k_{w} \left( {r,\theta ,z} \right) = k_{wo} \left( {1 + f_{1} rr_{o} + f_{2} r^{2} r_{o}^{ - 2} } \right)\cos \left( {\theta_{0} } \right)$$
(18a)
$$k_{p} \left( {r,\theta ,z} \right) = k_{po} \left( {1 + f_{1} rr_{o} + f_{2} r^{2} r_{o}^{ - 2} } \right)\cos \left( {\theta_{0} } \right).$$
(18b)

The torsional elastic foundation can be formulated as:

$$\chi_{r} = k_{r1} \left( {r,\theta } \right)\phi - r^{ - 1} \left( {r\phi_{,r} k_{r2} \left( {r,\theta } \right)} \right)_{,r} ,$$
(19)

Substituting \(\phi = {\raise0.7ex\hbox{${\partial u_{\theta } }$} \!\mathord{\left/ {\vphantom {{\partial u_{\theta } } {\partial r}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial r}$}}\) into Eq. (20) gives:

$$\chi_{r} = k_{r1} \left( {r,\theta } \right)u_{\theta ,r} - r^{ - 1} \left( {ru_{\theta ,rr} k_{r2} \left( {r,\theta } \right)} \right)_{,r}$$
(20)

These coefficients are considered as

$$k_{r1} \left( {r,\theta } \right) = \left( {1 + f_{1} rr_{o} + f_{2} r^{2} r_{o}^{ - 2} } \right)k_{r10} \sin \left( {\theta_{0} } \right)$$
(21a)
$$k_{r2} \left( {r,\theta ,z} \right) = \left( {1 + f_{1} rr_{o} + f_{2} r^{2} r_{o}^{ - 2} } \right)k_{r20} \sin \left( {\theta_{0} } \right).$$
(21b)

3.1 Solution procedure

To date, many studies showed that computer and numerical methods [63,64,65,66,67,68,69,70,71,72] are highly used for modeling different phenomena. In this research for solving the governing equations we apply DQM that have [19, 73]:

$$\,\frac{{\partial^{n} f}}{{\partial r^{n} }} = \sum\limits_{m = 1}^{M} {g^{\left( n \right)}_{j,m} f_{m,k} } ,$$
(22)

here, \(g^{(n)}\), can be extracted as below:

$$\begin{aligned} g_{ij}^{\left( 1 \right)} & = - \sum\limits_{j = 1,i \ne j}^{n} {g_{ij}^{\left( 1 \right)} } \quad i = j \\ g_{ij}^{\left( 1 \right)} & = \frac{{M\left( {x_{i} } \right)}}{{\left( {x_{i} - x_{j} } \right)M\left( {x_{j} } \right)}}\quad i,j = 1,2, \ldots ,n\,\,\,\,{\text{and}}\,\,\,\,i \ne j, \\ \end{aligned}$$
(23)

where:

$$M\left( {x_{i} } \right) = \prod\limits_{j = 1,j \ne i}^{n} {\left( {x_{i} - x_{j} } \right)} .$$
(24)

The derivatives of Eq. (24) can be written as the following equations [74]:

$$\begin{aligned} g_{ii}^{\left( n \right)} & = - \sum\limits_{j = 1,i \ne j}^{n} {g_{ij}^{\left( n \right)} } \quad 1 \le n \le N - 1\,\,{\text{while}}\,\,\,j,i = 1,2, \ldots ,N \\ g_{ij}^{\left( n \right)} & = r\left[ {g_{ij}^{{\left( {n - 1} \right)}} g_{ij}^{\left( 1 \right)} - \frac{{g_{ij}^{{\left( {n - 1} \right)}} }}{{\left( {x_{i} - x_{j} } \right)}}} \right]\quad i \ne j,\,2 \le n \le N - 1\,\,{\text{while}}\,\,j\,,i = 1,2, \ldots ,N. \\ \end{aligned}$$
(25)

In addition, via greed points of Chebyshev polynomials, the seed along with r-axes is as follows:

$$r_{i} = \frac{{R_{0} - R_{i} }}{2}\left( {1 - \cos \left( {\frac{{\left( {i - 1} \right)}}{{\left( {N_{i} - 1} \right)}}\pi } \right)} \right) + R_{i} \quad i = 1,2,3, \ldots ,N_{i} .$$
(26)

Besides, displacement fields of the HLNRACP/ HLNRAAP reinforced by GPLs are as:

$$u_{r} = \sum\limits_{m = 1}^{\infty } {\hat{u}_{r} } \sin \left( {\theta P_{m} } \right){, }u_{\theta } = \sum\limits_{m = 1}^{\infty } {\hat{u}_{\theta } } \cos \left( {P_{m} } \right), \, u_{z} = \sum\limits_{m = 1}^{\infty } {\hat{u}_{z} } \sin \left( {P_{m} } \right){, }$$
(27a)
$$\sigma_{r} = \sum\limits_{m = 1}^{\infty } {\hat{\sigma }_{r} } \sin \left( {\theta P_{m} } \right), \, \sigma_{\theta } = \sum\limits_{m = 1}^{\infty } {\hat{\sigma }_{\theta } } \sin \left( {\theta P_{m} } \right){, }\sigma_{z} = \sum\limits_{m = 1}^{\infty } {\hat{\sigma }_{z} } \sin \left( {\theta P_{m} } \right),$$
(27b)
$$\tau_{rz} = \sum\limits_{m = 1}^{\infty } {\hat{\tau }_{rz} } \sin \left( {\theta P_{m} } \right){, }\tau_{r\theta } = \sum\limits_{m = 1}^{\infty } {\hat{\tau }_{r\theta } } \cos \left( {\theta P_{m} } \right), \, \tau_{\theta z} = \sum\limits_{m = 1}^{\infty } {\hat{\tau }_{\theta z} } \cos \left( {\theta P_{m} } \right),$$
(27c)

where: Pm = m. We assumed, the following dimensionless form of equations:

$$\overline{E} = \frac{E}{{P_{0} }},\,\,\,\,\,\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\overline{\sigma }_{z} } & {\overline{\sigma }_{r} } & {\overline{\sigma }_{\theta } } \\ \end{array} } & {\overline{\tau }_{rz} } & {\overline{\tau }_{r\theta } } & {\overline{\tau }_{\theta z} } \\ \end{array} } \right) = \frac{1}{{E_{m} }}\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\hat{\sigma }_{z} } & {\hat{\sigma }_{r} } & {\hat{\sigma }_{\theta } } \\ \end{array} } & {\hat{\tau }_{rz} } & {\hat{\tau }_{r\theta } } & {\hat{\tau }_{\theta z} } \\ \end{array} } \right)$$
(28a)
$$\overline{r} = \frac{r}{{R_{m} }}{,}\,\,\,\,\left( {\begin{array}{*{20}c} {\overline{U}_{r} } & {\overline{U}_{\theta } } & {\overline{U}_{z} } \\ \end{array} } \right) = \frac{1}{h}\left( {\begin{array}{*{20}c} {u_{r} } & {u_{\theta } } & {u_{z} } \\ \end{array} } \right),\,\,\,\,S = \frac{h}{{R_{m} }},\,\,\,\overline{Z} = \frac{Z}{h},\,\,\,\overline{P}_{m} = P_{m}$$
(28b)
$${\text{P}}_{0} { = 1}\,\,{\text{[Mpa]}},\,\,\,\overline{p} = \frac{q}{{P_{0} }},\,\overline{g}_{ij} = g_{ij} R_{m} ,\,\hat{\overline{\mathbb{Q}}}_{ij} = \frac{{\overline{\mathbb{Q}}_{ij} }}{{P_{0} }},\,\,\,\overline{\sigma }_{0} = \frac{{\sigma_{0} }}{{P_{0} }}.$$
(28c)

Substitution of Eqs. (28a–b), (27a–b) and (22) into Eq. (14):

$$\frac{{\partial \overline{u}_{ri} }}{{\partial \overline{z}}} = - S\sum\limits_{j = 1}^{N} {\overline{g}_{ij} } \overline{u}_{zj} + \frac{{\overline{\tau }_{rzi} }}{{\hat{\overline{\mathbb{Q}}}_{55} }}$$
(29a)
$$\frac{{\partial \overline{u}_{\theta i} }}{{\partial \overline{z}}} = - S\overline{r}_{i}^{ - 1} P_{m} \overline{u}_{zi} + \frac{{\overline{\tau }_{z\theta i} }}{{\hat{\overline{\mathbb{Q}}}_{44} }}$$
(29b)
$$\frac{{\partial \overline{u}_{zi} }}{{\partial \overline{z}}} = \frac{{\overline{\sigma }_{zi} }}{{\hat{\overline{\mathbb{Q}}}_{33} }} - S\frac{{\hat{\overline{\mathbb{Q}}}_{13} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}\sum\limits_{j = 1}^{N} {\overline{g}_{ij} } \overline{u}_{rj} - S\overline{r}_{i}^{ - 1} \frac{{\hat{\overline{\mathbb{Q}}}_{23} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}\overline{u}_{ri} + S\overline{r}_{i}^{ - 1} \frac{{P_{m} \hat{\overline{\mathbb{Q}}}_{23} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}\overline{u}_{\theta i}$$
(29s)
$$\frac{{\partial \overline{\sigma }_{zi} }}{{\partial \overline{z}}} = - r_{i}^{ - 2} \sigma_{0} P_{m}^{2} \overline{u}_{zi} - S\sum\limits_{j = 1}^{N} {\overline{g}_{ij} } \overline{\tau }_{rzj} - S\overline{r}_{i}^{ - 1} \overline{\tau }_{rzi} - S\overline{r}_{i}^{ - 1} P_{m} \overline{\tau }_{z\theta i} {, }$$
(29d)
$$\begin{aligned} \frac{{\partial \overline{\tau }_{rzi} }}{{\partial \overline{z}}} & = - S\frac{{\hat{\overline{\mathbb{Q}}}_{13} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}\sum\limits_{j = 1}^{N} {g_{ij} } \sigma_{zj} - S\overline{r}_{i}^{ - 1} \left( {\frac{{\hat{\overline{\mathbb{Q}}}_{13} - \hat{\overline{\mathbb{Q}}}_{23} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}} \right)\sigma_{zi} - S^{2} \left( {\hat{\overline{\mathbb{Q}}}_{11} - \frac{{\hat{\overline{\mathbb{Q}}}_{13}^{2} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}} \right)\sum\limits_{j = 1}^{N} {\overline{g}_{ij}^{2} } \overline{u}_{rj} \\ & - S^{2} \overline{r}_{i}^{ - 1} \left( {\hat{\overline{\mathbb{Q}}}_{11} - \frac{{\hat{\overline{\mathbb{Q}}}_{13}^{2} }}{{\hat{\overline{Q}}_{33} }}} \right)\sum\limits_{j = 1}^{N} {\overline{g}_{ij} } \overline{u}_{rj} + P_{m}^{2} \overline{r}_{i}^{ - 2} \hat{\overline{\mathbb{Q}}}_{66} \overline{u}_{ri} + \sigma_{0} \overline{r}_{i}^{ - 2} \left( {P_{m}^{2} \overline{u}_{ri} - 2P_{m} \overline{u}_{\theta i} + \overline{u}_{ri} } \right) \\ & - S^{2} \overline{r}_{i}^{ - 2} \left( {\frac{{\hat{\overline{\mathbb{Q}}}_{12} \hat{\overline{\mathbb{Q}}}_{33} + \hat{\overline{\mathbb{Q}}}_{23}^{2} - \hat{\overline{\mathbb{Q}}}_{13} \hat{\overline{\mathbb{Q}}}_{23} - \hat{\overline{\mathbb{Q}}}_{22} \hat{\overline{\mathbb{Q}}}_{33} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}} \right)\overline{u}_{ri} \\ & + S^{2} \overline{r}_{i}^{ - 1} P_{m} \left( {\hat{\overline{\mathbb{Q}}}_{12} + \hat{\overline{\mathbb{Q}}}_{66} - \frac{{\hat{\overline{\mathbb{Q}}}_{13} \hat{\overline{\mathbb{Q}}}_{23} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}} \right)\sum\limits_{j = 1}^{N} {\overline{g}_{ij} } \overline{u}_{\theta j} \\ & + S^{2} \overline{r}_{i}^{ - 2} P_{m}^{2} \left( {\frac{{\hat{\overline{\mathbb{Q}}}_{12} \hat{\overline{\mathbb{Q}}}_{33} + \hat{\overline{\mathbb{Q}}}_{23}^{2} - \hat{\overline{\mathbb{Q}}}_{13} \hat{\overline{\mathbb{Q}}}_{23} - \hat{\overline{\mathbb{Q}}}_{22} \hat{\overline{\mathbb{Q}}}_{33} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}} \right)\overline{u}_{\theta i} \\ \end{aligned}$$
(29e)
$$\begin{aligned} \frac{{\partial \overline{\tau }_{\theta zi} }}{{\partial \overline{z}}} & = - S\frac{{P_{m} }}{{\overline{r}_{i} }}\frac{{\hat{\overline{\mathbb{Q}}}_{23} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}\overline{\sigma }_{zi} - S^{2} \frac{{P_{m} }}{{\overline{r}_{i} }}\left( {\hat{\overline{\mathbb{Q}}}_{12} + \hat{\overline{\mathbb{Q}}}_{66} - \frac{{\hat{\overline{\mathbb{Q}}}_{13} \hat{\overline{\mathbb{Q}}}_{23} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}} \right)\sum\limits_{j = 1}^{N} {\overline{g}_{ij} } \overline{u}_{rj} \\ & - S^{2} \frac{{P_{m} }}{{\overline{r}_{i}^{2} }}\left( {\hat{\overline{\mathbb{Q}}}_{22} + 2\hat{\overline{\mathbb{Q}}}_{66} - \frac{{\hat{\overline{\mathbb{Q}}}_{23}^{2} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}} \right)\overline{u}_{ri} \, - S^{2} \hat{\overline{\mathbb{Q}}}_{66} \sum\limits_{j = 1}^{N} {\overline{g}_{ij}^{2} } \overline{u}_{\theta j} - S^{2} \frac{{\hat{\overline{\mathbb{Q}}}_{66} }}{{\overline{r}_{i} }}\sum\limits_{j = 1}^{N} {\overline{g}_{ij} } \overline{u}_{\theta j} \\ & + S^{2} \frac{{P_{m}^{2} }}{{\overline{r}_{i}^{2} }}\left( {\hat{\overline{\mathbb{Q}}}_{22} - \frac{{\hat{\overline{\mathbb{Q}}}_{23}^{2} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}} \right)\overline{u}_{\theta i} + S^{2} \frac{{2\hat{\overline{\mathbb{Q}}}_{66} }}{{\overline{r}_{i}^{2} }}\overline{u}_{\theta i} + \frac{{\sigma_{0} }}{{r_{i}^{2} }}\left( {2P_{m} \overline{u}_{ri} - P_{m}^{2} \overline{u}_{\theta i} - \overline{u}_{\theta i} } \right), \\ \end{aligned}$$
(29f)

where:

$$\overline{u}_{ki} = \overline{u}_{k} (r,\theta ,z);\,\,\,(k = r_{i} ,\theta ,z),\,\,\,\overline{\sigma }_{ki} = \overline{\sigma }_{k} (r,\theta ,z),\,\overline{\tau }_{\theta zi} = \overline{\tau }_{\theta z} (r,\theta ,z)\,,\overline{\tau }_{rzi} = \overline{\tau }_{rz} (r,\theta ,z)\,\,\,$$
(30)

Substitution of Eqs. (15)–(16) into Eqs. (29a–f) gives the following state-space equations

$$\frac{{\partial \overline{\delta }_{{\text{b}}} }}{{\partial \overline{z}}} = \overline{G}_{{\text{b}}} \overline{\delta }_{{\text{b}}} ,$$
(31)

where \(\overline{\delta }_{{\text{b}}} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\overline{u}_{r} } & {\overline{u}_{\theta } } \\ \end{array} } & {\begin{array}{*{20}c} {\overline{u}_{z} } & {\overline{\sigma }_{z} } \\ \end{array} } & {\begin{array}{*{20}c} {\overline{\tau }_{rz} } & {\overline{\tau }_{\theta z} } \\ \end{array} } \\ \end{array} } \right\}^{{\text{T}}}\) is the column matrix of state variables. In addition, subscript, b in Eq. (31) denotes the state equation includes the boundary conditions[38, 75, 76].

By using a layer-wise technique, \(\overline{G}_{{\text{b}}}\) is decreased to the constant matrix and finally Eq. (31) can be solved analytically for Nt fictitious layer as the follows

$$\delta_{k} \left( {\overline{z}} \right) = \delta_{ok} \exp \left( {\overline{G}_{bk} \left( {\overline{z} - \overline{z}_{k - 1} } \right)} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\overline{z}_{k - 1} \le \overline{z} \le \overline{z}_{k} .$$
(32)

At the inner and outer radius of kth layer, the relation between the state variables can be given as follows:

$$\delta_{k} \left( {\overline{z}_{k} } \right) = \overline{M}_{k} \delta_{ok} .$$
(33)

In which \(\overline{M}_{k} = \exp \left( {\frac{{\overline{G}_{bk} \overline{h}_{f} }}{{N_{t} }}} \right)\).

3.2 Static analysis

Whereas for static analysis it is assumed following surface traction boundary condition.

$$\begin{aligned} \overline{\sigma }_{z} & = \chi ,\,\,\,\,\,\,\overline{\tau }_{rz} = 0,\,\,\,\,\,\overline{\tau }_{\theta z} = \chi_{r} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{at}}\,\overline{z} = - \frac{1}{2} \\ \overline{\sigma }_{z} & = \overline{p}\cos \left( {\theta_{0} } \right),\,\,\,\,\,\,\overline{\tau }_{rz} = \overline{\tau }_{\theta z} = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{at}}\,\overline{z} = \frac{1}{2}. \\ \end{aligned}$$
(34)

Applying Eqs. (33) and (34) gives the following homogenous equation:

$$\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\lambda_{12} } \\ {\lambda_{52} } \\ {\lambda_{62} } \\ \end{array} } & {\begin{array}{*{20}c} {\lambda_{13} + \lambda_{16} \chi_{r} } \\ {\lambda_{53} + \lambda_{56} \chi_{r} } \\ {\lambda_{53} + \lambda_{56} \chi_{r} } \\ \end{array} } & {\begin{array}{*{20}c} {\lambda_{14} + \lambda_{11} \chi } \\ {\lambda_{54} + \lambda_{51} \chi } \\ {\lambda_{64} + \lambda_{61} \chi } \\ \end{array} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\overline{u}_{r} } \\ {\overline{u}_{\theta } } \\ {\overline{u}_{z} } \\ \end{array} } \right\}_{{\overline{z} = - \frac{1}{2}}} = \left\{ {\begin{array}{*{20}c} {\overline{p}\cos \left( {\theta_{0} } \right)} \\ 0 \\ 0 \\ \end{array} } \right\}_{{\overline{z} = \frac{1}{2}}} .$$
(35)

In addition, \(\overline{p} = \{ \overline{p}_{1} , \ldots ,\overline{p}_{N} \}^{{\text{T}}}\). Displacements at the bottom surface can be obtained by solving Eq. (35) and then by using Eq. (33) transverse normal and shear stresses as well as displacements as a function of radial coordinated are determined. Finally, in-plane normal and shear stresses are computed from the following equations;

$$\overline{\sigma }_{ri} = \frac{{\hat{\overline{\mathbb{Q}}}_{13} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}\overline{\sigma }_{zi} + S\left( {\hat{\overline{\mathbb{Q}}}_{11} - \frac{{\hat{\overline{\mathbb{Q}}}_{13}^{2} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}} \right)\sum\limits_{j = 1}^{N} {\overline{g}_{ij} \overline{u}_{rj} + S\overline{r}_{i}^{ - 1} } \left( {\hat{\overline{\mathbb{Q}}}_{12} - \frac{{\hat{\overline{\mathbb{Q}}}_{13} \hat{\overline{\mathbb{Q}}}_{23} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}} \right)\left( {\overline{u}_{ri} - P_{m} \overline{u}_{\theta i} } \right)$$
(36a)
$$\overline{\sigma }_{\theta i} = \frac{{\hat{\overline{\mathbb{Q}}}_{23} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}\overline{\sigma }_{zi} + S\left( {\hat{\overline{\mathbb{Q}}}_{12} - \frac{{\hat{\overline{\mathbb{Q}}}_{13} \hat{\overline{\mathbb{Q}}}_{23} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}} \right)\sum\limits_{j = 1}^{N} {\overline{g}_{ij} \overline{u}_{rj} + } S\overline{r}_{i}^{ - 1} \left( {\hat{\overline{\mathbb{Q}}}_{22} - \frac{{\hat{\overline{\mathbb{Q}}}_{23}^{2} }}{{\hat{\overline{\mathbb{Q}}}_{33} }}} \right)\left( {\overline{u}_{ri} - P_{m} \overline{u}_{\theta i} } \right)$$
(36b)
$$\overline{\tau }_{r\theta i} = S\overline{r}_{i}^{ - 1} P_{m} \hat{\overline{\mathbb{Q}}}_{66} u_{ri} + S\hat{\overline{\mathbb{Q}}}_{66} \sum\limits_{j = 1}^{N} {\overline{g}_{ij} \overline{u}_{\theta j} + S\overline{r}_{i}^{ - 1} \hat{\overline{\mathbb{Q}}}_{66} } \overline{u}_{\theta i} .$$
(36c)

4 Result

Material properties of graphene nanoplates, matrix, and the poroelastic constants are presented in Refs. [77, 78].

4.1 Validation

The properties in this validation section can be written as:

$$E\left( z \right) = E_{m} \left( {\frac{h - 2z}{{2h}}} \right)^{n} + E_{c} \left[ {1 - \left( {\frac{h - 2z}{{2h}}} \right)^{n} } \right]$$
(37a)
$$E_{r} = 0.396, \, E_{c} = 125.83 \times 10^{9} , \, E_{m} = E_{c} \times E_{r}$$
(37b)
$$R_{o} = 1, \, h = 0.2 \times R_{o} ,\nu = 0.288.$$
(37c)

The properties dimensionless stress and displacement in this example can be written as:

$$\overline{w}_{0}^{F} = \frac{{64w_{0}^{F} D_{c} }}{{q_{0} R_{o}^{4} }} = \frac{{D_{c} }}{{\Omega_{1} }}\left[ {1 - \left( {\frac{r}{{R_{o} }}} \right)^{2} } \right]^{2} + \frac{8}{{3K_{s}^{2} \left( {1 - v_{c} } \right)}}\left( {\frac{h}{{R_{o} }}} \right)^{2} \left[ {1 - \left( {\frac{r}{{R_{o} }}} \right)^{2} } \right]\left( {\frac{1 + n}{{E_{r} + n}}} \right)$$
(37a)
$$\overline{u}_{0}^{F} = \frac{{64u_{0}^{F} D_{c} }}{{q_{0} R_{o}^{4} }} = \frac{{D_{c} }}{{\Omega_{1} }}\left[ {1 - \left( {\frac{r}{{R_{o} }}} \right)^{2} } \right]^{2} + \frac{8}{{3K_{s}^{2} \left( {1 - v_{c} } \right)}}\left( {\frac{h}{{R_{o} }}} \right)^{2} \left[ {1 - \left( {\frac{r}{{R_{o} }}} \right)^{2} } \right]\left( {\frac{1 + n}{{E_{r} + n}}} \right)$$
(37b)
$$\left( {\overline{\sigma }_{0}^{F} ,\overline{\tau }_{rz}^{F} } \right) = \left( {\frac{{\sigma_{0}^{F} }}{{q_{0} }},\frac{{\tau_{rz}^{F} }}{{q_{0} }}} \right).$$
(37c)

Table 1 presents a validation study for proving the result of the current paper. For this regard, the Non-dimensional maximum deflections in the conditions of various power index (n) value \(\overline{w}_{0}^{F} \left( {0,0} \right)\), \(\overline{u}_{0}^{F} \left( {0, - \frac{h}{2}} \right)\), \(\overline{\sigma }_{z}^{F} \left( {\frac{R}{2},0} \right)\) and \(\overline{\tau }_{rz}^{F} \left( {R,0} \right)\) are compared with those outcomes in the Ref. [79]. As shown in the comparison studies, this paper's results have a suitable agreement with the presented study in the literature. The difference between the present study and Ref. [79] using three-dimensional elasticity theory in the present study shows that this theory presents an exact method.

Table 1 Compare the \(\overline{w}_{0}^{F} \left( {0,0} \right)\) of functionally graded clamped circular plates with the result in Ref. [79]
Full size table

The impact of the N on the convergence condition is reported in Fig. 2 for investigation of bending response and stress analysis of FG-GPLRCAAP under initially stressed interacting with the gradient elastic foundations. In this regard, the static and bending behaviors of the structure are presented for four N. Based on the presented diagram in Fig. 2, we can report that when the N is more than seven, the stress and displacement fields don’t have a dependency on the number of grid points. As a conclusion from Fig. 2, the convergence condition of the GDQ method is achieved by employing seven grid points for the semi-analytical method.

Fig. 2
figure 2figure 2

Convergence number of grid points for an investigation of the displacement and stress fields of the FG-GPLRC annular plates. Ri = 0.5, Ro = 2Ri, h = 0.1Ri, \(\Lambda_{{{\text{GPL}}}}\)  = 1 (wt%), GPL-UD, Kwo = Kpo = 100, f1 = f2 = 0.1, Kr10 = Kr20 = 100, \(\theta_{0} = \pi /4\), \(\theta_{0} = \pi /4\) and Simply–Simply boundary conditions

Full size image

In Fig. 3 shows the influence of five kinds of GPLs patterns on the static and stress responses of the FG-GPLRC circular/annular plates under initially stressed interacting with the gradient elastic foundations. Generally, GPL-A structure has the best bending responses, but at the inner and outer layers, the structure with GPL-X and GPL-O patterns encounter us with the best static responses. In addition, the structure with the GPL-UD pattern provides the most uniform distribution of displacement and stress fields. In addition, the weakest system against bending responses is the structure with a GPL-V pattern. The normal stress in the structure with GPL-A is high, but the displacement is low. The higher shear stresses at the inner, middle, and outer layers can see in the composite disk with GPL-A, GPL-O, and GPL-V patterns.

Fig. 3
figure 3figure 3

Stress and displacement fields of the FG-GPLRC annular plate for different FG patterns with Ro/Ri = 2, h = 0.1Ri, \(\Lambda_{{{\text{GPL}}}}\)= 0.01 wt%, Kwo = Kpo = 100, f1 = f2 = 0.1, Kr10 = Kr20 = 10, \(\theta_{0} = \pi /4\), and Simply–Simply boundary conditions

Full size image

The static and bending behaviors of the FG-GPLRC circular/annular plates under initially stressed interacting with the gradient elastic foundations are presented in Fig. 4 by focusing on the effect of three kinds of boundary conditions. According to Fig. 4, when the structure is encountered with the clamped edges, the better bending response and the lowest stress are seen. In addition, in the middle layers cannot see any effect from boundary conditions on the normal axial stress, while in the inner and outer layers, when the structure is encountered with simple edges, we can see the highest axial normal stress. In addition, if the structure encounters the clamped edges (C–C and C–S boundary conditions), we cannot find a remarkable change in the radial bending response while having simply–simply edges, we can see an increase in the radial displacement filed. Besides, for each boundary condition, the maximum axial shear stress is seen in the middle layers, and the structure with clamped edges has the lowest shear stress along the thickness direction. In addition, boundary conditions on normal stress are more remarkable in the inner and outer layers. Last but not the list, bending, and static responses of the structure will improve by increasing the structure's rigidity.

Fig. 4
figure 4figure 4

Stress and displacement fields of the structure for three kinds of boundary conditions with Ro/Ri = 2, h = 0.1Ri, \(\Lambda_{{{\text{GPL}}}}\) = 0.01 wt%, GPL-X, Kwo = Kpo = 10, f1 = f2 = 0.1, Kr10 = Kr20 = 10, \(\theta_{0} = \pi /4\), and annular plate

Full size image

The purpose of Fig. 5 is an investigation about the effect of Winkler and Pasternak factors (\(K_{wo} \, {\text{and}} \, K_{po}\)) on the stress and displacement fields of the structure. Accordingly, as the Winkler and Pasternak factors of the foundation increase, the in-plane and out plane stress decrease. Also, the impact of Winkler and Pasternak factors on the in-plane or shear stress (\(\tau_{rz}\) and \(\tau_{\theta z}\)) is more remarkable at the middle layers. in addition, increasing the foundation factors is a reason to decrease the axial stress (\(\sigma_{z}\)) and this issue becomes bold by increasing \(z^{ - }\) or at the outer layers. Furthermore, the system's static stability and bending behavior improve due to increasing the value of Winkler and Pasternak factors, and the stress distribution becomes more uniform.

Fig. 5
figure 5figure 5

Investigation the effect of the foundation coefficients on the stress and displacement fields of the structure with Ro/Ri = 2, h = 0.01Ri, \(\Lambda_{{{\text{GPL}}}}\) = 0.01 wt%, GPL-X, f1 = f2 = 0.1, Kr10 = Kr20 = 10, \(\theta_{0} = \pi /4\), Clamped–Clamped boundary conditions, and annular plate

Full size image

Stress and displacement fields versus to weight fraction of GPLs (\(\Lambda_{{{\text{GPL}}}}\)) are presented in Fig. 6 for five kinds of GPLRC patterns. Generally, increasing \(\Lambda_{{{\text{GPL}}}}\) factor makes a positive impact on the structure's static and bending behaviors, and the mentioned relation is more considerable by employing the GPL-X pattern. In addition, when the GPL-UD pattern makes the structure, the weight fraction of GPLs has the lowest positive impact on stress and displacement fields. For all patterns, as the \(\Lambda_{{{\text{GPL}}}}\) factor increases, the displacement and stress fields decrease.

Fig. 6
figure 6figure 6

Maximum stress and displacement fields of the structure for the different volume fraction of GPLs with Ro/Ri = 2, h = 0.1Ri, Kwo = Kpo = 10, f1 = f2 = 0.1, Kr10 = Kr20 = 10, \(\theta_{0} = \pi /4\), \(\overline{\sigma }_{0} = 0\), Clamped–Clamped boundary conditions, and annular plate

Full size image

The purpose of Fig. 7 is an investigation about the effect of initial or residual internal stress on the stress and displacement fields of the FG-GPLRCACP/FG-GPLRCAAP under initially stressed interacting with the gradient elastic foundations. By having attention to Fig. 7 as the value of the initial stress increases, the system's bending properties improve. In addition, there are no effects from internal stress on the axial stress, but other components of stress fields decrease owning to increasing the initial internal stress. In addition, the impact of residual internal stress on the hoop and axial shear stress is bold at − 0.35 \(\le z^{ - } \le\) 0.15 and the influences of the internal stress on the displacement fields is more remarkable at the \(z^{ - }\) = − 0.5 and 0.5. Furthermore, the stress and displacement fields' distribution become more uniform due to increasing the initial stress. At \(z^{ - }\) = − 0.5, 0, and 0.5, we can find that initial stress doesn’t affect axial normal stress.

Fig. 7
figure 7figure 7

Stress and displacement fields of the structure for Effect of initially stressed with Ro/Ri = 2, h = 0.1Ri, \(\Lambda_{{{\text{GPL}}}}\) = 0.01 wt%, GPL-X, Kwo = Kpo = 10, f1 = f2 = 0.1, Kr10 = Kr20 = 10, \(\theta_{0} = \pi /4\), and clamped–clamped annular plate

Full size image

Stress and displacement fields the FG-GPLRCACP/FG-GPLRCAAP under initially stressed interacting with the gradient elastic foundations are presented in Fig. 8 by considering the effects of thickness and width of the GPLs. Generally, increasing thickness and width of the GPLs positively impact the bending behaviors of the structure. In addition, adding the length of the GPLs increases, the value of stress and displacement increases, so the system's static stability decreases.

Fig. 8
figure 8figure 8

Stress and displacement fields of the structure for size effect of graphene with Ro/Ri = 2, h = 0.1Ri, \(\Lambda_{{{\text{GPL}}}}\) = 0.01 wt%, GPL-X, Kwo = Kpo = 10, f1 = f2 = 0.1, Kr10 = Kr20 = 10, \(\theta_{0} = \pi /4\), clamped–clamped boundary conditions, and annular plate

Full size image

5 Conclusion

This article explored the bending response of the HLNRACP/ HLNRAAP reinforced by GPLs resting on gradient elastic foundation within non-polynomial framework under initially stresses for different cases of boundary conditions. The main advantage is that it benefited from the exact theory (three-dimensional elasticity theory) to describe the kinematics of the structure. The numerical results were determined using the fast converging DQM. The continuity condition was considered between each of the heterogenous sections to satisfy the equality of displacement terms at the contact surfaces. Finally, the most bolded results of this paper were as follows:

  • Among the five GPL distribution patterns considered in the present study, GPL-X works more effectively and results in the smallest displacement and stress, also GPL-O has the highest displacement and stress.

  • As the \({\Lambda }_{GPL}\) parameter increases the bending response in the structure improves.

  • When the structure is encountered with the clamped edges, the better bending response and the lowest stress happens in the sandwich disk.

  • The system's static stability and bending behavior improve due to increasing the value of Winkler and Pasternak factors, and the stress distribution becomes more uniform.

  • Increasing the thickness and width of the GPLs positively impacts the bending behaviors of the structure. In addition, adding the length of the GPLs increases, the value of stress and displacement increases, so the system's static stability decreases.