1 Introduction

Design of optimal structures has been a dynamic field of investigation from a recent couple of decades due to its widespread engineering applications such as bridges, towers, roof supports, building exoskeletons, space frameworks, mechanical parts, and industries. It has been recognizing that structural optimization with multiple and conflicting design objectives is a challenging task that requires efficient and robust optimization methods to search optimal solutions [29, 56]. The design of a truss basically consists of defining its elemental sizes, shape, and topology so as to get minimum weight or cost under safety constraints [23, 51, 52].

The application of meta-heuristics (MHs) in multi-objective truss design is currently receiving growing attention from researchers around the globe. Owing to the dominance of MHs over classical gradient-based methods as they are easy to study, need low computation cost, and are flexible in nature, recently lots of effort have been made for their implementation in truss optimization problems. Some of the well-recognized MHs for single-objective truss design problems are genetic algorithms (GAs) [12, 17], particle swarm optimization (PSO) [18], simulated annealing [27], teaching–learning-based optimization (TLBO) [51], cuckoo search algorithm [19], tug-of-war optimization algorithm [26], artificial bee colony algorithm [43], sine–cosine optimization algorithm [31], ray optimization [24], and flower pollination algorithm [13]. The literature also demonstrated the enhancement in the performance of original MHs with further modification, hybridization, integration, and improvement in solving more intricate truss design problems. Some prominent optimizers are modified symbiotic organisms search (SOS) [23], modified GA [25], modified TLBO [6], improved dolphin echolocation algorithm [20], hybrid gray wolf optimizer and self-adaptive differential evolution [35], improved fireworks algorithm [21], hybridized passing vehicle search [57], improved harmony search algorithms [14], and adaptive SOS [51].

Often, a designer poses a real-world truss design problem with more than one objective to be optimized, which is called multi-objective optimization. Such a problem has multiple-objective functions usually conflicting in nature causing design more intricate. Contrary to single-objective design which has one solution, a multi-objective design problem leads to a set of optimal solutions. This optimal set is termed as a Pareto optimal set if it is viewed in the design domain. Alternatively, it is called Pareto front if it is observed in the objective domain. The literature demonstrates the superiority of MHs in finding these non-dominated optimal solutions set in truss design problems due to their simplicity and flexibility. More importantly, MH can search for a Pareto front within one run. For dealing with multi-objective optimization problem, from the last two decades, a number of multi-objective meta-heuristics (MOMHs) have been developed such as multi-objective GA [17], multi-objective PSO [7], multi-objective immune optimizer [28], multi-objective symbiotic organism search [36], and NSGA-II [15]. The first objective is usually truss weight an indicator for cost, while another objective function can be added for structural performance maximization. The second objective thus can be stress, natural frequency, structure stiffness, and nodal displacement. Owing to more than one optimal solution set, more than one distinct optimization objective and further two distinct search arena multi-objective optimization problems constitute, inefficient MOMHs may fail in obtaining a reliable solution. Consequently, modification of and improvement in MOMHs are always interesting subjects for numerous researchers. Some successful modified and improved optimizers are modified dragonfly optimization optimizer [3], modified adaptive SOS [58], hybrid mutation PSO [62], improved multi-objective GA [34], improved multi-objective PSO [44], hybrid multi-objective evolutionary optimizer [63], multi-objective improved cuckoo search optimizer [30], improved multi-objective JAYA optimization optimizer [39], modified multi-objective Pareto genetic optimizer for [8], modified multi-objective game theory optimizer [40], modified multi-objective immune optimizer [45], hybrid multi-objective modified artificial bee colony, and cuckoo search optimizers [64].

A recently developed state-of-the-art and highly efficient MH called heat transfer search (HTS) [37] based on the principle of the heat transfer process is modified and implemented for multi-objective structure optimization problems. After HTS initial invention, it has been implemented in various optimization design problems [10, 16, 22, 41]. Furthermore, it has been modified and improved by numerous researchers [32, 33, 46, 53, 58]. The work presented by Savsani et al. [47] displays that MOHTS can accomplish results with more diverse Pareto fronts compared to NSGA-II. Also, the correlation of Pareto front extreme points illustrates the robustness of MOHTS being better than that of multi-objective uniform GA variety, integrated PSO–GA-based multi-objective EA and NSGA-II. In another finding, Tawhid and Savsani [50] proposed an effective \(\in\)-constraint multi-objective HTS algorithm, which results in superiority to other multi-objective forms of GA, PSO, DE, and WCA. Recently, Tejani et al. [56] implemented the HTS algorithm in a multi-objective truss optimization problem subject to discrete design variables. The effectiveness of the algorithm was examined by different benchmark problems, while it is compared with multi-objective ant system (MOAS), multi-objective ant colony system (MOACS), and multi-objective symbiotic organism search (MOSOS). The outcome demonstrates the dominance of HTS over the others. The MOHTS algorithm is applied for the investigation on optimum heat exchanger [42]. The findings show good promise between optimization and analysis of experiments. Shah et al. [48] analyzed a nanoscale irreversible Stirling engine by using HTS with two and three conflicting objectives. Prajapati and Patel [38] implemented HTS for the optimization of the nanofluid-based organic Rankine cycle with multiple objectives of thermal efficiency maximization and levelized energy cost minimization.

Accordingly, there is a gap for further research and analysis as the HTS optimizer has just been proposed. Moreover, as MOHTS has limited investigation records in the literature, its modification should be investigated for various problems. As a result, this examination is proposed to modify the viability of MOHTS by consolidating synchronized transmission of heat by conduction, convection, and radiation of fundamental HTS during the search process to maintain a good balance between local intensification and global diversification.

In this study, the proposed MOMHTS optimizer is applied for multi-objective truss optimization problems with objective functions being weight minimization and maximization of nodal displacement. Five constrained benchmarks truss optimization problems (i.e., 10-, 25-, 60-, 72-, and 942-bar trusses) are taken into account for checking the potential of MOMHTS. Moreover, the obtained results of MOMHTS are compared with other MOMHs, which manifest the dominance of the proposed modification.

The rest of the study is structured as follows: Sect. 2 illuminates the basic HTS with all three phases. Section 3 gives details about the proposed MOMHTS optimizer. Section 4 defines the multi-objective design problem with its formulation. Section 5 comprises a detailed discussion about the truss design problems and result obtained. The suggested work is recapitulated in Sect. 6 followed by its future prospects.

2 Heat transfer search (HTS)

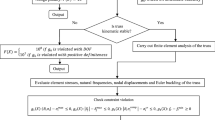
HTS is one of the advanced meta-heuristic proposed by Patel and Savsani [37]. HTS is inspired by the basic principle of heat transfer and thermodynamics. The law implies that, with conduction, convection, and radiation modes of heat transfer, a thermal system can achieve the thermal equilibrium within a system or its surroundings to make the system stable. Consequently, all three modes of heat transfer systems are assumed as the search procedures of the HTS optimizer. Here, it is presumed that all three modes will be fairly likely to participate in the search process. The equal selection probability of each mode in the search process is regulated in each iteration by the uniformly distributed random number ‘P,’ which ranges from 0 to 1. In the search process, conduction mode is picked when the value is \(P \in [ {0-0.3333} ]\), radiation mode is selected when \(P \in [ {0.3333-0.6666} ]\), and convection mode is selected if \(P \in [ {0.6666-1} ]\). Thus, based on the values of P, during the search process, the obtained results are updated as per the executed mode of heat transfer in each iteration.

In the HTS algorithm, the population resembles various molecules that experience the heat transfer process, while the design variables show the temperature levels of various molecules. Herein, the energy level of the system molecules is representing the value of the objective function while the surrounding mimicked the best solution. A population size is equivalent to ‘n’ number of molecules, and the design variables are equivalent to temperature level ‘m.’ In each generation ‘g’ the population is reproduced by randomly selecting one of the modes. The revised result in HTS will only be approved if it has a superior functional value.

2.1 Thermal conduction mode

In conduction, the molecules exchange heat due to the conduction mode between them. For achieving the thermal equilibrium, the molecules with higher energy state transfer energy to the lower energy-level molecules. The system and surrounding molecules can also exchange heat if they are in physical contact. This mode of the HTS algorithm is divided into two segments based on the number of iteration ‘i.’ The formulation for the new solution is shown in Eqs. (1) and (2):

Segment 1: when i ≤ Imax/CDF

$$ S_{a,\mu }^{'} = \left\{ {\begin{array}{*{20}c} {S_{b,\mu } + \left( { - P^{2} \times S_{b,\mu } } \right),\quad {\text{if}}\,\,F\left( {S_{a} } \right) > F\left( {S_{b} } \right)} \\ {S_{a,\mu } + \left( { - P^{2} \times S_{a,\mu } } \right),\quad {\text{if}}\,\, F\left( {S_{a} } \right) < F\left( {S_{b} } \right)} \\ \end{array} } \right. . $$
(1)

Segment 2: when i > Imax/CDF

$$ S_{a,\mu }^{'} = \left\{ {\begin{array}{*{20}c} {S_{b,\mu } + \left( { - p_{\beta } \times S_{b,\mu } } \right),\quad {\text{if}}\,\,F\left( {S_{a} } \right) > F\left( {S_{b} } \right)} \\ {S_{a,\mu } + \left( { - p_{\beta } \times S_{a,\mu } } \right),\quad {\text{if}}\,\,F\left( {S_{a} } \right) < F\left( {S_{b} } \right)} \\ \end{array} } \right. . $$
(2)

In the above equations, \(S_{a,\mu }^{'}\) symbolizes the updated molecules; \(a = 1,2,3, \ldots ,n\); \(b\) represents a solution which is selected at random; \(a \ne b\); \(b \in \left( {1,2,3, \ldots .,n} \right)\); \(\mu\) is a design variable index which is selected randomly; \(\mu \in \left( {1,2, \ldots ,m} \right)\); i is the current iteration; Imax is the maximum number of iteration; CDF is the conduction factor; probability variable is P where \(P \in \left[ {0,0.3333} \right]\); \(p_{\beta }\) is an arbitrary number varying from 0 to 1; \(P^{2}\) and \(p_{\beta }\) represent the Fourier’s equation [11]; conductance parameters \(S_{a}\) and \(S_{b}\) signify the temperature change of molecules; and CDF is assigned as 2 to balance the intensification and diversification [16, 37, 41]. It should be noted that, in each iteration, only one design variable is modified during the conductive process.

2.2 Thermal convection mode

In this HTS mode, the system continuously seeks to eliminate the existing energy-level disparity between the system and the surrounding by means of convection heat transfer. The system molecules (at \(S_{\text{mean}}\)) interrelate to establish thermal equilibrium with the surrounding (\(S_{\text{surr}}\)). The updated solution is obtained by the mathematical formulation as shown in Eqs. (3) and (4):

$$S_{a,\mu }^{'} = S_{a,\mu } + P \times \left( {S_{\text{surr}} - S_{\text{mean}} \times {\text{TCF}}} \right)$$
(3)
$$ {\text{TCF}} = \left\{ {\begin{array}{*{20}c} {{\text{abs}}\left( {P - p_{\beta } } \right),} & {{\text{if}}\,i \le I_{\hbox{max} } /{\text{COF}}} \\ {{\text{round}}\left( {1 + p_{\beta } } \right),} & {{\text{if}}\,i > I_{\hbox{max} } /{\text{COF}}} \\ \end{array} } \right. $$
(4)

where \(S_{a,\mu }^{'}\) serves as an updated solution; \(a = 1,2,3, \ldots ,n\); \(\mu \in \left( {1,2, \ldots ,m} \right)\); i is the function evaluations; COF is a convection factor; probability variable is P where \(P \in \left[ {0.6666,1} \right]\); \(p_{\beta }\) is an arbitrary number varying from 0 to 1; \(P^{2}\) and \(p_{\beta }\) represent the Newton’s law of cooling [11] convection parameters; \(S_{\text{surr}}\) is the surrounding temperature considered as a reference (the best solution) which remains constant; \(S_{\text{mean}}\) denotes the mean temperature of the system which changes during convection; TCF is a temperature change factor to trade-off between exploitation and exploration in the convection phase; and COF is assigned 10 [16, 37, 41].

2.3 Thermal radiation mode

In this process, due to its temperature level, heat transfer occurs due to radiation released in the form of electromagnetic waves. The system, therefore, interacts with the surrounding temperature or within the system (i.e., another solution) in order to achieve a thermal equilibrium state. This is governed by the Stefan–Boltzmann law of thermodynamics [11]. Here, the solution is updated continuously according to the mathematical formulation given in Eqs. (5) and (6):

$$ S_{a,\mu }^{'} = \left\{ {\begin{array}{*{20}c} {S_{a,\mu } + P \times \left( {S_{b,\mu } - S_{a,\mu } } \right),\quad {\text{if}}\,F\left( {S_{a} } \right) > F\left( {S_{b} } \right)} \\ {S_{a,\mu } + P \times \left( {S_{a,\mu } - S_{b,\mu } } \right),\quad {\text{if}}\,F\left( {S_{a} } \right) < F\left( {S_{b} } \right)} \\ \end{array} } \right.;\quad {\text{if}}\,i \le I_{\hbox{max} } /{\text{RDF}} $$
(5)
$$ S_{a,\mu }^{'} = \left\{ {\begin{array}{*{20}c} {S_{a,\mu } + p_{\beta } \times \left( {S_{b,\mu } - S_{a,\mu } } \right),\quad {\text{if}}\,F\left( {S_{a} } \right) > F\left( {S_{b} } \right)} \\ {S_{a,\mu } + p_{\beta } \times \left( {S_{a,\mu } - S_{b,\mu } } \right),\quad {\text{if}} \,F\left( {S_{a} } \right) < F\left( {S_{b} } \right)} \\ \end{array} } \right.;\quad {\text{if}}\,i > I_{\hbox{max} } /{\text{RDF}} $$
(6)

where \(S_{a,\mu }^{'}\) symbolizes the updated molecules; \(a = 1,2,3, \ldots ,n\); \(\mu \in \left( {1,2, \ldots ,m} \right)\); \(a \ne b\); \(b \in \left( {1,2,3, \ldots ,n} \right)\); \(b\) represents a randomly selected molecule; i is the current iteration; a probability variable is denoted as P \(\in\) [0.3333, 0.6666]; \(p_{\beta }\) is an arbitrary number varying from 0 to 1; \(P^{2}\) and \(p_{\beta }\) represent the Stefan–Boltzmann equation radiation parameters; and \(S_{a}\) and \(S_{b}\) signify the temperature difference in molecules of the system and the surrounding, respectively. The radiation factor is RDF which is set as 2 [16, 37, 41] to balance the intensification and diversification of the search process in the radiation phase. Here, all the design variables are modified during the course of the iteration process. The procedure of the MHTS optimizer is detailed in Fig. 1.

Fig. 1
figure 1

The heat transfer search algorithm

Full size image

3 Multi-objective modified heat transfer search (MOMHTS)

As a general rule, a MH optimizer can be efficient only if it poses some particular competencies. One of these is the potential to generate new solutions that can usually improve previous or existing solutions and should cover important areas of search where a global optimum can possibly be found. Another competency is that an optimizer should be able to leave the trap of local optima [60]. A good fusion of the above competencies under appropriate conditions will lead to the excellent performance of MHs. This often needs balancing two important mechanisms of as MH: exploration and exploitation (or diversification and intensification) [5, 59, 60]. Empirical knowledge of popular MHs and simulations of their convergence habit reveals that intensification tends to increase the convergence rate. Exploration, on the other hand, tends to reduce the rate of convergence. Notwithstanding, overly exploration augments the likelihood of discovering global optimality but with lesser efficiency, whereas large exploitation leads to premature convergence. Hence, the correct quantity of exploration and the accurate degree of exploitation should be in a fine balance [61]. This issue itself, however, is an unresolved task of optimization.

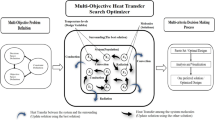
In HTS, the system molecules interact with the other system molecules and surrounding molecules through the transfer of heat to reduce the thermal imbalance. Also, at an instant energy transfer process, it is assumed to be done through one of the three modes of HTS. However, according to Patel and Savsani [37], the radiation process is more powerful in solving polynomial functions, while, for linear and nonlinear functions, the convection and conduction processes are efficient in providing solutions, respectively. Consequently, throughout the optimization process, if any phase gets more chance to work, then it will work efficiently for only one kind of function but might not work well for the rest. Nevertheless, a system transfers heat concurrently to speed up the thermal balance.

To alleviate these demerits, we come up with a modified version of HTS for multi-objective truss optimization leading to MOMHTS. In this modification, heat transfer proposed through all three modes in the fundamental HTS is synchronized. As the new solution in HTS is very much motivated by the mean solution, randomly selected solution, and the best solution of the population, there is a higher chance of premature convergence and local optima stagnation. This is due to the high proximity of solutions to each other. Therefore, based on the above facts we modified the basic HTS through the inclusion of synchronous heat transfer search, which results in a good balance between local intensification and global diversification of the optimizer. The details about the suggested modification are as follows:

3.1 Synchronous heat transfer

In the fundamental HTS optimizer, the energy interaction occurs in the form of heat between system molecules and surrounding molecules for achieving thermal equilibrium. It is assumed that this energy interaction is taken into account because of one of the three phases with equal likelihood throughout for all generations. However, heat transfer is likely to occur due to one or more than one of the three heat transfer modes being combined. Therefore, in the modified HTS optimizer, synchronized heat transfer is implemented resulting in speeding up the search process. The possibility of heat transfer modes in this state depends on probability factor for conduction mode (PFCD), probability factor for convection mode (PFCV), and probability factor for radiation mode (PFRD). Here, the values of these factors vary from 0 to 1, i.e., PFCD, PFCV, PFRD \(\in\) [0, 1] and PFCD + PFCV + PFRD = 1. Hence, during the activation of the conduction mode of heat transfer, the first one-third of the molecules in a population are updated. Similarly, the second one-third of solutions are updated during the activation of radiation mode, and the remaining solutions are updated using convection. In the original HTS optimizer, the conduction mode works better for nonlinear functions. The convection mode works more effectively for linear function, whereas the radiation mode works more efficiently for polynomial function. As a consequence, all the three operators should be activated in the synchronized form during optimization to obtain a more efficient HTS algorithm [22, 37]; Tejani et al. [52,53,54].

With such view, the PFCD, PFCV, and PFRD values are set at 0.3333 to take into account the effect of equal probability of each mode of energy interaction. Furthermore, to implement all three modes concurrently here three variables (i.e., P1, P2, and P3) are introduced to substitute the probability variable (P) where P1 is a conduction probability variable, P2 is a radiation probability variable, and P3 is a convection probability variable. This modification’s mathematical formulation is specified in the algorithm’s implementation steps. The procedure of the MOMHTS optimizer is detailed in Fig. 2.

Fig. 2
figure 2

Modified heat transfer search algorithm

Full size image

4 Problem definition

Essentially, almost all problems in the physical world are ideally suitable to be shown as multi-objective optimization problems consisting of multiple design objectives with diverse nature. Moreover, these real-world search and optimization problems mostly consist of nonlinear computational problems such as quadratic, cubic and polynomial, which are subject to multiple conflicting objectives. Formerly, due to deficiency of convenient solution techniques to obtain results these problems were transformed into a single objective artificially. The complexity of these problems is due to the generation of multiple optimal solutions, unlike single-objective problems that generate only one solution. Also, the designer has to make a trade-off between a set of multiple optimal solutions Pareto optimal sets as per the obligation. Furthermore, Pareto optimal solutions are typically unknown for a given problem. So, it becomes essential to search for multiple optimal solutions as much as possible within one run, rather than just one solution.

The formulation of the optimization of multi-objective truss problem is shown as follows:

$${\text{Find}},\,\,A = \left\{ {A_{1} , A_{2} ,.. ,A_{m} } \right\}$$
(7)

to minimize mass and maximize nodal deflection of truss

$$f_{1} \left( A \right) = \mathop \sum \limits_{i = 1}^{m} A_{i} \rho_{i} L_{i} \,{\text{and}}\,f_{2} \left( A \right) = \hbox{max} \left( {\left| {\delta_{j} } \right|} \right)$$

Subject to: Behavior constraints:

$$g(A):{\text{Stress}}\,{\text{constraints}},\,\,\,|\sigma_{i} | - \sigma_{i}^{max} \le 0$$

Side constraints:

$$\begin{aligned} & {\text{Discrete}}\,{\text{cross - sectional}}\,{\text{areas}},\quad A_{i}^{ \hbox{min} } \le A_{i} \le A_{i}^{ \hbox{max} } \\ & \quad {\text{where}},\, i = 1,2, \ldots ,m;\,j = 1,2, \ldots ,n. \\ \end{aligned}$$

Here, \(A_{i}\) stand for the design variable; \(\rho_{i}\) represents the mass density; \(L_{i}\) and \(E_{i}\) are the elemental length and Young modulus, respectively; and \(\sigma_{i}\) are elemental stress on the elements. ‘\(\delta_{j}\)’ are nodal displacements. The superscripts ‘max’ and ‘min,’ respectively, mean the upper and lower.

4.1 Dynamic penalty function

In handling design constraints such as the stress constraints expressed in (7) for use with MHs, a penalty function is the most popular choice as it provides an equivalent unconstrained problem to that with constraints. A good penalty function works in such a way that a feasible solution should have a better penalty function value than an infeasible solution. For two particular feasible solutions, one with a lower objective function is better. For two infeasible solutions, one with less constraint violation is the better. Given that objective function values which are all positive in the design domain, one of the most efficient penalty functions is the multiplication-based penalty function [26], which can be written as:

$$f\left( X \right)*\left( {1 + \varepsilon_{1} *{\text{C}}} \right)^{{\varepsilon_{2} }} ,\,{\text{C}} = \mathop \sum \limits_{i = 1}^{q} {\text{C}}_{i} ,{\text{C}}_{i} = \left| {1 - \frac{{p_{i} }}{{p_{i}^{*} }}} \right|$$
(8)

where pi is the dimension of requirement infringement having the limits as \(p_{i}^{*}\). The number of constraints is presented by q. The factors \(\varepsilon_{1}\) and \(\varepsilon_{2}\) are pre-specified by a user. In this investigation, the estimations of both \(\varepsilon_{1}\) and \(\varepsilon_{2}\) are set at 3, which were gotten from testing their impact on the parity of the investigation balance [51]; Tejani et al. [52,53,54,55].

5 Benchmark problems and discussion

The five benchmark truss problems are used to examine the proposed algorithms. These trusses have been examined by numerous researchers, including Angelo et al. [1, 2] and Tejani et al. [55,56,57]. This study considers the similar parameters used in the earlier studies [1, 2, 55,56,57]. Therefore, all five benchmark problems were executed with 100 population size and 50,000 functional evaluations. The considered algorithms are examined for 100 runs. The Pareto front hypervolume (PFHV) test is considered for the assessment. The average of the PFHV is measured to check the convergence rate of the algorithms and the standard deviation (SD) of PFHV is measured to check the algorithms’ reliability.

Likewise, a front spacing (S) measure is adopted to compute the comparative separation in the non-dominated set between the consecutive solutions [49]. Since a procedure of Pareto front P (having M objective functions) is obtained from using a specific method, the spacing of such a front is computed as:

$${\text{Spacing}} = \frac{1}{\left| P \right| - 1}\mathop \sum \limits_{i = 1}^{\left| P \right|} \left( {d_{i} - \bar{d}} \right)^{2}$$
(9)

where di is the Euclidian distance of the vector of objective function ‘i’ to its nearest neighbor. The expression |P| is the number of members in the set P. \(\bar{d}\) is the mean value of di.

The proportion of front expansion is:

$${\text{Extent}} = \mathop \sum \limits_{i = 1}^{M} \left| {f_{i}^{ \hbox{max} } - f_{i}^{ \hbox{min} } } \right|$$
(10)

where \(f_{i}^{ \hbox{max} }\) and \(f_{i}^{ \hbox{max} }\) are the minimum and maximum values, respectively, for an ith objective function shorted from all the members in P. The lower values of Spacing represent the superior Pareto front, while the higher value of Extent demonstrates the better Pareto front. The blend of the two indicators prompts another performance metric, which estimates both front spacing and extent, which is characterized as the proportion of spacing to the extent,

$${\text{Front}}\,{\text{Spacing - to - Extent}}\left( {\text{FSTE}} \right) = {\text{Spacing}}/{\text{Extent}} .$$
(11)

Equation (11) implies that the superior non-dominated front has a lower FSTE value.

Also, a statistical test, Friedman’s rank, is used to rank the various MHs. The truss optimization problems are presented in the following sections.

5.1 A 10-bar truss

The first benchmark problem which is broadly used, a 10-bar truss, is illustrated in Fig. 3. The figure also depicts geometrical information (i.e., elements, nodes, loading conditions, constraints, dimensions, etc.) of the truss. The details of design variables, material properties, and constraints are shown in Table 1. The design variables are considered from 42 discrete cross sections (i.e., 1.62, 1.8, 1.99, 2.13, 2.38, 2.62, 2.63, 2.88, 2.93, 3.09, 3.13, 3.38, 3.47, 3.55, 3.63, 3.84, 3.87, 3.88, 4.18, 4.22, 4.49, 4.59, 4.8, 4.97, 5.12, 5.74, 7.22, 7.97, 11.5, 13.5, 13.9, 14.2, 15.5, 16, 16.9, 18.8, 19.9, 22, 22.9, 26.5, 30, and 33.5 in.2) taken from Angelo et al. [2] and Tejani et al. [55,56,57].

Fig. 3
figure 3

The 10-bar truss

Full size image
Table 1 Design considerations of the truss problems
Full size table

The statistical results of the 10-bar truss are derived as the PFHV values presented in Table 2. The best PFHV, average PFHV, and SD of PFHVs are measured to check the effectiveness of the presented algorithms. The best average results found by using AS, ACS, SOS, HTS, and MHTS algorithms are 52,318.34, 55,094.06, 58,292.61, 58,735.88, and 58,849.96, respectively. Also, the SD of PFHVs found by using AS, ACS, SOS, HTS, and MHTS algorithms is 1307.00, 323.84, 149.79, 83.71, and 73.69, respectively. The results reveal that MHTS outperforms the other optimizers, while HTS and SOS rank second and third for the measure of search consistency. Also, a statistical test, Friedman’s rank, is used to compare the results of PFHVs obtained by three algorithms. The Friedman’s ranks for AS, ACS, SOS, HTS, and MHTS algorithms are 100, 200, 300, 413, and 487, respectively. As per the Friedman’s rank test at 95% significance, MHTS beats other algorithms followed by HTS and SOS. The results also show a considerable difference among the considered algorithms.

Table 2 The PFHV values for the 10-bar truss
Full size table

The front spacing-to-extent (FSTE) metric is tested, and the results are reported in Table 3. The Friedman’s rank shows that MHTS outperforms other MHs followed by HTS and AS, and similar solutions stated as per the mean value of FSTE. Also, MHTS is superior to its original version, HTS.

Table 3 The FSTE values for the 10-bar truss
Full size table

The median Pareto fronts of the considered algorithms obtained for the 100 independent runs are displayed in Fig. 4. This can be noted that the median Pareto fronts found for AS and ACS are discontinuous and broken. On the other hand, median Pareto fronts found by using the MHTS, HTS, and SOS are smooth, are continuous, and have a vast array of varied solutions, while the solutions are well spread. Overall, the assessments confirm that MHTS is the better algorithm among the considered algorithms and the considered modification advances the effectiveness of HTS.

Fig. 4
figure 4

Median Pareto fronts of the 10-bar truss

Full size image

5.2 A 25-bar 3D truss

The second benchmark problem, a 25-bar 3D truss, is shown in Fig. 5. The details of design variables, material properties, and constraints are depicted in Table 1. Loading conditions are considered as \(P_{x1} = 1\,{\text{Klb}},P_{y1} = P_{z1} = P_{y2} = P_{z2} = - 10\,{\text{Klb}},P_{x3} = 0.5\,{\text{Klb}}, \,{\text{and}}\,P_{x6} = 0.6\,{\text{Klb}}\). Also, 25 elements of the truss are grouped into eight groups by having structural symmetry with respect to planes x–z and y–z [1, 2, 55,56,57]. The design variables are considered from 30 discrete cross sections (i.e., 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2, 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.8, 3, 3.2, and 3.4 in.2) taken from Angelo et al. [1, 2] and Tejani et al. [55,56,57].

Fig. 5
figure 5

The 25-bar space truss

Full size image

The statistical results of the 25-bar truss are derived as the PFHV values and presented in Table 4. The best PFHV, average PFHV, and SD of PFHVs are measured to check the effectiveness of the presented algorithms. The best average results found by using AS, ACS, SOS, HTS, and MHTS algorithms are 1846.55, 1858.58, 1906.23, 1910.88, and 1913.17, respectively. Also, the SD of PFHVs found by using AS, ACS, SOS, HTS, and MHTS algorithms is 9.51, 13.90, 0.54, 0.51, and 0.38, respectively. The results reveal that MHTS presents the finest convergence and consistency in results’ accuracy, while HTS and SOS rank second and third, respectively, for the measure of search consistency. Also, a statistical test, Friedman’s rank, is used to compare the results of PFHVs obtained by the considered algorithms. The Friedman’s ranks for AS, ACS, SOS, HTS, and MHTS algorithms are 121, 179, 300, 400, and 500, respectively. It is revealed that MHTS is the best, while the second and third best, respectively, is HTS and SOS. The results also show a considerable difference among the considered algorithms.

Table 4 The PFHV values for the 25-bar truss
Full size table

The comparative FSTE values are given in Table 5. The Friedman’s rank MHTS, HTS, and SOS rank first, second, and third, respectively. The mean values of FSTE suggested a similar trend where MHTS outperforms its basic algorithm.

Table 5 The FSTE values for the 25-bar truss
Full size table

The median Pareto fronts of all the algorithms obtained for the 100 independent runs are shown in Fig. 6. The obtained figure demonstrates the broken and intermittent nature of AS and ACS median Pareto fronts, whereas the MHTS, HTS, and SOS median Pareto fronts are smooth, are continuous, and have a broad range of varied solutions with well spread. Overall, the assessments confirm that the proposed MHTS is the best algorithm among the considered algorithms.

Fig. 6
figure 6

Median Pareto fronts of the 25-bar truss

Full size image

5.3 A 60-bar ring truss

The third benchmark problem, a 60-bar ring truss, is presented in Fig. 7. The details of design variables, material properties, and constraints are given in Table 1. The design variables are considered from 45 discrete cross sections as [0.5, 0.6, 0.7,…, 4.9] in.2. Also, 60 elements of the truss are grouped into 25 groups by considering structural symmetry as per Angelo et al. [1, 2] and Tejani et al. [55,56,57]. Multiple loading conditions are considered as load case 1: \(P_{x1} = - 10\,{\text{Klb}}\,{\text{and}}\,P_{x7} = 9\,{\text{Klb}}\), load case 2: \(P_{x15} = P_{x18} = - 8\,{\text{Klb}}\) and \(P_{y15} = P_{y18} = 3\,{\text{Klb}}\), and load case 3: \(P_{x22} = - 20\,{\text{Klb}}\,{\text{and}}\,P_{y22} = 10\,{\text{Klb}}\).

Fig. 7
figure 7

The 60-bar ring truss

Full size image

The comparative results of the 60-bar truss are derived as the PFHV values and presented in Table 6. The best PFHV, average PFHV, and SD of PFHVs are computed to check the effectiveness of the presented algorithms. The best average results found by using AS, ACS, SOS, HTS, and MHTS algorithms are 3179.88, 3106.68, 4293.25, 4316.10, and 4324.61, respectively. Also, the SD of PFHVs found from the results of AS, ACS, SOS, HTS, and MHTS is 166.65, 74.18, 5.92, 2.04, and 1.51, respectively. The findings indicate that the MHTS obtains the best convergence and performance efficiency, while the second best is HTS. Also, the Friedman’s ranks for AS, ACS, SOS, HTS, and MHTS algorithms are 173, 127, 300, 400, and 500, respectively. MHTS is the best followed by HTS and SOS. Here, the obtained results from Friedman’s rank test also reflect the appreciable difference between the optimizers being considered.

Table 6 The PFHV values for the 60-bar truss
Full size table

The comparative FSTE results are shown in Table 7. The Friedman’s rank test shows that MHTS outperforms other MHs followed by HTS and SOS, while similar outcomes are obtained from ranking the mean values of FSTS. Also, MHTS is better than its original version.

Table 7 The FSTE values for the 60-bar truss
Full size table

Figure 8 displays the median Pareto fronts of the various algorithms obtained for 100 independent runs. This can be noted that the median Pareto fronts found for AS and ACS are irregular and spread in a tiny area. On the other side, Pareto fronts found by using the MHTS and HTS are continuous, diversified in nature, and well distributed.

Fig. 8
figure 8

Median Pareto fronts of the 60-bar truss

Full size image

5.4 A 72-bar space truss

The fourth benchmark problem, a 72-bar 3D truss, is illustrated in Fig. 9. The details of design variables, material properties, and constraints are reported in Table 1. The design variables are considered from 25 discrete cross sections as [0.1, 0.2, 0.3,…, 2.5] in.2. Also, 72 elements of the truss are grouped into 16 by considering structural symmetry as per Angelo et al. [1, 2] and Tejani et al. [55,56,57]. Multiple loading conditions are considered as load case 1: \(F_{1x} = F_{1y} = 5\,{\text{kips}}\,{\text{and}}\,F_{1z} = - 5\,{\text{kips}}\) and load case 2: \(F_{1z} = F_{2z} = F_{3z} = F_{4z} = - 5\,{\text{kips}}\).

Fig. 9
figure 9

The 72-bar 3D truss

Full size image

The results of the 72-bar truss are compared based on the PFHV values and presented in Table 8. The best PFHV, average PFHV, and SD of PFHVs are measured to check the effectiveness of the presented algorithms. The mean values of PFHV found by using AS, ACS, SOS, HTS, and MHTS algorithms are 2140.24, 2142.38, 2270.93, 2282.66, and 2285.37, respectively. Also, the SD of PFHVs found by using AS, ACS, SOS, HTS, and MHTS algorithms is 10.17, 19.50, 1.81, 0.63, and 0.39, respectively. It shows that MHTS is the best followed by HTS and SOS. The Friedman’s ranks for AS, ACS, SOS, HTS, and MHTS algorithms are 145, 155, 300, 400, and 500, respectively.

Table 8 The PFHV values for the 72-bar truss
Full size table

The result of comparing FSTE is shown in Table 9. The Friedman’s rank at 95% significant level shows that MHTS, HTS, and SOS are the top three performers in that order, while the mean values of FSTE also give similar results.

Table 9 The FSTE values for the 72-bar truss
Full size table

The median Pareto fronts of all the MHs obtained from performing 100 independent runs are displayed in Fig. 10. This can be noted that the median Pareto fronts found for AS and ACS are discontinuous and broken. On the other hand, Pareto fronts found by using MHTS, HTS, and SOS are continuously distributed and widely spread. The assessments affirm that MHTS is a superior performer to the other considered algorithms, which implies that the proposed modification improves the HTS performance.

Fig. 10
figure 10

Median Pareto fronts of the 72-bar truss

Full size image

5.5 A 942-bar tower truss

The fifth benchmark problem, a 942-bar tower truss, is shown in Fig. 11. Vertical loading along the axis of tower center (Z-direction) is − 3 kips, − 6 kips, and − 9 kips at each of the nodes in Sects. 1, 2, and 3, respectively; lateral loading along X-direction is 1.5 kips and 1 kips at each of the nodes on the right-hand side and left-hand side of the tower truss, respectively, and lateral loading along Y-direction is 1 kip at each node, respectively. The details of design variables, material properties, and constraints are depicted in Table 1. The design variables are considered from 200 discrete cross sections as [1, 2, 3,…, 200] in.2. Also, 200 elements of the truss are clustered into 59 groups by considering structural symmetry as per Angelo et al. [1, 2] and Tejani et al. [55,56,57].

Fig. 11
figure 11

The 942-bar tower truss

Full size image

The comparative results of the 942-bar truss based on the PFHV values are illustrated in Table 10. The best PFHV, average PFHV, and SD of PFHVs are measured to check the effectiveness of the presented algorithms. The mean values of PFHV found by using AS, ACS, SOS, HTS, and MHTS algorithms are 67,019,485.86, 67,205,495.61, 78,710,767.20, 83,582,579.55, and 84,034,459.15, respectively. Also, the SDs of PFHV found by using AS, ACS, SOS, HTS, and MHTS are 4,596,003.57, 1,247,239.78, 785,836.41, 135,436.80, and 85,499.11, respectively. The results reveal that MHTS performs the best followed by HTS and SOS. Also, a statistical test, Friedman’s rank, is considered to compare the results of PFHVs obtained by the considered algorithms. As per the rank check of the Friedman at a significant level of 95%, it is clear that the MHTS outperforms other optimizers, while HTS and SOS joined the second and third places in the ranking. This comparative results show the superiority of the proposed algorithm over the others for the design problem that can be considered a large-scale problem.

Table 10 The PFHV values for the 942-bar truss
Full size table

The FSTE values obtained from the various optimizers are given in Table 11. The Friedman’s rank at 95% significant level presents that MHTS, HTS, and SOS are the top three performers in that order. The comparative average results of FSTE also received similar solutions.

Table 11 The FSTE values for the 942-bar truss
Full size table

Figure 12 illustrates the median Pareto fronts of the optimizers where 100 independent runs for each method are performed. It is understood that in a small territory, the obtained median Pareto fronts are discontinuous and spread out for AS, ACS, and SOS optimizers. Contrary to this, the Pareto fronts are constantly distributed, are stable, and have a variety of different outcomes, when they are discovered using the MHTS and HTS optimizers. This obtained nature supports the supremacy of exploring Pareto fronts using MHTS and HTS over AS, ACS, and SOS. In conclusion, MOMHTS is superior to the methods available in the previous literature. Moreover, from the findings, it can be comprehended that the suggested modification leads to better MOHTS effectiveness.

Fig. 12
figure 12

Median Pareto fronts of the 942-bar truss

Full size image

6 Conclusions

This study presented an effective, modified version of a multi-objective HTS optimizer termed MOMHTS for truss optimization. The new algorithm is achieved by means of synchronizing the three heat transfer operators, which is further improved from the previous version of HTS. From the comparative results of the five standard test problems of truss optimization, it can be concluded that the proposed optimizer is superior to the others found in the literature and its original HTS. The gap between MOMHTS and the rest is even wider when the design problem is large scale. This implies that the proposed method is more suitable to the real word design of truss than the others.

For further work, one can utilize MOMHTS as a potential option for taking care of complex and real-world design problems that cannot be comprehended utilizing the current meta-heuristic optimizers. There is a fairly likely chance of further enhancement in the performance of the proposed optimizer which can be obtained with further modification, hybridization, integration, and improvement that can be used in solving more intricate truss design problems. Moreover, the application can be extended to the multi-objective problems with conflicting and dynamic constrained design problems.