1 Introduction

Sandwich structure is a type of advanced composites with high stiffness-to-weight ratio, long fatigue life as well as excellent sound and thermal insulation, which are widely used in the engineering application fields of marine, aerospace and automotive industries. However, a significant problem is that the delamination phenomenon would happen suddenly in the bonded surfaces between the two stiff face sheets and the soft core for the conventional sandwich-type structures. Fortunately, this problem can be avoided by using the functionally graded (FG) material instead of the isotropic homogenous material. The FG material is a type of material with its properties changed continuously from one surface to another. By virtue of the concept of FG sandwich design, setting the two face sheets of the sandwich as FG materials, or designing the core of sandwich as FG material can provide the smooth change behaviors in the interfaces, which can effectively avoid the interface and stress concentration problems in the conventional sandwich-type structures. The pioneering researcher on this structure is Zenkour [1] who has studied the vibration and buckling performances of FG sandwich structures on the basis of the shear deformation theory. Subsequently, many academic works were carried out to reveal the mechanical behaviors of these structures (Refs. [2,3,4,5].).

As is known to all, the FG material was firstly invented in 1980s to solve the problems of ultrahigh temperatures and extremely great temperature gradients in space planes [6]. Due to this fact, the FG sandwich structures also exhibit excellent application prospects in thermal tolerance, which indices that exploring their thermo-mechanical behaviors is a critical research area that needs to pay more attention. Recently, the thermo-elastic behaviors of FG and FG sandwich structures have been examined theoretically by a number of investigations. For FG structures, Tu et al. [7] utilized the higher-order shear deformation theory to conduct the thermo-elastic free vibration analyses of FG plates. Shen et al. [8, 9] studied the nonlinear thermo-elastic vibration of FG composite laminated rectangular and cylindrical panels reinforced by graphene on the basis of the higher-order shear deformation plate and shell theories, respectively. Besides, the buckling characteristics of FG orthotropic cylindrical shells in thermal environment were studied [10]. For FG structures, Liu et al. [11] presented a theoretical model for thermal–mechanical coupling buckling of FG sandwich beams with porosity defects based on the higher-order sinusoidal shear deformation theory. Besides, Zenkour and Alghamdi [12] studied the thermo-elastic bending performances of FG sandwich plates by employing the shear deformable plate theory. Tung [13] analyzed the nonlinear behavior of doubly curved FG sandwich panels under thermal environments. Other similar studies were also carried out by several different authors [14,15,16,17].

However, most of the aforementioned studies are limited to the FG sandwich structures under the macroscale. In recent years, with the rising demands in modern nanotechnologies, many advanced structures under nanoscale have been fabricated and are widely applied in various nanoelectromechanical systems (NEMS). A typical characteristic of these structures is that the size-dependent behavior will affect their mechanical performance significantly. To this end, developing methods to reveal their size-dependent behavior is an important task, in which experimental analysis and molecular dynamics (MD) simulation are two effective ways. Due to the complexity of small-scale experiments and the high time cost of MD simulation, the size-dependent continuum mechanics models including the nonlocal continuum model [18,19,20,21], strain gradient model [22] as well as couple stress model [23, 24] gain more popularity. Among them, the nonlocal continuum mechanics model is the most famous one [19, 25]. However, a shortcoming of this theory is that the nonlocal behavior can only present the stiffness-softening mechanism, which neglects the stiffness-hardening mechanism presented in many experiments and strain gradient elasticity. In the framework of the nonlocal strain gradient theory, Lim et al. [26] matched the dispersion curves of nanobeams with experiments and concluded that the nonlocal strain gradient theory can capture the size behavior of nanostructures more accurately. Recently, this theory has widely adopted to reveal the size-dependent behavior of FG nanostructures. For instance, Li and Hu [27, 28] studied bending, vibration and buckling behavior of FG nanobeam by using this theory. She et al. [29] studied the buckling characteristics of porous FG curved nanobeams. The hydro-thermal vibration behaviors of FG nanoplate were analyzed by Barati and Shahverdi [30] with the aid of this theory.

Apart from the mechanical behaviors of FG nanostructures under room temperature, the thermo-mechanical characteristics of these structures also have aroused a significant concern. Employing the nonlocal continuum mechanics model, Barati and Shahverdi [31] analyzed the vibration performance of FG nanoplate in thermal environment. Nami et al. [32] illustrated the thermal buckling behaviors of FG nanoplates. On the basis of this theory, the thermo-mechanical behaviors of FG nanobeams [33,34,35] were also widely investigated. Besides, the nonlocal strain gradient theory was also adopted to illustrate the thermo-mechanical behavior of FG nanostructures. For instance, Ebrahimi and Barati [36, 37] studied the influence of thermal environment on the vibration and buckling behaviors of FG nanobeams based on the nonlocal strain gradient theory. Similar studies were also carried out by Barati and Shahverdi [30] to show the thermo-vibration behavior of FG nanoplates. From these cited references, even though some academic studies have been conducted on thermo-mechanical behavior of FG nanostructures, there is no work available in the literature for the analysis of FG sandwich nanostructures subjected to thermal environment. One aim of the present study is to set up a theoretical model to detect the influence of thermal environment on the vibration performance of FG sandwich nanobeams.

Another novelty of the present work is that most previous studies are focused on the nanostructures with perfect geometry, and the geometric imperfection caused by the manufacturing error is often neglected. To provide more accurate predictions for mechanical behaviors of nanostructures, few theoretical models with consideration of the effect of geometric imperfection are presented. For instance, Ghayesh et al. [38,39,40,41] presented some systematical analyses to reveal the influence of geometric imperfection on the mechanical performances of microbeams and microplates by employing the modified couple stress theory. Based on the same theory, Dehrouyeh-Semnani et al. [42] investigated the thermal buckling of microbeams made of temperature-dependent FG materials. In another work, Sahmani et al. [43, 44] adopted the surface stress theory to investigate the effect of initial geometric imperfection on the nonlinear buckling and post-buckling characteristics of cylindrical nanoshells. Li et al. [45] studied the nonlinear vibration response of porous nanobeams involving geometric imperfection via the nonlocal strain gradient theory. Recently, the influence of geometric imperfection on the free vibration of FG sandwich nanobeam was analyzed by Liu et al. [46]. Moreover, Duc et al. [47] presented some related investigations on the nonlinear dynamics of FG sandwich macro-plate with initial geometrical curvature in thermal environment. However, the size-dependent effect is not taken into account in their studies.

According to the best of our knowledge, minimal research has been undertaken on thermo-mechanical behaviors of FG sandwich nanostructures by considering the effect of geometric imperfection. In this paper, the nonlinear vibration behaviors of FG sandwich nanobeams in the presence of initial geometric imperfection and subjected to thermal loadings are investigated on the basis of the nonlocal strain gradient theory. The material properties of the FG sandwich nanobeam are treated as temperature-dependent parameters. The governing equation of the imperfect FG sandwich nanobeam excited by transverse harmonic force is derived by using Hamilton’s principle, and the solution is obtained with the aid of the multiple-scale method. Firstly, the presented theoretical model is validated by comparing the obtained results with those presented in two previous works. Then, the numerical examples are presented to show the effects of various variables including size-dependent parameters, external temperature variation, geometric imperfection amplitude, gradient index and sandwich configuration on the nonlinear dynamic response of FG sandwich nanobeams in thermal environment.

2 Theoretical formulation

2.1 FG sandwich nanobeam

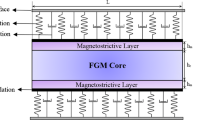
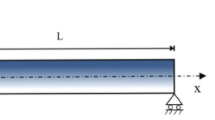
As presented in Fig. 1, a clamped supported FG sandwich nanobeam with thickness h, length L and width b is taken into account. Coordinates of points on the cross section are denoted as (x, z) in the Cartesian coordinate system. The range of coordinates along x and z directions are (0, L) and (− h/2, h/2), respectively. It is assumed that the FG sandwich nanobeams are composed of ceramic and metal materials whose properties are temperature dependent, and the volume fractions of materials vary continuously along z axis. The effective material properties P (e.g., Young’s modulus E, mass density ρ and thermal expansion coefficients αt) as a function of z and T can be expressed by the rule of mixture, i.e., [48]

$$P(z,T) = P_{{\text{c}}} (z,T)V_{{\text{c}}} (z) + P_{{\text{m}}} (z,T)V_{{\text{m}}} (z)$$
(1)
Fig. 1
figure 1

The schematic diagram of a geometrically imperfect FG sandwich nanobeam with b four material distribution configurations

Full size image

where V denotes the volume fraction; the subscript c and m represent ceramic and metal, respectively.

The material properties are denoted as functions of temperature as follows [49]:

$$P(T) = P_{0} \left( {P_{ - 1} T^{ - 1} + 1 + P_{1} T + P_{2} T^{2} + P_{3} T^{3} } \right)$$
(2)

in which Pi (i = − 1, 0, 1, 2, 3) are material parameters, and they are all temperature dependent.

FG sandwich nanobeams with four different material distribution configurations are considered in the paper, as shown in Fig. 1b. Two of them are asymmetric configurations, and the others are symmetric configurations. The material distribution configurations are given in the form of volume fraction of ceramic phase along the thickness direction. Particularly, the volume fractions of materials are continuous in the interfaces between different layers. As shown in Fig. 2, the volume fractions of ceramic phase along the thickness direction for these four material distribution configurations are presented, in which the symbol ‘1–1–1’ and ‘1–2–1’ represent the thickness ratio for each layer from the bottom to the top surfaces. From these figures, it is clear that Type A and Type B are asymmetric configurations, while Type C and Type D denote two symmetric configurations. The volume fraction of ceramic phase changes from 0 to 1 for Type A and Type B, but they are varied in different ways. Type C has the largest volume fraction of ceramic phase in the core, and it changes gradually from the top to bottom surfaces, respectively, while the volume fraction of ceramic phase for Type D is exhibited in an opposite way. The detail volume fractions of ceramic phase for each configuration are expressed as follows:

Fig. 2
figure 2

Volume fraction of ceramic (Vc) for FG sandwich nanobeams under several power law indexes: a Type A, b Type B, c Type C and d Type D

Full size image

Type A: FG nanobeams. The volume fraction of ceramic phase follows the exponential rule with exponent p as:

$$V_{{\text{c}}} (z) = \left( {\frac{z}{h} + \frac{1}{2}} \right)^{p}$$
(3)

Type B: FG sandwich nanobeams with FG core and homogeneous skins. The top and bottom surfaces are composed of full ceramic and full metal phases, respectively. The ceramic volume fraction Vc(i) in the ith layer is given as:

$$\left\{ {\begin{array}{*{20}l} {V_{{\text{c}}}^{(1)} (z) = 0,} \hfill & {{\text{for}}\;z \in \left[ {h_{0} ,h_{1} } \right]} \hfill \\ {V_{{\text{c}}}^{(2)} (z) = \left( {\frac{{z - h_{1} }}{{h_{2} - h_{1} }}} \right)^{p} ,} \hfill & {{\text{for}}\;z \in \left[ {h_{1} ,h_{2} } \right]} \hfill \\ {V_{{\text{c}}}^{(3)} (z) = 1,} \hfill & {{\text{for}}\;z \in \left[ {h_{2} ,h_{3} } \right]} \hfill \\ \end{array} } \right.$$
(4)

Type C: FG sandwich nanobeams with full ceramic core and FG skins. The material distribution is symmetric with respect to the geometric neutral plane. The volume fraction of ceramic is:

$$\left\{ {\begin{array}{*{20}l} {V_{{\text{c}}}^{(1)} (z) = \left( {\frac{{z - h_{0} }}{{h_{1} - h_{0} }}} \right)^{p} ,} \hfill & {{\text{for}}\;\;z \in \left[ {h_{0} ,h_{1} } \right]} \hfill \\ {V_{{\text{c}}}^{(2)} (z) = 1,{\kern 1pt} } \hfill & {{\text{for}}\;\;z \in \left[ {h_{1} ,h_{2} } \right]} \hfill \\ {V_{{\text{c}}}^{(3)} (z) = \left( {\frac{{z - h_{3} }}{{h_{2} - h_{3} }}} \right)^{p} ,} \hfill & {{\text{for}}\;\;z \in \left[ {h_{2} ,h_{3} } \right]} \hfill \\ \end{array} } \right.$$
(5)

Type D: similar to Type C with full metal core and FG skins. The ceramic distribution satisfies:

$$\left\{ {\begin{array}{*{20}l} {V_{{\text{c}}}^{(1)} (z) = 1 - \left( {\frac{{z - h_{0} }}{{h_{1} - h_{0} }}} \right)^{p} ,} \hfill & {{\text{for}}\;\;z \in \left[ {h_{0} ,h_{1} } \right]} \hfill \\ {V_{{\text{c}}}^{(2)} (z) = 0,{\kern 1pt} } \hfill & {{\text{for}}\;\;z \in \left[ {h_{1} ,h_{2} } \right]} \hfill \\ {V_{{\text{c}}}^{(3)} (z) = 1 - \left( {\frac{{z - h_{3} }}{{h_{2} - h_{3} }}} \right)^{p} ,} \hfill & {{\text{for}}\;\;z \in \left[ {h_{2} ,h_{3} } \right]} \hfill \\ \end{array} } \right.$$
(6)

It is assumed that FG sandwich nanobeam is exposed to the thermal environment with temperature varying linearly through the thickness, and the temperature is described as a function of z by [50]

$$T(z) = T_{0} + \Delta T_{1} + \Delta T_{2} \left( {\frac{1}{2} + \frac{z}{h}} \right)$$
(7)

where T0 is the reference temperature assumed to be 300 K. ΔT1 and ΔT2 are the uniform temperature increment and the temperature gradient, respectively.

2.2 Nonlocal strain gradient theory

According to the nonlocal strain gradient theory [26], the total stress tensor σij and the strain energy U can be separately expressed as:

$$\sigma_{ij} = \sigma_{ij}^{(0)} - \nabla \sigma_{{ij{\text{m}}}}^{(1)}$$
(8)
$$U = \frac{1}{2}\int_{V} {\left( {\sigma_{ij}^{(0)} \varepsilon_{ij} + \sigma_{{ij{\text{m}}}}^{(1)} \varepsilon_{{ij,{\text{m}}}} } \right)} {\text{d}}V$$
(9)

in which \(\sigma_{ij}^{(0)}\) and \(\sigma_{{ij{\text{m}}}}^{(1)}\) are stress tensor and its high-order term, respectively; \(\nabla\) denotes the Laplacian operator; εij and εij,m stands strain tensor and its gradient term. The stress tensor and its high-order term can be determined as

$$\begin{aligned} \sigma_{ij}^{(0)} & = C_{ijkl} \int_{V} {\alpha_{0} (\left| {{\varvec{x}} - {\varvec{x}}^{\prime } } \right|,e_{0} a)} \varepsilon_{kl} ({\varvec{x}}^{\prime } ){\text{d}}V \\ \sigma_{{ij{\text{m}}}}^{(1)} & = l^{2} C_{ijkl} \int_{V} {\alpha_{1} (\left| {{\varvec{x}} - {\varvec{x}}^{\prime } } \right|,e_{1} a)} \varepsilon_{{kl,{\text{m}}}} ({\varvec{x}}^{\prime } ){\text{d}}V \\ \end{aligned}$$
(10)

where α0 and α1 denote the kernel functions; e0a and e1a are the small-scale coefficients which indicate the effect of nonlocal stress field; l reflects the influence of strain gradient field; and all these small-scale parameters can be determined by matching the dispersion wave performance with the model of atomic lattice dynamics. Besides, Cijkl signifies the elastic constants. Suppose the kernel functions satisfy the Eringen’s nonlocal assumption [19, 25] and e = e0 = e1, the nonlocal strain gradient relation for a Euler–Bernoulli FG nanobeam can be denoted as

$$\left[ {1 - \left( {ea} \right)^{2} \nabla^{2} } \right]\sigma_{xx} = (1 - l^{2} \nabla^{2} )E(z)\varepsilon_{xx}$$
(11)

2.3 Governing equation of FG sandwich nanobeams

Based on Euler–Bernoulli beam theory, the displacement field is expressed as [42]

$$\begin{aligned} & u_{x} (x,z,t) = u(x,t) - z\frac{\partial w(x,t)}{{\partial x}} \\ & u_{y} (x,z,t) = 0 \\ & u_{z} (x,z,t) = w(x,t) + w_{0} (x) \\ \end{aligned}$$
(12)

where ux, uy and uz are the displacements along coordinate axes; u and w denote the axial and transverse displacements on the geometric neutral plane, respectively; w0 represents the initial geometric imperfection. Moreover, by considering the Von Karman geometric nonlinearity, the strain field εxx takes the following form [51]

$$\varepsilon_{xx} = \frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} - z\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{\partial w}{{\partial x}}\frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}$$
(13)

Applying Hamilton’s variational principle, we have

$$\int_{0}^{t} {(\delta K - \delta U + \delta V){\text{d}}t} = 0$$
(14)

where Eq. (14), K, U and V denote kinetic energy, strain energy and external work associated with harmonic excitations as well as thermal effects, respectively.

The virtual kinetic energy δK of the FG sandwich nanobeam is

$$\begin{aligned} \delta K & = \int_{V} {\rho (z)} \left[ {\frac{{\partial u_{x} }}{\partial t}\delta \left( {\frac{{\partial u_{x} }}{\partial t}} \right) + \frac{{\partial u_{z} }}{\partial t}\delta \left( {\frac{{\partial u_{z} }}{\partial t}} \right)} \right]{\text{d}}V \\ & = \int_{0}^{L} {\int_{{h_{0} }}^{{h_{3} }} {\rho (z)} } \left[ {\frac{{\partial u_{x} }}{\partial t}\delta \left( {\frac{{\partial u_{x} }}{\partial t}} \right) + \frac{{\partial u_{z} }}{\partial t}\delta \left( {\frac{{\partial u_{z} }}{\partial t}} \right)} \right]b{\text{d}}z{\text{d}}x \\ \end{aligned}$$
(15)

The above equation can be simplified as the following form by assuming ux ≈ u and uz ≈ w,

$$\begin{aligned} \delta K & \approx \int_{ - h/2}^{h/2} {\rho (z)b} {\text{d}}z\int_{0}^{L} {\left[ {\frac{\partial u}{{\partial t}}\delta \left( {\frac{\partial u}{{\partial t}}} \right) + \frac{\partial w}{{\partial t}}\delta \left( {\frac{\partial w}{{\partial t}}} \right)} \right]} {\text{d}}x \\ & = I_{0} \int_{0}^{L} {\left[ {\frac{\partial u}{{\partial t}}\delta \left( {\frac{\partial u}{{\partial t}}} \right) + \frac{\partial w}{{\partial t}}\delta \left( {\frac{\partial w}{{\partial t}}} \right)} \right]} {\text{d}}x \\ \end{aligned}$$
(16)

in which \(I_{0} = b\int_{ - h/2}^{h/2} {\rho (z)} {\text{d}}z\).

With the help of Eqs. (9) and (13), the virtual strain energy δU for the FG sandwich nanobeam incorporating the thickness effect can be expressed as [52,53,54,55]

$$\begin{aligned} \delta U & = \int_{V} {\left( {\sigma_{xx}^{(0)} \delta \varepsilon_{xx} + \sigma_{xxx}^{(1)} \delta \varepsilon_{xx,x} + \sigma_{xxz}^{(1)} \delta \varepsilon_{xx,z} } \right)} {\text{d}}V \\ & = \int_{V} {\left( {\sigma_{xx} \delta \varepsilon_{xx} + \sigma_{xxz}^{(1)} \delta \varepsilon_{xx,z} } \right){\text{d}}V} + \left. {\left[ {\int_{A} {\left( {\sigma_{xxx}^{(1)} \delta \varepsilon_{xx,x} } \right){\text{d}}A} } \right]} \right|_{0}^{L} \\ & = \int_{0}^{L} {\left( {N_{xx} \delta \frac{\partial u}{{\partial x}} + N_{xx} \frac{\partial w}{{\partial x}}\delta \frac{\partial w}{{\partial x}} + N_{xx} \frac{\partial w}{{\partial x}}\delta \frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}} \right.} \\ & \quad \left. { + N_{xx} \frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}\delta \frac{\partial w}{{\partial x}} - M\delta \frac{{\partial^{2} w}}{{\partial x^{2} }} - N_{zz}^{(1)} \delta \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right){\text{d}}x \\ & \quad + \left( {N_{xx}^{(1)} \delta \frac{\partial u}{{\partial x}} + N_{xx}^{(1)} \frac{\partial w}{{\partial x}}\delta \frac{\partial w}{{\partial x}} + N_{xx}^{(1)} \frac{\partial w}{{\partial x}}\delta \frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}} \right. \\ & \quad \left. {\left. { + N_{xx}^{(1)} \frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}\delta \frac{\partial w}{{\partial x}} - M^{(1)} \delta \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} \right|_{0}^{L} \\ \end{aligned}$$
(17)

in which the bending moments and axial forces are calculated as

$$\begin{aligned} M & = \int_{A} {z\sigma_{xx} {\text{d}}A} ,\quad M^{(1)} = \int_{A} {z\sigma_{xx}^{(1)} {\text{d}}A} , \\ N_{xx} & = \int_{A} {\sigma_{xx} {\text{d}}A,} \quad N_{xx}^{(1)} = \int_{A} {\sigma_{xx}^{(1)} {\text{d}}A} ,\quad N_{zz}^{(1)} = \int_{A} {\sigma_{xx,z}^{(1)} {\text{d}}A} {\kern 1pt} \\ \end{aligned}$$
(18)

Introduce \(M^{(0)}\) and \(N_{xx}^{(0)}\) as

$$\begin{array}{*{20}c} {M^{(0)} = \int_{A} {z\sigma_{xx}^{(0)} {\text{d}}A} ,} & {N_{xx}^{(0)} = \int_{A} {\sigma_{xx}^{(0)} {\text{d}}A} } \\ \end{array}$$
(19)

Then, the moment M and the axial force Nxx are converted to

$$\begin{gathered} M = \int_{A} {z\sigma_{xx} {\text{d}}A} = \int_{A} {z\left( {\sigma_{xx}^{(0)} - \frac{{\partial \sigma_{xx}^{(1)} }}{\partial x}} \right){\text{d}}A} = M^{(0)} - \frac{{\partial M^{(1)} }}{\partial x} \hfill \\ N_{xx} = \int_{A} {\sigma_{xx} {\text{d}}A} = \int_{A} {\left( {\sigma_{xx}^{(0)} - \frac{{\partial \sigma_{xx}^{(1)} }}{\partial x}} \right){\text{d}}A} = N_{xx}^{(0)} - \frac{{\partial N_{xx}^{(1)} }}{\partial x} \hfill \\ \end{gathered}$$
(20)

Besides, one can also obtain \(N_{zz}^{(1)} = - l^{2} A_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }}\) by using Eqs. (10), (13) and (18).

Combining Eqs. (11), (13) and (20), one has

$$\begin{aligned} M - \left( {ea} \right)^{2} \frac{{\partial^{2} M}}{{\partial x^{2} }} & = \left( {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)B_{xx} \left[ {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right. \\ & \quad \left. { + \frac{\partial w}{{\partial x}}\frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}} \right] - D_{xx} \left( {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} \\ \end{aligned}$$
(21)
$$\begin{aligned} N_{xx} - \left( {ea} \right)^{2} \frac{{\partial^{2} N_{xx} }}{{\partial x^{2} }} & = \left( {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)A_{xx} \left[ {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right. \\ & \quad \left. { + \frac{\partial w}{{\partial x}}\frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}} \right] - \left( {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)B_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} \\ \end{aligned}$$
(22)

where

$$\left( {A_{xx} ,B_{xx} ,D_{xx} } \right) = \int_{A} {E(z)\left( {1,z,z^{2} } \right){\text{d}}A}$$
(23)

The virtual external work induced by the harmonic excitations is written as

$$\delta V_{F} = \int_{0}^{L} {F\cos \left( {\Omega t} \right)\delta w{\text{d}}x}$$
(24)

In addition, the virtual external work of the thermal load is

$$\delta V_{{\text{T}}} = - \int_{0}^{L} {N_{{\text{T}}} \frac{\partial w}{{\partial x}}\delta \left( {\frac{\partial w}{{\partial x}}} \right){\text{d}}x}$$
(25)

where NT is axial force caused by thermal stress and can be calculated as [34]

$$N_{{\text{T}}} = \int_{A} {E(z,T)\alpha_{\text{t}} (z,T)} \left[ {T(z) - T_{0} } \right]{\text{d}}A$$
(26)

Substituting Eqs. (16), (17), (24) and (25) into Eq. (14), and setting the coefficients of δu and δw to zero, the following equilibrium equations can be obtained

$$\delta u:\frac{{\partial N_{xx} }}{\partial x} - I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} = 0$$
(27)
$$\begin{aligned} & \delta w: - I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} + \frac{\partial }{\partial x}\left[ {N_{xx} \left( {\frac{\partial w}{{\partial x}} + \frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}} \right)} \right] + \frac{{\partial^{2} N_{zz}^{(1)} }}{{\partial x^{2} }} \\ & \quad + N_{T} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} M}}{{\partial x^{2} }} + F\cos (\Omega t) = 0 \\ \end{aligned}$$
(28)

Furthermore, the boundary conditions at both ends of nanobeams are

$$\begin{aligned} & \begin{array}{*{20}c} {\delta u:} & {{\kern 1pt} N_{xx} = 0{\kern 1pt} \;or\;u = 0} \\ \end{array} , \\ & \begin{array}{*{20}c} {\delta \frac{\partial u}{{\partial x}}:{\kern 1pt} } & {N_{xx}^{(1)} = 0\;\;or\;\;\frac{\partial u}{{\partial x}} = 0} \\ \end{array} , \\ {\kern 1pt} & \begin{array}{*{20}c} {\delta w:{\kern 1pt} } & {N_{xx} \frac{\partial w}{{\partial x}} + N_{xx} \frac{{{\text{d}}w_{0} }}{{{\text{d}}x}} + N_{T} \frac{\partial w}{{\partial x}} + \frac{\partial M}{{\partial x}} = 0\;\;{\text{or}}\;\;w = 0} \\ \end{array} , \\ & \begin{array}{*{20}c} {\delta \frac{\partial w}{{\partial x}}:{\kern 1pt} } & {M - N_{xx}^{(1)} \left( {\frac{\partial w}{{\partial x}} + \frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}} \right) = 0\;\;{\text{or}}\;\;\frac{\partial w}{{\partial x}} = 0} \\ \end{array} , \\ & \begin{array}{*{20}c} {\delta \frac{{\partial^{2} w}}{{\partial x^{2} }}:{\kern 1pt} } & {M^{(1)} = 0\;\;{\text{or}}\;\;\frac{{\partial^{2} w}}{{\partial x^{2} }} = 0} \\ \end{array} \\ \end{aligned}$$
(29)

For the axial inertia is negligible in Eq. (27), we have

$$\frac{{\partial N_{xx} }}{\partial x} = 0$$
(30)

By view of Eq. (22), one has

$$N_{xx} = \left( {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\left\{ {A_{xx} \left[ {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \frac{\partial w}{{\partial x}}\frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}} \right] - B_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right\}$$
(31)

From Eq. (10), the relationship between \(N_{xx}^{(0)}\) and \(N_{xx}^{(1)}\) can be expressed as

$$N_{xx}^{(1)} = l^{2} \frac{{\partial N_{xx}^{(0)} }}{\partial x}$$
(32)

Combining Eqs. (20) and (32), one has

$$N_{xx} = N_{xx}^{(0)} - l^{2} \frac{{\partial N_{xx}^{(1)} }}{\partial x} = N_{xx}^{(0)} - l^{2} \frac{{\partial^{2} N_{xx}^{(0)} }}{{\partial x^{2} }} = \left( {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)N_{xx}^{(0)}$$
(33)

By inserting Eq. (31) into the above equation, we have

$$\begin{aligned} N_{xx}^{(0)} & = A_{xx} \left[ {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \frac{\partial w}{{\partial x}}\frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}} \right] - B_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }}, \\ N_{xx}^{(1)} & = l^{2} A_{xx} \left[ {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{\partial w}{{\partial x}}\frac{{{\text{d}}^{2} w_{0} }}{{{\text{d}}x^{2} }} + \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}} \right] \\ & \quad - l^{2} B_{xx} \frac{{\partial^{3} w}}{{\partial x^{3} }} \\ \end{aligned}$$
(34)

Substituting the equation \(N_{xx}^{(0)}\) into Eq. (33), the axial force \(N_{xx}\) can be denoted as

$$N_{xx} = A_{xx} \left( {\frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \frac{\partial w}{{\partial x}}\frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}} \right) - B_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{{\partial N_{xx}^{(1)} }}{\partial x}$$
(35)

For a FG sandwich nanobeam with two ends clamped, the displacements of both ends can be determined as

$$\left. u \right|_{x = 0} = \left. u \right|_{x = L} = 0,\;\;\left. {\frac{\partial w}{{\partial x}}} \right|_{x = 0} = \left. {\frac{\partial w}{{\partial x}}} \right|_{x = L} = 0,\;\;\left. {w_{0} } \right|_{x = 0} = \left. {w_{0} } \right|_{x = L} = 0$$
(36)

Moreover, according to Eq. (29), we have

$$\left. {N_{xx}^{(1)} } \right|_{x = 0} = \left. {N_{xx}^{(1)} } \right|_{x = L} = 0$$
(37)

Integrating both sides of Eq. (35) from 0 to L, leads to

$$N_{xx} = N_{0} = \frac{{A_{xx} }}{L}\int_{0}^{L} {\left( {\frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \frac{\partial w}{{\partial x}}\frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}} \right)} {\text{d}}x$$
(38)

As can be seen from Eq. (38), the axial force can be affected by both the deflection and initial geometric imperfection. By combining Eqs. (21), (22), (28) and (38), the bending moment can be obtained as

$$\begin{aligned} M & = \frac{{B_{xx} }}{{A_{xx} }}N_{0} + \left( {\frac{{B_{xx}^{2} }}{{A_{xx} }} - D_{xx} } \right)\left( {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} \\ & \quad + \left( {ea} \right)^{2} \left\{ {I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - N_{T} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{{\partial^{2} N_{zz}^{(1)} }}{{\partial x^{2} }}} \right. \\ & \quad \left. { - N_{0} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}{ + }\frac{{{\text{d}}^{2} w_{0} }}{{{\text{d}}x^{2} }}} \right) - F\cos (\Omega t)} \right\} \\ \end{aligned}$$
(39)

Substituting Eqs. (38) and (39) into Eq. (28), one has the governing equation

$$\begin{aligned} & \left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} + \left( {D_{xx} - \frac{{B_{xx}^{2} }}{{A_{xx} }}} \right)\left( {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} \\ & \quad + l^{2} A_{xx} \frac{{\partial^{4} w}}{{\partial x^{4} }} - \left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right]N_{T} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \left[ {1 - \left( {ea} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right] \\ & \quad \left\{ {\frac{{A_{xx} }}{L}\int_{0}^{L} {\left[ {\frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \frac{\partial w}{{\partial x}}\frac{{{\text{d}}w_{0} }}{{{\text{d}}x}}} \right]} {\text{d}}x} \right\}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{{\text{d}}^{2} w_{0} }}{{{\text{d}}x^{2} }}} \right) \\ & \quad - F\cos (\Omega t) = 0 \\ \end{aligned}$$
(40)

Following dimensionless quantities are introduced to rewrite the governing equation in the normalized form:

$$\begin{aligned} & r = \sqrt {\frac{I}{A}} ,\tilde{I}_{0} = \frac{{I_{0} }}{{\rho _{{\text{c}}} A}},\tilde{x} = \frac{x}{L},\tilde{w} = \frac{w}{r},\tilde{w}_{0} = \frac{{w_{0} }}{r}, \\ & \mu = \frac{{ea}}{L},\eta = \frac{l}{L},\gamma = \frac{L}{r},\tau = t\sqrt {\frac{{E_{{\text{c}}} I}}{{\rho _{{\text{c}}} AL^{4} }}} , \\ & \left( {\tilde{A}_{{xx}} ,\tilde{B}_{{xx}} ,\tilde{D}_{{xx}} } \right) = \left( {\frac{{A_{{xx}} }}{{E_{{\text{c}}} A}},\frac{{B_{{xx}} r}}{{E_{{\text{c}}} I}},\frac{{D_{{xx}} }}{{E_{{\text{c}}} I}}} \right), \\ & \tilde{\Omega } = \Omega /\sqrt {\frac{{E_{c} I}}{{\rho _{{\text{c}}} AL^{4} }}} ,\tilde{F} = \frac{{FL^{4} }}{{rE_{{\text{c}}} I}},\tilde{N}_{{\text{T}}} = \frac{{N_{{\text{T}}} L^{2} }}{{E_{{\text{c}}} I}} \\ \end{aligned}$$
(41)

in which A and I are, respectively, the area and moment of inertia of the cross section

$$\left( {A,I} \right) = b\int_{ - h/2}^{h/2} {\left( {1,z^{2} } \right){\text{d}}z}$$
(42)

Replacing quantities in Eq. (40) with the dimensionless one yields

$$\begin{aligned} & \left[ {1 - \mu^{2} \frac{{\partial^{2} }}{{\partial \tilde{x}^{2} }}} \right]\tilde{I}_{0} \frac{{\partial^{2} \tilde{w}}}{{\partial \tau^{2} }} + \left( {\tilde{D}_{xx} - \frac{{\tilde{B}_{xx}^{2} }}{{\tilde{A}_{xx} }}} \right)\left( {1 - \eta^{2} \frac{{\partial^{2} }}{{\partial \tilde{x}^{2} }}} \right)\frac{{\partial^{4} \tilde{w}}}{{\partial \tilde{x}^{4} }} \\ & \quad + \eta^{2} \gamma^{2} \tilde{A}_{xx} \frac{{\partial^{4} \tilde{w}}}{{\partial \tilde{x}^{4} }} - \left[ {1 - \mu^{2} \frac{{\partial^{2} }}{{\partial \tilde{x}^{2} }}} \right]\tilde{N}_{T} \frac{{\partial^{2} \tilde{w}}}{{\partial \tilde{x}^{2} }} - \left[ {1 - \mu^{2} \frac{{\partial^{2} }}{{\partial \tilde{x}^{2} }}} \right] \\ & \quad \left( {\frac{{\partial^{2} \tilde{w}}}{{\partial \tilde{x}^{2} }} + \frac{{{\text{d}}^{2} \tilde{w}_{0} }}{{{\text{d}}\tilde{x}^{2} }}} \right)\left\{ {\tilde{A}_{xx} \int_{0}^{1} {\left[ {\frac{1}{2}\left( {\frac{{\partial \tilde{w}}}{{\partial \tilde{x}}}} \right)^{2} + \frac{{\partial \tilde{w}}}{{\partial \tilde{x}}}\frac{{{\text{d}}\tilde{w}_{0} }}{{{\text{d}}\tilde{x}}}} \right]} {\text{d}}\tilde{x}} \right\} \\ & \quad - \tilde{F}\cos (\tilde{\Omega }\tau ) = 0 \\ \end{aligned}$$
(43)

2.4 Solution methods

In this section, the Galerkin method is applied to convert the governing equation to an ordinary differential equation. Then, the displacement function is expressed as

$$\tilde{w}_{n} \left( {\tilde{x},\tau } \right) = \theta_{n} \left( {\tilde{x}} \right)p\left( \tau \right)$$
(44)

where θn is the linear mode shape, and p is a time-dependent function.

For the FG sandwich nanobeam with clamped–clamped (C–C) boundary condition, one has

$$\tilde{w} = 0,\;\;\frac{{\partial \tilde{w}}}{{\partial \tilde{x}}} = 0$$
(45)

To satisfy the boundary condition, θn is assumed as [56]

$$\theta_{n} \left( {\tilde{x}} \right) = \cosh \left( {\lambda_{n} \tilde{x}} \right) - \cos \left( {\lambda_{n} \tilde{x}} \right) - \frac{{\cosh (\lambda_{n} ) - \cos (\lambda_{n} )}}{{\sinh (\lambda_{n} ) - \sin (\lambda_{n} )}}\left[ {\sinh \left( {\lambda_{n} \tilde{x}} \right) - \sin \left( {\lambda_{n} \tilde{x}} \right)} \right]$$
(46)

where λn is a constant and satisfies \(\cos (\lambda_{n} )\cosh (\lambda_{n} ) - 1 = 0\).

Suppose the initial geometric imperfection satisfies the first linear mode shape θ1, then the dimensionless initial imperfection can be written as [57]

$$\tilde{w}_{0} = A_{0} \theta_{1} (\tilde{x})$$
(47)

where A0 is the geometric imperfection. Substituting Eqs. (44)–(47) into Eq. (43) and integrating both sides with respect to \(\stackrel{\sim }{x}\), the following single mode approximation is obtained

$$\ddot{p}({\kern 1pt} \tau {\kern 1pt} ) + \beta_{1} p({\kern 1pt} \tau {\kern 1pt} ) + \beta_{2} p^{2} (\tau {\kern 1pt} ) + \beta_{3} p^{3} (\tau {\kern 1pt} ) = \hat{F}\cos \left( {\tilde{\Omega }\tau {\kern 1pt} } \right)$$
(48)

where new quantities can be calculated by

$$\begin{aligned} \beta_{1} & = \frac{{\left( {\tilde{D}_{xx} - \frac{{\tilde{B}_{xx}^{2} }}{{\tilde{A}_{xx} }}} \right)\left( {r_{4} - \eta^{2} r_{6} } \right) - \left( {r_{2\_1} - \mu^{2} r_{4\_1} } \right)A_{0}^{2} \tilde{A}_{xx} r_{11\_1} - \left( {r_{2} - \mu^{2} r_{4} } \right)\tilde{N}_{T} + \eta^{2} \gamma^{2} \tilde{A}_{xx} r_{4} }}{{\left( {r_{1} - \mu^{2} r_{2} } \right)\tilde{I}_{0} }}, \\ \beta_{2} & = \frac{{ - \left( {r_{2} - \mu^{2} r_{4} } \right)\tilde{A}_{xx} r_{11\_1} A_{0} - \left( {r_{2\_1} - \mu^{2} r_{4\_1} } \right)A_{0} \frac{{\tilde{A}_{xx} }}{2}r_{11} }}{{\left( {r_{1} - \mu^{2} r_{2} } \right)\tilde{I}_{0} }}, \\ \beta_{3} & = \frac{{ - \left( {r_{2} - \mu^{2} r_{4} } \right)\frac{{\tilde{A}_{xx} }}{2}r_{11} }}{{\left( {r_{1} - \mu^{2} r_{2} } \right)\tilde{I}_{0} }}, \\ \hat{F} & = \frac{{r_{0} \tilde{F}}}{{\left( {r_{1} - \mu^{2} r_{2} } \right)\tilde{I}_{0} }} \\ \end{aligned}$$
(49)

in which

$$\begin{aligned} r_{0} & = \int_{0}^{1} {\theta_{n} (\tilde{x}){\text{d}}\tilde{x}} ,\quad r_{1} = \int_{0}^{1} {\theta_{n} (\tilde{x})\theta_{n} (\tilde{x}){\text{d}}\tilde{x}} , \\ r_{11} & = \int_{0}^{1} {\left[ {\frac{{{\text{d}}\theta_{n} (\tilde{x})}}{{{\text{d}}\tilde{x}}}} \right]^{2} } {\text{d}}\tilde{x},\quad r_{11\_1} = \int_{0}^{1} {\left[ {\frac{{{\text{d}}\theta_{n} (\tilde{x})}}{{{\text{d}}\tilde{x}}}\frac{{{\text{d}}\theta_{1} (\tilde{x})}}{{{\text{d}}\tilde{x}}}} \right]} {\text{d}}\tilde{x}, \\ r_{2} & = \int_{0}^{1} {\frac{{{\text{d}}^{2} \theta_{n} (\tilde{x})}}{{{\text{d}}\tilde{x}^{2} }}\theta_{n} (\tilde{x}){\text{d}}\tilde{x}} ,\quad r_{2\_1} = \int_{0}^{1} {\frac{{{\text{d}}^{2} \theta_{1} (\tilde{x})}}{{{\text{d}}\tilde{x}^{2} }}\theta_{n} (\tilde{x}){\text{d}}\tilde{x}} , \\ r_{4} & = \int_{0}^{1} {\frac{{{\text{d}}^{4} \theta_{n} (\tilde{x})}}{{{\text{d}}\tilde{x}^{4} }}\theta_{n} (\tilde{x}){\text{d}}\tilde{x},} \quad r_{4\_1} = \int_{0}^{1} {\frac{{{\text{d}}^{4} \theta_{1} (\tilde{x})}}{{{\text{d}}\tilde{x}^{4} }}\theta_{n} (\tilde{x}){\text{d}}\tilde{x}} , \\ r_{6} & = \int_{0}^{1} {\frac{{{\text{d}}^{6} \theta_{n} (\tilde{x})}}{{{\text{d}}\tilde{x}^{6} }}\theta_{n} (\tilde{x}){\text{d}}\tilde{x}} , \\ \end{aligned}$$
(50)

Here, the primary resonance is considered. On the assumption that \(p\left( \tau \right) = \varepsilon q\left( \tau \right)\) and \(f = \hat{F}/\varepsilon^{3}\), Eq. (48) can be transformed into

$$\ddot{q}({\kern 1pt} \tau {\kern 1pt} ) + \omega_{0}^{2} q({\kern 1pt} \tau {\kern 1pt} ) + \varepsilon \gamma_{1} q^{2} (\tau {\kern 1pt} ) + \varepsilon^{2} \gamma_{2} q^{3} (\tau {\kern 1pt} ) = \varepsilon^{2} f\cos \left( {\tilde{\Omega }\tau {\kern 1pt} } \right)$$
(51)

where \(\omega_{0}^{2} = \beta_{1}\), \(\gamma_{1} = \beta_{2}\) and \(\gamma_{2} = \beta_{3}\). And the excitation frequency can be defined by [58]

$$\tilde{\Omega } = \omega_{0} + \varepsilon^{2} \sigma$$
(52)

in which ε and σ are a small dimensionless parameter and the detuning parameter, respectively.

According to the multiple-scale method, the solution of Eq. (51) can be expanded in the form

$$q({\kern 1pt} \tau {\kern 1pt} ) = q_{0} \left( {T_{0} ,T_{1} ,T_{2} } \right) + \varepsilon q_{1} \left( {T_{0} ,T_{1} ,T_{2} } \right) + \varepsilon^{2} q_{2} \left( {T_{0} ,T_{1} ,T_{2} } \right) + O\left( {\varepsilon^{3} } \right)$$
(53)

where Tn = εnτ. Moreover, T0 indicates the fast timescale, while Tn (n > 0) represents slow timescales. Time derivatives are determined as follows

$$\begin{aligned} \frac{{\text{d}}}{{{\text{d}}\tau }} & = D_{0} + \varepsilon D_{1} + \varepsilon^{2} D_{2} \\ \frac{{{\text{d}}^{2} }}{{{\text{d}}\tau^{2} }} & = D_{0}^{2} + 2\varepsilon D_{0} D_{1} + \varepsilon^{2} \left( {D_{1}^{2} + 2D_{0} D_{2} } \right) \\ \end{aligned}$$
(54)

in which \(D_{i} = \frac{\partial }{{\partial T_{i} }},\;\;i = 0,1,2\), and substituting Eqs. (52) and (53) into Eq. (51), as well as replacing the time derivatives with Di in Eq. (54), one can obtain

$$\varepsilon^{0} :\left( {D_{0}^{2} + \omega_{0}^{2} } \right)q_{0} = 0$$
(55)
$$\varepsilon^{1} :\left( {D_{0}^{2} + \omega_{0}^{2} } \right)q_{1} = - 2D_{0} D_{1} q_{0} - \gamma_{1} q_{0}^{2}$$
(56)
$$\begin{aligned} \varepsilon^{2} :\left( {D_{0}^{2} + \omega_{0}^{2} } \right)q_{2} & = - 2D_{0} D_{1} q_{1} - 2D_{0} D_{2} q_{0} - D_{1}^{2} q_{0} \\ & \quad - 2\gamma_{1} q_{0} q_{1} - \gamma_{2} q_{0}^{3} + f\cos \left( {\omega_{0} T_{0} + \sigma T_{2} {\kern 1pt} } \right) \\ \end{aligned}$$
(57)

The solution of Eq. (55) is given as

$$q_{0} = H(T_{1} ,T_{2} )\exp ({\text{i}}\omega_{0} T_{0} ) + \overline{H}(T_{1} ,T_{2} )\exp ( - {\text{i}}\omega_{0} T_{0} )$$
(58)

where H is an unknown complex function, and \(\overline{H}\) is the complex conjugate of H. Substituting Eq. (58) into Eq. (56) leads to

$$\left( {D_{0}^{2} + \omega_{0}^{2} } \right)q_{1} = - 2i\omega_{0} D_{1} H\exp (i\omega_{0} T_{0} ) - \gamma_{1} \left[ {H^{2} \exp (2i\omega_{0} T_{0} ) + H\overline{H}} \right] + cc$$
(59)

where cc stands for the complex conjugate. To avoid the secular term of q2, D1H must be set to zero. Accordingly, we have \(H = H(T_{2} ){\kern 1pt} {\kern 1pt} {\kern 1pt}\), and the solution of Eq. (56) is given by

$$q_{1} = \frac{{\gamma_{1} }}{{\omega_{0}^{2} }}\left( { - H\overline{H} + \frac{{H^{2} }}{3}\exp \left( {2{\text{i}}\omega_{0} T_{0} } \right)} \right) + cc$$
(60)

Substituting the expressions of q1 and q2 into Eq. (57), then eliminating the secular term, one can obtain the equation of H

$$2i\omega_{0} D_{2} H + \left( {3\gamma_{2} - \frac{{10\gamma_{1}^{2} }}{{3\omega_{0}^{2} }}} \right)H^{2} \overline{H} - \frac{1}{2}f\exp ({\text{i}}\sigma T_{2} ) = 0$$
(61)

To solve Eq. (61), express H in polar form is denoted as

$$H = \frac{1}{2}\alpha \exp \left( {i\phi } \right)$$
(62)

where \(\alpha\) and \(\phi\) are real functions of T2. Substituting Eq. (62) into Eq. (61) and separating the real and imaginary part, two differential equations of real variables are obtained

$$\left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}\alpha }}{{{\text{d}}T_{2} }} = \frac{{f\sin (\sigma T_{2} - \phi )}}{{2\omega_{0} }},} \hfill \\ {\alpha \frac{{{\text{d}}\phi }}{{{\text{d}}T_{2} }} = \frac{1}{{24\omega_{0}^{3} }}\left( {9\gamma_{2} \omega_{0}^{2} - 10\gamma_{1}^{2} } \right)\alpha^{3} - \frac{{f\cos (\sigma T_{2} - \phi )}}{{2\omega_{0} }}} \hfill \\ \end{array} } \right.$$
(63)

A new variable λ is introduced, which satisfies the relation \(\lambda = \sigma T_{2} - \phi\), and Eq. (63) is converted to

$$\left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}\alpha }}{{{\text{d}}T_{2} }} = \frac{f\sin (\lambda )}{{2\omega_{0} }}} \hfill \\ {\alpha \frac{{{\text{d}}\lambda }}{{{\text{d}}T_{2} }} = \sigma \alpha - \frac{1}{{24\omega_{0}^{3} }}\left( {9\gamma_{2} \omega_{0}^{2} - 10\gamma_{1}^{2} } \right)\alpha^{3} + \frac{f\cos (\lambda )}{{2\omega_{0} }}} \hfill \\ \end{array} } \right.$$
(64)

Considering steady-state conditions under which \(\frac{{{\text{d}}\alpha }}{{{\text{d}}T_{2} }} = 0\) as well as \(\frac{{{\text{d}}\lambda }}{{{\text{d}}T_{2} }} = 0\), the amplitude–frequency response can be derived as follows

$$\left[ {\sigma \alpha - \frac{1}{{24\omega_{0}^{3} }}\left( {9\gamma_{2} \omega_{0}^{2} - 10\gamma_{1}^{2} } \right)\alpha^{3} } \right]^{2} = \left( {\frac{f}{{2\omega_{0} }}} \right)^{2}$$
(65)

which presents the relation among the response amplitude, the excitation amplitude and the detuning parameter for the FG sandwich nanobeam.

3 Convergence and validation studies

Before performing numerical simulations, two comparison studies are conducted to check the validity and accuracy of the presented model. In the first comparison example, the linear fundamental frequencies for the nanobeam with Type A material distribution and slenderness ratio L/h = 100 in the thermal environment are calculated, which are compared with those obtained by Ebrahimi et al. [59]. As listed in Table 1, the FG nanobeams composed of SUS304 (as metal phase) and Si3N4 (as ceramic phase) with temperature-dependent material properties are taken into account. Besides, the effects of strain gradient size scale, Von Karman nonlinearity and geometric imperfection are all neglected in this convergence study. As presented in Fig. 3, it is clear that the linear non-dimensional fundamental frequency (\(\overline{\omega } = \omega L^{2} \sqrt {\rho_{{\text{c}}} A/EI_{{\text{c}}} }\)) shows almost the same change trend, which gives validation for the present model.

Table 1 Temperature-dependent material properties of SUS304/Si3N4 [42] used in the present study
Full size table
Fig. 3
figure 3

Comparison between the present work and Ebrahimi’s work [59] for the free vibration frequency of FG nanobeam under different temperature gradients

Full size image

The other comparison example is carried out to verify the nonlinear vibrational performances of the FG beam subjected to thermal loading without considering the size-scale effect. As depicted in Fig. 4, the nonlinear frequency–response curve of the Type A beam under different power law exponents are examined, which gives a comparison with Ansari’s work [60] without considering the surface elasticity effect. Similar to Ansari’s study, the material properties are treated as temperature independent, i.e., Em = 68.5 GPa, ρm = 3000 kg/m3, αtm = 23.6 × 10−6 K−1, νm = 0.35 and Ec = 210 GPa, ρc = 2331 kg/m3, αtc = 5 × 10−6 K−1, νc = 0.24. Besides, the initial imperfection and size-scale parameters of the present model are all neglected in the present model. The results show that the presented model can provide a reasonable nonlinear frequency–response curve, and the derivation between the present model and Ansari’s model [60] are small, indicating the present theoretical model can be used to predict the nonlinear vibration characteristics of FG sandwich nanobeams.

Fig. 4
figure 4

Comparison between the present work and Ansari’s model [60] for nonlinear frequency–response curve of the Type A beam under different power law exponents

Full size image

4 Results and discussion

In this section, the response of FG sandwich nanobeams subjected to the thermal environment with geometrical nonlinearity and initial perfection is presented. The temperature-dependent material properties of FG sandwich nanobeams are also derived from Table 1. The geometry parameters are chosen as h = b = 100 nm, L/h = 30. The bottom surface temperature and the uniform increment of the temperature are set as 300 K and 5 K, respectively. Unless otherwise stated, the thickness effect is not taken into consideration. Besides, the dimensionless size-scale parameters η = μ = 0.1, the power law exponent p = 0.5 and the excitation amplitude f = 0.5 are adopted in the following numerical analyses.

4.1 Initial imperfection amplitude

As shown in Fig. 5, the influence of material distribution pattern on the nonlinear frequency–response curves is given. Here, the parameters ΔT = 100 K, p = 0.5, μ = 0.1, η = 0.1 and f = 0.5 are adopted. Moreover, A0 = 0 represents perfect FG sandwich nanobeams, while A0 = 0.8 stands for the nanobeams with initial geometry imperfection. It is found that all frequency–response curves bend to the right, presenting a “hard-spring’’ behavior, which is due to the fact that the coefficient of q3 term is positive in Eq. (48). Besides, one can also conclude that the material distribution pattern plays an important role in the forced vibration behavior of nanobeams. Particularly, Type D and Type C have the largest and smallest response amplitude on stable branches for A0 = 0, respectively, whereas a contrary phenomenon is observed for A0 = 0.8, which suggests that Type D has the advantage of maintaining its mechanical properties for geometrically imperfect nanobeams.

Fig. 5
figure 5

Effects of material distribution pattern on the nonlinear frequency–response curve of a perfect and b imperfect FG sandwich nanobeams

Full size image

The effect of initial imperfection on the frequency–response curve of FG sandwich nanobeams with four different patterns is illustrated in Fig. 6. We set the temperature gradient ΔT = 100 K, power law exponent p = 0.5, nonlocal parameter μ = 0.1 and strain gradient parameter η = 0.1. As imperfection amplitude increases, the frequency–response curve bends more to the left, indicating that increasing the geometry imperfection results in intensifying the bending stiffness and reducing the hardening effect. It is also seen that the response amplitude on the left stable branch increases more for larger A0 as the detuning parameter is positive, indicating the initial imperfection amplitude has a significant effect on the frequency response of FG sandwich nanobeams.

Fig. 6
figure 6

Effects of initial geometric imperfection A0 on the nonlinear frequency–response curve of FG sandwich nanobeams with different patterns: a Type A, b Type B, c Type C and d Type D

Full size image

4.2 Temperature gradient

This subsection is devoted to examining the influence of temperature gradient. Figure 7 investigates the influence of temperature gradient through the thickness on frequency–response curves with different patterns as the initial geometric imperfection A0 = 0.8, power law exponent p = 0.5, nonlocal parameter μ = 0.1 and strain gradient parameter η = 0.1. As can be seen, the temperature gradient strengthens hardening behavior and exhibits a decreasing effect on the frequency–response curve. By comparing all four patterns, it can be demonstrated that the frequency response of Type D is the least sensitive to the temperature gradient.

Fig. 7
figure 7

Effects of temperature gradient ΔT on the nonlinear frequency–response curves of FG sandwich nanobeams with different patterns: a Type A, b Type B, c Type C and d Type D

Full size image

Figure 8 gives a more general view of the coupling effects of temperature gradient and initial imperfection. Here, the calculation parameters are specified as p = 0.5, μ = 0.1, η = 0.1 and f = 0.5. It can be observed that the increment of A0 makes the frequency–response curve bend to the left for the same temperature gradient, which is coincident with Fig. 6. However, for a given value A0, the temperature gradient has opposite effects on hardening behavior. It indicates that the initial imperfection cannot be neglected in the vibration analysis of temperature-dependent FG sandwich nanobeams.

Fig. 8
figure 8

Coupling effects of temperature gradient ΔT and initial geometric imperfection A0 on the nonlinear frequency–response curves of FG sandwich nanobeams with different patterns: a Type A, b Type B, c Type C and d Type D

Full size image

To provide a better understanding of the coupling effect of the temperature gradient and the initial imperfection amplitude on FG sandwich nanobeams, the nonlinear force–response curves are plotted in Fig. 9. In these figures, the power law exponent and size-scale parameters are, respectively, set as p = 0.5, η = 0.1 and μ = 0.1. The jump phenomenon can be observed in all types of FG sandwich nanobeams. For a given temperature gradient, on the lower stable branches, the vibration amplitude decreases with the increase in A0, while an opposite phenomenon is observed for the higher stable branches. For a given A0, curves of larger temperature gradient have smaller vibration amplitude on the lower stable branches. Furthermore, increasing the temperature gradient leads to larger forcing amplitude of the lower limit point bifurcation, whereas increasing the initial imperfection amplitude leads to a larger response amplitude of the higher limit point bifurcation.

Fig. 9
figure 9

Coupling effects of temperature change ΔT and initial geometric imperfection A0 on the nonlinear force–response curves of FG sandwich nanobeams with different patterns: a Type A, b Type B, c Type C and d Type D

Full size image

4.3 Power law exponent

Graphically presented in Fig. 10 is the influence of power law exponent p on the nonlinear frequency–response curves. Parameters ΔT = 300 K, A0 = 0.5, μ = 0.1 and η = 0.1 are used in this numerical calculation. It is evident that the increment of power law index reduces the hardening behavior and strengthens the bending stiffness for (a)–(c), while an inverse change trend can be found for (d). It can be deduced from Eqs. (3)–(6) that larger volume fraction of ceramic enhances the bending stiffness and reduces the nonlinear hardening effect.

Fig. 10
figure 10

Effects of power law index p on the nonlinear frequency–response curves of FG sandwich nanobeams with different patterns: a Type A, b Type B, c Type C and d Type D

Full size image

Figure 11 exhibits the effects of power law index on the force–response curves of FG nanobeams with different material distribution patterns. Here, ΔT = 300 K, A0 = 0.5, η = 0.1 and μ = 0.1 are used. It is shown that increasing volume fraction of ceramic results in higher response amplitude of the lower limit point, as well as lower response amplitude of the higher limit point. Besides, on the stable branches, curves of smaller volume fraction have larger response amplitudes at the same excitation amplitude. Moreover, the influence caused by the power law index p reduces as it increases, and Type B shows the least sensitive to the variation of p comparing with other material distribution patterns.

Fig. 11
figure 11

Effects of power law index p on the nonlinear force–response curves of FG sandwich nanobeams with different patterns: a Type A, b Type B, c Type C and d Type D

Full size image

Illustrated in Fig. 12 is the coupling effect of power law exponent and initial geometric imperfection on the frequency–response curves. In this numerical analysis, the temperature gradient ΔT = 300 K as well as the size-scale parameters μ = 0.1 and η = 0.1 are employed. It is demonstrated that the tendency of curves is similar to Fig. 10 and Fig. 6 as the value of p or A0 is specified. For all material distribution patterns, larger ceramic volume fraction and imperfection amplitude can cause larger bending stiffness and lower nonlinear hardening performances.

Fig. 12
figure 12

Coupling effects of power law index p and initial geometric imperfection A0 on the nonlinear frequency–response curves of FG sandwich nanobeams with different patterns: a Type A, b Type B, c Type C and d Type D

Full size image

4.4 Size-scale parameters

In this section, two dimensionless size-scale parameters, i.e., the nonlocal parameter μ and the material characteristic parameter η, are taken into consideration. The coupling effects of size-scale parameters and initial geometric imperfection on nonlinear frequency–response curves are demonstrated in Figs. 13 and 14, respectively. In all these figures, the temperature gradient ΔT = 300 K and power law exponent p = 0.5 are adopted, while the strain gradient and nonlocal parameters are fixed as η = 0.1 and μ = 0.1 for Figs. 13 and 14, respectively. From Fig. 13, it is illustrated that the nonlocal parameter enhances the nonlinear hardening effect no matter whether the effect of the initial imperfection is taken into account or not. In addition, within the given range of nonlocal parameter and imperfection amplitude, as μ increases, the effects of A0 is more significant on decreasing the hardening behavior and increasing the bending rigidity. It is revealed in Fig. 14 that increasing the material characteristic parameter strengthens the bending stiffness as well as decreases the hardening behavior when geometrically perfect beam is considered. However, the material characteristic parameter has an opposite effect on the bending stiffness and the hardening effect if the initial imperfection amplitude is taken into account. Furthermore, the influence caused by A0 and η is the least for the Type D pattern among all the four different configurations.

Fig. 13
figure 13

Coupling effects of nonlocal parameter μ and initial geometric imperfection A0 on the nonlinear frequency–response curves of FG sandwich nanobeams with different patterns: a Type A, b Type B, c Type C and d Type D

Full size image
Fig. 14
figure 14

Coupling effects of material length parameter η and initial geometric imperfection A0 on the nonlinear frequency–response curves of FG sandwich nanobeams with different patterns: a Type A, b Type B, c Type C and d Type D

Full size image

4.5 Effect of thickness

The influence of thickness on the nonlinear frequency–response of FG sandwich nanobeam is depicted in Fig. 15 under different power law indexes. In these numerical analyses, parameters μ = η = 0.05, ΔT = 100 K, f = 0.5 and A0 = 0 are adopted. Besides, the FG sandwich nanobeams with the material distribution pattern of Type A and C are employed in Fig. 15a, b, respectively. It is found that the power law index has great influence on the nonlinear frequency–response behavior of the FG sandwich nanobeam, i.e., larger volume fraction of ceramic can result in larger bending stiffness and lower nonlinear hardening effect no matter whether the thickness effect is taken into account or not. Comparing with the nonlinear frequency–response curve without the thickness effect, the nonlinear frequency–response curve bends to the left much more significant as the thickness effect is taken into consideration for all power law indexes, indicating the thickness effect can enhance the bending stiffness and reduce the hardening behavior of the FG sandwich nanobeam.

Fig. 15
figure 15

Influence of thickness on the nonlinear frequency–response curves of FG sandwich nanobeams with different patterns: a Type A and b Type C

Full size image

5 Conclusions

The present work is devoted to investigating the nonlinear forced vibrational behavior of FG sandwich nanobeams subjected to thermal environment with initial geometric imperfection. By considering the Von Karman geometrical nonlinearity, the governing equation of motion is derived with the aid of nonlocal strain gradient theory and Hamilton’s variational principle. The governing equation is converted to the ordinary differential equation through Galerkin technique, and the primary resonance behaviors are examined by means of the multiple-scale method. Four material distribution patterns of FG sandwich nanobeams with C–C boundary condition are taken into account. The influences of initial geometric imperfection, temperature gradient, power law exponent and size-scale parameters on the nonlinear responses of FG sandwich nanobeams are studied in detail. Not only the nonlinear hardening but also the softening behaviors are detected, and some important conclusions are drawn as follows:

  1. 1.

    The initial geometric imperfection can reduce the hardening behavior of FG sandwich nanobeams, while increasing the ceramic volume fraction and nonlocal parameter presents an opposite effect. For FG sandwich nanobeams with small initial imperfection amplitudes, the temperature gradient and material characteristic parameter will reduce the hardening behavior, while an inverse phenomenon can be observed for the counterparts with larger imperfection amplitude.

  2. 2.

    The frequency–response curve becomes much more sensitive to the variation of initial imperfection amplitude as its value enlarges. The influences caused by the temperature gradient and power law exponent on the response curves become less significant as the initial imperfection amplitude increases.

  3. 3.

    For force–response curves, larger initial imperfection amplitude makes the higher limit point bifurcation occurs at higher response amplitude, while larger temperature gradient leads to the lower limit point bifurcation happens at higher excitation amplitude.

  4. 4.

    Type D is the least distribution pattern that would be affected by the imperfection amplitude, the temperature gradient, and the power law exponent, while Type C is the most sensitive configuration to the variation of temperature gradient. Ceramic volume fraction presents the least influence on the frequency–response curve and force–response curve of Type B.