1 Introduction

Magnetostrictive materials are known as a type of smart materials that their size, shape and magnetization changes in response to the magnetic field and mechanical stress. Considering this fact, magnetostrictive materials can be used in sensors and actuators applications. Therefore, many investigators have been selected magnetostrictive materials as a research topic. For instance, Wang and Lin [1] described the design of new giant magnetostrictive structures for double-nut ball screw pre-tightening. A magnetomechanical coupling constitutive relation of the giant magnetostrictive material was investigated experimentally and theoretically by Yongping et al. [2]. Sheikholeslami and Aghdam [3] investigated the bending behavior of magnetostrictive beam. Mishrar et al. [4] conducted the experiments in a thermal environment on Tb–Dy–Fe film samples to determine their characteristic magnetization curves. A three-variable plate model was utilized by Ebrahimi and Dabbagh [5] to explore the wave propagation problem of smart sandwich nanoplate made of a magnetostrictive core and ceramic face sheets while subjected to thermo-magnetic loading. A nonlinear constitutive model of a giant magnetostrictive actuator was put forward for the application of effectively suppressing vibration by Zhang et al. [6]. Kumar et al. [5] analyzed the damping characteristics using distributed magnetostrictive layer bonded to an aluminum beam for different boundary conditions and coil configurations. They assumed that the magnetostrictive layer produces the actuating force required to control the vibration in the beam, based on a negative velocity feedback control law.

FGMs are innovative materials made of a combination of two material phases and can be classified as a recent improvement in composite materials. Due to this fact, FGMs are known as the materials with best properties and therefore can be applied in various fields such as the nuclear reactor and high-speed space craft industries. Numerous structural components of FGMs have beam-like configurations. Accordingly, investigating the buckling, vibration, dynamic response and wave propagation responses of FGM beams have been considered widely in the literature. Employing EBB theory and the physical neutral surface concept, the nonlinear governing equation for the FGM beam with two clamped ends and surface-bonded piezoelectric actuators was derived by the Hamilton’s principle by Fu et al. [7]. Fallah and Aghdam [8] investigated the thermo-mechanical buckling and nonlinear free vibration analysis of FG beams on nonlinear elastic foundation. Analytical relations between the critical buckling load of a FGM TB and that of the corresponding EBB subjected to axial compressive load were derived by Li and Batra [9] for clamped–clamped (C–C), simply supported-simply supported (S–S) and Clamped-free (C–F) edges. Shen and Wang [10] studied the large amplitude vibration, nonlinear bending and thermal postbuckling of FGM beams resting on an elastic foundation in thermal environments.

Sandwich structures consist of a thick core integrated with two relatively thin face sheets in their simplest forms. Since the core layer is always thick and also light, and the face sheets are selected among the high rigidity, sandwich structures are applied in structures with high rigidity and low weight aerospace, airplanes, sensors and actuators. Recently, considerable amount of investigation has been reported on mechanical responses of sandwich structures by several researchers. Transient responses and natural frequencies of sandwich beams with inhomogeneous FG core were investigated by Bui et al. [11]. Vibration and thermal buckling behaviors of sandwich beams with composite facings and viscoelastic core were studied by Pradeep et al. [12]. Free vibration of the FG sandwich beams was studied by a meshfree boundary-domain integral equation method by Yang et al. [13]. In another study, Vo et al. [14] presented finite element model for vibration and buckling of FG sandwich beams based on a refined shear deformation theory. They assumed that the core of sandwich beam is fully metal or ceramic and skins are composed of a FGM across the depth.

Recently, nanobeams are widely used in many nano- and micro-electromechanical systems (NEMS and MEMS) due to their unique mechanical, thermal and electronic properties. Owing to these properties, on the other hand, a large amount of researches have been carried out on the mechanical behavior of the functionally graded nanobeams (FGNBs). On the other hand, in order to study the mechanical characteristics of nanostructures accurately, size-dependent theories such as nonlocal elasticity, modified couple stress and modified strain gradient elasticity should be applied. Static bending and free vibration of FG microbeams were examined based on the MCST and various higher-order beam theories by Simsek and Reddy [15]. Nonlinear electromechanical behavior of nanobeams under electrostatic actuation based on the recently developed consistent couple stress theory was analyzed by Fakhrabadi and Yang [16]. Simsek [17] developed a non-classical beam theory for the static and nonlinear vibration analysis of microbeams based on a three-layered nonlinear elastic foundation within the framework of the MCST and EBB theory together with the von-Karman’s geometric nonlinearity. Akgoz and Civalek [18] addressed the stability problem of micro-sized beam based on the strain gradient elasticity and modified couple stress theories.

The surrounded elastic medium of nanobeams can be assumed as Winkler, Pasternak and visco-Pasternak. The Winkler foundation is capable of just normal load while Pasternak foundation is both capable of transverse shear and normal loads. Among these simulation visco-Pasternak medium which considers damping, shear and normal loads can be assumed as an accurate model for surrounding elastic foundation. Ghorbanpour Arani and Shokravi [19] discussed vibration of coupled double-layer grapheme sheet systems coupled with each other by an enclosing visco-Pasternak medium. In another attempt, Ghorbanpour Arani et al. [20] analyzed the nonlinear dynamic stability of single-layered grapheme sheets (SLGSs) integrated with zinc oxide (ZnO) actuators and sensors embedded on visco-Pasternak foundation. Linear transient response of FG higher-order nanobeams integrated with magnetostrictive layers using modified couple stress theory was investigated by Ghorbanpour Arani and Abdollahian [21]. They assumed the visco-Pasternak elastic medium and studied the effects of damping, shear and spring modulus on the linear transient response of FG nanobeams.

Consequences of motivation, in this paper nonlinear dynamic analysis of an embedded FGSNB integrated with magnetostrictive layers is studied using MCST. The FGMSNB is subjected to a time-dependent transverse load and the core is made of temperature-dependent FGM. Using the von-Karman nonlinear strain–displacement relationships and Hamilton’s principle as well as energy method, the governing motion equations and related boundary conditions are obtained for both EBB and TB models. The DQM in conjunction with Newmark-β method are applied to study the effects of small-scale parameter, geometrical parameters, surrounding elastic medium, magnetostrictive layers, material compositions of core layer, environment temperature and different boundary conditions.

2 Modified couple stress theory

Based on MCST, the strain energy density \(\varPi_{\text{s}}\) of a linear elastic material occupying region \(\varOmega\) with infinitesimal deformations can be expressed as [15, 22, 23]:

$$\varPi_{\text{s}} = \frac{1}{2}\int_{\varOmega }^{{}} {\left( {\sigma_{ij}^{{}} \varepsilon_{ij} + m_{ij}^{{}} \chi_{ij}^{{}} } \right)d\varOmega } ,\,\left( {i,j = 1,2,3} \right),$$
(1)

where \(\sigma_{ij}^{{}}\) is the Cauchy stress of sandwich nanobeam, \(\varepsilon_{ij}\) is the strain tensor, \(m_{ij}^{{}}\) is the deviatoric part of the couple stress tensor and \(\chi_{ij}^{{}}\) is the symmetric curvature tensor where:

$$\varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right),$$
(2a)
$$\chi_{ij}^{{}} = \frac{1}{2}\left( {\theta_{i,j} + \theta_{j,i} } \right),$$
(2b)
$$\theta_{i} = \frac{1}{2}e_{ijk} u_{k,j} ,$$
(2c)

in which \(u_{i}\), \(\theta_{i}\) and \(e_{ijk}\) are the displacement vector, the infinitesimal rotation vector and the alternate tensor, respectively.

3 Governing motion equations

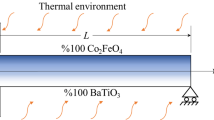
A uniform FGSNB with geometrical parameters of length \(L\), width \(b\), core thickness \(h_{\text{c}}\) and magnetostrictive layers thickness \(h_{\text{m}}\) is shown in Fig. 1. The nanobeam also embedded in visco-Pasternak medium and is subjected to time-dependent transverse load.

Fig. 1
figure 1

Configuration of an embedded FGSMNB

Full size image

3.1 Preliminaries

The displacement components of an arbitrary point of the FGSNB in terms of \(x\), \(y\) and \(z\) coordinates, denoted by \(u_{x} \left( {x,z,t} \right)\), \(u_{y} \left( {x,z,t} \right)\) and \(u_{z} \left( {x,z,t} \right)\) is written as follows [15]:

$$u_{x} \left( {x,z,t} \right) = u\left( {x,t} \right) - z\frac{{\partial w\left( {x,t} \right)}}{\partial x} + \varPhi \left( z \right)\gamma \left( {x,t} \right),$$
(3a)
$$u_{y} \left( {x,z,t} \right) = 0,$$
(3b)
$$u_{z} \left( {x,z,t} \right) = w\left( {x,t} \right).$$
(3c)

where \(u\left( {x,t} \right)\) and \(w\left( {x,t} \right)\) are the displacement components of the mid-plane in the axial and transverse directions, respectively. \(\gamma \left( {x,t} \right)\) denotes the transverse shear strain of any point on the neutral axis which can be written as [15]:

$$\gamma \left( {x,t} \right) = \frac{{\partial w\left( {x,t} \right)}}{\partial x} - \phi \left( {x,t} \right),$$
(4)

where \(\phi \left( {x,t} \right)\) is the total bending of the cross section at any point and \(t\) is time. For various beam models \(\varPhi \left( z \right)\) is defined as follows [15]:

  • Euler–Bernoulli beam theory (EBBT): \(\varPhi \left( z \right) = 0,\)

  • First-order shear deformation beam theory (FSDBT): \(\varPhi \left( z \right) = z,\)

  • Parabolic shear deformation beam theory (PSDBT): \(\varPhi \left( z \right) = z\left( {1 - {{4z^{2} } \mathord{\left/ {\vphantom {{4z^{2} } {3h_{l}^{2} }}} \right. \kern-0pt} {3h_{l}^{2} }}} \right),\)

  • Trigonometric shear deformation beam theory (TSDBT): \(\varPhi \left( z \right) = \frac{{h_{l} }}{\pi }\sin \left( {\frac{\pi z}{{h_{l} }}} \right),\)

  • Hyperbolic shear deformation beam theory (HSDBT): \(\varPhi \left( z \right) = h_{l} \sinh \left( {\frac{z}{{h_{l} }}} \right) - z\cosh \left( {\frac{1}{2}} \right),\)

  • Exponential shear deformation beam theory (ESDBT): \(\varPhi \left( z \right) = ze^{{ - 2\left( {{z \mathord{\left/ {\vphantom {z {h_{l} }}} \right. \kern-0pt} {h_{l} }}} \right)^{2} }} .\)

Based on Eqs. (2a) and (3), the strain–displacement relations are obtained as:

$$\varepsilon_{xx} = \frac{\partial u}{\partial x} - z\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \varPhi \left( z \right)\frac{\partial \gamma }{\partial x},\varepsilon_{yy} = \varepsilon_{zz} = \varepsilon_{xy} = \varepsilon_{yz} = 0,$$
(5a)
$$\gamma_{xz} = 2\varepsilon_{xz} = \frac{d\varPhi \left( z \right)}{dz}\gamma .$$
(5b)

From Eqs. (2c) and (3), the components of rotation vector are obtained as follows:

$$\theta_{x} = 0,$$
(6a)
$$\theta_{y} = \frac{1}{2}\frac{d\varPhi \left( z \right)}{dz}\gamma - \frac{\partial w}{\partial x},$$
(6b)
$$\theta_{z} = 0.$$
(6c)

Considering Eqs. (2b) and (6) yields the nonzero components of symmetric curvature tensor as follows:

$$\chi_{xy} = \frac{1}{4}\frac{d\varPhi \left( z \right)}{dz}\frac{\partial \gamma }{\partial x} - \frac{1}{2}\frac{{\partial^{2} w}}{{\partial x^{2} }},$$
(7a)
$$\chi_{yz} = \frac{1}{4}\frac{{d^{2} \varPhi \left( z \right)}}{{dz^{2} }}\gamma .$$
(7b)

The nonzero components of stress tensor and deviatoric part of the couple stress for core and magnetostrictive layers, without considering the effect of thermal load, can be written as [23]:

$$\sigma_{xx}^{c} = Q_{11}^{c} \varepsilon_{xx} ,$$
(8a)
$$\sigma_{xz}^{c} = Q_{55}^{c} \gamma_{xz} ,$$
(8b)
$$\sigma_{xx}^{l} = Q_{11}^{l} \varepsilon_{xx} - e_{31} H_{z} ,$$
(8c)
$$\sigma_{xz}^{l} = Q_{55}^{l} \gamma_{xz} ,$$
(8d)
$$m_{xy}^{c} = 2Q_{55}^{c} l^{2} \chi_{xy} ,$$
(8e)
$$m_{yz}^{c} = 2Q_{55}^{c} l^{2} \chi_{yz} ,$$
(8f)
$$m_{xy}^{l} = 2Q_{55}^{l} l^{2} \chi_{xy} ,$$
(8g)
$$m_{yz}^{l} = 2Q_{55}^{l} l^{2} \chi_{yz} ,$$
(8h)

where \(l\) is the material length scale parameter, \(Q_{ij}^{{}} \left( {i,j = 1,2, \ldots ,6} \right)\) are the elastic constants and the upper indexes \(l\) and \(c\) are related to magnetostrictive and core layers, respectively. Also:

$$Q_{11}^{c} = \frac{E}{{1 - \nu^{2} }},$$
(9a)
$$Q_{55}^{c} = \frac{E}{{2\left( {1 + \nu } \right)}},$$
(9b)
$$H_{z} = k_{\text{c}} c\left( t \right)\frac{\partial w}{\partial t},$$
(9c)

in which \(E\) and \(\nu\) are the Young’s modulus and Poisson’s ratio of the core, respectively. \(k_{\text{c}}\) is the coil constant and \(c\left( t \right)\) denotes the control gain [6]. The Young’s modulus, Poisson’s ratio and density \(\rho_{\text{c}}\) of the FGM core can be expressed as [24]:

$$E = \left( {E_{2} - E_{1} } \right)\left( {\frac{{2z + h_{\text{c}} }}{{2h_{\text{c}} }}} \right)^{{V_{f} }} + E_{1} ,$$
(10a)
$$\nu = \left( {\nu_{2} - \nu_{1} } \right)\left( {\frac{{2z + h_{\text{c}} }}{{2h_{\text{c}} }}} \right)^{{V_{f} }} + \nu_{1} ,$$
(10b)
$$\rho_{\text{c}} = \left( {\rho_{c2} - \rho_{c1} } \right)\left( {\frac{{2z + h_{\text{c}} }}{{2h_{\text{c}} }}} \right)^{{V_{f} }} + \rho_{c1} ,$$
(10c)

where \(E_{2}\) and \(E_{1}\) are the Young’s moduli, \(\nu_{2}\) and \(\nu_{1}\) are the Poisson’s ratio, \(\rho_{c2}\) and \(\rho_{c1}\) are the density of the constituent materials and \(V_{f}\) is the power law exponent, respectively [24]. Since most of FGMs are used in high-temperature applications, their properties must be assumed temperature dependent. Therefore, each property of the FGM core layer \(P_{i}\) is assumed to be the function of environment temperature \(T\left( K \right)\), as follows [24]:

$$P_{i} = P_{0} \left( {P_{ - 1} T^{ - 1} + 1 + P_{1} T^{1} + P_{2} T^{2} + P_{3} T^{3} } \right),$$
(11)

where \(P_{0}\), \(P_{ - 1}\), \(P_{1}\), \(P_{2}\) and \(P_{3}\) are temperature coefficients of the constituent materials.

3.2 Strain energy of FGSNB

Substituting Eqs. (5) and (7) into Eq. (1) yields the variation of the FGSNB strain energy as follows:

$$\int_{0}^{L} {\varPi_{\text{s}} \text{d}x} = \int_{0}^{L} {\left[ {N_{xx}^{t} \left( {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right) - M_{\text{c}}^{t} \frac{{\partial^{2} w}}{{\partial x^{2} }} + M_{nc}^{t} \frac{\partial \gamma }{\partial x} + Q_{x}^{t} \gamma + \frac{{Y_{2}^{t} }}{2}\frac{\partial \gamma }{\partial x} - Y_{1}^{t} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{Y_{3}^{t} }}{2}\gamma } \right]\text{d}x} ,$$
(12)

where:

$$N_{x}^{t} = \int_{{A_{t} }} {\sigma_{xx}^{{}} \text{d}A_{t} } = \int_{{{{ - h_{l} } \mathord{\left/ {\vphantom {{ - h_{l} } 2}} \right. \kern-0pt} 2}}}^{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} }2}} \right. \kern-0pt} 2}}} {\sigma_{xx}^{l} b\text{d}z} + \int_{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}}} 2}} \right. \kern-0pt} 2}}}^{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {\sigma_{xx}^{c} b\text{d}z} + \int_{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{l} } \mathord{\left/ {\vphantom {{h_{l} } 2}} \right. \kern-0pt} 2}}} {\sigma_{xx}^{l} b\text{d}z} ,$$
(13a)
$$M_{\text{c}}^{t} = \int_{{A_{t} }} {\sigma_{xx}^{{}} z\text{d}A_{t} } = \int_{{{{ - h_{l} } \mathord{\left/ {\vphantom {{ - h_{l} } 2}} \right. \kern-0pt} 2}}}^{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {\sigma_{xx}^{l} bz\text{d}z} + \int_{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {\sigma_{xx}^{c} bz\text{d}z} + \int_{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{l} } \mathord{\left/ {\vphantom {{h_{l} } 2}} \right. \kern-0pt} 2}}} {\sigma_{xx}^{l} bz\text{d}z} ,$$
(13b)
$$M_{nc}^{t} = \int_{{A_{t} }} {\sigma_{xx}^{{}} \varPhi \left( z \right)\text{d}A_{t} } = \int_{{{{ - h_{l} } \mathord{\left/ {\vphantom {{ - h_{l} } 2}} \right. \kern-0pt} 2}}}^{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {\sigma_{xx}^{l} \varPhi \left( z \right)b\text{d}z} + \int_{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {\sigma_{xx}^{c} \varPhi \left( z \right)b\text{d}z} + \int_{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{l} } \mathord{\left/ {\vphantom {{h_{l} } 2}} \right. \kern-0pt} 2}}} {\sigma_{xx}^{l} \varPhi \left( z \right)b\text{d}z} ,$$
(13c)
$$Q_{x}^{t} = \int_{{A_{t} }} {\sigma_{xz}^{{}} \frac{{\text{d}\varPhi \left( z \right)}}{{\text{d}z}}\text{d}A_{t} } = \int_{{{{ - h_{l} } \mathord{\left/ {\vphantom {{ - h_{l} } 2}} \right. \kern-0pt} 2}}}^{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {\sigma_{xx}^{l} \frac{{\text{d}\varPhi \left( z \right)}}{{\text{d}z}}b\text{d}z} + \int_{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {\sigma_{xx}^{c} \frac{{\text{d}\varPhi \left( z \right)}}{{\text{d}z}}b\text{d}z} + \int_{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{l} } \mathord{\left/ {\vphantom {{h_{l} } 2}} \right. \kern-0pt} 2}}} {\sigma_{xx}^{l} \frac{{\text{d}\varPhi \left( z \right)}}{{\text{d}z}}b\text{d}z} ,$$
(13d)
$$Y_{1}^{t} = \int_{{A_{t} }} {m_{xy}^{{}} \text{d}A_{t} } = \int_{{{{ - h_{l} } \mathord{\left/ {\vphantom {{ - h_{l} } 2}} \right. \kern-0pt} 2}}}^{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {m_{xy}^{l} b\text{d}z} + \int_{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {m_{xy}^{c} b\text{d}z} + \int_{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{l} } \mathord{\left/ {\vphantom {{h_{l} } 2}} \right. \kern-0pt} 2}}} {m_{xy}^{l} b\text{d}z} ,$$
(13e)
$$Y_{2}^{t} = \int_{{A_{t} }} {m_{xy}^{{}} \frac{{\text{d}\varPhi \left( z \right)}}{{\text{d}z}}\text{d}A_{t} } = \int_{{{{ - h_{l} } \mathord{\left/ {\vphantom {{ - h_{l} } 2}} \right. \kern-0pt} 2}}}^{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {m_{xy}^{l} \frac{{\text{d}\varPhi \left( z \right)}}{{\text{d}z}}b\text{d}z} + \int_{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {m_{xy}^{c} \frac{{\text{d}\varPhi \left( z \right)}}{{\text{d}z}}b\text{d}z} + \int_{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{l} } \mathord{\left/ {\vphantom {{h_{l} } 2}} \right. \kern-0pt} 2}}} {m_{xy}^{l} \frac{{\text{d}\varPhi \left( z \right)}}{{\text{d}z}}b\text{d}z} ,$$
(13f)
$$\begin{aligned} Y_{3}^{t} & = \int_{{A_{t} }} {m_{yz}^{{}} \frac{{\text{d}^{2} \varPhi \left( z \right)}}{{\text{d}z^{2} }}\text{d}A_{t} } \\ & = \int_{{{{ - h_{l} } \mathord{\left/ {\vphantom {{ - h_{l} } 2}} \right. \kern-0pt} 2}}}^{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {m_{yz}^{l} \frac{{\text{d}^{2} \varPhi \left( z \right)}}{{\text{d}z^{2} }}b\text{d}z} + \int_{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {m_{yz}^{c} \frac{{\text{d}^{2} \varPhi \left( z \right)}}{{\text{d}z^{2} }}b\text{d}z} \\ & \quad + \int_{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{l} } \mathord{\left/ {\vphantom {{h_{l} } 2}} \right. \kern-0pt} 2}}} {m_{yz}^{l} \frac{{\text{d}^{2} \varPhi \left( z \right)}}{{\text{d}z^{2} }}b\text{d}z} , \\ \end{aligned}$$
(13g)

where \(A_{t}\) is the total cross-sectional area of FGSNB. Equations (13) can be rewritten as follows using Eqs. (8):

$$N_{x}^{t} = A_{11} \frac{\partial u}{\partial x} - B_{11} \frac{{\partial^{2} w}}{{\partial x^{2} }} + E_{11} \frac{\partial \gamma }{\partial x} + \frac{{A_{11} }}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} - 2bh_{L} e_{31} k_{\text{c}} c\left( t \right)\frac{\partial w}{\partial t},$$
(14a)
$$M_{c}^{t} = B_{11} \frac{\partial u}{\partial x} - D_{11} \frac{{\partial^{2} w}}{{\partial x^{2} }} + F_{11} \frac{\partial \gamma }{\partial x} + \frac{{B_{11} }}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} ,$$
(14b)
$$M_{nc}^{t} = E_{11} \frac{\partial u}{\partial x} - F_{11} \frac{{\partial^{2} w}}{{\partial x^{2} }} + H_{11} \frac{\partial \gamma }{\partial x} + \frac{{E_{11} }}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} - E_{31} k_{\text{c}} c\left( t \right)\frac{\partial w}{\partial t},$$
(14c)
$$Q_{x}^{t} = B_{13} \gamma ,$$
(14d)
$$Y_{1}^{t} = \frac{1}{2}D_{13} l^{2} \frac{\partial \gamma }{\partial x} - A_{13} l^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }},$$
(14e)
$$Y_{2}^{t} = \frac{1}{2}B_{13} l^{2} \frac{\partial \gamma }{\partial x} - D_{13} l^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }},$$
(14f)
$$Y_{3}^{t} = \frac{1}{2}E_{13} l^{2} \gamma ,$$
(14g)

where

$$\left( {A_{11} ,B_{11} ,D_{11} } \right) = \int_{{{{ - h_{l} } \mathord{\left/ {\vphantom {{ - h_{l} } 2}} \right. \kern-0pt} 2}}}^{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {Q_{11}^{l} \left( {1,z,z^{2} } \right)b\text{d}z} + \int_{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {Q_{11}^{c} \left( {1,z,z^{2} } \right)b\text{d}z} + \int_{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{l} } \mathord{\left/ {\vphantom {{h_{l} } 2}} \right. \kern-0pt} 2}}} {Q_{11}^{l} \left( {1,z,z^{2} } \right)b\text{d}z} ,$$
(15a)
$$\left( {E_{11} ,F_{11} ,H_{11} } \right) = \int_{{{{ - h_{l} } \mathord{\left/ {\vphantom {{ - h_{l} } 2}} \right. \kern-0pt} 2}}}^{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {Q_{11}^{l} \varPhi \left( z \right)\left( {1,z,z^{2} } \right)b\text{d}z} + \int_{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {Q_{11}^{c} \varPhi \left( z \right)\left( {1,z,z^{2} } \right)b\text{d}z} + \int_{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{l} } \mathord{\left/ {\vphantom {{h_{l} } 2}} \right. \kern-0pt} 2}}} {Q_{11}^{l} \varPhi \left( z \right)\left( {1,z,z^{2} } \right)b\text{d}z} ,$$
(15b)
$$E_{31} = \int_{{{{ - h_{l} } \mathord{\left/ {\vphantom {{ - h_{l} } 2}} \right. \kern-0pt} 2}}}^{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {e_{31} \varPhi \left( z \right)b\text{d}z} + \int_{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{l} } \mathord{\left/ {\vphantom {{h_{l} } 2}} \right. \kern-0pt} 2}}} {e_{31} \varPhi \left( z \right)b\text{d}z} ,$$
(15c)
$$\begin{aligned} \left( {A_{13} ,B_{13} ,D_{13} ,E_{13} } \right) & = \int_{{{{ - h_{l} } \mathord{\left/ {\vphantom {{ - h_{l} } 2}} \right. \kern-0pt} 2}}}^{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {Q_{55}^{l} \left( {1,\varPhi_{,z} \left( z \right),\left[ {\varPhi_{,z} \left( z \right)} \right]^{2} ,\left[ {\varPhi_{,zz} \left( z \right)} \right]^{2} } \right)b\text{d}z} \\ & \quad + \int_{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {Q_{55}^{l} \left( {1,\varPhi_{,z} \left( z \right),\left[ {\varPhi_{,z} \left( z \right)} \right]^{2} ,\left[ {\varPhi_{,zz} \left( z \right)} \right]^{2} } \right)b\text{d}z} \\ & \quad + \int_{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{l} } \mathord{\left/ {\vphantom {{h_{l} } 2}} \right. \kern-0pt} 2}}} {Q_{55}^{l} \left( {1,\varPhi_{,z} \left( z \right),\left[ {\varPhi_{,z} \left( z \right)} \right]^{2} ,\left[ {\varPhi_{,zz} \left( z \right)} \right]^{2} } \right)b\text{d}z} , \\ \end{aligned}$$
(15d)

3.3 Kinetic Energy of FGSNB

The kinetic energy of the FGSNB is written as [15]:

$$\begin{aligned} \varPi_{k} & = \frac{1}{2}\int_{0}^{L} {\int_{{{{ - h_{l} } \mathord{\left/ {\vphantom {{ - h_{l} } 2}} \right. \kern-0pt} 2}}}^{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {\rho_{l} \left[ {\left( {\frac{\partial u}{\partial t} - z\frac{{\partial^{2} w}}{\partial x\partial t} + \varPhi \left( z \right)\frac{\partial \gamma }{\partial t}} \right)^{2} + \left( {\frac{\partial w}{\partial x}} \right)^{2} } \right]} } b\text{d}z\text{d}x \\ & \quad + \frac{1}{2}\int_{0}^{L} {\int_{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {\rho_{\text{c}} \left( z \right)\left[ {\left( {\frac{\partial u}{\partial t} - z\frac{{\partial^{2} w}}{\partial x\partial t} + \varPhi \left( z \right)\frac{\partial \gamma }{\partial t}} \right)^{2} + \left( {\frac{\partial w}{\partial x}} \right)^{2} } \right]} } b\text{d}z\text{d}x \\ & \quad + \frac{1}{2}\int_{0}^{L} {\int_{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{l} } \mathord{\left/ {\vphantom {{h_{l} } 2}} \right. \kern-0pt} 2}}} {\rho_{l} \left[ {\left( {\frac{\partial u}{\partial t} - z\frac{{\partial^{2} w}}{\partial x\partial t} + \varPhi \left( z \right)\frac{\partial \gamma }{\partial t}} \right)^{2} + \left( {\frac{\partial w}{\partial x}} \right)^{2} } \right]} } b\text{d}z\text{d}x, \\ \end{aligned}$$
(16)

where \(\rho_{l}\) are the density of magnetostrictive layers, respectively.

3.4 External forces

The total energy associated with external applied forces \(W_{{\text{ext}}}\) contains surrounding elastic medium and the distributed harmonically varying load \(f\) can be obtained as follows:

$$W_{{\text{ext}}} = \frac{1}{2}\int_{0}^{T} {\int_{0}^{L} {\left( {f - k_{\text{w}} w + k_{\text{g}} \frac{{\partial^{2} w}}{{\partial x^{2} }} - c_{\text{d}} \frac{\partial w}{\partial t}} \right)w\text{d}x} } ,$$
(17)

where \(k_{\text{w}}\), \(k_{\text{g}}\) and \(c_{\text{d}}\) are spring, shear and damping modulus, respectively, and:

$$f\left( {x,t} \right) = f_{0} \sin \left( {\frac{n\pi x}{L}} \right)e^{{\alpha_{t} t}} ,$$
(18)

in which \(f_{0}\) is a constant, \(\alpha_{t}\) is an integer and \(\omega\) is the frequency of variation of the load [25].

3.5 Hamilton’s principle

Hamilton’s principle on the interval time \(\left[ {0,T} \right]\) is defined as:

$$\delta \int_{0}^{T} {\left( {\varPi_{k} - \varPi_{\text{s}} + W_{\rm ext} } \right)dt} = 0,$$
(19)

Substituting Eqs. (12), (16) and (17) into Eq. (19), integrating by parts and setting the coefficients of \(\delta u\), \(\delta w\) and \(\delta \gamma\) to zero yields the motion equations of the FGSNB as follows

$$\delta u:\frac{{\partial N_{x}^{t} }}{\partial x} = I_{A} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{B} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} + I_{E} \frac{{\partial^{2} \gamma }}{{\partial t^{2} }},$$
(20a)
$$\begin{aligned} & \delta w:\frac{\partial }{\partial x}\left( {N_{x}^{t} \frac{\partial w}{\partial x}} \right) + \frac{{\partial^{2} M_{c}^{t} }}{{\partial x^{2} }} + \frac{{\partial^{2} Y_{1}^{t} }}{{\partial x^{2} }} + f - k_{\text{w}} w + k_{\text{g}} \frac{{\partial^{2} w}}{{\partial x^{2} }} - c_{\text{d}} \frac{\partial w}{\partial t} \\ & \quad = I_{A} \frac{{\partial^{2} w}}{{\partial t^{2} }} + I_{B} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }} - I_{D} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} + I_{F} \frac{{\partial^{3} \gamma }}{{\partial x\partial t^{2} }}, \\ \end{aligned}$$
(20b)
$$\delta \gamma :\frac{{\partial M_{nc}^{t} }}{\partial x} - Q_{x}^{t} + \frac{1}{2}\frac{{\partial Y_{2}^{t} }}{\partial x} - \frac{1}{2}Y_{3}^{t} = I_{E} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{F} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} + I_{H} \frac{{\partial^{2} \gamma }}{{\partial t^{2} }}.$$
(20c)

where

$$\left( {I_{A} ,I_{B} ,I_{D} } \right) = \int_{{{{ - h_{l} } \mathord{\left/ {\vphantom {{ - h_{l} } 2}} \right. \kern-0pt} 2}}}^{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {\rho_{l} \left( z \right)\left( {1,z,z^{2} } \right)b\text{d}z} + \int_{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {\rho_{\text{c}} \left( z \right)\left( {1,z,z^{2} } \right)b\text{d}z} + \int_{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{l} } \mathord{\left/ {\vphantom {{h_{l} } 2}} \right. \kern-0pt} 2}}} {\rho_{l} \left( z \right)\left( {1,z,z^{2} } \right)b\text{d}z} ,$$
(21a)
$$\begin{aligned} \left( {I_{E} ,I_{F} ,I_{H} } \right) & = \int_{{{{ - h_{l} } \mathord{\left/ {\vphantom {{ - h_{l} } 2}} \right. \kern-0pt} 2}}}^{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {\rho_{l} \left( z \right)\varPhi \left( z \right)\left( {1,z,\varPhi \left( z \right)} \right)b\text{d}z} + \int_{{{{ - h_{\text{c}} } \mathord{\left/ {\vphantom {{ - h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}} {\rho_{\text{c}} \left( z \right)\varPhi \left( z \right)\left( {1,z,\varPhi \left( z \right)} \right)b\text{d}z} \\ & \quad + \int_{{{{h_{\text{c}} } \mathord{\left/ {\vphantom {{h_{\text{c}} } 2}} \right. \kern-0pt} 2}}}^{{{{h_{l} } \mathord{\left/ {\vphantom {{h_{l} } 2}} \right. \kern-0pt} 2}}} {\rho_{l} \left( z \right)\varPhi \left( z \right)\left( {1,z,\varPhi \left( z \right)} \right)b\text{d}z} , \\ \end{aligned}$$
(21b)

And the related boundary conditions are obtained as:

$$x = 0,L:\,\,\,\,\,u = 0\,\,\,\,\,\text{OR}\,\,\,\,\,N_{x}^{t} = 0,$$
(22a)
$$x = 0,L:\,\,\,\,\,w = 0\,\,\,\,\,\text{OR}\,\,\,\,\,I_{B} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{D} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} + I_{F} \frac{{\partial^{2} \gamma }}{{\partial t^{2} }} - N_{x}^{t} \frac{\partial w}{\partial x} - \frac{{\partial M_{c}^{t} }}{\partial x} - \frac{{\partial Y_{1}^{t} }}{\partial x} = 0,$$
(22b)
$$x = 0,L:\,\,\,\,\,\frac{\partial w}{\partial x} = 0\,\,\,\,\,\text{OR}\,\,\,\,\,M_{c}^{t} + Y_{1}^{t} = 0,$$
(22c)
$$x = 0,L:\,\,\,\,\,\gamma = 0\,\,\,\,\,\text{OR}\,\,\,\,\,M_{nc}^{t} + \frac{1}{2}Y_{2}^{t} = 0.$$
(22d)

It is worth mentioning that the initial displacements and the initial velocities of the beam are assumed to be zero [25].

It is convenient to introduce the following dimensionless parameters as:

$$\begin{aligned} & X = \frac{x}{L},\left( {U,W} \right) = \left( {\frac{u}{h},\frac{w}{h}} \right),l_{0} = \frac{l}{h},\eta = \frac{h}{L},\varGamma = \gamma ,T = \frac{t}{L}\sqrt {\frac{{A_{11} }}{{I_{A}^{{}} }}} ,\varOmega = \omega L\sqrt {\frac{{I_{A} }}{{A_{11} }}} , \\ & \left( {\bar{B}_{11} ,\bar{D}_{11} ,\bar{E}_{11} ,\bar{F}_{11} ,\bar{H}_{11} } \right) = \left( {\frac{{B_{11} }}{{A_{11} L}},\frac{{D_{11} }}{{A_{11} L^{2} }},\frac{{E_{11} }}{{A_{11} h}},\frac{{F_{11} }}{{A_{11} h^{2} }},\frac{{H_{11} }}{{A_{11} h^{2} }}} \right),M_{31} = \frac{{2bh_{L} e_{31} k_{\text{c}} c\left( t \right)}}{{\sqrt {I_{A}^{{}} A_{11} } }}, \\ & M_{32} = \frac{{E_{31} k_{\text{c}} c\left( t \right)}}{{h\sqrt {I_{A} A_{11} } }},\left( {\bar{I}_{B} ,\bar{I}_{D} ,\bar{I}_{E} ,\bar{I}_{F} ,\bar{I}_{H} } \right) = \left( {\frac{{I_{B} }}{{I_{A} L}},\frac{{I_{D} }}{{I_{A} L^{2} }},\frac{{I_{E} }}{{I_{A} h}},\frac{{I_{F} }}{{I_{A} h^{2} }},\frac{{I_{H} }}{{I_{A} h^{2} }}} \right),\alpha_{T} = L\sqrt {\frac{{I_{A}^{{}} }}{{A_{11} }}} , \\ & \left( {\bar{A}_{13} ,\bar{D}_{13} ,\bar{B}_{13} ,\bar{E}_{13} } \right) = \left( {\frac{{A_{13} }}{{A_{11} }},\frac{{D_{13} }}{{A_{11} }},\frac{{B_{13} }}{{A_{11} }},\frac{{E_{13} L^{2} }}{{A_{11} }}} \right),K_{\text{c}} = \frac{{c_{\text{d}} L}}{{\sqrt {I_{A} A_{11} } }},K_{\text{w}} = \frac{{k_{\text{w}} L^{2} }}{{A_{11} }},K_{\text{g}} = \frac{{k_{\text{g}} }}{{A_{11} }},F_{0} = \frac{{f_{0} L^{2} }}{{A_{11} h}}. \\ \end{aligned}$$
(23)

Substituting Eqs. (14) into Eqs. (20) and (22) and using Eqs. (23), the dimensionless governing motion equations are derived as follows:

$$\frac{{\partial^{2} U}}{{\partial X^{2} }} - \bar{B}_{11} \frac{{\partial^{3} W}}{{\partial X^{3} }} + \bar{E}_{11} \frac{{\partial^{2} \varGamma }}{{\partial X^{2} }} + \eta \frac{\partial W}{\partial X}\frac{{\partial^{2} W}}{{\partial X^{2} }} - M_{31} \frac{{\partial^{2} W}}{\partial X\partial T} = \frac{{\partial^{2} U}}{{\partial T^{2} }} - \bar{I}_{B} \frac{{\partial^{3} W}}{{\partial X\partial T^{2} }} + \bar{I}_{E} \frac{{\partial^{2} \varGamma }}{{\partial T^{2} }},$$
(24a)
$$\begin{aligned} & \eta \frac{{\partial^{2} U}}{{\partial X^{2} }}\frac{\partial W}{\partial X} + \bar{E}_{11} \eta \frac{\partial W}{\partial X}\frac{{\partial^{2} \varGamma }}{{\partial X^{2} }} + \frac{{3\eta^{2} }}{2}\left( {\frac{\partial W}{\partial X}} \right)^{2} \frac{{\partial^{2} W}}{{\partial X^{2} }} - M_{31} \eta \frac{{\partial^{2} W}}{\partial X\partial T}\frac{\partial W}{\partial X} \\ & \quad + \eta \frac{\partial U}{\partial X}\frac{{\partial^{2} W}}{{\partial X^{2} }} + \bar{E}_{11} \eta \frac{\partial \varGamma }{\partial X}\frac{{\partial^{2} W}}{{\partial X^{2} }} - M_{31} \eta \frac{\partial W}{\partial \tau }\frac{{\partial^{2} W}}{{\partial X^{2} }} + \bar{B}_{11} \frac{{\partial^{3} U}}{{\partial X^{3} }} - \bar{D}_{11} \frac{{\partial^{4} W}}{{\partial X^{4} }} \\ & \quad + \bar{F}_{11} \eta \frac{{\partial^{3} \varGamma }}{{\partial X^{3} }} + \frac{1}{2}\bar{B}_{13} \eta l_{0}^{2} \frac{{\partial^{3} \varGamma }}{{\partial X^{3} }} - \bar{A}_{13} l_{0}^{2} \eta^{2} \frac{{\partial^{4} W}}{{\partial X^{4} }} + F_{0} \sin \left( {\varOmega T} \right)e^{{\alpha_{T} T}} \\ & \quad - K_{\text{w}} W + K_{\text{g}} \frac{{\partial^{2} W}}{{\partial X^{2} }} - K_{\text{c}} \frac{\partial W}{\partial T} = \frac{{\partial^{2} W}}{{\partial T^{2} }} + \bar{I}_{B} \frac{{\partial^{3} U}}{{\partial X\partial T^{2} }} - \bar{I}_{D} \frac{{\partial^{4} W}}{{\partial X^{2} \partial T^{2} }} + \bar{I}_{F} \eta \frac{{\partial^{3} \varGamma }}{{\partial X\partial T^{2} }}, \\ \end{aligned}$$
(24b)
$$\begin{aligned} & \bar{E}_{11} \frac{{\partial^{2} U}}{{\partial X^{2} }} - \bar{F}_{11} \eta \frac{{\partial^{3} W}}{{\partial X^{3} }} + \bar{H}_{11} \frac{{\partial^{2} \varGamma }}{{\partial X^{2} }} + \bar{E}_{11} \eta \frac{\partial W}{\partial X}\frac{{\partial^{2} W}}{{\partial X^{2} }} - M_{32} \frac{{\partial^{2} W}}{\partial X\partial T} - \frac{{\bar{D}_{13} }}{{\eta^{2} }}\varGamma + \frac{1}{4}\bar{D}_{13} l_{0}^{2} \frac{{\partial^{2} \varGamma }}{{\partial X^{2} }} \\ & \quad - \frac{1}{2}\bar{B}_{13} l_{0}^{2} \eta \frac{{\partial^{3} W}}{{\partial X^{3} }} - \frac{1}{4}\bar{E}_{13} l_{0}^{2} \varGamma = \bar{I}_{E} \frac{{\partial^{2} U}}{{\partial T^{2} }} - \bar{I}_{F} \eta \frac{{\partial^{3} W}}{{\partial X\partial T^{2} }} + \bar{I}_{H} \frac{{\partial^{2} \varGamma }}{{\partial T^{2} }}. \\ \end{aligned}$$
(24c)

And dimensionless boundary conditions are obtained as follows:

$$X = 0,L:\,\,\,\,\,U = 0\,\,\,\,\,\text{OR}\,\,\,\,\,\frac{\partial U}{\partial X} - \bar{B}_{11} \frac{{\partial^{2} W}}{{\partial X^{2} }} + \bar{E}_{11} \frac{\partial \varGamma }{\partial X} + \frac{\eta }{2}\left( {\frac{\partial W}{\partial X}} \right)^{2} - M_{31} \frac{\partial W}{\partial T} = 0,$$
(25a)
$$\begin{aligned} & X = 0,L:\,\,\,\,\,W = 0\,\,\,\,\,\text{OR}\,\,\,\,\,\bar{I}_{B} \frac{{\partial^{2} U}}{{\partial T^{2} }} - \bar{I}_{D} \frac{{\partial^{3} W}}{{\partial X\partial T^{2} }} + \bar{I}_{F} \eta \frac{{\partial^{2} \varGamma }}{{\partial T^{2} }} + \eta \frac{\partial U}{\partial X}\frac{\partial W}{\partial X} - \bar{B}_{11} \eta \frac{{\partial^{2} W}}{{\partial X^{2} }}\frac{\partial W}{\partial X} \\ & \quad + \bar{E}_{11} \eta \frac{\partial \varGamma }{\partial X}\frac{\partial W}{\partial X} + \frac{{\eta^{2} }}{2}\left( {\frac{\partial W}{\partial X}} \right)^{2} \frac{\partial W}{\partial X} - M_{31} \frac{\partial W}{\partial \tau }\frac{\partial W}{\partial X} - \bar{B}_{11} \frac{{\partial^{2} U}}{{\partial X^{2} }} \\ & \quad + \bar{D}_{11} \frac{{\partial^{3} W}}{{\partial X^{3} }} - \bar{F}_{11} \eta \frac{{\partial^{2} \varGamma }}{{\partial X^{2} }} - \bar{B}_{11} \eta \frac{\partial W}{\partial X}\frac{{\partial^{2} W}}{{\partial X^{2} }} - \frac{1}{2}\bar{B}_{13} l_{0}^{2} \eta \frac{{\partial^{2} \varGamma }}{{\partial X^{2} }} \\ & \quad + \bar{A}_{13} l_{0}^{2} \eta^{2} \frac{{\partial^{3} W}}{{\partial X^{3} }} - K_{\text{g}} \frac{\partial W}{\partial X} = 0, \\ \end{aligned}$$
(25b)
$$\begin{aligned} & X = 0,L:\,\,\,\,\,\frac{\partial W}{\partial X} = 0\,\,\,\,\,\text{OR}\,\,\,\,\,\bar{B}_{11} \frac{\partial U}{\partial X} - \bar{D}_{11} \frac{{\partial^{2} W}}{{\partial X^{2} }} + \bar{F}_{11} \eta \frac{\partial \varGamma }{\partial X} + \frac{1}{2}\bar{B}_{13} l_{0}^{2} \eta \frac{\partial \varGamma }{\partial X} - \bar{A}_{13} l_{0}^{2} \eta^{2} \frac{{\partial^{2} W}}{{\partial X^{2} }} \\ & \quad + \frac{{\bar{B}_{11} }}{2}\eta \left( {\frac{\partial W}{\partial X}} \right)^{2} = 0, \\ \end{aligned}$$
(25c)
$$\begin{aligned} & X = 0,L:\,\,\,\,\,\varGamma = 0\,\,\,\,\,\text{OR}\,\,\,\,\,\bar{E}_{11} \frac{\partial U}{\partial X} - \bar{F}_{11} \eta \frac{{\partial^{2} W}}{{\partial X^{2} }} + \bar{H}_{11} \frac{\partial \varGamma }{\partial X} - M_{32} \frac{\partial W}{\partial T} + \frac{1}{4}\bar{D}_{13} l_{0}^{2} \frac{\partial \varGamma }{\partial X} \\ & \quad + \frac{{\bar{E}_{11} }}{2}\eta \left( {\frac{\partial W}{\partial X}} \right)^{2} - \frac{1}{2}\bar{B}_{13} l_{0}^{2} \eta \frac{{\partial^{2} W}}{{\partial X^{2} }} = 0. \\ \end{aligned}$$
(25d)

Therefore, for simply supported end conditions, one can write the following expression:

$$\begin{aligned} & U = 0,W = 0,\bar{B}_{11} \frac{\partial U}{\partial X} - \bar{D}_{11} \frac{{\partial^{2} W}}{{\partial X^{2} }} + \bar{F}_{11} \eta \frac{\partial \varGamma }{\partial X} + \frac{1}{2}\bar{B}_{13} l_{0}^{2} \eta \frac{\partial \varGamma }{\partial X} - \bar{A}_{13} l_{0}^{2} \eta^{2} \frac{{\partial^{2} W}}{{\partial X^{2} }} + \frac{{\bar{B}_{11} }}{2}\eta \left( {\frac{\partial W}{\partial X}} \right)^{2} = 0, \\ & \bar{E}_{11} \frac{\partial U}{\partial X} - \bar{F}_{11} \eta \frac{{\partial^{2} W}}{{\partial X^{2} }} + \bar{H}_{11} \frac{\partial \varGamma }{\partial X} - M_{32} \frac{\partial W}{\partial T} + \frac{1}{4}\bar{D}_{13} l_{0}^{2} \frac{\partial \varGamma }{\partial X} + \frac{{\bar{E}_{11} }}{2}\eta \left( {\frac{\partial W}{\partial X}} \right)^{2} - \frac{1}{2}\bar{B}_{13} l_{0}^{2} \eta \frac{{\partial^{2} W}}{{\partial X^{2} }} = 0. \\ \end{aligned}$$
(26)

And for clamped end conditions:

$$U = 0,W = 0,\frac{\partial W}{\partial X} = 0,\varGamma = 0.$$
(27)

4 Solution method

In the present study, the DQM in conjunction with Newmark-β are employed to solve the governing motion equations. For this purpose, first, the DQM is applied. The main idea of this method is that the partial derivative of a function with respect to spatial variables at a given discrete point is approximated as a weighted linear sum of the function values at all discrete points chosen in the solution domain. Therefore, the functions \(U\), \(W\) and \(\varGamma\) and their derivatives with respect to \(X\) can be expressed as [22, 26]:

$$\left\{ {U,W,\varGamma } \right\} = \sum\limits_{m = 1}^{N} {l_{m} \left( X \right)\left\{ {U_{m} \left( {X_{m} ,t} \right),W_{m} \left( {X_{m} ,t} \right),\varGamma_{m} \left( {X_{m} ,t} \right)} \right\}} ,$$
(28a)
$$\left. {\frac{{\partial^{k} }}{{\partial X^{k} }}\left\{ {U,W,\varGamma } \right\}} \right|_{{X = X_{i} }} = \sum\limits_{m = 1}^{N} {C_{im}^{\left( k \right)} \left( X \right)\left\{ {U_{m} \left( {X_{m} ,t} \right),W_{m} \left( {X_{m} ,t} \right),\varGamma_{m} \left( {X_{m} ,t} \right)} \right\}} ,$$
(28b)

where \(N\) is the total number of grid points along \(X\), \(l_{m} \left( X \right)\) is the Lagrange interpolation polynomials and \(C_{im}^{\left( k \right)}\) represents the weighting coefficients, which can be found in [22, 26]. The Chebyshev polynomials are chosen for the positions of the grid points which can be expressed as:

$$X_{i} = \frac{1}{2}\left( {1 - \cos \left( {\frac{{\pi \left( {i - 1} \right)}}{N - 1}} \right)} \right),\,\,\,\,\,i = 1,2, \ldots ,N$$
(29)

Substituting Eqs. (28) into Eqs. (24) yields the following differential equations as:

$$\begin{aligned} & \sum\limits_{m = 1}^{N} {C_{im}^{\left( 2 \right)} U_{m} } - \bar{B}_{11} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 3 \right)} W_{m} } + \bar{E}_{11} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 2 \right)} \varGamma_{m} } + \eta \sum\limits_{m = 1}^{N} {C_{im}^{\left( 1 \right)} W_{m} } \sum\limits_{m = 1}^{N} {C_{im}^{\left( 2 \right)} W_{m} } \\ & \quad - M_{31} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 1 \right)} \dot{W}_{m} } = \ddot{U}_{i} - \bar{I}_{B} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 1 \right)} \ddot{W}_{m} } + \bar{I}_{E} \ddot{\varGamma }_{i} , \\ \end{aligned}$$
(30a)
$$\begin{aligned} & \eta \sum\limits_{m = 1}^{N} {C_{im}^{\left( 2 \right)} U_{m} } \sum\limits_{m = 1}^{N} {C_{im}^{\left( 1 \right)} W_{m} } + \bar{E}_{11} \eta \sum\limits_{m = 1}^{N} {C_{im}^{\left( 1 \right)} W_{m} } \sum\limits_{m = 1}^{N} {C_{im}^{\left( 2 \right)} \varGamma_{m} } + \frac{{3\eta^{2} }}{2}\left( {\sum\limits_{m = 1}^{N} {C_{im}^{\left( 1 \right)} W_{m} } } \right)^{2} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 2 \right)} W_{m} } \\ & \quad - M_{31} \eta \sum\limits_{m = 1}^{N} {C_{im}^{\left( 1 \right)} \dot{W}_{m} } \sum\limits_{m = 1}^{N} {C_{im}^{\left( 1 \right)} W_{m} } + \eta \sum\limits_{m = 1}^{N} {C_{im}^{\left( 1 \right)} U_{m} } \sum\limits_{m = 1}^{N} {C_{im}^{\left( 2 \right)} W_{m} } + \bar{E}_{11} \eta \sum\limits_{m = 1}^{N} {C_{im}^{\left( 2 \right)} W_{m} } \sum\limits_{m = 1}^{N} {C_{im}^{\left( 1 \right)} \varGamma_{m} } \\ & \quad - M_{31} \eta \dot{W}_{i} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 2 \right)} W_{m} } + \bar{B}_{11} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 3 \right)} U_{m} } - \bar{D}_{11} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 4 \right)} W_{m} } + \bar{F}_{11} \eta \sum\limits_{m = 1}^{N} {C_{im}^{\left( 3 \right)} \varGamma_{m} } \\ & \quad + \frac{1}{2}\bar{B}_{13} \eta l_{0}^{2} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 3 \right)} \varGamma_{m} } - \bar{A}_{13} l_{0}^{2} \eta^{2} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 4 \right)} W_{m} } + F_{0} \sin \left( {\varOmega T} \right)e^{{\alpha_{T} T}} - K_{\text{w}} W_{i} \\ & \quad + K_{\text{g}} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 2 \right)} W_{m} } - K_{\text{c}} \dot{W}_{i} = \ddot{W}_{i} + \bar{I}_{B} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 1 \right)} \ddot{U}_{m} } - \bar{I}_{D} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 2 \right)} \ddot{W}_{m} } + \bar{I}_{F} \eta \sum\limits_{m = 1}^{N} {C_{im}^{\left( 1 \right)} \ddot{\varGamma }_{m} } , \\ \end{aligned}$$
(30b)
$$\begin{aligned} & \bar{E}_{11} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 2 \right)} U_{m} } - \bar{F}_{11} \eta \sum\limits_{m = 1}^{N} {C_{im}^{\left( 3 \right)} W_{m} } + \bar{H}_{11} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 2 \right)} \varGamma_{m} } + \bar{E}_{11} \eta \sum\limits_{m = 1}^{N} {C_{im}^{\left( 1 \right)} W_{m} } \sum\limits_{m = 1}^{N} {C_{im}^{\left( 2 \right)} W_{m} } \\ & \quad \quad - M_{32} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 1 \right)} \dot{W}_{m} } - \frac{{\bar{B}_{13} }}{{\eta^{2} }}\varGamma_{i} + \frac{1}{4}\bar{B}_{13} l_{0}^{2} \sum\limits_{m = 1}^{N} {C_{im}^{\left( 2 \right)} \varGamma_{m} } - \frac{1}{2}\bar{D}_{13} l_{0}^{2} \eta \sum\limits_{m = 1}^{N} {C_{im}^{\left( 3 \right)} W_{m} } - \frac{1}{4}\bar{E}_{13} l_{0}^{2} \varGamma \\ & \quad = \bar{I}_{E} \ddot{U}_{i} - \bar{I}_{F} \eta \sum\limits_{m = 1}^{N} {C_{im}^{\left( 1 \right)} \ddot{W}_{m} } + \bar{I}_{H} \ddot{\varGamma }_{i} . \\ \end{aligned}$$
(30c)

where the over dot indicates the partial derivatives with respect to the dimensionless time. Also, inserting Eqs. (28) into Eqs. (26) and (27) yields the following equations for C–C, S–S and clamped-simply supported (C–S) boundary conditions as:

$$\begin{aligned} \text{C}{ - }\text{C}:\,\,\,U_{1} & = 0,W_{1} = 0,\sum\limits_{m = 1}^{N} {C_{1m}^{\left( 1 \right)} W_{m} } = 0,\varGamma_{1} = 0,\,\,\,\,\,\text{at}\,\,\,\,\,X = 0, \\ U_{N} & = 0,W_{N} = 0,\sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} W_{m} } = 0,\varGamma_{N} = 0,\,\,\,\,\,\text{at}\,\,\,\,\,X = 1 \\ \end{aligned}$$
(31a)
$$\begin{aligned} \text{S - S}:\,\,\, & \quad U_{1} = 0,W_{1} = 0, \\ & \quad \bar{B}_{11} \sum\limits_{m = 1}^{N} {C_{1m}^{\left( 1 \right)} U_{m} } - \bar{D}_{11} \sum\limits_{m = 1}^{N} {C_{1m}^{\left( 2 \right)} W_{m} } + \bar{F}_{11} \eta \sum\limits_{m = 1}^{N} {C_{1m}^{\left( 1 \right)} \varGamma_{m} } + \frac{1}{2}\bar{B}_{13} l_{0}^{2} \eta \sum\limits_{m = 1}^{N} {C_{1m}^{\left( 1 \right)} \varGamma_{m} } \\ & \quad - \bar{A}_{13} l_{0}^{2} \eta^{2} \sum\limits_{m = 1}^{N} {C_{1m}^{\left( 2 \right)} W_{m} } + \frac{{\bar{B}_{11} }}{2}\eta \left( {\sum\limits_{m = 1}^{N} {C_{1m}^{\left( 1 \right)} W_{m} } } \right)^{2} = 0, \\ & \quad \bar{E}_{11} \sum\limits_{m = 1}^{N} {C_{1m}^{\left( 1 \right)} U_{m} } - \bar{F}_{11} \eta \sum\limits_{m = 1}^{N} {C_{1m}^{\left( 2 \right)} W_{m} } + \bar{H}_{11} \sum\limits_{m = 1}^{N} {C_{1m}^{\left( 1 \right)} \varGamma_{m} } - M_{32} \dot{W}_{1} + \frac{1}{4}\bar{D}_{13} l_{0}^{2} \sum\limits_{m = 1}^{N} {C_{1m}^{\left( 1 \right)} \varGamma_{m} } \\ & \quad + \frac{{\bar{E}_{11} }}{2}\eta \left( {\sum\limits_{m = 1}^{N} {C_{1m}^{\left( 1 \right)} W_{m} } } \right)^{2} - \frac{1}{2}\bar{B}_{13} l_{0}^{2} \eta \sum\limits_{m = 1}^{N} {C_{1m}^{\left( 2 \right)} W_{m} } = 0.\,\,\,\,\,\text{at}\,\,\,\,\,X = 0, \\ & \quad U_{N} = 0,W_{N} = 0, \\ & \quad \bar{B}_{11} \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} U_{m} } - \bar{D}_{11} \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 2 \right)} W_{m} } + \bar{F}_{11} \eta \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} \varGamma_{m} } + \frac{1}{2}\bar{B}_{13} l_{0}^{2} \eta \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} \varGamma_{m} } \\ & \quad - \bar{A}_{13} l_{0}^{2} \eta^{2} \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 2 \right)} W_{m} } + \frac{{\bar{B}_{11} }}{2}\eta \left( {\sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} W_{m} } } \right)^{2} = 0, \\ & \quad \bar{E}_{11} \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} U_{m} } - \bar{F}_{11} \eta \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 2 \right)} W_{m} } + \bar{H}_{11} \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} \varGamma_{m} } - M_{32} \dot{W}_{N} + \frac{1}{4}\bar{D}_{13} l_{0}^{2} \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} \varGamma_{m} } \\ & \quad + \frac{{\bar{E}_{11} }}{2}\eta \left( {\sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} W_{m} } } \right)^{2} - \frac{1}{2}\bar{B}_{13} l_{0}^{2} \eta \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 2 \right)} W_{m} } = 0.\,\,\,\,\,\text{at}\,\,\,\,\,X = 1, \\ \end{aligned}$$
(31b)
$$\begin{aligned} \text{C - S}:\,\,\, & \quad U_{1} = 0,W_{1} = 0,\sum\limits_{m = 1}^{N} {C_{1m}^{\left( 1 \right)} W_{m} } = 0,\varGamma_{1} = 0,\,\,\,\,\,\text{at}\,\,\,\,\,X = 0, \\ & \quad U_{N} = 0,W_{N} = 0, \\ & \quad \bar{B}_{11} \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} U_{m} } - \bar{D}_{11} \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 2 \right)} W_{m} } + \bar{F}_{11} \eta \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} \varGamma_{m} } + \frac{1}{2}\bar{B}_{13} l_{0}^{2} \eta \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} \varGamma_{m} } \\ & \quad - \bar{A}_{13} l_{0}^{2} \eta^{2} \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 2 \right)} W_{m} } + \frac{{\bar{B}_{11} }}{2}\eta \left( {\sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} W_{m} } } \right)^{2} = 0, \\ & \quad \bar{E}_{11} \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} U_{m} } - \bar{F}_{11} \eta \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 2 \right)} W_{m} } + \bar{H}_{11} \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} \varGamma_{m} } - M_{32} \dot{W}_{N} + \frac{1}{4}\bar{D}_{13} l_{0}^{2} \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} \varGamma_{m} } \\ & \quad + \frac{{\bar{E}_{11} }}{2}\eta \left( {\sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 1 \right)} W_{m} } } \right)^{2} - \frac{1}{2}\bar{B}_{13} l_{0}^{2} \eta \sum\limits_{m = 1}^{N} {C_{Nm}^{\left( 2 \right)} W_{m} } = 0.\,\,\,\,\,\text{at}\,\,\,\,\,X = 1, \\ \end{aligned}$$
(31c)

Considering Eqs. (30) and (31) and explanations presented in “Appendix”, the governing motion equations can be obtained as follows:

$$\left[ M \right]\left\{ {\ddot{d}} \right\}_{\text{d}} + \left[ {C_{NL} + C_{L} } \right]\left\{ {\dot{d}} \right\}_{\text{d}} + \left[ {K_{NL} + K_{L} } \right]\left\{ d \right\}_{\text{d}} = \left\{ F \right\},$$
(32)

5 Numerical results and discussion

In this study based on the DQM for space discretization and Newmark-β method for time discretization, the nonlinear dynamic response of the embedded FGMSNB is obtained for C–C, S–S and C–S boundary conditions. The sandwich nanobeam consists of a FGM core integrated with magnetostrictive layers. The temperature-dependent material properties of FGM constituent materials which are taken from Ref. [24] are listed in Table 1.

Table 1 Material properties of the FGM core [24]
Full size table

It should be noted that in the present study, the room temperature (\(T = 25\;^\circ \text{C}\)) is assumed to calculate the material properties in Eq. (11). Also, the Young’s modulus for Terfenol-D magnetostrictive layer is \(E = 26.5\;\text{GPa}\) and the magnetostrictive coupling moduli are \(e_{31} = e_{32} = E^{m} d^{m}\) where \(E^{m} = 26.5\;\text{GPa}\), \(d^{m} = 1.67 \times 10^{ - 8} \;{\text{m} \mathord{\left/ {\vphantom {\text{m} \text{A}}} \right. \kern-0pt} \text{A}}\) [6]. Moreover, the following data used for geometry of the FGMSNB and elastic medium constants: the core thickness \(h_{\text{c}} = 1\;\left( {\text{nm}} \right)\), the thickness of each magnetostrictive layer \(h_{\text{m}} = 0.25\;\left( {\text{nm}} \right)\),the aspect ratio of length to the thickness \(L/h_{l} = 8\), the spring constant of elastic medium \(k_{\text{w}} = 100\;\left( {{{\text{MN}} \mathord{\left/ {\vphantom {{\text{MN}} {\text{m}^{2} }}} \right. \kern-0pt} {\text{m}^{2} }}} \right)\), the shear constant of elastic medium \(k_{\text{g}} = 1\;\left( {\text{nN}} \right)\) and the damping modulus constant of elastic foundation \(k_{\text{c}} = 3 \times 10^{ - 4} \;\left( {{{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {\text{ms}}}} \right. \kern-0pt} {\text{ms}}}} \right)\). Also the external harmonic load properties used for the presented results are \(F_{0} = 0.5\) and \(\alpha_{T} = - 0.1\).

5.1 Validation

In order to check the validity and accuracy of the presented solution, the linear results are compared with the exact solution obtained by Rao [25]. Using Eqs. (23), the dimensionless midpoint displacement for the S–S EBBT beam subjected to a harmonically varying load as \(F_{0} \sin \left( {\varOmega T} \right)\sin \left( {n\pi X} \right)\) is obtained as [25]:

$$\left. W \right|_{X = 0.5} = \frac{{F_{0} }}{{\bar{D}_{11} \left( {\pi^{4} - \varOmega^{2} } \right)}}\left( {\sin \left( {\varOmega T} \right) - \left( {\left( {\frac{\varOmega }{{\pi^{2} \sqrt {\bar{D}_{11} } }}} \right)\sin \left( {\pi^{2} \sqrt {\bar{D}_{11} } T} \right)} \right)} \right).$$
(33)

Figure 2a and b compares the dimensionless midpoint deflection of the S–S EBB FGMSNB obtained with the DQM in conjunction with Newmark-β method with the exact solution obtained in Eq. (33) and good agreement can be seen between them.

Fig. 2
figure 2

Dimensionless midpoint deflection of the S–S EBB FGMSNB obtained from the presented method and exact solution [23] a\(F_{0} = 1.0\), \(n = 1.0\) and b\(\varOmega = 0.5\), \(n = 1.0\)

Full size image

5.2 Convergence of numerical solution

In order to check the convergence and accuracy of the DQM, the appropriate number of grid points is obtained. For this purpose, the maximum dimensionless midpoint deflections (\(\left. W \right|_{X = 0.5}\)) of the FGSNB for different values of grid points for both linear and nonlinear analysis are presented in Tables 2, 3 and 4 for C–C, C–S and S–S boundary conditions, respectively. As can be seen, the maximum dimensionless midpoint deflection values are converged for \(N = 15\), \(N = 19\) and \(N = 13\) for C–C, C–S and S–S boundary conditions, respectively.

Table 2 Maximum values of dimensionless midpoint deflection for different number of grid points for C–C boundary conditions
Full size table
Table 3 Maximum values of dimensionless midpoint deflection for different number of grid points for C–S boundary conditions
Full size table
Table 4 Maximum values of dimensionless midpoint deflection for different number of grid points for S–S boundary conditions
Full size table

From Tables 2, 3 and 4, it can be found that results obtained from different theories are close to each other. Therefore from here to the end of the manuscript in order to obtain the results, PSDBT is chosen.

5.3 Small-scale parameter effect

Figure 3a–c shows the small-scale effects on the nonlinear time history of the dimensionless midpoint deflection of PSDBT model for C–C, C–S and S–S boundary conditions, respectively. It is seen form Fig. 3 that increasing small-scale parameter decreases the maximum midpoint dimensionless deflection for different boundary conditions. It is due to the fact that according to Eqs. (1) and (8) increasing the small-scale parameter increases the strain energy of the system which yields reduction in dimensionless deflection of the FGSNB. Moreover, the effect of small-scale parameter becomes more distinguished for C–C boundary conditions. Furthermore, comparing the dimensionless midpoint deflection values shows that the C–C end conditions yield lower deflection in comparison with other boundary conditions. Therefore, the obtained numerical results are consistent with physical results where the stiffer boundary conditions yields lower deflections. It should be mentioned that for the following sections, the \(l = 0.2h_{l}\) is selected for the small-scale parameter unless otherwise mentioned.

Fig. 3
figure 3

Small-scale effect on the time history of midpoint dimensionless deflection a C–C, b C–S and c S–S

Full size image

5.4 Geometrical parameters effect

In order to show the effects of geometrical parameters on the nonlinear midpoint deflection of the FGMSNB, Figs. 4 and 5 are plotted for different boundary conditions. To this purpose in the present section, the small-scale parameter is chosen \(l = 0.3\;\left( {\text{nm}} \right)\). In order to show the effect of magnetostrictive layers thickness on the dimensionless midpoint deflection, Fig. 4 is plotted for C–C FGSNB with \(L = 12\;\left( {\text{nm}} \right)\). It is seen from Fig. 4 that increasing the thickness of magnetostrictive layers decreases the midpoint deflection of the nanobeam. From the physically point of view, with increasing the thickness of magnetostrictive layers the bending rigidity of FGSNB increases, therefore, the deflection should be decreased. Therefore, the numerical results match the physical results.

Fig. 4
figure 4

Magnetostrictive layers thickness effect on the time history of midpoint dimensionless deflection

Full size image
Fig. 5
figure 5

FGSNB length effect on the time history of midpoint dimensionless deflection

Full size image

In Fig. 5, the length effect of the FGSNB on the time history of the dimensionless midpoint deflection is plotted. From Fig. 5, it is observed that increasing the length of the FGSNB decreases the midpoint deflection. Therefore, increasing the length of the FGSNB decreases the stability of the system.

5.5 Effect of environment temperature

To evaluate the influence of environment temperature on the midpoint deflection of the nanobeam for both linear and nonlinear solutions and C–C, C–S and S–S boundary conditions, Fig. 6 is plotted. From Fig. 6, it can be observed that the dimensionless midpoint deflection of the FGMSNB increases with increasing the environment temperature for both linear and nonlinear solutions and different boundary conditions. It is due to this fact that increasing the environment temperature makes the system looser which yields an increase in deflection of the system. Therefore, the effect of environment temperature on the properties of the FGM core should not be neglected in dynamic analysis. Also, the dimensionless midpoint deflections from linear solution are higher than those obtained from nonlinear solution. From Eqs. (12) and (14), it can be obtained that considering nonlinear terms increases the strain energy of the system. Therefore, the dimensionless deflections obtained from nonlinear solution should be lower than those obtained from linear solution.

Fig. 6
figure 6

Environment temperature effect on the time history of midpoint dimensionless deflection a C–C, b C–S and c S–S

Full size image

5.6 Surrounding elastic medium effect

Figures 7, 8 and 9 depict the effect of Winkler, Pasternak and visco-Pasternak elastic mediums, respectively, on the time history of the FGSNB nonlinear midpoint deflection. As can be seen, increasing each parameter of elastic medium such as spring, shear and damping constants of elastic medium decreases the midpoint dynamic deflection at a decreasing rate for different boundary conditions. Furthermore, increasing the damping modulus of elastic medium increases the period of midpoint deflection oscillations.

Fig. 7
figure 7

Winkler constant of elastic medium effect on the time history of midpoint dimensionless deflection a C–C, b C–S and c S–S

Full size image
Fig. 8
figure 8

Pasternak constant of elastic medium effect on the time history of midpoint dimensionless deflection a C–C, b C–S and c S–S

Full size image
Fig. 9
figure 9

Damping constant of elastic medium effect on the time history of midpoint dimensionless deflection a C–C, b C–S and c S–S

Full size image

5.7 Influence of magnetostrictive layers

Figure 10 illustrates the effect of magnetostrictive layers on the nonlinear midpoint dimensionless deflection for C–C, C–S and S–S boundary conditions, respectively. It is seen that increasing the velocity feedback gain (\(k_{\text{c}} c\left( t \right)\)) decreases the dimensionless midpoint deflection for different boundary conditions. Moreover, it can be concluded from Fig. 10 that the effect of velocity feedback gain is more prominent for S–S boundary conditions than others. Also, the effect of velocity feedback gain becomes more evident in results obtained from nonlinear solution.

Fig. 10
figure 10

Effects of magnetostrictive layers on the midpoint dimensionless longitudinal displacement a C–C, b C–S and c S–S

Full size image

5.8 Influence of material composition of the core

Figure 11 depicts the effect of material composition of the core layer by illustrating the variation of nonlinear dimensionless midpoint deflection versus the dimensionless time for different boundary conditions. It can be concluded for different boundary conditions, increasing the power law exponent leads to increasing the dimensionless midpoint deflection at a decreasing rate.

Fig. 11
figure 11

Effects of materials composition of core layer on the midpoint dimensionless longitudinal displacement a C–C, b C–S and c S–S

Full size image

6 Conclusion

Due to this fact that, dynamic analysis of nanobeam has been attracted much attention in NEMS, in this study the nonlinear dynamic analysis of FGMSNBs embedded in visco-Pasternak foundation was investigated using different beam models. The MCST was utilized to study the effect of small-scale parameter on the deflection of the nanobeam. Energy method and Hamilton’s principle were taken into account to obtain the governing motion equations and related boundary conditions. The results of this study were validated as far as possible with those obtained by Rao [25] and the influences of small-scale effect, geometrical parameters, environment temperature, surrounding elastic medium, magnetostrictive layers, material composition of core layer and boundary conditions were studied in detail. The obtained results would be beneficial for the design of sensors and actuators in NEMS. The following conclusions were made from the results:

  1. 1.

    Results obtained from different theories are close to each other; therefore, the PSDBT theory had been taken into consideration.

  2. 2.

    The dynamic response of the SNB is significantly influenced by the small-scale effect; increasing small-scale parameter decreases the maximum midpoint dimensionless deflection for different boundary conditions. Therefore, neglecting small-scale effects leads to inaccurate results.

  3. 3.

    Comparing results from different boundary conditions shows that the midpoint deflection for S–S boundary conditions is higher than those obtained from C–C and C–S boundary conditions.

  4. 4.

    Midpoint deflection values obtained from nonlinear solution are lower than those obtained from linear solution. It is due to the fact that considering nonlinear terms increases the strain energy of the system.

  5. 5.

    Increasing the velocity feedback gain increases the dimensionless deflection of the FGSNB.