Enhanced a hybrid moth-flame optimization algorithm using new selection schemes

Abstract

This paper presents two levels of enhancing the basic Moth flame optimization (MFO) algorithm. The first step is hybridizing MFO and the local-based algorithm, hill climbing (HC), called MFOHC. The proposed algorithm takes the advantages of HC to speed up the searching, as well as enhancing the learning technique for finding the generation of candidate solutions of basic MFO. The second step is the addition of six popular selection schemes to improve the quality of the selected solution by giving a chance to solve with high fitness value to be chosen and increase the diversity. In both steps of enhancing, thirty benchmark functions and five IEEE CEC 2011 real-world problems are used to evaluate the performance of the proposed versions. In addition, well-known and recent meta-heuristic algorithms are applied to compare with the proposed versions. The experiment results illustrate that the proportional selection scheme with MFOHC, namely (PMFOHC) is outperforming the other proposed versions and algorithms in the literature.

1 Introduction

Metaheuristic algorithms are classified into local search-based algorithms and population-based algorithms. Local search-based algorithms consider one solution at a time and try to enhance it using neighbourhood structures [44], such as hill climbing [26], tabu searches [16], $\beta$-hill climbing [2], and simulated annealing [25]. While the main advantage of these methods is rapid search speeds, the main drawback is their tendency to focus on exploitation rather than exploration, which, as a result, increases the likelihood of their getting stuck in local optima [43]. By contrast, population-based algorithms, which consider a population of solutions at a time, recombine the current solutions to generate one or more new solutions at each iteration. These methods are effective in identifying promising areas in the search space but are ineffective in exploiting the search space region being explored [45]. Evolutionary computation and swarm intelligence methods are classifications of population-based methods [1]. Both methods are based on the natural biological evolution or social interaction behaviour of natural creatures. Examples of swarm-based algorithms include particle swarm optimization (PSO) [24], krill herd algorithm (KHA) [13], the salp swarm algorithm (SSA) [31] and the moth-flame optimization (MFO) [28].

Swarm intelligence-based methods are inspired by animal societies and social insect colonies [4]. They mimic the behaviour of swarming social insects, schools of fish or flocks of birds. The main advantages of these methods are their flexibility and robustness [8]. MFO is a recent metaheuristic population-based method developed by Mirjalili [28] that imitate the moths’ movement technique in the night, called transverse orientation for navigation. Moths fly in the night depending on the moonlight, where they maintain a fixed angle to find their path. The behavior of moths has been formulated as a novel optimization technique. MFO can be utilized to solve a wide range of problems because its procedures are simple, flexible, and easily implemented [21]. On account of these merits, MFO was successfully applied to various optimization problems. For instance, scheduling [12], inverse problem and parameter estimation [3, 19], classification [58], economic [51], medical [53], power energy [57], and image processing [10].

As mentioned above, the basic MFO proved its efficiency to solve various problems. However, it suffers from a weak exploitation search, low diversity, and it slows the convergence rate. Therefore, Li et al. [27] applied multi-objective moth-flame optimization algorithm (MOMFA) to improve the efficiency of using water resources. The method assisted and utilized the original moth-flame optimization algorithm, opposition-based learning, and indicator-based selection efficient mechanisms to maintain the diversity and accelerate the convergence. The algorithm tested on the Lushui River Basin and many benchmarks [49]. The algorithm can determine the optimal tradeoff of the elements and can distribute non dominated outcomes for utilization problem of the multi-objective water resources. The result is verified and compared with other algorithms, it indicated to the ability to obtain well pareto solutions for standard problems. Also, Bhesdadiya et al. [6] introduced a hybrid optimization algorithm based on integration between particle swarm optimization (PSO) and MFO. The proposed algorithm is used to solve unconstrained engineering design optimization problems in power system context. MFO is applied to overcome the limitation of PSO algorithm by increasing the exploration search during solving high complex design problem. In the conducted experiment, four benchmarking functions are used to validate the proposed algorithm in terms of exploration and exploitation. Furthermore, the proposed algorithm is compared with the two traditional swarm-based algorithm namely, particle swarm optimization (PSO) and MFO to validate the performance. Overall experiment results illustrate that the performance of the proposed algorithm is better than the compared traditional methods. Moreover, in the context of image segmentation (automated food quality inspection), Sarma et al. [37] proposed a hybrid algorithm combined between physics-based algorithm [e.g., gravitational search algorithm (GSA)] and swarm-based algorithm (i.e., MFO). The proposed algorithm is applied to solve the problem of measuring the degree of food rottenness that cloud helps to minimize monetary losses due to food and storage. Both algorithm is combined because they complete each other. For example, MFO is important due to its effectiveness in exploratory nature. While, GSA is applied due to its effectiveness in team of exploitation. The experiment study is designed to test the hybrid optimization algorithm over thirteen unimodal functions and multimodal functions. Then, the experiment results are used to compare the proposed hybrid algorithm with traditional MFO and GSA algorithms. The comparison results show that the proposed hybrid algorithm is very fast and produces safe results. In [38], the authors proposed a nondominated MFO algorithm (NSMFO) method to solve multi-objective problems. Metaheuristics search techniques are used based on MFO instead of the different optimization techniques like cuckoo search, genetic algorithms, particle swarm optimization, and differential evolutions. The method utilized the crowding distance approach and sorting of the elitist non-dominated for preserving the diversity and obtaining variant nondomination levels, respectively, among the optimal set of solutions. It measured the effectiveness by multiobjective benchmark, engineering problems, distinctive feature, and the Pareto front generation [50]. The results of the method were compared with other algorithms and considered closer and better sometimes. While Reddy et al. [35] modified the MFO algorithm (MFOA) and examined characteristics of the local and global search of the basic algorithm. The algorithm is aimed to improve solving unit commitment (UC) problem by using the binary coded modified MFO algorithm (BMMFOA), the basic MFO is a natureinspired heuristic search approach that mimics the traverse navigational properties of moths around artificial lights tricked for natural moonlight, the algorithm used position update of a single-based approach between corresponding flame and the moth differently than many other swarm based approaches. The modified MFO algorithm (MMFOA) is used to improve the exploitation search of the moths and reduces the number of flames.

This paper highlights the two main weaknesses recognized in the performance trajectory of the basic version of the MFO: loss of the solutions’ diversity, which leads to a slow convergence manner. Because of these weaknesses, MFO requires further refinements, to be modified or hybridized with other algorithms components or local search techniques. As a result, an improved method, by hybridizing the basic MFO and hill-climbing (HC) search strategy called MFOCH. Moreover, using several promising selection schemes for enhancing the quality of the selected solutions. The following points are summarized the main contributions of this work.

• 1. A new hybridization method using MFO and HC (MFOCH) is developed to improve the exploitation search.

• 2. Alternative selection methods in the MFOCH for global optimization problems are investigated to maintain the diversity of the solutions, as well as improving their quality.

• 3. The performance of the proposed algorithms is tested using thirty basic benchmarks and five IEEE CEC 2011 real world problems.

The organization of this review is as follows. Section 2 introduces MFO, HC, and the selection schemes. Then, The proposed methods are described in Sect. 3. Section 4 shows experimental results and discussions. Finally, Sect. 5 presents conclusions and future directions.

2 Preliminaries

2.1 Moth-flame optimization algorithm

2.1.1 Origin

In nature, over 160,000 different species of moths have been documented, which are resemble butterflies in their life cycle (i.e., moth consists of two-level life: larvae and adult, where it converted to moth by cocoons) [48].

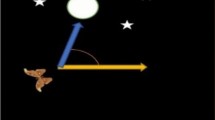
Interesting thing in the moths’ life is their special navigation methods at night. They have evolved to fly in the night using the moonlight. Also, they employed a mechanism called transverse orientation for navigation. This mechanism allows the moth to fly by preserving a stable angle with respect to the moon, a very effective mechanism for travelling long distances in a straight path [14]. Figure 1 illustrates a conceptual model of transverse orientation. Since the moon is far away from the moth, this mechanism guarantees flying in a straight line. The same navigation method can be done by humans. Suppose that the moon is in the south side of the sky and a human wants to go the east. If he keeps moon of his left side when walking, he would be able to move toward the east on a straight line.

Fig. 1

Moth’s transverse orientation

It can be observed in Fig. 2 the moths do not travel in a forward path, they fly spirally around lights. This is due to the transverse orientation method which is efficient just for the light source is very far (moonlight). In the human-made artificial light case, the moths attempt to preserve the same angle with the light source. Consequently, moths move in spirally paths around lights.

Fig. 2

Moth’s spiral flying path around a light source [46]

2.1.2 MFO algorithm

Moth-Flame optimization (MFO) algorithm was proposed by Mirjalili [28]. It is under the population-based metaheuristic algorithms. The flow data of the MFO starts by generating moths randomly within the solution space. Then, calculating the fitness values ( i.e., position) of each moth and tagging the best position by flame. After that, updating the moths’ positions depends on a spiral movement function to achieve better positions tagged by a flame, as well as updating the new best individual positions. Repeating the previous processes (i.e., updating the moths’ positions and generating new positions) until the termination criteria are met. Table 1 lists the characteristics of the MFO.

Table 1 Characteristic of the MFO algorithm

The MFO algorithm has three main steps. These steps as shown below. Followed by the pseudocode of the MFO as shown in Algorithm 1.

• 1. Generating the initial population of Moths:

  As mentioned in [28], Mirjalili assumed that each moth can fly in 1-D, 2-D, 3-D, or hyperdimensional space. The set of moths can be expressed:

  $$\begin{aligned} M=\begin{bmatrix} m_{1,1} &{} m_{1,2} &{} \cdots &{} \cdots &{} m_{1,d}\\ m_{2,1} &{} m_{2,2} &{} \cdots &{} \cdots &{} m_{2,d} \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ m_{n,1} &{} m_{n,2} &{} \cdots &{} \cdots &{} m_{n,d} \end{bmatrix} \end{aligned}$$

  (1)

  where n refers to the moths’ number and d refers to the dimensions’s number in the solution space. Also, the fitness values for all moths are memorized in an array as follows:

  $$\begin{aligned} OM=\begin{bmatrix} OM_{1}\\ OM_{2}\\ \vdots \\ OM_{n} \end{bmatrix} \end{aligned}$$

  (2)

  The rest elements in the MFO algorithm are flames. The following matrix showing the flames in the D-dimensional space followed by their fitness function vector:

  $$\begin{aligned} F= & {} \begin{bmatrix} F_{1,1} &{} F_{1,2} &{} \cdots &{} \cdots &{} F_{1,d}\\ F_{2,1} &{} F_{2,2} &{} \cdots &{} \cdots &{} F_{2,d} \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ F_{n,1} &{} F_{n,2} &{} \cdots &{} \cdots &{} F_{n,d} \end{bmatrix} \end{aligned}$$

  (3)
  $$\begin{aligned} {\text{OF}}= & {} \begin{bmatrix} {\text{OF}}_{1}\\ {\text{OF}}_{2}\\ \vdots \\ {\text{OF}}_{n} \end{bmatrix} \end{aligned}$$

  (4)

  It should be noted here that moths and flames are both solutions. The difference between them is the way we treat and update them in each iteration. The moths are actual search agents that move around the search space, whereas flames are the best position of moths that are obtained so far. In other words, flames can be considered as flags or pins that are dropped by moths when searching the search space. Therefore, each moth searches around a flag (flame) and updates it in case of finding a better solution. With this mechanism, a moth never loses its best solution.

• 2. Updating the Moths’ positions:

  MFO employs three different functions to convergent the global-optimal of the optimization problems. These functions are defined as follows:

  $$\begin{aligned} {\text {MFO}}=(I,P,T) \end{aligned}$$

  (5)

  where I refers to the first random locations of the moths ($I:\phi \rightarrow \left\{ M,OM \right\}$), P refers to motion the moths in the search space($P: M\rightarrow M$), and T refers to finish the search process ($T: M\rightarrow {{\text{true,false}}}$). The following equation represents I function, which use for implementing the random distribution.

  $$\begin{aligned} M(i,j )= ({\text {ub}}(i )-{\text {lb}}(j ))\times {\text {rand}}()+{\text {lb}}(i ) \end{aligned}$$

  (6)

  where lb and ub indicate the lower and upper bounds of variables, respectively. As mentioned previously, the moths fly in the search space using the transverse orientation. There are three conditions should abide when utilizing a logarithmic spiral subjected, as follows:

  • Spiral’s initial point should start from the moth.

  • Spiral’s final point should be the position of the flame.

  • Fluctuation of the range of spiral should not exceed the search space.

  Therefore, the logarithmic spiral for the MFO algorithm can be defined as follows:

  $$\begin{aligned} S(M_{i},F_j)=D_{i}\cdot e^{bt} \cdot { \cos}(2\pi t)+F_{j} \end{aligned}$$

  (7)

  where $D_{i}$ refers to the space between the i-th moth and the j-th flame (see the Eq. (8). b indicates a fix to define the shape of the logarithmic spiral, and t indicates a random number between [− 1, 1].

  $$\begin{aligned} D_{i}=\left| F_j-M_{i} \right| . \end{aligned}$$

  (8)

  In MFO, the balancing between exploitation and exploration are guaranteed by the spiral motion of the moth near the flame in the search space. Also, to avoid falling in the traps of the local optima, the optimal solutions have been kept in each repetition, and the moths fly around the flames (i.e., each moths flies surrounding the nearest flame) using the OF and OM matrices.

• 3. Updating the number of flames:

  This section highlights enhancing the exploitation of the MFO algorithm (i.e., Updating the moths’ positions in n various locations in the search space may decrease a chance of exploitation of the best promising solutions). Therefore, decreasing the number of flames helps to solve this issue based on the following equation:

  $$\begin{aligned} {\text {flame}}\; {\text {no}}={\text {round}}\left( N-l\times\frac{N-l}{T}\right) \end{aligned}$$

  (9)

where N is the maximum number of flames, l is the current number of iteration, and T indicates the maximum number of iterations.

2.2 Hill climbing

The hill climbing (HC) technique, called local search, is the most simplistic form of local development methods. It begins with one random initial solution (x), iteratively proceeds by moving from the current solution to a better neighboring solution till it reaches a local optimum (i.e., the local optimal solution does not have a better neighboring solution, no improvement in fitness function). It only takes downhill progress where the fitness function of a neighboring solution should be better than the current solution Shehab [41]. Consequently, it can converge to the local optima fast and suddenly. However, it can quickly get stuck in local optima, which in most situations is not satisfactory. Algorithm 2 presents the pseudo-code of the HC technique. After creating the first solution x and through the iterative improvement process, a group of neighboring solutions is created utilizing the procedure Improve(N(x)). This procedure seeks to discover the enhanced neighboring solution from the group of neighbors utilizing any used acceptance rule such as first improvement, best improvement, sidewalk, and random walk. But, all of these rules are stopped in local optima.

2.3 Selection schemes

In this section, the selection schemes are described that used in this paper.

2.3.1 Tournament selection scheme (TSS)

Tournament selection is among the most popular selection methods in genetic algorithms. It was initially proposed by Goldberg and Holland [17]. Algorithm 3 shows the principle of tournament selection work, which starts from the random selection of t individuals from P(t) population and then proceeds to the selection of the best individual from tournament t. This procedure is repeated N times. The best choice is frequently between two individuals, and this scheme is called binary tournament, where the choice is between t individuals called tournament size [7]. In other words, the efficiency of tournament selection scheme is based on the value of t. For instance, increasing the value of t will increase the diversity which leads to an increase in the quality of the selected solution, and vice versa [47].

There are several merits of the tournament selection scheme. For instance, low susceptibility to a takeover by dominant individuals [33], it has efficient time complexity (i.e., O(n)) [40], and no requirement for fitness scaling or sorting [32].

2.3.2 Proportional selection scheme (PSS)

The proportional selection scheme or so-called roulette wheel has been proposed in [20]. In other words, each element reserves a section in the roulette wheel, where the section’s size proportional with the element’s fitness. The mechanism of this method is choosing the probability based on the comparison between the fitness values of any solution and the fitness value of the stored solution in MFO. As shown in algorithm 4, r has been selected from U(0,1). Then, $s_{i}$ has accumulative determining the probabilities, the following equation shows the probability of solution x.

$$\begin{aligned} P_{i}=\frac{f(x_{i})}{\sum _{j=1}^{{\text {swarm size}}}f(x_{j})}. \end{aligned}$$

(10)

The advantage of proportional selection, it offers a chance for each element to be chosen. In contrast, in population converges, it suffers from selection pressure [40]. The time complexity of the proportional selection is O($n\ {\text {log}}\ n$).

2.3.3 Linear ranking selection scheme (LRSS)

To overcome the limitation of the proportional selection scheme, Goldberg and Holland [17] proposed Linear ranking selection scheme. It arranges the solutions based on their fitness ranks. Equation (11) shows the mechanism of calculation the selection probability by linear mapping of the solution ranks.

$$\begin{aligned} P_{i}=\frac{1}{N}\times \left( \eta ^{+} -\left( \eta ^{+}-\eta ^{-} \right) \times \frac{i-1}{N-1} \right) , \quad i \in {1,\ldots ,N}, \end{aligned}$$

(11)

where i is the rank of solution location $x^{j}$, $\eta ^{-}$ is the expected value of the worst location, $\eta ^{+}$ is the expected value of the best location. Both of $\eta ^{-}$ and $\eta ^{+}$ set the slope of the linear function. More details are shown in Algorithm 5.

The expected results of the linear ranking selection scheme with small $\eta ^{+}$ are close to the binary tournament selection. However, the linear ranking selection scheme with big $\eta ^{+}$ suffers from a stronger selection pressure (i.e., the time complexity is is O($n\ {\text {log}}\ n$)) [34].

2.3.4 Exponential ranking selection scheme (ERSS)

Unlike linear ranking completely, exponential ranking selection arranging the probabilities of the ranked elements by exponentially weighted [42]. The major of the exponent c which is situated between (0, 1), where it based on parameter s. For instance, the best solution has a value of $c_{1}=1$, followed by the second solution with $c_{2}=s$ ($\hbox {s} =0.99$), the third solution has $c_{3}=s^{2}$, and so on until the worst solution has $c_{{\text {swarm}}\, {{\text {size}}}}= s^{{\text {swarm}}\ {\text {size}}{-}1}$ [18]. Probabilities of the individuals calculated by

$$\begin{aligned} p_{i}=\frac{c^{N-i}}{\sum _{j=1}^{N}c^{N-j}} ; \quad i\in \{1,2,\ldots ,N \} \end{aligned}$$

(12)

The ${\sum _{j-1}^{N}c^{N-j}}$ normalizes the probabilities to ensure that ${\sum _{i=1}^{N}c^{N-j}}p_{i}=1$. As

${\sum _{j-1}^{N}c^{N-j}} = \frac{c^{N}-1}{C-1}$ it will be as a following equation:

$$\begin{aligned} p_{i}=\frac{c-1}{c^{N}-1}C^{N-i} ; \quad i\in \{1,2,\ldots ,N \} \end{aligned}$$

(13)

Algorithm 6 illustrates the exponential ranking selection algorithm, the similarity of structure between linear ranking selection and exponential ranking selection can be noticed. While the difference lies in the calculation of the selection probabilities. The time complexity of the exponential ranking selection is O($n\ {\text {log}}\ n$).

2.3.5 Greedy-based selection scheme (GSS)

The greedy selection scheme is called global best which was initially applied by Kennedy [23] in PSO. The technicality of greedy selection focuses to choose the three best solutions: $x_{\alpha }, x_{\beta }, {\text {and}} \,x_{\gamma }$ to avoid the local optima. Algorithm 7 shows the pseudo-code of the greedy selection scheme.

As mentioned above, the greedy choose the best three solutions and ignored the other solutions. Therefore, the diversity of the search space might be lost which leads to prematurely converge and quickly stagnate without efficient results. The time complexity of the greedy selection scheme is O($n\ {\text {log}}\ n$).

2.3.6 Truncation selection scheme (TrSS)

Truncation selection is considered as the simplest selection scheme comparing with other selection schemes. The truncation chooses elements by saving a certain percentage until reaching the population size [39]. This selection is equal to $\left( \mu ,\lambda \right)$ -selection utilized in development strategies with $T= \frac{\mu }{\lambda }$ [5].

From Truncation’s pseudo-code, it can be noticed that the ease of implementation of this selection. However, it neglects the solutions with a low fitness value which have an ability to improve into better solutions. This may lead to premature convergence. As a sorting of the population is required, truncation selection has a time complexity of O ($n\ ln\ n).$

3 The proposed methods

This section presents two new methods for improving basic MFO.

3.1 Hybrid Moth-flam optimization algorithm and hill climbing

The first improvement is hybridized basic MFO and HC (i.e., MFOHC) to enhance the exploitation mechanism as well as the convergence rate. As shown in Fig. 3, the flowchart of MFOHC starts by generating initial moth randomly, then calculating the moths’ fitness function and determining the best flam’s position. The usage of the HC components start in case the output of the first condition is “No”. In other words, if the fitness value of the selected moth is worse than the value of the best flam position, then it should search for another moth with better fitness value using the exploitation mechanism of the HC. After that, the selected solution will be compared again with the best flame position. The rest steps are similar to the basic MFO, such as updating the flam, calculating the distance between the moth and the updated flam, etc.

Fig. 3

Flowchart of the MFOHC algorithm

3.1.1 Computational complexity

Note that, the computational complexity for running the proposed MFOHC algorithm is depended on the number of salp solutions (X), the dimensions (d), and the maximum number of repetitions (t). Hence, the computational complexity of sorting procedure in each iteration is O($t \times n^2$) in the worst case. The computational complexity of the initialization procedure is O(n). Updating the positions of all search agents is O($t\times n\times d$). Therefore, the computational complexity of the basic MFO is O($n\ \text{log}\ n$) and O($n^2$) in the best and worst case, where n denotes the number of moths. Moreover, the time complexity to determine if the hill-climbing process has reach a local optimum is O($n^3$). Therefore, the final complexity of the MFOHC is O($T\times n^3(n^2 + n\times v)$), where T is the maximum number of iterations and v is the number of variables. Thus, the time complexity of each MOFHC’s version can be fined by adding the time complexity of each selection scheme as mentioned breviously. For instance, the time complexity of PMFOHC is estimated as ${O}(T\times n^3(n^2 + n\times v)) + {O}(n\ \text{log}\ n)$.

3.2 Improved MFOHC using various selection schemes

The second improvement is using new selection schemes to enhance the quality of the selected solution, as well as diversity. Six selection schemes have been chosen based on their features. For instance, TSS has the time complexity O(N) and diversity is inversely proportional to the t size. While PSS provides a probability for each solution to be selected based on their proportions. LRSS and ERSS focus on improving the convergence rate. GSS gives priority to the global search with avoiding the local optima. Finally, in TrSS, the worst six solutions (i.e., worst fitness values) will never be neglected, thus it will speed up the search processes.

In Fig. 3, the red rectangles show the locations of using each one of the selection schemes. In other words, the enhancing of the MFOHC using the selection schemes is presented after generating the population, where the selection schemes aid to select the best solution to compare it with the best flame. While the second location of using the selection scheme in the local search part, where it replace the basic selection in HC (i.e., random selection).

4 Simulations

4.1 Experiments settings

• Normalization measure is the process of regularizing data with respect to the difference in values between samples. In the experiments, the effects of different values of the dimensions and the search agents are compared with one another. This procedure is difficult due to the wide gap between solutions. Therefore, normalization improves data integrity [52]. In this work, normalization is calculated based on the following equation:

  $$\begin{aligned} z_{i}=\frac{x_{i}- \mu }{S}, \end{aligned}$$

  (14)

  where is $x=(x_{1},\ldots ,x_{n})$, n denotes the total number of data, $z_{i}$ denotes the normalized data for element ith, $\mu$ is the mean and S is the standard deviation. Finally, the minimum element of the data will be 1 in the normalization results.

• The best measure is utilized to calculate the best-obtained value by the algorithm to be evaluated for several predefined numbers of runs, which can be measured as follows:

  $$\begin{aligned} {\text {Best }}= \underset{1 \le i \le N_{r}}{\min } F_{i}^{*} \end{aligned}$$

  (15)

  where, $N_{r}$ denoted to the number of various runs and $F_{i}^{*}$ denoted to the best-obtained value.

• The average measure (avg) is utilized to calculate the mean of the best-obtained values by the algorithm to be evaluated for several predefined numbers of runs, which can be measured as follows:

  $$\begin{aligned} \mu _{F}=\frac{1}{N_{r}} \sum _{i=1}^{N_{r}} F_{i}^{*} \end{aligned}$$

  (16)

• The standard deviation (std) is a measure utilized to test if the algorithm to be evaluated can obtain the same best value in several various runs and examine the repeatability test of the algorithm results, which can be measured as follows:

  $$\begin{aligned} {\text {STD}}_{F}=\sqrt{\frac{1}{N_{r}-1}\sum _{i=1}^{N_{r}}(F_{i}-\mu _{F})^{2}} \end{aligned}$$

  (17)

Also, convergence trajectories are shown to display the behavior of the comparative algorithms to give the optimal value. Note, the parameters settings of the comparative algorithms are shown in Table 2.

Table 2 The parameters values of the comparative algorithms

There are two levels of evaluation performed in this work. The first step is evaluating the performance of the HMFO using a set of benchmark functions (see Sect. 4.1.1). The second step is applying the HMFO versions Using a set of IEEE CEC 2011 real world problems (see Sect. 4.1.2). All the experiments run using Matlab R2015a and Windows 7 Professional, Intel(R) Core(TM) i5-4590 CPU @ 3.30 GHz with a memory of 6.00 GB.

4.1.1 Benchmark functions

The proposed MFOHC method is verified based on using 30 classical benchmark test functions listed in tables 3, 4, and 5. This well-knowing benchmarks include 30 test functions, which are classified in to unimodal (it means optimization functions with only one local optimum) and multimodal (it means optimization functions that frequently contain multiple global and local optima) problems. Moreover, these functions are chosen with various dimensions and diverse difficulty levels including 10 scalable unimodal functions, 12 scalable multimodal functions, and 8 fixed-dimension multimodal functions. These features make the investigation process more fitting for testing the exploration and exploitation functions in the proposed method.

Table 3 Description of unimodal benchmark functions

Table 4 Description of multimodal benchmark functions

Table 5 Description of fixed-dimension multimodal benchmark functions

4.1.2 IEEE CEC 2011 real world problems

This subsection describes seven real-world problems that used in CEC 2011, more details can be found in [9]. These problems are utilized to evaluate the performance of HMFO versions.

• 1. CEC-P1: Static economic load dispatch (ELD) Problem

  This problem (i.e., static ELD) is focused on minimizing the fuel cost of producing units in a specific period, which is usually set by one hour. Thus, determining the optimal production dispatch during the operating units, as well as keeping the system load demand. The objective function is based on the non-smooth cost and smooth cost functions, more details are shown below:

  $$\begin{aligned} {\text {Minimizing}} :\; F = \sum _{i=1}^{N_{G}}F_{i}(P_{i}), \end{aligned}$$

  (18)

  where

  $$\begin{aligned} F_{i}(P_{i})=a_{i}P_{i}^{2}+b_{i}P_{i}+c_{i}, \; i=1,2,3,\ldots ,N_{G}, \end{aligned}$$

  (19)

  where $F_{i}(P_{i})$ refers to the cost function and $a_{i}$, $b_{i}$, and $c_{i}$ indicate to its cost coefficient. $N_(G)$ refers to the number of online producing units and $P_{i}$ the real power output in a time t. The following equation shows the cost function for the unit with valve point loading influence.

  $$\begin{aligned} F_{i}(P_{i})= a_{i}P_{i}^{2}+b_{i}P_{i}+c_{i}+\left| e_{i}{{\sin }} \left( f_{i}\left( P_{i}^{\min }-P_{i} \right) \right) \right| , \end{aligned}$$

  (20)

  where $f_{i}$ and $e_{i}$ indicate to the cost coefficients identical to the valve point loading influence.

• 2. CEC-P2: Optimal control of a non-linear stirred tank reactor

  In the chemical area, the chemical reaction proceeds in the continuous stirred tank reactor (CSTR) which can be included under the multimodal optimization problem. Thus, it can be used to evaluate the performance of the metaheuristic algorithms, exactly like the standard benchmark functions. The following equations illustrate the mathematical model of this problem.

  $$\begin{aligned} \dot{x_{1}}&=-(2+u)(x_{1}+0.25)+(x_{2}+0.5) \exp\left( \frac{25x_{1}}{x_{1}+2} \right) , \end{aligned}$$

  (21)
  $$\begin{aligned} \dot{x_{2}}&=0.5-x_{2}-(x_{2}+0.5) \exp\left( \frac{25x_{1}}{x_{1}+2} \right) , \end{aligned}$$

  (22)

  where u refers to the flow rate of the cooling fluid, $x_{1}$ and $x_{2}$ indicate to state temperature and deviation, respectively. The objective function is determined by an appropriate value of u to enhance the performance index, the following equation shows the calculation process.

  $$\begin{aligned} J=\int _{0}^{t_{f=0.72}}(x_{1}^2+x_{2}^{2}+0.1u^{2}){\text {d}}t. \end{aligned}$$

  (23)

• 3. CEC-P3: Large scale transmission pricing problem

  In modern power systems, the estimation price of the transmission considers a controversial problem [9]. The estimation price is based on various take-holders. Thus, it depends on different factors. The equivalent bilateral exchange (EBE) is one of the common factors (linearized model) used to estimate the price of the transmission. EBA creates a matrix of the load-generation interaction, the following equation illustrates the total of equivalent bilateral exchange.

  $$\begin{aligned} {\text {GD}}_{ij}=\frac{P_{Gi}P_{Dj}}{P_{D}^{{\text {sys}}}}, \end{aligned}$$

  (24)

  where i and j refer to generator and load, respectively. $P_{D}^{sys}$ refers to the total load. While Eq. (25) represents the portion of power flow pf inline k, which used (i.e., $pf_{k}$) to examine the all equivalent dual power exchanges.

  $$\begin{aligned} pf_{k}=\sum _{i} \sum _{j}\left| \gamma _{ij}^{k} \right| {\text {GD}}_{ij}. \end{aligned}$$

  (25)

• 4. CEC-P4: Hydrothermal scheduling problem

  Hydrothermal scheduling is divided into long term (i.e., from week(s) to months) and short term (i.e., 24 h and less) problems. This problem aims to schedule the power generations of the thermal and hydro units in a fixed period of time and minimum fuel cost. However, the hydrothermal system is very complicated and includes nonlinear connections of the resolution variables, water carry retards, and time connection among the consecutive schedules. So, detecting the minimum fuel cost is so difficult by utilizing the basic optimization algorithms.

  The main objective to achieve the maximum results of the hydro units, at the same time each unit consumed the lowest load. The description of the objective function is expressed below.

  $$\begin{aligned} F=\sum _{i=1}^{M}f_{i}(P_{Ti}), \end{aligned}$$

  (26)

  where M refers to the number of intervals. In Eq. (27), the $f_{i}$ indicates to the cost function connected with the identical thermal unit’s power producer $P_{Ti}$ :

  $$\begin{aligned} f_{i}(P_{Ti})=a_{i}P_{Ti}^{2}+b_{i}P_{Ti}+c_{i} +\left| e_{i}{{\sin }}\left( f_{i}\left( P_{Ti}^{\min }-P_{Ti} \right) \right) \right| . \end{aligned}$$

  (27)

• 5. CEC-P5: Spread spectrum radar polly phase code design

  waveform is considered as one of the most important factors in designing radar-system which is based on pulse compression. Various studies have been proposed for polyphase pulse compression code synthesis, especially those depending on the characteristic of the aperiodic autocorrelation function. Thus, CEC-P5 can be treated like a continuous optimization problem. The mathematical model is described in the following equations.

  $$\begin{aligned} {{\text {global}}}\; \underset{x\in X}{{\min }}f(x) =\max \left\{ \phi _{1}(x),\ldots , \phi _{2m}(x) \right\} , \end{aligned}$$

  (28)

  where $X=\left\{ (x_{1},\ldots ,x_{n})\in R^{n} \mid 0\le x_{j}\le 2 \pi , j=1,\ldots ,n \right\}$ and $m=2n-1$

  $$\begin{aligned} \phi _{2i-1}(x)&=\sum _{j=i}^{n}{{\cos }} \left( \sum _{k=\left| 2i-j-1 \right| +1}^{j} x_k\right) , \; i=1,\ldots ,n \end{aligned}$$

  (29)
  $$\begin{aligned} \phi _{2i}(x)&= 0.5+\sum _{j=i+1}^{n}{{\cos }} \left( \sum _{k=\left| 2i-j \right| +1}^{j} x_k\right) , \; i=1,\ldots ,n-1 \end{aligned}$$

  (30)
  $$\begin{aligned} \phi _{m+i}(x)&=-\phi _{i}(x),\; i=1,\ldots ,m \end{aligned}$$

  (31)

4.2 Results and discussions

4.2.1 Influence of control parameter

The experiments start with evaluating the parameter settings of the MFO to set them in subsequent experiments. It can be noticed that the parameters tuning include experiments of the population size (n) with a set of common values to determine the optimal value. After that, repeat the experiments with the selected value of the population size (n) and different common values for the dimension (D) to find its optimal value. Thus, the best values of the n and D will be uses in the rest of the experiments.

• 1. Population size: n

  To demonstrate the influence of the population sizes, the experiments are produced using several values for population sizes (i.e., $P = 5$, 10, 15, 20, 50, 100, 250, and 500) for the utilized 30 benchmark functions. Table 6 shows the results for different population sizes.

  As shown in Table 6, we can see that the best-normalized results for MFO with population sizes. The MFO obtained the best results (17 times) when the population size is equal to 15. Furthermore, for the 10 scalable unimodal functions, the MFO got the most of the best results when $P=20$, it got 7 out of 10 best cases. For 12 scalable multimodal functions, the MFO got the most of the best results when $P=20$, it got 6 out of 12 best cases. For the 8 fixed-dimension multimodal functions, the MFO got the most of the best results when $P=20$, it got 5 out of 8 best cases. It is clearly observed that when the population size is equal to 15, it is the most suitable size for all benchmark test functions.

• 2. Dimension: D

  In this part, to analyze the influence of the problem dimensional spaces, experiments are produced for several potential dimensional spaces (i.e., $D=5$, 10, 15, 20, 25, 30, 35, 40, 45, and 50) as reported in the literature using the utilized 30 benchmark functions. The results for 30 functions are illustrated in Table 7 using the best normalized values.

  As shown in Table 7, the MFO obtained the overall best results when $D=5$, it got the best results on 17 cases. Furthermore, for the 10 scalable unimodal functions, the MFO got the most of the best results when $D=5$, it got 7 out of 10 best cases in both dimensions. For 12 scalable multimodal functions, the MFO got the most of the best results when $D=12$, it got 6 out of 12 best cases. For the 8 fixed-dimension multimodal functions, the MFO got the most of the best results when $D=5$, it got 4 out of 8 best cases. From these results, we concluded that increasing the overall performance of MFO is observed by increasing the problem dimensional space. Usually, the MFO is unable to solve the problem before getting the maximum number of iterations. However, as seen, MFO gives better results for high-dimensional problems.

Table 6 The best normalized results for MFO with population sizes

Table 7 The best normalized results for MFO with different dimensional spaces

4.2.2 Comparisons MFOHC with other methods using the benchmark functions

For a clear comparison, as shown in Table 8, the proposed MFOHC is compared with the basic MFO [28] and other similar nine optimization algorithms, namely, Ant Bee Colony (ABC) Algorithm [22], Bat-inspired Algorithm (BA) Yang [56], Salp Swarm Optimization (SSA) [31] , Dragonfly Algorithm (DE) Mirjalili [29], Genetic Algorithm (GA) [17], Harmony Search (HS) Algorithm Geem et al. [15], Krill Herd (KH) Algorithm [13], and Grey Wolf Optimizer (GWO) Algorithm Mirjalili et al. [30]. Table 8shows the best, average (Avg), the standard division (Std) of fitness values obtained by all comparative algorithms over 30 runs, respectively.

As shown in Table 8, the basic MFO has some weakness (weak local search) in achieving excellent results in unimodal functions (i.e., F1, F2, F4, F5, F6, and F9). Consequently, the hybrid MFO with HC is proposed to improve the exploitation searchability of MFO. Thus, functions F1–F10 are scalable unimodal benchmarks since they have just one global optimum. These functions support assessing the exploitation ability of the examined optimization algorithms. It can be seen from Table 8 that MFOHC is a very competitive algorithm compared to other similar algorithms. Mainly, it was the most effective algorithm for functions F1 and F10 in most test problems. The proposed MFOHC hence provide perfect exploitation. MFOHC got better results in solving unimodal functions compared to the proposed MFOHC where, it almost obtained all best results in unimodal functions as well as other test functions (i.e., multimodal F11–F22 and fixed-dimension multimodal F23–F30). Although the results indicate that MFOHC also has excellent exploration searchability, it is possible to further improve the exploration search to make a balance between exploitation and exploration search. Moreover, performance, diversity, and the convergence rate of MFOHC can be enhanced.

Table 8 Best, average (Avg), and standard deviation (Std) for comparing the proposed MFOHC with basic MFO and other algorithms

4.2.3 A comparison of MFOHC versions using Benchmark functions

In this part, as shown in the previous section that the MFOHC can further improve its exploration search abilities, new experiments series conducted to investigate the skills of the selection schemes in enhancing the global search abilities. Various selection scheme mechanisms (tournament selection scheme (TMFOHC), proportional selection scheme (PMFOHC), linear ranking selection scheme (LRMFOHC), exponential ranking selection scheme (ERMFOHC), greedy-based selection scheme (GMFOHC), and truncation selection scheme (TrMFOHC)) have been tested on the MFOHC to improve its exploration search abilities, as well as, various versions of MFO from the literature have been used (i.e., LGCMFO [55], CLSGMFO [54], MFODE [11], and OMFO [36]) to evaluate the performance of the MOFHC versions.

Contrary to unimodal functions, multimodal functions cover many local optima, where number grows exponentially with the number of decision variables (problem size). Accordingly, this kind of benchmark functions becomes very beneficial if the objective is to evaluate the exploration search ability of an optimization algorithm.

Optimization of benchmark functions is a very challenging job because just a precise balance between exploration and exploitation supports local optima to be evaded. Optimization results listed in Table 9 show that the proposed hybrid MFO with HC using proportional selection scheme (PMFOHC) is almost the best optimizer in all test problems and overcomes other similar comparative algorithms¹. It is definitely demonstrated that the proposed PMFOHC support exploration and exploitation phases to be balanced. Moreover, the results indicate that PMFOHC also has excellent exploration search ability. However, the proposed PMFOHC always will be the most useful algorithm in the majority of function problems.

Table 9 Best, average (Avg), and standard deviation (Std) for comparing the MFOHC versions with other algorithms

The performance of the proposed versions of the MFOHC algorithm is further evaluated using Friedman’s statistical tests. Table 10 provides the average ranking of the proposed MFOHC versions against the comparative methods using Friedman’s test. It can be noticed that the proposed PMFOHC version is ranked first, followed by LRMFOHC, ERMFOHC, TrMFOHC, TMFOHC, and GMFOHC versions, which ranked second, fourth, fifth, sixth, and seventh, respectively. The overall P value computed by Friedman’s test is 9.43E−11, which is below the significant level (i.e., $\alpha =0.05$). This value indicates that there are significant differences between the performance of the comparative methods used.

Table 10 Average rankings based on Friedman’s test for CEC2011 problem

Figures 4 and 5 shows the convergence graphs of the unimodal benchmark functions ($F_{1}$, $F_{3}$, $F_{5}$, $F_{7}$, and $F_{9}$), multimodal benchmark functions ($F_{12}$, $F_{15}$, $F_{16}$, $F_{17}$, $F_{19}$, $F_{20}$, and $F_{21}$), and fixed-dimension multimodal benchmark functions ($F_{23}$, $F_{25}$, $F_{27}$, and $F_{30}$). The convergence graphs are plotted between the best solutions of each algorithm and the number of iterations based on the results acquired through 30 independent runs.

It is observed from the convergence graphs of the unimodal functions that the PMFOHC outperformed the other versions in $F_{1}$, $F_{5}$, and $F_{7}$. While it achieved close results from the LRMFOHC and ERMFOHC in $F_{3}$ and $F_{9}$ with superiority to LRMFOHC and ERMFOHC. Thus, it can be summarized that the PMFOHC is the most efficient version in dealing with unimodal benchmark functions. However, PMFOHC still has a weak at the beginning (i.e., from start until 200–400 iterations). Thus, it suffers from slow convergence when dealing with the local search functions.

Similar to the mentioned above (i.e., unimodal functions) the convergence performance of the PMFOHC achieved best results in 4 out of 7 multimodal benchmark functions [i.e., ($F_{12}$, $F_{15}$, $F_{16}$, and $F_{20}$)]. In $F_{17}$ and $F_{21}$ the PMFOHC is the fastest method for finding the best solutions in the first part, while in the last part (i.e, after iteration 600) the LRMFOHC was the best. In $F_{19}$ ERMFOHC achieved the best results compared with the other versions. Consequently, although PMFOHC outperformed the other algorithms, it needs more enhancements to achieve the best solutions in all global search functions.

In the fixed-dimension multimodal benchmark functions, PMFOHC got the best results in 3 of 4 of the functions ($F_{23}$, $F_{27}$, and $F_{30}$), while in $F_{25}$ the superiority was obvious to the LRMFOHC, followed by TrMFOHC and PMFOHC.

Fig. 4

Convergence graphs of the benchmark functions

Fig. 5

Convergence graphs of the benchmark functions

Based on the above, it can be noticed that PMFOHC proved its performance in most functions of the three categories of the benchmarks. The experiment results are convincing because of the structure of PMFOHC combines the feature of MFO in the exploration search, supported by the feature of HC in the exploitation search, and distinguished from the rest of the proposed methods by using the proportional selection schemes to increase the quality of the selected solutions.

4.2.4 A comparison of MFOHC versions using real world problems

Table 11 Best, average (Avg), and standard deviation (Std) for comparing the MFOHC versions using five CEC 2011 real-world problems

The real-world problems are presented in Sect. 4.1.2 where it can be considered as discrete or continuous problems. Thus, can be used to evaluate the performance of different metaheuristic algorithms. All results in Table 11 are gained by 50 separate runs on the five real-world problems.

PMFOHC determines the best solutions on three out of five real problems (except CEC–P3 and CEC–P4) followed by GMFOHC which achieved best solution in both CEC–P3 and CEC–P4. Regarding the mean solution, PMFOHC outperforms the other methods in all real problems. Finally, the std results show that the PMFOHC obtained the best results in CEC–P1, CEC–P3, and CEC–P4. GMFOHC obtained the best results in CEC–P2 and CEC–P5. The summary of the results in Table 11 refer that PMFOHC shows the best performance comparing with the other six methods.

5 Conclusion and future works

This paper presented new alternative methods using moth-flame optimization (MFO). The proposed methods include two main steps: in the first step, the basic MFO is hybridized with hill climbing (HC) local search to improve its exploitation search, called MFOHC. In the second step, six popular selection schemes are investigated, and the proportional selection scheme is selected as the best to improve the exploration search of the MFOHC by maintaining the diversity of the solutions, called PMFOHC.

Experiments are conducted using thirty benchmark functions and five IEEE CEC 2011 real-world problems. The results of the proposed algorithms are compared to several similar algorithms published in the literature. The effectiveness of each algorithm is evaluated by three measures, the best, average, standard deviation of the fitness values. The results illustrated that the PMFOHC version is almost the best optimizer in all test problems and it as a summary, the results for solving the real-world problems showed that the proposed PMFOHC has a promising ability to be very useful in solving the structural design problems with unfamiliar search spaces also overcoming other similar comparative algorithms. The proposed PMFOHC support exploration and exploitation phases to be balanced through, keeping the diversity of the solutions. However, it suffers from a weakness of slow convergence.

In future work, we will enhance the limitation of the proposed methods by using new search techniques such as stochastic hill-climbing and opposition-based learning. Also, we will utilize different optimization problems, as well as multi-objective problems to achieve better results.