1 Introduction

Most engineering structures are subjected to dynamic loads (e.g., fatigue, seismic, and shock loads) which can produce unwanted vibrations. The natural frequencies are essential parameters that are useful to avoid resonance and improve the dynamic behavior of a structure [1, 2]. In addition, engineering structures should be as light as possible. However, minimizing the weight of structures can be considered as a difficult problem to solve because the reduction of weight generates conflict with the frequency bounds. These constraints are highly non-linear, non-convex, and implied with respect to the variables of design [3]. Therefore, this has led to difficulty in the use of gradient-based optimizers [2]. Under such circumstances, the metaheuristic algorithms can serve as appropriate alternatives due to the ability to search global minima in highly modal and multidimensional spaces.

The first works to address this problem employed classical techniques such as Gauss method [4], bi-factor algorithm [5], optimality criteria [1, 6], and integrated force method [7, 8]. Since then many researchers in the field of structural optimization have introduced several metaheuristics for solving this kind of optimization problem. Table 1 presents the most important works that involve metaheuristics methods to solve this problem. Although several metaheuristics have been introduced to solve this problem, most of them are population based, undergo many steps along with several parameters that make them difficult to understand and code. Also, there are same procedures in recent metaheuristics which make them similar. Because of this, the researchers usually are confused to select a metaheuristic. According to the No Free Lunch Theorem in the field of optimization, there is no algorithm to solve all optimization problems. This indicates that a new improved algorithm has potential to solve a group of problems better than the existing algorithms.

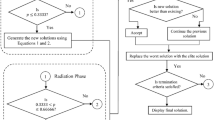
Table 1 Main works in optimization of truss structures with frequency constraints
Full size table

Contrary to the previous works, this paper aims to improve the performance of the recently proposed modified simulated annealing algorithm (MSAA) and adapt it better for structure design problems. MSAA is a simple single-solution algorithm based on the behavior of atomic arrangements in liquid or solid materials during the annealing process introduced by Millat et al. [29] for solving global optimization problems and it has been applied in structural optimization problems with success [30,31,32]. Regardless of the successful application of MSAA, this algorithm estimates the global optimum of a given problem in three phases: preliminary exploration, search step, and probability of accepting. First, a preliminary exploration is realized to choose the starting point of search. Second, the transition from the start point to the new point is done by a search step. Third, the range of probability of accepting a worse solution is reduced [29].

In the search step phase, the new solution for comparison is not randomly generated. From the starting point determined in the preliminary exploration phase, a search step is generated to determine the neighboring state. This step depends on a radius (R) of action that gradually decreases as the temperature of the system decreases. The transition from starting point to the new point (search step) is performed by the addition of random numbers that are between [− R, R]. This phase leads solution to jump into non-visited regions (exploration) and permits local search of visited regions (exploitation). However, the exploitation capability of this phase is considerably low as compared to the exploratory capability. This causes the algorithm to consume a large number of unused function evaluations (FEs) at low temperatures. To overcome this drawback, the aim of this work is to investigate whether the basic concepts underlying water wave optimization (WWO) can be exported to improve the MSAA. This variation pretends to allow a good balance between exploration and exploitation throughout the optimization process. The validity of the improved MSAA (based on WWO) is confirmed by testing for a diverse set of benchmark problems and applied to size optimization problems of truss structures with frequency constraints. Optimal results attained by I-MSAA are compared with other metaheuristics in the literature.

The remainder of this article is structured as follows. The MSAA is briefly presented in Sect. 2. Section 3 describes the improvement in the MSAA. In Sect. 4, the 30 benchmark functions proposed in the CEC2014 special session on single objective real-parameter numerical optimization [33] are used to demonstrate the effectiveness of the proposed algorithm. Section 5 describes the mathematical formulation of truss optimization with frequency constraints. Section 6 presents four most widely investigated benchmark numerical examples to illustrate the efficiency of the I-MSAA. Finally, in Sect. 7, our final conclusions are presented.

2 Modified simulated annealing algorithm

The MSAA [29] is a single-solution algorithm based on the cooling process of molten metals through annealing process. MSAA has three main stages that differentiate it from the simulated annealing (SA) proposed by Kirkpatrick [34]:

  1. 1.

    The starting point is not randomly generated but is selected by a preliminary exploration where the algorithm performs a scan in the search space and is given by the following equation:

    $${\mathbf{X}}_{P \times N} = {\mathbf{I}}_{P \times N} X_{\text{L}} + {\mathbf{rand}}_{P \times N} (X_{\text{U}} - X_{\text{L}} ),$$
    (1)

    where P is the number of points that are desired in the search space; N the number of dimensions of the problem; \({\mathbf{I}}_{P \times N}\) the identity matrix of size P × N; \(X_{\text{L}}\) the lower limit of the problem; \(X_{\text{U}}\) the upper limit of the problem, and \({\mathbf{rand}}_{P \times N}\) is the matrix of random numbers (pure randomness) between 0 and 1 of size P × N. To start the optimization process with MSAA, all points generated with (1) are evaluated in the objective function of the problem and the smallest value (in the case of searching the minimum value of the function) is chosen as the starting point of the search.

  2. 2.

    The new solution for comparison is not randomly generated. From the starting point determined in the preliminary exploration stage, a search step is generated to determine the neighboring state. This step depends on a radius (R) of action that gradually decreases as the temperature of the system decreases. The transition from the starting point to the new point is performed by the addition of random numbers that are within the defined radius. This enables the algorithm to execute a global exploration at high temperatures and a local exploration at low temperatures. The radius is updated as follows:

    $$R_{{{\text{i}} + 1}} = R_{\text{i}} \times \alpha ,$$
    (2)

    where \(R_{\text{i}}\) is the initial radius cycle and \(\alpha\) is the radius reduction coefficient.

  3. 3.

    If the cost function of the new solution is higher than the best value, the acceptance of the new solution depends on the following equation:

    $$P = \frac{1}{{1 + e^{{\left( {\Delta f/T} \right)}} }},$$
    (3)

    where P is the probability of accepting the new solution; \(\Delta f\) the difference between the quality of the new solution and the quality of the current solution; T the temperature of the system; and e is the Euler number. This probability is in a range between 0 and 0.5, allowing the algorithm to have a lower range of acceptance of worse solutions. For more details, see [29]. The flowchart of the MSAA is illustrated in Fig. 1.

    Fig. 1
    figure 1

    The MSAA flowchart

    Full size image

3 Improvement in the MSAA

The capability to balance intensification and diversification during a search determines the efficiency of a specific metaheuristic algorithm. Diversification (exploration) ensures, usually by randomization, that the algorithm explores the search space efficiently. Intensification (exploitation) aims to identify the best solution and select, during the process, a succession of best solutions. In the search step phase of the MSAA, the trial point is generated by the addition of random numbers that are defined within a radius (Fig. 1). This phase works mainly to improve exploitation capabilities of the search process. Although the MSAA has demonstrated its ability to find near global regions within a reasonable time, it is comparatively inefficient in performing local searches [31]. This is because the radius must be tuned for each problem, affecting the speed convergence of the algorithm. Thus, this paper proposes the I-MSAA as a new and superior MSAA algorithm variant to improve MSAA algorithm local search capabilities and balance-associated intensification and diversification components. The proposed algorithm introduces a concept drawn from water wave optimization (WWO) [35] to replace the search step phase.

WWO was introduced by Zheng [35] and is inspired by shallow water wave models. The WWO has three important phases for finding optimal solutions. They are: propagation, breaking, and refraction phase. In propagation phase, the wave is propagated to a random position exactly once in an iteration. If a wave attains a lower sea depth (for minimization), it breaks into solitary waves which are formed in the breaking phase. Thus, breaking is used for the intensive search (exploitation) in search spaces by producing random solitary waves around the current best position. While in the refraction phase, the algorithm explores the search space for any other best solution and avoids search inactiveness. As our interest is to improve the exploitation of the MSAA, the breaking phase used in WWO is implemented in the I-MSAA.

3.1 Breaking

According to Zheng [35], when a wave moves to a position where the water depth is below a threshold value, the wave crest velocity exceeds the wave celerity. Consequently, the crest becomes steeper and steeper, and finally the wave breaks into a train of solitary waves. In WWO, the breaking operation performs a local search around the wave to simulate wave breaking. In the problem-solving process, k is randomly selected (where k is a random number between 1 and a predefined number kmax), and at each dimension d generate a solitary wave x as:

$$x^{\prime}\left( d \right) = x\left( d \right) + N\left( {0,1} \right) \times \beta L\left( d \right),$$
(4)

where β is the breaking coefficient; N(0, 1) a Gaussian random number with mean 0 and standard deviation 1, and L(d) is the length of the dth dimension of the search space. According to Zheng [35], it is recommended to set β to 0.001–0.01, and kmax to min(12, D/2), where D is the dimension of the problem.

This concept is exported to MSAA. Thus, the search step phase of the MSAA is replaced by breaking phase to improve the convergence ability and set a good balance between exploration and exploitation.

4 The 30 benchmark functions of the CEC2014

The validity of the proposed I-MSAA is confirmed on 30 benchmark functions of the CEC2014 special session on single objective real-parameter numerical optimization [33]. The benchmark suite covers various types of function optimization problems, as summarized in Table 2. The algorithm is coded in Matlab program and executed using an Intel Core i7-3630QM system 2.4 GHz with 8 GB RAM. For result verification, the comparison is made between several optimization algorithms (IWO, BBO, GSA, HuS, BA, WWO, SOS, ISOS, MSAA, and I-MSAA). In this study, 30D functions are used with search ranges as [− 100, 100] and set the FEmax to 150,000. All results are collected from 60 independent runs on each test function. For all examples, the population size (preliminary exploration), initial temperature (Tinitial), final temperature (Tfinal), npmax, β, and kmax are set as 200, 1, 1 × 10−3, 300, 0.001, and min(12, D/2), respectively. Sensitivity analyses on these parameters are investigated in [29, 31, 32, 35]. Statistical tests are essential to check significance improvements by a proposed method over the existing methods. Therefore, the Friedman rank test on the results of I-MSAA, MSAA, and other state-of-the-art algorithms is used. The test is performed on the average and standard deviation (SD) of functional values obtained.

Table 2 Summary of the CEC 2014 benchmark functions [33]
Full size table

Table 3 shows the comparative average of fitness value. It can be seen that I-MSAA gives best results for unimodal functions, multimodal functions, and composition functions. In hybrid functions, I-MSAA is only surpassed by the WWO and IWO algorithms. Furthermore, I-MSAA ranks better compared to MSAA for all type functions. Finally, I-MSAA ranks first for overall performance. Table 4 shows the comparative SD of fitness value. The results indicate that I-MSAA is second best among the considered algorithms. These results confirm the merits of the proposed algorithm.

Table 3 Comparative average of fitness values of the CEC2014
Full size table
Table 4 Comparative SD of fitness values of the CEC2014
Full size table

5 Problem definition

The goal of the problem is designing the member sizes of the structure so that its weight is minimized while satisfying some constraints on the natural frequencies. Member cross-sectional areas are considered as continuous design variables. Each variable should be chosen within a permissible range. The mathematical formulation for this problem can be expressed as follows:

$$\begin{array}{*{20}l} {\text{Minimize}} \hfill & {W\left( A \right) = \mathop \sum \limits_{i = 1}^{n} \rho_{i} A_{i} L_{i} } \hfill \\ {{\text{Subject}}\;{\text{to}}} \hfill & {\left\{ {\begin{array}{*{20}l} {\omega_{j} \le \omega_{j}^{*} } \hfill \\ {\omega_{k} \ge \omega_{k}^{*} } \hfill \\ {A_{i,\hbox{min} } \le A_{i} \le A_{i,\hbox{max} } } \hfill \\ \end{array} } \right.} \hfill \\ \end{array} ,$$
(4)

where \(W\) is the weight of the structure; \(n\) the total number of members of the structure; \(\rho_{i}\), \(A_{i}\), and \(L_{i}\) stand for the material density, the cross-sectional area, and the length of the ith member, respectively; \(\omega_{j}\) and \(\omega_{k}\) the jth and kth natural frequencies of the structure, respectively; \(\omega_{j}^{*}\) and \(\omega_{k}^{*}\) the upper and lower bounds corresponding to \(\omega_{j}\) and \(\omega_{k}\), respectively; \(A_{i,\hbox{min} }\) and \(A_{i,\hbox{max} }\) are the lower and upper bounds of \(A_{i}\), respectively.

6 Truss problems and discussions

To evaluate the feasibility and validity of the I-MSAA, the following classical truss sizing problems (Fig. 2) are optimized and the results are compared with the previous results obtained through various existing metaheuristics: (1) 10-bar planar truss; (2) 72-bar space truss; (3) 120-bar dome truss, and (4) 200-bar planar truss. The design considerations of the problems are given in Table 5.

Fig. 2
figure 2

Benchmark trusses’ problems

Full size image
Table 5 Design considerations of the benchmark trusses
Full size table

In all design examples, the parameters used in the I-MSAA are: (1) as it is demonstrated in the previous studies [29, 31, 32], the population size (preliminary exploration), initial temperature (Tinitial), and final temperature (Tfinal) are set as 200, 1, 1 × 10−3, respectively; (2) according to [35], β and kmax are set as 0.001 and min(12, D/2), respectively; (3) according to [32], the maximum number of perturbations (npmax) at the same temperature can be chosen in the range of 100–300. Evidence gathered from sensitivity analysis led to set npmax as 200. These numbers of perturbations have been obtained in this work by examining its effect to find a balance between accuracy and computational cost for each of the problems.

The iterative process is terminated when the algorithm reaches the final temperature. The proposed I-MSAA algorithm and finite element analysis are coded in Matlab program and executed using an Intel Core i7-3630QM system 2.4 GHz with 8 GB RAM. Statistical results, obtained for 100 independent runs, are presented in terms of the best weight, average weight, standard deviation (SD), the corresponding iterations number (NI), and frequency responses. It is important to note that all presented I-MSAA designs are feasible. The results and discussions of the benchmark problems are explained in the following sections.

6.1 10-Bar planar truss

The first design example is the 10-bar planar truss structure shown in Fig. 2. A lumped mass of 454 kg is added in all free nodes. Table 6 presents a comparison of optimal results obtained by the proposed algorithm and other methods. The results indicate that I-MSAA (529.75 kg) achieves better optimal weight than DPSO, SBO, VPS, and MSAA algorithms, but slight heavier design than ReDe, ISOS, and AHEFA. However, the proposed algorithm requires less NI than ReDe (6200 NI for I-MSAA and 8300 NI for ReDe) to reach final solution. It can be seen that the convergence speed of the DPSO, ISOS, and AHEFA is faster than that of the I-MSAA (6000 NI for DPSO, 4000 NI for ISOS, 5860 for AHEFA); however, the I-MSAA is more stable than the DPSO, ISOS, and AHEFA through the best value of SD (0.11 kg for I-MSAA, 3.48 kg for ISOS, 1.92 kg for the AHEFA, and 4.02 kg for the DPSO). Finally, with respect to the SD, I-MSAA ranks second among the considered metaheuristics, only being surpassed by MSAA (0.01 kg). Natural frequencies optimal obtained by the I-MSAA show that none of the frequency constraints are violated. Figure 3 shows the convergence curve of the best design of I-MSAA for this problem.

Table 6 Optimal design parameters for the 10-bar planar truss by different algorithms
Full size table
Fig. 3
figure 3

Convergence curve of I-MSAA for the 10-bar planar truss

Full size image

6.2 72-Bar space truss

The 72-bar space truss shown in Fig. 2 is the second numerical example. The bars are categorized into 16 groups by considering geometrical symmetry. A lumped mass of 2770 kg is attached at all top nodes (nodes 1–4). Optimal results obtained by the I-MSAA and the other optimization algorithms published in the literature are reported in Table 7. It can be seen that the acquired result by the proposed algorithm (324.43 kg) is better than the other methods (327.51 kg for the CSS-BBBC, 327.65 kg for the DPSO, 327.55 kg for the SBO, 327.65 kg for the VPS, 325.01 kg for the ISOS, and 324.97 kg for the MSAA). Moreover, I-MSAA requires fewer NI than the DPSO, SBO, VPS, ReDe, AHEFA, and MSAA (6200 NI for I-MSAA, 20,000 NI for DPSO, 15,000 NI for SOB, 30,000 for VPS, 10,840 NI for ReDe, 8860 NI for AHEFA, and 7130 for MSAA). The average weight benefit for I-MSAA is 3.24, 3.16, 3.15, 4.95, and 0.61 kg as compared to those obtained from DPSO, SBO, VPS, ISOS, and MSAA, respectively. Finally, I-MSAA obtains a low SD (0.07 kg) that evidences the stability of the proposed algorithm. Natural frequencies indicate the feasibility of the obtained design by I-MSAA. The convergence curve of the best design of I-MSAA for this problem is shown in Fig. 4.

Table 7 Optimal design parameters for the 72-bar space truss by different algorithms
Full size table
Fig. 4
figure 4

Convergence curve of I-MSAA for the 72-bar space truss

Full size image

6.3 120-Bar dome truss

The third example is the 120-bar dome truss shown in Fig. 2. A lumped mass is attached to all free nodes as follows: 3000 kg at node one, 500 kg at nodes 2 through 13 kg, and 100 kg at the rest of the nodes. The members of the structure are categorized into seven groups using symmetry about the z axis. Table 8 compares the results of I-MSAA with other optimization methods. As observed, the I-MSAA provides the best result with 8707.01 kg while the others give larger weights, namely CSS-BBBC (9046.34 kg), DPSO (8890.48 kg), CBO (8889.13 kg), HALC-PSO (8889.96 kg), VPS (8888.74 kg), ReDe (8707.32 kg), ISOS (8710.06 kg), and MSAA (8707.39 kg). Moreover, I-MSAA requires 6200 NI to converge the optimal solution, while the HALC-PSO and VPS need 17,000 and 30,000 NI, respectively. From the obtained average weight (8707.42 kg) and SD (0.08 kg) values of the proposed method, it can be seen that the I-MSAA is stable. The SD obtained with I-MSAA ranks first among the considered metaheuristics. The convergence curve of the best design of I-MSAA for this problem is shown in Fig. 5.

Table 8 Optimal design parameters for the 120-bar dome truss by different algorithms
Full size table
Fig. 5
figure 5

Convergence curve of I-MSAA for the 120-bar dome truss

Full size image

6.4 200-Bar planar truss

The last design problem is the 200-bar planar truss (Fig. 2). A lumped mass is attached at all top nodes (nodes 1–5). The bars are grouped into 29 by seeing symmetry as reported in the previous studies. Table 9 provides a comparison of optimal results obtained by the I-MSAA and different metaheuristics. It can be seen that the best weight obtained by I-MSAA (2156.83 kg) is better than those given by AHEFA (2160.74 kg), CSS-BBBC (2298.61 kg), ISOS (2169.46 kg), SOS (2180.32 kg), and MSAA (2157.28 kg). The I-MSSA design is slightly worse than SBO (2156.51 kg) and HALC-PSO (2156.73 kg); however, the convergence speed of the I-MSAA is faster than these algorithms (23,000 NI for SBO and 13,000 NI for HALC-PSO). The results also indicate that, I-MSAA is more stable than SOS, ISOS, and MSAA with the smallest SD (1.13 kg for I-MSAA, 83.59 kg for SOS, 43.48 kg for ISOS, and 2.96 for MSAA). Frequency values show that all constraints of the 200-bar planar truss are satisfied by the I-MSAA. Figure 6 shows the convergence curve of the best design of I-MSAA for this problem.

Table 9 Optimal design parameters for the 200-bar planar truss by different algorithms
Full size table
Fig. 6
figure 6

Convergence curve of I-MSAA for the 200-bar planar truss

Full size image

7 Conclusions

This paper proposes how to improve the modified simulated annealing algorithm by including breaking operator, a concept borrowed from water wave optimization. The breaking operator is implemented to improve exploitation ability of MSAA in the search process. The new algorithm is called I-MSAA. Thirty benchmark functions of the CEC2014 and four classical truss sizing problems with frequency constraints are tested to verify the effectiveness and robustness of the proposed algorithm. In the benchmark functions, I-MSAA is better or competitive for obtaining results based on the mean and SD of functional values obtained over the stated runs as compared to MSAA and other metaheuristics. In the truss optimization, I-MSAA always achieve a better design than MSAA. Additionally, the numerical results show the ability of this algorithm to produce competitive results compared to those of the other metaheuristic algorithms presented in the literature in terms of best weight, SD, and NI required by the optimization process. The presented data on average weight and SD of optimized weight obtained from 100 independent runs prove the robustness of I-MSAA. The I-MSAA is simple to implement and it can be easy to extend for various engineering optimization problems such as: simultaneous shape and topology optimization of truss structures, frame optimization, and reliability-based design optimization problems.