Application of dual-Chebyshev wavelets for the numerical solution of boundary integral equations with logarithmic singular kernels

Abstract

In this paper, the discrete Galerkin method based on dual-Chebyshev wavelets has been presented to approximate the solution of boundary integral equations of the second kind with logarithmic singular kernels. These types of integral equations occur as a reformulation of a boundary value problem of Laplace’s equation with linear Robin boundary conditions. The discrete Galerkin methods for solving logarithmic boundary integral equations with Chebyshev wavelets as a basis encounter difficulties for computing their singular integrals. To overcome this problem, we establish the dual-Chebyshev wavelets, such that they are orthonormal without any weight functions. This property adapts Chebyshev wavelets to discrete Galerkin method for solving logarithmic boundary integral equations. We obtain the error bound for the scheme and find that the convergence rate of the proposed method is of $O(2^{-Mk})$. Finally, some numerical examples are presented to illustrate the efficiency and accuracy of the new technique and confirm the theoretical error analysis.

1 Introduction

The main purpose of this article is to propose a method for obtaining numerical solutions of logarithmic singular boundary integral equations of the second kind, namely

$$\begin{aligned} -\pi u(\mathrm{x})+ \int _{\partial D} u(\mathrm{y}) \left( p(\mathrm{y})\ln \Vert \mathrm{x}-\mathrm{y}\Vert +\frac{\partial \ln \Vert \mathrm{x}-\mathrm{y}\Vert }{\partial n_{\mathrm{y}}} \right) {d}s_{\mathrm{y}}=\int _{\partial D} g(\mathrm{y})\ln \Vert \mathrm{x}-\mathrm{y}\Vert {d}s_{\mathrm{y}},~~~~\mathrm{x} \in \partial D, \end{aligned}$$

(1)

where $D\subset \mathbb {R}^2$ is a bounded, open, simply connected region in the plane, $n_{x}$ is the outward unit normal on $\partial D$, $\Vert .\Vert$ is the Euclidean norm on $\mathbb {R}^2$, p(x) and g(x) are given functions on $\partial D$ with $p(\mathrm{x})\ge 0$, but $p \not \equiv 0$ and u(x) is the unknown function to be determined [10, 18]. Boundary integral equations of the second kind with logarithmic singular kernels deduce from reformulations of the boundary value problem for two-dimensional Laplace’s equation with linear Robin boundary conditions [10, 18], that is

$$\begin{aligned} \left\{ \begin{array}{rl} \Delta u(\mathrm{x})=0,~ ~~~~~~~~~~~~~~\mathrm{x}\in D\subset \mathbb {R}^2, &{} \\ \frac{\partial u(\mathrm{x})}{\partial n_{\mathrm{x}}}+p(\mathrm{x})u(\mathrm{x})=g(\mathrm{x}),~~~~\mathrm{x}\in \partial D. &{} \\ \end{array} \right. \end{aligned}$$

(2)

It should be noted that these integral equations are also used in connection with other types of partial differential equations arising in various branches of applied science such as solid and fluid mechanics, electrostatics, heat transfer, diffraction and scattering of waves, etc [10, 14, 15, 17, 32].

Boundary integral equations, especially in the singular case, are mostly difficult to solve analytically, so it is needed to obtain their approximate solutions [4, 24, 38]. The projection methods, including Galerkin and collocation methods, are the commonly used approaches for the numerical solutions of boundary integral equations which require a family of orthogonal basic functions, such as wavelets. Wavelets as well localized and multi-resolution functions [40, 41] are considerably powerful for solving singular integral equations and provide accurate solutions [2, 39, 42]. These methods usually require some quadrature formulae to estimate the logarithmic singular integral appeared in these schemes, such as Gauss-type quadrature rules [18, 22]. A useful research work conducted by authors of [31] has investigated a cell structure together with logarithmical Gaussian quadrature schemes for the numerical integration of boundary integrals. The wavelet technique also allows establishing fast algorithms for the solution of integral equations [3].

Legendre wavelets have been used to obtain the numerical solutions of boundary integral equations of the second kind with logarithmic singular kernels [18]. Spline wavelets have been applied to solve first kind boundary integral equations on polygons [36]. Biorthogonal wavelets have been established a method for solving boundary integral equations in three dimensions [21]. The numerical solutions based on the use of trigonometric wavelets have been presented for the second kind natural boundary integral equation (NBIE) with hyper-singular kernel [16, 19]. Daubechies interval wavelets have been utilized to give a numerical solution of boundary integral equations [35, 43]. The numerical solution of the natural boundary integral equation of the Laplace equation in the concave angle domains via Harr wavelet has been investigated in [26, 44]. The meshless discrete Galerkin (MDG) method [4, 27, 29] has been proposed to solve logarithmic boundary integral equations based on the moving least squares (MLS) approximation [6, 30]. In addition, radial basis functions (FBFs) have been used to obtain the numerical solutions of boundary integral equations [5, 7, 8].

Among wavelets, Chebyshev wavelets have significant applications in different problems of the numerical mathematics as one of the piecewise polynomial wavelets. The Chebyshev wavelets have been used to approximate the solution of differential equations [12], the second kind integral equations [11], the first kind Fredholm integral equations [1], Abel’s integral equations [34], nonlinear systems of Volterra integral equations [13], fractional nonlinear Fredholm integro-differential equations [45], time-varying delay systems [20], and fractional differential equations [37].

The adaptation of Chebyshev wavelets to Galerkin method for solving singular integral equations has some difficulties in computations. The dual-wavelet concept is defined for establishing an orthonormal basis from Chebyshev wavelets and improves these problems. Some good properties of Chebyshev wavelets, such as having vanish moments and local support, are resulted high accuracy approximation for dual-Chebyshev wavelets.

This article applies the dual-Chebyshev wavelets to solve the logarithmic boundary integral equations of the second kind (1). The scheme utilizes the dual-Chebyshev wavelets constructed on the unit interval to estimate the unknown function in the discrete Galerkin method. The discrete Galerkin method for solving singular integral equations usually needs a special integration rule to approximate their integrals. We utilize the composite non-uniform Gauss–Legendre (CNGL) quadrature formula for this aim. At first, by parameterizing $\partial D$, the boundary integral equation (1) converts to a weakly singular integral equation. Then, the properties of Chebyshev wavelets and dual of them are used to reduce this equation into solving a system of algebraic equations. The error bound and the convergence rate for the new method are obtained. The new technique is efficient, simple, computationally attractive and more flexible for most classes of boundary integral equations.

The outline of the current paper is as follows. In Sect. 2, dual-Chebyshev wavelets are introduced and used to approximate functions. A computational method for solving the integral equation (1) using dual-Chebyshev wavelets is presented in Sections 3. In Sect. 4, we provide the error analysis for the method. Numerical examples are given in Section 5. Finally, we conclude the article in Sect. 6.

2 Dual-Chebyshev wavelets

Chebyshev wavelets, $\psi _{n,m}(x)=\psi (k,n,m,x)$, have four arguments; $n=1,2,\dots ,2^{k-1}$, k can assume any non-negative integer, m is the degree of Chebyshev polynomial of the first kind, and x denotes an independent variable in [0, 1] [11]:

$$\begin{aligned} \psi _{n,m}(x)=\left\{ \begin{array}{rl} \alpha _m\sqrt{\frac{2^k}{\pi }} T_m(2^kx-2n+1), &{} \frac{n-1}{2^{k-1}}\le x< \frac{n}{2^{k-1}}, \\ 0, &{} \mathrm{otherwise},\\ \end{array} \right. \end{aligned}$$

(3)

where

$$\begin{aligned} \alpha _m=\left\{ \begin{array}{rl} 1, &{} m=0 , \\ \sqrt{2}, &{} m>0,\\ \end{array} \right. \end{aligned}$$

(4)

and $m=0,1,\dots ,M-1$ and $n=1,2,\dots ,2^{k-1}$. Here, $T_m(x),~m=0,1,\dots$ are Chebyshev polynomials of the first kind of degree m which are orthogonal with respect to the weight function $w(x)=\frac{1}{\sqrt{1-x^2}}$, on the interval $[-1,1]$, and satisfy the following formula:

$$\begin{aligned} T_m(\cos \theta )=\cos m\theta ,~~m=0,1,2,\dots . \end{aligned}$$

We should note that Chebyshev wavelets are the orthonormal basis for $L^2_{\bar{w}_k}[0,1]$ with respect to the weight function:

$$\begin{aligned} \bar{w}_{k}(x)=\left\{ \begin{array}{cccc} w_{1,k}(x),~~~ &{}~~~~0\le x<\frac{1}{2^{k-1}}, \\ w_{2,k}(x),~~~ &{}\frac{1}{2^{k-1}}\le x<\frac{2}{2^{k-1}}, \\ \vdots &{} \vdots \\ w_{2^{k-1},k}(x), &{} \frac{2^{k-1}-1}{2^{k-1}}\le x<1, \\ \end{array}\right. \end{aligned}$$

(5)

where $w_{n,k}(x)=w(2^{k-1}x-n+1)$ [1].

A function $f(x)\in L^2_{\bar{w}_k}[0,1]$ may be approximated by Chebyshev wavelets as [1, 11]

$$\begin{aligned} f(x)\approx \sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M-1}c_{n,m}\psi _{n,m}(x), \end{aligned}$$

(6)

where

$$\begin{aligned} c_{n,m}=<f(x),\psi _{n,m}(x)>_{\bar{w}_{k}}=\int _0^1f(x),\psi _{n,m}(x){\bar{w}_{k}}(x) \mathrm {d}x. \end{aligned}$$

(7)

2.1 Dual-Chebyshev wavelets

We define the dual-Chebyshev wavelet concept for establishing an orthonormal basis respect to the weight function $w(x)=1$ from Chebyshev wavelets which are an orthogonal basis for $L^2_{\bar{w}_k}[0,1]$ (not for $L^2 [0,1]$). The dual-Chebyshev wavelets basis of $\{\psi _{n,k}\}$ is defined as an orthogonal basis for $L^2[0,1]$ such as $\{\tilde{\psi }_{n,k}\}$, subject to the following assumptions:

• (I) $~\mathrm {span}\{\psi _{n,m}(x)\}=\mathrm {span}\{\tilde{\psi }_{n,m}(x)\},~~~m=0,1,\dots ,M-1,~n=1,2,\dots ,2^{k-1},$

• (II) $~ \langle \psi _{n,k},\tilde{\psi }_{n',k'}\rangle = \int _0^1\psi _{n,k}(x).\tilde{\psi }_{n',k'}(x) \mathrm {d}x = \delta _{k,k'}\delta _{n,n'}.$

By considering $i=M(n-1)+m+1$, we can relabel $\psi _i=\psi _{n,m}$ and $\tilde{\psi }_i=\tilde{\psi }_{n,m}$ where $i=1,2,...,2^{k-1}M$. From the assumption (I), it can be concluded that the dual-Chebyshev wavelets are a linear combination of Chebyshev wavelets, that is

$$\begin{aligned} \tilde{\psi }_{i}(x)=\sum _{j=1}^{2^{k-1}M}T_{ij}\psi _{j}(x), \end{aligned}$$

(8)

or in the matrix form

$$\begin{aligned} \tilde{\Psi }=\mathbf T \Psi ^T. \end{aligned}$$

(9)

In addition, we rewrite the assumption (II) in the matrix form as follows:

$$\begin{aligned} \int _0^1\tilde{\Psi }(x).\Psi ^T(x) \mathrm {d}t = \mathbf I , \end{aligned}$$

(10)

where

$$\begin{aligned} \Psi =[\psi _{1,0},\psi _{1,1},\dots ,\psi _{1,M-1},\psi _{2,0},\psi _{2,1},\dots ,\psi _{2,M-1},\dots , \psi _{2^{k-1},0},\dots ,\psi _{2^{k-1},M-1}]^T, \end{aligned}$$

(11)

$$\begin{aligned} \tilde{\Psi }=[\tilde{\psi }_{1,0},\tilde{\psi }_{1,1},\dots ,\tilde{\psi }_{1,M-1},\tilde{\psi }_{2,0},\tilde{\psi }_{2,1},\dots ,\tilde{\psi }_{2,M-1},\dots , \tilde{\psi }_{2^{k-1},0},\dots ,\tilde{\psi }_{2^{k-1},M-1}]^T, \end{aligned}$$

(12)

and $\mathbf I _{2^{k-1}M\times 2^{k-1}M}$ is the identity matrix.

Let $\mathbf L$ be a $2^{k-1}M\times 2^{k-1}M$ matrix with following entries:

$$\begin{aligned} l_{ij}=\int _{0}^{1}\psi _{i}(x)\psi _{j}(x)\mathrm {d}x. \end{aligned}$$

(13)

It is easy to obtain that $\mathbf T =\mathbf L ^{-1}$, because

$$\begin{aligned} \mathbf I = \int _{0}^{1}\tilde{\Psi }(x)\Psi ^T(x)\mathrm {d}x= \int _{0}^{1}{} \mathbf T \Psi (x)\Psi ^T(x)\mathrm {d}x =\mathbf T {} \mathbf L . \end{aligned}$$

(14)

Now, we need to calculate the entries of the matrix L for the numerical implementation to compute the matrix $\mathbf T$. For this purpose, by considering $i= M(n-1)+m +1$ and $j= M(n'-1)+m' +1$, we have

$$\begin{aligned} l_{ij}=2^k\int _{0}^{1}\tilde{T}_{m}(2^kx-2n+1)\tilde{T}_{m'}(2^kx-2n'+1)\mathrm {d}x. \end{aligned}$$

(15)

If $n\ne n'$, then the support of two functions in the integral (15) is disjoint and yields $l_{ij}=0$. In addition, if $n= n'$, by properties of Chebyshev polynomials, we have

$$\begin{aligned} l_{ij}= & {} 2^kd_{m,m'}\int _{\frac{n-1}{2^{k-1}}}^{\frac{n}{2^{k-1}}}T_{m}(2^kx-2n+1)T_{m'}(2^kx-2n+1)\mathrm {d}x \\ = & {} d_{m,m'}\int _{-1}^{1}T_{m}(\tau )T_{m'}(\tau )\mathrm {d}\tau \\ = & {} d_{m,m'}\int _{-1}^{1}\frac{1}{2}[T_{m+m'}(\tau )+T_{|m-m'|}(\tau )]\mathrm {d}\tau ,\end{aligned}$$

(16)

where

$$\begin{aligned} d_{m,m'}=\frac{1}{\pi } \left\{ \begin{array}{lr} 1 , &{} m=m'=0,\\ 2 , &{} m\ne 0\ne m',\\ \sqrt{2}, &{} \mathrm{otherwise}. \end{array} \right. \end{aligned}$$

The following recurrence relationship between Chebyshev polynomials and their differentials is

$$\begin{aligned} 2T_n(x)=\frac{T'_{n+1}}{n+1}-\frac{T'_{n-1}}{n-1}, \end{aligned}$$

so the integral of Chebyshev polynomials can be writhen as

$$\begin{aligned} \int _{-1}^{1}T_m(x)\mathrm {d}x=\left\{ \begin{array}{lr} \frac{1}{m+1}-\frac{1}{m-1}, &{} {m~ {\text{ i }s~ even}},\\ 0, &{} {m~ {\text{ i }s~ odd}}.~~ \end{array} \right. \end{aligned}$$

(17)

Overall, using Eq. (17), the matrix $\mathbf L$ is a blocked-diagonal matrix which has the following form:

$$\begin{aligned} \mathbf L =\mathrm {diag}( \underbrace{A,A,\ldots ,A}_{2^{k-1} \text {times}}), \end{aligned}$$

(18)

where $A=[A_{mm'}]$ is an $M\times M$ matrix with the following entries

$$\begin{aligned} {A}_{mm'} = \left\{ \begin{array}{rl} -d_{m,m'}\left( \frac{1}{(m+m')^2-1}+\frac{1}{(m-m')^2-1}\right) , &{} m+m'~{\text{ i }s~ odd},\\ 0,\quad &{} m+m'~{\text{ i }s~ odd}.\\ \end{array} \right. \end{aligned}$$

(19)

Remark 1

Note that, L is positive definite and strictly diagonally dominant matrix because of Eq. (19) shows a fast decreasing pattern of the magnitude of non-zero entries of A by increasing distance with main diagonal. It is clear that A is a strictly diagonally dominant matrix, and hence, it is invertible. The matrix A (and consequently $\mathbf L$) is a symmetric matrix and its eigenvalues are real and positive by Gershgorin’s circle theorem [33]. In addition, A is positive definite, because a symmetric strictly diagonally dominant matrix with real positive diagonal entries is positive definite. On the other hand, the magnitude of diagonal entries of A is bounded with $\frac{2}{\pi }$, because

$$\begin{aligned} |A_{mm}|=|-d_{m,m}(\frac{1}{4m^2-1}-1)|= \frac{2}{\pi } |1-\frac{1}{4m^2-1}| <\frac{2}{\pi },~~~m\ne 0. \end{aligned}$$

It yields that

$$\begin{aligned} \rho (A)\le \Vert A\Vert _1=\sum _{j=1}^{M}|A_{1,j}|=|A_{1,1}|+\sum _{j=2}^{M}|A_{1,j}|<\frac{4}{\pi }. \end{aligned}$$

Clearly, $\mathbf T$ can be written as a blocked-diagonal matrix as

$$\begin{aligned} \mathbf T =\mathrm {diag}(\underbrace{A^{-1},A^{-1},\dots ,A^{-1}}_{2^{k-1} \, \mathrm{times}}). \end{aligned}$$

(20)

2.2 Function approximation

A function $f(x)\in L^2[0,1]$ may be expanded by dual-Chebyshev wavelets for any integer $k> 0$ and a fixed number $M \in \mathbb {N}$ as follows:

$$\begin{aligned} f(x)\approx \sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M-1}{f}_{n,m}\tilde{\psi }_{n,m}(x)=\sum _{i=1}^{2^{k-1}M}f_i\tilde{\psi }_i(x)= {F}^T\tilde{\Psi }(x), \end{aligned}$$

(21)

where

$$\begin{aligned} {f}_{n,m}=<f(x),\tilde{\psi }_{n,m}(x)> = \int _0^1f(x)\tilde{\psi }_{n,m}(x) \mathrm {d}t, \end{aligned}$$

(22)

and

$$\begin{aligned} {F}^T= & {} [f_{1,0},f_{1,1},\dots ,f_{1,M-1},f_{2,0},f_{2,1},\dots ,f_{2,M-1},\dots , f_{2^{k-1},0},\dots ,f_{2^{k-1},M-1}]^T \nonumber \\= & {} [f_1,f_2,\dots ,f_{2^{k-1}M}]^T. \end{aligned}$$

In the following, the error estimate of the dual-Chebyshev wavelets is presented in terms of the parameter k in the mean norm. For this aim, we define the orthogonal projection operator $\mathcal {P}_{k,M}:~L^2[0,1]\rightarrow V_N$ as the Galerkin operator by

$$\begin{aligned} \mathcal {P}_{k,M}u(x)=\sum _{i=1}^{2^{k-1}M}c_i\tilde{\psi }_i(x),~~~~{x}\in [0,1], \end{aligned}$$

(23)

where the space $V_N=\mathrm {span}\{\tilde{\psi }_1,...,\tilde{\psi }_{2^{k-1}M}\}\subset L^2[0,1]$ with the dimension $d_N$ and the coefficients $\{c_1,...,c_{2^{k-1}M}\}$ determined by solving the linear system:

$$\begin{aligned}<u,\tilde{\psi }_j>=\sum _{i=1}^{2^{k-1}M}c_i<\tilde{\psi }_i,\tilde{\psi }_j>,~~~~j=1,...,2^{k-1}M. \end{aligned}$$

(24)

Theorem 2.1

Suppose that the functionu(x) is M times continuously differentiable on [0, 1], i.e.,$u\in C^M[0,1]$. Then, the functionu(x) can be expanded as the infinite sum of dual-Chebyshev wavelets (23) and this series converges to the functionu(x) like of$O(2^{-kM})$. Furthermore

$$\begin{aligned} \parallel u-\mathcal {P}_{k,M}u {\parallel } \le 2^{-kM} C_M \sup _{0 \le x \le 1} |u^{(M)}(x)|, \end{aligned}$$

(25)

where$C_M=\frac{2}{2^{M}M!}$.

Proof

Similar to [3], for dual-Chebyshev wavelets, we have

$$\begin{aligned} \parallel u-\mathcal {P}_{k,M}u {\parallel }= & {} \left( \int _0^1 [u(x)-\mathcal {P}_{k,M}u(x)]^2 \mathrm {d}x \right) ^{1/2}\\\le & {} \left( \sum _{n=1}^{2^{k-1}} \int _{\frac{n-1}{2^{k-1}}}^{\frac{n}{2^{k-1}}}\int _0^1 [u(x)-Q^n_{k,M}(x)]^2 \mathrm {d}x \right) ^{1/2}, \end{aligned}$$

where $Q^n_{k,M}(x)$ is the interpolation polynomial of degree M at the Chebyshev nodes of order M on $[{\frac{n-1}{2^{k-1}}},{\frac{n}{2^{k-1}}}]$ for the function u. Thus, utilizing the error bound for Chebyshev interpolation [33], we obtain

$$\begin{aligned} \parallel u-\mathcal {P}_{k,M}u {\parallel } \le 2^{-kM} \underbrace{\frac{2}{2^{M}M!}}_{C_M} \sup _{0 \le x \le 1} |u^{(M)}(x)|. \end{aligned}$$

Since $2^{-kM}$ vanishes as $k \rightarrow \infty$ it follows that $\mathcal {P}_{k,M}u$ converges (in the mean) to u.

Similarly, we can approximate the two-dimensional function $K(x,y)\in {L^2([0,1]\times [0,1])}$ by dual-Chebyshev wavelets as

$$\begin{aligned} K(x,y)\approx \sum _{i=1}^{2^{k-1}M}\sum _{j=1}^{2^{k-1}M}K_{ij}\psi _{i}{(x)}\psi _{j}{(y)}=\tilde{\Psi }^T(x)\mathbf K \tilde{\Psi }(y), \end{aligned}$$

(26)

where $\mathbf K ={[K_{ij}]}_{{1\le {i,j}} \le {2^{k-1}M}}$ with the entries

$$\begin{aligned} K_{ij}=\langle \tilde{\psi }_{i}(x),\langle K(x,y),\tilde{\psi }_{j}(y)\rangle \rangle = \int _{0}^{1}\int _{0}^{1}K(x,y)\tilde{\psi }_{i}(x)\tilde{\psi }_{j}(y) \mathrm {d}x \mathrm {d}y. \end{aligned}$$

(27)

3 Solution of Logarithmic Boundary Integral Equations

Consider the boundary Fredholm integral equation of the second kind with logarithmic singular kernel:

$$\begin{aligned} -\pi u(\mathrm {x})+ \int _{\partial D} u(\mathrm {y}) \left( p(\mathrm {y})\ln \Vert \mathrm {x}-\mathrm {y}\Vert +\frac{\partial \ln \Vert \mathrm {x}-\mathrm {y}\Vert }{\partial n_{\mathrm {y}}} \right) \mathrm {d}s_{\mathrm {y}}=\int _{\partial D} g(\mathrm {y})\ln \Vert \mathrm {x}-\mathrm {y}\Vert \mathrm {d}s_{\mathrm {y}},~~~~\mathrm {x} \in \partial D, \end{aligned}$$

(28)

where D is a bounded, open, simply connected region in the plane, $n_\mathrm {x}$ is the outward unit normal on $\partial D$, $p(\mathrm {x})$ and $g(\mathrm {x})$ are given functions on $\partial D$ with $p(\mathrm {x})\ge 0$ but $p \not \equiv 0$ and $u(\mathbf {x})\in C^1(\bar{D})\cap C^2(D)$ is the unknown function to be determined [10, 18].

We also assume that the boundary $\partial D$ is a smooth simple closed curve with a twice continuously differentiable [10] and parameterized by

$$\begin{aligned} \mathrm {r}(t)=(\xi (t),\eta (t)),~~~~0\le t \le 1, \end{aligned}$$

(29)

with $\mathrm {r} \in C^2[0,1],~|\mathrm {r'}(t)|\ne 0$ and the parametrization of $\partial D$ traverses in a counter-clockwise direction. The interior unit normal $\mathrm {n}(t)$ is introduced as

$$\begin{aligned} \mathrm {n}(t)=\frac{(-\eta '(t),\xi '(t))}{\sqrt{\xi '(t)^2+\eta '(t)^2}}, \end{aligned}$$

(30)

which is orthogonal to the curve $\partial D$ at $\mathrm {r}(t)$. Based on the parametrization of $\partial D$, we obtain the quantities:

$$\begin{aligned} \mathrm {d}s_{\mathrm {y}}=\sqrt{\xi '(t)^2+\eta '(t)^2} \mathrm {d}s, \end{aligned}$$

(31)

and

$$\begin{aligned} \frac{\partial \ln \Vert \mathrm {x}-\mathrm {y}\Vert }{\partial n_{\mathrm {y}}}=\left\{ \begin{array}{rl} \frac{-\eta '(s)[\xi (t)-xi(s)]+\xi '(s)[\eta (t)-\eta (s)]}{\sqrt{\xi '(s)^2+\eta '(s)^2}([\xi (t)-\xi (s)]^2+[\eta (t)-\eta (s)]^2)}, &{} s\ne t, \\ \frac{-\eta '(t)\xi ^{''}(t)+\xi '(t)\eta ^{''}(t)}{2\sqrt{\xi '(s)^2+\eta '(s)^2}(\xi '(t)^2+\eta '(t)^2)},~~~~~~~~~~~ &{} s=t. \\ \end{array} \right. \end{aligned}$$

(32)

By substituting Eqs. (31) and (32) into the integral equation (28), we reduce the boundary integral equations (28) to the following integral equation with the logarithmic kernel:

$$\begin{aligned} -\pi u(t)+\int _0^1 K(t,s) u(s) \mathrm {d}s=f(t),~~~~0\le t \le 1, \end{aligned}$$

(33)

where

$$\begin{aligned} f(t)=\int _0^1 g(\mathrm {r}(s)) \Vert \mathrm {r}^\prime(s)\Vert \ln \Vert \mathrm {r}(t)-\mathrm {r}(s)\Vert \mathrm {d}s, \end{aligned}$$

(34)

and

$$\begin{aligned} K(t,s)=p(\mathrm {r}(s)) \Vert \mathrm {r}^\prime(s)\Vert \ln \Vert \mathrm {r}(t)-\mathrm {r}(s)\Vert +q(t,s), \end{aligned}$$

(35)

with

$$\begin{aligned} q(t,s)=\left\{ \begin{array}{rl} \frac{-\eta '(s)[\xi (t)-\xi(s)]+\xi '(s)[\eta (t)-\eta (s)]}{[\xi (t)-\xi (s)]^2+[\eta (t)-\eta (s)]^2}, &{} s\ne t, \\ \frac{-\eta '(t)\xi ^{''}(t)+\xi '(t)\eta ^{''}(t)}{2(\xi '(t)^2+\eta '(t)^2)},~~~~~~~~~~~~ &{} s=t. \\ \end{array} \right. \end{aligned}$$

(36)

Note that in the integral Eq. (33), we have used $u(t)\equiv u(\mathrm {r}(t))$ for simplicity in notation.

Now, we want to utilize the Galerkin method with dual-Chebyshev wavelets constructed on [0, 1] as a basis for solving the integral Eq. (33). From the expansion (21), the solution u(t) can be approximated by dual-Chebyshev wavelets as

$$\begin{aligned} u(t)\approx \sum _{i=1}^{2^{k-1}M}u_i\tilde{\psi }_i(t) = {U}^T\tilde{\Psi }(t). \end{aligned}$$

(37)

Then, instead of u(t), we can replace the expansion (37) in the integral equation (33). Thus, we obtain

$$\begin{aligned} -\pi \tilde{\Psi }^T(t){U}+\int _{0}^{1}K(t,s)\tilde{\Psi }^T(s){U} \mathrm {d}s=f(t). \end{aligned}$$

(38)

By taking inner product $<\tilde{\Psi }(t),.>$ upon both sides of (38), we have

$$\begin{aligned} -\pi<\tilde{\Psi }(t),\tilde{\Psi }^T(t)>{U}+<\int _{0}^{1}K(t,s) \mathrm {d}s\tilde{\Psi }^T(s){U}, \tilde{\Psi }^T(t)>=< \tilde{\Psi }(t),f(t)>. \end{aligned}$$

(39)

The use of orthonormality of dual-Chebyshev wavelets yields

$$\begin{aligned} (-\pi \mathbf I + \mathbf K )U=F, \end{aligned}$$

(40)

where $\mathbf I _{{2^{k-1}M}\times {2^{k-1}M}}$ is the identity matrix and $F=[f_1,f_2,...,f_{2^{k-1}M}]^T$ with $f_j=<f(t),\tilde{\psi }_j>$.

This linear system of algebraic equations can be also written in the extended form as

$$\begin{aligned} -\pi u_j +\sum _{i=1}^{2^{k-1}M}u_i\int _{0}^{1}\int _{0}^{1}K(t,s)\tilde{\psi }_i(s)\tilde{\psi }_j(t) \mathrm {d}s\mathrm {d}t=\int _0^1 f(t)\tilde{\psi }_j(t) \mathrm {d}t,~~~~j=1,2,...,2^{k-1}M, \end{aligned}$$

(41)

for unknowns ${{{U}}^T}=[{u}_1,{u}_2,\dots ,{u}_{2^{k-1}M}]^T.$

The discrete Galerkin method arises when all integrals required in the Galerkin method are calculated using numerical integration. Therefore, we must approximate two types of integrals in the system (41) as

$f_j=\langle \tilde{\Psi }(t),f(t)\rangle=\int _0^1 f(t)\tilde{\psi }_j(t) \mathrm {d}t,$

$K_{ij}=\langle\tilde{\psi }_{i}(x),\rangle K(x,y),\tilde{\psi }_{j}(y)\rangle\rangle=\int _{0}^{1}\int _{0}^{1} K(t,s) \tilde{\psi }_i(s)\tilde{\psi }_j(t) \mathrm {d}s\mathrm {d}t.$

From (33) and (34), we obtain

$$\begin{aligned} f_j=\int _0^1 \int _0^1 g(\mathrm {r}(s)) \Vert \mathrm {r'}(s)\Vert \ln \Vert \mathrm {r}(t)-\mathrm {r}(s)\Vert \tilde{\psi }_j(t) \mathrm {d}s \mathrm {d}t, \end{aligned}$$

(42)

$$\begin{aligned} K_{ij}=\int _{0}^{1}\int _{0}^{1}\left\{ p(\mathrm {r}(s)) \Vert \mathrm {r'}(s)\Vert \ln \Vert \mathrm {r}(t)-\mathrm {r}(s)\Vert +q(t,s)\right\} \tilde{\psi }_i(s)\tilde{\psi }_j(t) \mathrm {d}s\mathrm {d}t. \end{aligned}$$

(43)

Since the function $\ln \Vert \mathrm {r}(t)-\mathrm {r}(s)\Vert$ is a logarithmic weakly singular function, the integrals (42) and (43) cannot be computed by the usual quadrature formulae, and so, we need a specific numerical integration rule. In the following, we consider a simple but efficient quadrature rule for computing such integrals presented in [18]. For approximating the integrals, we use the double composite $q_N$-point Gauss–Legendre (DCGL) rule with M non-uniform subdivisions.

Suppose that f(t, s) is defined on $(0, 1)\times (0, 1)$ and satisfies

$$\begin{aligned} \left| \frac{\partial ^{2q_N} f}{\partial t^{2q_N} }\right|<C_1 t^{-\epsilon -2q_N},~~~~\left| \frac{\partial ^{2q_N} f}{\partial s^{2q_N} }\right| <C_2t^{-\epsilon }, \end{aligned}$$

(44)

for all (t, s) and some $\epsilon \in (0,1)$. Let $\alpha _1(t), \alpha _2(t)$ be functions in $C^{2q_N}[0, 1]$. Then, for any given integer M, we have [18, 22]

$$\begin{aligned} \int _0^1\int _{\alpha _1(t)}^{\alpha _2(t)} f(t,s) \mathrm {d}t\mathrm {d}s=\sum _{q=1}^M\frac{\Delta t_q}{2}\sum _{k=1}^{q_N}w_k \frac{\Delta s(\theta _k^q)}{2}\sum _{r=1}^{M_{p,r}}\sum _{p=1}^{q_N}w_p f(\theta _k^q, \eta _p^r(\theta _k^q))+O\left(\frac{1}{M^{2q_N}}\right), \end{aligned}$$

(45)

where

$$\begin{aligned} \theta _k^q=\frac{\Delta t_q}{2}v_k+\bar{t}_q, ~\Delta t_q=t_q-t_{q-1}~and~\bar{t}_q=\frac{t_q+t_{q-1}}{2}, \end{aligned}$$

with

$$\begin{aligned} t_q=\left( \frac{q}{M}\right) ^\ell ,~~~\ell =\frac{2q_N+1}{1-\epsilon },~~~M_{p,r}=1+[M(\alpha _2(\theta _k^q)-\alpha _1(\theta _k^q))], \end{aligned}$$

$$\begin{aligned} \Delta s (\theta _k^q)=\frac{\alpha _2(\theta _k^q)-\alpha _1(\theta _k^q)}{M_{p,r}}~~~{and}~~~\eta _p^r(\theta _k^q)=\frac{\Delta s(\theta _k^q)}{2}s_p+\alpha _1(\theta _k^q)+\left(r-\frac{1}{2}\right)\Delta s(\theta _k^q). \end{aligned}$$

Note that the integrals (42) and (43) are singular along the diagonal $t=s$ (not only at point $t=0$) and also at the points (0, 1) and (1, 0) because $\partial D$ is a simple closed curve, so the quadrature rule (45) cannot be applied for them. The change of variables

$$\begin{aligned} u=t-s,~~~v=s+t, \end{aligned}$$

for these integrals transform the unit square $[0,1]\times [0,1]$ to the diamond $\{(u,v): |u|+|v-1|\le 1\}$ [18, 22]. Therefore, we have

$$\begin{aligned} f_j=\int_{-1}^1 \int _{\alpha _1(u)}^{\alpha _2(u)} {\frac{1}{2}g\left(\mathrm {r}\left(\frac{v-u}{2}\right)\right) \left\| \mathrm {r'}\left(\frac{v-u}{2}\right)\right\| \ln \left\| \mathrm {r}\left(\frac{v+u}{2}\right)-\mathrm {r}\left(\frac{v-u}{2}\right)\right\| \tilde{\psi }_j\left(\frac{v+u}{2}\right)} \mathrm {d}v \mathrm {d}u, \end{aligned}$$

(46)

and

$$\begin{aligned} K_{ij}=\int _{-1}^{1}\int _{\alpha _1(u)}^{\alpha _2(u)}{\frac{1}{2}K\left(\frac{v+u}{2},\frac{v-u}{2}\right)\tilde{\psi }_i\left(\frac{v-u}{2}\right)\tilde{\psi }_j\left(\frac{v+u}{2}\right)} \mathrm {d}v\mathrm {d}u. \end{aligned}$$

(47)

with

$$\begin{aligned} \alpha (u)=\max \{-u,u\}~~~\mathrm {and}~~~\beta (u)=\min \{2-u,2+u\}. \end{aligned}$$

The integrals of (46) and (47) have weakly singularity at $u=0,\pm 1$ and are sufficiently smooth for every v. To approximate these singular integrals via the quadrature rule (45), we give

$$\begin{aligned} f_j= & {} \int _{-1}^{\frac{-1}{2}} F(u) \mathrm {d}u +\int _{\frac{-1}{2}}^0 F(u) \mathrm {d}u+\int _{0}^{\frac{1}{2}} F(u) \mathrm {d}u+\int _{\frac{1}{2}}^1 F(u) \mathrm {d}u\nonumber \\= & {} \int _{0}^{\frac{1}{2}}[F(-u)+F(u)] \mathrm {d}u+\int _{\frac{1}{2}}^1[F(-u)+F(u)] \mathrm {d}u, \end{aligned}$$

(48)

where

$$\begin{aligned} F(u)=\int _{\alpha _1(u)}^{\alpha _2(u)} \frac{1}{2}g(\mathrm {r}(\frac{v-u}{2})) \left\| \mathrm {r'}(\frac{v-u}{2})\right\| \ln \left\| \mathrm {r}(\frac{v+u}{2})-\mathrm {r}(\frac{v-u}{2})\right\| \tilde{\psi }_j(\frac{v+u}{2}) \mathrm {d}v. \end{aligned}$$

It is easy to see by a simple changing variables that

$$\begin{aligned} f_j=\frac{1}{2}\int _{0}^{1}\left[F\left(\frac{-u}{2}\right)+F\left(\frac{u}{2}\right)+F\left(\frac{u}{2}-1\right)+F\left(1-\frac{u}{2}\right)\right] \mathrm {d}u. \end{aligned}$$

(49)

Similarly, we obtain

$$\begin{aligned} K_{ij}=\frac{1}{2}\int _{0}^{1}[H(\frac{-u}{2})+H(\frac{u}{2})+H(\frac{u}{2}-1)+H(1-\frac{u}{2})] \mathrm {d}u, \end{aligned}$$

(50)

where

$$\begin{aligned} H(u)=\int _{\alpha _1(u)}^{\alpha _2(u)} \frac{1}{2}K(\frac{v+u}{2},\frac{v-u}{2})\tilde{\psi }_i(\frac{v-u}{2})\tilde{\psi }_j(\frac{v+u}{2})\mathrm {d}v. \end{aligned}$$

The integrands of (49) and (50) are singular in $u=0$ and satisfy the condition (44) for any positive integer k and for any small positive number $\epsilon$ [18]. Now, using the quadrature rule (45), we compute

$$\begin{aligned} f_j= \sum _{k=1}^{q_N}w_k \sum _{q=1}^M\frac{\Delta u_q}{2}[\hat{F}(\frac{-\theta _k^q}{2})+\hat{F}(\frac{\theta _k^q}{2})+\hat{F}(\frac{\theta _k^q}{2}-1)+\hat{F}(1-\frac{\theta _k^q}{2})]+O(\frac{1}{M^{2q_N}}), \end{aligned}$$

(51)

where

$$\begin{aligned} \hat{F}(u)=\frac{1}{2}\frac{\Delta v}{2} \sum _{r=1}^{q_N}w_k \sum _{p=1}^M g(\mathrm {r}(\frac{\eta _r^p-u}{2})) \left\| \mathrm {r'}(\frac{\eta _r^p-u}{2})\right\| \ln \left\| \mathrm {r}(\frac{\eta _r^p+u}{2})-\mathrm {r}(\frac{\eta _r^p-u}{2})\right\| \tilde{\psi }_j(\frac{\eta _r^p+u}{2}), \end{aligned}$$

(52)

with

$$\begin{aligned} \theta _k^q=\frac{\Delta t_q}{2}v_k+\bar{t}_q,\quad \Delta t_q=t_q-t_{q-1},~~~\bar{t}_q=\frac{t_q+t_{q-1}}{2},~~~t_q=\left( \frac{q}{M}\right) ^s,~~~s=\frac{2q_N+1}{1-r}, \end{aligned}$$

$$\begin{aligned} \Delta s=\frac{\beta (t)-\alpha (t)}{M_t}~~\mathrm {and}~~\eta _r^p=\frac{\Delta s}{2}v_r+(p-\frac{1}{2})\Delta s. \end{aligned}$$

In addition, we have

$$\begin{aligned} K_{ij}= \sum _{k=1}^{q_N}w_k \sum _{q=1}^M\frac{\Delta u_q}{2}[\hat{H}(\frac{-\theta _k^q}{2})+\hat{H}(\frac{\theta _k^q}{2})+\hat{H}(\frac{\theta _k^q}{2}-1)+\hat{H}(1-\frac{\theta _k^q}{2})]+O(\frac{1}{M^{2q_N}}), \end{aligned}$$

(53)

where

$$\begin{aligned} \hat{H}(u)=\frac{1}{2}\frac{\Delta v}{2} \sum _{r=1}^{q_N}w_k \sum _{p=1}^M K(\frac{\eta _r^p+u}{2},\frac{\eta _r^p-u}{2})\tilde{\psi }_i(\frac{\eta _r^p-u}{2})\tilde{\psi }_j(\frac{\eta _r^p+u}{2}). \end{aligned}$$

(54)

Utilizing the numerical integration schemes (51) and (53) in the system (41) results the linear system of algebraic equations:

$$\begin{aligned} -\pi \hat{u}_j+ & {} \sum _{i=1}^{2^{k-1}M}\hat{u}_i\sum _{k=1}^{q_N}w_k \sum _{q=1}^M\frac{\Delta u_q}{2}[\hat{H}(\frac{-\theta _k^q}{2})+\hat{H}(\frac{\theta _k^q}{2})+\hat{H}(\frac{\theta _k^q}{2}-1)+\hat{H}(1-\frac{\theta _k^q}{2})]\nonumber \\= & {} \sum _{k=1}^{q_N}w_k \sum _{q=1}^M\frac{\Delta u_q}{2}[\hat{F}(\frac{-\theta _k^q}{2})+\hat{F}(\frac{\theta _k^q}{2})+\hat{F}(\frac{\theta _k^q}{2}-1)+\hat{F}(1-\frac{\theta _k^q}{2})], \end{aligned}$$

(55)

for the unknowns $\hat{u}=[\hat{u}_1,\hat{u}_2,\ldots,\hat{u}_N]$. The solution of this system eventually leads to the following numerical solution which can be approximated u(t) at any point $t\in [0,1]$:

$$\begin{aligned} \hat{u}(t)=\sum ^{2^{k-1}M}_{j=1}\hat{u}_j\tilde{\psi }_j(t). \end{aligned}$$

(56)

3.1 Notes on 3D boundary integral equations

The solution of boundary value problems for three-dimensional Laplace’s equations with linear Robin boundary conditions reduces to the solution of the following boundary integral equation [10]:

$$\begin{aligned} -\Omega (\mathbf {x}) u(\mathbf {x})+ \int _{\partial R} u(\mathbf {y}) \left( p(\mathbf {y})\frac{1}{\Vert \mathbf {x}-\mathbf {y}\Vert }+\frac{\partial }{\partial n_{\mathbf {y}}}\left[ \frac{1}{\Vert \mathbf {x}-\mathbf {y}\Vert } \right] \right) \mathbf {d}s_{\mathbf {y}}= \int _{\partial R} \frac{g(\mathbf {y})}{\Vert \mathbf {x}-\mathbf {y}\Vert } \mathbf {d}s_{\mathbf {y}},~~\mathbf {x} \in \partial R, \end{aligned}$$

(57)

where R is a bounded, open, simply connected region in $\mathbb {R}^3$ and the surface $\partial R$ denotes its boundary, $\Omega (\mathbf {x})$ indicates the interior solid angle at $x \in \partial R$, $n_\mathbf {y}$ is the outward unit normal on the surface $\partial R$, the known function $g(\mathbf {x},u)$ is assumed to be continuous on $\partial R \times \mathbb {R}$ and $f(\mathbf {x})$ is a given function on $\partial R$ and the unknown function $u(\mathbf {x})\in C^1(\bar{R})\cap C^2(R)$ must be determined.

Suppose that the surface $\partial R$ is a smooth parametric orientable surface given by the equation:

$$\begin{aligned} \mathrm {r}(t_1,t_2)=(\xi (t_1,t_2),\eta (t_1,t_2),\sigma (t_1,t_2)),\quad (t_1,t_2)\in [0,1] \times [0,1], \end{aligned}$$

(58)

and $\partial R$ is covered just once as $(t_1,t_2)$ ranges throughout the parameter domain $\mathcal {S}= [0,1] \times [0,1]$ with $\mathrm {r} \in C^2(\mathcal {S})$ and $\Vert \mathrm {r'}(t_1,t_2)\Vert \ne 0$. Based on the parametrization of $\mathrm {r}(t_1,t_2)$, the interior unit normal $\mathrm {n}(t)$ is obtained by

$$\begin{aligned} \mathrm {n}(t_1,t_2)= \frac{\mathrm {r}_{t_1}\times \mathrm {r}_{t_2}}{\Vert \mathrm {r}_{t_1}\times \mathrm {r}_{t_2}\Vert }. \end{aligned}$$

(59)

Moreover, we result that

$$\begin{aligned} \mathrm {d}s_{\mathrm {y}}=\Vert \mathrm {r}_{s_1}\times \mathrm {r}_{s_2}\Vert \mathrm {d}s_1\mathrm {d}s_2,~~~\mathbf {y} = \mathrm {r}(s_1,s_2), \end{aligned}$$

(60)

and

$$\begin{aligned} \mathrm {d}s_{\mathrm {x}}=\Vert \mathrm {r}_{t_1}\times \mathrm {r}_{t_2}\Vert \mathrm {d}t_1\mathrm {d}t_2,~~~\mathbf {x} = \mathrm {r}(t_1,t_2). \end{aligned}$$

(61)

To start the proposed method, we estimate the unknown function $u(t_1,t_2)$ utilizing dual-Chebyshev wavelets constructed on [0, 1] as follows:

$$\begin{aligned} u(t_1,t_2)\approx \bar{u}_{k,M}u(t_1,t_2)\sum _{i=1}^{2^{k-1}M}\sum _{i=1}^{2^{k-1}M} u_{i,j}\tilde{\psi }_i(t_1) \tilde{\psi }_j(t_2)=\tilde{\Psi }^T(t_1)\mathbf U \tilde{\Psi }(t_2),~~~(t_1,t_2) \in \mathcal {S}, \end{aligned}$$

(62)

where the matrix $\mathbf U ={[u_{ij}]}_{{1\le {i,j}} \le {2^{k-1}M}}$ is determined by solving the system which is obtained by replacing the expansion (62) with $u(t_1,t_2)$ in the boundary integral equation (33) and taking the inner product

$$\begin{aligned} \left<,\left<.,\tilde{\psi }_i(t_1)\right>,\tilde{\psi }_j(t_2)\right>=\int _{0}^{1}\int _{0}^{1}u(t_1,t_2)\tilde{\psi }_{i}(t_1)\tilde{\psi }_{j}(t_2) \mathrm {d}t_1 \mathrm {d}t_2,~~~i,j=1,...,2^{k-1}M, \end{aligned}$$

upon both sides. In addition, to compute the singular integrals on $\mathcal {S} \times \mathcal {S}$ appeared in the scheme, we need to choose a suitable quadrature formula based on the generalized non-uniform composite Gauss–Legendre quadrature rule. In fact, this work is not really easy for dimension bigger than 2 and increases the difficulties to apply the method. It should be noted that solving high dimensional boundary integral equations by the proposed method can be interesting for future researches.

4 Error analysis

In this section, we investigate the error estimate and the convergence rate in terms of the parameter k for the presented method. This discussion is mostly based on the error analysis of discrete Galerkin method in [10, 25].

The operator $\mathcal {K}:L^2[0,1]\rightarrow L^2[0,1]$ with weakly singular kernel is introduced as

$$\begin{aligned} \mathcal {K}u(t)= \int _{\partial D} u(\mathrm {y}) \left( p(\mathrm {y})\ln \Vert \mathrm {x}-\mathrm {y}\Vert + \frac{\partial \ln \Vert \mathrm {x}-\mathrm {y}\Vert }{\partial n_{\mathrm {y}}} \right) \mathrm {d}s_{\mathrm {y}} = \int _{0}^1 k(t,s)u(s) \mathrm {d}s. \end{aligned}$$

(63)

Therefore, we can rewrite the integral equation (28) in the operator form:

$$\begin{aligned} (-\pi +\mathcal {K})u=f, \end{aligned}$$

(64)

where

$$\begin{aligned} f(t)=\int _{\partial D} g(\mathrm {y})\ln \Vert \mathrm {x}-\mathrm {y}\Vert \mathrm {d}s_{\mathrm {y}}=\int _0^1 g(\mathrm {r}(s)) \Vert \mathrm {r}^\prime(s)\Vert \ln \Vert \mathrm {r}(t)-\mathrm {r}(s)\Vert \mathrm {d}s. \end{aligned}$$

(65)

If $\Vert \mathcal {K}\Vert <\pi$, then the operator $-\pi + \mathcal {K}$ is a contraction operator, by the Banach contraction mapping principle, Eq. (28) has a unique solution $u_0\in L_{}^2[0,1]$ [10]. Now, we present the definition of compact operators and the respective theorems from [10, 25] to establish the error analysis of the method.

Definition 4.1

[25] A linear operator $\mathcal {K}:L^2[0,1]\rightarrow L^2[0,1]$ is called compact if the set $\{\mathcal {K}u|\Vert u\Vert \le 1\}$ has compact closure in $L^2[0,1]$.

Theorem 4.1

[25] Compact linear operators are bounded.

Theorem 4.2

[10] The logarithmic integral operator $\mathcal {K}$ is a compact operator on$L^2[0,1]$.

We are ready to exchange Eq. (55) in the operator form by the operators (23) and (63) as

$$\begin{aligned} (-\pi +\mathcal {P}_{k,M}\mathcal {K}){u}=\mathcal {P}_{k,M} f. \end{aligned}$$

(66)

We introduce the discrete semi-definite inner product using the $q_N$-point Gauss–Legendre rule with M non-uniform subdivisions such that ($q_N\ge d_N$) as follows:

$$\begin{aligned} <f,g>_{q_N} = \sum _{k=1}^{q_N} \sum _{q=1}^M \frac{\Delta x(\theta _k^q)}{2} {w}_kf(\theta _k^q)g(\theta _k^q),~~~~f,g\in L^2[0,1], \end{aligned}$$

(67)

and, for every $g \in L^2[0,1]$, the discrete semi-norm

$$\begin{aligned} \Vert g\Vert _{q_N}=\sqrt{<g,g>_{q_N}}. \end{aligned}$$

(68)

The discrete projection operator $\mathcal {Q}_{k,M}:L^2[0,1]\rightarrow V_N$ is defined as

$$\begin{aligned} \mathcal {Q}_{{k,M}}u(x)=\sum _{k=1}^{{2^{k-1}M}}c_k\tilde{\psi }_k(x),~~~~{x}\in [a,b], \end{aligned}$$

(69)

where the coefficients $\{c_1,...,c_N\}$ determined by solving the linear system:

$$\begin{aligned}<u,\psi _j>_{q_N}=\sum _{k=1}^{2^{k-1}M}c_k<\tilde{\psi }_k,\tilde{\psi }_j>_{q_N}~~~~j=1,...,N. \end{aligned}$$

(70)

The family $\{\mathcal {Q}_{{k,M}}\}$ is uniformly bounded on $L^2[0,1]$ which is proved at some length in Atkinson and Bogomolny [9], namely

$$\begin{aligned} \Vert \mathcal {Q}_{{k,M}}\Vert \le m<\infty . \end{aligned}$$

(71)

Since $\mathcal {Q}_{k,M}$ is a projection operator and $\mathcal {P}_{{k,M}}u\in V_N$, we give $\mathcal {Q}_{k,M}(\mathcal {P}_{{k,M}}u)=\mathcal {P}_{{k,M}}u$ [10]. Therefore

$$\begin{aligned} u-\mathcal {Q}_{k,M}u= & {} u-\mathcal {P}_{{k,M}}u+\mathcal {P}_{{k,M}}u-\mathcal {Q}_{k,M}u\end{aligned}$$

(72)

$$\begin{aligned}= & {} u-\mathcal {P}_{{k,M}}u+\mathcal {Q}_{k,M}\mathcal {P}_{{k,M}}u-\mathcal {Q}_{k,M}u=(\mathcal {I}-\mathcal {Q}_{k,M}) (u-\mathcal {P}_{{k,M}}u). \end{aligned}$$

(73)

Now, we obtain

$$\begin{aligned} \Vert \mathcal {Q}_{k,M}u-u\Vert \le (1+m) \Vert u-\mathcal {P}_{{k,M}}u\Vert _{}. \end{aligned}$$

(74)

From Theorem 2.1, we have

$$\begin{aligned} \Vert \mathcal {Q}_{k,M}u-u\Vert \le (1+m) 2^{-kM} C_M\Vert u^{(M)}\Vert _{}, \end{aligned}$$

(75)

for every $u\in C^{M}([0,1])$.

A family of $q_N$-point Gauss–Legendre rule with M non-uniform subdivisions operators $\mathcal {K}_N:L^2[0,1] \rightarrow L^2[0,1]$ for approximating $\mathcal {K}$ is introduced by

$$\begin{aligned} \mathcal {K}_Nu(x)= \sum _{r=1}^{q_N}\sum _{p=1}^M {w}_r \frac{\Delta y(\theta _r^p)}{2} K(x,\theta _r^p)u(\theta _r^p),~~~N\ge 1. \end{aligned}$$

(76)

Note that $\{\mathcal {K}_N\}$ is a collectively compact family that is pointwise convergent to $\mathcal {K}$ on $L^2[0,1]$ of $O(\frac{1}{M^{2_{q_N}}})$ [10, 18]. Then, Eq. (55) can be rewritten as

$$\begin{aligned} (-\pi + \mathcal {Q}_{N}\mathcal {K}_N)\hat{u}_N=\mathcal {Q}_{N}f. \end{aligned}$$

(77)

To obtain the error analysis of the method, we present the following convergence theorem about the discrete Galerkin method [10].

Theorem 4.3

Let$u_0$ be a unique solution of the integral equation (28). Assume that for every$u \in L^2[0,1]$

$$\begin{aligned} \inf _{\phi \in V_N} \Vert u-\phi \Vert _{}\rightarrow 0,~~~~as~~~~N\rightarrow \infty . \end{aligned}$$

(78)

Then, the inverse operator $(\pi + \mathcal {Q}_{k,M}\mathcal {K}_N)^{-1}$ exists for all sufficiently large N and is uniformly bounded. Furthermore

$$\begin{aligned} (\pi + \mathcal {Q}_{k,M}\mathcal {K}_N)(u_0-\hat{u}_N)=(\mathcal {K}u_0-\mathcal {K}_Nu_0)+\mathcal {K}_N(I-\mathcal {Q}_{k,M})u_0. \end{aligned}$$

(79)

Here, we complete the error analysis by the following theorem:

Theorem 4.4

Having in mind the assumptions of Theorems4.3 and2.1. Assume that${u}_0 \in C^{\rho }[0,1],$ where$\rho =\max \{M,q_N\}$, is the unique exact solution of the boundary integral equation (28). Then, for all sufficiently largeN the proposed method has a unique solution${\hat{u}}_N$ which converges to$u_0$ as$N\rightarrow \infty$. Besides, the error bound follows as

$$\begin{aligned} \Vert u_0-\hat{u}_N\Vert _{} = O({M^{-2q_N}})+O(2^{-kM}). \end{aligned}$$

(80)

Proof

Since $\mathcal {P}_{{k,M}} \in V_N$ and from Theorem 2.1, we have

$$\begin{aligned} \inf _{\phi \in V_N} \Vert u-\phi \Vert _{}\le \Vert u-\mathcal {P}_{{k,M}}u\Vert _{} \le 2^{-kM} C_M \sup _{0 \le t \le 1} |u^{(M)}(t)|, \end{aligned}$$

for every $u\in C^M[0,1]$, and so, when $k\rightarrow \infty$, the condition (78) is satisfied. Therefore, Theorem 4.3 certifies that there exists ${M}> 0$ such that for every $N\ge {M}$, the inverse operators $(-\pi + \mathcal {Q}_{k,M}\mathcal {K}_N)^{-1}$ exist and are uniformly bounded, that is

$$\begin{aligned} \Vert (-\pi + \mathcal {Q}_{k,M}\mathcal {K}_N)^{-1}\Vert _{}\le C_1< \infty . \end{aligned}$$

(81)

Now, from Eq. (77), it is clear that the present method in this paper, for every $N\ge {M}$, has a unique solution as

$$\begin{aligned} {\hat{u}}_N=(-\pi +\mathcal {Q}_{k,M}\mathcal {K}_N)^{-1}\mathcal {Q}_{k,M}f. \end{aligned}$$

On the other hand, from Eq. (82), we obtain

$$\begin{aligned} \Vert u_0-\hat{u}_N\Vert _{}\le & {} \Vert (-\pi +\mathcal {Q}_{k,M}\mathcal {K}_N)^{-1}\Vert _{}\left[ \Vert \mathcal {K}u_0-\mathcal {K}_Nu_0\Vert _{}+\Vert \mathcal {K}_N(I-\mathcal {Q}_{k,M})u_0\Vert _{}\right] \nonumber \\\le & {} C_1\left[ \Vert \mathcal {K}u_0-\mathcal {K}_Nu_0\Vert _{}+\Vert \mathcal {K}_N\Vert _{}\Vert u_0-\mathcal {Q}_{k,M}u_0\Vert _{}\right] . \end{aligned}$$

(82)

The family ${\mathcal {K}}_N$ is a pointwise convergence sequence and from the principle of uniform boundedness (see [10], Theorem A.3 in the Appendix), we can assume that $\Vert {\mathcal {K}}_N\Vert _{}\le C_2$, so

$$\begin{aligned} \Vert \hat{u}_N-u_0\Vert _{}\le C_1\Vert \mathcal {K}u_0-\mathcal {K}_Nu_0\Vert _{}+C_1C_2\Vert u_0-\mathcal {Q}_{k,M}u_0\Vert _{}. \end{aligned}$$

(83)

The inequality (75) concludes the error bound

$$\begin{aligned} \Vert u_0-\mathcal {Q}_{k,M}u_0\Vert _{} \le C_M 2^{-kM} \sup _{0 \le t \le 1} |u^{(M)}(t)|, \end{aligned}$$

(84)

where $u_0 \in C^{M}[0,1]$ and also as $u_0 \in C^{q_N}[0,1]$, Eq. (45) implies $\mathcal {K}_N$ is convergence to $\mathcal {K}$ of order $\frac{1}{M^{2q_N}}$, namely

$$\begin{aligned} \Vert \mathcal {K}u_0-\mathcal {K}_Nu_0\Vert _{} \le \frac{C_3}{M^{2q_N}} . \end{aligned}$$

(85)

Altogether

$$\begin{aligned} \Vert \hat{u}_N-u_0\Vert _{}\le \frac{C_1C_3}{M^{2q_N}}+C_1C_2C_M 2^{-kM} \sup _{0 \le t \le 1} |u^{(M)}(t)|. \end{aligned}$$

(86)

This completes the proof.

Corollary 4.1

As a conclusion from Theorem4.4, it should be noted that for $q_N$ sufficiently large, the error of the dual-Chebyshev wavelet approximation is dominated over the error of integration rule, and so, increasing the number of integration nodes$q_N$ has no significant effect on the error. Therefore, by increasingk, the proposed method will be of $O(2^{-kM} )$.

We can estimate the solution of the boundary value problem with linear Robin boundary conditions (2) using the numerical solution $\hat{u}_N(\mathrm {x})$ of the boundary integral equation (28) as follows:

$$\begin{aligned} \tilde{u}_N(\mathrm {x})=\frac{1}{2\pi } \int _{\partial D} \hat{u}_N(\mathbf {y}) \left( p(\mathrm {y})\ln \Vert \mathrm {x}-\mathrm {y}\Vert +\frac{\partial \ln \Vert \mathrm {x}-\mathrm {y}\Vert }{\partial n_{\mathrm {y}}} \right) \mathrm {d}s_{\mathrm {y}}-\frac{1}{2\pi } \int _{\partial D} g(\mathrm {y})\ln \Vert \mathrm {x}-\mathrm {y}\Vert \mathrm {d}s_{\mathrm {y}},~~~~\mathrm {x} \in D. \end{aligned}$$

Based on the theoretical analysis in [28, 29], we can obtain an error bound for the approximate solution $\tilde{u}_N(\mathrm {x})$ which requires an error analysis of the dual-Chebyshev wavelet approximation in the Sobolev space norm. To this aim, we firstly consider

$$\begin{aligned} |{u}({\mathrm {x}})-{\tilde{u}}_N({\mathrm {x}})|= & {} \frac{1}{2\pi } \left| \int _{\partial D} (u({\mathrm {y}})-{\hat{u}}_N({\mathrm {y}})) \left( p({\mathrm {y}})\ln \Vert {\mathrm {x}}-{\mathrm {y}}\Vert +\frac{\partial \ln \Vert {\mathrm {x}}-{\mathrm {y}}\Vert }{\partial n_{\mathrm {y}}} \right) {\mathrm {d}}s_{\mathrm {y}}\right| \\\le & {} C_1\Vert u-{\hat{u}}_N\Vert _{H^{-(\gamma +2)}(\partial D)}\left\| p({\mathrm {y}})\ln \Vert {\mathrm {x}}-{\mathrm {y}}\Vert +\frac{\partial \ln \Vert {\mathrm {x}}-{\mathrm {y}}\Vert }{\partial n_{\mathrm {y}}} \right\| _{H^{\gamma +2}(\partial D)}. \end{aligned}$$

Suppose that there exists a non-negative integer $\gamma$ such that the dual-Chebyshev wavelets $\tilde{\psi }_i$ are $\gamma$-times continuously differentiable and the boundary $\partial D$ is a piecewise $C^{\gamma }$. If there exists a constant $\delta>0$ such that $d_\mathrm {x}\equiv d(\mathrm {x},\partial D)=\min _{\mathrm {y}\in \partial D}\{|\mathrm {x}-\mathrm {y}|\}\ge \delta$, then

$$\begin{aligned} \left\| \frac{\partial \ln \Vert \mathrm {x}-\mathrm {y}\Vert }{\partial n_{\mathrm {y}}}\right\| _{H^{\gamma +2}(\partial D)}= \left\| -\frac{1}{2\pi }\frac{\cos (\mathrm {y}-\mathrm {x},n_{\mathrm {y}})}{\Vert \mathrm {x}-\mathrm {y}\Vert }\right\| _{H^{\gamma +2}(\partial D)}\le \rho _1 \sum _{l=0}^{\gamma +2} d_\mathrm {x}^{-l-1}, \end{aligned}$$

(87)

and

$$\begin{aligned} \Big \Vert { \ln \Vert \mathrm {x}-\mathrm {y}\Vert }\Big \Vert _{H^{\gamma +2}(\partial D)}\le \rho _2 \left( |\ln d_\mathrm {x}|+\sum _{l=1}^{\gamma +2}d_\mathrm {x}^{-l}\right) , \end{aligned}$$

(88)

where $\rho _1,\rho _2>0$ are constants (for more details please see [28, 29]). Thus, we have

$$\begin{aligned} |{u}(\mathrm {x})-\tilde{u}_N(\mathrm {x})| \le C_1\Vert u-\hat{u}_N\Vert _{H^{-(\gamma +2)}(\partial D)} \left\{ \rho _2\rho _3\left( |\ln d_\mathrm {x}|+\sum _{l=1}^{\gamma +2}d_\mathrm {x}^{-l}\right) +\rho _1\sum _{l=0}^{\gamma +2}d_\mathrm {x}^{-l-1}\right\} , \end{aligned}$$

where $\Vert p(\mathrm {x})\Vert _{H^{\gamma +2}(\partial D)}\le \rho _3.$

5 Numerical examples

In this section, three boundary integral equations with logarithmic singular kernels are solved to demonstrate the efficiency and accuracy of the proposed method. These numerical examples are deduced from some mixed boundary value problems for Laplace’s equation. We utilize 10-points composite non-uniform Gauss–Legendre (CNGL) quadrature rule with $M = 10$ for approximating singular integrals in the scheme. In order to measure the accuracy of the method, the maximum error $\Vert e_k\Vert _{\infty }$ and the mean error $\Vert e_k\Vert _2$ have been used as follows:

$$\begin{aligned} \Vert e_k\Vert _{\infty }=\max _{\mathrm {x}\in \partial D}\{|u_{ex}(\mathrm {x})-\hat{u}_k(\mathrm {x})|\},~~~~\Vert e_k\Vert _2=\left( \int _{ \partial D } |u_{ex}(\mathrm {x})-\hat{u}_k(\mathrm {x})|^2 \mathrm {d}\mathrm {x} \right) ^{\frac{1}{2}}, \end{aligned}$$

where $\hat{u}(\mathrm {x})$ is the numerical solution of the exact solution $u_{ex}(\mathrm {x})$. We have also been reported the convergence rate of the presented method by

$$\begin{aligned} Ratio =\frac{\ln (\Vert e_{k}\Vert _{\infty })-\ln (\Vert e_{k+1}\Vert _{\infty })}{\ln (2)}. \end{aligned}$$

In addition, the results obtained in the numerical examples are compared with the method presented in [26] based on the use of Haar wavelets. Although Haar wavelets establish a simple algorithm, they have few vanish moments in comparison with dual-Chebyshev wavelets. Therefore, we expect that the scheme proposed in the current paper will be faster than the Haar wavelet method. We have written all routines in “Maple” software with the “Digits” 20 (Digits environment variable controls the number of digits in Maple) and a Laptop with 2.10 GHz of Core 2 CPU and 4 GB of RAM has been used to run these. To solve the final linear system of algebraic equations the “LinearSolve” command from “LinearAlgebra” package has been employed.

Table 1 Some numerical results for Example 5.1

Fig. 1

Distribution absolute error for Example 5.1

Fig. 2

Absolute error of Example 5.1 with $k=7$

Example 5.1

Consider the boundary value problem for Laplace’s equation [18]:

$$\begin{aligned} \Delta u(\mathrm {x})=0,\quad \mathrm {x}\in D=\left\{ (x_1,x_2): x_1^2+\frac{x_2^2}{4}<1\right\} , \end{aligned}$$

with the boundary condition:

$$\begin{aligned} \frac{\partial u(\mathrm {x})}{\partial n_\mathrm {x}}+u(\mathrm {x})=\frac{2x_1}{1+\sqrt{1+3x_1^2}}+x_1+1,~~~~\mathrm {x}\in \partial D=\left\{ (x_1,x_2): x_1^2+\frac{x_2^2}{4}=1\right\} . \end{aligned}$$

This problem is reduced to the following logarithmic boundary integral equation of the second kind:

$$\begin{aligned} -\pi u(\mathrm {x})+ \int _{\partial D} u(\mathrm {y}) \left( \ln \Vert \mathrm {x}-\mathrm {y}\Vert +\frac{\partial \ln \Vert \mathrm {x}-\mathrm {y}\Vert }{\partial n_{\mathrm {y}}} \right) \mathrm {d}s_{\mathrm {y}}=\int _{\partial D} g(\mathrm {y})\ln \Vert \mathrm {x}-\mathrm {y}\Vert \mathrm {d}s_{\mathrm {y}},~~~~\mathrm {x} \in \partial D, \end{aligned}$$

(89)

where

$$\begin{aligned} g(\mathrm {x})=g(x_1,x_2)=\frac{2x_1}{1+\sqrt{1+3x_1^2}}+x_1+1, \end{aligned}$$

with the exact solution $u_{ex}(\mathrm {x})=u_{ex}(x_1,x_2)=1+x_1$.

Table 1 reports $\Vert e\Vert _{\infty }$, $\Vert e\Vert _2$ and the values of the ratio at different numbers of k for $M=3$ and $M=4$. In addition, the results are compared with the Haar wavelet method [26] in this table. It is clear that the obtained results by the proposed scheme are better than the obtained results by the Haar wavelet method. From Table 1, we find that the ratio of error remains approximately constant ($\approx 3$) for $M=3$ and ($\approx 4$) for $M=4$. Therefore, numerical results confirm the theoretical error estimates in Theorem 4.4. The obtained errors of $M=2,3,4$ for different numbers of k are drawn in the logarithmic mode in Fig. 1. The absolute errors for $M=3,4$ and $k=7$ are graphically shown in Fig. 2.

Example 5.2

In this example, we solve the following Dirichlet problem:

$$\begin{aligned} \Delta u(\mathrm {x})=0,~~~~\mathrm {x}\in D=(0,\pi )\times (0,\pi ), \end{aligned}$$

(90)

with the boundary condition

$$\begin{aligned} u(0,x_2)=0,~~~~u(\pi ,x_2)=0, \end{aligned}$$

$$\begin{aligned} u(x_1,0)=0,~~~~u(x_1,\pi )=\sin x \sinh \pi . \end{aligned}$$

Using Green’s formula and conditions, we obtain the logarithmic boundary integral equation:

$$\begin{aligned} -\pi u(\mathrm {x})+ \int _{\partial D} u(\mathrm {y})\ln \Vert \mathrm {x}-\mathrm {y}\Vert + \mathrm {d}s_{\mathrm {y}}=\int _{\partial D} g(\mathrm {y})\ln \Vert \mathrm {x}-\mathrm {y}\Vert \mathrm {d}s_{\mathrm {y}},~~~~\mathrm {x} \in \partial D, \end{aligned}$$

(91)

where

$$\begin{aligned} g(\mathrm {x})=g(x_1,x_2)=\left\{ \begin{array}{rl} \sin x_1 \sinh x_2, &{} 0\le x_1 \le \pi ,~x_2=\pi , \\ 0,~~~~~~~~~~~~~~&{} otherwise,\\ \end{array} \right. \end{aligned}$$

with the exact solution $u_{ex}(\mathrm {x})=u_{ex}(x_1,x_2)=\sin x_1 \sinh x_2$.

Table 2 shows $\Vert e\Vert _{\infty }$, $\Vert e\Vert _2$ and the values of the ratio at different numbers of k for $M=3$ and $M=4$. To compare the presented method, we also solve the integral equation (91) utilizing the Haar wavelet method and the numerical results are given in Table 2.

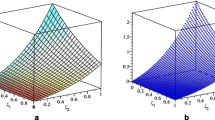
It should be noted that from Theorem 4.4, the results gradually converge to the exact values as the parameter k increases. In addition, the ratio of error, as $k\rightarrow \infty$, remains approximately constant for $M=2$, $M=3$ and $M=3$ nearly 2, 3, and 4, respectively, i.e., the proposed method is of $O(2^{-Mk})$. The obtained errors of $M=3,4$ for different numbers of k are drawn in the logarithmic mode in Fig. 3. The numerical solutions for $k=3,4,5,6$ and $M=2$ are graphically shown in Figure 4.

Fig. 3

Distribution absolute error for Example 5.2

Fig. 4

The numerical solutions of Example 5.2 with $M=2$

Table 2 Some numerical results for Example 5.2

Fig. 5

Approximate solutions with $k=4,5,6,7$,  $M=3$ for Example 5.3

Example 5.3

In this example, we solve the following Laplace’s equation:

$$\begin{aligned} \Delta u(\mathrm {x})=0,~~~~\mathrm {x}\in D=\left\{ (x_1,x_2): x_1^2+x_2^2-2x_2<0\right\} , \end{aligned}$$

with the boundary condition

$$\begin{aligned} \frac{\partial u(\mathrm {x})}{\partial n_\mathrm {x}}+\frac{x_1+x_2}{2(x_1+x_2+2)}u(\mathrm {x})=\frac{2x_1+2x_2-1}{2\sqrt{x_1+x_2+2}},~~~~\mathrm {x}\in \partial D=\left\{ (x_1,x_2): x_1^2+x_2^2-2x_2=0\right\} . \end{aligned}$$

This problem is reduced to the following logarithmic boundary integral equation of the second kind:

$$\begin{aligned} -\pi u(\mathrm {x})+ \int _{\partial D} u(\mathrm {y}) \left( \frac{(x_1+x_2)\ln \Vert \mathrm {x}-\mathrm {y}\Vert }{2(x_1+x_2+2)}+\frac{\partial \ln \Vert \mathrm {x}-\mathrm {y}\Vert }{\partial n_{\mathrm {y}}} \right) \mathrm {d}s_{\mathrm {y}}=\int _{\partial D} g(\mathrm {y})\ln \Vert \mathrm {x}-\mathrm {y}\Vert \mathrm {d}s_{\mathrm {y}},~~~~\mathrm {x} \in \partial D, \end{aligned}$$

(92)

where

$$\begin{aligned} g(\mathrm {x})=g(x_1,x_2)=\frac{2x_1+2x_2-1}{2\sqrt{x_1+x_2+2}}, \end{aligned}$$

with the exact solution $u_{ex}(\mathrm {x})=u_{ex}(x_1,x_2)=\sqrt{x_1+x_2+2}$.

Table 3 shows $\Vert e\Vert _{\infty }$, $\Vert e\Vert _2$ and the values of the ratio at different numbers of k for $M=3,4,5$. Also, the results are compared with the Haar wavelet method [26] in this table. As can be seen, the convergence rate for the proposed scheme is high in comparison with Haar wavelet method. We parameterize $\partial D$ by

$$\begin{aligned} \mathrm {r}(t)=(\cos (2\pi t),\sin (2 \pi t)+1),~~~~0\le t \le 1. \end{aligned}$$

(93)

Therefore, we can reduce the boundary integral equation (92) to the logarithmic singular Fredholm integral equation of the second kind for the known function $u(\mathrm {r}(t))$. In addition, the approximate solution $u(\mathrm {r}(t))$ for $M=3$ and $k=2,3,4,5$ is graphically shown in Fig. 5. It is remarkable that by increasing the parameter k, the results improves. Apparently, the method provides accurate numerical solutions for the logarithmic singular integral equation.

Table 3 Some numerical results for Example 5.3

6 Conclusion

This paper has investigated a numerical method for solving logarithmic singular boundary Fredholm integral equations of the second kind by combining dual-Chebyshev wavelets and discrete Galerkin method. The singular integrals occurring in the method are computed by a composite non-uniform Gauss–Legendre integration rule. The properties of dual-Chebyshev wavelets are used to reduce the problem to the solution of the linear system of algebraic equations. The error analysis is provided for the method. The convergence accuracy of the new method was examined in three boundary Fredholm integral equations which occur as reformulations of a boundary value problem for Laplace’s equation. All numerical results confirm the theoretical error estimates. We can also expand this method to various types of boundary integral equations with little additional works.