1 Introduction

First-order reliability method (FORM) is widely used for structural reliability analyses. In FORM, failure probability is estimated by the reliability index (\( \beta \)), which corresponds to minimum distance to the origin on the limit state function (LSF) in the standard normal space [1, 2]. The reliability index is computed based on most probable point (MPP, \( \varvec{U}^{\varvec{*}} \)) as \( \beta = \left\| {\varvec{U}^{\varvec{*}} } \right\| \), that the MPP is searched using the following optimization model [3, 4]:

$$ \begin{array}{*{20}l} {\text{Find}} \hfill & {\varvec{U}^{*} } \hfill \\ {\mathop {\text{Min}}\limits_{\varvec{U}} } \hfill & {\varvec{U}^{T} \varvec{U}} \hfill \\ {{\text{S}} . {\text{t}} .\,} \hfill & {g(\varvec{U}) = 0,} \hfill \\ \end{array} $$
(1)

where \( g\left( \varvec{U} \right) \) is the LSF in normal standard space, \( g\left( \varvec{U} \right) \le 0 \) stands the failure region, \( \varvec{U} \) is the standard normal variables, which includes random variables with zero means, unit standard deviations, and independent components.

The optimization schemes such as: the gradient projection method, the augmented Lagrangian method, and the sequential quadratic programming method were studied by Liu and Der Kiureghian [2] to solve the above optimization problem (Eq. 1). The conjugate optimization methods were applied to search MPP based on the Wolfe conditions by Keshtegar and Miri [5]. Computing reliability index by the optimization schemes are actually complex FROM formulation [6]. Hasofer and Lind [1] -Rackwitz and Fiessler [7] (HL-RF) method is applied to approximate the reliability index based on a general and simple formulation. However, the HL-RF scheme may provide unstable results such as periodic and chaotic solutions for highly nonlinear problems [8,9,10,11]. To improve the robustness of the FORM formula, several modified algorithm were suggested such as improved HL-RF method using a merit function [2], improved HL-RF based on the Armijo rule [4] and improved the HL-RF method by the Wolfe conditions and differentiable merit function [12]. Wang and Grandhi [13, 14] improved the FORM formula based on the intervening variables and considering the adaptive nonlinear two-point approximation of the limit state function. The instabilities of the FORM formula were controlled based on the stability transformation method (STM) using chaos feedback control [10, 15,16,17]. The robustness of the FORM formula is improved using the finite-step length method (FSL)-based steepest descent search direction [6]. The relaxed approach for FORM [3, 18, 19] was proposed using a dynamic step size with sufficient decent condition [3] and a second-order polynomial fitness to obtain the relaxed factor [18, 19]. Recently, Meng et al. [17] proposed the directional stability transformation method (DSTM) using modified chaos control method to improve the efficiency of the STM. The Hao et al. proposed the enhanced chaos control (ECC) [20] and applied the adaptive chaos control [21] for reliability analysis of complex engineering aircraft stiffened shell. The ECC [20] is formulated using the dynamical adaptive chaos control while the ACC [21, 22] is established using chaos control factor which is adapted using convexity criterion between 1 and 0.1. The STM is slowly converged, when the chaos control factor is selected a small value for both concave and convex reliability problems [23] and the FSL scheme is slowly converged in highly nonlinear LSFs [9, 24]. The modified FORM formulas-based steepest descent search direction were established using a step size less than 1 thus the efficiency of the modified FORM formulas in STM [10, 11], FSL [6], RHL-RF [19], improved HL-RF [2, 4, 12], and DSTM [17] is less than the HL-RF for moderately nonlinear performance functions.

The conjugate methods such as conjugate HL-RF (CHL-RF) using finite-step-length [25], chaotic conjugate search direction of chaos control approach [9, 24], the modified conjugate search direction using limited Fletcher-Reeves (LFR) [8] and hybrid conjugate search direction [23] can be applied to control the instabilities of FORM formula. The efficiency and robustness are important issues to develop the conjugate search direction in the reliability analyses. The steepest descent search direction may be produced unstable results as chaotic and periodic solutions for highly nonlinear problems [23, 24]. However, the conjugate search direction methods were applied to improve the robustness the FORM formula, more successfully [8, 23, 26, 27]. The conjugate method using FROM is particularly efficient for solving optimization problems due to its simplicity and low storage (it does not need the storage of any matrices i.e., the Hessian matrix of limit state functions) with good numerical performances [28,29,30,31]. These methods can be control the instabilities of FORM formula to search the MPP [8, 23]. Nevertheless, the efficiency of these algorithms is a one of major challenges in the reliability problems. The evaluating convergence performance of the existing conjugate FORM to approximate the reliability index is a new interesting filed in structural reliability analysis as well as optimization problems.

In this paper, three conjugate search directions using Fletcher-Reeves (FR) method [32] including improved FR (IFR), modified FR (MFR) and spectral-variant FR (SVFR) are proposed to approximate the reliability index. The FR method is improved with a limited scalar conjugate factor and an adaptive finite-step length in IFR. The IFR, MFR, and SVFR ensured the sufficient descent property to control the instability of FORM. The adaptive finite step length is computed using the new and pervious iterations. Finally, the convergence performances of proposed IFR, MFR and SVFR methods are compared with FR, LFR [8], CHL-RF [25], HL-RF, and FSL [6] through five nonlinear LSFs. Numerical results show that the FORM formulas using conjugate search direction are provided stable results compared to HL-RF and FSL methods. The proposed modified FR methods are effective approaches as well as the FSL, but are more robust and efficient. The adaptive finite-step length can be controlled the instabilities of the FORM using the FSL method.

2 First-order reliability methods

The main effort of the reliability analysis is to estimate failure probability, which is computed by the following integral [33, 34]:

$$ P_{\text{f}} = \int\limits_{{g(\varvec{X}) \le 0}} { \cdots \int {f_{\varvec{X}} (x_{1} , \ldots ,x_{n} ){\text{d}}x_{1} \ldots {\text{d}}x_{n} \approx \varPhi ( - \beta )} ,} $$
(2)

where \( f_{\varvec{X}} (x_{1} , \ldots ,x_{n} ) \) is the joint probability density function for the basic random variables X and \( \varPhi \) is the standard normal cumulative distribution function. A closed form solution of the above integral is not available for general cases in nonlinear limit state functions with many basic random variables. The FORM can be provided good balance between accuracy and efficiency for engineering reliability analysis [11]. In FORM, failure probability is estimated based on the reliability index (\( \beta \)) using three steps as follows:

Step 1 Transfer the random variables in X-space (the original space), into U-space (standard normal space) based on the Rosenblatt transformation i.e., \( u = \varPhi^{ - 1} \{ F_{X} (x)\} \). Using first-order Taylor’s series expansion and Rosenblatt transformation, the random variable can be defined at MPP (x*) in the U-space as follows:

$$ u = \varPhi^{ - 1} \{ F_{X} (x^{*} )\} + \frac{\partial }{\partial x}(\varPhi^{ - 1} \{ F_{X} (x^{*} )\} )\left| {_{x*} } \right.(x - x^{*} ). $$
(3)

It can be conducted that

$$ \frac{\partial }{\partial x}(\varPhi^{ - 1} \{ F_{X} (x^{*} )\} ) = \frac{{f_{X} (x^{*} )}}{{\phi (\Phi^{ - 1} \{ F_{X} (x^{*} )\} )}}. $$
(4)

By Substituting Eq. (4) in Eq. (3) and rearranging, it is obtained

$$ u = \frac{{x - x^{*} + [\varPhi^{ - 1} \{ F_{X} (x^{*} )\} ]\varphi (\varPhi^{ - 1} \{ F_{X} (x^{*} )\} )/f_{X} (x^{*} )}}{{\varphi (\varPhi^{ - 1} \{ F_{X} (x^{*} )\} )/f_{X} (x^{*} )}}. $$
(5)

According to Eq. (5), the equivalent mean (\( \mu_{x}^{e} \)) and the standard deviation (\( \sigma_{x}^{e} \)) at point x for non-normal random variables are given as [4]:

$$ \sigma_{x}^{e} = \frac{1}{{f_{X} (x)}}\varphi \left[ {\varPhi^{ - 1} \left\{ {F_{X} (x)} \right\}} \right], $$
(6)
$$ \mu_{x}^{e} = x - \sigma_{x}^{e} \varPhi^{ - 1} \left[ {F_{X} (x)} \right], $$
(7)

where \( f_{X} (x) \) and \( F_{X} (x) \) are the probability and cumulative distribution function of random variable \( x \), respectively. \( \varPhi^{ - 1} \) is the inverse standard normal cumulative distribution function and \( \varphi \) is the standard normal probability density function.

Step 2 Find the most probable point (MPP) \( \varvec{U}^{*} = (u_{1}^{*} ,u_{2}^{*} , \ldots u_{n}^{*} )^{T} \) using an iterative process as

$$ \varvec{U}_{k + 1} = \left( {\frac{{\varvec{U}_{k}^{T} \nabla g(\varvec{U}_{k} ) - g(\varvec{U}_{k} )}}{{\varvec{\alpha}_{k}^{T} \nabla g(\varvec{U}_{k} )}}} \right)\varvec{\alpha}_{k} , $$
(8)

where \( \nabla^{{}} g(\varvec{U}_{k}^{{}} ) \) is gradient vector of the LSF in the standard normal space at the design point \( \varvec{U}_{k} \) i.e. \( \nabla g(\varvec{U}) = [\partial g/\partial u_{1} ,\partial g/\partial u_{2} , \ldots ,\partial g/\partial u_{n} ]^{T} \) and \( \varvec{\alpha}_{k}^{{}} \) is negative unit normal vector, which is computed in some iterative schemes as

2.1 The HL-RF method [8]

$$ \varvec{\alpha}_{k} = - \frac{{\nabla g(\varvec{U}_{k} )}}{{\left\| {\nabla g(\varvec{U}_{k} )} \right\|}}. $$
(9)

2.2 The finite-step-length (FSL) method [6]

$$ \varvec{\alpha}_{k}^{{}} = \frac{{\varvec{U}_{k + 1}^{\lambda } }}{{\left\| {\varvec{U}_{k + 1}^{\lambda } } \right\|}}, $$
(10)

in which point \( \varvec{U}_{k + 1}^{\lambda } \) is along the direction of the negative gradient vector, which is determined as follows:

$$ \varvec{U}_{k + 1}^{\lambda } = \varvec{U}_{k}^{{}} - \lambda \nabla g\left( {\varvec{U}_{k} } \right), $$
(11)

where \( \lambda > > 0 \) is the finite-step-length. The FSL iterative algorithm is adjusted to the HL-RF method when \( \lambda \to \infty \).

2.3 Conjugate HL-RF method [25]

$$ \varvec{\alpha}_{k} = \frac{{\varvec{U}_{k + 1}^{C\lambda } }}{{\left\| {\varvec{U}_{k + 1}^{C\lambda } } \right\|}}, $$
(12)

where point \( \varvec{U}_{k + 1}^{C\lambda } \) is along the direction of the negative conjugate gradient vector at design point \( \varvec{U}_{k}^{{}} \) which is determined by the following relation

$$ \varvec{U}_{k + 1}^{C\lambda } = \varvec{U}_{k} + \lambda \varvec{d}_{k} , $$
(13)

where \( \varvec{d}_{k}^{{}} \) is conjugate search direction, which is computed as

$$ \varvec{d}_{k}^{{}} = - \nabla g(\varvec{U}_{k}^{{}} ) - \frac{{\left| {\left| {\nabla g(\varvec{U}_{k}^{{}} )} \right|} \right|^{2} }}{{\,\,\left\| {\nabla g(\varvec{U}_{k - 1}^{{}} )} \right\|^{2} }}\varvec{d}_{k - 1} . $$
(14)

The CHL-RF approach is more robust than the HL-RF and is more efficient than the FSL scheme [8, 24] but, it may be converged computationally inefficient for highly nonlinear LSFs [9, 23].

Step 3 Calculate the reliability index based on the MPP (\( \varvec{U}^{*} \)) i.e. \( \beta = \left\| {\varvec{U}^{*} } \right\| \).

In highly nonlinear performance functions, the unit normal vector-based steepest descent search direction at the point \( \varvec{U}_{k + 1}^{{}} \) (\( \varvec{\alpha}_{k}^{{}} \)) may be paralleled to the previous unit normal vector e.g., \( \varvec{\alpha}_{k - 2} \). This means that \( \varvec{\alpha}_{k}^{{}} \) is equal to \( \varvec{\alpha}_{k - 2} \). Therefore, \( \varvec{U}_{k + 1}^{{}} = \varvec{U}_{k - 1}^{{}} \), which indicates that \( \varvec{U}_{k - 1}^{{}} \) and \( \varvec{U}_{k + 1}^{{}} \) are located in fixed position. Consequently, the FORM formula using steepest descent search direction may be captured the periodic oscillating points. To reduce the parallel risk of the unit normal vectors in the steepest descent search direction methods, the conjugate search direction can be used for reliability analysis using FROM. This idea is generally applied to control instabilities of FORM formula for searching the MPP.

3 Enriched conjugate FR methods

The conjugate gradient method can avoid the computation of the Hessian matrix of limit state function in reliability analyses [29]. The search direction vector is determined in conjugate gradient optimization methods as follows [28, 31]:

$$ \varvec{d}_{k} = \left\{ {\begin{array}{ll} { - \nabla g(\varvec{U}_{k} )} & {k = 0} \\ { - \nabla g(\varvec{U}_{k} ) + \theta_{k} \varvec{d}_{k - 1} } & {k \ge 1} \\ \end{array} ,} \right. $$
(15)

where \( \theta_{k} \) is a scalar. One of the well-known conjugate gradient method is the Fletcher-Reeves approach [32], in which \( \theta_{k} \) is defined as

$$ \theta_{k}^{\text{FR}} = \frac{{\left| {\left| {\nabla g(\varvec{U}_{k} )} \right|} \right|^{2} }}{{\,\,\left\| {\nabla g(\varvec{U}_{k - 1} )} \right\|^{2} }}. $$
(16)

The FR method is applied to improve the HL-RF method based on the conjugate HL-RF (CHL-RF) for evaluating the failure probabilities of corroded pipeline [25]. Recently, Keshtegar [8, 9, 23, 24] showed that the CHL-RF using FR approach is converged to stable results with more computational efforts compared to modified versions of conjugate FORM. The simple approach is applied using limited FR (LFR) by Keshtegar [8] that the LFR can be provided stable results using the modified search direction which is satisfied the sufficient descent condition. The improved versions of FR approaches can be applied for reliability analysis using the conjugate FORM formula based on the sufficient descent condition. The conjugate search direction of MFR is generated as follows:

$$ \varvec{d}_{k}^{\text{MFR}} = - \eta_{k} \nabla g(\varvec{U}_{k} ) + \theta_{k}^{FR} \varvec{d}_{k - 1} . $$
(17)

The variant spectral-type FR (VSFR) method is defined as follows:

$$ \varvec{d}_{k}^{\text{VSFR}} = - \eta_{k} \nabla g(\varvec{U}_{k} ) + \theta_{k}^{\text{VFR}} \varvec{d}_{k - 1} . $$
(18)

A simple conjugate method is applied based on the limited conjugate search direction (Eq. 15), which is proposed by Keshtegar [8] in IFR as below:

$$ \theta_{k}^{\text{IFR}} = \hbox{min} \{ \delta ,\,\theta_{k}^{\text{FR}} \} , $$
(19)

where

$$ \eta_{k} = \frac{{\varvec{d}_{k - 1}^{T} [\nabla g(\varvec{U}_{k} ) - \nabla g(\varvec{U}_{k - 1} )]}}{{\left\| {\nabla g(\varvec{U}_{k - 1} )} \right\|^{2} }}, $$
(20)
$$ \theta_{k}^{\text{VFR}} = \frac{{\left| {\left| {\nabla g(\varvec{U}_{k} )} \right|} \right|\,.\,\left| {\nabla^{T} g(\varvec{U}_{k - 1} )\nabla g(\varvec{U}_{k} )} \right|}}{{\,\,\left\| {\nabla g(\varvec{U}_{k - 1} )} \right\|^{3} }}, $$
(21)

and \( \delta \) is limited scale factor i.e., \( 0.5 < \delta \le 1.0 \). The limited scalar factor of FR method in Eq. (19) \( \theta_{k}^{\text{IFR}} \) satisfies as

$$ \theta_{k}^{\text{IFR}} \le \theta_{k}^{\text{FR}} \le \delta . $$
(22)

Inspired by the idea of conjugate gradient search direction, three iterative formulas are proposed to search the MPP based on the Eqs. (17)–(19). The reliability index, LSF, and iterative points and the conjugate search directions in the two-dimensional standard normal space are shown in Fig. 1 as (a) FR, (b)IFR, (c) MFR and (d) VSFR methods. It is obvious that the conjugate vector (\( \varvec{d}_{k}^{{}} \)) at point (\( \varvec{U}_{k}^{{}} \)) is not along direction \( - \nabla g(\varvec{U}_{k}^{{}} )\,\, \). Therefore, \( \varvec{\alpha}_{k}^{{}} \) is not parallel to the normalized conjugate search direction vector (\( \varvec{\alpha}_{k}^{c} \)) at point (\( \varvec{U}_{k + 1}^{C\lambda } \)). This implies that the conjugate search direction vector can be provided stable results compared to the FORM formulas-based steepest descent search direction for highly nonlinear problems. The conjugate search direction for modified FR methods is obtained different. Two parameters \( \theta_{k} \) and \( \eta_{k} \) are affected on the participation of the new gradient (\( \nabla g(\varvec{U}_{k}^{{}} )\,\, \)) and previous conjugate (\( \varvec{d}_{k - 1}^{{}} \)) vectors to compute the search direction in various modified FR approaches.

Fig. 1
figure 1

An iterative procedure of the different conjugate algorithms a FR, b IFR, c MFR and d VSFR

Full size image

The iterative formula of the conjugate FORM is rewritten using Eq. (8) as follows:

$$ \varvec{U}_{k + 1} = \left( {\frac{{\varvec{U}_{k}^{T} \nabla g(\varvec{U}_{k} ) - g(\varvec{U}_{k} )}}{{\varvec{\alpha}_{k}^{cT} \nabla g(\varvec{U}_{k} )}}} \right)\varvec{\alpha}_{k}^{c} , $$
(23)

in which, \( \varvec{\alpha}_{k}^{c} \) is normalized conjugate search direction vector, which is given as

$$ \varvec{\alpha}_{k}^{c} = \frac{{\varvec{U}_{k + 1}^{c\lambda } }}{{\left\| {\varvec{U}_{k + 1}^{c\lambda } } \right\|}}, $$
(24)

where

$$ \varvec{U}_{k + 1}^{c\lambda } = \varvec{U}_{k} + \lambda_{k} \varvec{d}_{k} . $$
(25)

Step length (\( \lambda \)) and the conjugate search direction (d) are two important factors in the FORM-based conjugate search direction. If \( \lambda \) is well-defined then the modified FR algorithms using scalar factors in Eqs. (17), (18), and (19) can be converged, efficiently and robustly. An adaptive finite-step length \( \lambda \) is suggested for conjugate FORM. The finite-step length is adapted based on the sufficient descent condition and Armijo-type rule as follows:

$$ \lambda_{\hbox{max} } \le M\frac{{\left\| {\varvec{d}_{k} } \right\|^{2} }}{{\left\| {\nabla g(\varvec{U}_{k} )} \right\|^{2} }}. $$
(26)

It is supposed that the finite-step length implies the sufficient descent condition i.e., \( \nabla^{T} g(\varvec{U}_{k + 1}^{{}} )\,\varvec{d}_{k + 1}^{{}} < - c_{1} \left\| {\nabla g(\varvec{U}_{k + 1}^{{}} )} \right\|^{2} \), in which \( 0 < c_{1} < 1 \). Therefore, \( \lambda \le c_{1} \lambda_{\hbox{max} } \) and \( M > > 1 \). If \( \left\| {\varvec{U}_{k + 1}^{{}} - \varvec{U}_{k}^{{}} } \right\| > \left\| {\varvec{U}_{k}^{{}} - \varvec{U}_{k - 1}^{{}} } \right\| \) (\( \left\| {\nabla g(\varvec{U}_{k + 1}^{{}} )} \right\| > \left\| {\nabla g(\varvec{U}_{k}^{{}} )} \right\| \)) then \( \lambda_{k} = c_{k} \lambda_{k - 1} \) and \( c_{k} \) is dynamical adjusting coefficient. This step length holds the sufficient descent condition as follows:

$$ \lambda_{k} = \left\{ {\begin{array}{*{20}c} {\lambda_{k - 1} } & {\left\| {\varvec{U}_{k - 1} - \varvec{U}_{k} } \right\| < \left\| {\varvec{U}_{k} - \varvec{U}_{k - 1} } \right\|} \\ {c_{k} \lambda_{k - 1} } & {\left\| {\varvec{U}_{k - 1} - \varvec{U}_{k} } \right\| \ge \left\| {\varvec{U}_{k} - \varvec{U}_{k - 1} } \right\|} \\ \end{array} .} \right. $$
(27)

The sufficient descent condition is satisfied based on dynamic adjusting coefficient and maximum step length. The maximum step length is given based on the Eq. (28) as below:

$$ \lambda_{0} = \frac{100}{{\left\| {\nabla g\left( {\left. \varvec{U} \right|_{{\varvec{U} =\varvec{\mu}}} } \right)} \right\|}}, $$
(28)

in which \( \nabla g\left( {\left. \varvec{U} \right|_{{\varvec{U} =\varvec{\mu}}} } \right) \) is gradient vector at the mean point in normal standard space, and \( \lambda_{0} \) is the initial step length. The dynamic adjusting coefficient for finite-step length is proposed as below:

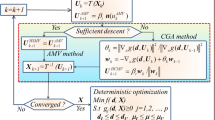
$$ c_{k} = \hbox{min} \left\{ {0.95,\,\frac{3}{10}\frac{{\left\| {\nabla g(\varvec{U}_{k} )} \right\|^{2} }}{{\left| {\nabla^{T} g(\varvec{U}_{k} )\,\varvec{d}_{k} } \right|}}} \right\}. $$
(29)

The adaptive finite-step length is computed using initial step length (Eq. 28) and adjusting coefficient (Eq. 29) without merit function or Wolfe condition. The maximum finite-step length and adjusting factor in adaptive finite-step length are two major differences between the proposed modified FR methods and LFR method. The initial step size in the LFR method is selected a constant value in the range from 5 to 100, while the initial step size is dynamically adapted using Armijo rule based on Eq. (28) in the modified FR methods. However, the scalar factor in the IFR is limited between 0 and 1 that this scalar factor holds as well as the LFR the sufficient descent condition, theoretically. Consequently, the IFR can be provided sable results for reliability analysis. The steps of the IFR method for reliability analysis are summarized as follows:

Step 0

Given probability parameters of random variables, constants stopping criterion \( \varepsilon = 10^{ - 6} \) and \( \delta \in [0.5,\,1.0] \) for IFR, let \( k = 0 \), and choose an initial point \( \varvec{X}_{0}^{{}} =\varvec{\mu} \) \( \varvec{d}_{\varvec{0}}^{{}} = \varvec{0} \)

Step 1

Normalize random variable based on Eqs. (5) to Eq. (7)

Compute the performance function and gradient vector at point \( \varvec{U}_{k}^{{}} \)

If \( k = 0 \) then compute the initial step length using Eq. (28)

Step 2

Compute \( \theta_{k}^{\text{FR}} \) using Eq. (16), \( \eta_{k} \) by Eq. (20), \( \theta_{k}^{\text{VFR}} \) using Eq. (21).

Determine \( \varvec{d}_{k}^{{}} \) using Eqs. (15) and (19) for IFR, by Eq. (17) for MFR and Eq. (18) for VSFR

Determine new point in terms of Eqs. (23)–(25)

If \( k \ge 3 \) then adjust the new step length based on Eqs. (27) and (29)

Let the next iterate be \( \varvec{X}_{k + 1}^{{}} =\varvec{\mu}_{X}^{e} +\varvec{\sigma}_{X}^{e} \varvec{U}_{k + 1}^{{}} \) and \( k = k + 1 \)

Step 3

If \( \left\| {\varvec{U}_{k + 1}^{{}} - \varvec{U}_{k}^{{}} } \right\| < \varepsilon \) then stop and compute the reliability index \(\left(\beta = \left\| {\varvec{U}_{k + 1}^{{}} } \right\| \right)\), else Go to Step 1

The formwork of the modified versions of FR is plotted in Fig. 2. As seen, this approach (IFR) is as simple as the LFR but the adaptive finite-step length may improve the efficiency and robustness of FORM compared to the FSL and HL-RF methods.

Fig. 2
figure 2

Framework of the conjugate first-order reliability method

Full size image

4 Results of numerical examples

Five numerical experiments with the nonlinear mathematical and the complex structural/mechanical performance functions are used to demonstrate the robustness and efficiency of the proposed VSFR, MFR, and IFR methods compared with FR method for each example. The same stopping criterion (\( \varepsilon = 10^{ - 6} \)) is used and, the initial step size and adaptive adjusting coefficient are computed based on Eqs. (27) and (29) in all conjugate reliability methods. The limited scalar factor is selected as δ = 0.75 in IFR method. The number of gradient vector evaluations \( \nabla g(\varvec{U}) \) (Iter) and the reliability index (\( \beta \)) are used to compare the robustness and efficiency of these algorithms.

Example 1

A highly non-linear limit state function is given as [14]

$$ g(\varvec{X})\; = \;x_{1}^{3} \; + \;x_{1}^{2} x_{2} \; + \;x_{2}^{3} \; - \;18, $$
(30)

where \( x_{1}^{{}} \) and \( x_{2}^{{}} \) are normal random variables whose means and standard deviations are \( \mu_{1}^{{}} = 10 \), \( \mu_{2}^{{}} = 9.9 \) and \( \sigma_{1}^{{}} = \sigma_{2}^{{}} = 5 \), respectively. The reliability index is extracted from Wang and Grandhi [14] and Keshtegar and Miri [5] as 2.2983 and 2.29825, respectively. Table 1 gives the convergence results of the FR, MFR, VSFR, and IFR algorithms. The results show that the IFR converges with the same number of iterations as VSFR and MFR. IFR, VSFR, and MFR are much more efficient than the FR method with convergence rate four-times faster than FR.

Table 1 Convergent results of the conjugate algorithms for Example 1
Full size table

Example 2

A vehicle side-impact performance function, which is given as follows [35]:

$$ g(\varvec{X}) = 0.489x_{3}^{{}} x_{7}^{{}} + 0.843x_{5}^{{}} x_{6}^{{}} - 0.0432x_{9}^{{}} x_{10}^{{}} + 0.0556x_{9}^{{}} x_{11}^{{}} + 0.000786x_{11}^{2} - 0.75, $$
(31)

where \( i = 1\sim 7\,\,\,x_{i}^{{}} \sim N(1,\,\,0.005),\,\,i = 8\sim 9\,\,\,x_{i}^{{}} \sim N(0.3,\,\,0.006),\,i = 9\sim 10\,\,\,x_{i}^{{}} \sim N(0,\,\,10.0)\, \). Table 2 gives the reliability index, iterations, and the MPP (\( \varvec{X}^{*} \)) obtained from the conjugate methods i.e., FR, MFR, VSFR, and IFR. It can be conducted the IFR and VSFR iterative algorithms are more efficient than MFR and FR methods. The IFR and VSFR are converged to stable results about twice faster than the FR algorithm. The MFR is also converged faster than the FR method. Therefore, the proposed methods are more efficient than the FR algorithm for this example.

Table 2 Convergence results of the conjugate algorithms for Example 2
Full size table

Example 3

A automobile front axle to carry the weight of the automobile that the front axle beam is schematically shown Fig. 3, is studied by the following LSF based on bending moment and torque loads [36].

Fig. 3
figure 3

The schematic view of automobile front axle [36]

Full size image
$$ g = \sigma_{\text{s}}^{{}} - \sqrt {\sigma_{\text{m}}^{2} + 3\tau^{2} } , $$
(32)

where \( \sigma_{\text{s}}^{{}} \) is the limit stress of yielding which is considered as 460 Mpa. \( \sigma_{\text{m}}^{{}} \) and \( \tau \) are, respectively, the maximum normal stress and shear stress subjected to the bending moment and torque loads, which are expressed as follows:

$$ \begin{aligned} \sigma_{\text{m}}^{{}} = \frac{M}{{W_{x} }} \hfill \\ \tau = \frac{T}{{W_{\rho } }}, \hfill \\ \end{aligned} $$
(33)

in which \( M \) and \( T \) are the bending moment and torque, \( W_{x} \) and \( W_{\rho } \) are section factor and polar section factor, which are given as

$$ \begin{aligned} W_{x} & = \frac{{a(h - 2t)^{3} }}{6h} + \frac{b}{6h}\left[ {h^{3} - (h - 2t)^{3} } \right] \\ W_{\rho } & = 0.8bt^{2} + 0.4\frac{{a^{3} (h - 2t)}}{t}, \\ \end{aligned} $$
(34)

where \( a,\,b,\,t,\, \) and \( h \) are the geometry parameters of I-beam (see in Fig. 3) distribution parameters of six normal variables are listed in Table 3 for automobile front axle.

Table 3 Distribution parameters of random variables for automobile front axle
Full size table

Table 4 summarizes the convergence results of MPP and reliability index obtained from FR, MFR, VSFR, and IFR schemes. As seen, the proposed algorithms are as robust as the FR but the IFR is more efficient than the FR method. The IFR scheme is converged to stable results of \( \beta \) = 2.064536 which is very close to the safety index obtained by Zhang et al. [37].

Table 4 The convergent results of conjugate methods for Example 3
Full size table

Example 4

A conical structure as indicated in Fig. 4 is used by the following the buckling failure mode for the LSF [9]:

Fig. 4
figure 4

The schematic view of conical structure [9]

Full size image
$$ g = 1 - \frac{{\sqrt {3(1 - v^{2} )} }}{{\pi \,E\,t^{2} \cos^{2} \alpha }} \times \left( {\frac{P}{0.66} + \frac{M}{{0.41\,r_{1} }}} \right), $$
(35)

in which \( P \) and \( M \) are the compressive axial load and bending moment, and \( v = 0.3 \) [9].

Table 5 gives the random variables of conical example.

Table 5 The random variables for conical structure
Full size table

After 17 iterations, the proposed method (IFR) obtained the reliability index as 4.627765 and the MPP as X* = [65378.078, 0.002096, 0.52747, 0.88874, 108411.745, 72707.579]. Based on the reliability analysis undertaken using the conjugate search direction algorithms using FR, MFR and SVFR, the safety index are obtained as 4.723984 (FR method after 101 iterations), 4.635483 (MFR method after 30 iterations), and 4.635342 (VSFR method after 30 iterations). The converged results of this example show that the IFR is more efficient than the other proposed conjugate gradient methods but the MFR and VSFR methods are more efficient than IF, more remarkably.

Example 5

A two degree of freedom primary-secondary dynamic system as shown in Fig. 5 is employed by the LSF as follows [23, 24]:

Fig. 5
figure 5

Two-degree of freedom dynamic system

Full size image
$$ g = F_{s} - K_{s} \; \times \;P(E[x_{s}^{2} ])^{1/2} , $$
(36)

where \( F_{s} \) denotes force capacity, P is the peak factor as P = 3, and \( E[x_{s}^{2} ] \) is mean-square relative displacement response of the secondary spring which is given by

$$ E[x_{s}^{2} ] = \frac{{\pi S_{0} }}{{4\xi_{s} \omega_{s} }}\left[ {\frac{{\xi_{a} \xi_{s} }}{{\xi_{p} \xi_{s} (4\xi_{a}^{2} + \theta^{2} ) + \gamma \xi_{a}^{2} }} \times \frac{{(\xi_{p} \omega_{p}^{3} + \xi_{s} \omega_{s}^{3} )\omega_{p} }}{{4\xi_{a} \omega_{a}^{4} }}} \right], $$
(37)

in which \( \gamma = \frac{{M_{s} }}{{M_{p} }} \) is mass ratio, \( \omega_{a} = \frac{{\omega_{p} + \omega_{s} }}{2} \) and \( \xi_{a} = \frac{{\xi_{p} + \xi_{s} }}{2} \) are average frequency and damping ratio of the two systems, respectively. \( \theta = \frac{{\omega_{p} - \omega_{s} }}{{\omega_{a} }} \) is a tuning parameter and \( S_{0} \) is intensity of the white noise and subscripts p and s are the primary and secondary oscillators. Table 6 gives the mean and standard deviation of eight Lognormal random variables.

Table 6 Random variables of Example 5
Full size table

Based on reliability analysis using FORM extracted from Keshtegar [24], the converged results are as reliability index of β = 2.016348 and the MPP of X* = [1.00191, 0.01009, 1.10209, 0.01115, 0.02799, 0.01211, 103.7171, 13.7360]. The reliability index and MPP are obtained as \( \beta \) = 2.014604 and X* = [1.00184, 0.01009, 1.10186, 0.01115, 0.0280, 0.01212, 103.7115, 13.7343] after 23 iterations using the IFR method. As seen, these stable results from IFR are very close agreement with the results from Refs [23, 24, 27].

Figure 6 shows the iteration histories of the FR, MFR, VSFR and IFR algorithms. It can be seen that the FR, MFR, and IFR algorithms accurately converged to the same reliability index i.e., \( \beta \) = 2.014604 and the MFR scheme more efficient than the other algorithms. The VSFR method is converged to reliability index (i.e., \( \beta \) = 2.869749) that this reliability index is more different with the reliability index obtained using the MFR and IFR methods. Based on schematic iterative view for different reliability methods in Fig. 1, the conjugate search direction in Eq. (18) for SVFR is developed using the scalar factor \( \theta_{k}^{\text{VFR}} \) while the FR, IFR and MFR is formulated based on the FR conjugate scalar factor in Eq. (16). Consequently, the conjugate search direction using scalar factor \( \theta_{k}^{\text{VFR}} \) provides an inaccurate FORM reliability index, while scalar factor \( \theta_{k}^{\text{FR}} \) is a suitable conjugate scalar factor for evaluating the conjugate search direction for this nonlinear problem. It illustrates that the MFR method is the most efficient than the other methods and it is converged about twice faster than the FR, more robustly.

Fig. 6
figure 6

Iterative history comparison of reliability index for Example 5

Full size image

5 Discussions

This section involves three applications including the effects of search direction for MPP search in the first application, in second application; the adaptive finite-step length is investigated to improve the robustness of FORM, and finally, proposed enriched FR methods are compared with several existing reliability methods. For all the studies, the limited scalar factor (\( \delta \)) is selected as 0.75 and \( \varepsilon = 10^{ - 6} \).

5.1 Effects of search direction

Effects of the search directions based on the HL-RF [2], FSL [6], CHL-RF [25], and proposed IFR methods are evaluated based on a constant finite-step length equal to 20 for all Examples 1–5. The FORM formula using IFR is similar to LFR when a constant finite-step length is selected. Consequently, the IFR iterative formula is equal to the LFR for this evaluation with λ = 20. The convergence results are tabulated in Table 7 to illustrate the effects of search direction vector in different FORM algorithms. The HL-RF method is failed in problems 1, 2, 4, and 5 and the FSL approach in not converged to stable solutions in Examples 1, 2, and 5. The CHL-RF and IFR (LFR) is robustly converged in compression with the FORM-based steepest descent search direction i.e., HL-RF and FSL methods for all of examples.

Table 7 Result comparison of HL-RF, FSL, CHL-RF, and IFR (LFR)
Full size table

The parallel risk of the unit vector at the new point with previous points is reduced using conjugate search direction in CHL-RF and IFR (LFR) methods. The IFR (LFR) method is as robust as the CHL-RF method but is more efficient for all examples.

Figure 7 shows the convergence histories of the HL-RF, FSL, CHL-RF, and IFR (LFR) methods for Example 2. The CHL-RF and IFR (LFR) schemes are converged to stable results but, the IFR is more efficient. As it can be seen, the HL-RF and FSL methods are converged to the periodic-4 and periodic-2 solutions as (3.1757, 2.0351, 1.9180, 1.2957) and (3.2556, 3.2681), respectively. Moreover, the IFR is more robust than the HL-RF and FSL algorithms.

Fig. 7
figure 7

Iterative history of reliability index using FORM algorithms with λ = 20 for Example 2

Full size image

Figure 8 illustrates the iterative histories of reliability index for Example 5 based on the HL-RF, FSL, CHL-RF, and IFR (LFR) methods. It can be seen that the HL-RF and FSL methods did not converge and exhibited an unstable solutions as periodic-2 for the reliability index as (4.2170, 4.9807) and (3.7343, 4.2447), respectively. However, the CHL-RF and IFR (LFR) method with step length \( \lambda = 20 \) are robustly converged. The direction vector is more important factor to obtain stable results. As results of that, the HL-RF and FSL methods are yielded unstable solutions for highly nonlinear problems (Examples 1, 2, and 5) while the CHL-RF and IFR (LFR) are produced the stable results, more accurately.

Fig. 8
figure 8

Iterative history of reliability index using FORM algorithms with λ = 20 for Example 5

Full size image

5.2 Effect of step length

The effects of step length are investigated using adaptive finite-step length (Eq. 27). Table 8 gives the convergence results of the FSL, CHL-RF, and IFR methods. It is shown that the FSL method is converged to stable reliability index with the proposed finite-step length.

Table 8 Comparing the self-adaptive step length (25) on convergence results of FSL, CHL-RF and IFR
Full size table

The self-adaptive step length improved the efficiency of CHL-RF in Examples 2, 4 and IFR methods in Examples 1, 2, 4, and 5 compared to the IFR (LFR) with constant finite-step length. As seen, the step length can be enhanced the robustness of the FSL method and improved the efficiency of CHL-RF. The results in Tables 7 and 8 show that IFR based on self-adaptive step length is converged about twice faster than the IFR (LFR) with constant step length (\( \lambda = 20 \)) in Examples 4 and 5. It is shown form Table 8 that the FSL algorithm is more efficient than CHL-RF method in Examples 1, 3, and 4 but, the CHL-RF is more efficient than FSL in Example 2 and 5.

It is clear from Tables 7 and 8 that the CHL-RF and IFR (LFR) algorithms are more robust than the HL-RF scheme. The adaptive finite-step length can be increased the convergence rate of the FORM formula, adaptively. Thus, the search direction vector and step size are two important factors to improve instabilities and efficiency of FORM formula.

5.3 Comparative studies

Three proposed conjugate methods for structural reliability analyses including IFR, MFR and VSFR which are used the adaptive finite-step length in Eq. (27) are compared with the existing conjugate search direction methods such as CHL-RF [25] with parameters as \( \lambda_{0} = 50 \) and c = 0.95, LFR [8] with parameters as \( \lambda_{0} = 50 \) and δ = 0.75 and also the steepest descent search direction-based FSL [6] method with parameters as \( \lambda_{0} = 50 \) and c = 0.95. The number of evaluating the gradient vector (Iter), CPU-run times (T) and the reliability index (β) are used to illustrate the convergence performances of these reliability methods. The convergence results of different reliability methods using and Monte Carol simulation (MCS) are tabulated in Table 9. The results of Table 9 showed that modified FORM formulas-based conjugate search direction are robustly converged as well as the FSL method but the conjugate search directions-based LFR, CHL-RF, MFR, IFR, and VSFR are more efficient than the FSL method for highly concave Examples 1, 2, and 5. The LFR is more efficient than the MFR and VSFR method for Examples 4, while the MFR is more efficient than the LFR for Examples 1 and 5. The IFR is remarkably more efficient than the LFR and it converges twice faster than the LFR for highly nonlinear examples 1 and 5. This means that the adaptive finite-step length can be improved the efficiency of the FORM formula compared to the CHL-RF and LFR method with a constant initial step size \( \lambda_{0} = 50 \). The conjugate search directions and the adaptive finite-step size can be provided stable results for nonlinear performance function, more efficiently.

Table 9 Convergence results of different reliability methods including FSL, CHL-RF, LRF, MFR, SVFR and IFR
Full size table

6 Conclusion

Three modified versions of conjugate search direction using Fletcher-Reeves (FR) search direction scheme called as improved FR (IFR), modified FR (MFR), and spectral-variant FR (SVFR) are proposed for first-order reliability method (FORM). A adaptive finite-step length is established to control the instabilities of FORM formula. The IFR, MFR, and VSFR schemes are compared with the conjugate algorithms including FR, CHL-RF, and LFR and the FORM-based steepest search direction methods including the HL-RF and FSL through five nonlinear structural/mechanical reliability problems.

The IFR, MFR, and SVFR algorithms are successfully applied in reliability analysis and are more robust than the FORM-based HL-RF and FSL without adjustment for step size. The IFR is strongly more efficient among the existing conjugate gradient methods. The proposed search direction in IFR can be controlled the instabilities of the iterative FORM formula and can be improved its efficiency.

The adaptive finite-step length improves the efficiency of iterative FORM formula using CHL-RF and enhances the robustness of FSL scheme. The FSL method with adaptive finite- step length is more robust than the HL-RF and FSL with constant step length for highly nonlinear limit state functions.