An octree-based dual contouring method for triangular and tetrahedral mesh generation with guaranteed angle range

Abstract

This paper presents a novel octree-based dual contouring (DC) algorithm for adaptive triangular or tetrahedral mesh generation with guaranteed angle range. First, an adaptive octree is constructed based on the input geometry. Then the octree grid points are adjusted such that we can maintain a minimum distance from the grid points to the input boundary. Finally, an improved DC method is applied to generate triangular and tetrahedral meshes. It is proved that we can guarantee the obtained triangle mesh has an angle range of (19.47°, 141.06°) for any closed smooth curve, and the tetrahedral mesh has a dihedral angle range of (12.04°, 129.25°) for any closed smooth surface. In practice, since the straight line/planar cutting plane assumption inside each octree leaf is not always satisfied, there is a small perturbation for the lower and upper bounds of the proved angle range.

1 Introduction

Due to its simplicity and convenience, triangular and tetrahedral meshing is the most common form of 2D/3D unstructured mesh generation in the application of finite element analysis and computer graphics. Octree-based [17, 22], Delaunay-based [2, 3, 16, 18, 19] and advancing front [9, 10, 11, 12, 15] methods are the three most popular techniques currently in use. Among the octree-based methods, the marching cubes (MC) technique is widely used, but it often results in cracks between adjacent octree cells at different levels, which need to be resolved with additional work. In contrast, the dual contouring (DC) method can produce crack-free contours on any quadtree or octree grid. It is also capable of reproducing sharp geometry features when Hermite data are available. However, the traditional DC method cannot guarantee mesh quality. For the octree method, only a few algorithms can guarantee the angle range. The isosurface stuffing method [5] generates tetrahedral meshes with all the dihedral angles between 10.78° and 164.74°, but it requires a uniform mesh on the boundary surface. For non-uniform tetrahedra on the boundary surface, the angle bounds become 1.66° and 174.72°. Later, an improved algorithm [20] was developed to guarantee a minimal dihedral angle 5.71° for an adaptive tetrahedral mesh.

In this paper, we introduce a novel DC algorithm for adaptive triangular or tetrahedral mesh generation with a better angle range guaranteed. This algorithm is based on quadtree or octree structure, and can generate interior and exterior meshes with conformal boundary. It is proved that following the three steps of our algorithm, we can guarantee the obtained triangle mesh has an angle range of (19.47°, 141.06°) for any given closed smooth curve, and the tetrahedral mesh has a dihedral angle range of (12.04°, 129.25°) for any given closed smooth surface. In practice, since the straight line/planar cutting plane assumption is not always satisfied, there is a small perturbation for the lower and upper bounds of the proved angle range. This algorithm provides a fundamental study on guaranteed-quality mesh generation, which is suitable for computer graphics or visualization. For real finite element applications, adjustments need to be made to meet various requirements from different physical problems.

The reminder of this paper is organized as follows: Sect. 2 reviews related previous work. Section 3 explains the detailed algorithm for guaranteed-quality triangular meshing using DC. Section 4 extends the 2D DC method to 3D tetrahedral meshing. Section 5 shows some application results. Finally, Sect. 6 presents our conclusion and future work.

2 Previous work

Most triangular and tetrahedral meshing techniques currently in use can be classified into three main categories: octree, Delaunay and advancing front. The octree technique [17, 22] subdivides the bounding cube recursively until the stopping criterion is reached. Tetrahedra are constructed from both the irregular cells on the boundary and the regular internal cells. The Delaunay triangulation technique [2, 3, 16, 18, 19] is based on a criterion called “empty circle” or “empty sphere”, which requires that no node is contained within the circumcircle of any triangle or the circumsphere of any tetrahedra within the mesh. Advancing front is another popular triangular and tetrahedral mesh generation algorithm [11, 12]. In this method, tetrahedra are built progressively inward from the surface. An active front is maintained where new tetrahedra are formed. As the algorithm progresses, the front will advance to fill the remainder of the area. Various advancing front algorithms have been developed for tetrahedral meshing [9, 10, 11, 15].

For the octree method, there are two popular techniques based on isocontouring: MC and DC. The classic MC algorithm [14] classifies cubic cells into 14 unique cases after considering symmetry and complementary. For each case, an approximation of the isosurface is created. MC is straightforward and easy to implement, but it has several drawbacks. First, it requires a uniform octree structure. Second, vertices are located on the cell edges, which can easily produce many elements with small angles. Finally, because of the uncategorized ambiguities in MC, it is possible to have discrepancy in connecting the shared face of two adjacent cells. Extended MC has been developed to solve the above problems [21, 13, 26]. The DC method combines SurfaceNets [3] and the extended MC algorithm, and has the capability to handle adaptive octree. It was first introduced for the isocontouring from Hermite data [4] and then extended to tetrahedral and hexahedral mesh generation [24, 23]. DC can also work on domains with heterogeneous materials [25].

However, only a few octree-based algorithms can guarantee the angle range. By using the body centered cubic tetrahedral lattice and adjusting the cutting points, an isosurface stuffing method [5] guarantees that all the dihedral angles are between 10.78° and 164.74° for a uniform boundary, and between 1.66° and 174.72° for an adaptive boundary. Later, another method was developed in [20] to guarantee a minimal dihedral angle 5.71° for an adaptive tetrahedral mesh. In this paper, we will introduce an improved DC method, which can guarantee a better dihedral angle range.

3 Triangular meshing with guaranteed quality

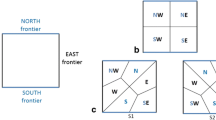
For a given planar and closed smooth curve ${{\mathcal{C}}}$, we introduce an algorithm to generate an adaptive triangular mesh for the regions enclosed by ${{\mathcal{C}}}$ with guaranteed angle bounds. Three steps are designed as shown in Fig. 1, including (1) adaptive quadtree construction, (2) grid points adjusting, and (3) improved DC method.

Fig. 1

Flow chart of triangular meshing with guaranteed quality. a Curve decomposition, b adaptive quadtree construction, c grid points adjusting, d improved dual contouring method and e the final result. In (c), pink grid points are moved toward the curve, and yellow grid points are moved away from the curve

3.1 Adaptive quadtree construction

Similar to [6, 7], we first decompose the input curve ${{\mathcal{C}}}$ into a set of non-uniform points ${{\mathcal{X}}}$ based on its local curvature, which satisfies two requirements: the angle formed by any three neighboring points is $\in [180^{\circ} - \varepsilon, 180^{\circ} + \varepsilon]$, where $\varepsilon \leq 10^{\circ}$; and the approximation error of each line segment is less than a given threshold δ (here δ = 0.05). Figure 1a shows an example.

For the obtained non-uniform points ${{\mathcal{X}}}$, a function is first defined as s(i) = min(d _ij ), where d _ij is the distance between two points, and ${j\,(i, j \in {\mathcal{X}}}$ and i ≠ j). Then, the points ${{\mathcal{X}}}$ are enclosed in a bounding box, which corresponds to the root of the quadtree. This box is either a square cell or a rectangle with multiple square cells. A cell, c, is defined as crowded if its size is greater than s(i) of any point i within c or if the quadtree level difference around c is more than one. By splitting any crowded cell recursively until there is no more crowded cell, we obtain an adaptive quadtree, see Fig. 1b. If the input ${{\mathcal{C}}}$ consists of multiple components or narrow regions, we need to ensure that no any cell in the quadtree intersects with more than one curve. Otherwise, these cells need to be further refined, such that the topology of the input can be preserved during mesh generation.

3.2 Grid points adjusting

In previous work [24], a triangular mesh can be immediately generated using the DC method. However, no angle range can be guaranteed in the resulting mesh. When some grid points in the quadtree are very close to the curve ${{\mathcal{C}}}$, triangles with small angles may be constructed. To obtain guaranteed-quality meshes, we need to adjust these grid points.

A size function grid(i) is defined for each grid point i, which represents the shortest edge length from all the edges sharing i. We also define dist(i) as the distance between point i and the curve ${{\mathcal{C}}}$. Then we compare grid(i) with dist(i). If ${\rm dist}(i) \leq \frac{1}{4}{ \rm grid}(i)$, point i is moved toward ${{\mathcal{C}}}$, see Fig. 2a. Otherwise, if $\frac{1}{4}{\rm grid}(i) < {\rm dist}(i) < \frac{1}{2} \rm {grid}(i)$, pointi is moved away from the curve along the normal direction such that ${\rm dist}(i) = \frac{1}{2} {\rm grid}(i)$, see Fig. 2b. Here $\frac{1}{4}$ and $\frac{1}{2}$ are heuristically chosen. By doing this, we can guarantee each grid point off the curve has a minimum distance of $\frac{1}{2}{\rm grid}(i)$ to the curve, as shown in Fig. 1c.

Fig. 2

Grid points adjusting. a Case 1: |AA′| < 0.25 |AE|, point A is moved to A′ and b case 2: 0.25 |AE| < |AA′| < 0.5 |AE|, point A is moved to A″ along the normal direction (at A′) such that |A′A″| = 0.5 |AE|. A′ is the projection of A onto the input curve

3.3 Improved dual contouring method for 2D

In the traditional DC method, each cell needs a minimizer. There are various methods to calculate the position of minimizers [24]. In this paper, we use the projection method. First, all the grid points are classified into three types: interior node (with a “+” sign), exterior node (with a “−” sign), and boundary node (with a “o” sign). For each cell, if all its nodes have the same sign, the minimizer point locates at the cell center; otherwise, we choose the projection of the cell center to the curve as the minimizer. Figure 3 illustrates the process for minimizer calculation. Usually the projected minimizer is inside the cell. If it is outside the cell, we calculate the middle of the two intersecting points, and project the middle point to the curve as the minimizer, see Fig. 3(d).

Fig. 3

Minimizer calculation. a The inner element with four interior nodes, b the element with one exterior node, c the element with two exterior nodes, and d special case. Node denoted as plus symbol is an interior node, node denoted as minus symbol is an exterior node. Grey circle is original minimizer located in the center, and red circle is the recalculated minimizer

Then, we need to build the triangular mesh by connecting the minimizers with grid points. An edge-based connecting method is adopted in this paper. For each inner edge whose two ending nodes have the same sign, a triangle is constructed by connecting this edge with an adjacent minimizer, see Fig. 4a. For each sign change edge whose two ending nodes have different signs, a triangle is generated by connecting an ending node with two adjacent minimizers, see Fig. 4b. Note that for an inner cell whose four nodes have the same sign, it can be simply split into two triangles without adding a minimizer.

Fig. 4

Triangle element construction. a For the inner edge, connect it with one minimizer and b for the sign change edge, connect each grid node with two adjacent minimizers

Only one minimizer point is allowed for each cell in the traditional DC method. In adaptive triangular meshing, small element angles can be induced, see Fig. 5a, c, since the minimizer is very close to the edges. In this paper, we improve the DC method by allowing an extra minimizer point for the cells whose minimizer has a distance to the cell center greater than 1/4 of the edge length of the cell (outside the dash circle in Fig. 5b, d). The extra minimizer is initially placed at the center, but can be adjusted within the circle to ensure a good minimum angle. When connecting to the sign change edge or the interior edge, for the two minimizers inside the cell, we always choose the one that can provide a better angle range.

Fig. 5

Extra minimizer insertion. a Case 1: before improvement, b case 1: after improvement (D is inserted), c case 2: before improvement and d case 2: after improvement (E is moved to E′ and E′ is inserted). The radius of the circle is 1/4 of the edge length

As to be proved in Sect. 3.4, the minimum angle we can achieve is 19.47°. In Fig. 6, the original minimizer point C for the yellow cell may form an angle $\angle ACD < 19.47^{\circ}$ or $\angle BCE < 19.47^{\circ}$. In this special case, the minimizer C is adjusted along the curve to a new position C′ such that |AD|/|C′D| = |BE|/|C′E|, resulting in both $\angle AC'D$ and $\angle BC'E \ge 19.47^{\circ}$.

Fig. 6

Example for minimizer adjusting. Grey dot is the original minimizer, red dot is the adjusted minimizer, squares are the projection points of Points A and B. C is moved to C′ for better angles

3.4 Proof of guaranteed angle bounds

Based on the above three steps, we are able to prove that our algorithm offers a guaranteed angle range for the generated mesh.

Proposition 1

The angle range for a triangular mesh generated using the above method is (30°, 120°) for uniform quadtree, and (19.47°, 141.06°) for adaptive quadtree.

Proof

In the following proof, we assume that the curve inside each leaf cell is locally straight. For the uniform mesh, we only need to consider two cases: inner edge and sign change edge. For the inner edge, it can be verified that the worst case happens in an inner cell with one or more nodes adjusted. As shown in Fig. 7a, we only need to consider that D′ moves on the circle and we check the minimal angle in triangles ABD′ and BCD′. D′ shown here indicates the case with the minimal angle $\angle AD'B$. Here, |D′D| = 0.25|CD|, |AD| = |CD|, and $\angle ADD' = 135^{\circ}$. Then we get $|AD'|^2 = |AD|^2 + |DD'|^2 - 2|AD||DD'|{\rm cos}(\angle ADD')$ and |AD′| ≈ 1.19|CD|. Since $|AD|/{\rm sin}(\angle AD'B) = |AD'|/{\rm sin}(\angle ADD')$, we have $\angle AD'B = {\rm arcsin}(|AD|*{\rm sin}(\angle ADD')/|AD'|) \approx 36.46^{\circ}$. So, for the inner edge case, the minimal angle is about 36.46°.

Fig. 7

Uniform quadtree. a Inner edge and b sign change edge. Green lines are the input curve, red square points are minimizers, circle points are original grid points and solid points are adjusted grid points

For the sign change edge, as shown in Fig. 7b, the dashed circles are the adjusted areas, in which the radius |CC′| = |DD′| = 0.25|CD|. The worst case happens when the input curve tangents with the two dashed circles C and D. As required in Sect. 3.2, C and D move away from the curve, and reach C′ and D′. Then we need to find out the minimal angle in triangles D′′EF and C′FE $(\angle D'EF)$. Obviously, D′E//CD, |D′E| = |CD|, and |D′F| = 2|DF| = 2*0.25|CD| = 0.5|CD|, therefore, we have |D′F| = 0.5|D′E|. Because D′F ⊥ EF, we can obtain that $\angle D'EF = 30 ^{\circ}$. Therefore, for the sign change edge case, the minimal angle is 30°.

Now we will figure out the angle range for the adaptive quadtree. The worst case comes from the sign change edge. For the sign change edge without a hanging node, see Fig. 8a, the input curve DEF tangents to the two circles A and C. Points D, E, and F are the minimizer points. Two triangles A′DE and C′EF are generated, which are identical. We need to check the minimal angle $\angle A'ED$. Obviously, we have AD ⊥ DE, DE ⊥ BE and $\angle ABE = 45^{\circ}$. Since |A′D| = 0.25 |AB|, and $|DE| = 1/2|AC| = \sqrt{2}/2 |AB|$, we have the minimum angle $\angle A'ED = {\rm arc tan}(|A'D|/|DE|) \approx 19.47^{\circ}$.

Fig. 8

Adaptve quadtree. a Case 1 and b case 2. Green lines are the input curve, triangle points are intersecting points, red square points are minimizers, circle points are original grid points, and solid points are adjusted grid points

For the sign change edge with a hanging node, see Fig. 8b, the worst case happens when cricles A and E are tangential to the input curve FG at F and I. Their radius $|AF| = |EI| = \frac{1}{4}|AE| = \frac{1}{8}|CD|$. The minimizer point G is the projection point of the center J on the input curve. Therefore, |EJ| = 0.5|CD| and $\angle JGI = 90^{\circ}$. In this case, two triangles E′FG and A′GF are generated and we need to check the minimal angle in them, which is $\angle A'GF$. Similar to the proof of the sign change edge in a uniform quadtree in Fig. 7b, we can obtain $\angle EHI= \angle E'FI = 30^{\circ}$. Considering that triangle EIK is similar to triangle JGK and also triangle HIE, it is easy to obtain that $\angle IEK = \angle GJK = \angle EHI = 30^{\circ}$, and $|GI| = |GK|+|KI| = |KJ|{\rm sin}(\angle GJK)+|EK|{\rm sin}(\angle IEK) = (|KJ|+|EK|){\rm sin}30^{\circ} = 0.5|EJ| = 0.25|CD|$. Since triangle AFH is identical to triangle EIH, we can obtain $\angle AHF = \angle EHI = 30^{\circ}$ and $|FH| = |HI| = |AF|*{\rm ctan}(\angle AHF) = 1/8|CD|*{\rm ctan}30^{\circ} \approx 0.2165|CD|$. Then, we have |FG| = |FH| + |HI| + |GI| = (0.2165 + 0.2165 + 0.25)|CD| = 0.683|CD| and $\angle A'GF = {\rm arc tan}(|A'F|/|FG|) = {\rm arc tan}(1/4|CD|/0.683|CD|) \approx 20.10^{\circ}$. Therefore, for this case, the minimal angle is about 20.10°.

In summary, we can conclude that the minimum angle is 30° for a uniform mesh, and 19.47° for an adaptive mesh. Similarly, we can derive that the maximum angle is 120° for uniform quadtree, and 141.06° for adaptive quadtree. Therefore, the angle range for the triangular mesh is (30°, 120°) for uniform meshing, and (19.47°, 141.06°) for adaptive meshing. Note that this conclusion is based on the straight line assumption which may not be satisfied in real models. A small perturbation is expected. □

4 Tetrahedral meshing with guaranteed quality

The algorithm in the previous section can be extended to 3D adaptive tetrahedral meshing with some modifications. There are still three steps: adaptive octree construction, grid points adjusting, and improved DC.

4.1 Adaptive octree construction

For a given triangular/quadrilateral surface mesh, we choose the approach described in [18] to build the adaptive octree. As the first step, we generate a large cube (or a row of several cubes) which bounds the given surface mesh. This cube is defined as the root of the octree and marked as level 0. Cells constructed after refining the ith-level cell will be marked as level (i + 1). To decide whether a cell needs to be refined or not, a feature sensitive error function [24] is defined: ${\rm ERROR} = \sum_{i=1}^{27}{\frac{|f^{i+1}(P) - f^{i}(P)|}{|\nabla f^{i}(P)|}}$, in which f ⁱ(P) is the distance from node P at level i to the surface. This error function estimates the surface difference between two neighboring levels by measuring a total of 27 nodes for each cell. For a cell at level i, the function values of the 8 vertices are calculated directly, and the function values of 12 edge middle points, 6 face middle points and 1 center point can be obtained through a trilinear interpolation. For a preset error tolerance $\varepsilon$, we refine any cell if its ${\rm ERROR} > \varepsilon$. Moreover, to preserve the original topology, it is not allowed to have any cell intersecting with more than one cutting plane. Otherwise, such cells need to be refined. Note that in our algorithm, we do not consider non-manifold surface. In addition, to generate meshes with good aspect ratio, we enforce the octree to be strongly balanced, which limits the level difference between adjacent cells to be no more than one. Finally, we obtain an adaptive octree.

4.2 Grid points adjusting

The grid points adjusting in 3D is similar to that in 2D. We need to adjust grid points close to the input surface ${{\mathcal{S}}}$. We use the same definition for grid(i), and redefine dist(i) as the distance between point i and the surface ${{\mathcal{S}}}$. Then we still compare grid(i) with dist(i). If ${\rm dist}(i) \leq \frac{1}{4} {\rm grid}(i)$, point i is moved toward ${{\mathcal{S}}}$. Otherwise, if $\frac{1}{4}{\rm grid}(i) < {\rm dist}(i) < \frac{1}{2} {\rm grid}(i)$, point i is moved away from the curve along the normal direction such that ${\rm dist}(i) = \frac{1}{2}{\rm grid}(i)$. By doing that, we can guarantee each grid point i off the surface has a minimum distance of $\frac{1}{2}{\rm grid}(i)$ to the surface.

4.3 Improved dual contouring method for 3D

In this step, the main differences between 2D and 3D DC are the minimizer calculation, and the insertion of extra minimizers.

In Sect. 4.1, we enforce that the cutting plane inside each boundary cell is planar, and each cell is limited to have at most one cutting plane. As a result, for the minimizer calculation in a boundary cell, we only need to consider five cases, as shown in Fig. 9, in which there are 0, 1, 2, 3 or 4 interior grid points, respectively. For the interior cell, we choose the cell center as the minimizer. For each boundary cell, we first calculate the intersecting plane, and then choose the projection of the geometric center onto the intersecting plane as the minimizer.

Fig. 9

Minimizer calculation in 3D. a The interior cell, b the cell with one interior grid node, c the cell with two interior grid nodes, d the cell with three interior grid nodes and e–f the cells with four interior grid nodes. Node denoted as plus symbol is an interior node, node denoted as minus symbol is an exterior node. Red circle is the minimizer

Then, we adopt the edge-based connecting method to construct the tetrahedral mesh by connecting the minimizers with grid points. For each inner edge whose two ending nodes have the same sign, we build a tetrahedron by connecting this edge with two adjacent minimizers, see Fig. 10a. For each sign change edge whose two ending nodes have different signs, there are two cases we need to take into consideration. For the sign change edge shared by four elements, one pyramid (the yellow one in the top) is built by connecting the interior ending node with four adjacent minimizers separately, see Fig. 10b, then this pyramid is split into two tetrahedra by connecting the diagonal which can maximize the minimum dihedral angles of the tetrahedra. For the sign change edge shared by three elements, which happens only in the adaptive octree, a tetrahedron (the yellow one in the top) is constructed by connecting the interior ending nodes with three adjacent minimizers, see Fig. 10c. For exterior mesh generation, the bottom pyramid in Fig. 10b and the bottom tetrahedron in Fig. 10c are constructed.

Fig. 10

Tetrahedral element construction. a For the inner edge, build a tetrahedron by connecting it with two minimizers, b for the sign change edge shared by four elements, build a pyramid by connecting the interior node with four adjacent minimizers and c for the sign change edge shared by three elements, build a tetrahedron by connecting the interior node with three adjacent minimizers

Similar to the triangular DC, we also need to insert extra minimizers in the adaptive octree to improve the minimal dihedral angle of the generated tetrahedral elements. Figure 11a shows an example with only one minimizer. We can observe that some tetrahedra have very sharp angles. Therefore, an extra minimizer is inserted in the larger cube, as shown in Fig. 11b. We insert an extra minimizer if the distance from the minimizer to the cell center is greater than 1/4 of the edge length. The extra minimizer is initially positioned at the center of the cube, but can be adjusted for optimization. The insertion of the extra minimizer produces better dihedral angles with a few more elements.

Fig. 11

Extra minimizer insertion for 3D. a Before inserting an extra minimizer, and b after inserting an extra minimizer. Red dots are minimizers on the surface ${{\mathcal{S}}}$, green dots are interior cell centers, and yellow dots are extra minimizers

In the above illustrations, for simplification, we only consider interior and exterior grid points. For grid points lying on the curve, they can be treated as either interior or exterior points. When connected with interior points, they are considered as an interior point, vice versa.

4.4 Proof of guaranteed angle bounds

Based on the above three steps, our method offers a guaranteed dihedral angle range for the generated mesh, as shown in the following proposition.

Proposition 2

All the dihedral angles in the generated adaptive tetrahedral mesh are in the range of (12.04°, 129.25°).

Proof

Because there are an infinite number of possible positions for the grid points and minimizers, here we utilize a computer-aided proof method to numerically verify the dihedral angle range, and thus simplify the analysis. There are five cases we need to take into consideration:

• 1. An interior edge shared by two same-size cells;

• 2. An interior edge shared by two different-size cells;

• 3. A sign change edge shared by four same-size cells;

• 4. A sign change edge shared by four different-size cells;

• 5. A sign change edge shared by three different-size cells.

For each case, we first assume a planar plane inside each cell, then adjust the grid points according to Sect. 4.2, and generate the minimizers (and extra minimizers if required) according to Sect. 4.3. Then we can construct tetrahedra, and obtain the corresponding dihedral angle range. An arbitrary planar plane can be formed by three non-colinear sampling points in three different cells. If the testing case has only two cells, we place two points in one cell and the third point in the other cell. By testing all the possible cutting plane, we are able to identify the worst cases for the above five cases, and illustrate them in Fig. 12. The corresponding dihedral angle bounds are also given in the figure.

Fig. 12

a The worst shape for an interior edge in the uniform grid, with a dihedral angle range of (13.10°, 128.70°); b the worst shape for an interior edge in the adaptive grid, with a dihedral angle range of (12.04°, 129.25°); c the worst shape for a sign change edge shared by four same-size elements, with a dihedral angle range of (14.55°, 125.39°); d the worst shape for a sign change edge shared by four different-size elements, with a dihedral angle range of (12.84°, 128.48°) and e the worst shape for a sign change edge shared by three different size elements, with a dihedral angle range of (18.63°, 122.17°)

In summary, we can conclude that the overall dihedral angle range for an adaptive tetrahedral mesh is (12.04°, 129.25°). Note that in the above proof, the planar cutting plane assumption is applied, which may not be satisfied for arbitrary models. Therefore, a perturbation is expected. This can happen because the input surface is a triangular mesh, and the dihedral angle of two adjacent triangles is usually not 180°. In the extreme case when sharp features exist in the surface ${{\mathcal{S}}}$, our algorithm may not guarantee the dihedral angle range in the sharp feature regions. □

4.5 Discussion

In 2D triangular meshing, we theoretically proved that the minimal angle of the obtained mesh is 19.47°, which is the optimal angle we can achieve. Differently, in 3D tetrahedral meshing, we utilized a computer-aided approach to numerically determine the minimal angle. Since we have tested all the possible cutting planes inside a cell, the obtained minimal angle should also be an optimal one.

5 Results

The presented triangular and tetrahedral meshing algorithms have been implemented in Visual C++, and were tested on a PC configured with a 2.93 GHz Intel X3470 CPU and 8 GB of Memory. We have applied our algorithm to a variety of 2D and 3D models.

For adaptive triangular meshing, we have applied our algorithm to three models: an S curve in Fig. 13, a mouse in Fig. 14, and the China map in Fig. 15. Statistics of these meshes are listed in Table 1. We can observe that all the three models have an angle range of (19.47°, 141.06°), with a 1.27° perturbation. This perturbation is induced by the restriction of the quadtree level we preset in the code which limits the number of vertices and elements generated in the final mesh. However, this restriction makes the straight cutting line assumption invalid for some cells, and enlarges the angle range in a small amount. This is a trade-off between the mesh size and angle range. This happens to the adaptive tetrahedral meshing algorithm as well. Due to the property of quadtree, the interior elements have angles of 45° or 90°, instead of the ideal 60° for triangles, see Fig. 16.

Fig. 13

Triangular mesh for an S curve with an angle range of (19.4°, 125.9°)

Fig. 14

Triangular mesh for a mousy curve with an angle range of (18.8°, 133.8°)

Fig. 15

Triangular mesh for China map with an angle range of (18.2°, 134.3°)

Table 1 Mesh statistics of the triangular meshing models

Fig. 16

Angle histograms. a The S curve, b the mousy curve and c the China map. Span size is 1° for all the three histograms

For adaptive tetrahedral meshing, we have also applied our approach to three models: the bladder in Fig. 17, a head model in Fig. 18, and the Igea model in Fig. 19. Corresponding mesh information is given in Table 2. We can observe that all the three models have a dihedral angle range of (12.04°, 129.25°), with 2.5° perturbation. As mentioned above, this perturbation is cause by the incomplete enforcement of planar cutting plane condition. Furthermore, due to the property of octree and DC, most of the interior tetrahedra have dihedral angles of either 60° or 90°, see Fig. 20.

Fig. 17

Tetrahedral mesh for the bladder model, with the dihedral angle range of (13.3°, 130.1°)

Fig. 18

Tetrahedral mesh for the head model, with the dihedral angle range of (12.0°, 130.2°)

Fig. 19

Tetrahedral mesh for the Igea model, with the dihedral angle range of (11.4°, 131.9°)

Table 2 Mesh statistics of the tetrahedral meshing models

Fig. 20

Dihedral angle histograms. a Bladder, b head and c Igea. Span size is 1° for all the three histograms

Since projection is adopted for minimizer calculation, the boundary of the meshes automatically conform to the given curve/surface, demonstrating a good fidelity to the original input. We can also conclude from Tables 1 and 2 that the time complexity of our algorithm depends on the obtained mesh size and the geometric complexity of the input.

Note that in the three steps of our algorithm, no coupling exists between octree cells and no propagation is required. Therefore, it is easy to parallelize the implementation. We tested Fig. 15 as a 2D example and Fig. 19 as a 3D example using different threads. The parallel performance of our algorithm is shown in Fig. 21. We can observe that a nearly linear speed-up is achieved for two threads. However, the performance curve is flattened out and converges to a constant value with the increase of threads. This is because a small portion of the implementation cannot be parallelized, which limits the overall performance according to the Amdahl’s Law [1].

Fig. 21

Parallel performance of the adaptive triangular (China map) and tetrahedral (Igea) mesh generation

6 Conclusion

In this paper, we introduce a novel octree-based DC algorithm for adaptive triangular or tetrahedral mesh generation. Using this algorithm, we can guarantee the obtained triangle mesh has an angle range of (19.47°, 141.06°) for any given closed smooth curve, and the tetrahedral mesh has a dihedral angle range of (12.04°, 129.25°) for any given closed smooth surface. In practice, since the straight line/planar cutting plane assumption is not always satisfied, there is a small perturbation for the lower and upper bounds of the proved angle range. Our adaptive tetrahedral meshing algorithm can provide a better dihedral angle range than the algorithms presented in [5] in which the dihedral angle range is (1.66°, 174.72°), and in [20] in which the minimal dihedral angle is 5.71°. Generally speaking, the resulting mesh quality is not affected by the input mesh much once it can define a good boundary surface. However, if the input mesh quality is not good, it may result in more elements in the final mesh. This algorithm cannot handle face-interior point constraints. Sharp feature was not considered either. In the future, we will include sharp feature in our algorithm and explore the possible angle range we can achieve.