Convex strategyproofness with an application to the probabilistic serial mechanism

Abstract

We consider two natural notions of strategyproofness in random object-assignment mechanisms based on ordinal preferences. The two notions are stronger than weak strategyproofness but weaker than strategyproofness. We demonstrate that the two notions are equivalent, provide a geometric characterization of the new intermediate property which we call convex strategyproofness, and then show that the (generalized) probabilistic serial mechanism is, in fact, convexly strategyproof. We finish by showing that the property of weak envy-freeness of the random serial dictatorship can be strengthened in an analogous manner.

1 Introduction

We consider some questions of strategyproofness arising in mechanisms for the random assignment of heterogeneous indivisible objects among participating agents, based on their reported ordinal preferences over the objects. The two main (ex-ante symmetric) such mechanisms considered in the literature are the random serial dictatorship (Abdulkadiroğlu and Sönmez 1998), and the probabilistic serial (PS) mechanism (Bogomolnaia and Moulin 2001). The main trade-off between the two mechanisms is that while the PS mechanism satisfies a stronger efficiency property, it fails to be strategyproof. Instead, it satisfies a weaker condition, called weak strategyproofness. Here, we define two natural intermediate incentive properties that are stronger than weak strategyproofness but weaker than strategyproofness. We show that these two concepts are equivalent and call the resulting property convex strategyproofness. Then, using a simple geometric characterization, we show that the PS mechanism and its generalization due to Budish et al. (2013) are convex strategyproof.

More specifically, weak strategyproofness means that, holding the reports of the other agents constant, an agent deviating to a false report cannot induce a probability distribution over the available objects that strictly first-order stochastically dominates the outcome that a true report would induce.¹ Equivalently, for any outcome corresponding to a false report, there exists a utility function compatible with the agent’s true ordinal preferences, under which the truth-telling outcome has higher expected utility. Strategyproofness, on the other hand, means that the outcome corresponding to the true report first-order stochastically dominates all outcomes corresponding to false reports. Equivalently, for any utility function compatible with the agent’s true ordinal preferences, the agent’s expected utility from the truth-telling outcome is weakly greater than her expected utility for any other outcome. Note that, by contrast, weak strategyproofness does not even guarantee the existence of a single utility function compatible with the agent’s preferences, under which the truth-telling outcome is the best one (see Example 1 in Sect. 3).

This observation gives us the first natural candidate for an intermediate property: requiring the existence of a compatible utility function, such that truth-telling maximizes utility. The second one is similar to weak strategyproofness but allows for mixed strategies: namely, this version of strategyproofness holds if no mixed reporting strategy induces a probability distribution that strictly first-order stochastically dominates the truth-telling outcome. As noted above, we show that these two properties are equivalent.

This paper is related most closely to Mennle and Seuken (2013) who also study an intermediate strategyproofness concept, which they call partial strategyproofness, and apply it to convex combinations (hybrids) of the random serial dictatorship and the PS mechanism. In particular, they show that the set of utility functions for which the hybrid mechanism is strategyproof (i.e. truth-telling maximizes utility) is increasing as we increase the weight placed on the random serial dictatorship. We can view convex strategyproofness as a form of minimal partial strategyproofness. Note that the two papers are logically unrelated.² Kojima and Manea (2010) study a different aspect of the incentive properties of the PS mechanism. They show that it becomes strategyproof if there are sufficiently many copies of each object. By comparison, we show that, for markets of all sizes, the PS mechanism satisfies an incentive property that is stronger than weak strategyproofness.

2 Set-up

In what follows, we present a simplified representation of the strategic situations that agents participating in object-assignment mechanisms face. At the end of this section, we further discuss how this set-up pertains to the incentive compatibility of such mechanisms.

We assume that an agent with unit demand (the decision maker or the DM) can take several actions. Each action is associated with some probability distribution over the available objects which the DM receives. The DM has some strict ³ preference order over the objects, which, via first-order stochastic dominance, induces a partial order over the possible probability distributions.

Assume that there are $n+1$ different objects⁴ (numbered $1,2,\ldots$) and, without loss of generality, that the DM prefers objects with smaller indices (i.e. $1\succ 2\succ \cdots \succ n+1$). We assume that the probability shares of the objects in each probability distribution sum up to 1. This is also without loss of generality since we can always add a least-preferred “null object” to the list of objects and assign the rest of the probability weight to it. Thus we can denote any possible probability distribution as an element of

$$\begin{aligned} P:=\left\{ x\in \mathbb {R}^n:\sum _{i=1}^n x_i\le 1,x\ge 0\right\} . \end{aligned}$$

Consider all utility vectors compatible with the DM’s preferences, which have been normalized so that $u_{n+1}=0$. Denote them by

$$\begin{aligned} \mathscr {U}:=\left\{ u\in \mathbb {R}^n:u_1>u_2>\cdots >u_n>0\right\} . \end{aligned}$$

For a given utility vector $u\in \mathscr {U}$, the von Neumann-Morgenstern expected utility the DM derives from a probability distribution $p\in P$ is $u\cdot p=\sum _{i=1}^n u_i p_i$.

A probability distribution $p\in P$ is said to first-order stochastically dominate a probability distribution $q\in P$ (with respect to $\succ$) if $\sum _{i=1}^j p_j\ge \sum _{i=1}^j q_j$ for all $j=1,\ldots ,n$. We say that p strictly first-order stochastically dominates q if p first-order stochastically dominates q and $p\ne q$. We write $p\succsim ^{FOSD} q$ and $p\succ ^{FOSD} q$, respectively. A useful fact is that a probability distribution $p\in P$ first-order stochastically dominates $q\in P$ if and only if $u\cdot p\ge u\cdot q$ for all $u\in \mathscr {U}$ (Hadar and Russell 1969). Note that the partial order $\succsim ^{FOSD}$ can be extended from P to $\mathbb {R}^n$ using the same definition of first-order stochastic dominance. Abusing notation, we call that order $\succsim ^{FOSD}$ as well.

Let the DM’s set of (finitely many) possible actions (e.g. possible reports of her preferences) be $A=\{a,b^1,\ldots ,b^k\}$ and let the function $g:A\rightarrow P$ associate each action with a probability distribution. Note that if the DM chooses a mixed action strategy, she can induce any probability distribution in the convex hull of the set $\{g(a),g(b^1),\ldots ,g(b^k)\}$, which we denote ${\text {co}}\{g(a),g(b^1),\ldots ,g(b^k)\}$ as usual. The converse is, naturally, also true—any mixed action strategy induces a probability distribution in that convex hull. We say that the action a is a dominant strategy if g(a) first-order stochastically dominates all $g(b^i)$’s. We say that the action a is an undominated strategy if no $g(b^i)$ first-order stochastically dominates g(a). We say that the action a is compatible with utility maximization if there exists $u\in \mathscr {U}$ such that $u\cdot g(a)\ge u\cdot g(b^i)$ for all i. Finally, we say that the action a is convexly undominated if there doesn’t exist a mixed action strategy that induces a probability distribution that strictly first-order stochastically dominates g(a). This is equivalent to saying that there is no $p\in {\text {co}}\{g(a),g(b^1),\ldots ,g(b^k)\}$ such that $p\succ ^{FOSD} g(a)$. The preceding four concepts were defined with respect to particular set A and function g but the definition of these objects will be always clear from the background and we will suppress their mention.

Assume that f is a random object-assignment mechanism; i.e. f is a map between the reported preferences of a set of participating agents and a profile of probability-share distributions for each agent. Each element of the action set of each agent corresponds to some possible preference order over the objects. Each possible report by an agent i is mapped into a probability-share distribution by the function $f_i(\cdot ,\succ _{-i})$, where $\succ _{-i}$ denotes the fixed preference profile of the other agents participating in the mechanism. A mechanism is strategyproof (resp. weakly strategyproof) at a given profile $(\succ _i,\succ _{-i})$ if for every participating agent i reporting truthfully is a dominant strategy (resp. an undominated strategy) with respect to $f_i(\cdot ,\succ _{-i})$. Furthermore, a mechanism is (weakly) strategyproof if it is (weakly) strategyproof at all possible preference profiles.

2.1 Convex cones and polyhedra

We provide another useful characterization of first-order stochastic dominance using convex cones. A convex cone $C\subseteq \mathbb {R}^n$ is a set such that for all $x,y\in C$ we have $\alpha x+\beta y\in C$ for all $\alpha ,\beta \ge 0$. For every partial order $\succsim$ on $\mathbb {R}^n$ compatible with the vector-space operations⁵ on $\mathbb {R}^n$, there exists a convex cone $C_{\succsim }$ such that $p\succsim q$ if and only if $p\in \{q\}+C_{\succsim }$, where $\{q\}+C_{\succsim }:=\{q+x: x\in C_{\succsim }\}$ is the usual Minkowski set summation. In fact, one can show $C_{\succsim }=\{x\in \mathbb {R}^n:x\succsim \mathbf {0}\}$ (e.g. see Aliprantis and Border 2006, Section 8.1). The convex cone $C:=C_{\succsim ^{FOSD}}$ then satisfies $C=\{x\in \mathbb {R}^n:x\succsim ^{FOSD}\mathbf {0}\}$ or, in other words, $C=\{x\in \mathbb {R}^n:\sum _{i=1}^j x_i\ge 0 \text{ for } \text{ all } j=1,\ldots ,n\}$. Using the convex cone C, we can easily give a geometric characterization of an undominated strategy directly from its definition: given a set $A=\{a,b^1,\ldots ,b^k\}$ and a function $g:A\rightarrow P$, the action a is undominated if and only if

$$\begin{aligned} (\{g(a)\}+C)\cap \{g(a),g(b^1),\ldots ,g(b^k)\}=\{g(a)\}. \end{aligned}$$

In this section, we also state a result due to McLennan (2002). Before we do that, we introduce a couple of additional convex-analysis concepts. Any subset of $\mathbb {R}^n$ that is a finite intersection of closed half-spaces is called a polyhedron. It is easy to verify that the convex hull of any finite set is a polyhedron, as is the convex cone C corresponding to $\succsim ^{FOSD}$. The set of all finite affine combinations of elements of a set $S\subseteq \mathbb {R}^n$ is called the affine hull of S and we denote it by ${\text {aff}}(S)$:

$$\begin{aligned} {\text {aff}}(S):=\left\{ \sum _{i=1}^k \alpha _i s_i:s_1,\ldots ,s_k\in S, \alpha \in \mathbb {R}^k,\sum _{i=1}^k\alpha _i=1\right\} . \end{aligned}$$

It is easy to verify that if $p\cdot s$ is constant for some $p\in \mathbb {R}\setminus \{\mathbf {0}\}$ and all $s\in S$, then $p\cdot s'=p\cdot s$ for all $s\in S$ and all $s'\in {\text {aff}}(S)$. In other words, if a set is entirely contained within a hyperplane, then so is its affine hull.

Given a polyhedron P, the empty set, P itself, and any set of the form $P\cap H$ for a hyperplane H, one of whose closed half-spaces contains P, are called faces of P. Finally, McLennan (2002, Lemma 2) shows that for any convex subset S of a polyhedron P, there exists a smallest face of P that contains S. That Lemma permits us to state the following theorem, which is also due to McLennan (2002).

Theorem 1

(The Polyhedral Separating Hyperplane Theorem) For two polyhedra $P_1,P_2\subset \mathbb {R}^n$, let $F_1$ and $F_2$ be the smallest faces of, respectively, $P_1$ and $P_2$ that contain $P_1\cap P_2$. Let also ${\text {aff}}(F_1\cup F_2)\ne \mathbb {R}^n$. Then there exists $u\in \mathbb {R}^n,u\ne \mathbf {0}$ such that $u\cdot p_1>u\cdot f_1=u\cdot f_2>u\cdot p_2$ for all $p_i\in P_i\setminus F_i,f_i\in F_i$ for $i=1,2$.

3 The characterization result

Proposition 1

Given a set $A=\{a,b^1,\ldots ,b^k\}$ and a function $g:A\rightarrow P$, the following are equivalent:

• (i) action a is compatible with utility maximization;

• (ii) action a is convexly undominated;

• (iii) $(\{g(a)\}+C)\cap {\text {co}}\{g(a),g(b^1),\ldots ,g(b^k)\}=\{g(a)\}$, where C is the convex cone corresponding to the partial order induced by first-order stochastic dominance.

Proof

• (i) $\Rightarrow$(ii) We know that there exists some $\overline{u}\in \mathscr {U}$ such that $\overline{u}\cdot g(a)\ge \overline{u}\cdot g(b^i)$ for all i. This implies $\overline{u}\cdot g(a)\ge \overline{u}\cdot x$ for all $x\in {\text {co}}\{g(a),g(b^1),\ldots ,g(b^k)\}$. Assume toward contradiction that there exists some $y\in {\text {co}}\{g(a),g(b^1),\ldots ,g(b^k)\}$ that strictly first-order stochastically dominates g(a). As remarked above, however, this implies $u\cdot y>u\cdot g(a)$ for all $u\in \mathscr {U}$, which is a contradiction since $\overline{u}\in \mathscr {U}$.

• (ii) $\Rightarrow$(iii) This follows from the facts that the set ${\text {co}}\{g(a),g(b^1),\ldots ,g(b^k)\}$ equals the set of elements in P that can be induced by a mixed action strategy, and that the set of points that strictly first-order stochastically dominates g(a) is the set $(\{g(a)\}+C)\setminus \{g(a)\}$.

• (iii) $\Rightarrow$(i) For notational simplicity, denote the convex hull ${\text {co}}\{g(a),g(b^1),\ldots ,g(b^k)\}$ by D. First, note that $\{g(a)\}+C$ (a translation of the polyhedron C) and D (a convex hull of a finite set) are both polyhedra. Additionally, it is clear that the smallest face of $\{g(a)\}+C$ containing $\{g(a)\}$ is the singleton $F_1:=\{g(a)\}$. Now consider $F_2$—the smallest face of D that contains $\{g(a)\}$. Note that we have $F_1=\{g(a)\}\subseteq F_2$. So, in order to invoke McLennan’s theorem, it suffices to show that ${\text {aff}}(F_2)\ne \mathbb {R}^n$.

Note that g(a) is on the boundary of D (since $g(a)+\varepsilon (1,\ldots ,1)\in \{g(a)\}+C$ for all $\varepsilon >0$). Then there exists a hyperplane H separating g(a) and D: i.e. $g(a)\in H$ and D is entirely contained in one of the closed half-spaces defined by H. Therefore, $H\cap D$ is a face of D containing g(a), and the smallest such face $F_2$ must satisfy $F_2\subseteq H\cap D\subset H$. As noted above, if a set is entirely contained within a hyperplane H, then so is its affine hull. Therefore, ${\text {aff}}(F_2)\subseteq H\subsetneq \mathbb {R}^n$. Thus the two sets satisfy the conditions of the Polyhedral Separating Hyperplane Theorem and there exists $\overline{u}\in \mathbb {R}^n,\overline{u}\ne \mathbf {0}$ such that $\overline{u}\cdot x>\overline{u}\cdot g(a)\ge \overline{u}\cdot y$ for all $x\in (\{g(a)\}+C)\setminus \{g(a)\}$ and $y\in D$.⁶

Now, it suffices to show that $\overline{u}_1>\overline{u}_2>\cdots >\overline{u}_n>0$. Indeed, denoting the standard basis vectors by $e_1,\ldots , e_n$, note that $g(a)+e_i-e_j\in (\{g(a)\}+C)\setminus \{g(a)\}$ for $i<j$ and $g(a)+e_n\in (\{g(a)\}+C)\setminus \{g(a)\}$. Hence, we have the inequalities $\overline{u}\cdot (g(a)+e_i-e_j)>\overline{u}\cdot g(a)$ for $i<j$ and $\overline{u}\cdot (g(a)+e_n)>\overline{u}\cdot g(a)$. They imply $\overline{u}_i>\overline{u}_j$ whenever $i<j$ and $\overline{u}_n>0$, respectively. $\square$

We say that a mechanism is convexly strategyproof at a given preference profile if for every agent reporting truthfully is either convexly undominated or, equivalently, compatible with utility maximization. As above, we also say that a mechanism is convexly strategyproof if it is convexly strategyproof at all possible preference profiles. It is obvious that convex strategyproofness is strictly weaker than strategyproofness and that it implies weak strategyproofness. The converse is not true, as the following example demonstrates.

Example 1

Consider a set $A=\left\{ a,b^1,b^2\right\}$ and $g:A\rightarrow P$, such that for $n=2$:

$$\begin{aligned} g(a)&=\left( .3, .3\right) \\ g(b^1)&=\left( .29, .7\right) \\ g(b^2)&=\left( .41, 0\right) . \end{aligned}$$

The action a is undominated since g(a) is not first-order stochastically dominated by either $g(b^1)$ (because $g(b^1)_1<g(a)_1$) or $g(b^2)$ (because $\sum g(b^2)_i<\sum g(a)_i$). However, a is not convexly undominated (or, equivalently, not compatible with utility maximization) because the convex combination

$$\begin{aligned} \frac{1}{2}g(b^1)+\frac{1}{2}g(b^2)=\left( .35, .35 \right) \end{aligned}$$

first-order stochastically dominates g(a). Since weak strategyproofness is defined via undominatedness and convex strategyproofness via convex undominatedness, this also implies that convex strategyproofness is strictly stronger than weak strategyproofness. Furthermore, it is straightforward to check that this example can be generalized to show that convex strategyproofness is strictly stronger than weak strategyproofness as long as $n>1$.

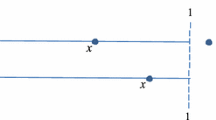
See also Fig. 1 for a geometric illustration of the difference between undominated and convexly undominated actions and thus between weak and convex strategyproofness. The Figure illustrates two possible scenarios with $n=2$ and 5 possible actions, which are then mapped into probability-share distributions via the function g. In both panels, taking action a is undominated since none of the other actions result in first-order stochastic dominance improvement. In other words, none of the other actions result in a probability-share distribution that lies in the set $\{g(a)\}+C$. However, the action a is convexly undominated only in panel (a), where no element of the convex hull ${\text {co}}\{g(b^1),g(b^2),g(b^3),g(b^4)\}$ lies in $\{g(a)\}+C$. In panel (b), however, it is clear that a convex combination of the actions $b^1$ and $b^2$ can result in first-order stochastic dominance improvement over a.

Fig. 1

Undominated (UD) vs. convexly undominated (cUD) actions. a Action a is UD and cUD. b Action a is UD but not cUD

4 The probabilistic serial mechanism

We start this section with a brief description of the PS mechanism. While being executed, it treats each object as one unit of infinitely divisible probability shares. Time runs continuously, starting at $t=0$. The mechanism then allows each agent to continuously claim probability shares of her favorite object among those that have not been entirely claimed yet. The speed with which each agent claims probability shares is equal to 1. The mechanism runs until $t=1$, when each agent will have claimed a total of one unit of probability shares. The probability shares claimed by each agent represent the probability-share distribution induced by the PS mechanism for that agent. For a more detailed and formal definition, see Bogomolnaia and Moulin (2001).

Bogomolnaia and Moulin (2001) show that the PS mechanisms is weakly strategyproof.⁷ In this section, we extend their arguments to show that the PS mechanism is also convexly strategyproof. As above, we will call the agent of interest the DM and we will assume that her true preferences (denoted by $\succ$) are as above: she strictly prefers objects with lower indices over those with higher ones. We will denote the fixed preference profile of the other agents by $\succ _{-}$ and $PS(\cdot )$ will be a function that maps a preference profile to the probability distribution that the PS mechanism assigns to the DM for that preference profile.

Let us first briefly examine the idea behind the proof of weak strategyproofness in Bogomolnaia and Moulin (2001). The authors show that if the DM reports a preference $\succ '$ (which is potentially different from $\succ$) that yields a probability-share distribution $q=PS(\succ ',\succ _{-})$ such that $q_1\ge p_1$ for $p=PS(\succ ,\succ _{-})$, then this is possible only if $q_1=p_1$. The authors then iterate this argument to establish weak strategyproofness. The iterated argument can be summarized in the following lemma.⁸

Lemma 1

Let $p:=PS(\succ ,\succ _{-})$ and $q:=PS(\succ ',\succ _{-})$ and let some $j=1,\ldots ,n$ be given. If $p_i=q_i$ for all $i<j$ and if $q_{j}\ge p_{j}$, then $q_j=p_j$.

The implicit understanding in the statement of Lemma 1 is that if $j=1$, the only condition is $q_{1}\ge p_{1}$. We omit the proof of Lemma 1 as it can be straightforwardly derived from arguments in Bogomolnaia and Moulin (2001) as outlined above.

Proposition 2

The PS mechanism is convexly strategyproof.

Proof

Consider an agent (our decision maker) with true preference $\succ$. Let some possible preferences over the objects be $\succ ^1,\ldots ,\succ ^k$ (not necessarily different from each other or from $\succ$). Finally, let $p=PS(\succ ,\succ _{-})$ and $q^i=PS(\succ ^i,\succ _{-})$ for $i=1,\ldots ,k$. Assume toward contradiction that the truthful report of DM’s preferences (i.e. reporting $\succ$) is not convexly undominated, which would imply that the PS mechanism is not convexly strategyproof.

By the definition, this means that there exist some $\alpha ^1,\ldots ,\alpha ^{k}\ge 0$ with $\sum _{i=1}^{k}\alpha ^i=1$ such that

$$\begin{aligned} \sum _{i=1}^k\alpha ^i q^i\succ ^{FOSD} p \end{aligned}$$

(1)

In fact, without loss of generality, we can assume $\alpha ^1,\ldots ,\alpha ^{k}>0$. Then note that (1) implies

$$\begin{aligned} \sum _{i=1}^k\alpha ^i q_1^i\ge p_1. \end{aligned}$$

This is possible only if there exists i such that $q_1^i>p_1$ or if $q_1^i=p_1$ for all i. By Lemma 1, the first case is impossible. Therefore we have $q_1^i=p_1$ for all i.

We can extend the argument inductively. Consider the induction step: assume that $p_l=q^i_l$ for all $l\le j$. Now (1) implies

$$\begin{aligned} \sum _{i=1}^k\alpha ^i q_{j+1}^i\ge p_{j+1}. \end{aligned}$$

Analogously to the above, this implies either $q^i_{j+1}>p_{j+1}$ for some i or $q^i_{j+1}=p_{j+1}$ for all i. Using the inductive hypothesis, Lemma 1 implies that the first case is impossible. Therefore, $q^i_{j+1}=p_{j+1}$ for all i.

We conclude that $p=q^1=\cdots =q^k$. But then (1) doesn’t hold. Contradiction!

$\square$

We end by considering a related question regarding envy-freeness and the random serial dictatorship mechanism. The random serial dictatorship mechanism (Abdulkadiroğlu and Sönmez 1998) starts by drawing from a uniform distribution over all possible strict priority orders over the participating agents. Then the first agent in the resulting priority order is assigned her most preferred object, the second agent in the order is assigned her most preferred object among the remaining objects etc. The mechanism clearly induces a profile of probability-share allocations.

As above, we denote the probability-share allocation of agent i under a random-assignment mechanism f and a preference profile $\succ$ by $f_i(\succ )$. Then f is said to be envy-free if we have $f_i(\succ )\succsim _i^{FOSD} f_j(\succ )$ for all i, j and $\succ$. We say that f is weakly envy-free if there is no pair of agents i and j such that $f_j(\succ )\succ _i^{FOSD}f_i(\succ )$. Analogously to the way we define convex strategyproofness, we can also define convex envy-freeness by saying that f is convexly envy-free if for all agents i and $\succ$, there exists a utility vector $u\in \mathbb {R}^n$ that is compatible with $\succ _i$ such that $u\cdot f_i(\succ )\ge u\cdot f_j(\succ )$ for all agents j. Proposition 1 implies that this is equivalent to saying that there is no convex combination of elements in $\{f_j(\succ )\}_{j\ne i}$ that strictly first-order stochastically dominates $f_i(\succ )$. Bogomolnaia and Moulin (2001) show that while the random serial dictatorship is strategyproof, it is only weakly envy-free. The method of their proof can be summarized in a statement that is essentially identical to Lemma 1, except in that it concerns the probability-share allocations of the other agents rather than the probability-share allocations an agent can induce by misreporting. The method used in the proof of Proposition 2 can then be applied to show that the random serial dictatorship is in fact convexly envy-free.⁹ We can summarize the results of this section in the following stronger version of Bogomolnaia and Moulin (2001)’s Proposition 1:

Proposition 3

• (i) The PS mechanism is only convexly strategyproof but envy-free;

• (ii) The random serial dictatorship is strategyproof but only convexly envy-free.