The influence of splattering on the development of the wall film after horizontal jet impingement onto a vertical wall

Abstract

Liquid jet impingement is used in industries for cleaning or cooling the surfaces, since this process is characterized by high heat or mass transport rates. The impinging jet spreads radially outwards and creates a wall film flow, which is bounded by a hydraulic jump. The existing models describing the extent of the radial flow zone and the position of hydraulic jump are only applicable for small nozzle-to-target distances and low flow rates. In this work, the model is extended to include the effect of splattering liquid, which may reduce the extent of the radial flow zone considerably. The splattering in combination with the hydraulic jump position is investigated experimentally for a liquid jet impinging horizontally onto a vertical wall. In addition, the high-speed images of the jet and of the impingement region provide further insight into the splattering mechanisms. It is found that for large nozzle-to-target distances the splattered mass fraction is determined only by the jet Weber number. The hydraulic jump position can be predicted using the extended model with deviations of less than 20% in this region.

Graphic abstract

1 Introduction

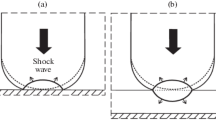
Impinging jets are used for either cooling, or cleaning purposes in different industrial branches, such as steel production as well as the chemical, pharmaceutical, and food industries. The impingement of an initially circular liquid jet onto a solid vertical wall is accompanied by development of a radial flow zone (RFZ), in which the velocity is dominated by its radial component (Aouad et al. 2016). Above and on its sides, this zone is bounded by a hydraulic jump, which is not circular as in the case of a normal impingement onto horizontal surfaces (e.g., (Craik et al. 1981; Liu and Lienhard 1993)), but has an arc shape. Downstream of the hydraulic jump outside RFZ the flow is dominated by its azimuthal velocity component and forms the circumferential flow region. Below the point of impingement, the RFZ merges with the circumferential flow forming a gravity-dominated draining film (Wilson et al. 2012), as shown in Fig. 1. This leaves the RFZ without a clearly visible and sharp boundary below the point of impingement. However, Aouad et al. (2016) suggest that the extent of the RFZ below and to its sides is comparable.

Fig. 1

Schematics of the liquid flow pattern studied in the current work. R is the position of the hydraulic jump at the azimuthal angle $\varphi$ measured from point of impingement (POI). $X$ and $Y$ are the positions of the hydraulic jump in the horizontal and vertical direction. a Top view, b sectional view through z–y-plane at POI

The extent of the RFZ on the container walls is extremely important for many applications, especially for cleaning of tanks, which are in the most of the cases vertically oriented, since this extent is directly related to the area that can be efficiently cleaned. Wilson et al. (2012) have developed a model for predicting the position of the hydraulic jump. The model is based on a momentum balance under an assumption of a parabolic velocity profile in the liquid film. The effect of gravity is neglected, and the film flow is assumed to be laminar. The hydraulic jump is assumed to be situated at the locations where the momentum of the film is balanced by the surface tension force. In the case of small nozzles (${\text{nozzle diameter }}d_{\text{N}} \le 4$ mm) and high jet velocities ($Re_{{d_{\text{N}} }}$ > $10^{4}$), the model of Wilson for the position of the hydraulic jump $X$ reduces to the following relation (Wilson et al. 2012; Wang et al. 2013a):

$$X = 0.276\left[ {\frac{{\dot{M}^{3} }}{\mu \gamma \rho }} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0pt} \!\lower0.7ex\hbox{$4$}}}} ,$$

(1)

where $\dot{M}$ denotes the jet mass flow rate, $\gamma$ is the surface tension, $\mu$ is the dynamic viscosity and $\rho$ is the density of the liquid. The jet Reynolds number is defined as

$$Re_{{d_{\text{N}} }} = \frac{{\overline{u}_{\text{jet}} d_{\text{N}} }}{\nu },$$

(2)

where $\bar{u}_{\text{jet}}$ denotes the mean jet velocity and $\nu$ denotes the kinematic viscosity of the liquid.

This model has been extended to include gravity (Wang et al. 2013b) or a transition to turbulent flow (Bhagat and Wilson 2016). In the latter case, a quartic velocity profile has been assumed in the film upstream from the location of transition to turbulence and a (1/7)-power velocity profile downstream (Bhagat and Wilson 2016). All these models have in common that they show good agreement when compared to experimental data at a low nozzle-to-target distance (nozzle distance) $L/d_{\text{N}} < 20$ and $Re_{{d_{\text{N}} }} \; < \;2\; \times \;10^{4 }$, but fail to describe the position of the hydraulic jump, if the nozzle distance is high ($L/d_{\text{N}} > 80)$ and $Re_{{d_{\text{N}} }} > 3.7 \times 10^{4 }$ (Feldung Damkjær et al. 2017). Feldung Damkjær et al. (2017) carried out an extensive experimental study of jet impingement at high flow rates up to 50 l/min ($Re_{{d_{\text{N}} }} \approx 1.9 \times 10^{5 }$) and found that Eq. (1) overpredicts the hydraulic jump position in up to a 2.5-fold factor in the range $200 < L/d_{\text{N}} < 550$.

This discrepancy can be explained by the fact that an increasing nozzle distance leads to growing disturbances of the jet surface and eventually to the jet disintegration before reaching the wall. The impact of disturbed jet and impact of separate drops may lead to splattering of liquid from the wall film. This phenomenon affects the mass and momentum balances within the liquid film and, therefore, the position of hydraulic jump. To understand the splattering phenomena, the dynamics of jet should be taken into account.

For standard ambient conditions, the disintegration of liquid jets in stagnant gases can take place in the Rayleigh breakup (I), first wind-induced (II), second wind-induced (III), or the atomization (IV) regimes. The borders between the different regimes have been initially proposed in Miesse (1955) and Ohnesorge (1936) in terms of the jet Reynolds number and Ohnesorge number:

$$Z = \frac{\mu }{{\sqrt {\rho \gamma d} }} ,$$

(3)

where $d$ denotes the jet diameter. In Lin and Reitz (1998), the regime map has been modified by taking into account the effect of surrounding gas. The new borders between different regimes include the gas Weber number, defined in the following form:

$$We_{\text{g}} = \frac{{\rho_{\text{g}} u_{\text{jet}}^{ 2} d}}{\gamma } ,$$

(4)

where $\rho_{\text{g}}$ is the density of the gas. The boundaries between different regimes as defined in Lin and Reitz (1998) are listed in Table 1.

Table 1 Regimes of jet disintegration with according borders (Lin and Reitz 1998)

In the Rayleigh regime, disintegration happens due to the dynamically unstable form of the initially cylindrical round jet, since the specific surface energy is not minimal (Rayleigh-Plateau instability). The surrounding gas plays a negligible role (Lin and Reitz 1998; Rayleigh 1878). All axisymmetric disturbances with a wavelength $\lambda$ larger than the jet perimeter are unstable, and the maximum growth rate is found for $\lambda = 4.51 d$ (Rayleigh 1878). The first wind-induced regime (II) is related to the Kelvin–Helmholtz instability, which mainly leads to the growth and propagation of axisymmetric disturbances, and the wavelength of the fastest growing disturbance decreases with increasing jet velocity, since protruding disturbances result in a lower pressure in the nearby gas phase which amplifies the former and vice versa. The physical mechanism of the jet disintegration remains capillary pinching, as in (I) (Weber 1931; Haenlein 1931). With further increase of the jet velocity, the disintegration takes place in the regime (III), dominated by interaction with the surrounding gas. In this regime, both symmetric and asymmetric disturbances grow and propagate due to aerodynamic forces. Even higher jet velocities will eventually lead to jet atomization. In these regimes (III) and (IV), different from the two regimes mentioned previously, surface tension plays a dampening role (Haenlein 1931; Lin and Creighton 1990). Besides the influence of liquid and gas properties, several authors report the influence of the flow inside the nozzle on the jet break-up (Lin and Creighton 1990; Grant and Middleman 1966; Reitz 1978; Sallam et al. 2002). This flow can be influenced using different nozzle designs such as pipe or convergent nozzles (Xu and Antonia 2002). In this work, the liquid jets will be in the first and second wind-induced regime although features of the atomization regime are already visible.

As the disturbed jet impinges onto the wall, the surface disturbances of the jet lead to surface waves in the wall film flow. If amplified, these waves grow along the flow direction and eventually form droplets which detach from the film surface at a certain distance from the impingement point known as the droplet departure radius (Bhunia and Lienhard 1994a; Lienhard et al. 1992; Errico 1986). It was shown that the jet surface disturbances lead to splattering only in the case if a certain threshold based on the jet velocity and the bulge height (Lienhard et al. 1992), or alternatively on the root mean square roughness of the film surface (Bhunia and Lienhard 1994b), is reached. The higher the jet velocity, the smaller disturbance is required for splattering.

Lienhard et al. (Errico 1986) study the influence of splattering on cooling by impingement of vertical jets emerged from a pipe nozzle onto a horizontal heated wall. They measure the speed of the droplets leaving the wall flow. Then, assuming that the droplet velocity is equal to the velocity of film surface at the position of drop departure, they calculate the droplet departure radius. Lienhard et al. come to conclusion that the droplet departure radius is approximately constant, $r_{\text{s}} \approx 5.71 d_{\text{N}}$. They also propose a model for the splattered mass fraction $\xi$ = $\xi \left( \omega \right)$ for vertical impact onto a horizontal wall, in which $\omega$ (Eq. 6) is a scaling factor that represents the roughness of the jet surface at point of impact and depends on jet Weber number and the nozzle distance (Errico 1986). This model is based on an assumption that the surface disturbances originate from turbulent pressure fluctuations at the nozzle outlet and grow exponentially in time in the Rayleigh mode. Bhunia and Lienhard (1994a, b) improved this model by extending it to a wider range of parameters and derived a correlation for the splattered mass fraction on basis of experimental data for a wider range of parameters compared to (Errico 1986):

$$\xi = - \;0.258\; + \;7.85\; \times \;10^{ - 5} \omega \; - \;2.51\; \times \;10^{ - 9} \omega^{2} ,$$

(5)

where

$$\omega = We_{{d_{\text{N}} }} \exp \left( {\frac{0.9710 }{{\sqrt {We_{{d_{\text{N}} }} } }}\frac{L}{{d_{\text{N}} }}} \right)$$

(6)

$$We_{{d_{\text{N}} }} = \frac{{\rho_{l} \bar{u}_{\text{jet}}^{2} d_{\text{N}} }}{\gamma } .$$

(7)

Correlation (5) is valid in the range of parameters $1.2 \le L/d_{\text{N}} \le 110,$ $1400 \le We_{{d_{\text{N}} }} \le 31,000$, and $4400 \le \omega \le 10,000$ (Bhunia and Lienhard 1994a) for vertical impingement onto a horizontal wall. Wang et al. (2013b) report a poor agreement between their experimental data and correlation (5) and suggest that the reason for the discrepancy is the difference in the nozzle design. In Wang et al. (2013b), a convergent nozzle has been used. In addition, Wang et al. have performed experiments on horizontal jet impingement onto a vertical wall, which could be an additional reason for deviation from Eq. (5), derived for jet impact onto horizontal walls.

This work has two major goals: first, to enlighten the influence of the different nozzle types (Wang et al. 2013b; Bhunia and Lienhard 1994a, b), which influence the jet disintegration (Grant and Middleman 1966), on the splattering phenomena, since they have never been studied systematically. Second, the development of a predictive model describing the extent of RFZ at high nozzle distances by taking into account the splattering of liquid from the wall film, since this phenomenon becomes significant at high nozzle distances ($L/d_{\text{N}} > 100$). Toward these aims, the splattered mass fraction is measured for the horizontal jet impact onto a vertical wall in a wide range of parameters. The measured splattered mass fraction is taken into account in the momentum balance equation for determination of the size of RFZ. The resulting predicted hydraulic jump positions in the vertical ($Y$) and horizontal ($X$) directions are compared with the measured values. Since the nozzle type has been reported to affect the phenomenon of splattering, both convergent and pipe nozzles have been used in our experiments. High-speed imaging of the jet and the impingement region has been used to examine the morphology and evolution of jet and of the wall film. In addition, the influence of tube deflections upstream the nozzle, which are common in tank cleaning systems, such as rotatory jet heads, on the splattering phenomenon and the hydraulic jump position is investigated.

2 Methods

2.1 Experimental setup

The main part of the test setup used in this work is the open water circuit pictured in Fig. 2. The water used in the test stand is a mixture of tap water provided by the city of Darmstadt and deionized water (1:3). This procedure results in soft and non-corrosive water. The surface tension was measured (DCAT 25, Data Physics) to $\gamma = \left( {72.3\; \pm \;0.3} \right)\; \times \;10^{ - 3} \;\;{\text{N/m}}$ after mixing and after 6 weeks in the test stand. During the measurement, the water is pumped from the tank (1) by a multi-stage centrifugal pump (2, IN-VB 2-140, Speck) passing the Coriolis mass flow meter (TME 5, Heinrichs Messtechnik GmbH). Before and after the pump, two pressure sensors are installed. The water temperature is kept at $20 \; \pm \; 0.5 \;\;^\circ {\text{C}}$ using counter flow heat exchanger and a bath thermostat (not depicted). The sectional valves (3, EV210B, Danfoss) are used to rapidly shut off the water from the nozzle (4) and lead it to the tank instead. Behind the valves, the water flows through a 19 mm hose and then through a 500 mm long 25 mm pipe before entering the nozzle, where a liquid jet is formed. This jet enters the wet cell (9) (1200 high, 1000 mm deep and 700 mm wide) through a 100 mm diameter hole. Thereafter, the jet impinges onto the transparent wall (5), having passed the nozzle distance $L$. After impingement, a part of liquid with the mass flow rate $\dot{M}_{\text{s}}$ is splattered, and the rest of the liquid with the mass flow rate $\dot{M}_{\text{r}}$ remains and spreads on the wall. The splattered liquid collected by the tub (6), and the liquid spread on the wall is collected by the tub (7). The liquid from both tubs can be withdrawn from the circuit at the sampling point (8) into two separate containers. The nozzle is mounted to a circular positioning device (CPD, part no. 21161, Norelem©), which is placed on a sled to be able to vary the distance. Each nozzle was positioned by driving the nozzle against the wall for zeroing and then to the desired nozzle distance $L$. To guarantee a horizontal impact (normal to $Y$ axis, Fig. 1), the nozzle was slightly inclined using the CPD. The angle $\alpha$ between the nozzle axis and horizontal direction has been calculated using the parabolic throwing, neglecting drag (Eq. 8) and reached a maximum of 7°.

$$2\alpha = \sin^{ - 1} \left( {\frac{2Lg}{{\bar{u}_{\text{jet}}^{2} }}} \right)$$

(8)

Fig. 2

Schematic of the test stand used in this work: tank (1), centrifugal pump (2), sectional valves (3), nozzle (4), transparent wall (5), collecting tubs (6) and (7), sampling position (8), and wet cell (9)

The CPD was leveled for each nozzle. This was done using a precision spirit level for the pipe nozzles, or stitched images resulting from high-speed images (see Sect. 2.5) have been used for the other nozzle configurations (Table 2). For guaranteeing normal impact to the $X$ axis, the sled was driven back and forth while the mounting was adjusted until the POI remained on vertical line.

Table 2 Nozzle dimensions and experimental parameters

Two different nozzle types have been used in experiments: pipe nozzles and convergent nozzles. Figure 3 illustrates the setup with the 4 mm pipe nozzle at $L/d_{\text{N}} = 33$. In Table 2, all nozzle dimensions and the experimental parameters investigated with the corresponding nozzle are listed. $Re_{{d_{\text{N}} }}$ (Eq. 2) and $We_{{d_{\text{N}} }}$ (Eq. 7) are calculated from the mean velocity. The values of uncertainty in brackets are calculated based on the maximum deviation in the mass flow rate (3%) from the mean value, since the influence of other sources of uncertainties was much weaker (the temperature remained in a narrow range and the uncertainty of the nozzle diameter was less than 1 µm). It is known that the maximum velocity in the nozzle flow does not significantly differ from the mean velocity for fully turbulent pipe flows ($u_{ \hbox{max} } \approx 8/7 \bar{u}$). Since the boundary layer in convergent nozzles is much thinner than in pipe nozzles, this difference is even less for the convergent nozzles (Xu and Antonia 2002).

Fig. 3

Image of jet originating from 4 mm pipe nozzle impinging on transparent wall inside wet cell. ($L/d_{\text{N}} = 33$, without meshes for visibility)

The two pipe nozzles of diameters $d_{\text{N}} =$ 3 mm and 4 mm have a length to diameter ratio $l_{\text{N}} /d_{\text{N}} = 42$. This configuration facilitates the development of fully turbulent flow within the nozzle for the whole range of $Re_{{d_{\text{N}} }}$ listed in Table 2 (Herwig 2008). The two convergent nozzles (TE20A652, Alfa Laval Mid Europe GmbH) also have the diameters 3 mm and 4 mm and are much shorter $l_{\text{N}} /d_{\text{N}} =$ 3.3 (2.5, respectively). All four nozzles were carefully treated with a reamer of the appropriate diameter to provide a smooth inner surface. For the 4 mm convergent nozzle, two modifications were used in addition to the plain nozzle. To simulate the situation in tank cleaning, a 2 × 90° deflection was included before the inlet of the 4 mm convergent nozzle in these modifications. Modification 1 (convD) is the 4 mm convergent nozzle mounted in front of the deflection. In modification 2 (convDS), the same deflection is used, while a strainer was inserted into the nozzle by Alfa Laval Mid Europe GmbH, which was supposed to suppress large eddy distortions and swirl in the flow. Including these two modifications, we used 6 nozzle configurations.

2.2 Splattered mass fraction

For measuring the splattered mass fraction, the target wall has been positioned in a way that—besides pinches of created mist—only water from the draining film has entered one tub, while the splattering water enters the other. Toward this goal, the edge of the transparent target wall was put close to the wall of the collection container leaving a gap of about 10 mm. The gap between the transparent wall and the wet cell walls was closed with a foil. The remaining cell walls were covered with fine (mesh count 100) and coarse (mesh count 30) stainless steel mesh to avoid splash back from the cell walls to the transparent target wall. Before starting the measurement, the wet cell walls were initially wetted and drained. Then, the water was turned toward the nozzle for 90 s. Water was collected during the impingement and 30 ± 5 s after to allow time for drainage. After that time little amount of water (< 30 g) would still flow from the sampling position for splattered water but, as the ball valves were closed, remained in the tubing. This amount leads to an underestimation of the splattered mass fraction to a maximum of 0.4%. The containers, filled with the splattered mass $M_{\text{s}}$ and the mass drained from the transparent wall $M_{\text{r}}$, are then weighed with a Kern 572-55 scale. After the weighing, the water was filled back into the circuit. The procedure was repeated three times for each parameter setting and the splattered mass fraction was calculated using the equation

$$\xi = \frac{{M_{\text{s}} }}{{M_{\text{r}} + M_{\text{s}} }}.$$

(9)

2.3 Position of the hydraulic jump

The extent of the RFZ was measured at two positions, vertically and horizontally, from the point of impingement. For this aim, a high-speed camera (MotionBlitz EoSens Cube 7, Mikrotron GmbH) was mounted behind the transparent wall, which was enlightened from the side of the nozzle. The images were taken with a frame rate ${\text{fr}} = 1 \;\;{\text{kHz}}$ and a shutter time $t_{\text{s}} = 10$ μs. The position of the hydraulic jump was then measured manually. For each parameter set, an average image was created from 200 images taken in a time span of 200 ms. An example of a single image and an average image is shown in Fig. 4. The distance in pixels has been converted to millimeters using a reference image for the set camera position, giving 0.289 mm/Pi. The fluctuations of the hydraulic jump position in horizontal direction within this time interval were in the order of 1 cm, which is why the hydraulic jump is rather smeared in the mean image.

Fig. 4

Single high-speed image of the jet impingement taken through the transparent wall (left). Mean image of 200 succeeding images (right). The measured positions X and Y are shown. (${\text{fr}} = 1 \;\;{\text{kHz}},\;\;t_{\text{s}} = 10$ μs)

The fluctuations in the vertical direction were less than half of that. The uncertainty, therefore, amounts to ± 0.8 cm in $X$ direction and ± 0.4 cm in $Y$ direction. The presented $X$ values are the mean values derived from the left and right of the POI.

2.4 Model for the prediction of the hydraulic jump position

It is assumed that following the normal jet impingement the liquid spreads on the wall in such a way that the water is distributed equally in all directions along the circumference. Following Wang et al. (2013b), the momentum balance on a streamline is given by the following relation:

$$\frac{\text{d}}{{{\text{d}}r}}\left( {\frac{6}{5}\rho h\bar{u}^{2} r} \right) = - \tau r - rh\rho g\cos \varphi .$$

(10)

In this equation, $r$ is the distance from the point of impingement, $\varphi$ is the inclination angle to the vertically upward direction, $g$ is the gravitational constant, $h = h\left( {r,\varphi } \right)$ is the film thickness, $\bar{u}$  =  $\bar{u}\left( {r,\varphi } \right)$ is the average velocity and $\tau = \tau \left( {r,\varphi } \right)$ is the shear stress at the wall. A parabolic velocity profile, which is characteristic for a hydrodynamically developed laminar flow, is assumed

$$u = u_{{max} } \left( {2\frac{z}{h} - \frac{{z^{2} }}{{h^{2} }}} \right),\;\;\bar{u} = \frac{2}{3}u_{{max} } ,$$

(11)

where $z$ is the coordinate normal to the wall. The shear stress can be determined from the relation

$$\tau = 3\frac{{\mu \bar{u}}}{h}.$$

(12)

Mass balance together with the assumption of equal distribution of mass flow in all directions leads to the following relation:

$$\dot{M} = 2\pi rh\rho \bar{u}.$$

(13)

Combining Eqs. (10) with (13) leads to:

$$\frac{\text{d}}{{{\text{d}}r}}\bar{u} = - 10\pi^{2} \frac{{\mu \rho_{l} \bar{u}^{2} r^{2} }}{{\dot{M}^{2} }} - \frac{5g\cos \varphi }{{6\bar{u}}}.$$

(14)

This ordinary differential equation is then solved to determine $\bar{u}\left( r \right)$ for each $\varphi$. It is assumed that the flow is terminated as soon as the surface tension force balances the momentum flow, which, according to Craik et al. (1981), happens at the location where the average velocity reaches the threshold value

$$\bar{u}_{\gamma } = \gamma \frac{5r\pi }{{3\dot{M}}}.$$

(15)

This relation is valid for $\dot{M} > 1 \;\;{\text{kg/min}}$, where the extent of the RFZ becomes independent of the substrate properties (Wang et al. 2013a).

Splattering affects the distribution of film thickness and average velocity, because the liquid mass and momentum are leaving the wall flow in the form of droplets. To take this phenomenon into account, we modify Wang’s procedure and solve Eq. (14) in two distinct regions. We assume that the splattering occurs at the radial position $r = r_{\text{s}} = 5.71 d_{\text{N}}$ (Errico 1986). In the vicinity of the impingement point, as long as no splattering has taken place ($r \le r_{\text{s}}$), Eq. (14) is solved with the measured jet mass flow rate $\dot{M}$. The jet speed $\bar{u}_{\text{jet}}$ is used as an initial condition, $\bar{u}\left( {r = d_{\text{N}} /2} \right) = \bar{u}_{\text{jet}}$. We assume that the splattered mass leaves the wall flow instantly at $r_{\text{s}}$. Therefore, for $r \ge r_{\text{s}}$, we solve the modified Eq. (16), whereas the mass flow rate $\dot{M}$ is replaced with $\dot{M}_{\text{r}} = \dot{M}\left( {1 - \xi } \right)$, using $\bar{u}\left( {r = r_{\text{S}} } \right)$ as start condition:

$$\frac{\text{d}}{{{\text{d}}r}}\bar{u} = - 10\pi^{2} \frac{{\mu \rho_{l} \bar{u}^{2} r^{2} }}{{\dot{M}_{\text{r}}^{ 2} }} - \frac{5g\cos \varphi }{{6\bar{u}}}.$$

(16)

The velocity corresponding to the position of hydraulic jump is modified accordingly

$$\bar{u}_{\gamma } = \gamma \frac{5r\pi }{{3\dot{M}_{\text{r}} }}$$

(17)

2.5 High-speed images of the jet and jet surface roughness

To gain a deeper understanding of the influence of the different nozzle types on splattering phenomenon, we used high-speed imaging of the jet at different nozzle distances $L$. In this case, the nozzle was driven into the field of view of the camera having the size a × b, the objective lens was focused on the nozzle and then the nozzle was driven back to the desired distance $L$. The nozzle angle was arranged in a way that the jet passed the field of view horizontally. For imaging, the shadow method was applied using a 200 W LED light source and diffusive Plexiglas^® panel on one side of the jet. The high-speed camera (MotionBlitz EoSens Cube 7, Mikroton) was placed at the opposite side of the jet at a distance of 550 mm. In this arrangement, the pixels were converted to millimeters using a reference scale, giving 0.0451 mm/Pi. The images were then taken with a frame rate ${\text{fr}} = 3.5,\;\; 5$ or $15\;\; {\text{kHz}}$ and a shutter time of $t_{\text{s}} = 10$ μs. The frame rate was changed in case the image height had to be increased, to be able to capture the entire jet width, which spread with increasing nozzle distance. Each measurement was carried out during at least 1 s. The images contain the information of the jet shape between the distance $L$ and $L + b$ from the nozzle at the time $t$. The images were processed using Matlab™ and combined into a stitched image representing the temporal evolution of the jet shape at the nozzle distance L, so that overlapping is eliminated (detailed procedure in the “Appendix”). The results of each measurement were distributed into 5 stacks of images, to reduce the matrix size. Neglecting the change of the surface shape within the time span between two frames ($\Delta t$ = 0.067 ms, 0.2 ms or 0.29 ms for the frame rates of 15 kHz, 5 kHz and 3.5 kHz, respectively), we extract the coordinates of the upper, $y^{\text{u}} \left( t \right)$, and lower, $y^{\text{l}} \left( t \right)$ boundaries of the jet at the desired distance $L$ over the time of experiment. A Fourier analysis justifies neglecting these changes, since no peaks at a frequency corresponding to the frame rate are visible. Note that for this setting the temporal resolution is thereby independent of the frame rate but only depends on the jet velocity and the scaling factor of 0.0451 mm/Pi. This results in 235,000–535,000 Pi/s.

Finally, the root mean square (RMS) roughness $R_{\text{q}}$ of the jet surface was calculated for upper and lower border of the jet, $y^{\text{u}}$ and $y^{\text{l}}$, using the following equations:

$$R_{\text{q}}^{\text{u}} = \left( {\frac{1}{n}\mathop \sum \limits_{i}^{n} \left( {y_{i}^{\text{u}} - \bar{y}^{\text{u}} } \right)^{2} } \right)^{1/2} ,\;\;R_{\text{q}}^{\text{l}} = \left( {\frac{1}{n}\mathop \sum \limits_{i}^{n} \left( {y_{i}^{\text{l}} - \bar{y}^{\text{l}} } \right)^{2} } \right)^{1/2} .$$

(18)

In Eq. (18), $\bar{y}$ denotes the mean value of $y$. After that the average of the values $R_{\text{q}}^{\text{u}}$ and $R_{\text{q}}^{\text{l}}$, $R_{\text{q}}$, was computed. This procedure results in five values—one for each stack of images—for each parametric setting. We present the mean as well as the minimum and maximum of those five values in the following section. For $L/d_{\text{N}} \ge 167$ ($L/d_{\text{N}} \ge 100$ for $Re_{{d_{\text{N}} }} \approx 41,000)$, the jet was disintegrated using pipe nozzles. In these cases, calculating $R_{\text{q}}$ was performed excluding the data points where no jet was found. In addition, $R_{\text{q}}$ becomes less accurate in these cases, since drops or ligaments overlapped with the jet at the horizontal positions at some points. Examples of non-binary stitched images showing these conditions are provided in the “Appendix” for illustration purposes and were not used for the roughness measurements.

3 Results

The results are reported in the following order. At first, the measured values of the splattered mass fraction are presented. The dependency of $\xi$ on the nozzle distance, mass flow rate and nozzle type is presented and rationalized by relating the splattering phenomena to the behavior of jet obtained from the high-speed images and measured jet surface roughness $R_{\text{q}}$. A correlation for the splattered mass fraction at high nozzle distances is given. Finally, the measured hydraulic jump positions in directions X and Y are compared with the model predictions.

3.1 Splattering

The splattered mass fraction was measured for all 6 nozzle configurations for different nozzle distances and mass flows. The results are presented for different nozzle types and jet Reynolds numbers versus the nozzle distance in Fig. 5 (for $d_{\text{N}}$ = 3 mm) and Fig. 6 (for $d_{\text{N}}$ = 4 mm). In Fig. 5, we compare the results for the pipe and the convergent nozzle with 3 mm diameter for four Reynolds numbers. It can be seen that the splattered mass fraction $\xi$ reaches values up to almost 0.7. The variation of the mass flow rate (max. 3%) is the most probable cause for the data scattering among measurements of the same parameter settings, which is generally below 3% (see the error bars). Two major conclusions can be drawn by comparing these two nozzles. First, $\xi$ reaches significantly higher values for $L/d_{\text{N}} = 17 \ldots 167$, if a pipe nozzle is used instead of a plain convergent nozzle (without modifications). For the pipe nozzles, a local maximum of splattered mass fraction is observed at $L/d_{\text{N}} \approx 33$ and $Re_{{d_{\text{N}} }} \ge 51,100$. In this region, $L/d_{\text{N}} = 17 \ldots 67$, $\xi$ increases strongly with the jet Reynolds number. For example, increasing the Reynolds number 41,000–71,400 (mass flow rate from 5.85 to 10.1 kg/min) leads to the increase of $\xi$ from 0.35 to 0.63. The remaining mass flow rate $\dot{M}_{\text{r}}$ decreases accordingly.

Fig. 5

Splattered mass fraction $\xi$ for a pipe (solid) and a convergent (dashed) 3 mm nozzle for different nozzle distances and mass flows

Fig. 6

Splattered mass fraction $\xi$ for different nozzle distances and mass flows for 4 mm nozzles of different type: pipe (solid), convergent (dashed), convergent with deflection (dotted) and convergent with deflection and strainer (dashed/dotted)

Second, at higher nozzle distances ($L/d_{\text{N}} \ge 250$) the $\xi$ values do not depend significantly on the nozzle type. Comparison between the data presented in Fig. 5 and in Fig. 6 shows that the behavior of pipe nozzles and plain convergent nozzles is qualitatively similar for the nozzles with 3 mm and 4 mm orifices.

To relate the splattering phenomenon to the hydrodynamics of the impacting jets, the jet morphologies are examined at several distances from the nozzle. In Fig. 7, the stitched images of jets from the 4 mm pipe nozzle (upper left) are compared with those of the 4 mm convergent nozzle (upper right) for several nozzle distances. For $L/d_{\text{N}} = 8$, the jet on the left appears thicker, although the orifice has the same diameter for both jets. This is due to the three-dimensional distortions of the jet surface that are projected into the two-dimensional image. In fact, at distances of $L/d_{\text{N}} = 8 \ldots 67$ the surface of the jet originating from the pipe nozzle differs significantly from that of a convergent nozzle. The former shows disturbances with larger amplitude and shorter wavelength than the latter. The reason is that the pipe nozzles, which are significantly longer than the convergent nozzles (see Table 2), are characterized by the fully developed turbulent pipe flow. As soon as water leaves the constricting nozzle walls of the pipe nozzle, turbulent eddies lead to short wave surface roughness. For the convergent nozzles, the turbulence is not fully developed, the turbulent eddies are larger (Herwig 2008) and their intensity does not suffice to lead to significant surface roughness directly after the nozzle exit. As shown by Lin and Creighton (1990), surface tension suppresses disturbances with short wavelength and, therefore, prevents their development into droplets which could be detached from the jet. In contrast, disturbances with higher wavelength are enhanced and lead to jet break up by capillary pinching (Rayleigh 1878; Haenlein 1931). However, if the jet impinges onto the target plate, while short wavelength disturbances are apparent (for relatively small nozzle-to-target distances), splattering is increased. Since the intensity of turbulence fluctuations increases with increasing Reynolds number (Wolf et al. 1995; Mansour and Chigier 1994), Reynolds number exerts a strong influence on the jet surface dynamics at small distances. Since the short wave disturbances are reduced along the jet flow direction, these disturbances are only apparent for $L/d_{\text{N}} \le 33$, which leads to the maximum in the $\xi$ vs. $L/d_{\text{N}}$ curve, and the shape of the jets originating from the different pipe and plain convergent nozzles look similar at $L/d_{\text{N}} \ge 100$ for the presented Reynolds number. The distance $L/d_{\text{N}}$, from which the jet shape is only weakly influenced by the nozzle type, decreases with increasing Reynolds number. In addition, for the Reynolds number 41,600 (51,000, 59,600, 74,800), the jet from the pipe nozzle is disintegrated at $L/d_{\text{N}} = 100 \left( {133, 133, 167} \right)$, while the jet from the convergent nozzle is disintegrated at $L/d_{\text{N}} = 167$ for all Reynolds numbers. This finding is valid for both the 3 mm and 4 mm nozzles and is in agreement with the finding of Grant and Middleman, who state that a jet originating from a short nozzle $\left( {l_{\text{N}} /d_{\text{N}} = 6.9} \right)$ is more stable than a jet from a pipe nozzle $\left( {l_{\text{N}} /d_{\text{N}} \ge 26} \right)$ in the first and second wind-induced regimes (Grant and Middleman 1966).

Fig. 7

Stitched images of a water jet originating from a 4 mm pipe or convergent nozzle as well as from a convergent nozzle with two 90° deflections upstream the nozzle entering at different nozzle distances. $\left( {{Re}_{{d_{\text{N}} }} = 59,600} \right)$

The jet surface roughness $R_{\text{q}}$ is plotted versus $L/d_{\text{N}}$ for all 4 mm nozzles and two values of the Reynolds number in Fig. 8. $R_{\text{q}}$ increases in the range $L/d_{\text{N}} = 33 \ldots 6 7$ for the pipe nozzle, whereas $\xi$ is reduced in the same range (see Fig. 6). The jet speed does not change with the nozzle distance in this range. Therefore, the jet speed $u_{\text{jet}}$ and $R_{\text{q}}$ alone do not fully describe the splattering behavior by jet impingement of a given liquid, as suggested by Bhunia and Lienhard (1994a, b). It can be assumed that the typical scale, or the wavelength of the disturbance, which is not reflected in the roughness parameter $R_{\text{q}}$, also plays a role. Note that the data presented in Bhunia and Lienhard (1994a, b) also tend to show a local maximum in the range of nozzle distances mentioned above.

Fig. 8

Surface roughness of jets originating from 4 mm nozzle configuration for different nozzle distances and mass flows: pipe (solid), convergent (dashed), convergent with deflection (dotted) and convergent with deflection and strainer (dashed/dotted). Filled markers represent values with a disintegrated jet

In the following, the influence of the modifications of the convergent nozzles is discussed. It is seen in Fig. 6 that using a 2 × 90° deflection in front of the convergent nozzle increases the degree of splattering. For the two highest $Re_{{d_{\text{N}} }}$, the $\xi$ values without strainer exceed those for the pipe nozzles, and the corresponding $\xi$ versus $L/d_{\text{N}}$ curves exhibit weak local maxima at $L/d_{\text{N}} \approx 67$. At this distance, the $\xi$ values exceed those of the plain convergent nozzle by a factor of 1.5–3. Additionally, it can be seen Fig. 7 (Figs. 18, 19 in the Appendix) that the jet tends to spread in the plane spanned by the vertical and the jet axis, as the images remained sharp and did not become blurry. This could be due to Dean vortices in the flow, which are known to appear in and downstream a bend flow (Röhrig et al. 2015; Dutta et al. 2016) and probably also occur in the present sharp turns. This spreading also seemed to have a periodical component with a frequency of about 4 Hz. Starting from $L/d_{\text{N}} = 67$, the vertical undulations of the jet shape become visible in Fig. 7.

It is clearly seen in Fig. 7 that the strainer strongly suppresses the jet undulation caused by the deflection. As a result, the jet roughness (see Fig. 8) and also the degree of splattering are reduced accordingly (see Fig. 6). The splattered mass fraction exceeds the corresponding values for the plain convergent nozzle, but is lower than that for the pipe nozzle.

One of the important practical implications of the presented data is the existence of a local maximum in the $\xi$ versus $L/d_{\text{N}}$ curve. This behavior has been observed for pipe nozzles and for convergent nozzles combined with sharp bending immediately preceding the nozzle. For the applications where these nozzle types are used and splattering should be minimized, the nozzle distance should be chosen in such a way that the maximum for splattering is avoided.

It can be seen from Figs. 5 and 6 that for $L/d_{\text{N}} \le 167$ the splattered mass fraction $\xi$ depends on the nozzle type and cannot be expressed as a function of $Re_{{d_{\text{N}} }}$ and $We_{{d_{\text{N}} }}$. Moreover, even including $R_{\text{q}}$, it is impossible to correlate the data. An attempt of describing the amount of splattering as a sole function of $Re_{{d_{\text{N}} }}$, $We_{{d_{\text{N}} }}$, and jet roughness $R_{\text{q}} /d_{\text{N}}$ did not lead to distinct results. However, for higher nozzle distances, which are typical for the tank cleaning systems, splattering can be correlated well using the Weber number alone. This can be explained by the fact that at high distances from the nozzle the jet is already disintegrated or the jet disturbances have at least grown to a large extent. Therefore, the impingement is less than that of an impinging jet but rather that of a sequence of drops onto a thin liquid film. The splattering of a sequence of impinging drops on a well-defined point of impingement on a horizontal substrate has been investigated by Yarin and Weiss (1995). They have correlated the onset of splashing well using the dimensionless velocity

$$U = Ca \lambda_{\text{drop}}^{{\frac{3}{4}}} \approx 17,$$

(19)

where $Ca = \bar{u}_{\text{drop}} \mu /\gamma$ is the capillary number and $\lambda_{\text{drop}}$ is the dimensionless distance between successive impacting droplets, depending on the drop frequency $f$ in the order of 20 kHz:

$$\lambda_{\text{drop}} = \left( {\frac{v}{f}} \right)^{{\left( {\frac{1}{2}} \right)}} \sigma /\left( {\rho v^{2} } \right)$$

(20)

The distance $\lambda_{\text{drop}}$ affects the splashing threshold, since it determines the thickness of the liquid film on which the drops impinge. However, the drop frequency in the present work is in the range of 0.7–1.4 kHz and the drops are not aligned (see Fig. 7). Following the approach of (Yarin and Weiss 1995) did not lead to a well-described correlation.

Splattered mass fraction depends, besides the Weber number and the nozzle-to-target distance, on the nozzle type. However, $\xi$ values for the configuration convD (largest values of $R_{\text{q}} /d_{\text{N}} \approx 1.6$, at $L/d_{\text{N}} = 333$) are only about 8% higher than that for the plain convergent nozzle (lowest value of $R_{\text{q}} /d_{\text{N}} \approx 0.6$, at $L/d_{\text{N}} = 333$). Therefore, we suggest the following correlation for the splattered mass fraction, based on the presented experimental data:

$$\xi = 0.045 We_{{d_{\text{N}} }}^{0.275} \;{\text{for}}\;L/d_{\text{N}} \ge 250,\;5000 < We_{{d_{\text{N}} }} < 25,000$$

(21)

This correlation is illustrated in Fig. 9 together with the experimental data. It is seen that all the data deviate from the proposed correlation not more than by 10%. The proposed correlation is used in the model describing the position of hydraulic jump (Sect. 2.2).

Fig. 9

The splattered mass fraction $\xi$ plotted versus $We_{{d_{\text{N}} }}$ for different nozzles and different nozzle distances in the range $L/d_{\text{N}} = 250 \ldots 570$. Symbols: experimental data; solid line: Eq. (21); dash-dotted lines: Eq. (21) $\pm 10\%$

For the lowest nozzle distances $L/d_{\text{N}} = 3$ for the pipe nozzle and $L/d_{\text{N}} = 8$ for the convergent nozzle, no actual splattering took place. The measured values of the splattered liquid mass result from frequent dripping from the very thick hydraulic jump. For higher nozzle distances, small droplets leaving the wall flow may collide with the hydraulic jump. This seems to suppress the formation of big drops.

3.2 Position of the hydraulic jump

During the measurements of the hydraulic jump position, we could observe what is often described in the literature: the point of impingement is surrounded by a smooth surface region. Even for turbulent jets, the wall flow is initially laminarized by the pressure gradient in the stagnation region. At some distance from the point of impingement, the surface of the wall film becomes rough, which is usually interpreted as the turbulent boundary layer reaching the surface of the wall jet (Liu et al. 1991; Azuma and Hoshino 1984). This transition to turbulent flow has been observed at low nozzle distances whenever a plain convergent nozzle was used. For the pipe nozzles, this behavior was not observed for the range of $Re_{{d_{\text{N}} }}$ and $L/d_{\text{N}}$ presented in this work: the film surface was rough within the whole RFZ. Either turbulent fluctuations were still apparent during the development of the wall flow, or the initial jet roughness (although small) leads to the disturbed surface of the wall flow.

As explained in Sect. 2.4, splattering affects the mass and momentum balances in the wall film and, therefore, influences the film thickness and velocity and, as a consequence, the position of the hydraulic jump. The results of the measurements of the hydraulic jump position in the vertical direction (denoted as $Y$ in Fig. 1) are shown in Fig. 10 compared to the prediction using Eqs. (16) and (17) for the 4 mm pipe nozzle (a) and convergent nozzle (b). The correlation (21) has been used for computation of $\dot{M}_{\text{r}}$ for distances $L/d_{\text{N}} \ge 250$, while the measured values were used for lower nozzle distances. For comparison, the results of the model prediction without splattering (Eqs. (14) and (15), $\xi = 0$) are depicted as a solid line. In the case of the pipe nozzle, high discrepancy between the results of the measurement and prediction for the lowest nozzle distance is observed. This can be attributed to the fact that for this nozzle distance the jet turbulence at the nozzle outlet is not dissipated before the jet impinges onto the wall (Mansour and Chigier 1994). If the wall jet is not laminarized and the film flow is turbulent, the shear stress at the wall is much higher than that assumed in Eq. (12), and the average velocity within the film decreases much faster than that in the case of laminar film flow. As a result, the critical velocity corresponding to the formation of hydraulic jump is reached at a much lower distance from the point of impingement. For nozzle distances $L/d_{\text{N}} \ge 17$, where the assumption of a laminar wall film flow is justified, the agreement between the predicted and measured position of hydraulic jump is very good. It is noteworthy that $Y$ shows a local minimum for $L/d_{\text{N}} = 33$ in the whole range of mass flow rates, corresponding to the local maximum of splattered mass fraction. Additionally, the numerical results tend to slightly underpredict the hydraulic jump position for smaller nozzle distances and to overpredict the measured $Y$ values for high nozzle distances. One possible reason for this discrepancy is that the assumption of the constant radius of splattering $r_{\text{s}}$ does not perfectly describe the process. Figures 11 and 12 show sets of succeeding images of the wall film for different nozzle distances to follow the evolution of a surface wave into splattering droplets. The images show that for the lower nozzle distance $L/d_{\text{N}} = 17$ (Fig. 11) smaller and more frequent waves are formed on the surface of the wall jet than for $L/d_{\text{N}} = 67$ (Fig. 12). In the latter case, some liquid seems to detach from the wall film at the crest of these high waves at locations ahead of $r_{\text{s}}$ and, thereby, splattering is likely to take place at a smaller radius for the higher nozzle distance. This suggests that the splattering position depends on the impinging jet roughness.

Fig. 10

Measured and calculated position of the hydraulic jump for different nozzle distances for the 4 mm pipe nozzle (a) and the 4 mm convergent nozzle (b). Dash-dotted lines and empty markers: solution of Eqs. (16) and (17) including splattering computed using Eq. (21) for $L/d_{\text{N}} \ge 250$. Filled markers: experimental results. Marker shape corresponds to the nozzle distance (see legend). Solid line: solution of Eqs. (14) and (15) (splattering neglected)

Fig. 11

Set of succeeding images of jet impingement originating from a 4 mm pipe nozzle. $Re_{{d_{\text{N}} }} = 51,000,L/d_{\text{N}} = 17, {\text{fr}} = 2 \;\;{\text{kHz}}$

Fig. 12

Set of succeeding images of jet impingement originating from a 4 mm pipe nozzle. $Re_{{d_{\text{N}} }} = 51,000, L/d_{\text{N}} = 67, {\text{fr}} = 2 {\text{ kHz}}$

Note that determining where the actual splattering takes place is difficult. Therefore, calculating the droplet departure radius from the measured droplet speed as suggested in (Errico 1986) is a feasible alternative.

For the convergent nozzle, the $Y$ values decrease monotonically with increasing nozzle distance without showing any local minimum. The agreement between the predicted and measured position of hydraulic jump is very good, and the deviation between them is independent of the nozzle distance for convergent nozzles. In Fig. 13, the results of computations obtained by solving Eqs. (16) and (17) in the $Y$ versus $X$ plane in comparison with the measurement results are shown for the 4 mm pipe nozzle and $Re_{{d_{{_{\text{N}} }} }} = 59,600$ and different nozzle distances. The results show the features mentioned above, particularly the shortcoming of the prediction for $L/d_{\text{N}} = 3$, whereas a good agreement for larger nozzle distances is observed.

Fig. 13

2-D results of calculated position of the hydraulic jump for different nozzle distances for the 4 mm pipe nozzle and $Re_{{d_{\text{N}} }} = 59,600$ compared to measurement results. Solid lines and empty markers: solution of Eqs. (16) and (17) including splattering computed using Eq. (21) for $L/d_{\text{N}} = 333$. Filled markers: experimental results for $Y$ and $X$

In Fig. 14, the quotient of the measured and predicted values of X and Y, $\left( {X^{*} = \frac{X}{{X_{\text{num}} }},\;\;Y^{*} = \frac{Y}{{Y_{\text{num}} }}} \right)$, is plotted for all data collected in experiments. Note that for all nozzle configurations, the measured values deviate to a maximum of 20% from the solution of Eqs. (16) and (17) for $L/d_{\text{N}} \ge 100$. These nozzle distances are typical for tank cleaning applications. Neglecting splattering leads to an overestimation of the distance between the impact point and hydraulic jump position by up to a factor of 1.7.

Fig. 14

Quotient of predicted hydraulic jump position and measured value for different mass flow rates and nozzles. Filled markers represent $X^{*}$ hollow markers represent $Y^{*}$

Finally, we present the hydraulic jump position in the vertical versus the hydraulic jump position in the horizontal direction (Fig. 15). The solid line represents the results of computations according to Eqs. (14) and (15), and the experimental data are represented by the symbols. It is clear that the most of the data fall on one master line, that is slightly below the computation and the agreement between the experimental data and the model prediction is good, except for the data in the range $L/d_{\text{N}} = 17 \ldots 33$ in configuration “convDS”. For these data, the vertical position is smaller with respect to the horizontal position in comparison to other nozzles and/or nozzle distances. This could be due to the nozzle internal flow or an oval shaped jet.

Fig. 15

Vertical position plotted versus the horizontal position of the hydraulic jump. Solid line results from the ratio calculated by Eqs. (14) and (15). Oval comprises values for 4 mm convDS and $L/d_{\text{N}} = 17 \ldots 33$

4 Conclusions

In this paper, water jets impinging horizontally on a vertical wall were investigated regarding the amount of splattering and the position of the hydraulic jump position using six different nozzle configurations. The jet Reynolds number was varied in a range of $41,000 \le Re_{{d_{\text{N}} }} \le 75,000$ and the nozzle distance was varied in a range of $3 \le L/d_{\text{N}} \le 570$. This range significantly extends the work of previous research concerning the amount of splattering (Wang et al. 2013b; Bhunia and Lienhard 1994a, b) and concerning the prediction of the hydraulic jump positions for horizontal impingement onto a vertical wall (Wilson et al. 2012; Wang et al. 2013b; Bhagat and Wilson 2016). For almost all the set parameters, splattering took place.

Using pipe nozzles leads to a significantly higher amount of splattering in the range $17 \le L/d_{\text{N}} \le 167$ compared to plain convergent nozzles. For pipe nozzles, a maximum of the splattered mass fraction has been detected at $L/d_{\text{N}} \approx 33$ for $Re_{{d_{\text{N}} }} \ge 51,000$. This finding has not been reported before and can be explained by the presence of short wave disturbances on the jet surface, which probably originate from initial jet turbulence, and which could be observed for $L/d_{\text{N}} \le 33$. For higher values of $L/d_{\text{N}}$, these disturbances are not present, while the RMS Roughness $R_{\text{q}}$ increases monotonically with the increase of $L/d_{\text{N}}$. Besides pipe nozzles, two configurations with two 90° deflections before the inlet of the convergent nozzles were used, which also increased the amount of splattering compared to plain convergent nozzles.

The splattered mass fraction was, therefore, shown to significantly depend on the nozzle configuration for nozzle distances $L/d_{\text{N}} \le 167$. For $L/d_{\text{N}} \ge 250$, a simple correlation has been developed for splattered mass fraction $\xi$ as a function of the jet Weber number.

The hydraulic jump position was measured in the vertical and horizontal directions from the point of impingement. A momentum balance in the wall film was used to predict the position of the hydraulic jump, in which the splattering was taken into account and assumed to take place at a fixed distance $r_{\text{s}} \approx 5.71 d_{\text{N}}$ from the point of impingement. By inclusion of the splattering effect into the momentum equation, the prediction of the hydraulic jump position has been significantly improved to a fold factor of 0.9–1.3 to prior models, which showed fold factors of up to 1.7 in the same parameter range. For practical application, this showed how splattering affects the hydraulic jump position and the effective amount of water downstream of the impingement region and thereby reduces the area which can be cleaned.

Appendix

1.1 Image processing for characterization of jet surface roughness

See Figs. 16, 17, 18, 19.

Fig. 16

Illustration of image processing operations: a raw cropped image, b image after background subtraction, c detected edges, d processed image

Fig. 17

Illustration of image stitching: a processed image at $t$ with a predefined detail to find in (box), b processed image at $t + \Delta t$ with a predefined area to search in (box), c result of 2D cross correlation (pink and green areas show deviations between a and b, and d ongoing stitched image with the inserted cropped detail

Fig. 18

Stitched image of a water jet originating from a 4 mm convergent nozzle with two 90° deflections upstream the nozzle entering (convU) at $L/d_{\text{N}} = 100$ and $Re_{{d_{\text{N}} }} =$ 59,600. The imperfect stitching of the formed droplets due to their lower velocity is clearly visible

Fig. 19

Stitched image of a water jet originating from a 4 mm convergent nozzle with two 90° deflections upstream the nozzle entering (convU) at $L/d_{\text{N}} = 167$ and $Re_{{d_{\text{N}} }} =$ 59,600

To create the stitched images, the recorded images were stored in 5 stacks of equal size, to reduce the size of the stitched images and thereby increase the speed of the roughness calculation. The images were processed using the following steps, some of them illustrated in Fig. 16:

• Cropping the relevant region of the image

• Subtraction of background image

• Conversion of 8bit grayscale image into Boolean image with edge detection, using the “Canny method” (Canny 1986)

• Adding a “true” line to the rear and back of the image

• Filling of closed geometries

• Eliminating droplets one order of magnitude smaller than the largest object (jet).

After processing, the images were correlated and stitched as illustrated in Fig. 17. Parts (a) and (b) of this figure show processed images at the time $t$, and $t + \Delta t$ respectively. The region within the box of Fig. 17a was correlated with the region in the box of Fig. 17b, which was predefined by the expectancy of the jet speed and a tolerance. Note, that the left side of the box was set to the position, at which the nozzle showed at the set up (compare Sect. 2.5). In Fig. 17c, the result of the correlation is shown. The pink areas at the border of the jet highlight regions where a jet is present in the box of Fig. 17a, but not in the found position in Fig. 17b, vice versa for the green area. These minor deviations are due to the change of the jet surface during the period $\Delta t = 1/{\text{fr}}$. The region of Fig. 17a was then cropped at the right to reach a width of the travelled distance and stitched to the ongoing stitched image of Fig. 17d. In this way, images counting up to 100 kPi (equivalent to a length of ca. 4.5 m) in length were constructed.

Clips of the derived binary stitched images are shown in Fig. 7 for jets originating from all 4 mm nozzle configurations with $Re_{{d_{\text{N}} }} =$ 59,600, while non-binary images are shown in the following Figs. 18 and 19 for a jet originating from a 4 mm convergent nozzle with two 90° deflections upstream the nozzle entering for illustration purposes.