1 Introduction

The collision phenomenon between droplets and solid walls is widespread in nature, daily life, and industrial and agricultural production. Studies show that during the liquid–solid collision process, the transient impact force between the droplet and the wall is the key factor affecting the droplet morphology and erosion phenomenon (Field et al. 1989; Field 1999; Zhang et al. 2002). Therefore, a growing interest in the theoretical analysis, experimental research, and numerical simulation of droplet impact force has been encouraged in recent years by the required comprehensive understanding of the collision phenomenon in extensively used technological processes, such as scouring, inkjet printing, pesticide spraying, jet cutting, and spray axial fans.

In the early days, many scholars devoted themselves to deriving the mathematical model of impact force between droplets and solid surfaces. The most popular is the water-hammer pressure model, which was proposed by Cook (1928), who intended to study the blade erosion mechanism. According to his expression, the water-hammer pressure is sufficient to cause erosion of steam turbine blades. On the basis of 1D analysis incorporated with variable shock wave velocity, Heymann (1968) extended Cook’s water-hammer relation by multiplying a modification coefficient. In 1969, Heymann (1969) further developed a 2D approximation model that is valid for the “initial” phase of the impact, that is, the stage before the occurrence of the lateral outflow of the droplet. Lesser (1981) pointed out that the envelope of the shock wave can be regarded as the superposition of the disturbance elements formed by the solid–liquid contact particles at different times. For droplet collision with low speed, existing theoretical models tend to focus on the value of the collision force of the entire solid–liquid contact surface when the droplet impacts the wall. Imeson et al. (1981) used the momentum theorem to estimate the average collision force of a droplet throughout the collision process. Soto et al. (2014) estimated the maximum value of the droplet collision force according to the momentum theorem. Both models assume that the velocity of the droplet in the normal direction is equal to the initial velocity during the entire collision process, but the velocity of the droplet is affected by pressure fluctuations. Philippi et al. (2016) analyzed the process of self-similar structure, both for the velocity field and the pressure field. A total net normal force imparted by an impacting drop on the underlying substrate at early times was given as \(F(t)=6\sqrt 3 \rho U{}^{{5/2}}{R^{3/2}}\sqrt t\). This formula could predict the initial impact force well which has been verified through experiment by Gordillo et al. (2018).

Owing to the limitation of theoretical analysis, the time domain process of impact force cannot be quantitatively analyzed, and the morphological changes of a droplet contacting a wall cannot be intuitively seen. Therefore, experimental research is necessary. Given the transient process of droplet collision, a piezoelectric sensor is suitable for such measurement owing to its high natural frequency and fast response. Grinspan et al. (2010) used a self-made piezoelectric film sensor to measure the time domain process of impact force of three different droplets under varied impact speed conditions. However, a large negative value process appeared in the late stage of the impact force. A negative impact force was also observed in the research of Mitchell et al. (2016). According to the momentum theorem, the momentum of the droplet along the normal direction of the wall surface points to the wall during the collision between the droplet and the wall surface, which means that the impact force cannot be negative. Portemont et al. (2004) found that the presence of air in the sensor cavity affects the accuracy of impact pressure measurement. Therefore, designing experiments properly and setting up reliable laboratory furniture to obtain accurate droplet impact force are keys to further exploring the influence of impact force on droplet collision. In the studies of Li et al. (2014) and Zhang et al. (2017), an experimental setup with a piezoelectric transducer was established to record the impact force evolutions of low-speed droplets, and a high-speed camera was used to capture the droplet shape. The results proved the reliability of the experiment rig.

Given the difficulty of experimental platform construction and numerous uncontrollable factors in the experimental process, many scholars focus on adopting numerical methods to discuss and analyze the impact process. Adler (1995) developed a 3D viable finite element model to investigate the pressure distribution in water droplets and the stress distribution in solid plates during droplet–solid collision. The impact process of a 2 mm-diameter water droplet with velocity of 305 m/s on a zinc surface was simulated, and the general behavior of the water droplet impact on deformable surfaces appeared to be adequately represented. Keegan et al. (2013) employed the Explicit Dynamics software package to model a rain droplet colliding with an epoxy resin plate at speeds ranging from 40 to 140 m/s. The simulated impact forces and pressures were consistent with the data obtained from standard analytical relations. Zhou et al. (2008) simulated the quasi-3D (axisymmetric) impact process, and the results were specified for water drop impact on 1Cr13, with impact speed varying from 10 to 500 m/s. In some works (Mehdi-Nejad et al. 2003; Fujimoto et al. 2007; Lunkad et al. 2007; Li et al. 2014), the volume of fluid method was used to study the deformation and dynamic behavior of the impacting droplet with solid surfaces. However, the traditional grid method requires grid encryption and adaptive adjustment to accurately track the free interface, which often consumes considerable computing time and resources. Accordingly, several scholars began to pay attention to meshless methods because of their unique advantages. These methods, which are inherently well suited for simulating large deformation flows owing to their mesh-free feature, could handle convection-dominated flows without numerical diffusion. Thus, particle methods provide substantial potential for simulating free-surface flows, especially those involving large deformations and fragmentations. Smoothed particle hydrodynamics (SPH) is one of the earliest particle methods and was introduced by Lucy (1977) and Gingold and Monaghan (1977) in astrophysics for studying the collision of galaxies. This method was later extended to deal with different hydrodynamic problems (Xu et al. 2012; Liu 2011; Wang 2011). Zhang et al. (2007, 2008) used the SPH method to simulate free-surface and solidification problems. The method was applied to a droplet impacting substrates with different roughness. Their works demonstrated the SPH model to be a powerful tool for studying transport phenomena in problems with free-surface deformation and solidification. In the research of Kordilla et al. (2013), they used a 3D multiphase SPH model to simulate flow on smooth fracture surfaces. They modeled droplet and film flow over a wide range of contact angles and Reynolds numbers encountered in such flows on rock surfaces. They proved that the SPH model can be used to study flow on rough surfaces. Xu et al. (2014) extended a truly incompressible SPH algorithm combined with an effective model to simulate the dynamic process of multiple droplets impacting a liquid film in 2D and 3D. All numerical results obtained were consistent with the available data.

The droplet shape is usually irregular before colliding with a solid surface because of oscillation. Some studies investigated the oscillation and deformation of droplets under the influence of various external forces and surface tension. Tian et al. (1995) presented a theoretical analysis for the shape oscillations of droplets suspended in air; they found that the oscillation frequency is determined by the surface tension for droplets of surfactant solutions, and the free-damping constant depends on the surface viscoelasticity. Fujii et al. (2000) investigated the effect of the shape change of a droplet on the surface oscillation using the electromagnetic levitation method under microgravity. Thus, ensuring that the droplets are perfectly spherical when they fall and collide with the solid wall is difficult in real environments. Although studies on the drop collision phenomenon received considerable attention in the past, minimal research has been reported on the effects of droplet shape on impact force and the erosion effects on solids. In the present study, an experimental rig is established to perform a low-velocity droplet collision test, and the accuracy of the experiment is verified with the momentum theorem. The SPH and FEM coupling methods are used to calculate the morphology and impact force of 3D single droplet collision with the solid wall, and the simulation results are compared with experimental results to verify the accuracy of the algorithm. Subsequently, an ellipsoid droplet model is constructed, and the influence of droplet shape on the impact force is further discussed. Moreover, the erosion effect of the droplet on the solid wall is analyzed.

2 Experimental setup

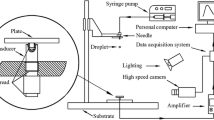
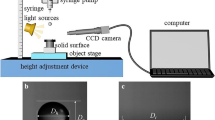
A schematic of the experimental setup is shown in Fig. 1. The droplet was generated by using a flat-tipped needle that was connected to a high-precision syringe pump. Water droplets dropped off the needle under gravity and fell freely. An aluminum plate with a machined and polished upper surface, which had a diameter of 15 mm and thickness of 2 mm, was used to receive the falling droplet. A plate with a thread on its bottom surface was screwed vertically into a Kistler model 9215 force transducer. The natural frequency of the transducer was greater than 50 kHz, and its maximum useful frequency could reach 15 kHz with an accuracy of 10%, 10 kHz with an accuracy of 5%, and 5 kHz with an accuracy of 1%, according to the specification in the user menu. In the present experiment, the maximum frequency of the impact force of the droplet is below 5 kHz which could be obtained by frequency spectrum. Thus, the precision of the measured impact forces can be guaranteed. The charge signal from the transducer was amplified by a Kistler model 5018A charge amplifier. The charge amplifier converted the charge signal to voltage signal, which was recorded by the computer via a data acquisition system (Dewe-43), for further analysis. According to Nyquist sampling theorem, the sample rate was set to 100 kHz, which was far more than twice that of the maximum frequency of the concerned signal. Furthermore, the apparatuses, such as the syringe pump and a personal computer, were insulated from the substrate in which the transducer was screwed to prevent the background noise caused by equipment vibrations.

Fig. 1
figure 1

Schematic of experimental setup

Full size image

The time evolution of the droplet shape was recorded by a high-speed camera (Phantom V711) at 40,000 frames per second. The droplet diameter could be measured from the images before the droplet collided with the plate surface. The droplet before collision might not be perfectly spherical, so the equivalent diameter of the droplet is defined as \(D=\sqrt[3]{{D_{{\text{h}}}^{2}{D_{\text{v}}}}}\), where \({D_{\text{h}}}\) and \({D_{\text{v}}}\) are the horizontal and vertical diameters in the images, respectively (Li et al. 2012). Impact velocity was measured from consecutive images before the droplet impacted the plate with a known interval time. Droplet diameter was changed by needles of different sizes, and the impact velocity of the droplet was altered by varying the distance between the needle tip and plate surface. Aside from the impact force data, the vibration signal of the aluminum plate caused by droplet collision could be recorded by the transducer. In our previous studies, a theoretical analysis and elaborate experiments were performed to determine how the plate affects the signal. The results indicated that a light plate mass, with the aid of a low-pass filtering process, can eliminate the influence of the plate on the impact force signal. Detailed information about the experimental setup and filtering procedure is available in the references (Li et al. 2014; Zhang et al. 2017).

To validate the accuracy of our measurements of impact force, both the sensibility and repeatability analyses were carried out. Figure 2 exhibits the different droplet (diameter = 2.48 mm) impact positions on the impact plate. Position A was placed at the center of the impact plate, while Position B was 3 mm offset to the center. To avoid the unexpected perturbation of occasional breeze, the droplet was designed to drip from the needle at a height of 100 mm above the impact plate, and the corresponding impact velocity was 1.36 m s− 1. The experiment for one fixed droplet impact position was repeated five times and the mean value of impact force was therefore obtained to further reduce the error.

Fig. 2
figure 2

Various droplet impact positions on the impact plate

Full size image

Table 1 compares the average peak values of impact force and the mean square errors of two different droplet impact positions. The average peak values of impact force were calculated as 8.89 mN at Position A and 8.98 mN at Position B, reporting a deviation of merely 1% within the eccentric distance of 3 mm based on the present layout of our experimental setup. The mean square errors of two positions are 0.0002 and 0.0001, which can also demonstrate good repeatability of our measurement. What is more, during the process of our experiments, two major methods were adopted to improve the repeatability of the droplet impact point. Firstly, most of the droplet impact positions were located near the center of the impact plate based on the precise design of the droplet generation system. Secondly, through the images of high-speed photography, only a portion of droplets which precisely impact on the plate center are selected to further investigate their impact forces.

Table 1 The influence of the droplet impact position on the peak value of impact force
Full size table

3 Simulation method

3.1 SPH method

The SPH method has been widely used in problems of large deformation based on continuous media and fluid–solid coupling (Chen and Beraun 2000; Cleary et al. 2006; Fang and Owens 2006). The unique adaptability of this meshless method is demonstrated in the solution process. Simulating the deformation problem of droplet and jet flow with the SPH method can effectively prevent the problem of grid stiffness and negative volume using FEM. Moreover, the discrete nature of SPH particles enables simulating liquid splashes. Relative to the large deformation of the liquid, the deformation of the solid material in the impact process is small, which can be completely simulated with FEM and an appropriate material model (Wang et al. 2008).

Unlike in FEM, the nodes of the SPH method are discrete, that is, the particle number and distribution within the smooth length around each particle are unfixed owing to the absence of cell connection. For any unknown continuous smooth field function, Eq. (1) is used to approximate the ordinary function value of a certain point, where < > is the Kernel approximation operator; W is the smoothing function, which has the nature of peak and regularization constraints similar to the Dirac δ function; and h is the smooth length, which defines the affect region of W. Particle approximation is used to convert the continuous integral expression to a discretized form of superposition and summation for all particles in the support domain, as shown in Fig. 3. The particle approximation formula at particle i can be written as Eq. (2); that is, any function value at particle i can be weighed and averaged by approximating the function value of all the particles in the support region with smoothing function. Here,

Fig. 3
figure 3

Schematic of particle approximation

Full size image
$$<f(x)>= \int_{\Omega } {f({x^\prime })} W(x - {x^\prime },h){\text{d}}{x^\prime },$$
(1)
$$<f({x_i})>= \sum\limits_{{j=1}}^{N} {\frac{{{m_j}}}{{{\rho _j}}}} f({x_j}) \cdot {W_{ij}}.$$
(2)

The discrete Navier–Stokes equations (Liu 2003) obtained by the SPH method are as follows:

Continuity equation:

$$\frac{{{\text{d}}{\rho _i}}}{{{\text{d}}t}}=\sum\limits_{{j=1}}^{N} {{m_j}v_{{ij}}^{\beta } \cdot \frac{{\partial {W_{ij}}}}{{\partial x_{i}^{\beta }}}} .$$
(3)

Momentum equation:

$$\frac{{{\text{d}}v_{i}^{\alpha }}}{{{\text{d}}t}}=\sum\limits_{{j=1}}^{N} {{m_j}\left( {\frac{{\sigma _{i}^{{\alpha \beta }}}}{{\rho _{i}^{2}}}+\frac{{\sigma _{j}^{{\alpha \beta }}}}{{\rho _{j}^{2}}}} \right)\frac{{\partial {W_{ij}}}}{{\partial x_{i}^{\beta }}}} .$$
(4)

Energy equation:

$$\frac{{{\text{d}}{e_i}}}{{{\text{d}}t}}=\frac{1}{2}\sum\limits_{{j=1}}^{N} {{m_j}\left( {\frac{{{p_i}}}{{\rho _{i}^{2}}}+\frac{{{p_j}}}{{\rho _{j}^{2}}}} \right)} v_{{ij}}^{\beta }\frac{{\partial {W_{ij}}}}{{\partial x_{i}^{\beta }}}+\frac{{{\mu _i}}}{{2{\rho _i}}}\varepsilon _{i}^{{\alpha \beta }}\varepsilon _{j}^{{\alpha \beta }},$$
(5)

where N is the particle number in the smooth length range; \({m_j}\) is the mass of particle j; \(v_{{ij}}^{\beta }\) is the relative velocity component in direction β of two particles; \(x_{i}^{\beta }\) is the coordinate in direction β of particle i; \(\sigma _{i}^{{\alpha \beta }}\) and \(\sigma _{j}^{{\alpha \beta }}\) are stress and strain tensors, respectively; p is the pressure; and µ is the viscosity coefficient of fluid.

3.2 FEM method

The solid part is solved with FEM, because many SPH particles used in the simulation will require a large computational memory and a long calculation time. In addition, given the small deformation rate in solid materials, the algorithm does not need a strong capability to deal with deformation problems. The equations for the solid part are as follows:

Kinematic equation:

$${\sigma _{ij,j}}+\rho {f_i}=\rho {\ddot {u}_i}.$$
(6)

Geometric equation:

$${\varepsilon _{ij}}=\frac{1}{2}({u_{i,j}}+{u_{j,i}}).$$
(7)

Physical equation:

$${\sigma _{ij}}=\lambda {\varepsilon _{kk}}{\delta _{ij}}+2\mu {\varepsilon _{ij}}.$$
(8)

3.3 Contact algorithm

The interfacial coupling between the droplet and solid surface is achieved by the point–surface contact penalty function algorithm in the SPH method. During the calculation process, each slave node is examined for penetration of the major surface. If penetration occurs, then an interface force that is equal to the product of the contact stiffness, k, and the penetration are applied between the node and the contact point. The effect is equivalent to that of placing a spring on the interface. The contact stiffness k is given by Eq. (9), where f is the scale factor of the contact stiffness, A is the interfacial area of the contact element, K is the bulk modulus of the contact element, and Vol is the volume of the contact element.

$$ k=\frac{{f{A^2}K}}{{{{Vol}}}}.$$
(9)

3.4 Physical parameters and boundary conditions

The physical parameters and boundary conditions in the numerical simulation are consistent with the experimental data. The properties of the liquid are selected according to pure water with 22 °C under atmospheric pressure, as shown in Table 2. Referring to the experiment data, the droplet diameter and impact velocity are set to 2.7 mm and 2.67 m/s, respectively. The surface tension model is not considered in this study owing to the physical parameters of droplets. \( {{Re}}\) is 7355, and \( {{We}}\) is 261, which mean that the droplet is in the inertia-dominated zone (Zhang et al. 2017), and the effect of viscosity and surface tension on the impact force can be neglected.

Table 2 Physical parameters of water droplet
Full size table

In addition to the material parameters, the equation of state for the liquid is given as follows (Liu et al. 2002):

$${p_{\text{a}}}={\text{(}}\gamma - 1{\text{)}}\frac{\rho }{{{\rho _0}}}e,$$
(10)

where \(\gamma\) is the adiabatic exponent and has a value of 1.4, e is the internal energy of unit reference volume, and the initial value of pressure \({p}_{a}\) is 101,325 Pa. Given the compressibility of droplets, the Gruneisen state equation must be added as follows:

$$p=\frac{{{\rho _0}{C^2}\mu \left[ {1+\left( {1 - \frac{{{\gamma _0}}}{2}} \right)\mu - \frac{a}{2}{\mu ^2}} \right]}}{{{{\left[ {1 - \left( {{S_1} - 1} \right)\mu - {S_2}\frac{{{\mu ^2}}}{{\mu +1}} - {S_3}\frac{{{\mu ^3}}}{{{{\left( {\mu +1} \right)}^2}}}} \right]}^2}}}+\left( {{\gamma _0}+a\mu } \right)E,$$
(11)

where C is the Y-intercept of curve US–Up (US is the velocity of shock wave, and Up is the particle velocity); \({\gamma }_{0}\) is the Gruneisen coefficient, \(\mu =\frac{\rho }{{\rho }_{0}}-1\); \(a\) is the first-order correction factor of \({\gamma }_{0}\); and \({S}_{1}, {S}_{2},{ \text{and} S}_{3}\) are the coefficients of the slope formula of curve US–Up. The values of the parameters are shown in Table 3 (Steinberg 1987).

Table 3 Determined coefficient
Full size table

An aluminum alloy plate is selected to be the solid material, and the relevant parameters are shown in Table 4. The plate size is set to 20 mm × 20 mm × 1 mm; rigid constraint condition and non-reflecting boundaries are set for four side surfaces.

Table 4 Physical parameters of solid material
Full size table

In this work, we control the particle number around 170,000 and FEM grid number 500,000 for each case, which could ensure the convergence and accuracy of calculation. For a case of a droplet with a diameter of 2.70 mm and velocity of 2.67 m/s, the validation of particle number independence is shown in Table 5. The time step in these simulations is all below 2.32 × 10−9 s.

Table 5 Verification of particle number independence
Full size table

4 Results and discussion

4.1 Validation of experimental results

The reliability and accuracy of the impact force data obtained from the experiment are the bases for a thorough understanding of the characteristics of the droplet impact force and the verification of the numerical model. The momentum theorem provides an effective method for verifying the accuracy of impact force. The integral of the impact force and time is the impulse on the wall surface, which is the experimental impulse. The droplet is under the upward support of wall and gravity in the normal direction when it collides with the horizontal wall, and the gravity value is negligible compared with the value of support force (numerically equals impact force). Therefore, according to the momentum theorem, the momentum change (the theoretical impulse \( m{\varDelta} U\)) and the impulse of the droplet in the normal direction of the wall surface during the collision (the experimental impulse) are numerically equal.

Figure 4 shows a comparison between experimental and theoretical impulses of droplets with diameters of 2.70, 2.90, and 3.54 mm at five collision speeds (1.36, 1.92, 2.32, 2.67, and 2.99 m/s). The experimental impulses of the droplet with 3.54 mm diameter which were obtained by numerically integrating the measured force curves are 91–94% of the theoretical impulses, and the experimental impulses of drops with diameters of 2.90 and 2.70 mm reach 97–99% of the theoretical impulses. The similarity between the experimental impulse and the theoretical impulse values indicates that the impact force data obtained in this experiment are accurate and reliable. By contrast, the experimental impulse of the 2.90 mm drop impact force measured in the literature (Mitchell et al. 2016) is only approximately 60% of the theoretical impulse under the condition of similar velocity in this work. In the literature (Grinspan et al. 2010), the experimental impulse of 3.57 mm drop impact force is approximately thrice the theoretical impulse, which contradicts the momentum theorem. The comparison results indicate that the data obtained in this experiment are more reliable than those in the literature.

Fig. 4
figure 4

Comparison between experimental and theoretical impulses

Full size image

4.2 Verification of numerical method

To verify the numerical model, a qualitative comparative analysis of the droplet shape obtained by the numerical calculation and the high-speed imaging is first performed, as shown in Fig. 5. The left side of the figure shows a droplet with a diameter of 2.70 mm and velocity of 2.67 m/s (obtained by high-speed photography), and the right side is the droplet phase diagram by 3D numerical calculation. The initial contact moment between the droplet and the solid wall is defined as 0 µs. The time interval for each frame of the experiment and numerical simulation step length are 25 µs. The left high-speed photographic images show that at the initial stage, the droplet shows a spherical shape with the bottom sheared, and no visible jet or liquid film is observed, such as the droplet shape at 50 µs. The liquid film begins to appear on the edges of the droplet at 100 µs and is evident at 200 µs. The spreading diameter of the liquid film of the droplet gradually increases with time, and the height of the droplet gradually decreases. Given that the present study focuses on the initial stage in this study, only the changes of droplet morphology during the pre-collision period are compared. The comparison between the numerical and experimental results indicates that a good agreement in the droplet morphology is achieved.

Fig. 5
figure 5

Morphology comparison between experiment and simulation results

Full size image

Figure 6 quantitatively compares the experimental and numerical values of the impact force of droplet during the collision process. The two curves fit well in the entire range. A rapid rising stage and a relatively slow falling stage are clearly observed in both curves, and the final impact force values all approach 0 N. In addition, the maximum value of force (peak force) calculated by simulation, which is 0.04345 N, is only 3.4% smaller than the experimental peak force, which is 0.04499 N. Figures 5 and 6 illustrate that the numerical method used in this paper can predict not only the morphological changes of droplets, but also the time domain process of the collision force.

Fig. 6
figure 6

Comparison of impact force between experiment and simulation results

Full size image

4.3 Effect of morphological changes of droplet on impact force

The droplet can hardly maintain its perfect sphere during the falling period owing to the oscillation in the actual environment. To study the impact force of the irregular droplet collision in the actual situation and explore the erosion of the solid further, the shape of the droplet before colliding is assumed to be an ellipsoid, as shown in Fig. 7. The ellipsoid drop falls in the negative direction of the Z axis, where a, b, and c are the lengths of the ellipsoid in the X, Y, and Z directions, respectively. Letting a = b, the ellipsoid droplet is further simplified to facilitate the calculation; that is, the droplet is circular in a section parallel to the wall surface. For describing the ellipsoidal shape easily, the concept “horizontal-to-vertical ratio” is introduced here.

Fig. 7
figure 7

Schematic of a rotational ellipsoid

Full size image
$$k=\frac{b}{c}.$$
(12)

When \(k\) < 1, the ellipsoid shows a slender shape in the falling direction; when k = 1, the droplet is a spherical droplet; when \(k\) > 1, the droplet is flat and stretched horizontally. It is necessary to ensure that the ellipsoid droplets of different aspect ratios have the same volume and collision velocity as the spherical droplet of 2.70 mm in diameter in the numerical calculation; that is, the droplets of different shapes have the same momentum when they are in contact with the wall surface.

Figure 8 shows the impact force evolution of droplets with the horizontal-to-vertical ratio of 0.5, 0.8, 1.0, 1.2, and 1.5, respectively. The peak force gradually increases with the increase of k. For example, the peak force of the droplet with k of 0.5 is only 0.0245 N, but the value can reach 0.0809 N when k equals 1.5. By contrast, the time when the peak force appears decreases with the increase of k. For instance, the time to peak force is 625 µs when k is 0.5, whereas only 80 µs is needed to reach the maximum value when k equals 1.5.

Fig. 8
figure 8

Comparison of impact force with different k

Full size image

Figure 9 shows the influence of k on the peak force and the time required to reach the maximum value intuitively. The peak force increases with the increase of k with a power tendency. On the contrary, the power trend of timing to peak force decreases with k. The error of peak force exists sometimes, and part of the experimental results must be screened and eliminated because the droplet shape could not always be a sphere at the moment before the collision in the experiment. According to Fig. 8, we use the peak force when k equals 1 as the reference. On the principle of guaranteeing the error range of 5%, we can obtain the range of k of the available droplets, which is 0.96–1.04 during the experiment of spherical droplet collision. Therefore, some experiment data in which k is beyond this range due to droplet deformation can be eliminated through analyzing the photos taken by high-speed camera. It can be regarded as a reliable criterion to select available spherical droplets.

Fig. 9
figure 9

Fitting curves of peak force with different k

Full size image

4.4 Comparison of impact force and erosion effect between oblate and spherical droplets

Field (1999) proposed that when the water droplet is in a “flat state” (when the aspect ratio of the water droplet is greater than 1), the effect of the collision process between the droplet and the solid wall surface is equivalent to that of a large-sized spherical droplet, which will cause serious erosion of the material. However, no explicit explanations and in-depth discussions were given. Based on the conclusion from the previous section, we find that oblate droplet causes enhanced peak force similar to that of a large-sized spherical droplet on the wall surface. Therefore, this issue is researched in detail in the present study.

In this work, given the impact velocity of 2.67 m/s, the droplet volume is used instead of diameter to facilitate the discussion of irregular droplets. Droplets with five different volumes are chosen in the experiments. The fitting curve of the relationship between peak force and spherical droplets is shown in Fig. 10. Using these droplet volumes, five horizontal-to-vertical ratios are chosen for each volume. After calculation using the SPH method, the fitting curves between the peak force and k can be obtained as shown in Fig. 11. If the peak forces remain equal, then V′ (which is Vsphe originally) is the equivalent volume of a spherical droplet; taking V (droplet volume with random k) and k as independent variables, the fitting surface is obtained as shown in Fig. 12. The fitting formula shown in Eq. (13) means that the equivalent volume V′ can be determined when the volume of different-sized droplet (V) and k are given. We can find the volume relation between the spherical and ellipsoid droplets with the same peak force. For example, given an ellipsoid droplet with volume of 10.31 mm3 (V) and k of 1.5, a large-sized spherical droplet with equivalent volume of 24.52 mm3 (V′) is needed to achieve the same peak force according to Eq. (13).

Fig. 10
figure 10

Fitting curve of peak force with different volumes

Full size image
Fig. 11
figure 11

Fitting curves of peak force with different volumes and k

Full size image
Fig. 12
figure 12

3D-fitting surface of V′

Full size image
$${V^\prime }=0.09{V^{1.55}}{k^{2.75}}+0.04{V^{1.55}}+3.462{k^{2.75}}+2.268.$$
(13)

For further analysis, an ellipsoid droplet with volume 10.31 mm3 and k of 1.5, and an equivalent large-sized spherical droplet with volume 24.52 mm3 are chosen to be simulated for comparison. The 2D front view of two droplets before colliding on the wall is shown in Fig. 13. The impact force curves of the two droplets are calculated as shown in Fig. 14. With the error of peak force less than 5%, the curves at the rise stage coincide, especially the stage before 60 µs. Two lines are drawn to demonstrate the positions when two droplets reach peak forces, as shown in Fig. 13. Line 1 represents the contact position of the oblate droplet reaching peak force, and line 2 represents that of the spherical droplet. Compared with Fig. 14, the two droplets have similar radii of curvature in the initial contact area. The area below line 1 has the same radius of curvature with little difference, which corresponds to the overlapping period shown in Fig. 14. Therefore, we assume that the radius of curvature is the key factor affecting the impact force of the initial collision stage. Through calculation, the maximum radius of curvature of this ellipsoid which is the point contacting with the wall firstly is \({r_{{\text{max}}}}=\frac{{{b^2}}}{{{c^2}}}=\frac{{{{0.00155}^2}}}{{{{0.00103}^2}}}=0.00233\;{\text{m}}\), where b is the semi-major axis and c is the semi-minor axis of the ellipse. This value is 1.3 times that of large-sized spherical droplet. As the collision goes on, the radius of curvature of the ellipsoid in the contact region decreases, while that of the sphere remains unchanged which means the curvature gap of two shapes further narrows. Keeping the shape and volume consistent with the spherical one makes the oblate droplet be regarded as the same as that of the spherical droplet in the initial collision process. This is the reason for overlapping force curves and similar peak forces.

Fig. 13
figure 13

2D front view of the two droplets before impact

Full size image
Fig. 14
figure 14

Impact forces of the two droplets

Full size image

According to water-hammer theory, the impact of the droplet on the wall surface is in a compressible state at the initial stage. The water-hammer pressure generated at this time is the main factor that causes erosion and destruction of the wall surface. The high pressures are generated over a radius of contact given by \({R_{{\text{high}}}}=rU/C\), where \(C\)is the shock velocity of liquid, U is the impact velocity, and r is the radius of curvature of the drop in the region of contact (Field 1999; Bowden 1964). Based on this equation, the radius of curvature r is the key factor that impacts the initial impact process. However, extensive works (Philippi 2016; Gordillo 2018) have shown that the peak impact force (especially under the low-speed collision velocity) arises due to the self-similar pressure field, instead of the water-hammer pressure. Philippi et al. (2016) analyzed the process of self-similar structure both for the velocity field and the pressure field. Also, a total net normal force imparted by an impacting drop on the underlying substrate at early times was given as \(F(t)=6\sqrt 3 \rho U{}^{{5/2}}{R^{3/2}}\sqrt t\). For the convenience of discussion, Eq. 14 could be obtained if radius R is replaced with diameter D:

$$F(t)=\frac{{3\sqrt 6 }}{2}\rho U{}^{{5/2}}{D^{3/2}}\sqrt t .$$
(14)

In addition, dimensional peak force can be calculated according to the expression (Zhang 2017):

$${F_{\text{p}}}=0.84\rho {U^2}{D^2}.$$
(15)

These two formulas which only depend on liquid density, impact velocity and droplet diameter could predict initial impact force well, which has been verified through experiment by Gordillo et al. (2018). However, their works are all based on spherical droplets. Figure 15 shows the comparison between the prediction of initial impact force based on self-similar theory and the simulation results of both ellipsoid and spherical droplets. Great coincidence demonstrates that droplet with rotational ellipsoid shape also has self-similar properties in initial impact stage. In particular, D here used in this case should have equivalent diameter calculated through Eq. 13. To better compare the results and further analyze the relationship between impact force and time in the early stage, an lg–lg graph is shown in Fig. 16. Eight points for each case are used between 10 and 80 µs, which is the period the three curves coincide well in Fig. 15. Through Eq. 14, a linear relation with a slope of 0.5 is obtained after the logarithm operation. It can be seen from Fig. 16 that in the early stage, especially before 60 µs, the impact force follows the square root of t dependence well for both cases with different sizes and shapes. Regarding the prediction of peack force, Table 6 shows the comparison between calculation results through Eq. 15 (D is the equavalent diameter obtained through Eq. 13) and simulation results of the droplets with 10.31 mm3, 2.67 m/s and various k.

Fig. 15
figure 15

Comparison between the prediction of initial impact force based on self-similar theory and the simulation results of both ellipsoid and spherical droplets

Full size image
Fig. 16
figure 16

Comparison between self-similar theory and the simulation results in the early stage in double logarithm coordinate

Full size image
Table 6 Comparison between theoretical and simulation results
Full size table

It can be seen that within the margin of error, the dimensional peak force can be calculated according to Eq. 15, in which the equivalent diameter of a specific spherical droplet should be used. In addition, the dimensionless force of an ellipsoid droplet in initial impact process could also be expressed by:

$$F{^{*}}=\frac{F}{{\rho {U^2}{D^2}}},$$
(16)

which is generally used in the inertial force scale of a spherical droplet (Zhang 2017).

In conclusion, droplets with rotational ellipsoid shape could be regarded as equivalent spherical droplets in the initial impact stage. Radius of curvature in the contact area is the key factor of specific transformational relation. To verify this conclusion, we compare an ellipsoid model with a volume of 10.31 mm3 and k of 1.5 and a semi-ellipsoid model that retains the lower half of the geometry. The curves of the collision forces are shown in Fig. 17. Before the semi-ellipsoid droplet reaches the peak force, the three collision force curves nearly coincide, which validates the conclusion of the curvature effect. Even though the semi-ellipsoid is not a regular shape, the self-similar theory is also suitable due to the same curvature. Moreover, according to the discussion in Sect. 3.4, the peak force increases with the volume, so the peak force of the semi-ellipsoid is smaller than the entire ellipsoid, and the peak forces of the two do not coincide.

Fig. 17
figure 17

Comparison of impact force between whole and half ellipsoid

Full size image

To study the effect of the oblate droplet and large-sized droplet on the internal corrosion of materials, we simulate and obtain the internal stress variation of a 2 mm aluminum alloy plate subjected to droplet impact. The values of maximum stress and time to it are shown in Table 7. The comparison shows that the values of maximum stress are nearly equal and appear earlier after impact by the oblate drop, and this result is similar to that of the laws of peak force discussed above.

Table 7 Value of and time to reach maximum effective stress
Full size table

5 Conclusions

The impact force during the collision between the droplet and the wall has great importance for understanding the mechanism of droplet erosion phenomenon and exploring the cause of droplet shape change. In the present study, an experimental setup was built to measure the impact force and record the droplet shape. The influences of droplet shape change on the time domain process of impact force and peak force were investigated through numerical simulation. In addition, the erosion effect to the material between a small-sized oblate droplet and a large-sized spherical droplet was compared.

  1. 1.

    The impact force measurement system with a high-sensitivity piezoelectric sensor can accurately measure the transient impact force variation during the droplet–wall collision process. The 3D numerical model based on the SPH method can accurately predict the impact force and initial droplet morphology change.

  2. 2.

    Given the same volume and collision velocity, the peak impact force increases by a power function trend with the increase of the horizontal–vertical ratio of the droplet, and the time when the collision force reaches the maximum value decreases.

  3. 3.

    The collision force and erosion effect are closely related to the curvature radius of the droplet in the contact region, especially at the initial stage. Ellipsoid droplet, which could be regarded as an equivalent spherical one, has the same self-similar properties in the early collision stage. Given the same collision speed, peak force and effective stress with little difference can be found after impact of a small-sized oblate droplet and a large-sized spherical droplet.