1 Introduction

The phenomenon of a droplet impacting a solid surface has been observed in many fields and is considered a problem or a solution depending on the circumstances in which it appears. For example, the phenomenon is a solution for designers who adopt high-speed droplet streams or jets for equipment cleaning, coal mining, rock cutting and spray generation (Aguilar et al. 2001; Brook and Summers 1969; Li et al. 2012a; Sharma et al. 2011). By contrast, the phenomenon is a problem for engineers who try to avoid or alleviate the droplet impact damage in designing machines or instruments. These circumstances or machines include the steam turbines having wet stages (Gardner 1963; Mann and Arya 2003; Staniša and Ivušić 1995), aircraft and missiles under rainy conditions (Field 1999; Gohardani 2011), and soil splash in heavy rain in the first stage of soil erosion (Mouzai and Bouhadef 2011). In these processes or machines, the impact force or pressure of a droplet colliding with solid surfaces is an essential factor (Engel 1973; Field et al. 1985, 1989; Haller et al. 2003; Heymann 1969; Keegan et al. 2013; Lee et al. 2002). Therefore, studying the major factors that affect impact force is necessary.

Impact velocity is one of the most critical parameters that affect droplet impact force. Ahmad et al. (2009) discovered that the erosion rate of the materials increases with impact velocity in a power law relation with exponents varying from 3.3 to 5, when they conducted the experiments on the erosion resistance of five steam turbine blade materials. The strong effect of impact velocity on erosion has also been observed in many other studies (Gujba et al. 2016; Mahdipoor et al. 2015a, b; Oka et al. 2007). To explain the mechanism underlying the blade erosion, Cook (1928) proposed the water hammer pressure model as a pioneer. The model was further modified by Heymann (1969). Both researchers indicated that impact pressure is directly proportional to impact velocity. In addition, the simulations of the evolution history of pressure distribution in water droplets and stress distribution in solids by Zhou et al. (2009) indicated that the computed impact pressure is consistent with water hammer pressure at a low impact velocity (10–30 m/s), whereas at a high impact velocity (200–500 m/s), the pressure at the impact center is approximately 1.5–2 times the water hammer pressure. On the other hand, some experimental studies were conducted to investigate the effect of the impact velocity of a droplet on the impact force or pressure on a solid surface by using piezoelectric sensors (Haboussa et al. 2008; Li et al. 2014; Mitchell et al. 2016; Nearing et al. 1986; Portemont et al. 2004; Sahaya Grinspan and Gnanamoorthy 2010). In the study of Sahaya Grinspan and Gnanamoorthy (2010), a polyvinylidene fluoride piezoelectric film was used to measure the impact force of three types of droplets. The results showed that impact force increases exponentially with increasing impact velocity. Li et al. (2014) used a piezoelectric transducer to study the impact force of water droplets with different impact velocities and found that the peak impact force increases with impact velocity through a power law relation in which the power exponent is close to two. (Mitchell et al. 2016) examined the impact force evolution of a 2.9 mm water droplet at different impact velocities by using a piezoelectric force sensor. They discovered that the average force increases with impact velocity quadratically and the experimental impulse increases with impact velocity linearly.

Droplet diameter critically affects erosion as revealed by many investigations (Adler 1995; Ahmad et al. 2013; Hattori and Lin 2011; Pouchot 1969). Hattori and Lin (2011) and Ahmad et al. (2013) used an erosion test rig to relate volume loss per droplet impact against water droplet diameter with a simple power law expression, namely, \(\sim D^{n}\). The value of n was determined to be 4.67 in the study of Hattori and Lin (2011) and 3.2–3.5 in the study of Ahmad et al. (2013). The analytical models and numerical simulations showed that the magnitude of impact pressure is unrelated to droplet diameter (Cook 1928; Zhou et al. 2009); therefore, the increase in material erosion rate with increasing droplet diameter is suspected to be caused by impact duration (Bowden and Field 1964). This postulation was confirmed by the numerical investigation of Zhou et al. (2009), who discovered that impact duration is a linear function of droplet size at initial stages. Li et al. (2014) experimentally studied the effect of droplet diameter on the impact force evolution of a low-speed water droplet. They found that time duration, which is defined as the period of the entire droplet impact force process, increases with droplet diameter in a similar manner. This finding further verifies the statement that the increase in material erosion rate with increasing droplet diameter mainly results from increased impact time or duration.

Liquid density also plays an important role in droplet impact erosion. According to the water hammer model (Cook 1928), water hammer pressure is directly proportional to the liquid density of a droplet. The experiments of Rochester and Brunton (1974) and Hancox and Brunton (1966), who used a small wheel and jet apparatus to investigate the erosion of solids through repeated liquid impacts, verified the deduction that large liquid density results in large impact pressure and leads to a serious erosion rate. Soto et al. (2014) experimentally studied the effect of liquid density on impact force, and found that the impact force is directly proportional to the liquid density.

Many studies have been conducted on the effects of impact velocity, density and droplet diameter on impact force. However, only a few studies have investigated the effects of viscosity and surface tension on droplet impact forces. In many practical applications, the viscosity and surface tension of droplets may vary remarkably when different liquids are used. In numerical cases, researchers tend to disregard the influence of viscosity and surface tension on impact force or pressure. For example, Haller et al. (2002) studied the fluid dynamics of a droplet impacting a rigid substrate by using a high-resolution axisymmetric solver for Euler equations. The researchers established the assumption that viscosity and surface tension exert no effect on impact pressure and speculated that a high Reynolds (Re) number or a high Weber (We) number implies that inertial force dominates the progress. The same assumption was also adopted in the numerical investigation of Li et al. (2011). Although this assumption has been adopted in many numerical simulations, the following questions remain. Is such an assumption feasible? Under what situation is it feasible? Furthermore, do general rules exist to determine the effect of different parameters on impact force? These questions emphasize the need for basic experimental research on the effects of different parameters on the force of droplet impingement.

In the present paper, an experimental setup with a piezoelectric transducer was established to record the impact force evolutions of low-speed droplets. A high-speed camera was used to capture the droplet shape. The Re and We numbers were used to investigate the affecting factors systematically. It is found that the impact process can be categorized by the Re number, which is the major affecting dimensionless parameter. In addition, a universal variation trend of the dimensionless impact force is found.

2 Experimental setup

2.1 Experimental apparatuses

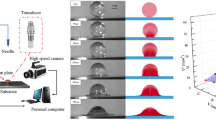
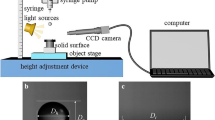
As shown in Fig. 1, a droplet was generated with a flat-tipped needle connected to a high-precision syringe pump, which drove the liquid steadily and continuously. The droplet that formed at the tip of the needle fell freely on a flat polished aluminum plate that was screwed vertically into a piezoelectric force transducer (Kistler Model 9215). The high-precision force transducer has a natural frequency of about 57 kHz and response time of about 3 μs. The useful frequency can reach 5 kHz with amplitude error of 1%, 10 kHz with amplitude error of 5% and 15 kHz with amplitude error of 10%. As illustrated in the zoomed circle in Fig. 1, the upper thread of the force transducer was used to fix the aluminum plate and deliver impact force to the internal sensor. The middle thread was employed to mount the transducer on the substrate firmly. The thread in the lower part was used to fix the cable that delivered the original signal from the transducer to the charge amplifier (Kistler Model 5018A). The signal acquisition equipment (Dewe-43) was utilized to transform the amplified analog signal into the digital signal, which was subsequently recorded and analyzed with the data acquisition software (DewesoftX) in a personal computer. The resolution of the force measurement system is 0.001 N.

Fig. 1
figure 1

Schematic of the experimental setup

Full size image

The time evolution of the droplet shape was recorded by a high-speed camera (Phantom V711) at 40,000 frames per second. The image resolution was 0.056 mm/pixel, which was calibrated by placing a Vernier caliper in the scope of the images. The camera recorded images when the impact force increased above 0.001 N in DewesoftX. Image recording and processing were performed with Phantom camera control software, and the memory function enabled the software to record the images before the trigger moment. The camera was placed on the same level as the flat plate to facilitate the side-view observation of the impact process.

Different liquids, namely, water, ethanol, pure glycerin and aqueous glycerin solutions, were used in the experiments. These liquids are nontoxic and have been widely used by former researchers (Bakshi et al. 2007; Banks et al. 2014; Mongruel et al. 2009; Šikalo et al. 2005). The properties of the liquids, which were determined from published data in References (Association GP 1963; Khattab et al. 2012), are indicated in Table 1. Water, ethanol and glycerin were pure analytical reagents. The concentration of the aqueous glycerin solutions was in weight percent and ranged from 50 to 90% at an interval of 10%. For concise expression, the aqueous glycerin solutions were labeled as AG50, AG60, AG70, AG80 and AG90. The working temperature of the aqueous glycerin solutions was 20 °C. Pure glycerin droplets at three different temperatures were also used to study the effect of viscosity on impact force. The liquid and aluminum plate had the same temperature during the impact process, and temperature uncertainty was less than 0.2 °C.

Table 1 Physical properties of different liquids used in the present study
Full size table

Droplet diameter can be determined with the mass conservation law, \(D = \left( {{{6m} \mathord{\left/ {\vphantom {{6m} {\pi \rho }}} \right. \kern-0pt} {\pi \rho }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}}\), where \(\rho\) and m are the liquid density and droplet mass, respectively. To reduce the measurement error, usually the total mass of n droplets (n is 100 in the present experiments) were measured by a balance with accuracy of 0.001 g. The single droplet mass was the average of the total mass of n droplets. Droplet diameter can also be measured from the images before the droplet collides with the plate surface. The droplet before collision might not be perfectly spherical, so the equivalent diameter of the droplet is defined as \(D = \left( {D_{\text{h}}^{ 2} D_{\text{v}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}}\), where \(D_{\text{h}}\) and \(D_{\text{v}}\) are the horizontal and vertical diameters in the images, respectively (Li et al. 2012b; Rioboo et al. 2002). The differences in the diameters of water, ethanol and pure glycerin droplets determined with these two methods are all within 2%. The former method was employed in the present study to obtain all the diameters of the aqueous glycerin droplets, to ease the processing of the experimental data.

Impact velocity was measured from consecutive images before the droplet impacted the plate with a known interval time. This method can reduce the overestimated velocity calculated by the free fall law, which does not consider the influence of air drag. Our tests show that the differences between the two methods increase with increasing fall distance. The differences between the two methods are within 1.7 and 4.5% when the fall distances of droplets are 100 and 500 mm, respectively. Droplet diameter was changed by needles of different sizes; the impact velocity of the droplet was altered by varying the distance between the needle tip and plate surface. During the tests, droplet diameters were varied between 2.03 and 3.64 mm, and impact velocities were varied from 1.36 to 2.99 m/s.

2.2 Measurement of droplet impact force

A plate with a diameter of 15 mm was used to record the entire history of the impact force of a droplet colliding on a surface. However, the presence of the plate affects the obtained signals of impact force. Aside from the impact force data, the vibration signal of the aluminum plate caused by droplet collision can be also recorded by the transducer. In our previous study (Li et al. 2014), a theoretical analysis and elaborate experiments were performed to determine how the plate affects the signal. We discovered that a light plate mass, with the aid of a low-pass filtering process, can eliminate the influence of the plate on the impact force signal. For further detailed information on the experimental setup and filtering procedure, readers may refer to reference (Li et al. 2014).

Figure 2 shows the time duration of the filtered impact force and the seven images of impact shape for a 2.70 mm water droplet colliding with the plate at 2.99 m/s. The images begin at the impact instant of 0 μs. For the subsequent impact instants, the droplet shape resembles a truncated sphere without a visible spread lamella, similar to the description of the initial phase in the study of Rioboo et al. (2002). The image at 50 μs is presented as a typical impact shape. In the following impact progress, the lamella begins to appear and spread along the plate surface, similar to that in the image of the droplet shape at 100 μs. The impact force reaches its peak value at about 200 μs. At that moment, the droplet shows an apparent spread lamella. Subsequently, the impact force decreases at a relatively slow rate as the droplet spreads continuously. As the height of the droplet is about of the thickness of the spread lamella or when the vertical velocity of the droplet becomes nearly zero, the impact force decreases to zero (1600 μs). The droplet continues spreading along the surface until it reaches its maximum spread diameter at about 2500 μs. During this period, the droplet is mainly in the shape of a water film.

Fig. 2
figure 2

Impact force evolution and corresponding impact images of a water droplet

Full size image

In Fig. 2, the area under the filtered force curve, i.e., the integration of impact force with time, is named as the ‘experimental impulse’ of the impacting water droplet. According to the momentum theorem, this impulse should be equal to the change of the momentum (theoretical impulse) of the droplet in the impact direction, that is, the product of \(m\Delta V\), where m and \(\Delta V\) are the mass of the droplet and the change in velocity, respectively. The experimental and theoretical impulses of different droplets at five impact velocities are plotted in Fig. 3. The experimental impulse of a droplet at each impact velocity is the average of five repeated test results. It can be seen that the experimental impulse increases linearly with velocity for a given mass of droplet. In addition, Fig. 3 shows that the experimental impulses are almost equal to the theoretical impulses, which means the present measured experimental data are accurate and reliable.

Fig. 3
figure 3

Theoretical and experimental impulses of different droplets

Full size image

3 Results and discussion

3.1 Dimensionless parameters for the impact force evolution of a droplet

In the present experiments, impact force is the function of the following variables:

$$F = f(V,D,\rho ,\mu ,\sigma ,t),$$
(1)

where F, V, D, ρ, μ, σ, and t are impact force, impact velocity, droplet diameter, liquid density, dynamic viscosity, surface tension and time, respectively.

Dimensional analysis was conducted with Eq. (1) by the Buckingham pi theorem. Four dimensionless parameters were obtained as follows: \(F^{*} = \frac{F}{{\rho V^{2} D^{2} }}\), \(t^{*} = \frac{tV}{D}\), \(Re = \frac{\rho VD}{\mu }\) and \(We = \frac{{\rho V^{2} D}}{\sigma }\), where \(F^{*}\) and \(t^{*}\) denote dimensionless impact force and time. Equation (1) can then be written in a dimensionless form as

$$F^{*} = f(Re,We,t^{*} ).$$
(2)

The effects of viscosity and surface tension are embedded in Re and We numbers. Accordingly, the discussions of the experimental results are organized on the basis of Re and We numbers.

3.2 Dimensionless impact force curves in the zone of inertia-dominated impacts

3.2.1 Effect of droplet shape on dimensionless impact force

Twenty impact tests were conducted on water droplets by using four droplet diameters, namely, 2.70, 2.90, 3.07 and 3.53 mm. Five impact velocities, namely, 1.36, 1.92, 2.32, 2.67 and 2.99 m/s, were adopted for each of the diameters. To provide an example, the dimensional impact forces of these droplets are shown in Fig. 4. The droplet with the same diameter would exert a larger impact force on the plate at a larger velocity; the same trend applies to the droplet with the same impact velocity but with a different diameter.

Fig. 4
figure 4

Dimensional force evolution of water droplets: \(3746 < Re < 10{,}769\) and \(68 < We < 428\)

Full size image

The plots of dimensionless force versus dimensionless time for the 20 cases in Fig. 4 are presented in Fig. 5. All of the 20 curves of dimensionless force coincide with one another. In the initial stage of the impact process, the curves collapse into almost one single curve. By contrast, the dimensionless peak forces of the curves disperse to some extent. Such dispersion applies to the curves at their decline stage (from the peak force to zero). These dispersions can be attributed to the shape deformation of the oscillating droplets before collision. Field (1999) reported that if a drop is flattened, it will have a higher radius of curvature in the contact region and will behave effectively as a larger drop and thus be more damaging. As shown in the upper-right corner of Fig. 5, the 3.53 mm droplet at 1.36 m/s possesses a vertical ellipsoid shape, which means that its horizontal diameter, \(D_{\text{h}}\), is smaller than the vertical diameter, \(D_{\text{v}}\). Actually, its horizontal-to-vertical ratio, \(k = {{D_{\text{h}} } \mathord{\left/ {\vphantom {{D_{\text{h}} } {D_{\text{v}} }}} \right. \kern-0pt} {D_{\text{v}} }}\), is only 0.88, smaller than one. According to Field (1999), the impact peak force of this droplet with a small value of k should be small. The measured force of the case of the 3.53 mm droplet at 1.36 m/s agrees with above inference.

Fig. 5
figure 5

Dimensionless force evolution of water droplets: \(3746 < Re < 10{,}769\) and \(68 < We < 428\)

Full size image

3.2.2 Effect of Re and We numbers on dimensionless impact force of water droplets

Figure 6 shows the dimensionless forces of water droplets with only slight deformation, which are identified from the abovementioned water droplets. The curves in Fig. 6 coincide more closely with one another than the curves in Fig. 5. The range of Re and We numbers in Fig. 6 is similar to that in Fig. 5. The curves in Fig. 6 show that dimensionless force is independent of Re and We numbers in the experimental ranges, that is, \(3746 < Re < 10{,}769\) and \(68 < We < 428\). Dimensional impact force is directly proportional to density, square of impact velocity and square of the droplet diameter.

Fig. 6
figure 6

Dimensionless force evolution of water droplets with different Re and We numbers and with small deformation (\(0.98 < \kappa < 1.04\))

Full size image

The Re number is the ratio of the inertia force to the viscous force of a fluid element, and the viscous effect is small or even negligible for large Re number flows. Therefore, the above impact flow is an inertia-dominated flow, and the effect of viscosity can be disregarded. In addition, the We number is an index of the inertial force to the surface tension acting on a fluid element. Considering that the experimental results are unaffected by the changes in the We number, surface tension exerts no effect on impact force for an impact with a large We number.

The present experimental data validates the assumptions in Haller et al. (2002) and Li et al. (2011), i.e., the effect of viscosity and surface tension on impact pressure is negligible. The Re numbers in the studies of Haller et al. (2002) and Li et al. (2011) are in the order of \(5 \times 10^{4}\) and \(1 \times 10^{6}\), respectively, and the We numbers are in the order of \(3.5 \times 10^{5}\) and \(7.1 \times 10^{6}\), respectively.

3.3 Dimensionless impact force curves in the zone of viscosity-dominated impacts

Table 1 shows that the magnitude of the viscosity of pure glycerin is three orders higher than that of water at 22 °C. Therefore, glycerin droplet can be used to investigate the dimensionless impact force behavior at low Re numbers. Figure 7 shows the dimensionless impact forces of glycerin droplets at 22 °C with different diameters and impact velocities. Evident differences are observed between the peak forces. For example, the dimensionless peak force increases by nearly 14% with decreasing the Re number from 9.5 to 3.8. The horizontal-to-vertical ratios for the droplets are from 0.99 to 1.04, which indicates that the glycerin droplets are nearly spherical, and the influence of the droplet deformation could be neglected. The We numbers of the glycerin droplets are in a similar range as those of the previous water droplets. However, the Re numbers of the glycerin droplets (\(3.8 < Re < 9.5\)) are much smaller than those of water droplets in Figs. 5 and 6 (\(3746 < Re < 10{,}769\)). The change in the low Re number causes the variation in the dimensionless peak force in Fig. 7.

Fig. 7
figure 7

Dimensionless impact force of glycerin droplets at different Re and We numbers; \(0.99 < \kappa < 1.04\)

Full size image

To verify this speculation, a comparison is performed between the water and glycerin droplets, which are characterized by similar We numbers (280 versus 290) but different Re numbers (7900 against 7.0). As shown in Fig. 8, a significant difference is observed. First, the dimensionless peak force of the glycerin droplet is 1.4 times higher than that of the water droplet. Second, the dimensionless impact force of the glycerin droplet decreases to a low value at a much quicker rate than that of the water droplet, which leads to a shorter impact time or duration. In the two cases, the We numbers are close to one another. This means that it is the Re number that results in the large difference. The effect of viscosity cannot be disregarded when the Re number is not sufficiently large. This condition suggests that viscosity plays an important role in this type of droplet impact.

Fig. 8
figure 8

Comparison of dimensionless impact force evolutions between water and glycerin droplets

Full size image

As shown in Table 1, when the temperature increases from 19 to 26 °C, the density and surface tension of glycerin decrease by only 0.3 and 0.6%, but its viscosity decreases by 43.2%. This characteristic was employed to study the effect of viscosity on impact force further. In the following experiments, three glycerin droplets with diameters of 3.03 mm at 19 °C, 3.04 mm at 22 °C, and 3.02 mm at 26 °C impacted the plate at the same velocity of 2.32 m/s. The Re numbers were 5.8, 7.8 and 10.1 for the glycerin droplets at 19, 22 and 26 °C, respectively, with nearly the same We number (about 324). Figure 9 shows the dimensionless impact forces of the glycerin droplets at different temperatures. A decrease of 4.3 in the Re number leads to an increase of about 17% in the peak dimensionless force. This figure confirms that viscosity results in a evident variation in impact force, and the impact process is a viscosity-dominated impact flow. Therefore, the viscosity effect should be considered in analytical models and numerical simulations when the impact force of droplets are studied at small Re numbers.

Fig. 9
figure 9

Effect of viscosity on dimensionless force evolution using glycerin droplets at different temperatures

Full size image

3.4 Effect of Re and We numbers on dimensionless impulse

Impulse is an important parameter to characterize the impact force. Here, a dimensionless impulse, \(I_{(t)}^{*}\), is defined as \(I_{(t)}^{*} = \frac{{I_{(t)} }}{{I_{\text{total}} }}\), where subscript t means time, \(I_{(t)}\) is the impulse which is the integration of impact force with time from 0 to t, and \(I_{\text{total}}\) is the total impulse when t reaches the end of the impact process.

The effect of Re number on the dimensionless impulse is shown in Fig. 10a, in which the impulse data is calculated by the same data of the impact process shown in Fig. 8. It can be seen that, at initial impact, the growth rate of dimensionless impulse of glycerin droplet is larger than that of water droplet. This is consistent with the rapid increase in the dimensionless force of glycerin droplet at the initial impact in Fig. 8. In addition, the dimensionless impulse of the glycerin droplet is always larger than that of the water droplet during the process. At the dimensionless time of 0.2, 0.6 and 1, the dimensionless impulses of glycerin droplet are 37.1, 24.1 and 3.6% higher than those of water droplet, respectively. These clear differences between the dimensionless impulses of the two droplets are attributed to the difference in Re number.

Fig. 10
figure 10

a Effect of Re number on dimensionless impulse; b Effect of We number on dimensionless impulse

Full size image

The effect of We number on dimensionless impulse is shown in Fig. 10b. With almost the same Re number (3746 vs. 3747), the We number of the ethanol droplet is about 7.5 times larger than that of the water droplet. Despite such a large difference in the We number, the two curves almost coincide with each other. At the dimensionless time of 0.2, 0.6 and 1, the differences between the dimensionless impulses of the two curves are only 3.2, 2.1 and 2.7%, respectively. The closeness of the two curves further indicates that the We number has little effect on the dimensionless impulse.

3.5 Relations of dimensionless peak force with Re and We numbers

Determining the ranges of inertia-dominated and viscosity-dominated zones is necessary. All the liquids in Table 1 were, thus, used in experiments to keep the Re and We numbers changing in a continuous manner. The lower limit of the We number is 68 when the water droplet experiments are conducted, and the upper limit of the We number is about 858 when experiments on the ethanol droplet are performed. Concurrently, the Re number ranges from 2.9 to 10,769, and pure glycerin and water droplets are used at the limit boundary.

Given that the peak force is the typical value of an impact process, dimensionless peak force is selected for comparison and discussion. Figure 11 shows the variation trend of dimensionless peak force \(F_{\text{p}}^{ *}\) with the We number, in which the corresponding Re numbers of these data range from 230 to 10,769. Dimensionless peak forces have a constant mean value of around 0.84. Clearly, the We number does not affect dimensionless peak force, or the variation in surface tension exerts minimal influence on peak force in the range of \(68 < We < 858\). The present experiment data do not cover data with We numbers smaller than 68. In the future, attention should be paid to the relation between dimensionless impact force and We number with low values.

Fig. 11
figure 11

Effect of We number on dimensionless peak force

Full size image

To verify the present experimental trend, the experimental data in the references (Mitchell et al. 2017; Mitchell et al. 2016; Soto et al. 2014) are added in Fig. 11. The added data fall in the range of the present experimental dimensionless peak force. In addition, the lower limit of the We number is extended to 52 when the water droplet experiments in Soto et al. (2014) are adopted, and the upper limit of the We number is extended to 1958 when experiment on an ethanol droplet in Mitchell et al. (2017) is included.

The relation between the dimensionless peak force and Re number of all the tested droplets, with several large distorted ones being discarded, is shown in Fig. 12. These data have the same range of the We number in Fig. 11. \(F_{\text{p}}^{*}\) decreases rapidly at low Re numbers then decreases gradually and finally becomes a flat line at large Re numbers. The curve suggests that the impact process can be categorized into three zones: viscosity-dominated, transition and inertia-dominated zones.

Fig. 12
figure 12

Effect of Re number on dimensionless peak force

Full size image

In the viscosity-dominated zone (\(2.9 < Re < 20\)), dimensionless peak force decreases rapidly with Re number in a power law relation, namely, \(F_{\text{p}}^{*} = 1.79Re^{ - 0.21}\). The R-squared value of 0.9 indicates a good fit. The apparent influence of the Re number on dimensionless peak force means that viscosity plays an important role in the impact process and should be considered in numerical simulations. Why does impact force increase rapidly with a decrease in the Re number in the viscosity-dominated zone? For droplets with the same size and velocity, a low Re number indicates that the droplet is a high-viscosity liquid. Given that viscosity is a property of liquid to resist shear deformation, large viscosity means high resistance to droplet deformation. For a case in which liquid viscosity was infinite, the liquid droplet would be treated as a rigid ball. The time duration of a rigid ball colliding with a rigid surface is much shorter than that of a liquid droplet. According to the momentum theorem, \(F\Delta t = m\Delta V\), the impact force of a rigid ball is much larger than that of a liquid droplet when the change in their momentum is the same.

In the inertia-dominated zone where the Re number is larger than 230, dimensionless peak force remains constant, which indicates that the effect of viscosity could be neglected, and inertial force dominates the impact process. In addition, the average value of dimensionless peak force in this zone is 0.84 with a standard deviation of 0.04. The peak impact force depends only on density, droplet diameter and impact velocity and can be expressed as \(F_{\text{p}} = 0.84\rho V^{2} D^{2}\). This expression is almost similar to Eq. (4) in Li et al. (2014), with a relative error of 0.5% in the constant coefficient, when the density of water in Table 1 is considered.

In the transition zone (\(20 < Re < 230\)), the dimensionless peak force decreases slowly with increasing Re number. The impact force/process is mainly the balanced results of both the inertial and viscosity forces. Which factor weights heavier is dependent on the specific Re number of the droplet involved.

The relation between dimensionless peak force and Re number in Fig. 12 provides valuable information for future analytical or numerical work, for example, to facilitate proper assumptions in simulations. In addition, the present data verify the simulated results of Roisman and Tropea (2009) on the impact pressure fields of droplet impacts. In their numerical investigations, little changes in the dimensionless pressure curves can be observed for two cases (We = 761, Re = 83 and We = 1165, Re = 104). Considering the scopes of the We and Re numbers, the results in Roisman and Tropea (2009) agree with the prediction of the present data.

The experimental data in Mitchell et al. (2016, 2017) and Soto et al. (2014) are also included in Fig. 12. The upper limit of Re number is extended from 10,769 to 12,831. The upper limit of 12,831 is taken from the experiment on water droplets in Soto et al. (2014). Generally, the added experimental data agree with the present experimental results and have the same trend.

4 Conclusions

The impact force evolutions of different droplets colliding with a solid surface were measured by employing a piezoelectric transducer. Droplet shape was recorded with a high-speed camera. Several conclusions can be drawn as follows:

  1. 1.

    The type of impact force of low-speed droplets colliding with a solid wall can be categorized into three zones: viscosity-dominated (\(2.9 < Re < 20\)), transition (\(20 < Re < 230\)) and inertia-dominated (\(Re > 230\)) zones.

  2. 2.

    In the inertia-dominated zone, a universal curve of dimensionless impact force exists; in other words, dimensionless force is independent of the Re number and the We numbers. In addition, dimensional peak force can be calculated according to the expression \(F_{\text{p}} = 0.84\rho V^{2} D^{2}\). The effect of viscosity on impact force can be neglected in the inertia-dominated zone.

  3. 3.

    In the viscosity-dominated zone, dimensionless peak force decreases rapidly with the Re number in a power law relation, namely, \(F_{\text{p}}^{*} = 1.79Re^{ - 0.21}\). The effect of viscosity plays an important role in the process and should be considered in numerical simulations. Moreover, the dimensionless impact duration for the droplet in this zone is shorter than that in the inertia-dominated zone.

  4. 4.

    The We number exerts small effect on dimensionless impact force in the range of \(68 < We < 858\). The effect of surface tension on impact force can be disregarded when simulating the impact.

  5. 5.

    The shape deformation of the oscillating droplet due to perturbation when leaving the needle tips affects impact force. The small horizontal-to-vertical ratio of the droplet shape leads to the small impact force and vice versa.