On the loss-of-correlation due to PIV image noise

Abstract

The effect of image noise on the uncertainty of velocity fields measured with particle image velocimetry (PIV) is still an unsolved problem. Image noise reduces the correlation signal and thus affects the estimation of the particle image displacement. However, a systematic quantification of the effect of the noise level on the loss-of-correlation is missing. In this work, a new method is proposed to estimate the loss-of-correlation due to image noise $F_{\sigma }$ from the autocorrelation function of PIV images. Furthermore, a new definition of the signal-to-noise ratio (SNR) for PIV images is suggested, which results in a bijective relation between $F_{\sigma }$ and SNR. Based on the newly defined SNR, it becomes possible to estimate the signal level and the noise level itself. The presented method is very general because the estimation of $F_{\sigma }$ and SNR works independently of various parameters, including the particle image intensity, the particle image density, the particle image size, the image noise distributions and the laser light-sheet profile. The findings lead to an extension of the fundamental PIV equation $N=N_{\mathrm {I}} F_{\mathrm {I}} F_{\mathrm {O}} F_{\Delta }$ and enable PIV users to optimize their measurement setup with respect to the image noise and not only based on the loss-of-correlation due to in-plane motion, out-of-plane motion and displacement gradients. Furthermore, the new definition of SNR allows for a characterization and comparison of PIV images. The new approaches are validated by using synthetic images, and the predictions are confirmed by using experimental data.

1 Introduction

Thanks to the enormous improvements regarding the quality of the equipment and the evaluation techniques during the last decades, nowadays PIV provides reliable velocity field distributions in transparent fluids even when the in-plane and out-of-plane loss-of-pairs is significant and strong gradients are present (Stanislas et al. 2003, 2005, 2008; Kähler et al. 2016). The valid detection probability of a shift vector depends on the height of the correlation peak with respect to the correlation noise. Keane and Adrian (1992) showed that the formation of a well-detectable correlation peak is sufficiently likely if the number of particle images within the interrogation window is $N_{\mathrm {I}} >7$. For larger numbers of particle images, the contrast of the correlation function further increases. However, using a larger number of particle images is not efficient in terms of spatial resolution. The interrogation window size and thus $N_{\mathrm {I}}$ must be selected carefully to compromise between valid detection probability and spatial resolution. It is well known that loss-of-correlation due to in-plane motion $F_{\mathrm {I}}$, out-of-plane motion $F_{\mathrm {O}}$ or displacement gradients $F_{\Delta }$ leads to a decreased probability for the detection of valid displacement vectors (Raffel et al. 2007; Adrian and Westerweel 2010). To keep these effects into account, the optical magnification, the seeding concentration, the light-sheet thickness and the size of the interrogation windows should be selected such that the effective number of particle images is $N=N_{\mathrm {I}}F_{\mathrm {I}}F_{\mathrm {O}}F_{\Delta } >7$. Usually, the one-quarter rule proposed by Keane and Adrian (1990) ensures a sufficiently high value of $F_{\mathrm {I}}$ for the first evaluation pass. For following evaluation passes, the in-plane loss-of-pairs is compensated by multi-pass interrogation techniques using window shifting (Willert 1996), such that $F_{\mathrm {I}}=1$ (at least for the final pass) for state-of-the-art multi-pass PIV evaluation methods. In-plane gradients can be compensated by combining multi-pass interrogation techniques with window deformation approaches (Scarano 2001). In the case of dominant out-of-plane motion, the time separation between the double images $\Delta t$ must be selected carefully to find a compromise between a large dynamic velocity range and a small amount of loss-of-pairs (Adrian 1997; Scharnowski and Kähler 2016).

After optimizing the probability in detecting a valid vector the problem of quantifying the uncertainty of the results emerged. Promising approaches for the uncertainty quantification are published by Timmins et al. (2012), Charonko and Vlachos (2013), Sciacchitano et al. (2013, 2015), Wilson and Smith (2013), Christensen and Scarano (2015), Neal et al. (2015), Wieneke (2015), Xue et al. (2015), Scharnowski and Kähler (2016), Kähler et al. (2012a, b). It was shown that the uncertainty of PIV measurements depends on many parameters in a complex manner, including particle image size, particle image density, turbulent fluctuations, noise level, velocity gradients and many more. Knowledge about the individual parameters is not necessarily required in order to estimate the shift vectors uncertainty if one analyzes the shape of the correlation function (Wieneke 2015). However, knowledge about the effect of the different parameters on the uncertainty certainly is desirable to identify the most important error sources and to optimize PIV experiments efficiently. To do so, it is necessary to determine not only the uncertainty with respect to the parameters, which can be done with the help of synthetic PIV images, but also to determine the value of these parameters from the PIV images.

One important parameter, which is difficult to determine from experimental PIV images, is the image noise level or the signal-to-noise ratio. Image noise is mainly generated by statistical processes during the collection of photons, the generation of photoelectrons and during the readout and amplification of the electrons in the camera sensor. The photon noise is characterized by a Poisson distribution, and the readout and amplification noise can be approximated by Gaussian noise (Jähne 2013; Hain et al. 2007). The noise level depends on the signal level itself. Thus, PIV images with bright background are also characterized by a higher noise level. Furthermore, the noise level is different for different camera sensors and also changes with its temperature due to thermal excitation of electrons.

Image noise reduces the correlation function’s contrast of cross-correlated PIV images and therefore raises the uncertainty for the shift vector estimation. Figure 1 illustrates, based on synthetic images, that the noise level $\sigma _{n}$, which is the standard deviation of random noise, affects the shift vector uncertainty $\Delta X_{\mathrm {rms}}$ quite strongly. While the particle image diameter D was kept constant, different numbers of particle images per pixel $N_{\mathrm {ppp}}$ were tested. The lower the particle image density is the higher the shift vector uncertainty becomes. Interestingly, the effect of $N_{\mathrm {ppp}}$ on $\Delta X_{\mathrm {rms}}$ becomes larger with increasing noise levels. This illustrates that knowledge about all individual parameters is required to optimize PIV measurements.

Fig. 1

Shift vector uncertainty $\Delta X_{\mathrm {rms}}$ computed from synthetic PIV images as a function of the image noise level $\sigma _{n}/I_{0}$ for different particle image densities $N_{\mathrm {ppp}}$. Particle image diameter and interrogation window size were set to $D=3.0$ px and $32\times 32\,$ px, respectively

Unfortunately, no method exists to determine the image noise level reliably from PIV images. To overcome this problem, a new method to estimate the loss-of-correlation due to image noise $F_{\sigma }$ from the height of the autocorrelation function is proposed in this work. It will be shown that a new definition of the signal-to-noise ratio SNR allows for an analytical solution for the loss-of-correlation due to image noise with respect to SNR.

Synthetic images are used to analyze the effect of different parameters on the correlation function and the shift vector uncertainty. The generation of the synthetic images is briefly discussed in the following section. Section 3 describes how the loss-of-correlation is determined from PIV images, and Sect. 4 discusses the new SNR definition. Section 5 shows how the shift vector uncertainty can be estimated from height of the autocorrelation function for a specific PIV evaluation algorithm. Finally, the developed methods for the estimation of $F_{\sigma }$ and SNR are applied to an experimental example to prove the theoretical and numerical predictions.

2 Synthetic PIV images

The generation and analysis of synthetic PIV images is a well-established method to investigate the effect of different parameters on the shift vector uncertainty, as discussed in Kähler et al. (2012a), Stanislas et al. (2003, 2005, 2008) and other works. The main advantages of synthetic PIV image analysis is that all parameters can be precisely controlled and varied independently over a range not achievable in experiments. On the other hand, all important parameters must be considered in order to generate realistic data.

All synthetic images were generated using MATLAB functions, as discussed in detail in Scharnowski and Kähler (2016). The controlled image parameters include: the maximum particle image intensity $I_0$, the particle image diameter D (width at which the intensity drops to $I_0/e^2$), number of particle images per pixel $N_{\mathrm {ppp}}$, noise level and others. The image noise was simulated as homogeneous background noise with constant standard deviation $\sigma _{n}$, referred to as noise level in the following, and a mean intensity of $5\sigma _{n}$. This approach accounts for PIV images with high background intensity that can reach the particle image intensity. Photon shot noise, which becomes very important for high particle image intensities combined with low background intensities, was not included in the synthetic images. In order to account for a three-dimensional particle distribution, the intensity of the particle images was computed based on their z-position. For most of the images a top-hat laser profile was simulated as this resembles quite nicely the intensity distribution of typically used Nd:YAG lasers. However, in Sect. 4.2 the effect of different light-sheet profile is discussed in detail. The discrete pixels’ gray values were computed from the integral over the pixels’ areas, corresponding to a sensor fill-factor of 1. Image noise with different distributions was added to the images. Gaussian noise was simulated for most of the images, but other distributions are tested in Sect. 4.1. Between the first synthetic PIV image A and the second one B a small particle image displacement of ${\pm }1\,$ px, with a constant gradient in y-direction, was simulated to capture all possible subpixel displacements in the analysis. This is important to achieve representative results. To account for the discrete nature of digital images, the intensity distribution was converted to 16-bit unsigned integer numbers. The image parameters were varied to study the effect of the noise level on the loss-of-correlation and the shift vector uncertainty. Figure 2 shows small sections ($100\times 100\,$ px) of example images with different noise levels and different particle image densities. The full size of the synthetic images was $1024\times 1024\,$ px.

Fig. 2

Examples of synthetic PIV images with constant particle image diameter $D=3\,\hbox{px}$, varying particle image density (from top to bottom) but increasing noise level (from left to right)

3 Loss-off-correlation

The function of the cross-correlation coefficient $C\left( \xi ,\psi \right)$ of a PIV image pair is computed from the averaged product of the intensity variations normalized by the product of the standard deviations of the intensity variations within the interrogation windows of the two images A and B:

$$\begin{aligned} C\left( \xi ,\psi \right) =\frac{\sum _{x=1}^{X} {\sum _{y=1}^{Y}{I^\prime _{A}\left( x,y\right) \cdot I^\prime _{B}\left( x-\xi ,y-\psi \right) }}}{X\cdot Y\cdot \sigma _{A} \cdot \sigma _{B}} \end{aligned}$$

(1)

where $\left( x,y\right)$ are coordinates of the image plane within the interrogation window, $\left( \xi ,\psi \right)$ are the displacements and $\sigma _{A}$ and $\sigma _{B}$ are the standard deviations of the intensity variations within the interrogation windows of the images A and B, respectively. The intensity variations are computed from the image intensity I and the mean intensity $\langle I\rangle$:

$$\begin{aligned} I^\prime \left( x,y\right) =I\left( x,y\right) -\langle I\rangle \end{aligned}$$

(2)

for both images A and B.

If random noise is added to the image intensity the shape of the correlation function, computed from Eq. (1), remains unchanged on average. However, the denominator in Eq. (1) increases. The standard deviation of a noisy image $\sigma _{A,n}$ is:

$$\begin{aligned} \sigma _{A,n}=\sqrt{\sigma _{A}^2 + \sigma _{n}^2} \end{aligned}$$

(3)

where $\sigma _{n}$ is the standard deviation of the noise level. Thus, image noise results in a decreased correlation signal. The loss-of-correlation due to image noise can be defined as the ratio of the averaged correlation function with and without image noise:

$$\begin{aligned} F_{\sigma }=\frac{\langle C_{n}\rangle }{\langle C\rangle }=\frac{\sigma _{A} \cdot \sigma _{B}}{\sqrt{\sigma _{A}^2 + \sigma _{n}^2} \cdot \sqrt{\sigma _{B}^2 + \sigma _{n}^2}}. \end{aligned}$$

(4)

It is important to note that the loss-of-correlation due to image noise $F_{\sigma }$ not only depends on the noise level but also on the standard deviation of the PIV images, where $\sigma _{A}$ is a function of the maximum particle image intensity $I_0$, the particle image diameter D and the particle image density. Based on the analysis of synthetic images, it can be shown that for $2\le D\le 10$ and $0.01\le N_{\mathrm {ppp}}\le 0.1$ the standard deviation of a noise-free PIV image is in good approximation given by

$$\begin{aligned} \sigma _{A}=\frac{I_0}{2} \sqrt{N_{\mathrm {ppp}}\cdot \left( \frac{\pi }{4}D^2 -1\right) } \end{aligned}$$

(5)

with an error of ${<}2\,\%$. $D^2 \cdot \pi / 4$ is the area at which the intensity is larger than $I_0 /{e}^2$.

While the loss-of-correlation due to image noise $F_{\sigma }$ is superimposed by the loss-of-correlation due to out-of-plane motion $F_{\mathrm {O}}$, in-plane motion $F_{\mathrm {I}}$ and velocity gradients $F_{\Delta }$ in the case of the cross-correlation [see Adrian (1988), Soria and Willert (2012) or Scharnowski et al. (2012)], the height of the autocorrelation function only depends on the noise alone. Figure 3 illustrates the normalized autocorrelation function R for three different noise levels. The center value of the normalized autocorrelation function always equals one due to the self-correlation of the noise. By using the intensity of the surrounding pixels without the center pixel to approximate the discrete autocorrelation function by a Gaussian fit function, the estimation of the loss-of-correlation from the peak height of the fit function $F_{\sigma }$ becomes possible. It is evident from the figure that $F_{\sigma }$ decreases with increasing noise level. The MATLAB code for the application of the fit function is provided in the “Appendix.”

Fig. 3

Autocorrelation distribution (left) and cross section (right) computed from synthetic PIV images with $D=3\,$ px and $N_{\mathrm {ppp}}=0.1$ for $\sigma _{A}/\sigma _{n}=1,\,2,\,5$ (from top to bottom). The gray bars represent the autocorrelation value, while the red line is the result of the Gaussian fit applied to pixels ($17\times 17\,$ px) around the peak

According to Eqs. (4) and (5) the loss-of-correlation due to image noise varies with D and $N_{\mathrm {ppp}}$ for a constant noise level. This is shown in Fig. 4, where the maximum intensity of the particle images $I_0$ and the image noise standard deviation $\sigma _{n}$ were kept constant, while D and $N_{\mathrm {ppp}}$ were changed over a broad range. It becomes clear from the figure and from Eq. 5 that the ratio $I_0/\sigma _{n}$, which is often used as signal-to-noise ratio for PIV images, is not suited for the estimation of the loss-of-correlation due to image noise. This is obvious for the following two reasons: First, not only the center of the particle images contributes to the correlation function but also the lower intensity values located around the maximum. Thus, larger particle images lead to higher signal and to less loss-of-correlation if the particle image intensity is kept constant. Second, more particle images increase the standard deviation of the image intensity, according to Eq. (5), which results in a reduced effect of the noise level on the loss-of-correlation, according to Eq. (4). Thus, higher particle image densities also represents higher signals and lead to less loss-of-correlation.

Fig. 4

Loss-of-correlation due to image noise as a function of the particle image size and the particle image density for a fixed noise level of $\sigma _n=0.2\cdot I_0$ and a fixed particle image intensity of $I_0=1000$. The contour lines indicate the levels $F_{\sigma }=0.2$ to 0.9 in steps of 0.1

It is important to note that in the case of large particle images combined with high particle image densities massive overlapping can occur. On average, the image area is fully covered for $N_{\mathrm {ppp}}\ge 4/(\pi \cdot D^2)$. Furthermore, for the estimation of $F_{\sigma }$ from the height of the autocorrelation function without center peak, the peak width and thus the particle image diameter must be significantly larger than $1\,$ px.

4 Signal-to-noise ratio

The maximum of the Gaussian fit function $F_{\sigma }$ of the autocorrelation function is equal to the loss-of-correlation of the correlation function. Thus, $F_{\sigma }$ in Eq. (4) can be computed from image A, assuming that A and B have the same maximum intensity and noise level:

$$\begin{aligned} F_{\sigma }=\frac{\sigma _{A}^2}{\sigma _{A}^2+\sigma _{n}^2}. \end{aligned}$$

(6)

Based on this equation, it is proposed to use the ratio of the standard deviations of the image intensity and the noise as signal-to-noise ratio:

$$\begin{aligned} {\text {SNR}}=\sigma _{A}/\sigma _{n}, \end{aligned}$$

(7)

which results in

$$\begin{aligned} F_{\sigma }=\left( 1+\frac{1}{\text {SNR}^2}\right) ^{-1} . \end{aligned}$$

(8)

Following the definition of Eq. (7), the SNR becomes 1 if $\sigma _{A}$ and $\sigma _{n}$ are equal. In this case the loss-of-correlation due to image noise is 50 %. For smaller noise levels $F_{\sigma }$ becomes larger and reaches $80\,\%$ for SNR $= 2$ or $96\,\%$ for SNR $\approx$ 5, respectively.

The proposed definition of SNR, shown in Eq. (7), is universal, because it results in a unique relation between $F_{\sigma }$ and SNR, which includes the effects of the particle image size and the particle image density, according to Eq. (5). Figure 5 illustrates the estimated $F_{\sigma }$ from synthetic PIV images with varying image intensity and varying noise level. For each symbol type in the figure, the particle image diameter was varied between $2\le D\le 10\,$ px and the particle image density varied between $0.01\le N_{\mathrm {ppp}}\le 0.1$, like in Fig. 4. The results clearly show that all estimated values collapse nicely with the theoretical curve given by Eq. (8). It is evident from Fig. 5 that the often used definition, $I_0 /\sigma _{n} = \text {SNR}$, does not result in a constant loss-of-correlation. The ratio $I_0 /\sigma _{n}$ only represents the same SNR as $\sigma _{A} /\sigma _{n}$ if $N_{\mathrm {ppp}}=4/\left( D^2\cdot \pi /4 -1 \right)$, according to Eq. (5). For $D=3\,$ px, for instance, the number of particle images per pixel must be $N_{\mathrm {ppp}}\approx 0.65$ to fulfill the condition $I_0=\sigma _{A}$, which is a rather high particle image density.

Fig. 5

Loss-of-correlation due to image noise as a function of the signal-to-noise ratio as defined in Eq. (7). Each symbol contains a variation of D and $N_{\mathrm {ppp}}$

On the one hand, the effect of particle image density on the loss-of-correlation is very small for low noise levels ${\text {SNR}} >10$ (red symbols in Fig. 5). In this region, improving SNR has only little effect on $F_{\sigma }$. On the other hand, at higher noise levels, particle image density and particle image diameter strongly affect $F_{\sigma }$, in agreement with the results of Fig. 4. The steepest slope of the function $F_{\sigma }\left( \text {SNR}\right)$ is at $\text {SNR}=1$, where $\sigma _{A}=\sigma _{n}$ and $F_{\sigma }=0.5$. In this region, improving SNR by increasing the particle image intensity or increasing the particle image density is most efficient and results in the best gain for $F_{\sigma }$.

4.1 Effect of noise distribution

So far, only Gaussian noise with a standard deviation of $\sigma _{n}$ and a mean value of $\mu =5\cdot \sigma _{n}$ was considered. To investigate the effect of different noise distributions on the relation between SNR and $F_{\sigma }$, two more distributions were tested. For noisy PIV images it is sometimes favorable to suppress noise by subtracting a constant value from the image intensity in a preprocessing step. To simulate such filtered PIV images, a noise distribution, which covers only the positive half of a Gaussian (with zero mean) was analyzed. Additionally, a slightly skewed Poisson-like distribution was simulated and tested. Figure 6 illustrates the three considered noise distributions normalized by their standard deviation. The vertical lines in the figure indicate the mean noise intensity.

Fig. 6

Distribution of the three simulated images noise intensities. The vertical lines indicate the mean values

For the three noise distributions, synthetic PIV images with $D=3\,$ px, $I_0=1024\,$ counts and $N_{\mathrm {ppp}}=0.1$ were generated. Thus, the image standard deviation is $\sigma _{A}\approx 400\,$counts, according to Eq. (5). To achieve SNR values between 0.1 and 100, the noise level was varied between $\sigma _{n}=4000$ and $\sigma _{n}=4$. Figure 7 shows that the estimated loss-of-correlation nicely collapses on the theoretical function for $F_{\sigma }\left( \text {SNR}\right)$ from Eq. (8) for all tested noise distributions. It can be concluded that the standard deviation $\sigma _{n}$ is the only relevant parameter of the noise distribution. Consequently, $F_{\sigma }$ and SNR can be reliably estimated from the height of the autocorrelation function. Figure 7 also includes a variation of the laser light-sheet profile, which is discussed in the following paragraph.

Fig. 7

Loss-of-correlation due to image noise as a function of the signal-to-noise ratio as defined in Eq. (7) for different image noise distributions and different laser light-sheet shape factors s

4.2 Effect of light-sheet profile

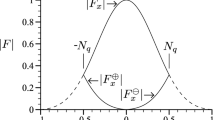
In order to account for a three-dimensional particle imaged distribution, the intensity of the particle images was adapted to their z-position according to the laser light-sheet intensity profile:

$$\begin{aligned} I\left( z\right) =I_{0}\cdot \exp \left[ -\frac{1}{\sqrt{2\pi }} \left| \left( \frac{2z}{\Delta z_{0}}\right) ^{s}\right| \right] ,\,\,\,\,\,\, s\ge 2. \end{aligned}$$

(9)

$I_{0}$ is the maximum intensity in the light-sheet center and $\Delta z_0$ is the width at which the intensity drops to $I_0\cdot \exp \left( -1/\sqrt{2\pi }\right) \approx 0.67\cdot I_0$. The factor $1/\sqrt{2\pi }$ ensures that the squared intensity is independent of the shape factor s for a fixed light-sheet thickness. As a result of this, different intensity profiles lead to the same image standard deviation $\sigma _{A}$, if the spatial density of particle images is kept constant. Consequently, a Gaussian light-sheet profile results in more particle images than a top-hat profile. However, for a top-hat profile, all particle images have a comparable intensity value in contrast to the Gaussian profile case. For $s=2$ the intensity profile is Gaussian, and for larger values it becomes closer to a top-hat profile, as illustrated in Fig. 8. In the previous analysis, only top-hat profiles with $s=10^4$ were simulated.

Fig. 8

Laser intensity profile according to Eq. (9) for different shape factors

To investigate the effect of the light-sheet shape on the relation between SNR and $F_{\sigma }$, the three shape factors $s=[2,10,10^4]$, shown in Fig. 8, were analyzed. As before, synthetic PIV images with $D=3\,$ px, $I_0=1024\,$ counts and $N_{\mathrm {ppp}}=0.1$ were generated. It is important to note that $N_{\mathrm {ppp}}$ refers to the top-hat case. For the generation of the synthetic images, the number of particle images was increased by a factor of four and the simulated z-location spans $\pm 2\Delta z_0$ to ensure a homogeneous distribution in z-direction.

Figure 7 shows that the theoretical function $F_{\sigma }\left( \text {SNR}\right)$ from Eq. (8) is also valid for all laser light-sheet shapes examined. Two important conclusions follow from this result. First, the effective light-sheet thickness is the width at which the intensity drops to $0.67\cdot I_0$. Second, the effective number of particle images in a non-top-hat light-sheet is the number of particle images with a maximum intensity higher than $0.67\cdot I_0$.

4.3 Estimation of σ _n and σ _A

The signal-to-noise ratio is estimated from the height of the autocorrelation function. The inverse function of Eq. (8) is:

$$\begin{aligned} {\text {SNR}}=\frac{\sigma _{A}}{\sigma _{n}}= \left( \frac{1}{F_{\sigma }}-1\right) ^{-0.5}. \end{aligned}$$

(10)

If $F_{\sigma }$ is measured, the ratio $\sigma _{A}/\sigma _{n}$ can be computed. The absolute values of $\sigma _{A}$ can be directly computed from Eq. (6):

$$\begin{aligned} \sigma _{A}=\sigma _{A,n}\sqrt{F_{\sigma }}, \end{aligned}$$

(11)

because the standard deviation of the noisy image $\sigma _{A,n}$ and $F_{\sigma }$ are measurable quantities. The noise level $\sigma _{n}$ follows from Eqs. (6) and (11):

$$\begin{aligned} \sigma _{n}=\sigma _{A,n}\sqrt{1-F_{\sigma }}. \end{aligned}$$

(12)

Thus, the signal $\sigma _{A}$ and the noise level $\sigma _{n}$ can be extracted from PIV images, theoretically.

Therefore, $F_{\sigma }$ must be estimated with high confidence. Figure 9 illustrates how the window size affects the estimation of $F_{\sigma }$. As before, synthetic PIV images with $D=3\,$ px, $I_0=1024\,$ counts and $N_{\mathrm {ppp}}=0.1$ were generated. Gaussian noise was added to the images to obtain different values for the loss-of-correlation. The window size from which the autocorrelation function was computed varied between $32\times 32\,$ px and $256\times 256\,$ px. The markers in the figure represent the mean value of the estimated $F_{\sigma }$ averaged over 100 windows, and the error bars correspond to the standard deviation. The figure shows that the smallest window size considered ($32\times 32\,$ px) results in a rather large scatter of the estimated $F_{\sigma }$. For a window size of $64\times 64\,$ px and $128\times 128\,$ px, the estimated $F_{\sigma }$ scatters much less. However, it seems to be slightly underestimated in the range between $F_{\sigma }\approx 0.2$ and 0.8, for these window sizes. The largest windows investigated ($256\times 256\,$ px) allow for a reliable estimation of $F_{\sigma }$. Thus, it can be concluded that several thousand particle images are required for the estimation of the loss-of-correlation due to image noise from the autocorrelation function. For a particle image density of $N_{\mathrm {ppp}}=0.1$, for instance, a window size of $128\times 128\,$ px or larger is recommended. In this work, the autocorrelation function was computed from $1024\times 1024\,$ px, if not stated differently. In principle, the autocorrelation function can also be computed from averaged window correlation (Meinhart et al. 2000) or single-pixel ensemble-correlation (Westerweel et al. 2004; Kähler et al. 2006).

Fig. 9

Estimated versus simulated loss-of-correlation due to image noise for different interrogation windows

The estimation of $\sigma _{n}$ for different interrogation window sizes is illustrated in Fig. 10. The smallest window size considered ($32\times 32\,$ px) results in a rather large scatter. Additionally, for $\sigma _{n}/I_0\le 0.2$, the image noise is slightly overestimated for a window size of $128\times 128\,$ px or smaller. The largest window investigated ($256\times 256\,$ px) allows for a reliable estimation of $\sigma _{n}$ down to $\sigma _{n}/I_0\approx 0.03$. It can be concluded that for $0.03\le \sigma _{n}/I_0<1.0$, corresponding to $0.4<{\text {SNR}}\le 30$, the image noise level can be estimated accurately from $F_{\sigma }$.

Fig. 10

Estimated versus simulated noise level $\sigma _{n}$ for different interrogation windows

5 PIV uncertainty due to image noise

The analysis of the autocorrelation function reveals the loss-of-correlation due to image noise. With the new definition of SNR, the ratio $\sigma _{A}/\sigma _{n}$ can now directly be measured. In order to estimate the shift vector uncertainty based on image noise for experimental PIV images, it is necessary to generate a look-up table from synthetic images by using the same evaluation software and the same settings. Figure 11 shows the relation between the shift vector uncertainty and $F_{\sigma }$ computed from synthetic images with $D=3\,$ px, $I_0=1024\,$ counts and $N_{\mathrm {ppp}}=0.1$ and different noise levels. The displacement fields were computed by using the software DaVis 8.2.3 (LaVision GmbH), including multi-pass processing with iterative image deformation and Gaussian window weighting. It is important to keep in mind that the shift vector uncertainty depends not only on the image noise level, but also on many other parameters, as discussed in Scharnowski and Kähler (2016) in more detail. Thus, the results from Fig. 11 do not enable for the uncertainty estimation on its own. In general, a multi-dimensional look-up table, covering all relevant parameters, is required (Timmins et al. 2012; Wilson and Smith 2013). Nevertheless, the image parameters used for Fig. 11 are representative and the trends are rather universal.

Fig. 11

Shift vector uncertainty as a function of the loss-of-correlation due to image noise for different interrogation window sizes

It becomes clear from Fig. 11 that the shift vector uncertainty strongly depends on the image noise, in agreement with the results of case B of the third PIV challenge (Stanislas et al. 2008). Particularly, for $0.8\le F_{\sigma }\le 1.0$, which is the relevant region for high quality experiments, the slope is rather steep. Thus, in order to be able to estimate the uncertainty from the effect of individual parameters, as discussed by Wilson and Smith (2013) or Timmins et al. (2012), it is important to precisely know the value of the image noise parameter.

6 Experimental example

In order to prove the proposed methods for the estimation of $F_{\sigma }$ and SNR on real PIV images, a wind tunnel experiment was performed. The experimental setup to measure the open jet flow is sketched in Fig. 12. The flow velocity was set to $u_\infty = 19.0\,$ m/s and the air was seeded with DEHS (Di-Ethyl-Hexyl-Sebacat) droplets with an average size of 1 μm (Kähler et al. 2002). Downstream of the nozzle ($360\,$ mm in diameter) the seeding droplets in the center of the jet were illuminated by a double-pulse Nd:YAG PIV laser with a pulse energy of up to $E_{\mathrm {max}}\approx 18\,$ mJ. A Zeiss macroplanar objective lens with $100\,$ mm focal length and an f-number of 2 was selected to image the scattered light to the sensor of a PCO sCMOS camera. To avoid perspective errors, a working distance of $400\,$ mm and a field of view of $12\,$ mm were used. Only the center part of the camera sensor ($512 \times 512\,$ px) was evaluated. To ensure uniform flow conditions, the measurement location was in the core of the free jet flow $100\,$ mm downstream of the nozzle’s exit.

Fig. 12

Top view of the experimental PIV setup for the investigation of the effect image noise on the shift vector uncertainty

By varying the laser pulse energy, PIV images with different SNR values were generated. For 18 pulse energy levels, ranging from 4 to $100\,\%$, 100 image pairs were recorded for each case. Figure 13 shows a $200\times 200\,$ px section of the images for four laser pulse energies E. The particle image intensity increases with increasing laser energy and more and more particle images become visible, as expected. The time between the laser pulses was set to $20\,{\upmu}$s corresponding to a maximum shift vector length of $\Delta X\approx 15\,$ px to obtain a good relative measurement uncertainty. Due to the uniform flow, uncertainties based on out-of-plane motion (Scharnowski and Kähler 2016) and bias errors due to strongly curved streamlines (Scharnowski and Kähler 2013) are negligible.

Fig. 13

Examples of experimental PIV images with varying laser pulse energy intensity

For all 18 laser pulse energy levels, $F_{\sigma }$ was estimated from the height of the normalized autocorrelation, whereas the autocorrelation function of both images A and B was averaged to account for differences between the two images. For each pulse energy $F_{\sigma }$ was determined by averaging the value over all 100 image pairs. The top part of Fig. 14 shows that $F_{\sigma }$ increases strongly for laser energies below $25\,\%$ from $0.4$ to $0.8$ and decreases slowly for higher energies. The reason why $F_{\sigma }$ does not reach values close to 1 is the relatively high optical magnification, which causes low particle image intensity and low particle image density. Both quantities directly affect the image standard deviation, according to Eq. (5), and thus the SNR and $F_{\sigma }$. The bottom part of Fig. 14 shows the estimated SNR, computed from Eq. (10), as a function of the laser pulse energy. The SNR increases strongly for laser energies below $25\,\%$ from $0.8$ to $2.0$ and decreases slowly for higher energies. At maximum laser power, the SNR is reduced to 1.7 compared to $25\,\%$ power. In order to achieve a higher SNR, one could try to increase the seeding density.

Fig. 14

Loss-of-correlation due to PIV image noise (top) as well as signal-to-noise ratio, image noise level and image signal level (bottom) for experimental PIV images with varying laser pulse energy

The noise level of the experimental PIV images was estimated from $F_{\sigma }$ and $\sigma _{A,n}$ by using Eqs. (11) and (12). Figure 14 shows the estimated $\sigma _{A}$ and $\sigma _{n}$, respectively. On the one hand, the signal increases with increased laser energy. On the other hand, the noise level increases at a comparable rate. As a result, increasing the laser energy to values of more than $25\,\%$ does not result in increased SNR for this experiment.

To investigate the effect of the laser pulse energy on the shift vector uncertainty, 100 instantaneous velocity fields were computed for each selected laser energy by using the software DaVis 8.2.3 (LaVision GmbH). Therefore, multi-pass PIV evaluation including iterative image deformation and Gaussian window weighting was applied. Three different final interrogation window sizes were investigated: $16\times 16\,$ px, $32\times 32\,$ px and $64\times 64\,$ px with an overlap of $50\,\%$, respectively. It was shown in Scharnowski and Kähler (2016) that the turbulence level of the flow facility is well below $1\,\%$ of the free stream velocity. Thus, shift vector fluctuations larger than $0.05\,$ px are assumed to be directly related to the measurement uncertainty. Figure 15 illustrates the standard deviation of the estimated shift vector’s horizontal component, where ${\Delta } X_{\mathrm {rms}}$ is at first computed locally from the 100 velocity fields for each interrogation window and thereafter averaged over the field of view.

Fig. 15

Shift vector uncertainty for experimental PIV images with varying laser pulse energy

Figure 15 shows that the shift vector uncertainty decreases rapidly with increasing laser pulse energy. Furthermore, $\Delta X_{\mathrm {rms}}$ decreases with increasing interrogation window size, as expected. Depending on the interrogation window size, ${\Delta } X_{\mathrm {rms}}$ remains constant from a certain laser pulse energy. For the $32\times 32\,$ px and the $64\times 64\,$ px interrogation windows, the constant uncertainty value starts approximately at the maximum of SNR ($25\,\%$ of laser energy). In the case of the smallest interrogation windows ($16\times 16\,$ px), ${\Delta } X_{\mathrm {rms}}$ remains constant from significantly higher laser pulse energy (${\approx } 50\,\%$). The increasing number of particle images with the laser pulse energy is probably more important than the SNR value for this window size. The lowest uncertainty is achieved for $64\times 64\,$ px at laser pulse energies between 0.4 and 0.65. Here, ${\Delta } X_{\mathrm {rms}}$ reaches values of ${\approx } 0.05\,$ px, which corresponds to a relative uncertainty of $0.05\,$ px$/15\,\hbox{px}$ $\,\approx 0.003$.

The discussed experiment shows that the proposed methods for the estimation of the loss-of-correlation due to image noise, for the signal-to-noise ratio, for the image noise level and for the signal level are well suited for real PIV images. The estimation of $F_{\sigma }$, SNR, $\sigma _{n}$ and $\sigma _{A}$ allow for a quantitative comparison of different PIV images and makes their quality quantitatively accessible.

7 Summary and discussion

The loss-of-correlation due to image noise $F_{\sigma }$ depends on the particle image intensity, the particle image density, the particle image size and the image noise in a complex manner. The presented approach shows that the loss-of-correlation can be determined from the distribution of the autocorrelation function with high confidence if the central peak is rejected. Furthermore, it is shown that the ratio of the standard deviations of the (noise-free) PIV image and the image noise is a useful and quite universal definition for SNR. The definition includes the effect the particle image intensity, the particle image density, the particle image size and the image noise. Due to the unique relation between SNR and $F_{\sigma }$, the newly defined SNR can directly be determined from the autocorrelation function, for the first time. The relation between SNR and $F_{\sigma }$ is very general. The findings are also valid for different noise distributions and different light-sheet profiles. It was shown that not only the SNR but also the noise level $\sigma _{n}$ and the signal level $\sigma _{A}$ can be estimated from of PIV images. The variation of the light-sheet shape factor showed that the effective thickness of a Gaussian light-sheet is 1.8 times the standard deviation (there the intensity drops to 0.67 times the maximum intensity). A top-hat intensity profile of the same width results in the same image standard deviation and thus in the same loss-of-correlation and the same shift vector uncertainty. The measurable quantity $F_\sigma$ allows for the estimation of the effect of the image noise on the shift vector uncertainty.

The findings of this work are an important step toward a full characterization of PIV images. Knowledge about SNR enables PIV users to compare their measurements quantitatively and to optimize the measurement setup. Furthermore, due to the effect of the image noise on the autocorrelation function, special care needs to be taken when estimating further properties from the autocorrelation function, like the particle image diameter or the particle image density (Warner and Smith 2014).

Finally, this analysis implies that the classical rule proposed by Keane and Adrian (1992), $N=N_{\mathrm {I}}F_{\mathrm {I}}F_{\mathrm {O}}>7$, which was extended by the loss-of-correlation due to gradients $F_{\Delta }$ by Westerweel (2008), must also be extended by the loss-of-correlation due to image noise. Hence, the effective number of particle images is $N=N_{\mathrm {I}}F_{\mathrm {I}}F_{\mathrm {O}}F_{\Delta }F_{\mathrm {\sigma }}$. The recommendation $N>7$ in the interrogation window is still valid, in order to keep the number of spurious vectors sufficiently low, such that they can be reliably detected.

Appendix

The MATLAB code for the estimation of $F_{\sigma }$, SNR, $\sigma _{A}$ and $\sigma _{n}$ is shown in the following: