Wake instabilities of a blunt trailing edge profiled body at intermediate Reynolds numbers

Abstract

Experiments have been conducted to identify and characterize the instabilities in the wake of a blunt trailing edge profiled body, comprised of an elliptical leading edge and a rectangular trailing edge, for a broad range of Reynolds numbers ($2{,}000\le Re(d)\le 50{,}000$ based on the thickness of the body). These experiments, which include measurements of the wake velocity field using hot-wire anemometry and particle image velocimetry, complement previous studies of the wake flow for the same geometry at lower and higher Reynolds numbers. The spatial characteristics of the primary wake instability (the von Kármán vortex street) are found to have relatively little variation in the range of Reynolds numbers investigated, in spite of the transition of the boundary layer upstream of the trailing edge from a laminar to a turbulent state. The dominant secondary instability, identified based on the structure of velocity and vorticity fields in the wake extracted using proper orthogonal decomposition, is found to have features similar to the ones described numerically and experimentally by Ryan et al. (J Fluid Mech 538:1–29, 2005), and Naghib-Lahouti et al. (Exp Fluids 52:1547–1566, 2012) at lower Reynolds numbers. The findings suggest that the spatial characteristics of the dominant primary and secondary wake flow instabilities have little dependence on the state of the flow upstream of the separation points, in spite of the distinct change in the normalized vortex shedding frequency upon the transition of the boundary layer.

1 Introduction

Periodic shedding of vortices dominates the wake of nominally two-dimensional bluff bodies as the primary instability, beyond a threshold Reynolds number. This phenomenon, which occurs due to the interaction of the separated shear layers, starts at Reynolds numbers as low as $Re(d)=49$ in the case of a circular cylinder (Williamson 1996) and continues to dominate the wake as the Reynolds number increases. The trend of variation of the vortex shedding frequency with Reynolds number, changes for bluff bodies with different profile geometries. This variation in the shedding frequency often includes discontinuities, due to the emergence of secondary instabilities, and transition of the flow in the wake and the shear layer to turbulence (Eisenlohr and Eckelmann 1988; Petrusma and Gai 1996).

Since the role of secondary instabilities on the flow structure of bluff body wakes was highlighted by Oertel (1990), extensive studies have been conducted to identify and describe them. Based on these studies, these instabilities have been characterized in detail in the case of a circular cylinder. As shown experimentally by Williamson (1996) and numerically by Wu et al. (1996), the first secondary instability, known as Mode-A, occurs in the wake of a circular cylinder at $Re(d)=194$ . This instability is replaced by a secondary instability with a different mechanism, known as Mode-B, at $Re(d)=230{-}260$. Both secondary instability modes appear as spanwise wave-like undulations in von Kármán vortices, which evolve into pairs of counter-rotating streamwise vortices further downstream. However, as first noted by Brede et al. (1996), the two modes have different spanwise wavelengths and vorticity structures. In the Mode-A instability, which has a spanwise wavelength of $3\le \lambda _{\rm z}/d\le 5$, the sense of rotation of the streamwise vortices alternates every half shedding cycle. However, in the case of Mode-B, which has a smaller spanwise wavelength of $\lambda _{\rm z}/d=1$, the streamwise vortices retain their sense of rotation over multiple shedding cycles. This behavior suggests that the streamwise vortices in the Mode-B instability may be originating from the instabilities in the boundary layer before separation. The studies of Bays-Muchmore and Ahmed (1993), Lin et al. (1995) and Hangan et al. (2001) confirm that the Mode-B instability continues to exist at Reynolds numbers of the order of $10^4$.

Studies involving bluff bodies with other profile geometries have shown that the secondary instability mechanisms for bluff bodies with non-circular profiles can be significantly different from those of a circular cylinder. For a square cylinder with fixed separation points at the trailing edge, Robichaux et al. (1999) have reported a Mode-A-type instability with a wavelength of $\lambda _{\rm z}/d=5.2$ , initiating at $Re(d)=162$, followed by a Mode-B-type instability with a wavelength of $\lambda _{\rm z}/d=1.2$, at $Re(d)=190$. They have also reported a third instability mechanism with a wavelength of $\lambda _{\rm z}/d=2.4{-}2.8$, in which the sense of rotation of the streamwise vortices alternates every full shedding cycle. This instability mechanism, which has been named Mode-S due to its sub-harmonic nature, becomes dominant at Reynolds numbers larger than $Re(d)=200$ and is therefore thought to play a key role in transition of the wake flow to turbulence. The experimental results of Dobre and Hangan (2004), which involve a square cylinder at $Re(d)=22{,}000$, indicated that a similar secondary instability mechanism continues to exist at higher Reynolds numbers. They report a secondary instability with a spanwise wavelength of $\lambda _{\rm z}/d=2.4$. The secondary instability has a general mechanism similar to Mode-A of a circular cylinder; however, its vorticity structure is distinguished from Mode-A by a staggered pattern of streamwise vorticity, in which the regions of negative streamwise vorticity are slightly shifted in the streamwise direction.

Other examples of secondary instability mechanisms that are qualitatively and quantitatively different from those of a circular cylinder have been reported in the case of elliptical cylinders (Sheard 2007), inclined square cylinders (Sheard et al. 2009), spheres, and torus-shaped bodies (Hourigan et al. 2007). Based on these differences, Hourigan et al. (2007) conclude that the wake transition sequence of a circular cylinder is not universal, and the wake of bluff bodies with other profile geometries may undergo transition to turbulence through different sequences, which may involve modes with spanwise wavelengths, threshold Reynolds numbers, and vorticity structures different from those of a circular cylinder.

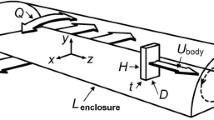
In the present study, instabilities in the wake of a bluff body with an elongated profile, comprised of an elliptical leading edge and a rectangular trailing edge, are investigated. This geometry, shown schematically in Fig. 1, will be referred to as a blunt trailing edge profiled body hereafter. From the point of view of practical applications, the blunt trailing edge profiled body can be regarded as a simplified representation of blunt trailing edge airfoils, which are of special interest in the aeronautical and wind power industries, due to their favorable upper surface pressure distribution, superior lift characteristics, and structural strength (Baker et al. 2006).

Fig. 1

The blunt trailing edge profiled body: a geometry and horizontal plane PIV measurement area, and b the model-endplate arrangement

The small-scale secondary instability in the wake of a blunt trailing edge profiled body has been investigated for the first time by Ryan et al. (2005), through direct numerical simulations and Floquet stability analysis at Reynolds numbers up to $Re(d)=650$. Their results indicated that the characteristics of the secondary instability for this bluff body depend on the chord length to thickness ratio $(l/d)$. The threshold Reynolds numbers for the onset of the secondary instability were found to be in the range of $400\le Re(d)\le 475$, which is significantly higher than the threshold Reynolds numbers of circular and square cylinders. For profiles with $l/d=2.5$ and 7.5, a Mode-A-type mechanism with spanwise wavelengths of $\lambda _{\rm z}/d=3.5$ and 3.9, respectively, was found to be the first mode to become unstable. In the case of profiles with $l/d=12.5$ and 17.5, the first mode to become unstable was a Mode-B-type mechanism, in which streamwise vortices retain their sense of rotation over multiple shedding cycles. However, this secondary instability mechanism was found to have features that distinguish it from the Mode-B instability of a circular cylinder. For instance, it has a larger spanwise wavelength of $\lambda _{\rm z}/d=2.2$, and a different distribution of vorticity in the formation region, which leads to traces of streamwise vorticity of the opposite sign accompanying the streamwise vortices at any given spanwise location. To emphasize these distinct features, this secondary instability mechanism has been named Mode-$\hbox {B}^{\prime }$ by Ryan et al. (2005). For profiles with $l/d>17.5$, this instability mechanism is replaced by one with a vorticity structure similar to Mode-S of a square cylinder, with a smaller spanwise wavelength of $\lambda _{\rm z}/d=1$. This secondary instability mechanism has been named Mode-$\hbox {S}^{\prime }$, to emphasize its different wavelength.

The experimental study by Naghib-Lahouti et al. (2012) confirmed the existence of a Mode-B′ instability in the wake of a blunt trailing edge profiled body with $l/d=12.5$. The Mode-B′ instability was found to be the dominant secondary mechanism at $550\le Re(d)\le 2{,}150$. The vortex structure of this instability, as well as its spanwise wavelength, which varies between $\lambda _{\rm z}/d=2.0$ at $Re(d)=550$ and $\lambda _{\rm z}/d=2.5$ at $Re(d)=2{,}150$, was found to be consistent with the Mode-$\hbox {B}^{\prime }$ instability predicted by Ryan et al. (2005).

Doddipatla (2010) investigated the secondary instabilities in the wake of a similar blunt trailing edge profiled body with $l/d=12.5$ experimentally at $Re(d)=24{,}000$ and 46,000. His finding indicates a dominant secondary instability with a near-wake structure similar to the Mode-$\hbox {B}^{\prime }$ mechanism predicted by Ryan et al. (2005), and a spanwise wavelength of $\lambda _{\rm z}/d=2.0{-}2.8$.

The objective of the present study is to extend the findings about primary and secondary wake instabilities of the blunt trailing edge profiled body to intermediate Reynolds numbers, through a series of experiments conducted at Reynolds numbers ranging between $Re(d)=2{,}000$ and 50,000. This range of Reynolds numbers has been chosen to bridge the gap between the low Reynolds number studies by Ryan et al. (2005) and Naghib-Lahouti et al. (2012), and the study by Doddipatla (2010), and is also relevant to the previously mentioned applications of this bluff body geometry. The present study also includes an investigation of the effects of the flow conditions upstream of the shear layer separation points on the characteristics of the wake instabilities. Specifically, the range of Reynolds numbers in the present study covers the transition of the boundary layer upstream of the trailing edge from laminar to turbulent. In comparison, the experiments by Naghib-Lahouti et al. (2012) involved a natural laminar upstream boundary layer, and the experiments by Doddipatla (2010) involved a fully turbulent boundary layer. In addition, the experiments conducted by Naghib-Lahouti et al. (2012), Doddipatla (2010), and the present experiments have been conducted at three different facilities with different freestream flow conditions corresponding to turbulence intensities between 0.05 and 0.9 %. From this perspective, comparison of the present results with those reported by Naghib-Lahouti et al. (2012) and Doddipatla (2010) makes it possible to assess the sensitivity of the three-dimensional wake flow structure to variations in the boundary layer state and freestream flow conditions. This paves the way for establishing a consistent description of the structure and instabilities of the flow in the wake of the blunt trailing edge profiled body over a broad range of Reynolds numbers and upstream flow conditions.

2 Experimental setup

The experiments have been carried out in a closed-circuit subsonic wind tunnel at the University of Toronto Institute for Aerospace Studies. The tunnel is able to generate a maximum freestream velocity of 40 m/s in a closed test section, which is 1.2 m wide, 0.8 m high, and 5.0 m long. It has been shown through hot-wire measurements at a freestream velocity of 10 m/s that variation of the mean velocity is less than 5 % of the average within a 0.3 m radius of the center of the test section, and freestream turbulence intensity is 0.05 %. It should be noted that the low Reynolds number experiments by Naghib-Lahouti et al. (2012) and the high Reynolds number experiments by Doddipatla (2010), which are referred to for comparison throughout the present work, were conducted using facilities which both had a higher freestream turbulence intensity of 0.9 %.

The blunt trailing edge profiled body model, shown schematically in Fig. 1, has a thickness of $d=0.0254$ m, which generates a blockage ratio of 3.2 % in the test section. The profile geometry of the model is comprised of a semi-elliptical leading edge with a length of $2.5d$, followed by a rectangular section. The total chord length to thickness ratio of the model is $l/d=12.5$. These geometric proportions are similar to those used in the studies by Ryan et al. (2005), Doddipatla (2010) and Naghib-Lahouti et al. (2012), to facilitate comparison with these studies. The model, which has a span of $27d$, is bounded by two transparent acrylic endplates, to isolate it from the effects of the sidewalls of the tunnel. The endplates, shown schematically in Fig. 1, extend $10d$ upstream of the leading edge, $20d$ downstream of the trailing edge, and $15d$ in the vertical direction on either side of the model. The model has a surface finish typical of finely machined aluminum. Throughout all experiments, a spanwise obstacle with a semi-circular cross section and a height of $5\times 10^{-4}$ m was placed at the beginning of the rectangular section $(x/d=2.5)$, to ensure the uniform transition of the boundary layer across the span of the model.

Hot-wire anemometry was used to measure the vortex shedding frequency $(f_{\rm s})$ and convective velocity $(U_{\rm c})$ in the wake. Hot-wire measurements were carried out using two single-wire probes, connected to a constant temperature anemometry (CTA) system, operated at an overheat ratio of 1.6. The CTA was built at the University of Newcastle, Australia, based on the anemometer design of Miller et al. (1987). The probes were calibrated in situ, immediately before each experiment, at 12 reference velocities ranging between 0.75 m/s and $1.5U_\infty$, using the Kings law curve fit. Reference velocities were measured using a pitot-static tube connected to an MKS Barotron Type 225A 1 Torr pressure transducer. Temperature in the test section was measured simultaneously, and a linear temperature correction (Bearman 1971) was applied to the measurements. In all cases, temperature variations during the experiments were maintained within $1.5\,^{\circ }\hbox {C}$ of the calibration temperature. The average error in velocity measurements, estimated using the methods described by Jorgensen (2002) and Moffat (1988), was found to be ±1.2 %.

One hot-wire probe was positioned at the wake centerline $(y/d=0)$, and the other one was positioned in the shear layer $(y/d=0.6)$. Both probes were traversed simultaneously in the streamwise direction, and measurements were made at 75 positions between $x/d=0.25$ and $x/d=5.3$, with the streamwise interval between the measurement locations increasing from $0.04d$ near the trailing edge to $0.16d$ at the farthest downstream position. For each measurement point, data were recorded at a sampling rate of 18.5 kHz, for a duration of 60 s. For measurement of the frequency spectra used to determine the vortex shedding frequency, the data recording time was increased to 200 s at selected downstream locations.

PIV measurements were carried out in the wake, at vertical $(xy)$ and horizontal $(xz)$ planes, to investigate the spatial characteristics of the primary and secondary wake instabilities, respectively. A LaVision FlowMaster system equipped with an Imager ProX 4M CCD camera with a resolution of $2{,}048\times 2{,}048$ pixels and a 200 mJ Nd:YAG laser was utilized. Lenses with focal lengths of 60 and 105 mm were used for imaging during the wake and boundary layer measurements, respectively. The laser beam was converted into a diverging light sheet using a cylindrical lens with a focal length of −25 mm and focused to a thickness of 0.9 mm in the measurement area using a spherical lens with a focal length of 500 mm. Bis(2-ethylhexyl) sebacate oil was used to generate seeding particles with an average size of 0.25 μm. In each experiment involving one combination of Reynolds number and measurement plane, 3,000 image pairs were recorded, with a recording rate of 5 image pairs per second. Velocity vector fields were obtained by cross-correlating the interrogation region in one frame to the search region in the second frame, using $32\times 32$ pixel interrogation windows with 50 % overlap, to obtain an array of $128\times 128$ vectors for each image pair. The size of the measurement area was chosen to make it possible to study the evolution of the wake over multiple shedding cycles of the von Kármán vortices in each image in the vertical plane, and to capture multiple wavelengths of the secondary instability in the horizontal plane. The vertical $(xy)$ plane measurements covered a $7.5d\times 7.5d$ area located at the mid-span of the model $(z/d=0)$, with the trailing edge of the model at the mid-height of the imaging area. The horizontal plane $(xz)$ measurements were carried out in a $7.5d\times 7.5d$ area located at $y/d=0.5$, as shown schematically in Fig. 1. Measurements of the boundary layer velocity field were carried out in an area measuring $2d$ in the streamwise direction and $1.4d$ in the wall-normal direction, centered at $0.8d$ upstream of the trailing edge. Velocity vectors were obtained using $16\times 16$ pixel interrogation windows with 50 % overlap. A combination of matte black paint and Kapton^® was used to limit surface reflections during the boundary layer measurements to the first 32 pixels in the wall-normal direction. As a result, valid vectors were obtained as close as 0.5 mm to the wall, with a resolution of 0.17 mm in the wall-normal direction. The number of vectors in the wall-normal direction within the boundary layers varied between 41 and 66, depending on $Re(d)$. The average normalized error in velocity measurements $(\Delta u/u)$, estimated using the method described by Cowen and Monismith (1997), was found to be 1.8 % in the vertical $(xy)$ plane and 2.2 % in the horizontal $(xz)$ plane.

3 Primary characteristics of the wake

In this section, the behavior of a number of principal characteristics of the von Kármán vortex street (the primary wake instability) over the range of Reynolds numbers covered by the present experiments are investigated. These characteristics include vortex shedding frequency, the length of the vortex formation region, and the streamwise wavelength, which have been determined based on the results of hot-wire and PIV measurements in the vertical $(xy)$ plane. As mentioned in Sect. 1, one of the objectives of the present study is to investigate the effect of the state of the boundary layer upstream of the trailing edge separation points on the characteristics of the wake flow. To determine the state of the boundary layer, PIV measurements have been carried out as described in detail in Sect. 2, at Reynolds numbers between $Re(d)=2{,}000$ and 30,000. Examples of the boundary layer velocity profiles at $0.5d$ upstream of the trailing edge are shown in Fig. 2a, in comparison with typical velocity profiles of laminar and turbulent boundary layers with the same thickness and boundary layer edge velocity (Schlichting 1979). Up to $Re(d)=8{,}000$, the velocity profiles are representative of a laminar boundary layer in a pressure gradient, similar to the one described by Niebles-Atencio et al. (2012). However, for $Re(d) \ge 10{,}000$, the velocity profiles are turbulent. The variation of the boundary layer shape factor, given by the ratio of the displacement thickness to the momentum thickness $(H=\delta ^{*}/\theta )$, with Reynolds number, is shown in Fig. 2b. The figure confirms the transition of the boundary layer from laminar to turbulent between $Re(d)=8{,}000$ and 10,000.

Fig. 2

a Boundary layer velocity profiles measured at $x=0.5d$ upstream of the trailing edge, in comparison with typical laminar and turbulent profiles, and b variation of the boundary layer shape factor $(H=\delta ^{*}/\theta )$ with Reynolds number

The vortex shedding frequency $(f_{\rm s})$ has been determined based on the power spectral density of the streamwise velocity $(u)$, given by

$$\begin{aligned} {\text{PSD}}=\frac{(\Delta t)^2}{T} \left|\sum \limits _{n=1}^{N} u_ne^{-i \omega n} \right|^2, \end{aligned}$$

(1)

which is obtained from hot-wire measurements in the shear layer $(x/d=2.0\,,\,y/d=0.6)$. In Eq. 1, $\Delta t$ is the time interval between samples, $N$ is the number of samples, and $T=N\Delta t$ is the total sampling time. Plots of power spectral density of $u$ for $Re(d)=5{,}000$, 12,000 and 24,000 are shown in Fig. 3, in terms of the normalized vortex shedding frequency $(\text{St}(d)=f_{\rm s}d/U_{\infty })$. The dominant peaks in the plots correspond to the vortex shedding frequency, and the smaller peaks, which occur at integer multipliers of the frequency associated with the dominant peak, represent the harmonics of the vortex shedding frequency.

Fig. 3

Power spectral density of streamwise velocity, measured at $x/d = 2.0,\,y/d = 0.6$. The graphs for $Re(d)=5{,}000$ and 24,000 have been offset by $10^{-1}$ and $10^{+1}$, respectively, to facilitate visualization

Figure 4 shows the variations of the vortex shedding frequency, expressed

Fig. 4

Variation of normalized vortex shedding frequency (expressed in terms of the Roshko number $Ro(d^{\prime })$) with Reynolds number

in terms of the Roshko number, $Ro(d^{\prime })={\text{St}}(d^{\prime })Re(d^{\prime })$, as a function of $Re(d^{\prime })$. The reference length in Fig. 4 is the thickness of the wake at the trailing edge, defined as $d^{\prime }=d+2\delta ^*$, in which $\delta ^*$ is the displacement thickness of the boundary layer. Using $d^{\prime }$ as reference length minimizes the effect of boundary layer thickness as an independent parameter and makes it possible to compare the data obtained from experiments involving blunt trailing edge profiled bodies with various length to thickness $(l/d)$ ratios and Reynolds numbers. Therefore, this reference length has been used throughout the manuscript to normalize the parameters representing the spatial characteristics of the wake. Comparison of the vortex shedding frequencies with previously published data indicates that the results of the present experiments follow the trend of the data from Naghib-Lahouti et al. (2012) at lower Reynolds numbers, and closely agree with the value reported by Doddipatla (2010) at the highest Reynolds number.

In previous studies, linear relationships between $Ro(d^{\prime })$ and $St(d^{\prime })$ have been observed for circular (Roshko 1954) and square cylinders (Yen and Yang 2011), as well as blunt trailing edge profiled bodies (Bull et al. 1995) at Reynolds numbers of order $10^4$. Bull et al. (1995) have established linear relationships between $Ro(d^{\prime })$ and ${\text{St}}(d^{\prime })$ based on their experiments involving blunt trailing edge profiled bodies at $Re(d)\le 15{,}000$, with slopes of 0.286 and 0.229 for bodies with laminar and fully turbulent boundary layers, respectively. In the present experiments, for $Re(d^{\prime })\ge$13,100 $Ro(d^{\prime })$ follows a linear trend with a slope of 0.231 (with a coefficient of determination $R^2=0.996$), which is close to the slope proposed by Bull et al. (1995) for the body with a fully turbulent boundary layer. For $Re(d^{\prime })\le 8,750,\,Ro(d^{\prime })$ varies with a slope of 0.289 $(R^2=0.998)$, which is comparable to the slope associated with the body with a laminar boundary layer. This change in the slope of $Ro(d^{\prime })$ vs. ${\text{St}}(d^{\prime })$ is another indicator of the transition of the boundary layer upstream of the trailing edge from laminar to turbulent between $Re(d) = 8{,}000$ and $Re(d)=12{,}000$.

The length of the vortex formation region $(L_{\rm f})$ is one of the important characteristics of the wake flow, since it is strongly correlated with the drag resulting from vortex shedding (Bearman and Tombazis 1993). Figure 5 shows the variations of $L_f$ with Reynolds number, based on the PIV measurements in the vertical $(xy)$ plane. As shown in Fig. 5, $L_{\rm f}$ is defined as the position of the downstream edge of the recirculation zone along the wake centerline, determined based on the sectional streamlines of the mean flow field. This position also corresponds with the location on the wake centerline where fluctuations of the streamwise velocity component reach a maximum (Williamson 1996). The results reported by Naghib-Lahouti et al. (2012) indicate that $L_{\rm f}$ decreases rapidly when the Reynolds number increases from $Re(d)=550$ to 2,150. According to the results of the present study, the rate of variation decreases at higher Reynolds numbers, and no significant change in $L_{\rm f}$ is observed when the boundary layer upstream of the trailing edge undergoes transition from laminar to turbulent between $Re(d)=8{,}000$ and $Re(d) = 10{,}000$. The trend of variation of $L_{\rm f}$ at higher Reynolds numbers in the turbulent regime is similar to the one reported by Pastoor et al. (2008) for a bluff body with a circular leading edge and rectangular trailing edge, in which a slight increase in $L_{\rm f}$ is observed when $Re(d)$ is increased from 23,000 to 70,000.

Fig. 5

a Contours of streamwise turbulence intensity and sectional streamlines of the mean flow at $Re(d) = 30{,}000$, showing the definition of vortex formation length $(L_{\rm f})$, and b variation of vortex formation length with Reynolds number

The wavelength of the primary instability $(\lambda _{\rm x})$ is another important characteristic of the wake flow, which quantifies the spatial structure of the von Kármán vortex street downstream of the formation region. It is defined as the streamwise spacing between two consecutive vortices shed from the same corner of the trailing edge and can be determined using

$$\begin{aligned} \lambda _{\rm x}=U_{\rm c}/f_{\rm s}, \end{aligned}$$

(2)

where $U_{\rm c}$ is the mean velocity on the wake centerline $(y/d=0)$, also known as the convective velocity. Figure 6 shows examples of $U_{\rm c}$ along the wake centerline, based on PIV measurements. The values of $U_{\rm c}$ obtained based on hot-wire measurements at $Re(d)=12{,}000$ are also shown for comparison and indicate that the velocities obtained using hot-wire deviate from those obtained using PIV when $x/d\le 2.0$. This deviation is believed to be due to the increasing magnitude of the vertical component of velocity $(v)$ relative to its streamwise component $(u)$ in the vicinity of the recirculation zone $(x/d\le 2)$, as well as the occurrence of flow reversal $(u<0)$ in the recirculation zone $(x/d\le 1)$. To verify this effect, the mean value of velocity magnitude $\overline{\left( u^2+v^2\right) ^{0.5}}$, obtained from PIV measurements, is also included in Fig. 6. The figure indicates that the velocity measured by hot-wire is in fact in close agreement with the mean value of velocity magnitude, rather than the streamwise velocity, due to the above-mentioned factors. When $x/d\ge 3.5$, however, the values obtained using PIV and hot-wire match closely, and the convective velocity shows little variation, indicating that $\lambda _{\rm x}$ remains relatively constant in this region as well. Based on this observation, and to obtain values comparable to those obtained by Naghib-Lahouti et al. (2012) at $x/d=4.0$ according to Eq. 2, $\lambda _{\rm x}$ has been calculated here using the value of $U_{\rm c}$ at $x/d=4.0$. Figure 6 indicates that while $\lambda _{\rm x}$ decreases considerably from $4.9d\,(3.2d^{\prime })$ to $3.7d$ $(2.9d^{\prime })$ when $Re(d)$ increases from 550 to 2,150 (Naghib-Lahouti et al. 2012), it shows relatively little dependence on $Re(d)$ at higher Reynolds numbers, with variation between $3.5d$ and $3.7d$ ($3.0d^{\prime }$ and $3.3d^{\prime }$) for $3{,}000\le Re(d) \le 50{,}000$. In particular, no significant change in $\lambda _{\rm x}$ is observed when the boundary layer upstream of the trailing edge undergoes transition from laminar to turbulent.

Fig. 6

a Convective velocity $(U_{\rm c})$ on the wake centerline $(y/d=0)$ based on PIV measurements. The results of hot-wire measurement and the mean value of velocity magnitude $\overline{\left( u^2+v^2\right) ^{0.5}}$ based on PIV measurements at $Re(d) = 12{,}000$ are included for comparison. b Variation of the wavelength of the primary wake instability $(\lambda _{\rm x})$ with Reynolds number

In summary, the present results indicate that the transition of the boundary layer upstream of the trailing edge results in a distinct change in the normalized vortex shedding frequency $({\text{St}}(d^{\prime }))$ from 0.231 to 0.289. However, the spatial characteristics of the primary wake instability ($L_{\rm f}$ and $\lambda _{\rm x}$) have been found to be less sensitive to variation of Reynolds number within the range investigated in the present study $(2{,}000\le Re(d)\le 50{,}000)$. Considering the close relationship between the spatial characteristics of the small-scale secondary instability and those of the primary instability, the limited variation of $\lambda _{\rm x}$ over the range of Reynolds numbers studied here suggests that the effect of Reynolds number on the small-scale secondary instability may be similarly limited, as will be discussed in the next section.

4 Secondary instabilities

The results of PIV velocity field measurements in the horizontal $(xz)$ plane are analyzed in this section to characterize the small-scale secondary instability. The objective is to determine the spanwise wavelength $(\lambda _{\rm z})$ and identify the spatial structure of the instability, in comparison with the low Reynolds number small-scale secondary instability modes observed by Ryan et al. (2005) and Naghib-Lahouti et al. (2012), shown schematically in Fig. 7.

Fig. 7

Schematic representation of vorticity structure of the secondary instability (adapted from Naghib-Lahouti et al. (2012))

4.1 Wavelength of the small-scale secondary instability

Figure 8 shows an example of the instantaneous distribution of streamwise velocity $(u)$ in the horizontal $(xz)$ plane located at $y/d=0.5$, measured at $Re(d)=5{,}000$. Effects of both large- and small-scale secondary instabilities can be observed in the figure. The large-scale secondary instability appears as dislocations in the von Kármán vortices, which distort the vortices in the streamwise direction, as previously described by Williamson (1996) in the case of a circular cylinder.

Fig. 8

Instantaneous contours of streamwise velocity $(u)$ in the horizontal $(xz)$ plane located at $y/d=0.5$, for $Re(d)=5{,}000$. The spanwise variations of $u$ are associated with the small-scale instability. The dashed line highlights the dislocation in the von Kármán vortex due to the large-scale instability

The small-scale secondary instability originates as streamwise undulations in von Kármán vortices, which evolve into pairs of counter-rotating vortices further downstream. These streamwise undulations in the von Kármán vortices are associated with spanwise variations of streamwise velocity $(u)$, which are visible in Fig. 8. As shown by Mansy et al. (1994) and Wu et al. (1996), in the case of a circular cylinder, and El-Gammal and Hangan (2008) and Naghib-Lahouti et al. (2012) for a blunt trailing edge profiled body, a correlation exists between the small-scale secondary instability and the spanwise variations of the streamwise velocity $(u)$ in the near-wake region, in which both have the same spanwise wavelength. Based on this correlation, the streamwise velocity data, acquired by PIV measurements in the horizontal $(xz)$ plane, are analyzed to determine the wavelength of the small-scale secondary instability.

Proper orthogonal decomposition (POD) analysis is used here to obtain a simplified, energy-based representation of the velocity field, which facilitates the identification of the small-scale secondary instability. The computational cost of POD analysis can be reduced using the method of snapshots (Sirovich 1987) when the number of vectors in each sample $(n_{\rm V})$ is considerably larger than the number of samples $(N)$. Therefore, this method has been utilized to carry out the POD analysis in the present study, where $n_{\rm V} =$16,384 and $N=3{,}000$. To ensure that the results of POD analysis using 3,000 snapshots represent the POD mode shapes and the associated eigenvalues accurately at higher Reynolds numbers, additional POD analysis has been carried out using independent data ensembles containing 500 to 3,000 snapshots, acquired at $Re(d)=16{,}000$, as a representative of the turbulent boundary layer–turbulent wake regime. Very little variation in the individual mode shapes, and a maximum variation of 2.5 % in the eigenvalues of the first 32 modes have been observed when the results obtained using 2,000- and 3,000-snapshot data ensembles are compared, indicating that $N=3{,}000$ is adequate for POD analysis at higher Reynolds numbers.

In order to study the features of the small-scale secondary instability, including its spanwise wavelength, a combination of the POD modes which adequately represents the original data ensemble should be used. Such a POD representation should preserve the features of the original data ensemble by including sufficient number of modes. The ratio of the cumulative energy contained by a POD representation, based on $M\le N$ modes, to that of the original data ensemble, is used here as a criterion for the adequacy of the POD representation. This ratio is based on the eigenvalues $(\lambda ^n)$, which represent the relative energy of the respective POD modes, and is given by

$$\begin{aligned} E_{\rm c}= \sum _{n=1}^{M}\lambda _{\rm n}\bigg / \sum _{n=1}^{N}\lambda _{\rm n}. \end{aligned}$$

(3)

Figure 9 shows the variation of $E_{\rm c}$ with the number of POD modes, for $2{,}000\le Re(d)\le 24{,}000$. The figure shows that at higher Reynolds numbers, an increasingly larger part of the total energy is contained by the higher modes. In particular, a distinct shift of energy toward higher POD modes can be observed between $Re(d) = 8{,}000$ and $Re(d) = 12{,}000$, where the boundary layer upstream of the trailing edge undergoes transition to turbulence. This behavior implies that a larger number of modes is required for the POD representation to preserve a given proportion of the total energy at higher Reynolds number. As a quantitative criterion, the number of modes to be included in the POD representation for each Reynolds number is selected such that at least 70 % of the cumulative energy is preserved. This number is $M=16$ for $Re(d)\le 5{,}000,\,M=20$ for $Re(d)=8{,}000$, and $M=32$ for $Re(d)\ge 12{,}000$.

Fig. 9

Normalized cumulative energy $(E_{\rm c})$ of the first 150 POD modes of streamwise velocity $(u)$ (The inset shows $E_{\rm c}$ for the first 8 modes.)

Examples of the superimposed POD mode shapes obtained using the above-mentioned numbers of modes are shown in Fig. 10. The mode shapes show the alternating spanwise variations of streamwise velocity due to the small-scale instability. The distortion in the superimposed POD mode shapes (marked by the dashed line in Fig. 10) is a result of the streamwise dislocations caused by the large-scale instability.

Fig. 10

Contours of the reconstructed fluctuating component of streamwise velocity $(\tilde{u})$ based on superimposed POD mode shapes of $u$ in the horizontal $(xz)$ plane: a $Re(d) = 2{,}000$, 16 modes, b $Re(d) = 5{,}000$, 16 modes, c $Re(d) = 16{,}000$, 32 modes, and d $Re(d) = 24{,}000$, 32 modes. The dashed line highlights the dislocation in the von Kármán vortex due to the large-scale instability

The spanwise wavelength of the small-scale secondary instability is determined based on spanwise variations of the reconstructed fluctuating component of streamwise velocity $(\tilde{u})$ extracted from the superimposed POD mode shapes, which have been shown at selected streamwise locations in Fig. 11. The average wavelength of the secondary instability $(\lambda _{\rm z})$, defined as the average spanwise distance between the relative maxima or minima of streamwise velocity, varies between $2.3d$ and $2.5d$ for the range of Reynolds numbers investigated here. Figure 12 shows the variation of $\lambda _{\rm z}$ with Reynolds number, in comparison with previously published data, using $d^{\prime }$ as the normalizing length scale. The normalized wavelength obtained at $Re(d)=5{,}000$ is very close to the value reported by Naghib-Lahouti et al. (2012) at $Re(d)=2{,}150$. The value of $\lambda _{\rm z}/d^{\prime }$ at $Re(d)=24{,}000$ is also in good agreement with the one reported by Doddipatla (2010). Between these two extremes, $\lambda _{\rm z}$ shows relatively little variation. Most notably, no significant variation in $\lambda _{\rm z}$ is observed between $Re(d) = 8{,}000$ and 12,000, where the boundary layer upstream of the trailing edge undergoes transition to turbulence. These observations support the relationship between the instability wavelengths in the streamwise and spanwise directions, mentioned in Sect. 3, as both parameters show a similar trend of variation at intermediate Reynolds numbers.

Fig. 11

Examples of spanwise variation of the reconstructed fluctuating component of streamwise velocity $(\tilde{u})$ based on the superimposed POD mode shapes, for a $2{,}000\le Re(d)\le 8{,}000$, and b $12{,}000\le Re(d)\le 24{,}000$

Fig. 12

Variation of the wavelength of the small-scale secondary instability $(\lambda _{\rm z})$ with Reynolds number. The uncertainty bars indicate the combination of the statistical uncertainty resulting from the standard deviation of multiple measurements of $\lambda _z$ in each superimposed mode shape, and the systematic uncertainty of spatial coordinates due to the discretized nature of velocity field measurements in PIV

The limited variation of $\lambda _{\rm z}$ over a relatively broad range of Reynolds numbers, involving various flow conditions upstream of the trailing edge, is significant from the point of view of flow control. For flow control approaches based on interaction with secondary instabilities at their natural wavelength, such as the ones examined by Naghib-Lahouti et al. (2012), Doddipatla (2010) and Park et al. (2006), a relatively constant $\lambda _{\rm z}$ makes it possible to implement the flow control approach in a broad range of flow regimes with minimum modification to its physical arrangement (i.e., the spanwise spacing of actuators).

4.2 Flow structure of the secondary instability

Based on their flow visualizations and measurements at low Reynolds numbers $(550\le Re(d)\le 2{,}150)$, Naghib-Lahouti et al. (2012) have described the mechanism of secondary instability in the wake of the blunt trailing edge profiled body, as shown schematically in Fig. 7. The schematic diagram in Fig. 7 relates the spanwise undulations in von Kármán vortices to the sense of rotation and spanwise position of the streamwise vortices, and depicts a flow structure that is qualitatively similar to the Mode-B secondary instability of a circular cylinder, in which the counter-rotating streamwise vortices retain their sense of rotation over multiple shedding cycles. The results of the present measurements in the horizontal $(xz)$ plane are investigated in this section to determine whether a similar instability mechanism continues to exist at higher Reynolds numbers, in a manner similar to those described in Sect. 1 in the case of circular and square cylinders.

One of the features described by Naghib-Lahouti et al. (2012) is the alternating spanwise undulations in the von Kármán vortices shed from the two corners of the trailing edge in a shedding cycle, which is a characteristic of Mode-B-type secondary instabilities. Due to this alternating behavior, the spanwise position of the regions of high- and low-streamwise velocity also alternates, so that in each shedding cycle, high-velocity regions in one half-cycle are followed by low-velocity ones at the same spanwise positions, in the next half-cycle. Investigation of the individual streamwise velocity POD modes shown in Fig. 13 indicates a similar behavior in the present results. The figure shows the POD modes for two Reynolds numbers that are representative of the cases with laminar and turbulent boundary layers upstream of the trailing edge. In both cases, a staggered pattern for all mode shapes can be observed, with regions of high and low velocity appearing alternatively at the same spanwise position. Another example of the same behavior is shown in Fig. 14. The figure shows a sample of instantaneous distribution of streamwise velocity $(u)$ at $Re(d)=24{,}000$, in which the high-velocity regions in one half-cycle (marked by + signs) are followed by low-velocity regions in the next half-cycle (marked by − signs).

Fig. 13

The first 8 POD modes of streamwise velocity $(u)$ in the horizontal $(xz)$ plane located at $y/d=0.5$, for a $Re(d)=5{,}000$ and b $Re(d) = 24{,}000$

Fig. 14

An example of instantaneous contours of streamwise velocity $(u)$ in the horizontal $(xz)$ plane located at $y/d=0.5$, at $Re(d)=24{,}000$, showing the pattern of high and low velocities in the vortices shed from opposite corners

The vorticity structure in the wake in the present experiments is also found to be consistent with the mechanism shown in Fig. 7. This can be demonstrated by the results of POD analysis of the vertical vorticity component $(\omega _{\rm y}=\partial w/\partial x-\partial u/\partial z)$ in the horizontal $(xz)$ plane. Figure 15 shows examples of superimposed POD mode shapes of $\omega _{\rm y}$. For both Reynolds numbers (representing laminar and turbulent upstream boundary layers), the mode shapes show regions of positive and negative $\omega _{\rm y}$ across the span, with an average spanwise spacing between positives or negatives that is approximately half of the wavelength of the secondary instability $(\lambda _{\rm z})$. This behavior can be interpreted based on the relative position of the horizontal measurement plane and the streamwise vortices, which has been illustrated in Fig. 16. The figure shows the phase-averaged sectional streamlines of the flow in the vertical $(xy)$ plane, at $Re(d) = 12{,}000$. The streamwise vortices appear as braids that connect consecutive von Kármán vortices (Williamson 1996). The braids can be represented topologically by connecting focal points through saddle points by sectional streamlines (Dobre and Hangan 2004), as highlighted in Fig. 16. The location of the horizontal measurement plane is also marked with the horizontal dashed line. As shown in Fig. 16, the horizontal measurement plane intersects with the braids connected to each von Kármán vortex at two locations (marked by circles in the figure). These two intersections are located on the braids connecting the von Kármán vortex to the ones upstream and downstream, which are shed from the opposite corner of the trailing edge. In the Mode-$\hbox {B}^{\prime }$ instability (shown schematically in Fig. 7), the streamwise vortices represented by both braids have the same sense of rotation, therefore, the vertical vorticity $(\omega _{\rm y})$ of these vortices will have opposite signs. As a result, the two intersections will appear as one region with $\omega _{\rm y}<0$ and another one with $\omega _{\rm y}>0$ in the horizontal plane, as is the case for the present measurements (Fig. 15).

Fig. 15

Distribution of vertical vorticity $(\omega _{\rm y})$ in the near-wake region, based on the first 8 POD modes, at a $Re(d)=5{,}000$, and b $Re(d)=24{,}000$

Fig. 16

Phase-averaged sectional streamline plot at $Re(d)=12{,}000$, showing the relative position of the horizontal measurement plane and the wake vortices. The letters N and S indicate the approximate locations of the nodes and saddle points, respectively, and the arrows indicate the sense of rotation of the streamwise vortices

A similar discussion applies to the other streamwise vortex in a pair of counter-rotating streamwise vortices, which has an opposite sense of rotation, and is not visible in Fig. 16 due to its spanwise separation. This vortex also generates regions of positive and negative $\omega _{\rm y}$ in the horizontal plane; however, the signs of these regions are opposite of those generated by the other vortex, as shown schematically in Fig. 7. As a result, the intersection of the horizontal measurement plane with each pair of counter-rotating streamwise vortices will result in two adjacent regions of positive and negative $\omega _{\rm y}$, separated in the spanwise direction. In other words, the spanwise spacing between regions of positive or negative $\omega _{\rm y}$ in the horizontal plane will be half of the spanwise spacing of the pairs of counter-rotating streamwise vortices, or $\lambda _{\rm z}/2$. In contrast, a Mode-A-type instability, in which each streamwise vortex changes its sense of rotation every half shedding cycle, would result in regions of positive and negative $\omega _{\rm y}$ with a spanwise spacing equal to $\lambda _{\rm z}$ in the horizontal plane. Therefore, the spanwise distribution and spacing of vertical vorticity $(\omega _{\rm y})$, shown in Fig. 15, is consistent with the description presented above for Mode-$\hbox {B}^{\prime }$, and therefore supports the existence of this instability in the wake for the range of Reynolds numbers investigated here.

5 Conclusions

The characteristics of the primary and secondary instabilities, and the associated three-dimensional flow structure in the wake of a blunt trailing edge profiled body have been analyzed based on experiments at Reynolds numbers ranging between $Re(d)=2{,}000$ and $Re(d)=50{,}000$. The range of Reynolds numbers in the present study bridges the gap between the experimental results reported by Naghib-Lahouti et al. (2012) for $Re(d)\le 2{,}150$, and those reported by Doddipatla (2010) for $Re(d) \ge 24{,}000$. Moreover, this range of Reynolds numbers includes the transition of the boundary layer upstream of the trailing edge from laminar to turbulent, that occurs between $Re(d) = 8{,}000$ and 10,000, thus allowing an investigation of the effect of the state of the boundary layer on the wake flow characteristics.

The von Kármán vortex street dominates the flow in the wake, as the primary wake instability. The non-dimensional vortex shedding frequency is in close agreement with the values reported by other investigators at the two extremes of the range. Similar to previous studies involving circular and square cylinders and blunt trailing edge profiled bodies, a linear relationship is found to exist between $Ro(d^{\prime })={\text{St}}(d^{\prime })Re(d^{\prime })$ and $Re(d^{\prime })$ in the present results. When $Re(d)\le 8{,}000$, the slope of the linear relationship is in close agreement with the one reported by Bull et al. (1995) for similar bodies with laminar boundary layers, while for $Re(d)\ge 12{,}000$, it changes to a value very close to the one reported for bodies with turbulent boundary layers.

The effect of Reynolds number on the spatial characteristics of the wake has been studied by investigating the variations of the length of the vortex formation region $(L_{\rm f})$ and the wavelength of the von Kármán vortex street $(\lambda _{\rm x})$. While the results reported by Naghib-Lahouti et al. (2012) indicate a rapid decrease of both parameters when $Re(d)$ increases from 550 to 2,150, the present results show relatively small variation in both parameters for Reynolds numbers between $Re(d) = 2{,}000$ and 50,000. Specifically, neither of the two parameters change significantly when the boundary layer upstream of the trailing edge undergoes transition between $Re(d) =8{,}000$ and 12,000.

The secondary wake instabilities have been characterized based on the measurements and POD analysis of the wake velocity field in the horizontal $(xz)$ plane located at $y/d=0.5$. The results indicate that large- and small-scale secondary instabilities are simultaneously present in the wake. The large-scale secondary instability appears as dislocations in the von Kármán vortices, which distort the vortices in the streamwise direction, as previously described by Williamson (1996) in the case of a circular cylinder. The effect of the small-scale instability appears as spanwise variations of streamwise velocity in the velocity field. These spanwise variations correspond to undulations in von Kármán vortices, which are associated with the formation of pairs of counter-rotating streamwise vortices.

The POD mode shapes and instantaneous snapshots of streamwise velocity field indicate that the velocity variations follow a staggered pattern, in which the spanwise position of the regions of high and low velocity alternates every half shedding cycle. This behavior is one of the features of the Mode-$\hbox {B}^{\prime }$ instability mechanism described by Naghib-Lahouti et al. (2012) for the same bluff body at low Reynolds numbers between $Re(d)= 550$ and 2,150. The distribution of the vertical component of vorticity $\omega _{\rm y}$ in the present results is also found to be consistent with the features of the aforementioned instability mechanism. Furthermore, the average spanwise wavelength of the small-scale instability, which varies between $\lambda _{\rm z}/d^{\prime }=2.0$ and 2.2 $(\lambda _{\rm z}/d=2.3-2.5)$ for the range of Reynolds numbers studied herein, is found to be within the range of wavelengths reported by Ryan et al. (2005) and Naghib-Lahouti et al. (2012) for the Mode-$\hbox {B}^{\prime }$ instability at low Reynolds numbers. Based on these findings, it can be concluded that the Mode-$\hbox {B}^{\prime }$ small-scale instability mechanism continues to exist at the intermediate Reynolds numbers investigated here, with relatively little variation in the normalized spanwise wavelength $(\lambda _{\rm z}/d^{\prime })$. Most remarkably, no significant variation in $\lambda _{\rm z}/d^{\prime }$ is observed between $Re(d)=8{,}000$ and 12,000, where the boundary layer upstream of the trailing edge undergoes transition to turbulence.

The results of the present study indicate that the spatial characteristics of the wake, including the structure and spanwise wavelength of the small-scale secondary instability, have limited dependence on the state of the boundary layer upstream of the separation point. This finding is significant since it confirms that the boundary layer plays a limited role in the dynamics of the separated flow in the wake of nominally two-dimensional bluff bodies, as suggested by the results of previous studies involving circular cylinders (Bays-Muchmore and Ahmed 1993; Lin et al. 1995; Hangan et al. 2001) and square cylinders (Dobre and Hangan 2004).