Secondary wake instabilities of a blunt trailing edge profiled body as a basis for flow control

Abstract

Flow in the wake of a blunt trailing edge profiled body, comprised of an elliptical leading edge and a rectangular trailing edge, has been investigated experimentally, to identify and characterize the secondary instabilities accompanying the von Kármán vortices. The experiments, which involve laser-induced fluorescence for visualization and particle image velocimetry for quantitative measurement of the wake instabilities, cover Reynolds numbers ranging from 250 to 2,150 based on thickness of the body, to include the wake transition regime. The dominant secondary instability appears as spanwise undulations in von Kármán vortices, which evolve into pairs of counter-rotating vortices, with features resembling the instability mechanism predicted by Ryan et al. (J Fluid Mech 538:1–29, 2005). Feasibility of a flow control approach based on interaction with the secondary instability using a series of discrete trailing edge injectors has also been investigated. The control approach mitigates the adverse effects of vortex shedding in certain conditions, where it is able to amplify the secondary instability effectively.

1 Introduction

The flow structure in the wake of nominally two-dimensional bluff bodies is dominated by periodic shedding of vortices, due to the interaction between the shear layers separated from the two sides of the body that occurs beyond a threshold Reynolds number. This process, which starts at Reynolds numbers as low as Re(d) = 49 in the case of circular cylinder (Williamson 1996), continues to remain the primary instability mechanism in the wake, although its intensity and frequency vary as Reynolds number increases. While the trend of variation of vortex shedding frequency with Reynolds numbers is different for different profile geometries, this trend is often found to be affected by discontinuities, which have been attributed to secondary instabilities, as noted by Eisenlohr and Eckelmann (1988), Bull et al. (1995), and Petrusma and Gai (1996).

Since the secondary instability mechanisms were acknowledged by Oertel (1990), these instabilities have been extensively studied through experiments and numerical simulations, especially for circular cylinders. It is now well established that the cylinder wake is affected by two secondary instabilities, known as Modes A and B, which occur at Re(d) = 194 and Re(d) = 230–260 (Williamson 1996; Wu et al. 1996). As first reported by Brede et al. (1996), Modes A and B have different spanwise wavelengths and vorticity structures. The Mode-A instability appears as undulations or waves in the spanwise wake vortices (also known as von Kármán vortices), which evolve into pairs of counter-rotating streamwise vortices connecting the von Kármán vortices, with a spanwise wavelength of 3d ≤ λ _z  ≤ 5d. In Mode-A, the sense of rotation of the streamwise vortices alternates every half shedding cycle. The Mode-B instability also appears as pairs of counter-rotating streamwise vortices; however, unlike Mode-A, the streamwise vortices retain their sense of rotation over multiple shedding periods. This suggests that the Mode-B streamwise vortices may be originating from the instabilities existing in the shear layer prior to separation, which then undergo stretching between the von Kármán vortices. The Mode-B instability, which has a spanwise wavelength of λ _z  = 1d, continues to exist at higher Reynolds numbers in the order of 10⁴, as shown by Bays-Muchmore and Ahmed (1993), Lin et al. (1995), and Hangan et al. (2001).

The secondary wake instability mechanisms for bluff bodies with other profile geometries can be significantly different from those of the circular cylinder. In the case of a square cylinder, which represents forced shear layer separation, Robichaux et al. (1999) have shown that a Mode-A instability with a spanwise wavelength of λ _z  = 5.2d occurs at Re(d) = 162, followed by a Mode-B instability with λ _z  = 1.2d at Re(d) = 190. They have also reported an intermediate-wavelength secondary instability mode named Mode-S, which is not observed in the case of a circular cylinder. Mode-S has a spanwise wavelength of λ _z  = 2.4d–2.8d, and a subharmonic streamwise vorticity structure, in which the sense of rotation of the streamwise vortices alternates every full shedding cycle. This mode becomes the dominant secondary instability when Reynolds number increases beyond Re(d) = 200 and is thought to play an important role in transition of the wake into turbulence. The experimental study of the wake flow structure of a square cylinder at Re(d) = 22,000 by Dobre and Hangan (2004) indicates that the differences between the secondary instabilities in the wake of square and circular cylinders continue to exist at higher Reynolds numbers. The secondary instability reported by Dobre and Hangan (2004) has features that distinguish it from Mode-A of a circular cylinder, despite the general similarity between the two mechanisms. These features include a spanwise wavelength of λ _z  = 2.4d, and a staggered pattern of streamwise vorticity, in which the negative concentrations of streamwise vorticity are slightly shifted downstream.

Other studies on the wake of elliptical cylinders (Sheard 2007), inclined square cylinders (Sheard et al. 2009), rings, and spheres (Hourigan et al. 2007) have also shown secondary instability mechanisms that are qualitatively and quantitatively different from those of a circular cylinder. Hourigan et al. (2007) conclude that the wake transition sequence of a circular cylinder is not universal, and the wake of other bluff bodies may undergo transition to turbulence through different sequences involving modes with different vorticity structures and wavelengths.

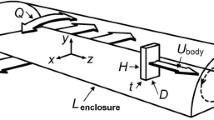
In the present study, we aim at experimental identification and characterization of the secondary instability mechanism in the wake of a blunt trailing edge profiled body, comprised of an elliptical leading edge and a rectangular trailing edge (Fig. 1). Ryan et al. (2005) have carried out a numerical study of the secondary wake instabilities of this geometry using direct numerical simulations and Floquet stability analysis, at Reynolds numbers up to Re(d) = 650. They have found out that depending on the profile thickness to length ratio (l/d), the secondary instabilities emerge at Reynolds numbers ranging from Re(d) = 400–475, which are considerably higher than the threshold Reynolds number of Re(d) = 194 and 162 for circular and square cylinders. For profiles with l/d = 2.5 and 7.5, they predict Mode-A instabilities with λ _z  = 3.5 and 3.9d, to be the first modes to become unstable. However, for l/d = 12.5 and 17.5, the predicted instability mode has a wavelength of λ _z  = 2.2d. In this mode, the streamwise vorticity at any spanwise location retains its sense of rotation over multiple shedding cycles in a manner generally similar to Mode-B of circular cylinder; however, it also carries traces of streamwise vorticity with opposite sign, due to a different distribution of vorticity in the formation region. This mode has been named mode-B’, due to these differences in wavelength and near-wake vorticity distribution. Finally, for l/d > 17.5, the instability shows a vorticity structure similar to that of Mode-S of a square cylinder, with a smaller wavelength of λ _z  = 1d. This instability has been named Mode-S’.

Fig. 1

Geometry of the blunt trailing edge profiled body

The lack of experimental evidence to support the predictions of Ryan et al. (2005) and to provide further insight into the mechanism of the secondary instability is the primary motivation of the authors of the present study to carry out a qualitative and quantitative experimental investigation of the flow structure in the wake of this bluff body geometry. The present experiments also extend the range of Reynolds numbers at which the secondary instabilities have been studied to 250 ≤ Re(d) ≤ 2,150, to cover the wake transition regime.

Moreover, from the practical point of view, the blunt trailing edge profiled body can be considered as a precedent to blunt trailing edge airfoils, which are gaining popularity in wind power generation because of superior lift characteristics, as shown, for example, by Baker et al. (2006). Application of these airfoils, however, is hindered by the adverse effects of vortex shedding from the blunt trailing edge, which highlights the need for efficient wake flow control methods.

The present study also includes an investigation of feasibility of a flow control approach based on the secondary wake instabilities, for mitigation of vortex shedding and reduction in drag. The flow control approach applied herein interacts with the von Kármán vortices through excitation of the secondary instabilities by a series of discrete trailing injectors. It therefore falls in the category of “three-dimensional forcing” in the classification by Choi et al. (2008), in which spanwise-periodic geometric modifications or actuators are employed to interact with the von Kármán vortices through secondary instabilities. This class of flow control approaches has emerged concurrently with the development of knowledge on the secondary wake instabilities since early 1990s. The first examples of applying this approach for a blunt trailing edge profiled body are the studies by Selby and Miandoab (1990) who achieved a 50% base pressure recovery at Re(d) = 10⁵, and Bearman and Tombazis (1993) who achieved a 35% base pressure recovery at Re(d) = 40,000, using spanwise-periodic geometric perturbations at the trailing edge to alter the wake flow structure.

Several investigators have noted that the three-dimensional forcing flow control approach is most effective when the spanwise periodicity or wavelength of the flow control perturbations is equal to the wavelength of the dominant secondary wake instability (λ _z ). Darekar and Sherwin (2001) have shown numerically that for a square cylinder at 10 ≤ Re(d) ≤ 150, with spanwise sinusoidal perturbations at the leading and trailing edges, the maximum base drag reduction (about 14%) is achieved when the perturbation wavelength is 5.6d. This wavelength is reasonably close to the Mode-A instability wavelength of a square cylinder, reported by Robichaux et al. (1999) for similar Reynolds numbers. In another example, Kim and Choi (2005) have applied three-dimensional forcing in the form of spanwise-periodic suction and injection through a slot, to the wake of a circular cylinder at Re(d) = 40–3,900, in a series of numerical simulations. They have reported the maximum reduction in mean and fluctuating drag for wavelengths between 3.14d and 5d, which correspond to the range of λ _z established for the Mode-A instability of a circular cylinder (Williamson 1996). Similarly, Dobre et al. (2006) have achieved significant attenuation of von Kármán vortices using spanwise sinusoidal perturbations with a wavelength of 2.4d at the trailing edge of a square cylinder at Re(d) = 12,500. This wavelength is equal to that of the Mode-A like secondary wake instability of a square cylinder at Re(d) = 22,000, reported by Dobre and Hangan (2004).

A similar relationship can be observed in the recent research work on applying three-dimensional forcing to the wake of the blunt trailing profiled body. Park et al. (2006) have reported a maximum base pressure recovery of 33%, using an array of small vertical tabs across the trailing edge of a blunt trailing edge profiled body at Re(d) = 20,000–60,000, with a spanwise spacing of 1.67–2.5d between the tabs. This spacing encompasses the wavelength Mode-B’ instabilities (λ _z  = 2.2d) predicated by Ryan et al. (2005). Also, the study by Doddipatla et al. (2008), who have used spanwise sinusoidal perturbations to control the wake of a blunt trailing edge profiled body at Re(d) = 25,000, indicates significant attenuation of base pressure fluctuations with a spanwise perturbation wavelength of 2.4d due to excitation of the small-scale instabilities. The control wavelength is very close to that of the Mode-B’ instability predicted by Ryan et al. (2005) and the Mode-A like instability identified by Dobre and Hangan (2004).

This trend can be explained at a more fundamental level based on the experimental study of growth rates for perturbations induced in the wake of a flat plate with a rectangular trailing edge, by Julien et al. (2003). They have shown that of all three-dimensional perturbations with various spanwise wavelengths, the highest growth rate belongs to the ones that match the wavelength of the secondary instability modes (λ _z ). Therefore, any flow control approach seeking to manipulate of three-dimensional secondary instabilities should excite them so that their growth rate is maximum, and this is best achieved when the excitation wavelength matches λ _z .

The flow control experiments in the present study follow the same trend for Reynolds numbers in the range of 700 ≤ Re(d) ≤ 1,280. The discrete injectors are arranged across the trailing edge with a spanwise spacing equal to the spanwise wavelength of the secondary instabilities (λ _z ), determined through the experiments described in Sect. 3. Details of the flow control experiments and the effects of this control approach on the wake flow structure will be presented in Sect. 4.

The geometric configuration of the body studied herein (an elliptical leading edge followed by a rectangular section) is similar to the ones studied by Selby and Miandoab (1990), Bearman and Tombazis (1993), Petrusma and Gai (1996), Kim et al. (2004), Mills et al. (2005), Park et al. (2006), Pastoor et al. (2008), and Stanlov et al. (2010). The geometric proportions of the body (shown in Fig. 1) are chosen exactly similar to the ones used in the studies by Ryan et al. (2005), Doddipatla et al. (2008), and Naghib-Lahouti and Hangan (2010), to facilitate comparisons of the observations.

2 Methodology

Qualitative and quantitative experimental techniques have been used to characterize the wake flow structure. Planar laser-induced fluorescence (LIF) has been utilized for visualization of the wake instabilities. Quantitative measurements of the velocity field in the wake have been carried out using particle image velocimetry (PIV), to study the wake instabilities, and the effects of flow control on the wake flow structure. Proper orthogonal decomposition (POD) analysis has been employed to characterize the secondary instabilities, and to study the effect of flow control on wake organization and modal energy distribution.

2.1 Experimental setup

The experiments have been carried out using the water tunnel facility of the Boundary Layer Wind tunnel Laboratory (BLWTL) at the University of Western Ontario, which is a closed test section, open return circuit water tunnel, with a 0.610-m-wide, 0.305-m-high, and 3.0-m-long test section. The tunnel is able to generate a maximum free stream velocity of 0.19 m/s. Velocity variations across the test section are within 1% of the free stream velocity, and the free stream turbulence intensity is 0.1% (Sarathi 2009).

The thickness of the experimental model is d = 0.0127 m, which generates a blockage ratio of 4.2% in the test section. The total span of the model is 48d; however, two transparent end plates have been used to isolate the center 34d portion of the span from the boundary layer developing on the sidewalls of the tunnel, as well as the secondary flow supply tubing, connected to the two extreme ends of the span of the model. The end plates extend 8d forward of the leading edge, 20d aft of the trailing edge, and 9.5d in the vertical direction from the upper and lower surfaces of the body. In order to minimize the effects of flow separation from the end plates, the leading and trailing edges are faired with elliptic profiles. A schematic drawing of the model-end plate arrangement is shown in Fig. 2a.

Fig. 2

Schematic views of the experimental model-end plate arrangement (a) and the experimental setup for horizontal (XZ) plane LIF and PIV experiments (b)

The imaging area is illuminated using a 120 mJ Nd-YAG pulse laser, with a wavelength of 532 nm, and pulse rate of 30 Hz. During the LIF flow visualization experiments, the Rhodamine 6G fluorescent dye is introduced to the flow through a spanwise slot located 1d upstream of the lower corner of the trailing edge (Fig. 2b). The dye generates a 560 nm fluorescent light when exposed to the 532 nm laser light. The fluorescent light is captured by a CCD camera, through a 550 nm filter that blocks the laser light and its reflections. The CCD camera captures images with a resolution of 1,600 × 1,200 pixel, at the rate of 30 frames per second. Flow visualizations have been carried out in the vertical (XY) plane to visualize the evolution and characteristics of the von Kármán vortex street, and in the horizontal (XZ) plane to visualize the secondary instabilities. A schematic drawing of the experimental setup is shown in Fig. 2b.

The same experimental setup (except for the 550 nm filter) has been used for the PIV velocity field measurement experiments in horizontal (XZ) and vertical (XY) planes. The vertical plane measurements are used to determine the principal characteristics of the von Kármán vortex street and to study the effects of flow control, while the horizontal (XZ) measurements are used for identification of the small-scale instabilities. The horizontal plane measurements cover a 9 × 7d area, shown in Fig. 2. The vertical plane measurement area extends 11.5d downstream of the trailing edge and 8.5d in the vertical direction, with the trailing edge at the mid-height of the imaging area. The size of the imaging area makes it possible to study the evolution of the wake over multiple shedding cycles of the von Kármán vortices in each image and to capture multiple wavelengths of the secondary instabilities in the horizontal plane.

In each PIV experiment involving one combination of measurement plane, Reynolds number, and control actuation (in case of the flow control experiments), 3,000 image pairs have been recorded with a sampling rate of 15 image pairs per second. Velocity vector fields are obtained by cross-correlating the interrogation window in one image to the search region in the other image. Using 32 × 32 pixel interrogation windows with 50% overlap, an array of 99 × 74 velocity vectors is generated based on each pair of 1,600 × 1,200 pixel images.

The normalized error of velocity measurement (${\raise0.7ex\hbox{${\Updelta u}$} \!\mathord{\left/ {\vphantom {{\Updelta u} u}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$u$}}$) has been estimated using the process described in Naghib-Lahouti (2010). The average error is approximately 1.6% in the vertical (XY) plane and 1.8% in the horizontal (XZ) plane.

2.2 Proper orthogonal decomposition (POD)

Proper orthogonal decomposition (POD) has been used for analyzing the velocity field data. This technique projects a data ensemble, built by acquiring N samples of a vector field variable u _i (x _i , t), onto N orthogonal eigenvectors or modes $\phi^{n} (x_{i} )$, so that the first mode accounts for as much variability in the data as possible, and each succeeding mode accounts for as much of the remaining variability as possible. In other words, the modes obtained by the POD technique are energetically optimal, and if the first M ≤ N POD modes are used to reconstruct the original data ensemble, the result will contain more energy than any other reconstruction using a similar number of modes obtained on any other basis.

Each POD mode $\phi^{n} (x_{i} )$ is accompanied by a time-varying amplitude coefficient a ⁿ(t), and the combination of these two can be used to reconstruct the original data ensemble using the following equation:

$$ u_{i}^{ * } (x_{i} ,t) = \sum\limits_{n = 1}^{M} {a^{n} (t)\varphi^{n} (x_{i} )} $$

(1)

In Eq. 1, $u_{i}^{ * } (x_{i} ,t)$ is an approximate reconstruction of the original data ensemble using M ≤ N modes. As shown by Holmes et al. (1996), the modes $\phi^{n} (x_{i} )$ can be obtained by finding the eigenvalues and eigenvectors in the following problem:

$$ \int {\left\langle {u_{i} (x_{i} ,t) \cdot u_{i} (x_{i}^{'} ,t)} \right\rangle } \varphi^{n} (x_{i}^{'} )dx_{i}^{'} = \lambda^{n} \varphi^{n} (x_{i} ) $$

(2)

in which the $\left\langle \cdot \right\rangle$ operator represents spatial autocorrelation. The detailed procedure for discretization and solution of this problem can be found in the works of Smith et al. (2005), and Shlens (2009). Once the modes are obtained, the amplitude coefficients can be found by projecting the original data onto the POD modes using Eq. 3.

$$ a^{n} (t) = \int {u_{i} (x_{i} } ,t).\varphi^{n} (x_{i} )dx_{i} $$

(3)

It is then possible to reconstruct the data ensemble using Eq. 3, to obtain what is known as a low-dimensional representation of the original data when M < N. The eigenvalues λ ⁿ in Eq. 2 represent the energy contained by each mode.

The unique properties of the POD technique, including orthonormality and the optimal representation of energy by the modes, make it an ideal tool for filtering out the noise in a complex data ensemble, in order to reveal the often hidden, simplified underlying structures. In the present study, this technique has been used to reconstruct a simplified representation of the velocity field data, which makes it possible to identify and quantify the three-dimensional wake instabilities more easily. In the flow control experiments, the same technique is used to study the redistribution of energy among the wake instabilities, and the effect of flow control on the organization of the von Kármán vortices.

3 Wake instabilities

In the following paragraphs, the results of the experiments in the vertical (XY) will be analyzed to determine the principal characteristics of the von Kármán vortex street, and the results in the horizontal (XZ) plane will be analyzed to identify the secondary wake instabilities.

3.1 The von Kármán vortex street

Flow in the wake of the body is found to be dominated by the von Kármán vortices for all Reynolds numbers studied herein. LIF flow visualization images of the von Kármán vortex street are shown in Fig. 3, for Reynolds numbers ranging from Re(d) = 550 to Re(d) = 2,150. Transition from a laminar wake to a turbulent one is indicated by the increased dispersion of the fluorescent dye at higher Reynolds numbers.

Fig. 3

LIF visualizations of the von Kármán vortex street at Re(d) = 550 (a), 850 (b), 1,150 (c), 1,320 (d), 1,705 (e), and 2,150 (f) (The streamwise extent of the images is 13.6d, approximately.)

Figure 3 also shows an increasingly tighter streamwise spacing between consecutive von Kármán vortices at higher Reynolds numbers, which is indicative of a smaller wavelength of the primary wake instability (λ _x ). This behavior is verified quantitatively in Fig. 4, which shows variations of λ _x with Reynolds number. The figure indicates that λ _x decreases when Reynolds number increases, until it reaches an asymptotic value of 3.6d, that is similar to the value reported by Doddipatla et al. (2008) for the same geometry at Reynolds numbers in the order of 10⁴. The streamwise wavelengths in Fig. 4 have been determined by measuring the average distance between consecutive von Kármán vortices over multiple shedding periods, in the near-wake region (x/d ≤ 10), with the starting point for the measurements located 4–5d downstream of the trailing edge. Figure 4 also shows the length of the vortex formation region (L _f ), based on the PIV velocity field data. L _f is defined as the location along the wake centerline where fluctuations of the streamwise velocity component (indicated by u _rms) reach a maximum (Williamson 1996). The figure indicates that L _f decreases when Reynolds number increases.

Fig. 4

Variation of the wavelength (λ _x ) of the primary wake instability (the von Kármán vortex street) and the length of the vortex formation region (L _f ) with Reynolds number

The decrease in the streamwise wavelength (λ _x ) and formation length (L _f ) is accompanied by an increase in vortex shedding frequency (f _S ), as shown in Fig. 5. The figure shows variations of the normalized shedding frequency ${\text{St}}(d^{'} ) = {{f_{S} d^{'}} \mathord{\left/ {\vphantom {{f_{S} d^{'} } {U_{\infty } }}} \right. \kern-\nulldelimiterspace} {U_{\infty } }}$, based on the frequency spectra of the velocity time series obtained from PIV experiments (Fig. 6), as a function of $\text{Re} (d^{'} )$. The reference length in ${\text{St}}(d^{'} )$ and $\text{Re} (d^{'} )$ is the thickness of the wake at the trailing edge, defined as $d^{'} = d + 2\delta^{ * }$, in which $\delta^{ * }$ is the displacement thickness of the boundary layer. Using $d^{'}$ instead of d as reference length makes it possible to compare data obtained for blunt trailing edge profiled bodies with different thickness to chord (l/d) ratios such as the data from Eisenlohr and Eckelmann (1988). Figure 5 indicates a good agreement between the values from the present study and the data from Eisenlohr and Eckelmann (1988), and verifies their suggested asymptotic value of ${\text{St}}(d^{'} ) = 0.286$. The error bars in Fig. 5 correspond to the smaller, secondary peaks in the vicinity of the dominant peak in the frequency spectra (Fig. 6). Petrusma and Gai (1996) have observed similar secondary peaks and have attributed them to the effects of the large-scale secondary wake instability described by Williamson (1996), which appears as streamwise dislocations of the von Kármán vortices due to phase variations of vortex shedding across the span. Due to their transient nature, these phase variations lead to long-period modulation of shedding frequency (f _S ) at any spanwise location, with a period that can be as several times longer than the shedding period (Wu et al. 2005). Horizontal plane flow visualizations and velocity field measurements of the present study (Figs. 7, 10) verify the existence of the large-scale instability at all Reynolds numbers, including those at which the small-scale secondary instabilities have not yet emerged.

Fig. 5

Variation of normalized vortex shedding frequency St (d) with Reynolds number Re(d′), with data from Eisenlohr and Eckelmann (1988) for comparison

Fig. 6

Single-sided amplitude spectra of the vertical velocity component (v) at x/d = 2, y/d = 0.5 based on PIV measurements at Re(d) = 700 (The arrows point to the secondary peaks attributed to the effects of the large-scale secondary instabilities.)

Fig. 7

Flow visualization in the XZ plane at y/d = −0.5, showing: parallel shedding at Re(d) = 250 (a), vortex dislocation at Re(d) = 250 (b), small-scale instability at Re(d) = 400 (c), and small-scale instability at Re(d) = 550 (d)

3.2 Secondary instabilities

LIF flow visualization images captured in the horizontal (XZ) plane show the evolution of the secondary instabilities qualitatively. Samples of the flow visualization images recorded at Reynolds numbers ranging from Re(d) = 250 to Re(d) = 550 with the horizontal laser sheet located at y/d = −0.5 are presented in Fig. 7. At Re(d) = 250, the wake is mostly dominated by parallel shedding of von Kármán vortices (Fig. 7a), which are occasionally distorted by large-scale secondary instabilities appearing as vortex dislocations (Fig. 7b). No indication of secondary small-scale instabilities is observed at this Reynolds number.

At Re(d) = 400, intermittent traces of small-scale secondary instabilities start to appear at certain instances. Figure 7c shows one such instance, in which a pattern of streamwise vortices can be observed. The streamwise vortex pairs seem to retain their sense of rotation in one shedding period (marked with the first pair of arrows), but alternate in the next period (marked by the second pair of arrows). This behavior, together with the spanwise wavelength of the structures observed in Fig. 7c (which is close to 1d), resembles the features of the Mode-S’ instability predicted by Ryan et al. (2005). However, the highly intermittent and irregular behavior of the instability at Re(d) = 400 makes it difficult to verify this observation quantitatively.

At Re(d) = 550, the von Kármán vortices are affected by a persistent small-scale instability, with a relatively regular behavior (Fig. 7d). This instability appears as upstream undulations in the von Kármán vortex closest to the trailing edge. Further downstream, the undulations evolve into pairs of counter-rotating streamwise vortices, connecting the von Kármán vortices. The undulations in the von Kármán vortices are marked with (►) symbols, and the pairs of counter-rotating streamwise vortices are marked with (◄) symbols in the figure. The average instantaneous spanwise wavelength of the secondary instability observed in Fig. 7d is λ _z  = 2.1d, approximately. The instability has two distinct features that are consistent with the Mode-B’ instability predicted by Ryan et al. (2005): Fig. 8 shows the visualization of a pair of counter-rotating vortices in two consecutive vortex shedding periods. The figure clearly indicates the persistent nature of the vortex pair and its relatively constant spanwise position over multiple shedding periods. This implies that the sign of streamwise vorticity would also remain constant at any given spanwise location. The other feature is the spanwise wavelength, which will be determined quantitatively in the following paragraphs, and is very close to the value of λ _z  = 2.2d predicted by Ryan et al. (2005). These features lead the authors to believe that the instability observed in Figs. 7d, 8 is an experimental visualization of Mode-B’, in line with the prediction of Ryan et al. (2005) about this mode being the first secondary instability to be observed experimentally in the wake of the blunt trailing edge profiled body with l/d = 12.5.

Fig. 8

Visualizations of a pair of counter-rotating streamwise vortices (marked by arrows) in two consecutive shedding periods, at Re(d) = 550. The visualization image at the top precedes the one at the bottom by one shedding period, approximately

A more detailed investigation of the flow visualization images reveals another interesting feature of the secondary instability. This feature can be observed in Fig. 8 as the alternating variation in the spanwise distance of the two opposite-sign vortices in the vortex pair, marked by the horizontal arrows. The distance between the opposite-sign streamwise vortices connecting the von Kármán vortex shed in the near side of the wake (i.e., the side directly illuminated by the laser light sheet) to the one shed from the far side of the wake, decreases in the upstream direction. Conversely, the distance between the opposite-sign streamwise vortices connecting the far side von Kármán vortex to the near side one increases in the upstream direction.

Considering the evolution of the pairs of counter-rotating vortices from the upstream undulations of the von Kármán vortices, this alternating behavior suggests that the spanwise position of the upstream undulations the von Kármán vortices also alternates every half shedding period. While the far side von Kármán vortices are not visible in the flow visualization images, further evidence to confirm this behavior can be found in the results of the PIV measurements, which will be presented in the following paragraphs.

Extreme dispersion of the fluorescent dye at higher Reynolds numbers above Re(d) = 550 makes it impossible to visually recognize any regular features associated with the small-scale instabilities and limits the application of the LIF flow visualization technique to relatively low Reynolds numbers. To study the secondary instability over a broader range of Reynolds numbers, and to quantify its wavelength (λ _z ), PIV velocity field measurements in the horizontal (XZ) plane and POD analysis have been carried out at Re(d) = 550, 850, 1,200, and 2,150.

The streamwise undulations observed in the von Kármán vortices in Fig. 7d are accompanied by spanwise variations of the streamwise velocity component (u), in which the “valleys” of the undulations in the upstream direction (marked with ► symbols in Fig. 7d) correspond to lower streamwise velocities. As shown by Mansy et al. (1994) and Wu et al. (1996) in the case of a circular cylinder, and El-Gammal and Hangan (2008) in the case of a blunt trailing edge airfoil, a correlation exists between the small-scale secondary instabilities and spanwise variations of streamwise velocity (u) in the near-wake region, in which both have a similar spanwise wavelength. Considering this correlation, the streamwise velocity (u) data acquired from the PIV measurements have been used here to determine the wavelength of the secondary instabilities.

The use of a simplified, low-dimensional representation of the velocity field, which can be obtained using POD analysis as described in Sect. 2.2, can facilitate the identification of the secondary instabilities. However, the POD representation should also preserve the principal features of the original data ensemble. This can be verified for a POD representation by comparing the cumulative energy contained by the POD reconstruction based on M ≤ N modes to that of the original data ensemble, using Eq. 4, in which the eigenvalues (λ ⁿ) represent the relative energy of the respective POD modes.

$$ E_{M} = {{\sum\limits_{n = 1}^{M} {\lambda^{n} } } \mathord{\left/ {\vphantom {{\sum\limits_{n = 1}^{M} {\lambda^{n} } } {\sum\limits_{n = 1}^{N} {\lambda^{n} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{n = 1}^{N} {\lambda^{n} } }} $$

(4)

The relative cumulative energy ($E_{M}$) for the first 500 POD modes of streamwise velocity, measured in the horizontal (XZ) plane located at y/d = 0, is shown in Fig. 9 for Re(d) = 550, 850, 1,200, and 2,150. It can be observed that the relative cumulative energy contained by any given number of POD mode decreases as Reynolds number increases. This means that for higher Reynolds numbers, more energy is contained by the higher POD modes (i.e., the ones with smaller spatial and temporal scales), which is indicative of the gradual transition of the wake into a turbulent one.

Fig. 9

Relative cumulative energy of the first 500 POD modes of streamwise velocity (u), measured in the horizontal (XZ) plane at y/d = 0.5

To reconstruct the streamwise velocity field in time and space, the first 32 POD modes have been used. For this reconstruction, E _M varies between 80% at Re(d) = 550, and 60% Re(d) = 2,150, indicating that a significant proportion of the energy of the original data ensemble is retained by the reconstruction. Figure 10 shows samples of the reconstructed spanwise and temporal variations of streamwise velocity at x/d = 2 and y/d = 0, for Re(d) = 550, 850, and 1,200. The figure clearly shows the alternating spanwise variations of streamwise velocity, which result from streamwise undulations in the von Kármán vortices due to the small-scale secondary instabilities. It should be noted that since the reconstructed velocity field is based on POD modes, which are calculated following subtraction of the mean velocity, the quantitative values in Fig. 10 correspond to the fluctuating component of velocity. The positive areas in Fig. 10 correspond to the high-speed regions between each two upstream undulations in the von Kármán vortex shed from the near side of the trailing edge, while the negative areas correspond to the upstream undulations in the von Kármán vortex shed from the far side of the trailing edge and therefore follow the high-speed regions with a half-period lag. As highlighted by the rectangles in Fig. 10, these areas of positive and negative velocity, which correspond to the two opposite-sign Kármán vortices in a shedding cycle, appear at similar spanwise positions. This pattern of the velocity field is an evidence of the alternating spanwise position of the upstream undulations and confirms the behavior described based on Fig. 8.

Fig. 10

Spatial and temporal variations of streamwise velocity (u) at x/d = 2.0, y/d = 0.5, based on the first 32 POD modes, at Re(d) = 550 (a), 850 (b), and 1,200 (c). Note that quantitative values in the plots represent the fluctuating component of velocity, as mean velocity is subtracted in POD analysis

The effects of large-scale instabilities are also visible as dislocations in the velocity field. Due to the limited temporal resolution of the PIV measurements, no attempt has been made to generate a plot of spatial and temporal variations of u at Re(d) = 2,150.

Based on the features observed in the flow visualization images and the reconstructed velocity fields, a schematic representation of the wake vortex structure has been developed for the secondary instability described herein. This representation, shown in Fig. 11, reflects a number of well-established features of the Mode-B secondary instability of a circular cylinder. As previously documented by Williamson (1996), the instability manifests as pairs of counter-rotating streamwise vortices, which retain their sense of rotation over multiple shedding period in an in-line arrangement. Another feature observed in the present flow visualizations, which is reflected by the schematic representation of Fig. 11, is the alternating variation of the spanwise distance between the opposite-sign vortices in a vortex pair, between half shedding cycles. This feature has also been observed in the Mode-1 vortex pattern of a perturbed plane wake, reported by Meiburg and Lasheras (1988), which has been found to have a three-dimensional vortex structure and symmetry similar to Mode-B of a circular cylinder (Leweke and Williamson 1998). Based on the flow visualizations and the velocity fields presented in Figs. 8 and 10, the present schematic representation also relates the alternating undulations in von Kármán vortices to the arrangement of streamwise vortices.

Fig. 11

Schematic representation of the wake vortex structure for the secondary instability described in the present work

The vortex structure and symmetry of the secondary instability reported herein is qualitatively similar to that of a circular cylinder. However, its quantitative features (including threshold Reynolds number and spanwise wavelength) are different from those of a circular cylinder.

The average spanwise wavelength of the secondary instability can be determined based on the spanwise variations of streamwise velocity (u) extracted from the superimposed POD mode shapes used to generate the flow field reconstructions shown in Fig. 11. Figure 12 shows the spanwise variations of u based on superposition of the first 32 POD modes. The average wavelength of the secondary instabilities, defined as the average distance between the relative maxima or minima in Fig. 12, is λ _z  = 2.0d at Re(d) = 550, and λ _z  = 2.4d at Re(d) = 850, and λ _z  = 2.5d at Re(d) = 1,200, and 2,150.

Fig. 12

Spanwise variations of streamwise velocity (u) at x/d = 2.0, y/d = 0.5, based on the first 32 POD modes

The trend of variation of the wavelength (λ _z ) has been illustrated in Fig. 13, using $d^{'}$(as defined in Sect. 3.1) as the length scale to normalize λ _z and calculate Reynolds number. The figure also compares the wavelengths with the ones reported in previous studies for the same geometry. It can be observed that the wavelength determined at Re(d) = 550 is in close agreement with the ones predicted by Ryan et al. (2005) and Naghib-Lahouti and Hangan (2010) for Reynolds numbers between Re(d) = 500 and 610. Also, a good agreement can be observed between the wavelength determined at Re(d) = 1,200 and the one reported by Naghib-Lahouti and Hangan (2010).

Fig. 13

Variations of the normalized wavelength of the small-scale instability (λ _z /d′) with Reynolds number, with data from Ryan et al. (2005) and Naghib-Lahouti and Hangan (2010) for comparison. (The error bars represent the uncertainty due to the scatter in the measured wavelengths and the errors in spatial measurements.)

A comparison of the trend of variation of λ _z observed herein, and the average value of $\lambda_{Z} /d^{'} = 1.86$ reported for the same geometry at Re(d) = 24,000 by Doddipatla (2010), indicates very little variability of the normalized wavelength over a relatively broad range of Reynolds numbers, which can have significant implications on flow control strategies.

4 Flow control

Bearman (1965) has shown that pressure at the base of a blunt trailing edge profiled body is proportional with formation length (L _f ), and an increase in L _f leads to reduction in drag. This effect has been attributed to the reduced influence of the unsteady, low-pressure vortex cores at the base, when von Kármán vortices are formed farther from the base of the bluff body. Since streamwise dislocations of von Kármán vortices lead to local variations of L _f , Tombazis and Bearman (1997) conclude that inducing the formation of positive dislocations in the streamwise directions can be used as a flow control approach for drag reduction. As discussed in Sect. 1, this control approach is usually implemented by introducing spanwise-periodic geometric perturbations to the leading and/or trailing edge of the body. In the present study, however, this flow control approach is implemented using a series of discrete injectors, located near the upper and lower corners of the trailing edge, as shown schematically in Fig. 14.

Fig. 14

Schematic view of the flow control mechanism (Size of the injection ports is exaggerated.)

Several studies involving various bluff bodies, flow conditions, and disturbance techniques indicate that this flow control approach is most effective in reducing drag when the spanwise wavelength at which vortex dislocations are induced is close to the characteristic spanwise scale in of the flow structure, which is the wavelength of the dominant secondary instability. Although a straightforward physical interpretation for this relationship is yet to appear, it is believed that this is due to “forcing” of the natural secondary instability into organized existence by the flow control mechanism (Darekar and Sherwin 2001). In the present experiments, the spanwise spacing of the injectors has been set to 2.4d, to match λ _z at Re(d) = 815. Therefore, one can expect the control to be most effective at Reynolds numbers close to this value. The experiments have been carried out at Re(d) = 700, 815, and 1,280, to investigate this assumption.

Control is applied by constant injection of a secondary flow through 20 injection ports distributed across the span, on each side of the trailing edge. The injectors, which have a diameter of 0.8 mm, and are located 2.5 mm upstream of the trailing edge, are fed by a common source of secondary flow. Unlike the three-dimensional forcing approaches involving geometric perturbations, the present approach allows the amplitude of flow control actuation to be adjusted without any changes to the geometry, and by adjusting the injection flow rate at each Reynolds number. The usual measure of efficiency for flow control approaches involving a secondary flow is the momentum coefficient (C _μ ), defined as the ratio of the flow control momentum flux to the free stream momentum flux through the section of the body affected by the flow control mechanism. For the present flow control approach, this coefficient can be expressed as:

$$ C_{\mu } = \frac{2na}{bd}\frac{{u_{i}^{2} }}{{U_{\infty }^{2} }} $$

(5)

In Eq. 5, n is the number of injection ports on each side of the trailing edge, a is the area of each injection port, and b is the span of the body. To determine the appropriate injection flow rate for the above-mentioned experiments, a series of PIV velocity field measurements have been carried out in the vertical (XY) plane coincident with the injection port located at mid-span, at Re(d) = 750. Considering the relationship between the effectiveness of flow control, and wake parameters including vortex formation length (L _f ) and the intensity of velocity fluctuations (u _rms) near the base, which will be described in detail in the following paragraphs, the effect of injection on these parameters has been used to select the appropriate injection rate. Figure 15 shows the effect of injection at rates ranging between u _i /U _∞ = 0.7 and 2.0 on L _f , and u _rms at (x/d = 0.25, y/d = 0.5). The figure indicates that all injection rates studied herein have led to an increase in L _f . However, only the three highest injection rates (u _i /U _∞ = 1.5, 2.0, and 2.5) have caused a reduction in u _rms. The reduction in u _rms at u _inj/U _∞ = 1.5 is found to be marginal, which suggests that the one of the higher injection rates (u _inj/U _∞ = 2.0 or 2.5) should be considered. A comparison between the two highest injection rates (u _inj/U _∞ = 2.0 and 2.5) shows that increasing the injection rate from u _inj/U _∞ = 2.0 to 2.5 leads to an 8% reduction in u _rms, and a 6% increase in formation length. This improvement, however, is offset by a 25% increase in injection flow rate, and thereby a 56% increase in the flow control momentum coefficient (C _μ ). Considering C _μ as the measure for efficiency of the flow control approaches involving a secondary flow, using the injection rate of u _inj/U _∞ = 2.0 can be regarded as a reasonable compromise, as it achieves improvements in L _f and u _rms that are very close to those achieved at u _inj/U _∞ = 2.0, with a considerably smaller C _μ . Based on this observation, an injection flow rate of u _inj/U _∞ = 2.0 through each injection port, which is equivalent to a control momentum coefficient of C _μ  = 0.01, has been maintained at all three Reynolds numbers.

Fig. 15

The effect of secondary flow injection rate (u _i /U _∞) on vortex formation length (L _f ) and velocity fluctuations (u _rms) at x/d = 0.25, y/d = 0.5 (Lines added to aid visualization.)

Four sets of PIV velocity field data, each based on 3,000 image pairs, have been recorded at each Reynolds number. One set corresponds to the case in which no injection is applied (the base case) and is recorded in the plane coinciding with the injection port located at the mid-span of the model. The other three data sets correspond to the case in which injection is applied, and are recorded in three equally spaced vertical (XY) planes, as shown in Fig. 16. One measurement plane coincides with the injection port, and the other two are located at spanwise distances of ${\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 4$}}\lambda_{Z}$ and ${\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}\lambda_{Z}$ from the injection port.

Fig. 16

Schematic view of the location of the three PIV measurement planes used in the flow control experiments

The velocity field data have been analyzed to investigate the effect of flow control on the wake flow structure, and its effectiveness in attenuation of the adverse effects of vortex shedding.

4.1 Effect of flow control on wake flow structure

Figure 17 shows the effect of the present flow control approach on vortex formation length (L _f ) at Re(d) = 700, 815, and 1,280, based on measurements in the planes shown in Fig. 16. The figure indicates that flow control has led to increased formation length in the injection plane at all three Reynolds numbers. At Re(d) = 815, where flow control is found to be most effective in increasing L _f , this effect has well propagated to the other two spanwise locations, leading to an average increase of 23% in L _f , compared to the base case. The effect of flow control on L _f at Re(d) = 700 and 1,280, however, is more localized and is mostly limited to the injection plane. The 15% average increase in L _f at Re(d) = 700 is due to this local effect. At Re(d) = 1,280, the average increase in L _f is 1%, which is within the range of measurement uncertainty.

Fig. 17

Effect of flow control on formation length (L _f ). (Injection plane is located at z = 0, and data points have been reflected about z = ½λ _z to aid visualization.)

As described in the previous paragraphs, the increase in formation length is accompanied by reduction in the influence of the von Kármán vortices and therefore reduction in velocity fluctuations at the base of the body. The frequency spectra of velocity near the base can be used to verify this effect. Figure 18 shows the single-sided amplitude spectra of the streamwise velocity component (u), extracted near the base in the upper shear layer (x/d = 0.25, y/d = 0.5), in the planes shown in Fig. 16. The peaks in the spectra correspond to the vortex shedding frequency (f _S ) at each Reynolds number.

Fig. 18

Effect of flow control on amplitude spectra of streamwise velocity (u) at x/d = 0.25, y/d = 0.5, for Re(d) = 700 (a), 815 (b), and 1,280 (c)

A comparison of the peak amplitudes of the spectra from the control experiments with that of the base case at Re(d) = 815 (Fig. 18b) indicates a consistent attenuation of the peak amplitude in all three measurement planes, leading to an average decrease of 48% of the peak amplitude compared to the base case.

At Re(d) = 700 (Fig. 18a), the amplitude attenuation due to flow control is again mainly limited to the injection plane. No significant amplitude attenuation can be observed in the other two planes, and the 15% average decrease in the peak amplitude at this Reynolds number is mainly due to the effect of control in the injection plane. Finally, at Re(d) = 1,280 (Fig. 18c), no consistent attenuation of peak amplitude of the spectra can be observed in any of the three measurement planes.

In general, the effect of flow control on the peak amplitudes of the near-base streamwise velocity spectra is found to be consistent with the effects of flow control on vortex formation length. The observed changes in formation length and the peak amplitude of the spectra imply that the flow control approach has the ability to attenuate the fluctuating component of drag for specific Reynolds numbers where these changes are significant. This effect will be investigated in the following paragraph.

4.2 Effect of flow control on drag

To investigate the effect of flow control on drag, the force estimation method proposed by van Oudheusden et al. (2007) has been used. Equation 6 summarizes this method, which is intended to estimate the forces based on planar velocimetry data, in absence of direct force or base pressure measurements.

$$ \bar{F}_{i} = - \rho \iint\limits_{S} {\bar{u}_{i} \bar{u}_{j} n_{j} ds - \rho \iint\limits_{S} {\overline{{u_{i}^{'} u_{j}^{'} }} n_{j} ds} + \mu \iint\limits_{S} {\left(\frac{{\partial \bar{u}_{i} }}{{\partial x_{j} }} + \frac{{\partial \bar{u}_{j} }}{{\partial x_{i} }}\right)n_{j} ds} - \iint\limits_{S} {\bar{p}}n_{i} ds} $$

(6)

The first three terms in Eq. 6 can be calculated based on the measured values of mean and fluctuating velocities at the boundaries of the control volume surrounding the body. The last term represents the effect of pressure field at the boundaries, for which no direct measurement is available. However, it has been shown that this term can be estimated based on the velocity field measurements. In order to estimate the pressure term, we use the formulation proposed by Bohl and Koochesfahani (2009). In this formulation, which has been applied successfully to determine the force based on velocity field measurements in a problem similar to the one studied herein (i.e., the wake of an oscillating airfoil, dominated by periodic vortices of alternating sign), the mean pressure profile on the downstream surface of the control volume is estimated as follows:

$$ \frac{{\partial \bar{p}}}{\partial y} = - \rho \frac{{\partial v_{\text{rms}}^{2} }}{\partial y} $$

(7)

Based on the above-mentioned formulation, Eq. 6 can be rewritten to estimate the drag coefficient (C _D ) as follows:

$$ C_{D} = \frac{2}{A}\int\limits_{W} {\frac{{\bar{u}}}{{U_{\infty } }}\left( {1 - \frac{{\bar{u}}}{{U_{\infty } }}} \right)dy - } \frac{2}{A}\int\limits_{W} {\left( {\frac{{u_{\text{rms}} }}{{U_{\infty } }}} \right)^{2} dy} + \frac{2}{A}\int\limits_{W} {\left( {\frac{{v_{\text{rms}} }}{{U_{\infty } }}} \right)^{2} dy} + \frac{2\mu }{{U_{\infty }^{2} A}}\int\limits_{W} {\left( {\frac{{\partial \bar{u}}}{\partial y} + \frac{{\partial \bar{v}}}{\partial x}} \right)dy} $$

(8)

Table 1 summarizes the effect of flow control on the first three terms of Eq. 8. In Table 1, $\overline{{C_{D} }}$ represents the estimated drag component resulting from mean momentum transfer (the first term in Eq. 8), and $\tilde{C}_{D}$ represents the estimated drag component resulting from fluctuating momentum transfer (the second and third terms in Eq. 8). The fourth term in Eq. 8, which represents the mean viscous stresses, has not been shown in the table, since its contribution to the total drag coefficient has been found to be 0.1% or less, depending on Reynolds number.

Table 1 Effect of flow control on the estimated drag components

The effect of flow control on the estimated drag coefficients is found to be consistent with its effect on vortex formation length and velocity spectra (Sect. 4.1). As expected, the most favorable effect is observed at Re(d) = 815, where flow control has caused an 19% reduction in $\tilde{C}_{D}$, accompanied by a 5% reduction in $\overline{{C_{D} }}$, resulting in a 8% reduction in total drag. At Re(d) = 700, flow control shows a favorable effect on $\tilde{C}_{D}$, but an adverse effect on $\overline{{C_{D} }}$, which has led to a 9% increase in total drag coefficient. Finally, at Re(d) = 1,280, the effect of flow control on both drag components is found to be very small and within the range of the measurement uncertainty.

4.3 Discussion: the role of secondary instabilities in flow control

POD analysis of the velocity field data can help to illustrate the role of the secondary instabilities in the present flow control experiments and to explain the variability of the effectiveness of the flow control approach with Reynolds number.

Deane et al. (1991) have shown through reconstruction of the von Kármán vortices that a significant part of the features of the von Kármán vortex street is contained by the first two pairs of POD modes of the velocity field in the vertical (XY) plane, which have the highest relative energy content, and display closely related spatial and temporal behaviors. Based on this relationship, which has been verified for the blunt trailing edge profiled body (Doddipatla et al. 2008; Naghib-Lahouti 2010), the relative energy of POD modes can be regarded as an indicator of the dominance of von Kármán vortices in comparison with other dynamic content of the wake, including secondary instabilities.

Figure 19 shows the effect of flow control on the relative energy of the first 15 POD modes. At Re(d) = 815 (Fig. 19b), flow control has led to a visible transfer of relative energy from the lower POD modes representing the von Kármán vortices, to the higher ones representing smaller scale dynamic structures, in all three measurement planes. Figure 19a shows that at Re(d) = 700, energy transfer to higher modes is limited to the injection plane, and a transfer of energy to lower modes occurs in the other two planes (see inset of Fig. 19a). At Re(d) = 1,280, no consistent transfer of energy to higher modes by the flow control can be observed. The Reynolds numbers and planes at which flow control has caused effective energy transfer from the modes representing von Kármán vortices to the higher modes representing the secondary instabilities, are similar to the ones at which favorable effects in terms of formation length and amplitude of the velocity spectra were observed in Sect. 4.1. This observation leads the authors to believe that the present flow control approach interacts with secondary instabilities and achieves favorable effects when it is able to amplify the secondary instabilities effectively.

Fig. 19

Relative POD mode energies in the vertical (XY) plane at Re(d) = 700 (a), 815 (b), and 1,280 (c)

Investigation of the time-varying coefficients of the POD modes (a _i (t)) can provide further insight into the role of secondary instabilities in the present flow control approach. Perrin et al. (2007) have shown that a 90° phase difference exists between the time-varying coefficients of the first two POD modes representing the von Kármán vortices and have used this relationship successfully to determine the shedding phase angle. This relationship makes it possible to study the effect of flow control on the organization of the von Kármán vortices, by investigating the phase plots (Lissajous curves) of the two normalized time-varying coefficients ($a_{2} (t)/\sqrt {2\lambda_{2} }$ vs. $a_{1} (t)/\sqrt {2\lambda_{1} }$). Ideally, the phase plots would appear as perfect circles if the von Kármán vortex street (as represented by POD modes 1 and 2) were the only dynamic mechanism in the flow field. However, transient dislocations in von Kármán vortices, caused by secondary instabilities, lead to transient variations in amplitude and phase of the time-varying coefficients, which would appear as increased scatter in the phase plots.

The phase plots for Re(d) = 700 and 815 are shown in Fig. 20. As expected, flow control has led to increased scatter at Re(d) = 815 in all three measurement planes (Fig. 20b). As a quantitative measure, the percentage of snapshots that fall within a ± 0.2 interval of a typical radius of $\left[ {(a_{1} /\sqrt {2\lambda_{1} } )^{2} + (a_{2} /\sqrt {2\lambda_{2} } )^{2} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} = 0.9$ decreases by 9, 5, and 19%, in the injection, ¼-, and ½-planes, respectively, compared to the base case. This is another indicator of consistent amplification of secondary instabilities by flow control at this Reynolds number, which does not occur at the other two Reynolds numbers.

Fig. 20

Phase plots based on POD modes 1 and 2, at Re(d) = 700 (a) and 815 (b)

When control is applied at Re(d) = 700 (Fig. 20a), the percentage remains virtually unchanged in the injection plane, and slightly increases in the other two measurement planes, compared to the base case. The phase plots for Re(d) = 1,280 do not indicate any significant changes due to flow control and are therefore not shown.

Two factors affect the effectiveness of the present flow control approach: the spanwise wavelength of excitation, which is dictated by the spanwise spacing of the injectors, and control power, which is quantified by C _μ. At Re(d) = 815, an adequate combination of these two factors has led to the attenuation of the adverse effects of vortex shedding, without any penalty in terms of total drag. However, the results at the two other Reynolds numbers suggest that this adequate combination has not been maintained, due to the passive nature of the control approach.

The significant effects of control in the injection plane at Re(d) = 700 indicate that it does not suffer from lack of power at this Reynolds number; however, the effects do not propagate effectively to other spanwise locations. The trend implied by previous control approaches involving “three-dimensional forcing” suggests that a mismatch between the excitation wavelength and the natural wavelength of the secondary instability (λ _z ) may be responsible for this limited effectiveness at this Reynolds number. As mentioned before, the spanwise spacing of the injectors in the control experiments is 2.4d. However, the trend of variation of λ _z with Reynolds number, shown in Fig. 13, suggests a smaller value of λ _z  ≈ 2.2d at Re(d) = 700.

At Re(d) = 1,280, the relatively small increase in formation length (L _f ) in the injection plane suggests that the control is not as powerful as lower Reynolds numbers. Furthermore, the effects of the control do not propagate effectively to the other measurement planes, although the difference between the excitation wavelength and λ _z is very small. This may be the result of the discrete and passive nature of the control approach. When Reynolds number increases from Re(d) = 815 to Re(d) = 1,280, the balance of energy shifts naturally from the lower POD modes to the higher ones, as indicated by Fig. 9. Specifically, the relative energy of the POD modes 1–4, which contain most of the features of the von Kármán vortices, decreases from ${{\sum\nolimits_{i = 1}^{4} {\lambda_{i} } } / {\sum\nolimits_{i = 1}^{N}{\lambda_{i} } }} = 0.34$ to ${{\sum\nolimits_{i = 1}^{4} {\lambda_{i} } } / {\sum\nolimits_{i = 1}^{N} {\lambda_{i} } }} = 0.20$. This redistribution of energy is due to the increased dynamic content of the wake in the process of transition to turbulence, which can be visualized by comparing the relatively regular behavior of the long-duration spatial and temporal variations of the reconstructed fluctuating velocity field at Re(d) = 815 (Fig. 21a), with the more irregular behavior seen at Re(d) = 1,280 (Fig. 21b). In these conditions, the control must interact with a broader, more energetic range of secondary instabilities for effective propagation of its effect. The present control approach, which interacts with a fixed spanwise wavelength and through discrete injectors, has not been able to achieve this objective, as illustrated by its inability to alter the POD mode energy distribution in favor of the higher modes in any of the measurement planes (Fig. 19c).

Fig. 21

Long-duration samples of spatial and temporal variations of streamwise velocity (u) at x/d = 2.0, y/d = 0.5, based on the first 32 POD modes, at Re(d) = 815 (a) and 1,280 (b)

5 Conclusions

A series of experiments have been conducted to characterize the instabilities in the wake of a blunt trailing edge profiled body at Reynolds numbers between Re(d) = 250 and Re(d) = 2,150. These experiments complement previous studies involving the same bluff body geometry, such as the instability analysis and numerical simulations by Ryan et al. (2005) at Reynolds numbers up to Re(d) = 650 and the experiments by Doddipatla et al. (2008) at Re(d) = 25,000, by covering the transition of the wake to turbulence, and providing a more detailed description of the dominant small-scale secondary instability.

Large-scale instabilities have been found to affect the von Kármán vortices at Reynolds numbers as low as Re(d) = 250. Intermittent traces of a small-scale secondary instability have been observed at Re(d) = 400; however, the continuous presence of the secondary instability in the wake has been found to occur at Re(d) ≥ 550. This is in accordance with the findings of Ryan et al. (2005), who predict a transition Reynolds number of Re(d) = 475 for the secondary instability in the wake of the same bluff body, based on numerical simulations and stability analysis.

The dominant secondary instability at Re(d) ≥ 550 appears as undulations in the von Kármán vortices in the near-wake region, which evolve into pairs of counter-rotating streamwise vortices further downstream. The pairs of counter-rotating streamwise vortices at any given spanwise location are found to persist over multiple shedding periods, with an average spanwise wavelength (λ _z ) that varies between 2.0d at Re(d) = 550 and 2.5d at Re(d) = 2,150. This range of wavelengths encompasses the value of λ _z  = 2.2d, predicted numerically by Ryan et al. (2005) for the dominant secondary wake instability of the same bluff body at 550 ≤ Re(d) ≤ 610. The similarities between the flow structure and wavelength of the secondary instability mechanism reported herein, and the Mode-B’ instability predicted numerically by Ryan et al. (2005) for the same bluff body geometry at 550 ≤ Re(d) ≤ 610, verify the existence and dominance of this mode experimentally at Reynolds numbers up to Re(d) = 2,150. Based on the features observed in flow visualization and velocity field measurements, a schematic representation of the wake vortex structure has been proposed.

The findings of the present study confirm that the sequence of transition of the laminar wake of a bluff body into a turbulent one is not universal, and that the wake of a blunt trailing edge profiled body undergoes transition through a secondary instability mechanism distinguished from that of a circular cylinder by unique features, and at a higher Reynolds number.

A flow control approach based on interaction with the secondary instability observed in the present study has been proposed. Feasibility of the flow control approach in attenuation of the adverse effects of vortex shedding has been investigated experimentally at Re(d) = 700, 815, and 1,280. At Re(d) = 815, the flow control approach has been able to increase formation length (L _f ) and attenuate the peaks in the amplitude spectra of streamwise velocity in all measurement planes. This effect, which is accompanied by disorganization of the POD modes associated with the von Kármán vortices, and transfer of energy to higher POD modes, is indicative of interaction with, and amplification of the secondary instability, and has led to an 19% reduction in the estimated drag component caused by velocity fluctuations ($\tilde{C}_{D}$) and a 8% reduction in total drag.

At Re(d) = 700, the effect of flow control is mostly local, and limited to the injection plane, possibly due to a mismatch between the excitation wavelength and λ _z . The 8% decrease in $\tilde{C}_{D}$ at this Reynolds number is accompanied by a 9% penalty in total drag.

Finally, at Re(d) = 1,280, the effect of flow control on the wake flow and the estimated drag components has been found to be very small, with no noticeable amplification of the secondary wake instabilities. This lack of effectiveness can be attributed to the more widespread modal energy distribution in the wake in the process of transition to turbulence at Re(d) = 1,280, and the increasingly smaller share of the specific instability excited by the control approach at a fixed spanwise wavelength, in the dynamic content of the wake.

An active control scheme, in which the spanwise excitation wavelength is adjusted according to the actual wavelength of the secondary instabilities, can address the diminished effectiveness of the present flow control approach at lower Reynolds numbers. However, for transitional and turbulent regimes, designing an ideal control approach is more challenging, as it should be able to excite a broad range of secondary instabilities through an active scheme. A control approach that is powerful enough to force the wake flow into a given secondary instability mode, similar to passive approaches involving large-amplitude spanwise geometric perturbations, might also be worth investigating.