Direct measurements of local bed shear stress in the presence of pressure gradients

Abstract

This paper describes the development of a shear plate sensor capable of directly measuring the local mean bed shear stress in small-scale and large-scale laboratory flumes. The sensor is capable of measuring bed shear stress in the range $\pm$200 Pa with an accuracy up to $\pm$1 %. Its size, 43 mm in the flow direction, is designed to be small enough to give spatially local measurements, and its bandwidth, 75 Hz, is high enough to resolve time-varying forcing. Typically, shear plate sensors are restricted to use in zero pressure gradient flows because secondary forces on the edge of the shear plate caused by pressure gradients can introduce large errors. However, by analysis of the pressure distribution at the edges of the shear plate in mild pressure gradients, we introduce a new methodology for correcting for the pressure gradient force. The developed sensor includes pressure tappings to measure the pressure gradient in the flow, and the methodology for correction is applied to obtain accurate measurements of bed shear stress under solitary waves in a small-scale wave flume. The sensor is also validated by measurements in a turbulent flat plate boundary layer in open channel flow.

1 Introduction

For environmental flows, the bed shear stress is an important quantity, but measuring it accurately continues to pose a challenge. We are motivated by the flows in the nearshore region: the surf and the swash zone, where incident waves propagate over a sloping bottom into shallower water and break, creating a swash and a moving shoreline. The flow near the bed, where the bed shear stress, has direct consequences for sediment transport, in such environments is not very well understood. Such flows are characterised by their shallow depths, unsteadiness, boundary layer flow reversals and air entrainment from wave breaking. Thus, it is a challenging environment to make measurements in.

Methods for measurement of bed friction or wall shear stress have been widely discussed in the literature, see for example, Hanratty and Campbell (1996). Broadly, they can be classified into direct methods and indirect methods (Haritonidis 1989). Indirect methods include pressure difference methods (e.g. the Preston tube) and correlation methods that use mass or heat transfer as a proxy for the velocity gradient at the wall. Sumer et al. (2011) recently used hot film sensors to measure the bed shear stress under plunging waves. However, the direction of the shear stress was not measured by hot films and so additional velocity measurements very close to the bed were also required. The calibration of hot films also requires assumptions about the nature of the flow very close to the boundary and so an in situ calibration is needed. For recent developments in hot film sensors, as well as other indirect methods, see Fernholz et al. (1996). Cowen et al. (2003) showed that it is possible to obtain estimates of the bed friction in the nearshore region from measurements of the velocity field using particle image velocimetry (PIV). This is done with the assumption of the existence of a logarithmic layer in the turbulent boundary layer on a smooth bed. Cox et al. (1996) obtained estimates for the bed friction in the same way for a rough bed.

Direct measurement devices, referred to as shear plate sensors herein, measure the force exerted by the bed shear stress on a small element of the wall that is separated from the rest of the boundary by a small gap. The principal advantage of shear plate sensors is that no assumptions about the boundary layer flow are needed since the force is measured directly. Additionally, the difficulties of nearshore flows mentioned above (shallow depths, presence of air bubbles, flow reversals, etc.) are handled more easily by shear plate sensors. They also distinguish whether the shear stress was in the positive streamwise direction, or negative. There is a compromise in the design between the size of the sensor and the desire to measure forces accurately: smaller sensors provide more local measurements, but produce smaller forces that need to be measured. For coastal and hydraulic engineering applications, the most common configuration has been the use of an eddy-current proximity probe, which is able to measure small deflections with high accuracy, combined with simple mechanisms that provide stiffness against the force of the fluid. Such a configuration was employed by Simons et al. (1992, 1994) to make measurements of bed shear stress in wave-current interactions, by Boers (2005) to measure the bed shear stress in the surf zone, by Mirfenderesk and Young (2003) to measure bed shear stress under surface gravity waves, and recently by Barnes et al. (2009) and Seelam et al. (2011) to measure bed shear stress in a bore driven swash and under solitary waves, respectively. Other methods of transducing the force have also been used. Riedel and Kamphuis (1973) measured the bed shear stress in oscillatory flow using strain gauges to measure the shear plate deflection, whereas Rankin and Hires (2000) used a linear variable differential transformer to measure the shear plate deflection. You and Yin (2007) also directly measured the bed shear stress under surface gravity waves, but their sensor used a Wheatstone half bridge circuit to generate an output voltage proportional to the horizontal force on the shear plate. A review of past sensors can be found in Kolitawong et al. (2010). Generally, the most severe limitation for shear plate sensors is that pressure gradients in the flow introduce large errors in measurement of the wall shear stress via an extra force exerted on the edge, or lip, of the shear plate. Their applicability has therefore been limited to zero pressure gradient flows or very mild pressure gradients where this error is negligible. This issue is re-addressed in this paper to extend the applicability of shear plate sensors to flows with pressure gradients.

The layout of the paper is as follows. In Sect. 2, we describe the shear plate sensor design and calibration. In Sect. 3, we discuss the error introduced by secondary forces that reduce the utility of shear plate sensors. We address the issue of pressure gradients and propose a new methodology to compensate for this extra force. In Sect. 4, we present validation experiments conducted to show the results of bed shear stress measurements in turbulent flat plate boundary layer flow and under transient long waves. We end with the conclusions in Sect. 5.

2 Shear plate sensor design and calibration

2.1 Design

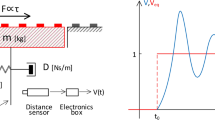
The design schematic for the shear plate sensor is shown in Fig. 1. The principle of transduction is that the shear plate is connected to four links that provide resistance to shear plate deflections from fluid forces, and these forces are inferred from measurements of the deflection. We are motivated by the study of the nearshore region in small-scale and large-scale laboratory wave flumes. The bed shear stress in such flows can be $O\left( 100\right)$ Pa even at moderate Reynolds numbers (Barnes et al. 2009; Sumer et al. 2011). The flow is primarily 2D, varying in the $x$ (cross-shore) direction and $z$ (vertical) direction, but with negligible variation in the spanwise (long-shore) direction of the flume. To obtain a local measurement of the bed shear stress, the length of the shear plate in the cross-shore direction needs to be much less than $O\left( 1\right)$ m, the typical length scale of waves in laboratory flumes, and the deflection of the shear plate needs to be as small as possible to cause minimal disturbance to the flow, but to be large enough to be measured accurately. The typical compromises in the design of shear plate sensors are discussed in Hanratty and Campbell (1996), Haritonidis (1989), Winter (1979).

For the current design, the brass (alloy 260) shear plate is 43.0 mm long, 136.0 mm wide and 0.8 mm thick. It is rigidly attached to 4 cylindrical brass (also alloy 260) links of diameter 1.6 mm and length 62.2 mm. The bottom ends of the cylindrical links are rigidly clamped to an aluminium base plate of thickness 6.4 mm. Such a configuration creates a parallel linkage mechanism, which provides stiffness to the shear plate deflections in the horizontal direction and support in the vertical direction. This type of mechanism also minimises the tilting of the shear plate from small deflections in the horizontal direction. The mechanism is installed into an acrylic housing via bolts through the aluminium base plate such that the top surface of the shear plate (its active area) is flush with the top surface of the acrylic housing. There exists a small gap of 1 mm along the perimeter of the shear plate between the shear plate and the housing to allow for small deflections. The acrylic housing can in turn be installed into laboratory flumes with the top surface flush with the flume bottom. When installed into our laboratory flume, in situ measurements of the vertical alignment of the active area of the shear plate with the bottom of the flume with the use of a vertical test dial indicator revealed that the misalignment around the perimeter of the shear plate was smaller than 0.2 mm. Additionally, there are two pairs of pressure tappings to enable measurement of pressure gradients above the shear plate (external) and underneath the shear plate (chamber). The external pressure tappings are of diameter 6.4 mm, located 95.4 mm apart equidistant from the centreline of the shear plate. The chamber pressure tappings are of diameter 1.2 mm located 45.0 mm apart on the side walls of the acrylic housing. The centre of the chamber pressure tappings is 1.8 mm below the active area of the shear plate. The deflection of the shear plate in the horizontal direction is detected by an eddy-current proximity probe (Lion Precision ECL-202, probe U8), which measures the distance to a small vertical target plate rigidly attached to the bottom face of the shear plate. The eddy-current proximity probe has a range of 2 mm with a resolution of 0.001 mm. A photograph of the shear plate sensor is shown in Fig. 2.

Fig. 1

Schematic side-view sketch of the shear plate sensor. Flow is in the x-direction. 1 eddy-current proximity sensor, 2 target plate, 3 cylindrical links, 4 base plate, 5 shear plate, 6 external pressure tappings, 7 chamber pressure tappings, 8 gap, 9 acrylic housing

Fig. 2

Photograph of the shear plate sensor

2.2 Calibration

To convert the displacement of the shear plate into a force, it is necessary to know the stiffness of the parallel linkage mechanism. The stiffness was measured by applying known forces and recording displacements. The first method used weights and a pulley system and the second method used a spring force meter. Figure 3 shows the data from a typical stiffness measurement. Combining the data from the repeated measurements of the stiffness gave a value of 9,800 N/m with a 95 % confidence interval of $\pm 100\, \hbox {N}/\hbox {m}$. The measured stiffness value using the two different methods several times over the course of the duration of the experiments remained constant to within 2 % of its original value. This measured stiffness can be compared to the expected stiffness from such a mechanism using simple beam structural mechanics since the deflections are small compared to the length of the links. The links will deflect as clamped guided beams maintaining a right angle to the shear plate as well as to the base plate. A clamped guided beam is equivalent to two cantilevered beams of half the length each and so a clamped guided beam has a stiffness four times in magnitude to that of a cantilevered beam of the same dimensions. Using the Young’s Modulus for brass as 110 GPa and dimensions of the links, the expected stiffness of the four links acting in parallel is calculated as 9,900 N/m. The predicted value and the measured value agree to within the uncertainty levels giving confidence in the response of the mechanism.

Fig. 3

Typical measurement of stiffness. Negative forces and displacements refer to the opposite direction

In the presence of unsteady loading, the dynamic response also becomes important. The frequency of oscillation of the shear plate in water puts an upper bound on the frequencies of forcing for which the instrument can make reliable measurements. The dynamic response was studied by modelling the system as a linear, second-order lumped parameter system of a mass, spring and dashpot. The equation of motion for this system [e.g. see den Hartog (1956)] is given by

$$\begin{aligned} \frac{\ddot{\chi }}{\omega _{n}^{2}}+2c\frac{\dot{\chi }}{\omega _{n}}+\chi =\frac{F}{k}, \end{aligned}$$

(1)

where $F$ is the total force on the shear plate in the x-direction and $\chi$ measures the deflection in the x-direction. The natural frequency of oscillation is given by $\omega _{n}=\sqrt{k/m}$, where $m$ is the mass of the shear plate, $k$ is the spring constant. The damping ratio is given by $c=\lambda /(2\sqrt{km})$, where $\lambda$ is the dashpot constant, and the damped natural frequency is given by $\omega _{d}=\omega _{n}\sqrt{1-c^{2}}$. The undamped natural frequency was estimated at 79 Hz using the measured stiffness and mass. The damped natural frequency was measured directly by measuring the impulse response in air and in water. The shear plate was given a small impulse by hand with a hammer and left to oscillate until the oscillations died out. The results are shown in Fig.  4, which plots the spectrum of the impulse response with the location of the peak indicating the damped natural frequency. The damped natural frequencies for air and water were found to be 69 and 54 Hz, respectively. Using this information, calculating the harmonic response of the mechanism revealed that the bandwidth (the upper limit on the frequency that the sensor can measure, or more specifically, the frequency where the output falls to −3 dB) of the shear plate sensor in water was 75 Hz. This is high enough to be able to resolve typical time scales of forcing in laboratory flumes (e.g. period of surface gravity waves).

Fig. 4

Spectra of impulse response measured in different fluids. Reflected portion of the spectrum not plotted

The shear plate sensor has been designed so that the size of its active area is small compared to typical length scales of the flow (e.g. typical laboratory flume dimensions, wavelength of free surface gravity waves). Thus, the shear plate sensor provides essentially local measurements of the shear stress. In laminar flow, this is usually a true local bed shear stress (unless there are strong spatial gradients in bed shear stress, e.g. near a separation point), whereas in the presence of turbulence, scales of motion much smaller than the streamwise length of the shear plate are averaged out.

The use of an eddy-current proximity probe that is able to measure small deflections with high accuracy, combined with a simple parallel linkage mechanism, which provides stiffness that does not require in situ calibration and minimises shear plate rotations, thus provides a powerful, inexpensive and robust way to measure the bed shear stress directly in laboratory flumes. The range of the shear stress sensor, given by the maximum force measurable divided by the active area of the shear plate, is $\pm 200\hbox { Pa}$. The accuracy of the shear plate sensor due to the combined uncertainty in the shear plate displacement and the stiffness of the parallel linkage mechanism is calculated [e.g. see Taylor (1997)] to be $\pm 1\,\%$. However, the true accuracy of the shear plate sensor is more likely to depend on the errors introduced by secondary forces on the shear plate. These are discussed in the following section.

3 Secondary forces for shear plate sensors

3.1 Analysis of pressure gradient force

Flows in laboratory flumes in the presence of surface gravity waves have time-varying streamwise pressure gradients. This may result in a significant secondary force on the edge of the shear plate. As illustrated in Fig. 5, the existence of a streamwise pressure gradient caused by the tilting of the free surface creates, for example, a higher pressure on the upstream edge of the plate compared to the downstream edge. Frei and Thomann (1980), making measurements in wind tunnels, provided a solution to the problem of pressure gradient forces by filling the gap and chamber with a fluid. However, this introduces additional surface tension forces and the applicability of such a technique in water flows may be limited. For the case where the chamber and gaps are open to the fluid flow, the ratio of the pressure gradient force to the shear force on the shear plate is estimated by the expression

$$\begin{aligned} \frac{\alpha l_{pt}}{u_{\tau }^{2}}, \end{aligned}$$

(2)

where $l_{pt}$ is the thickness of the shear plate as shown in Fig. 5, $\alpha =\left| -\frac{1}{\rho }\frac{\partial P}{\partial x}\right|$ is the magnitude of the kinematic pressure gradient (or alternatively, the free stream acceleration), and $u_{\tau }=\sqrt{\frac{\tau _{b}}{\rho }}$ is the friction velocity of the flow. For $\frac{\alpha l_{pt}}{u_{\tau }^{2}}\ll 1$, the effect of the pressure gradient force on the shear stress measurement is likely negligible. In many applications, especially under surface gravity waves, the pressure gradient force could be of the same order of magnitude as the force of the shear stress and needs to be accounted for from the total force on the shear plate. However, as pointed out by Riedel and Kamphuis (1973), Brown and Joubert (1969) and others, the constriction of the gaps forces the pressure gradient in the chamber to decay from its value in the external flow. Thus, it is insufficient to measure just the external pressure gradient to correct for the pressure gradient force; it is also necessary to know the rate of decay of the pressure gradient in the gaps. To account for this decay, we introduce an effective pressure gradient that acts on the shear plate: let $f_{PG}$ denote the effective fraction of the external flow pressure gradient that acts on the edge of the shear plate. If the value of $f_{PG}$ is known and the external flow pressure gradient is also known, the shear stress can be calculated by

$$\begin{aligned} \tau _{b}=\frac{1}{A_{plate}}\left( F-f_{PG}\frac{\partial P}{\partial x}V_{plate}\right) , \end{aligned}$$

(3)

where $V_{plate}$ is the volume of the shear plate and $A_{plate}$ is the active area of the shear plate. Equation 3 is also valid for time-varying quantities for frequencies within the bandwidth of the sensor.

Fig. 5

Schematic of shear plate sensor showing different forces on the shear plate

The concept of an effective fraction of the external flow pressure gradient has been introduced by others, e.g. Riedel and Kamphuis (1973), Allen (1977) and Seelam et al. (2011). The usual method to estimate the value of $f_{PG}$ is to measure the pressure gradient at some vertical distance below the active area of the shear plate and assume a linear decay of the pressure gradient in the vertical direction from the active area of the shear plate to the measurement location. Alternatively, it is common to assume $f_{PG}=0.5$ by the following reasoning: the pressure gradient decays linearly from the external value at the active area of the shear plate to a value of zero at the bottom surface of the shear plate with the fluid in the chamber at a pressure that is the mean of the pressure above the upstream and downstream gaps (e.g. see Acharya et al. 1985; Allen 1977; Brown and Joubert 1969; Coles 1953; Winter 1979). However, the most likely scenario is that $f_{PG}$ has a value between $0.5$ and $1$.

We conduct a simplified analysis for the flow in the chamber of the shear plate sensor to estimate the value of $f_{PG}$. The following assumptions are made: (1) deflections of the shear plate are ignored since they are small and do not have a large effect on the flow; (2) only the two-dimensional flow field is considered since typical laboratory flows have very little spanwise variation; (3) the pressure gradient is constant over the area of the shear plate; (4) the pressure just above the gaps is not modified by the flow perturbations due to the gaps, i.e. the flow in the chamber is essentially forced by the external flow without the external flow being significantly altered. Thus, the boundary conditions to the flow in the chamber are known and it is implied that the flow velocities in the chamber are small, an assumption required for the shear plate to report accurate values of the total shear force anyway. To proceed, we introduce the following dimensionless quantities for the flow in the chamber:

$$\begin{aligned} \tilde{u}=\frac{u}{U_{ch}};\;\tilde{t}=\frac{t}{T};\; \tilde{\nabla }=l_{g}\nabla ;\;\tilde{P}=\frac{P}{\rho \alpha l_{g}}, \end{aligned}$$

(4)

where $U_{ch}$ is the velocity scale in the chamber, $T$ is a relevant timescale of the external flow, $l_{g}$ is the size of the gap as defined in Fig. 5, $\alpha =\left| -\frac{1}{\rho }\frac{\partial P}{\partial x}\right|$ is the magnitude of the kinematic pressure gradient in the external flow. The pressure gradients in the chamber scale with the external flow pressure gradient since it is this external pressure gradient that drives the flow in the chamber. The dimensionless momentum equation is then given by

$$\begin{aligned} \frac{l_{g}^{2}}{\nu T}\frac{\partial \tilde{u}}{\partial \tilde{t}}+\frac{U_{ch}l_{g}}{\nu }\tilde{u}\cdot \tilde{\nabla }\tilde{u}=\frac{\alpha l_{g}^{2}}{\nu U_{ch}}\tilde{\nabla }\tilde{P}+\nabla ^{2}\tilde{u}. \end{aligned}$$

(5)

With the intention of linearising the equation, and under the assumption that the velocities in the chamber are small due to viscous forces in the chamber flow and mild pressure gradients in the external flow, we may derive the chamber velocity scale by requiring that the viscous term be of the same order as the pressure gradient term. This gives

$$\begin{aligned} U_{ch}=O\left( \frac{\alpha l_{g}^{2}}{\nu }\right) . \end{aligned}$$

(6)

The above is consistent with the intuition for the scale of the chamber velocity, i.e. $U_{ch}=U_{ch}\left( \alpha ,\, l_{g},\,\nu \right)$. Using this chamber velocity scale, we may evaluate the importance of the non-linear term in Eq. 5 by the magnitude of its coefficient, the chamber flow Reynolds number

$$\begin{aligned} Re_{ch}=\frac{\alpha l_{g}^{3}}{\nu ^{2}}. \end{aligned}$$

(7)

If $Re_{ch}\ll 1$, we may neglect the non-linear advective acceleration and greatly simplify the problem of calculating $f_{PG}$, since taking the divergence of the remaining terms in Eq. 5 and invoking continuity reveals that the pressure in the chamber follows Laplace’s equation

$$\begin{aligned} \tilde{\nabla }{}^{2}\tilde{P}=0. \end{aligned}$$

(8)

The boundary conditions are the Dirichlet boundary conditions above the gaps prescribed by the external pressure gradient and Neumann boundary conditions at the walls such that the wall normal pressure gradient is zero, implying that the pressure gradient in the chamber simply scales with the external pressure gradient and its decay depends only on the sensor geometry. The Neumann boundary condition follows directly from the kinematic no-flux boundary condition for velocity. To calculate $f_{PG}$, an aribitrary pressure gradient is imposed above the plate by imposing different pressures above the upstream and downstream gaps. The pressure field in the chamber is then obtained via a numerical solution to Eq. 8. From this solution, the vertical variation of the pressure gradient over the thickness of the plate can be calculated. The value of $f_{PG}$ is just the average pressure gradient that the plate feels divided by the pressure gradient imposed above the plate. This process for calculating $f_{PG}$ is convenient since its value only needs to be calculated once for a given sensor geometry. Figure 6 shows the numerical solution to Eq. 8 for the shear plate sensor using a second-order accurate finite difference scheme. A pressure difference of 1 is imposed with the a pressure of 1 above the left gap and a pressure of 0 above the right gap. Using grid refinement studies to ensure there is convergence of the solution, it was found that $f_{PG}=0.8$ for the shear plate sensor to 1 significant figure.

Fig. 6

Solution to Eq. 8 for the shear plate sensor geometry. Left full geometry. Right zoomed into top left corner. $P=1$ is imposed above the left gap and $P=0$ above the right gap. Lines are contours of pressure; adjacent contour lines are separated by a magnitude of 0.1. Estimated $f_{PG}=0.8$

To investigate how $f_{PG}$ varies with the geometry of the sensor, we postulate that

$$\begin{aligned} f_{PG}=f_{PG}\left( \frac{l_{pt}}{l_{g}},\frac{l_{g}}{l_{pl}}\right) , \end{aligned}$$

(9)

where the variations of $l_{h}$ are considered unimportant and have been ignored because they do not significantly alter the solution as long as $l_{h}$ is of the same order of magnitude as $l_{pl}$. Figure 7 shows the variation of $f_{PG}$ with the shear plate thickness to gap size ratio $\frac{l_{pt}}{l_{g}}$ and gap size to shear plate length ratio $\frac{l_{g}}{l_{pl}}$. Figure 7 shows similar trends to those observed by Acharya et al. (1985) who studied the variation of $f_{PG}$ experimentally: $f_{PG}$ tends to decrease towards a value of $0.5$ as the thickness to gap size ratio is increased. Increasing the gap size to shear plate length ratio, while holding the shear plate thickness to gap size ratio constant, also reduces the value of $f_{PG}$.

Fig. 7

Variation of $f_{PG}$ with geometric ratios of the shear plate sensor from solution to Eq. 8. $l_{h}/l_{pl}=1$ for all cases

3.2 Misalignment forces and intrusiveness

Misalignment of the shear plate relative to the rest of the bed can add extra forces to the shear plate. Small protrusions, recessions and shear plate rotations can create complex flow patterns that add extra forces as is obvious from considerations of streamlines in these cases. Such extra forces can be large, but it is not generally possible to account for them. Allen (1977, 1980) and Kolitawong et al. (2010) provide further discussion on this matter. The developed shear plate sensor was constructed to minimise these errors by the use of a parallel linkage mechanism that minimises shear plate tilting and by careful construction so that the active area of the shear plate is flush with the surrounding boundary.

There may also be secondary forces on the shear plate due to non-zero chamber velocities and the exchange of momentum between the external flow and the chamber, as also pointed out by Brown and Joubert (1969). The accompanying velocity perturbations may also disturb the near wall flow and change the shear stress being measured. Intuitively, we may expect that the intrusion due to the gaps will be small if the gap size is of the order of the viscous lengthscale, or equivalently, that the Reynolds number based on the gap size and friction velocity is $O\left( 1\right)$. This Reynolds number is defined as

$$\begin{aligned} l_{g+}=\frac{u_{\tau }l_{g}}{\nu }. \end{aligned}$$

(10)

However, using experimental evidence of turbulent boundary layers over gaps, Dhawan (1953) provides a rule of thumb that in fact, the gradient of the velocity profile is unaltered by the presence of the gaps up to $l_{g+}<100$. Flow visualisations with coloured dye were used to check whether the shear plate sensor suffers from large chamber velocities and is thus intrusive to the external flow. No significant perturbations were observed.

4 Validation

The validation experiments presented in this section cover only a fraction of the range of bed shear stress that the shear plate sensor is capable of measuring. Given that the shear plate sensor was designed for flow environments that are not well understood and challenge other measurement techniques, it was not possible to generate a flow in which high bed shear stress values measured by the shear plate sensor could be verified by other methods. However, the accuracy of the shear plate sensor is fully validated by the following experiments since they test the sensor at low values of bed shear stress, where it is most prone to errors.

4.1 Turbulent flat plate boundary layer

Unidirectional flow was established in an 8 m long open channel flume with glass side walls and acrylic bed in the DeFrees Hydraulics Laboratory at Cornell University. Simultaneous measurements of the bed shear stress were made with the shear plate sensor and from the velocity data obtained using particle image velocimetry (PIV). The setup of the experiment is shown in Fig. 8. The shear plate sensor and the PIV field of view (FOV) coincided in the streamwise direction but were at different spanwise locations, allowing for a direct comparison of the shear stress. Both the shear plate sensor and the PIV FOV were sufficiently far from the side walls to be unaffected by the side wall boundary layer. Also at the same streamwise location, but separate spanwise location was an acoustic doppler velocimeter (ADV, Nortek Vectrino with plus firmware), which was used to monitor the mean velocity of the flow.

Fig. 8

Experimental setup for turbulent flat plate boundary layer experiments. The shear plate sensor, ADV and PIV field of view are co-located in the streamwise direction but separated in the spanwise direction

The FOV was illuminated by a dual-head Spectra Physics Nd:YAG laser operating at 10 Hz for each head, allowing for 10 Hz velocity data. The laser beams were expanded into a vertical light sheet using a cylindrical lens. The FOV measured $4\times 3$  cm with 4 cm in the horizontal to match the shear plate length of 4.3 cm. The images were taken with a 1,600 × 1,200 14-bit camera (Vision Research, Phantom v9.1) fitted with a Nikon 105 mm f/2.8D AF Micro-Nikkor lens. Images were taken for 200 s, at 20 Hz yielding 4,000 images and the time between images $\left( \Delta t\right)$ ranged from 0.7 to 0.4 ms. Image pairs were analysed using dynamic sub-window PIV method outlined in Cowen and Monismith (1997) after removing the background image from each image pair. Sub-pixel peak location was obtained with the use of the spectral shifting technique given in Liao and Cowen (2005), which has been shown to reduce peak-locking and improve accuracy. The final pass of the image analysis was done with 32 × 32 pixels sub-windows with 50 % overlap giving a velocity vector array of $97\times 71\,\left( x\times z\right)$ for every image pair. The PIV algorithm produces around 90 % valid vectors; the number of valid vectors suffered slightly due to small differences in illumination intensity between images in an image pair due to the difficulty of achieving identical power from both laser heads.

The PIV velocity data were decomposed into mean quantities and fluctuating quantities using the Reynolds decomposition

$$\begin{aligned} q=\left\langle q\right\rangle +q', \end{aligned}$$

(11)

where $q$ is a quantity of interest, $\left\langle q\right\rangle$ is its ensemble mean and $q'$ is its instantaneous turbulent fluctuation. For this flow, the ensemble mean is the mean of the quantity in time and the x-direction. The mean horizontal velocity profiles $\left\langle u\left( z\right) \right\rangle$ were thus computed from 194,000 data points at each vertical elevation. Using the mean velocity profile, the momentum thickness of the flow is given by Pope (2000)

$$\begin{aligned} \theta =\int\limits_{0}^{\infty }\frac{\left\langle u\right\rangle }{U_{0}}\left( 1-\frac{\left\langle u\right\rangle }{U_{0}}\right) dz, \end{aligned}$$

(12)

from which the momentum thickness Reynolds number, $Re_{\theta }=\frac{U_{0}\theta }{\nu }$, was calculated. The mean horizontal velocity profile scaled by the friction velocity, $u_{\tau }=\sqrt{\tau _{b}/\rho }$, gives the well-known law of the wall

$$\begin{aligned} u_{+}=\frac{1}{\kappa }\ln \left( z_{+}\right) +C, \end{aligned}$$

(13)

where $u_{+}=u/u_{\tau },\, z_{+}=u_{\tau }z/\nu ,\, \kappa =0.41$ and $C=5.5$ (Pope 2000).

Using the PIV velocity measurements, the friction velocity was found in two ways: (1) by least squares fit of the mean velocity profile to the law of the wall with the friction velocity, which gives $u_{\tau ,1}$; (2) linear extrapolation of the Reynolds stress profile from $z/h>0.075$ to $z=0$, which gives $u_{\tau ,2}$. Figure 9 shows the mean horizontal velocity profiles normalised with $u_{\tau ,1}$. The law of the wall is also plotted in Fig. 9 for comparison and shows good agreement with the data. The data also show good agreement with the direct numerical simulation (DNS) dataset of Spalart (1988), which was done at $Re_{\theta }=1,410$. Figure 10 shows the profiles of the Reynolds stress normalised with $u_{\tau ,2}$.

Fig. 9

Normalised horizontal mean velocity profiles: PIV experimental data (open symbols). Law of the wall (dashed line); Spalart (1988) DNS data (solid line). Law of the wall calculated using $\kappa =0.41$ and $C=5.5$

Fig. 10

Normalised Reynolds stress profiles: PIV experimental data (open symbols, same as Fig. 9)

Table 1 Summary of results for turbulent flat plate boundary layer experiments

The deflection of the shear plate was recorded simultaneously with the PIV data at 50 Hz. To obtain the deflection, the mean position of the shear plate after the flow was stopped and the fluid returned to rest was subtracted from the mean position of the shear plate during the flow. The measured deflection was converted to force using the stiffness, and this force was divided by the active area of the shear plate to obtain a mean shear stress. The results are summarised in Table 1. Values for $\tau _{b,1}$ and $\tau _{b,2}$ refer to the shear stress estimates from PIV measurements, corresponding to $u_{\tau ,1}$ and $u_{\tau ,2}$, respectively, and values for $\tau _{b,SPS}$ refer to the direct measurements of shear stress using the shear plate sensor. Table 1 also gives estimates of the 95 % confidence intervals on all measurements of the shear stress. Following Moffat (1988), the uncertainty in the measurements was split into bias error and random error. For $\tau _{b,SPS}$, the estimated 95 % confidence intervals were calculated by a root-sum-square combination of the 1 % bias error found in the calibration and the random error, which was found by applying the bootstrap technique (Efron and Tibshirani 1993) on the mean of the deflection of the shear plate. The combined error is reported to 1 significant figure. For the PIV results, the major bias error resulting from peak-locking effects is difficult to estimate quantitatively, but qualitatively, probability density functions of the measured velocities can show the peak-locking effect (Liao and Cowen 2005). These were examined and showed there was little peak-locking, consistent with the use of the spectral shifting technique for finding sub-pixel peak location. However, the are several sources of random error in determining the particle displacement, e.g. camera thermal noise [see Raffel (2007) for a comprehensive list] as well as sources of uncertainty in determination of $u_{\tau ,1}$ and $u_{\tau ,2}$, e.g. uncertainty in the coefficients of linear regression. The total random error was found by applying the bootstrap technique on the entire process of finding $u_{\tau ,1}$ and $u_{\tau ,2}$ from the raw velocity vectors. The uncertainty from PIV data in $u_{\tau ,1}$ and $u_{\tau ,2}$ was propagated to $\tau _{b,1}$ and $\tau _{b,2}$ [e.g. see Taylor (1997)]. The results, with vertical error bars representing the estimated 95 % confidence intervals, are plotted in Fig. 11.

For these experiments, the streamwise pressure gradients are negligible and there is no need to include a correction term in the calculation of shear stress. Flow visualisation with coloured dye injected into the chamber showed very little flow motion in the chamber and through the gaps. This is in accordance with the prediction of Eq. 6 since the streamwise pressure gradients in these experiments are negligible. Comparison between the direct measurement of shear stress by the shear plate sensor and the indirect measurement of shear stress with the use of PIV velocity data are generally good. With the exception of U2 and U5, the shear plate sensor data agree to within 10 % of the values of shear stress obtained from the PIV velocity data. Some of the discrepancy with the shear plate sensor data may be explained by the fact that for the low values of shear stress in these experiments, the shear plate sensor is more susceptible to additional errors such as small shifts in the zero position of the shear plate caused by vibration noise of the variable frequency pumps used to drive the flow in the channel.

Fig. 11

Bed shear stress measurements for turbulent flat plate boundary layer experiments. Shear stress data from $u_{\tau ,1}$ (squares); shear stress data from $u_{\tau ,2}$ (triangles); shear plate sensor measurements (circles). Vertical bars represent 95 % confidence intervals

4.2 Boundary layer under solitary waves

In water of constant depth and in the absence of viscosity, the solitary wave is an elevation wave of permanent form propagating at a constant celerity. The wave is fully characterised by the still water depth that it travels in, $h$, and the maximum elevation of the free surface above the still water depth, i.e. its height, $H$. The normalised wave height is expressed as $\epsilon =H/h$, which is typically a small parameter. Grimshaw (1971) provides a solution to the solitary wave that is accurate up to second order, i.e. up to $O\left( \epsilon ^{2}\right)$, which will be used to compare to experimental data. In the presence of viscosity, there exists thin boundary layers at the bed and at the free surface that introduce damping to the solitary wave as it propagates (Liu et al. 2007). The bottom boundary layer of the solitary wave has been previously studied by Keulegan (1948), and Liu and Orfila (2004) have developed a general theory for the bottom boundary layer of transient long waves. Liu et al. (2007) applied the analysis of Liu and Orfila (2004) specifically to solitary waves and experimentally examined the laminar boundary layer under three solitary waves of different heights. Here we repeat two of those cases to compare the direct bed shear stress measurements from the shear plate sensor to indirect bed shear measurements from velocity field data using PIV in the boundary layer. We also compare the bed shear stress measurements to the linear boundary layer theory as presented by Liu et al. (2007).

Table 2 Characteristics of solitary waves generated

The solitary waves were generated in a 15-m wave flume equipped with a piston-type wave-maker of stroke of 1.2 m in the DeFrees Hydraulics Laboratory at Cornell University. Table 2 summarises the characteristics of the solitary waves generated in these experiments, including their effective wavelengths, $L_{0}$, and their effective periods, $T_{0}$. The trajectory of the wave-maker to generate a solitary wave was computed using the method provided in Goring (1978) with the wavelength cut-off corresponding to where the free surface displacement is at 1 % of the wave height. The setup of the experiment is shown in Fig. 12. The still water depth was kept at 10.0 cm, and shear plate sensor was mounted with the active area flush with the rest of the bed of the flume. The centre of the shear plate was at a distance of 7.1 m from the wave-maker in its retracted position. There was a 1:10 slope installed at the other end of the flume, but the toe of the slope was sufficiently far from the shear plate so that wave reflections did not contaminate the data. An acoustic wave gauge (Banner Engineering, S18U; resolution $\pm$0.5 mm) was positioned directly above the centre of the shear plate sensor to record the free surface elevation. Two differential pressure gauges (Omega Engineering, PX26; resolution $\pm$7.5 Pa) were used to record the pressure difference between the external pressure tappings and the chamber pressure tappings (see Fig. 1). To increase the signal-to-noise ratio of the shear plate sensor for the low values of shear stress in these experiments, the results shown are the ensemble average of 40 repetitions of each wave. Measurements of the free surface elevation confirmed that the repetitions were aligned in phase and highly repeatable. An additional repetition of each wave was done where an ADV was also installed to measure the water velocity 2 cm above the bed, which is outside the boundary layer for both wave cases. It was operated at 40 Hz with a sampling volume of diameter 6 mm and height 7 mm.

Fig. 12

Setup of experiments for solitary wave boundary layer

Figure 13 shows measurements of free surface elevation for the solitary wave of $H=0.83$ cm and Fig. 14 shows ADV measurements of the water velocity 2 cm above the bed. Both show very good agreement with Grimshaw’s theoretical solution. The measurements for the solitary wave of $H=2.00$ cm show similarly good agreement.

Fig. 13

Measurements of free surface elevation of W1: $H=0.83$ cm. Wave gauge data (circles); Grimshaw (1971) solution (solid line)

Fig. 14

Measurements of water velocity 2 cm above the bed of W1: $H=0.83$ cm. $u$ is the water velocity in direction of wave propagation and $w$ is the water velocity in the vertical direction. ADV data (circles); Grimshaw (1971) solution (solid line)

It is noted that the wavelengths of the waves are much larger than the streamwise length of the shear plate sensor, and thus, the value of the streamwise pressure gradient can be assumed constant over the shear plate. Measurements of the external pressure difference are converted to a pressure gradient by dividing by the distance separating the external pressure tappings. Figure 15 shows that the pressure gradient measured in this way for the solitary wave of $H=0.83$ cm compares very well to the solution to pressure given by Grimshaw (1971) theory. There is similar good agreement for the solitary wave of $H=2.00$ cm.

Fig. 15

Measurements of streamwise pressure gradient of W1: $H=0.83$ cm. Measurements (circles); Grimshaw (1971) solution (solid line)

As noted previously, for surface gravity waves, the streamwise pressure gradients will act as a secondary force on the shear plate. To characterise the importance of this force and the influence streamwise pressure gradients have on the flow in the chamber, an order of magnitude scale of the pressure gradient under a solitary wave is derived as $\alpha _{sw}=\frac{1}{\rho }\left( \frac{\rho gH}{L_{0}/2}\right)$, which is the average steepness of the wave assuming the pressure is hydrostatic (a valid assumption for $\epsilon \ll 1$). The ratio of the pressure gradient force to the shear force on the shear plate, Eq. 2, is estimated using $\alpha _{sw}$ together with the an order of magnitude scale for the bed shear stress (converted to units of velocity) obtained from the linear boundary layer solution of Liu et al. (2007). $\alpha _{sw}$ is also used to calculate the chamber flow Reynolds number as defined in Eq. 7. These quantities are presented in Table 2. It can be seen that the pressure gradient force is of the same order of magnitude as the shear force. Additionally, $Re_{ch}\gg O\left( 1\right)$ implying that the linearisation of the chamber flow is not justified and the pressure gradient is large enough to drive some flow in the chamber. Nonetheless, we proceed to use a constant value of $f_{PG}$ in Eq. 3 to account for the streamwise pressure gradients and calculate the shear stress. Figure 16 shows the measurements of shear stress from: (1) shear plate sensor using $f_{PG}=0.8$ in Eq. 3; (2) PIV velocity measurements in the boundary layer from Liu et al. (2007) and Park (2009). Both sets of measurements are compared to the shear stress obtained from the linearised solution to the boundary layer flow equations in Liu and Orfila (2004) and Liu et al. (2007).

Measurements from the shear plate sensor show good agreement with the data of Park (2009) and the linearised boundary layer solution of Liu et al. (2007) even though the magnitude of the pressure gradient force is comparable to the shear force, $\frac{\alpha l_{pt}}{u_{\tau }^{2}}=O\left( 1\right)$, and the flow is outside the validity of a constant value of $f_{PG}$. The most notable discrepancy is in the case of the solitary wave of $H=2.00$ cm where the shear plate sensor fails to capture the negative portion of the shear stress that occurs behind the wave crest as a result of the adverse pressure gradient on the boundary layer. Measurements of pressure difference in the chamber, plotted in Fig. 17, during this time show that the pressure on the downstream chamber wall was higher than the pressure on the upstream chamber wall. The resolution of the pressure difference measurements has been improved to $\pm$1.2 Pa from ensemble averaging of 40 repetitions of the wave. For the majority of the wave period, the pressure gradient in the chamber was still too small to measure. However, for a very short time under the wave crest and just behind it, the measured pressure difference may be indicative of flow velocity in the chamber in the same direction as the external flow. This suggests that the chamber flow was important only during a short period of time and that during that period the measurements of the shear stress may be affected by secondary flows. This is in accordance with the high value of the chamber flow Reynolds number, which predicted that there may be flow in the chamber that is not negligible. Thus, the negative part of the shear stress may not have been captured because the shear plate sensor suffered from local secondary flows during that phase of the flow.

Fig. 16

Measurements of bed shear stress from shear plate sensor. Left $H=0.83$ cm; Right $H=2.00$ cm. Shear plate sensor data (circles); PIV velocity field data from Liu et al. (2007) and Park (2009) (crosses); linearised boundary layer flow solution from Liu et al. (2007) (solid line)

Fig. 17

Measurements of streamwise pressure difference in chamber of W2: $H=2.00$ cm. Negative $\Delta P$ means downstream pressure is higher than upstream pressure

5 Conclusions

Accuracy of shear plate sensors suffer primarily due to the secondary forces on the shear plate; in particular, the force of streamwise pressure gradients acting on the edges of the shear plate. This force has been carefully examined, and a new methodology for its correction is presented: the effective fraction of the streamwise pressure gradient that acts on the shear plate, $f_{PG}$, can be calculated a priori and independently of the flow by the solution to Laplace’s equation for the pressure field in the chamber so long as the chamber flow Reynolds number, $Re_{ch}=\frac{\alpha l_{g}^{3}}{\nu ^{2}}$, is small.

A shear plate sensor has been designed, built and validated in an open channel flow experiments. The sensor is capable of measuring shear stresses in the range $\pm$200 Pa with a bandwidth of 75 Hz. The accuracy of the sensor is $\pm$1 %, but in practice, it depends primarily on the importance of secondary forces on the shear plate and the accuracy with which their values are known. For the developed shear plate sensor, $f_{PG}=0.8$, which is valid for pressure gradients up to $\alpha =O\left( 10^{-3}\right)$. This can be still be a constraint under surface gravity waves, especially in small-scale flumes where the magnitude of the shear stress is very low and the error due to pressure gradient forces is large. Nonetheless, the shear plate sensor has been shown to be able to measure the bed shear stress in the laminar boundary layer under solitary waves in a small-scale laboratory wave flume.

The design of the shear plate sensor makes it an especially suitable sensor to measure the bed shear stress in the nearshore region of a large-scale flume. Such a flow environment presents severe difficulties for indirect methods to measure the bed shear stress due to the shallow flow depth often containing air bubbles, transient flow that that covers a large range of shear stress values (that can also change direction), and lack of optical access. The shear plate sensor, however, can make good measurements in these conditions since the pressure gradients are relative mild and the magnitudes of bed shear stresses are high. This makes it a powerful tool to study the flow processes in the nearshore region.