Abstract
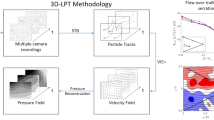
Three-dimensional time-resolved velocity field measurements are obtained using a high-speed tomographic Particle Image Velocimetry (PIV) system on a fully developed flat plate turbulent boundary layer for the estimation of wall pressure fluctuations. The work focuses on the applicability of tomographic PIV to compute the coherence of pressure fluctuations, with attention to the estimation of the stream and spanwise coherence length. The latter is required for estimations of aeroacoustic noise radiation by boundary layers and trailing edge flows, but is also of interest for vibro-structural problems. The pressure field is obtained by solving the Poisson equation for incompressible flows, where the source terms are provided by time-resolved velocity field measurements. Measured 3D velocity data is compared to results obtained from planar PIV, and a Direct Numerical Simulation (DNS) at similar Reynolds number. An improved method for the estimation of the material based on a least squares estimator of the velocity derivative along a particle trajectory is proposed and applied. Computed surface pressure fluctuations are further verified by means of simultaneous measurements by a pinhole microphone and compared to the DNS results and a semi-empirical model available from literature. The correlation coefficient for the reconstructed pressure time series with respect to pinhole microphone measurements attains approximately 0.5 for the band-pass filtered signal over the range of frequencies resolved by the velocity field measurements. Scaled power spectra of the pressure at a single point compare favorably to the DNS results and those available from literature. Finally, the coherence of surface pressure fluctuations and the resulting span- and streamwise coherence lengths are estimated and compared to semi-empirical models and DNS results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The spanwise coherence of pressure fluctuations at the wall under a turbulent boundary layer is of great importance in aeroacoustics, for instance for the estimation of trailing edge noise, and in vibro-structural problems. Several authors (Amiet 1976; Howe 1999) have discussed diffraction theory in the framework of trailing edge noise, relating the power spectral density and the spanwise coherence length of hydrodynamic pressure fluctuations to an estimation of the acoustic far-field spectrum. It is assumed that incident pressure fluctuations on the wall below the turbulent boundary convect over the trailing edge, an impedance discontinuity, where these fluctuations are scattered in the form of acoustic waves. In the past, the aforementioned theory has been applied using both, numerical and experimental data. For instance, Christophe (2011) applied data obtained from Large Eddy Simulation (LES) as input for the model. Brooks and Hodgson (1981) have performed surface pressure measurements on a NACA0012 aerofoil model and demonstrated very good agreement with acoustic measurements.
Nevertheless, measurements of the space-time coherence of the pressure field require complex instrumentation involving several surface pressure transducers or microphones, installed inside the model or flush mounted on the model’s surface, at multiple points. Furthermore, transducer based measurements of pressure within the turbulent boundary layer have been proven difficult due to the intrusiveness of the methods and the obstacles encountered in installing a large number of pressure sensors closely spaced within thin geometries, such as sharp trailing edges.
In recent years, the development of high-speed PIV time-resolved velocity field measurement techniques opened new possibilities for the investigation and understanding of complex flows including turbulent flow phenomena and aeroacoustic sources. In particular, analysis of aeroacoustic problems and sources based on time-resolved PIV approaches has become of interest (Morris 2011). Examples include the estimation of turbulence-structure interaction noise (Lorenzoni et al. 2012) and cavity noise (Koschatzky et al. 2011). Under the assumption of incompressible flow, the momentum equation provides a relation between the spatially and temporally resolved velocity field and the hydrodynamic pressure. Therefore, within the limitations of this assumption, reconstruction of the pressure field becomes possible with time-resolved PIV, which provides a non-intrusive and more flexible alternative for the determination of pressure fluctuations within the flow.
Early application of pressure reconstruction based on PIV is due to Liu and Katz (2006). Further studies concentrated on the assessment of the measurement accuracy and robustness of different pressure reconstruction methods (Charonko et al. 2010). de Kat and van Oudheusden (2012) investigated the quality of pressure reconstruction methods in the turbulent flow past a square cylinder and proposed guidelines regarding the required temporal and spatial resolution of the measurements. In more recent experiments Ghaemi et al. (2012) have obtained the single point wall pressure spectrum under a turbulent boundary layer using a time-resolved thin-volume tomographic PIV approach. In their study, the measurement volume was aligned with the dominant flow direction and the results were compared to the signal captured by a single pinhole microphone measuring the surface pressure and a good agreement was found. However, the spatio-temporal structure of the wall pressure field cannot be assessed in this configuration due to the limited depth of the measurement volume.
The estimation of the coherence function and coherence length requires the evaluation of the wall pressure auto- and cross-power spectral densities. Restrictions on the spatial dynamic range pose a limit on the attainable imaging resolution for a given choice of the measurement volume. This limitation becomes particularly severe when operating the system at hight frequencies (here 10 kHz), where the energy per laser pulse and therefore the illumination intensity is significantly less when compared to lower repetition rates. Therefore, the measurement volume cannot be extended to include the entire boundary layer. Despite of this limitation, Ghaemi et al. (2012) have demonstrated that uniform and constant boundary conditions can be applied within the boundary layer maintaining the spectral content of pressure fluctuations over a wide range of frequencies. Therefore, a measurement configuration with a thin volume parallel to the wall could respond to the requirements of a measurement domain of sufficient stream- and spanwise extent. This measurement configuration is not new, for instance Schröder et al. (2008) applied it to fully developed boundary layers, and Atkinson et al. (2011) assessed the inner region of the boundary layer in a similar way. However, time-resolved experiments have not been performed in this configuration, which is required for the current experiment. The present study aims at determining the feasibility of an experimental approach based on volumetric time-resolved velocity field data from tomographic PIV to obtain wall pressure spatio-temporal characteristics and in particular an estimation of its coherence length. Because little reference data is available on this specific issue, the assessment of this approach is corroborated with a Direct Numerical Simulation (DNS) at similar conditions as those encountered experimentally. Moreover, simultaneous pressure measurements by a pinhole microphone are used to compare the pressure evaluated with PIV.
2 Wall pressure fluctuations and estimation
2.1 Wall pressure fluctuations
The properties of the wall pressure spectrum, especially for channel flows and zero pressure gradient boundary layers, have been thoroughly investigated in the past (Bull 1996). Research converged on the fact that single scaling approaches do not lead to a satisfactory collapse of experimental data over the entire frequency range, even when transducer-resolution effects are taken into account. This is ascribed to the complexity of the pressure field and its dependency on all parts of the domain, which involves the convection of turbulent velocity fluctuations at different characteristic velocities, depending for instance on the distance from the wall. A subdivision of the pressure spectrum \(\varPhi\left(\omega\right)\) in dependence on the angular frequency ω = 2πf into four parts has been proposed: The low, mid, universal, and high frequency range (Bull 1996) and the suitability of the scaling rules over different frequency ranges mostly depends on the Reynolds number. In a recent work due to Hwang et al. (2009) the scaling of the wall pressure spectrum and empirical models are reviewed.
Two different scaling rules are most commonly applied in literature, demonstrated by a better collapse of the low or high frequency range, respectively. The pressure spectrum scaled using outer flow variables, namely the free stream velocity \(u_\infty,\) displacement thickness \(\delta^\star,\) and dynamic pressure \(q_\infty=1/2 \rho u_\infty^2,\) is expressed as \(\tilde{\varPhi}_o \left( \tilde{\omega}_o \right) = \varPhi \left( \omega \right) u_\infty / q_\infty^2 \delta^\star,\) where \(\tilde{\omega}_o = \omega \delta^\star / u_\infty.\) Based on inner flow variables, namely the kinematic viscosity ν, wall shear stress \(\tau_w=\rho \nu \partial u/\partial y\vert_{y=0},\) shear velocity \(u_\tau=\sqrt{\tau_w/\rho},\) and viscous wall unit δν = ν/u τ, the pressure spectrum is scaled with \(\tilde{\varPhi}_i \left( \tilde{\omega}_i \right) = \varPhi \left( \omega \right) u_\tau^2 / \tau_w^2 \nu,\) where \(\tilde{\omega}_i=\omega \nu / u_\tau^2\) (Goody 2004). The outer scaling shows a better collapse at low frequencies, while the inner scaling applies at high frequencies and shows a generally accepted decay rate of ω −5 in the limit of high frequencies.
A model describing the pressure spectrum with dependence on Reynolds number has been proposed by Goody (2004). The dependence on Reynolds number is introduced through a parameter representing the ration between outer and inner time scales \(R_T = \delta u_\tau^2/\nu u_\infty,\) where δ is the boundary layer thickness. The model has been calibrated for a range of Reynolds numbers (based on the boundary layer momentum thickness θ) 1,400 < Re θ < 23,400 with empirical constants C 1 = 0.5, C 2 = 3, and C 3 = 1.1.
Schewe (1983) presents experimental data for a flat surface in air and conditions of similarly low Reynolds number Re θ = 1,400 as considered in the present study and will therefore be recalled for comparison. The displacement thickness in these experiments is reported to be \(\delta^\star=4.6\,{\rm mm}\), the free stream velocity \(u_\infty=6.3\,\hbox{m}/\hbox{s}\) and the ratio of outer and inner boundary layer time scales is Re T ≈ 25. As pointed out by Hwang et al. (2009) the universal range showing a decay in \(\varPhi(\omega)\) of approximately ω −0.7 between \(0.6 \leq \omega \delta^\star / u_\infty \leq 1.2\) for low Reynolds number flows is narrow. At higher frequencies the model converges to the generally accepted ω −5 decay.
2.2 Definition and estimation of coherence and coherence length
The coherence length is defined in terms of the coherence function (Eq. 2), which involves the auto-power and cross-power density of the signals, where \(\varPhi(\omega,z_1,z_2)\) denotes the cross-power spectral density between two points along a given dimension and \(\Updelta z=z_2-z_1\) is their spatial separation.
Note that this representation applies for the case that the flow statistics are homogeneously distributed along the spatial dimension, stationary in time and for an infinite observation period. For a flat plate boundary layer the first condition is fulfilled when considering the spanwise dimension and, with restriction to short separations, for the streamwise direction.
By definition, the coherence length is related to the integral of the coherence function \(\gamma(\omega,\Updelta z)\) over the spatial separation \(\Updelta z\) and therefore reduces to a function of frequency only (Eq. 3).
Several models for the spatial structure of the wall pressure spectrum have been proposed and a review has been provided by Graham (1997). Corcos (1964) proposed a model for the cross-spectrum of the turbulent wall pressure field (Eq. 4), implying that the normalized cross-power spectral density \(\varPhi\left(\omega,0,\Updelta z\right)/\varPhi\left(\omega,0,0\right)\) can be represented by a function depending on a single dimensionless variable \(\left(\omega \Updelta z/U_c\right),\) with U c a characteristic convection velocity of the pressure fluctuations.
A model for the coherence length (Eq. 5) is based on its definition in Eq. 3 and the expression for the pressure cross-spectrum in Eq. 4. It is often referred to as Corcos model.
Amiet (1976) suggests a value of α1 = 1/2.1, while later literature suggests a value of α1 = 0.77 for an estimation of the spanwise coherence length, but slightly different values have been reported (Graham 1997). An extension of the model to low frequencies has been proposed by Efimtsov (1982).
In principle, the coherence length can be obtained on the basis of its definition in Eq. 3 by numerical integration. Due to convergence issues also observed by Christophe (2011) for LES data and a finite observation period, the coherence does not approach zero for large separations \(\Updelta z\) and therefore, the integral in Eq. 3 is unbounded. Instead, a curve fitting approach based on an exponential function has been used by Palumbo (2012) as a more robust approach in the case of limited time series. The fit is performed for each discrete frequency and assumes the form in Eq. 6, which is consistent with the form of the pressure cross-spectrum in Eq. 4.
2.3 Pressure evaluation from PIV
In incompressible flows, the pressure field can be determined from time-resolved velocity field measurements as discussed extensively in de Kat and van Oudheusden (2012). The method invokes the use of the momentum equation further reformulated in the form of the Poisson equation. Knowledge of the pressure gradient and of the value of the pressure on the boundary of the measurement domain is required at every time instant in order to close the problem. In the past, even planar PIV data has been used as basis for pressure reconstruction approaches, however, it was demonstrated that three-dimensional measurements enable a more accurate evaluation of the pressure gradient (de Kat and van Oudheusden 2012), when compared to planar input data. In most cases, the pressure reconstruction technique is based on a form of the momentum equation. For incompressible flow the momentum equations reduce to Eq. 7, where u is the velocity vector.
For time-resolved data, the material derivative, can be evaluated by means of a Lagrangian computational approach as proposed by Liu and Katz (2006). Violato et al. (2011) have shown that, when dealing with convection dominated flows such as in wakes and boundary layers, the Lagrangian approach yields more accurate estimates of the material derivative when compared to the Eulerian scheme.
In the present study, the material derivative is estimated using a new method based on a least squares fit of the velocities along a reconstructed particle trajectory. Starting at time t 0 an estimate of the particle location at \(t_{\pm i}=\pm i \Updelta t + t_0\) for \(i=1\ldots M\) is obtained through the following recurrence relation:
Assuming a constant acceleration over the evaluation time, the components of the material acceleration vector Du j /Dt, corresponding to the velocity components u j , are related to the time differences \(\Updelta t_i = \left(t_i-t_0\right)\) and the velocity differences \(\Updelta u_j(\Updelta t_i) = u_j({\bf x}(t_i),t_i)-u_j({\bf x}(t_0),t_0)\) as follows:
Here, \(\Updelta {\bf t}=\left[\Updelta t_{-M} \Updelta t_{-M+1} \ldots \Updelta t_{M} \right]^T\) with M the number of forward and backward steps used for the reconstruction of the particle trajectory, and similarly \(\Updelta {\bf u_j}\) for the velocity differences. An approximation of the acceleration component \(\widehat{D u_j/D t}\) is subsequently obtained through the Least Squares estimate:
Application of the continuity equation for incompressible flow leads to a cancelation of the viscous terms and to a form of the Poisson equation 11.
The above Poisson equation is discretized using a second order accurate central difference scheme on the regular grid of velocity vector data obtained from tomographic PIV measurements and the resulting system of linear equations is solved by a pre-conditioned iterative method (GMRES). Ragni et al. (2011) applied this approach based on phase-locked stereoscopic PIV measurements in a volume.
In the present work, the component of the gradient normal to the boundary surface (Neumann boundary condition) is derived from the momentum Eq. 7 and applied on all boundary surfaces but the one closest to the free stream, where the value for the pressure is prescribed (Dirichlet boundary condition). Figure 1 shows a schematic of the reconstruction domain, where D and N denote Dirichlet and Neumann boundary conditions, respectively. The evaluation of the velocity in close proximity of the wall is affected by increasing noise level due to the combined effect of the interrogation volume overlapping with the wall and the large rate of shear. Therefore, an artificial interface is introduced at y/δ > 0 at which the pressure is computed. The analysis conducted on the DNS data shows that this procedure does not affect significantly the results of the surface pressure fluctuations for the range of frequencies considered to be well measured.
In the framework of pressure reconstruction, de Kat (2012) has proposed Dirichlet boundary conditions based on an extended version of the Bernoulli equation, corrected for an unsteady advective perturbation. Following this approach, the Dirichlet boundary conditions in form of the unsteady pressure fluctuations p′ are expressed through a Reynolds decomposition of the velocity field \({\bf u}=\overline{{\bf u}}+{\bf u}'\) as:
Ghaemi et al. (2012) suggests that also constant boundary conditions can be imposed at y/δ > 0.5 without greatly influencing the pressure fluctuations close to the wall within a certain frequency range, indicating that the local structure of the flow field dominates the pressure fluctuations away from this boundary.
3 Experimental set-up
Planar and time-resolved tomographic PIV experiments are performed on a flat plate of 60 cm chord, wetted span 40 cm, and 10 mm thickness in a low speed wind tunnel facility (W-Tunnel) at Delft University of Technology. The leading edge is formed elliptically, while it terminates in a sharp trailing edge at a surface angle of 2.4° with respect to the free stream. The boundary layer is tripped 10 cm downstream of the leading edge using a 5 mm wide strip with 3D roughness elements of 0.84 mm nominal grain size.
The measurement volume is located at the center of the span 43.5 cm downstream of the leading edge on the flat section of the plate. At a free stream velocity of \(u_\infty=10\,\hbox{m}/\hbox{s}\) the Reynolds number based on the local boundary layer thickness δ = 9.4 mm is Re δ≈ 6,240 and that based on the momentum thickness is Re θ≈ 730.
3.1 Planar PIV measurements
The characterization of the boundary layer is performed with planar PIV as it is possible to measure the flow statistics over its entire thickness. A single LaVision HighSpeedStar CMOS camera (1,024 × 1,024 px2, 12 bit, pixel pitch 20 μm) equipped with a Nikon Micro-Nikkor 105 mm prime lens records images taken over a field of view (FOV) of 58 × 58 mm2. The numerical aperture is set to f # = 2.8 to maximize the amount of collected light. At such a value of the numerical aperture the particle image diameter is lower than 1 px at the plane of focus, which would lead to large bias errors. Therefore, the plane of focus is slightly shifted away from the illumination plane leading to defocused particle images encompassing approximately 2 pixels. The boundary layer is illuminated from behind the plate, which strongly reduces light reflections from the wall. A light sheet of approximately 2 mm thickness is formed in the field of view. Illumination is provided by a Quantronix Darwin Duo Nd:YLF laser (2 × 25 mJ/pulse at 1 kHz). The tracer particles seeding the flow are water-glycol droplets of mean diameter 1μm.
With a magnification M = 0.37 one pixel is equivalent to 54 μm in the object plane. The recording comprises 4,500 image pairs at 125 Hz. The pulse separation is set to dt = 80 μs, corresponding to a displacement of approximately 0.8 mm (15 px) in the free stream. The illumination and imaging system are synchronized with a LaVision High-Speed-Synchronizer controlled by their DAVIS 8 software. The latter is also used for the image pre-processing and interrogation.
An iterative, multigrid correlation with window deformation procedure 75 % overlap yields velocity vectors on a grid with a pitch of 0.16 mm (4 px). For the correlation procedure, the wall region is masked and for the final pass elongated Gaussian weighted windows are used with an aspect ratio of 4:1, resulting in a rectangular window size of approximately 1.5 × 0.37 mm2 (28 × 7 px2). Effects of Gaussian weighting and other weighting functions have been theoretically investigated and reported by Astarita (2007). The main advantage of Gaussian compared to top hat weighting is the reduction in random errors due to signal truncation at the edges. Table 1 gives an overview of the parameters for the planar PIV experiment.
3.2 Tomographic PIV
Four LaVision HighSpeedStar CMOS cameras equipped with Nikon Micro-Nikkor 105 mm prime lenses are arranged as indicated in Fig. 2 and their optical axes deviates from the surface normal by an angle of approximately 25° in the y–z plane and 15° in the x–y plane. The numerical aperture is adjusted to f # = 11 for the tomographic experiments. Scheimpflug adapters adjust the lens plane such that the measurement median plane is parallel to the focal plane. To maximize the scattered light intensity, a multi-pass light amplification system consisting of an arrangement of two mirrors and knife-edges is used (Schröder et al. 2008; Ghaemi and Scarano 2010) and illumination is provided by a Quantronix Darwin Duo Nd:YLF laser. Figure 2a shows a photograph of the experimental apparatus as installed and Fig. 2b shows a schematic for clarity.
At an average magnification of M = 0.45 the voxel size in the object space is 42.3 μm. The image sequence is recorded at a frequency f = 10 kHz and the resulting particle displacement in the free stream is approximately u ∞/f≈ 1 mm (24 voxels, vxl). The region of interest (ROI) of the CMOS cameras is halved at this framing rate and the active sensor size is 512 × 1,024 px2. On average the particle image diameter is d τ = 1.8 px (standard deviation 0.4 px) and the seeding density is 0.07 ppp (particles per pixel).
LaVision DAVIS 8 is used for volume self-calibration (Wieneke 2008) and the MART algorithm is applied for iterative reconstruction (Elsinga et al. 2006) over a domain of 19.7 × 4.2 × 41.3 mm3. To obtain the vector field, the sequence of objects is analyzed with a volume deformation iterative multigrid technique with a final interrogation volume size of 32 × 16 × 32 vxl3 at 75 % overlap resulting in vector spacing of 0.16 mm along the wall-normal and 0.33 mm in the other coordinate directions. The high-speed acquisition allows to strengthen the correlation signal by a short-time sliding-average correlation technique, whereby the interrogation kernel encompasses four subsequent objects (three object pairs), and has recently been compared to other approaches for multi-frame interrogation (Sciacchitano et al. 2012). The no-slip condition at the wall is imposed by setting to zero the velocity vectors at or below the position of the wall during the iterative correlation process. This condition has been shown to stabilize the interrogation and reduces the number of spurious vectors (Theunissen et al. 2008). The normalized time step and measurement frequency are \(\Updelta t u_\infty/\delta=0.011\) and \(f \delta/u_\infty=9.4 \quad (\omega \delta^\star / u_\infty=9.4)\), respectively. Table 2 Footnote 1 gives an overview of the parameters for the tomographic PIV experiment.
3.3 Surface pressure fluctuations
The fluctuating pressure at the surface of the plate is measured at a single point within the measurement volume using a Sonion 8010T condenser microphone. Sensitivity charts provided by the manufacturer specify the response of this microphone to be constant between 300 Hz and 7 kHz with equivalent noise levels of about 15 dB sound pressure level (equivalent to approximately p rms = 100 μPa). The sensor is installed in a cavity below a pinhole with a diameter of 200 μm. Further details on the installation are documented in (Ghaemi et al. 2012).
The microphone measurement is performed simultaneously with tomographic PIV at a frequency of 30 kHz, where the acquisition sequence was triggered through the PIV synchronization system. For the purpose of obtaining converged statistics of the wall pressure measurements, a sequence of 30 s duration is recorded.
3.4 Direct numerical simulation
A compressible DNS of a turbulent boundary layer at a Reynolds number of Re θ = 1,000 and a Mach number of Ma = 0.3 is performed. The numerical algorithm is described by Pirozzoli (2010) and Bernardini and Pirozzoli (2011). Reference length and velocity scales are the boundary layer thickness at the center of the computational domain and the free stream velocity, respectively. Data are sampled on a domain extending over L x /δ = 45 streamwise, L y /δ = 2.25 wall-normal, and L z /δ = 4.5 in span. For the purpose of the present study, the spatio-temporal resolution of the DNS data is redundant. Therefore, the data are sub-sampled with a factor two in each coordinate direction, which results in a temporal sampling of \(\Updelta t u_\infty/\delta=0.045 \quad (\omega \delta^\star/u_\infty=25.4)\) and a vector spacing of \(\Updelta x/\delta=0.033\) and \(\Updelta z/\delta=0.030\) in streamwise and spanwise direction, respectively. In wall-normal direction the sampling resolution ranges from \(\Updelta y/\delta=0.004\) near the wall to \(\Updelta y/\delta=0.1\) in the free stream. For the present study, a subset of 3,000 samples equivalent to a non-dimensional time interval of T u ∞/δ = 137 is considered.
4 Results
4.1 Characterization of boundary layer
Outer scales have been determined by trapezoidal integration based on the time-averaged velocity fields obtained from planar PIV and the solution of the DNS. For the simulation, the friction velocity \(u_\tau/u_\infty\) is determined based on a linear fit in the inner region of the boundary layer. Instead, for the experiment, where this information is not accessible, the friction velocity is determined based on a fit in the logarithmic region (Clauser 1956) with constants κ = 0.4 and B = 4.0 (Buschmann and Gad-el-Hak 2003), which are likely to apply at low Reynolds number (Re θ = 730) and also confirmed by the DNS results. Figure 3 shows the mean velocity data scaled based on the constants determined with the procedures outlined above. Table 4 lists the parameters of the turbulent boundary layer at the measurement location and Table 5 provides a comparison of the dimensionless parameters relevant to both experiment and simulation.
In the experiment, a shape factor of \(H=\delta^\star/\theta=1.45\) confirms the presence of a fully developed turbulent boundary layer. Average velocity profiles and components of the Reynolds stress tensor for experimental data and simulation are shown in Fig. 4 and show a good agreement. For the given choice of the measurement domain, the tomographic PIV measurement encompasses only the lower half of the boundary layer.
The tomographic PIV data exhibit slight deviations within 3 % of the free stream velocity. The distributions of the normal components of the Reynolds stress tensor is shown in Fig. 4b. The two measurements agree very well with the DNS data in the outer region. Approaching the wall, the streamwise velocity fluctuations measured with planar PIV overestimate the maximum given by the DNS. Instead, the tomographic data show a lower value of the peak, which is ascribed to the averaging effect of the interrogation volume.
As an indication for the outer time scale the eddy turn over time is estimated with \(\delta/u_\infty \approx\) 1ms or a non-dimensional frequency of \(\omega \delta^\star/u_\infty\) = 1. Inner time scales correspond to δν/u τ = 56 μs or \(\omega \delta^\star/u_\infty\) = 18. The acquisition frequency of 10kHz therefore appears to be sufficient for resolution of the outer time scale, but not the inner one. The ratio of inner and outer time scales Re T = 16.8 is required as parameter in the model of Goody (2004) for the wall pressure spectrum. In the remainder of this study \(\delta^\star/u_\infty\) and \(\delta^\star\) are used as outer time and length scale, respectively, while δν/u τ and δν = ν/u τ are used as inner scales.
As illustrated with the Poisson equation, the velocity field turbulent fluctuations are profoundly linked to pressure fluctuations. The spatial organization of the turbulent velocity fluctuations is compared qualitatively by means of snapshot visualization (Fig. 5). The salient features of the turbulent boundary layer are represented by means of the streamwise velocity component iso-surface (\(u/u_\infty\) = 0.6) that return the organization of the flow into streamwise aligned low- and high-speed regions (Fig. 5a, c). The spacing between regions of low and high-speed velocity in the inner region of the boundary layer, about half the spanwise distance between two velocity iso-surfaces, is on the order of 100 viscous lengths δν = ν/u τ≈ 2.9 mm, typical for Reynolds numbers Re θ ≤ 6,000 (Robinson 1991). Pirozzoli (2012) has investigated the size of the energy-containing eddies in the outer turbulent wall layer and found a typical integral length scale of 0.3δ for the streamwise velocity fluctuations. Examination of the instantaneous pressure coefficient in a plane parallel to the wall shows slightly spanwise elongated patches of low and high pressure on the same order of magnitude for simulation and experiment (Fig. 5b, d).
4.2 Velocity spectrum and coherence
The spectral energy distribution and the coherence are first examined for the streamwise and wall-normal velocity components. For this comparison, data are sampled in a plane parallel to the surface at y/δ = 0.1. Figure 6 depicts the average power spectral density of the velocity fluctuations. Note that streamwise velocity fluctuations show a higher energy content at lower frequency, likely caused by streamwise coherent regions of low speed fluid protruding from the viscous sublayer into the upper regions of the boundary layer. On the other hand, wall-normal velocity fluctuations are associated with ejection and sweep events of smaller extent (Robinson 1991). In the experiment, for both velocity components the spectra start to level off at \(\omega \delta^\star/u_\infty=2.5\) and converge to a plateau at approximately \(\varPhi u_\infty/\delta^\star=3\cdot 10^{-5}\) for higher frequencies, indicating the threshold for random errors. Assuming the random error to be uniformly distributed over the measured frequency range at this level, this is equivalent to fluctuations of 0.1 m/s or an error of roughly 0.2vxl.
This difference between streamwise and wall-normal velocity components is emphasized when examining the coherence of the streamwise and wall-normal fluctuating velocity components in Figs. 7 and 8, respectively: The streamwise velocity component exhibits a larger streamwise coherence at low frequencies when compared to the wall-normal component in Figs. 7a and 8a. For frequencies \(\omega \delta^\star / u_\infty \lesssim 1.5\) the streamwise coherence of the streamwise velocity component compare well for experimental data and the DNS solution, while the comparison for the wall-normal component is less favorable. The more pronounced loss in coherence of the latter might be explained with the arrangement of the measurement volume, which implies an unfavorable condition for the measurement of the wall-normal velocity component, and therefore, a larger random error. The hatched area indicates the frequency range exceeding 2.5 kHz which was identified in Fig. 6 as dominated by measurement noise.
Further note the large difference in the length scale between streamwise and spanwise velocity fluctuations. For separations equal to the displacement thickness \(\delta^\star\) and frequencies \(\omega \delta^\star / u_\infty \lesssim 1\) both velocity components show a streamwise coherence greater than 0.4. The spanwise coherence falls below this value within approximately half of the distance, which approaches the resolution of PIV in this case.
The limitations in the experimental determination of the velocity coherence presented in this section might be regarded as upper bounds for the estimation of the pressure coherence. Both, maximum frequency and spatial resolution define these bounds.
4.3 Point pressure frequency spectrum
The pressure in the measurement domain is reconstructed following the methodology presented Sect. 2.3 with convection correction Bernoulli boundary conditions (Eq. 12) and compared to the fluctuating wall pressure measured by the pinhole microphone. Note that the artificial interface for the reconstruction process is located at y/δ = 0.07. The power spectral density based on the PIV data is estimated with a window averaging procedure (Welch 1967) with windows of 96 samples and an overlap of 50 % and applying the Hamming window function to each segment. The same procedure is applied to the DNS data (windows of 192 samples) and for the microphone signal (288 samples).
Random noise can influence the estimation of the power spectral density and coherence to a large extent. For the attenuation of the random noise component, a larger number of time steps should be considered in the reconstruction of the particle path and evaluation of the material derivative. Figure 9 shows the influence of this parameter on the spectral estimate and the microphone measurement for comparison. For small stencils M = 2 (4\(\Updelta t\)) random noise leads to an overestimation of the power over almost the entire measured frequency range. With increasing stencil size M = 3 (6\(\Updelta t\)) and M = 4 (8\(\Updelta t\)) the spectral estimate converges to the results obtained by the direct measurements, showing a dynamic range extending over two decades.
Since no single scaling rule leads to a collapse of boundary layer pressure spectra over the entire frequency range, two scaling rules based on inner and outer flow variables are adopted following previous works. In general, scaling based on outer variables is expected to yield a satisfactory collapse in the low frequency range, the opposite is true for higher frequencies.
Figure 10a shows a comparison of the pressure spectra scaled based on outer flow variables. The data obtained using the PIV approach (M = 4), microphone measurements and the DNS solution are shown together with the data of Schewe (1983) for comparison and at y/δ = 0.1 are indicated. The solid line indicates an estimation of the spectrum provided by the model of Goody (2004) for the present data, while the dashed line indicates the modeled spectrum for the data of Schewe (1983). For the present experiment, the measured and reconstructed spectrum show a very good agreement for frequencies between \(0.8\leq \omega \delta^\star / u_\infty \leq 2.5\). Over the this frequency range also the DNS data at y/δ = 0.05 agrees well with the data at the wall. For higher and lower frequencies the reconstruction results and measurements agree within approximately 3dB. At low frequencies the PIV based spectra tend to overestimate the levels provided by the microphone, while an underestimation is observed at higher frequencies up to the range where noise starts to dominate the spectrum. A plateau corresponding to the random noise level is encountered for frequencies exceeding \(\omega \delta^\star / u_\infty \approx 3.5\) at a level of \(\varPhi u_\infty/q_\infty^2 \delta^\star = 3\cdot10^{-7}.\) Therefore, an estimate of the noise level for the fluctuating pressure is \(\tilde{p}/q_\infty=10^{-3},\) obtained by assuming a uniform noise level equal to the value at the plateau over the frequency range.
As expected, in this outer scaling representation, the collected data collapse well at lower frequencies up to \(\omega \delta^\star / u_\infty \approx 1.\) Due to the lower value for the ratio of outer and inner time scales in the experiments Re T , the spectrum starts to fall off at lower frequencies when compared to the DNS and reference data at higher Reynolds number, in line with the model.
The pressure spectrum scaled on inner flow variables in Fig. 10b is consistent with previous works as the data show an improved collapse for higher frequencies and a constant slope of ω−5 is retrieved in the high frequency range. The indicated slope of ω−1 is characteristic for the overlap range, which, however, becomes narrow for low Reynolds numbers (Goody 2004). The levels obtained from numerical data and simulation agree well over the entire frequency range, but show a discrepancy with respect to the model and measured data of Schewe (1983). The model has been calibrated based on the data of Schewe (1983) for low Reynolds numbers, and thus, the perfect agreement for this case should not be surprising. On the other hand, the lack of reference data at low Reynolds numbers might provide an explanation for the discrepancy.
4.4 Wall pressure fluctuations
For the computation of the correlation coefficient, both signals are band-pass filtered for \(0.3 \leq \omega \delta^\star / u_\infty \leq\) 3 (300 Hz ≤ f ≤ 3 kHz) and the microphone signal is sub-sampled to match the sampling frequency of the tomographic PIV system. Figure 11a shows a comparison of the time signals for a subset of the data. The cross-correlation coefficient reaches a maximum close to 0.6 (Fig. 11b).
With regard to the spatial structure of the pressure fluctuations, the averaged spatial correlation of the pressure field shows slightly spanwise elongated iso-contours (Fig. 12) for experiment and simulation, a drop of the correlation to 0.1 within approximately twice the displacement thickness for the streamwise coordinate, and negative values for larger separations. These features resemble closely the generic shape of the wall pressure correlation function reported by Bull (1967). In his later review, Bull (1996) comments that small scale structures contribute to circular contours, while large-scale fluctuations preferably contribute to spanwise elongated oval contours as observed for the instantaneous snapshots in Fig. 5b, d.
4.5 Span- and streamwise coherence of pressure
Based on the reconstructed pressure fields, the coherence defined in Eq. 2 can be evaluated by estimating cross- and auto-spectral densities. Choosing the spatial separation along the spanwise coordinate direction \(\Updelta z\) yields spanwise coherence function \(\gamma_p\left(\omega,\Updelta z\right).\) Similarly, varying the streamwise separation leads to the streamwise coherence function \(\gamma_p\left(\omega,\Updelta y\right).\)
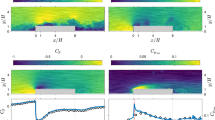
For the coherence in streamwise direction a clear difference can be observed for stencils of different length (M = 2, 3, and 4) as demonstrated by the contour plots in Fig. 13a through 13c in comparison to results obtained from the DNS solution, respectively. The size of the interrogation window used during the correlation procedure is indicated for reference (dashed line) and the hatched area indicates the frequency range not regarded to be well measured as indicated for the measured velocity spectra in Fig. 6.
In general, the coherence along the streamwise direction attains higher values at low frequency and decays beyond the resolvable scales at higher frequencies \(\omega \delta^\star/u_\infty>2.5.\) For larger stencils results compare increasingly better with the reference, indicating that random noise causes the underestimation of the coherence function for M = 2. The results for larger stencils appear to converge as also observed for the power spectra in Fig. 9 and show a very good agreement with the reference over a comparatively large frequency range \(0.5<\omega \delta^\star/u_\infty<2.5.\)
The spanwise coherence estimated based on the measurements in Fig. 13d shows a larger discrepancy by overestimating the coherence when compared to the DNS data. Moreover it barely shows a frequency dependence, with only a slow decay over the considered range of frequencies. Considering the decay of the square coherence below levels of 0.2 over the width of one interrogation volume, it has to be considered that the overestimation stems from limits imposed by the spatial resolution.
Comparison to the coherence of the wall-normal velocity component in Fig. 8 reveals similar tendencies. Coherence of pressure fluctuations over the span show a substantially faster decay compared to the streamwise direction, indicating the measurement resolution in this dimension to be a critical parameter. The data displayed in Fig. 13c, d provides the basis for data fitting to estimate the coherence lengths.
4.6 Estimation of coherence length
The estimation of the coherence length in Eq. 3 involves an integration of the pressure coherence function over its spatial coordinate. Direct integration is prone to convergence issues, since limitations in the total number of samples prevent the coherence function to converge to zero. The exponential fit discussed earlier significantly improves the robustness of the estimation. Note that the limited resolution and overlap between neighboring interrogation volumes in the correlation process of PIV provides a lower limit for the coherence since velocity vectors are correlated over the this scale.
Figure 14a demonstrates the exponential fit leading to the streamwise coherence length for two discrete frequencies, \(\omega \delta^\star/u_\infty=0.73\) and 1.47 based on the PIV data. The fitting procedure has been applied to the first 20 data points shown in the graph. Similarly, Fig. 14b demonstrates the exponential fit for the spanwise coherence. Comparison indicates the comparatively small spanwise coherence length and marginal differences between the frequencies displayed, pointing to the relative difficulty of the estimation in this dimension.
An estimation for the error \(\epsilon_\gamma\) on the coherence is evaluated through the root mean square estimator based on the fitted data points with respect to the exponential fit, under the assumption that the error is uniform all spatial separations. The error bars in Fig. 14 indicate the assumed error distribution (2\(\epsilon_\gamma\) one-sided, 95.4 % confidence level).
Based on this fitting procedure the coherence length is determined for each frequency, shown in Fig. 15a, b. Comparison confirms that the streamwise coherence length assumes substantially larger values than its spanwise counterpart for lower frequencies. The estimation obtained using the empirical models of Corcos (1964) and Efimtsov (1982), with \(\alpha_1 = 0.1 \left(0.77\right),\) is added for comparison. The horizontal line at \(l/\delta^\star=0.87\) indicates the measurement resolution of the PIV measurements.
The estimated error on the coherence function \(\epsilon_\gamma\) is assumed to be normally distributed with zero mean and propagated to the value for the coherence length \(\epsilon_l\) through a Monte Carlo simulation with 10,000 iterations. Error bars in Fig. 15 indicate the estimated error for this case (2\(\epsilon_l\) one-sided, 95.4 % confidence level).
The streamwise coherence length estimated by Corcos and Efimtsov models (Fig. 15a) starts to collapse at approximately \(\omega \delta^\star/u_\infty\) = 1.5. PIV and DNS results show a similar behavior with almost identical slope for 0.8\(\leq \omega \delta^\star/u_\infty \leq\)2, but with values of the coherence length lower than predicted by the models (\(l_x/\delta^\star=\) between 1 and 4). Note that both models rely on empirical constants and have been validated for considerably higher Reynolds numbers, which might explain the discrepancy. Interestingly, at lower frequencies, the PIV results suggest a constant or decaying value of l x , consistently with the extended model of Efimtsov. Instead, the DNS simulation indicates a increase to far larger values of l x . These discrepancies are not fully understood and need further attention and scrutiny. The current measurements and simulations yield a decaying value of l x for increasing frequency, consistent with both models.
Both predictions and measurements are more challenging in the spanwise direction. Here, the baseline value for the coherence length is significantly smaller than that in the streamwise direction (Fig. 15a). Both, the Corcos and Efimtsov models start collapsing at \(\omega \delta^\star/u_\infty>\)1. However, in the latter range, the estimate of l z is only a fraction of \(\delta^\star,\) which implies very small structures also of rather small amplitude. Estimates from PIV and DNS appear to agree with the model predictions in a fairly limited range (\(\omega\delta^\star/u_\infty<\)0.7). The spatial resolution and measurement dynamic range are considered as the main limiting factors, since the value of the estimated length converges to the value of the window size.
5 Conclusion
In the present study, information on the spatio-temporal structure of the pressure field below a turbulent boundary layer at low Reynolds numbers has been obtained using volumetric velocity fields measured by high-speed tomographic PIV. Results have been compared to reference data from literature, empirical scaling models, pinhole microphone measurements and a DNS solution for a zero pressure gradient boundary layer at similar Reynolds number.
Estimates of the wall pressure spectrum and coherence function depend on an appropriate choice of the scheme to estimate the material derivative. Small stencils lead to a large random noise component and therefore to an underestimation of the coherence function and coherence length.
The estimation of the single point pressure wall spectrum obtained using tomographic PIV compares very well with the measurement of fluctuating surface pressure obtained using pinhole microphones. Compared with the DNS solution and data available from literature, a good collapse of the data is demonstrated. This collapse is obtained for higher frequencies when scaled on inner and for lower frequencies when scaled on outer flow variables, consistent with previous results in literature. Measurement noise causes a substantial deviation from the measured wall pressure spectrum at about \(\omega \delta^\star/u_\infty>\)3.
In the case of streamwise coherence, PIV based results show a very good agreement with the reference data obtained from the DNS simulation over a comparatively large range of frequency range \(0.5<\omega \delta^\star/u_\infty<2.5.\) In contrast, the spanwise resolution of the coherence function is limited by the small spanwise coherence length relative to the measurement resolution and a consistent overestimation of the coherence function is observed.
For estimating the stream and spanwise coherence length, an exponential fit is applied. For the streamwise coherence length, results compare well with the DNS solution for a frequency range 0.8\(\leq \omega \delta^\star/u_\infty \leq\)2.5. PIV and DNS results follow similar trends when compared to the models of Corcos (1964) and Efimtsov (1982). At frequencies exceeding \(\omega \delta^\star/u_\infty=\)2.5 the estimate of the coherence length is questionable due to limits on the spatial and temporal resolution available in the experiment.
Notes
The vector spacing for PIV is one quarter the interrogation element size (overlap factor 75 %).
References
Amiet R (1976) Noise due to turbulent flow past a trailing edge. J Sound Vib 47(3):387–393
Astarita T (2007) Analysis of weighting windows for image deformation methods in PIV. Exp Fluids 43(6):859–872
Atkinson C, Coudert S, Foucaut J-M, Stanislas M, Soria J (2011) The accuracy of tomographic particle image velocimetry for measurements of a turbulent boundary layer. Exp Fluids 50(4):1031–1056
Bernardini M, Pirozzoli S (2011) Wall pressure fluctuations beneath supersonic turbulent boundary layers. Phys Fluids 23(8):085102
Brooks TF, Hodgson TH (1981) Trailing edge noise prediction from measured surface pressures. J Sound Vib 78(1):69–117
Bull MK (1967) Wall-pressure fluctuations associated with subsonic turbulent boundary layer flow. J Fluid Mech 28(4):719–754
Bull MK (1996) Wall-pressure fluctuations beneath turbulent boundary layers: some reflections on forty years of research. J Sound Vib 190(3):299–315
Buschmann MH, Gad-el-Hak M (2003) Debate concerning the mean-velocity profile of a turbulent boundary layer. AIAA J 41(4):565–572
Charonko JJ, King CV, Smith BL, Vlachos PP (2010) Assessment of pressure field calculations from particle image velocimetry measurements. Meas Sci Technol 21(10):105401
Christophe J (2011) Application of hybrid methods to high frequency aeroacoustics, PhD thesis, Université libre de Bruxelles
Clauser FH (1956) The turbulent boundary layer. Adv Appl Mech 4:1–51
Corcos GM (1964) The structure of the turbulent pressure field in boundary-layer flows. J Fluid Mech 18(3):353–378
de Kat R (2012) Instantaneous planar pressure determination from particle image velocimetry, PhD thesis, Delft University of Technology
de Kat R, van Oudheusden BW (2012) Instantaneous planar pressure determination from PIV in turbulent flow. Exp Fluids 52(5):1089–1106
Efimtsov BM (1982) Characteristics of the field of turbulent wall pressure flucuations at large Reynolds numbers. Sov Phys Acoustics 28(4):289–292
Elsinga GE, Scarano F, Wieneke B, van Oudheusden BW (2006) Tomographic particle image velocimetry. Exp Fluids 41(15):933–947
Ghaemi S, Scarano F (2010) Multi-pass light amplification for tomographic particle image velocimetry applications. Meas Sci Technol 21(12):127002
Ghaemi S, Ragni D, Scarano F (2012) PIV-based pressure fluctuations in the turbulent boundary layer. Exp Fluids 53(6):1823–1840
Goody MC (2004) Empirical spectral model of surface pressure fluctuations. AIAA J 42(9):1788–1794
Graham WR (1997) A comparison of models for the wavenumber-frequency spectrum of turbulent boundary layer pressures. J Sound Vib 206(4):541–565
Howe MS (1999) Trailing edge noise at low mach numbers. J Sound Vib 225(2):211–238
Hwang YF, Bonness WK, Hambric SA (2009) Comparison of semi-empirical models for the turbulent boundary layer wall pressure spectra. J Sound Vib 319:199–217
Koschatzky V, Moore PD, Westerweel J, Scarano F, Boersma BJ (2011) High speed PIV applied to aerodynamic noise investigation. Exp Fluids 50(4):863–876
Liu X, Katz J (2006) Instantaneous pressure and material acceleration measurements using a four-exposure PIV system. Exp Fluids 41(2):227–240
Lorenzoni V, Tuinstra M, Scarano F (2012) On the use of time-resolved particle image velocimetry for the investigation of rod-airfoil aeroacoustics. J Sound Vib 331(23):5012–5027
Morris SC (2011) Shear-layer instabilities: particle image velocimetry measurements and implications for acoustics. Ann Rev Fluid Mech 43(1):529–550
Palumbo D (2012) Determining correlation and coherence lengths in turbulent boundary layer flight data. J Sound Vib 331(16):3721–3737
Pirozzoli S (2010) Generalized conservative approximations of split convective derivative operators. J Comput Phys 229(19):7180–7190
Pirozzoli S (2012) On the size of the energy-containing eddies in the outer turbulent wall layer. J Fluid Mech 702:521–532
Ragni D, Oudheusden BW, Scarano F (2011) 3D pressure imaging of an aircraft propeller blade-tip flow by phase-locked stereoscopic PIV. Exp Fluids 52(2):463–477
Robinson S (1991) Coherent motions in the turbulent boundary layer. Ann Rev Fluid Mech 23(1):601–639
Schewe G (1983) On the structure and resolution of wall-pressure fluctuations associated with turbulent boundary-layer flow. J Fluid Mech 134:311–328
Schröder A, Geisler R, Elsinga GE, Scarano F, Dierksheide U (2008) Investigation of a turbulent spot and a tripped turbulent boundary layer flow using time-resolved tomographic PIV. Exp Fluids 44(2):305–316
Sciacchitano A, Scarano F, Wieneke BG (2012) Multi-frame pyramid correlation for time-resolved PIV. Exp Fluids 53:1087–1105
Theunissen R, Scarano F, Riethmuller ML (2008) On improvement of PIV image interrogation near stationary interfaces. Exp Fluids 45(4):557–572
Violato D, Moore P, Scarano F (2011) Lagrangian and Eulerian pressure field evaluation of rod-airfoil flow from time-resolved tomographic PIV. Exp Fluids 50(4):1057–1070
Welch P (1967) The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans Audio Electroacoustics 15(2):70–73
Wieneke B (2008) Volume self-calibration for 3D particle image velocimetry. Exp Fluids 45(4):549–556
Acknowledgments
This research is supported by the European Community’s Seventh Framework Programme (FP7/2007–2013) under the AFDAR project (Advanced Flow Diagnostics for Aeronautical Research). Grant agreement No.265695. The authors acknowledge the Italian computing center CINECA for the availability of high performance computing resources and support through the 2010-2011 ISCRA Award.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is part of the Topical Collection on Application of Laser Techniques to Fluid Mechanics 2012.
Rights and permissions
About this article
Cite this article
Pröbsting, S., Scarano, F., Bernardini, M. et al. On the estimation of wall pressure coherence using time-resolved tomographic PIV. Exp Fluids 54, 1567 (2013). https://doi.org/10.1007/s00348-013-1567-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-013-1567-6