1 Background

Since its general acceptance as a powerful measurement tool for fluid mechanics, researchers have been searching for means of increasing the dimensionality of PIV above the standard two component velocity measurement over a plane. Throughout the paper the mDnC notation will be used, where m represents the dimension of the measurement volume and n represents the dimension of the resolved displacements. As an example, two component velocity measurements over a plane are expressed as 2D2C measurements in this notation.

For three components of velocity vectors over a measurement plane, stereo PIV (SPIV) was one of the first variations in PIV methodology to be introduced. Since its first development (Arroyo and Greated 1991) through to more recent advances (Fouras et al. 2007a, 2008), SPIV has been becoming better understood, more accurate and simpler to implement. With 2D3C systems, six of the nine terms of the velocity gradient tensor are available. In order to obtain all nine terms of the velocity gradient tensor, a pseudo 3D3C system is available by conducting SPIV on two adjacent planes. Multi-plane SPIV (Schroder and Kompenhans 2004; Kahler 2004) allows for differentiation across planes to obtain those additional three spatial velocity gradients.

Holographic PIV (HPIV) (Barnhart et al. 1994; Zhang et al. 1997) allows for truly 3D3C velocity measurements. This broad range of techniques has, in its various forms, advantages and disadvantages. In-line HPIV, and more recently available Digital In-line HPIV, is perhaps the simplest and easiest to implement, but is limited by signal to noise ratio (SNR). Furthermore, there is a limit to the total number of particles that can be resolved and therefore a limited number of vectors is achievable. Off-axis HPIV, which does not have this limitation, is dramatically more complex to implement and requires considerable greater laser power. Although HPIV has demonstrated ability to accurately resolve 3D3C velocity fields, due to complexity and expense of implementation, HPIV has not enjoyed wide popularity.

An approach different to that of holography is tomographic image reconstruction. Tomographic PIV (Elsinga et al. 2006) utilises multiple cameras in different positions to image an illuminated volume. A 3D image pair is reconstructed and 3D cross-correlation analysis is performed. This technique, although recent, shows promise as an alternative 3D3C measurement tool. Unfortunately, like other techniques that reconstruct the image rather than the velocity field, this approach is also limited by the number of particles that can be resolved.

A simpler to implement, elegant technique that achieves 3D3C results is defocusing PIV (Willert and Gharib 1992; Pereira et al. 2000). This technique utilises a lens mask to alter the point spread function (PSF) of the imaging system. The mask creates a PSF that is asymmetric about the focal plane. Particles out of focus appear as triangles, which invert as they cross the focal plane. Despite the elegance and utility of this technique, this technique allows particles to be tracked throughout the illuminated volume, producing 3D3C particle tracking velocimetry (PTV). PTV is clearly distinguishable from PIV both by seeding density levels and the use of correlation functions for measurement of displacement. As a PTV variant, this technique is necessarily limited in the number of particles that can be individually identified. Furthermore, the introduction of the lens mask substantially reduces the light gathering power of the imaging system. Despite these limitations, the technique is gaining popularity and has achieved some considerable success recently (Forouhar et al. 2006). Another development similar to defocusing PIV is based on deconvolution imaging (Park and Kihm 2006). This once again allows the direct identification and measurement of particles in 3D space allowing 3D3C PTV.

As discussed, many techniques are available that have successfully resolved 3D3C vector fields. However, these techniques are typically based on the reconstruction of particle images, followed by either 3D cross-correlation or particle tracking analysis, which limits maximum spatial resolution. Furthermore, these techniques require additional or modified hardware not required for traditional PIV. This paper proposes a novel approach to gaining 3D velocity vector fields without this spatial resolution limitation. The key principle is to conduct further analysis of the calculated correlation function, of single camera PIV images, to obtain the 3D information. This results in a system that is identical to traditional PIV implementations, differing only in the analysis of images post-acquisition. The technique is based on 3D decomposition of the correlation function into various contributions at different depths.

2 Introduction

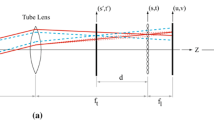
It is well understood that particle images appear differently when they are not on the focal plane. Olsen and Adrian (2000b) discuss the effect of these out-of-focus particles on the measurement of the velocity field. In micro-PIV (μPIV) systems, the entire volume is illuminated. Therefore several aspects of an out-of-focus particle contribute to the velocity measurements, such as the variation in particle image intensity and diameter as a function of distance from the focal plane. A schematic diagram of the optical and geometrical parameters including the coordinate system is shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of generic apparatus including coordinate system. The object plane (also the focal plane) is at the distance s 0 from the objective. The origin of the coordinates is the center of the object plane

Full size image

For a given particle diameter d p and a given set of magnification M, focal number f # and lens aperture diameter D a , Olsen and Adrian (2000b) derived the expression of the effective diameter and the intensity distribution of that given particle as a function of depth as seen in the image plane:

$$ d_e(z)^2 = M^2 d_p^2 + 5.95(M+1)^2\lambda^2f^{\#2} + {\frac{M^2z^2D^2_a}{(s_0 + z)^2}}, $$
(1)
$$ I(r,z)= I_0 \exp\left({\frac{-4\beta^2r^2} {d^2_e}} \right), $$
(2)

with

$$ I_0= {\frac{J_p D_a^2 \beta^2}{4\pi d^2_e (s_0+z)^2}}, $$
(3)

where λ is the wavelength of the laser, J p the flux of light emitted from the particle and β2 = 3.67 (Adrian and Yao 1985). The key assumptions are uniform particle diameter and laser intensity, isotropic light emission and that both the geometric optics term and the diffraction term can be approximated as Gaussian. To illustrate this, Eqs. (1) and (2) are represented in Fig. 2, for M = 5, f # = 1, d p  = 0.5 μm, and D a  = 9000 μm. The effect of out-of-focus particles is shown also in Fig. 3. Figure 3 shows the increase of the effective particle diameter and decrease of the peak light intensity emitted as the distance between the particle and the object plane (or focal plane) increases.

Fig. 2
figure 2

Normalised particle image intensity, and effective diameter as a function of depth, distance from focal plane z, following Eqs. (1) and (2), represented by the solid and dashed line, respectively (Olsen and Adrian 2000b)

Full size image
Fig. 3
figure 3

Example of particle images at nine different depth from the focal plane, with depth increasing from left to right, top to bottom

Full size image

Of interest, Meinhart et al. (2000a) and Olsen and Adrian (2000b) introduced the depth of correlation parameter. It defines the depth over which particles significantly contribute to the correlation function 2z corr for “simple flowfields”. This relation must be modified if the flowfield contains either significant Brownian motion (Olsen and Adrian 2000a) or out-of-plane motion (Olsen and Bourdon 2003). Here, z corr is given by:

$$ z_{\rm corr} = \left[{\frac{1-\sqrt{\varepsilon}}{\sqrt{\varepsilon}}} \left( f^{\# 2}d_p(z)^2 + {\frac{5.95(M+1)^2\lambda^2f^{\# 4}} {M^2}} \right) \right]^2, $$
(4)

where ε is the ratio of the correlation contribution of a particle of z = 0 to the correlation contribution at z. Typically, the choice of ε = 0.01 is reasonable (Olsen and Adrian 2000b). It is important to note that for cases where the PSF does not match aforementioned Eqs. (1) and (2), it has been shown (Bourdon et al. 2004) that the PSF can be readily measured experimentally.

It had previously been thought (Meinhart et al. 2000a; Olsen and Adrian 2000b) that the major problem in μPIV is the bias caused by the contribution of out-of-focus particles to the correlations. Therefore, several attempts have been made to overcome these difficulties by filtering, subtracting, and then tracking these particles. It is proposed here that the additional information provided by these out-of-focus particles should not be discarded. Instead, it provides the opportunity to resolve the displacement as a function of depth.

3 Description of new technique

The technique described in this paper is derived from an X-ray PIV method capable of measuring 3D2C velocity fields under certain flow conditions (Fouras et al. 2007b). The differences in approach and results are a direct consequence in the differences between imaging modalities. In the X-ray imaging system described in Fouras et al. (2007b), the effective depth of focus is infinite and hence no depth information is recorded.

This proposed technique is based on the proposition that at any (x,y) location, the full cross-correlation function C full of the image pairs at that location is equal to the sum of cross-correlation functions at each depth, C 2D, each with its own δ x , δ y and PSF. This can be expressed as:

$$ C_{\rm 2D}(\hat x, \hat y, z)= \alpha I_0(z)\exp\left(-{\frac{\| {\underline {\hat x}}-{\underline {\delta}} \|^2}{2\sigma(z)}}\right), $$
(5)
$$ C_{\rm full}(\hat x,\hat y)=\alpha \sum_{z=z_{\rm min}}^{z_{\rm max}}C_{\rm 2D}(\hat x, \hat y,z), $$
(6)

where σ = Md e is the effective particle diameter in the image plane measured in pixels, and z min and z max are the boundaries of the illuminated particle field.

To further assist in the description of the technique, the Couette flow is considered; that is, a uniform shear through a channel of depth h. Synthetic image pairs of particles (separated by a given δ t) within the whole channel have been generated, using Eqs. (1) and (2). The synthetic image pairs are then cross-correlated to yield the cross-correlation function.

Figure 4 shows the measured cross-correlation function, C meas, obtained for this flow viewed at a 45° angle. The coordinates in the cross-correlation space are \(\hat x\) and \(\hat y.\) It can be seen that the pattern is not representative of a Gaussian distribution, as one would expect from cross-correlation of focused particles, but is stretched along λ, the direction of the flow. Therefore, the pattern populates all the velocities occurring in the illuminated field. It is clear that if one were to take the maximum of the peak—as is done in classical PIV—the displacement obtained would be a complex function of both the velocity profile and the PSF. This justifies previous attempts of narrowing the depth of field in order to minimised this bias.

Fig. 4
figure 4

An averaged cross-correlation function for a Couette flow. The curvilinear coordinate λ represents the relationship between \(\hat x\) and \(\hat y,\)the direction of the flow. Note that for this flow λ lies on the maximum envelope of the cross-correlation peak

Full size image

In the case of Couette flow, or any other unidirectional flow, the λ coordinate can be trivially expressed with \((\hat x, \hat y).\) The aim as stated earlier in the section is to find a \(\underline{\delta}\) (z) such that \(C_{\rm full}(\hat x, \hat y)\) approaches \(C_{\rm meas}(\hat x, \hat y).\) This approach is only valid while I 0 and d e are unique for all z in the measurement volume. As Eqs. (1) and (2) are symmetric about the focal plane, this uniqueness is achieved by placing the focal plane outside the measurement volume. The ideal case is to utilise the linear region of the I 0(z) and d e (z) functions. However the maximum intensities of particles far from the focal plane also need to be considered in combination with the bit depth of the acquisition system.

This solution is implemented via a non-linear least squares solver. To achieve this, it is most convenient to express the solution δ x (z) and δ y (z) as continuous analytical functions. The choice of these functions is arbitrary but selected here are the piece-wise linear and cubic spline functions.

4 Results and discussion

The technique described in this paper has been rigorously validated by the use of a both synthetically generated image data sets and a laboratory experiment.

4.1 Validation by synthetic data sets

A uniform channel geometry, depth h = 6 μm, has been used to validate this technique. Four different flow profiles have been selected, namely a Couette flow (linear in z); Poiseuille flow (parabolic in z); separated channel flow (cubic in z); mixing-layer flow profile (hyperbolic tangent in z). Finally, a generalisation of the technique is proposed via a skewed (general) boundary layer profile.

For the sake of simplicity of explanation, these four seminal cases have been implemented with δ y  = 0. In cases such as these, where λ is a straight line (δ x and δ y are linearly related), the solution is independent of the orientation of λ. In this circumstance, λ lies on the maximum envelope of the cross-correlation function and hence is easily found.

Figure 5 shows a schematic of the geometrical configuration used as well as the coordinate system. Synthetic image pairs have been generated for particles of diameter d p  = 0.5 μm magnification, M = 5, focal number f # = 1 and aperture diameter D a  = 9,000 μm, typical of a μPIV setup. Similar results have been obtained for other μPIV optical configurations. The particles were located over the entire channel depth. As discussed earlier, to achieve optimal conditions for linearity without exceeding depth of correlation, a measurement volume spanning from z 0 = 2 to 8 μm was chosen. These pairs were successively cross-correlated then averaged and normalised. As pointed out by Meinhart et al. (2000b), averaging the cross-correlation samples overcomes problems such as insufficient seeding density and poor signal to noise ratio. Unless otherwise specified, the number samples used for each average in this study is 1,024.

Fig. 5
figure 5

Schematic diagram of the channel (depth h) including coordinate system. The object plane (also the focal plane) is at the distance s 0 from the objective, and at distance z 0 from the channel. The origin of the coordinates is the center of the object plane. The principal flow direction is out of the page

Full size image

Figure 6 shows the results of the analysis for the test cases described above. It can be seen that in all cases the solution has successfully captured the flow over the entire depth. Furthermore, these calculated velocities are obtained with a zero initial guess. While not necessary, the computational time is improved if the practitioner has a priori knowledge of the flow. However, in the case where such knowledge is not available, and for complicated topologies, the spline can be supplemented with a more robust piece-wise linear approach as a first step, followed by the more refined spline implementation. An example of this approach is demonstrated in Fig. 6c for the separated flow. Interestingly the accuracy does not vary with the magnitude of shear, as illustrated by the increasing rates of shear from Fig. 6a–d. As the functions used to evaluate the velocity data can be densely evaluated, the true resolution of these velocity measurements are only limited by the particle size, seeding density and number of image pairs utilised in the measurement.

Fig. 6
figure 6

Calculated values of the displacement δ x as a function of depth for a Couette, b Poiseuille, c separated, d mixing layer. The solid line represents the exact solution. Squares represent the knots for the spline solution (dashed lines). The separated flow example illustrates the iterative approach consisting of first a linear guess (circles and dotted line) followed by a spline scheme

Full size image

Finally the authors wish to stress that all of the above examples relate to the volumetric correlation analysis of cross-correlation peaks at a single interrogation window location. These depth resolved measurements would be available at each sampling window location throughout a PIV measurement region. Figure 7 shows both the effect of the number of samples N of the PIV interrogation window and the effect of the particle seeding density ρ on the r.m.s. of the calculated solution. Clearly, increasing the number of samples increases the accuracy of the resolved displacement field. However, even for low numbers of samples (N = 16), the results qualitatively follow the exact solution. Furthermore, it can be seen that for low N the velocity profiles is biased towards the focal plane. The effect of seeding density follows an interesting trend, which is that after significant benefit for increases in density at low values of density, a plateau is attained for a large range of seeding density.

Fig. 7
figure 7

Left effect on δ x of the number of samples N of the PIV interrogation window; N = 1024, 256, 64, 16. All solutions are obtained with a 5 knotted spline (solid squares with dashed line) with a zero initial guess. Solid line represents the exact solution. Right effect of the particle seeding density ρ on the r.m.s. of the calculated solution. Data shown are for N = 1,024

Full size image

To demonstrate the general applicability of this technique, we extended the analysis to different channel depths with their appropriate optical configuration. The objective lenses chosen are typical in μPIV as they are inexpensive and readily available.

Figure 8 demonstrates the applicability of the technique to channels of various depths. The selected range varies from a few microns depth to over a hundred microns depth. More precisely, the notion of depth is purely arbitrary, just as is the field of view in the laser plane; in a volumetric sense the field of view is selected by the practitioner through the choice of lenses, cameras, magnification tube, etc.

Fig. 8
figure 8

Parabolic profile for typical objectives and associated channel depth. Left channel from 2 to 13 μm with a 20 × 0.3 objective. Right 42–155 μm with 5 × 0.12 objective

Full size image

The final step of validation described in this section is the more general case where the velocity profile is skewed. Figure 9 shows two examples of flow geometries that would produce such skewed boundary layers. In this case δ y cannot be expressed as a simple linear function of δ x and λ is curved as can be seen in Fig. 10.

Fig. 9
figure 9

Left sketch of a skewed boundary layer caused by a cylinder. Taken from Schlichting and Gersten (2003) ©Springer-Verlag 2000. Right example of a geometry producing skewed boundary-layer (Lo Jacono et al. 2005)

Full size image
Fig. 10
figure 10

a Average cross-correlation function for the skewed boundary layer flow. The curvilinear coordinate λ represents the relationship between δ x and δ y . Note that for this flow λ does not lie on the maximum envelope of the cross-correlation peak

Full size image

Figure 11 shows the calculated values of the displacement field δ x and δ y as a function of depth for the skewed boundary layer flow. Solid lines represent exact solution. Crosses and circles represent the δ x and δ y components, respectively, using the piece-wise linear approach. It can be seen in this general case that the technique has worked to a high degree of accuracy, further validating the technique.

Fig. 11
figure 11

Calculated values of the displacement field δ x and δ y as a function of depth for the skewed boundary layer flow. Solid lines represent exact solution. Crosses and circles represent δ x and δ y component, respectively, using the piece-wise linear approach

Full size image

4.2 Experimental validation

As a final validation, this technique has been applied to the flow in a microchannel. As a preliminary step, the imaging system was characterised to avoid errors that might result from assuming a theoretical PSF. The PSF was characterised in a manner similar to that described in Bourdon et al. (2004). A thin sample of particles was traversed through the focal plane and nearby region. At each plane the auto-correlation function was evaluated throughout the image and an average auto-correlation function for each value of z was established. An increased number of averages can be achieved by taking a number of images at different positions within that z plane. A Gaussian function was then fitted to the auto-correlations, and values for intensity and half width established from the fit.

For the validation in this paper, a 5 × 0.15 NA objective was used in conjunction with a 2.5× tube lens for a total magnification of 12.5× and an overall pixel size of 0.71 μm. The normalised intensity and half-width (σ) are shown in Fig. 12. Of course the practitioner must take care that if the calibration is not performed within the same fluid medium as the measurements, a mapping of co-ordinates that takes refractive index into account must be performed. It can be seen in Fig. 12 that σ is unique (monotonic) and nearly linearly varying over a large range of z beyond approximately 20 μm. For this imaging system, maximum values of z are limited by two main factors. The most obvious is the bit depth and signal to noise ratio—specifically the ability to resolve peaks with very low intensities. The next limitation is the limitation on spatial resolution (in the xy-plane) that is a function of the peak size and the necessary increase in sampling window size that also results from a very large particle image.

Fig. 12
figure 12

a Normalised particle image intensity and correlation half width as a function of distance from the focal plane, b Values of streamwise flow velocity for on the centerline of the microchannel for Reynolds number of 0.7. Circles represent nine separate measurements made by scanning micro PIV. Squares and associated 100 point spline shown as dashed line represent the volumetric correlation measurements. Spline knots at the wall have been fixed using the non-slip boundary condition. The solid line represents the expected parabolic flow profile. The lines are in near-perfect superposition from the near wall to the centerline of the micro-channel

Full size image

The channel used had a nominally elliptical cross section with a 10:1 aspect ratio and a depth at the centerline of 112 μm. The working fluid was a 45:55 water/glycerol mixture of refractive index 1.40 and was seeded with 3 μm fluorescent microspheres. Illumination was achieved with a double pulsed Nd:YAG and images were achieved with the standard epi-fluorescent imaging mode. The Reynolds number based on maximum flow velocity and channel depth was approximately 0.7. On the centerline of the ellipse this flow is expected to be parabolic in profile.

The same spline approach used for the synthetic data was used in this case also. The only modification for laboratory data was due to a reduction in seeding density near to the walls. The approach was adjusted by simply not including data within 1.5 particle diameters from both walls. The near wall of the channel was positioned 34 μm from the focal plane. Due to the refractive index of the working fluid, the effective region of the calibration used was from 34 to 114 μm. A sequence of 200 image pairs was acquired and analysed as described in Sect. 3. The resultant flow field (expressed as δ x vs. depth position) at one sampling window location on the centerline of the microchannel can be seen in Fig. 12b.

While there is some deficit towards the far wall, the technique has accurately captured the details of the flow. A nearly parabolic flow profile has been measured and the maximum flow that agrees well with the expected flow profile and also with the scanning μPIV. The flow is an almost perfect match with the expected values for the first half of the channel, but errors appear to increase with distance from the near wall. A number of explanations for this increase in error are available. While there is no technical limit to the use of low intensity peaks far from the near wall, these peaks have to compete with background noise and limits on camera bit depth. Additionally, the nearly linear increase in σ with depth means that there is a reduction in relative differentiation of σ levels as z increases. These matters are the subject of further investigation, as are approaches to the improvement of accuracy over the entire range of z values. There is also excellent agreement between the 100 measurement points on the volumetric PIV spline taken from a single measurement and the 9 points of scanning μPIV taken from 9 separate measurements.

5 Conclusions

A method has been proposed that allows 3D2C measurements to be made in any volume illuminated by a light sheet of finite thickness. The method is based on the decomposition of the cross-correlation function into various contributions at different depths in the light sheet. This technique does not suffer from many of the limitations of other techniques designed to improve the dimensionality of PIV. A number of examples of the viability of this technique have been demonstrated by use of synthetic images which simulate micro-PIV experiments. These examples vary from trivial cases of linear variation of one velocity component over depth to a general case where both velocity components vary by different complex functions over depth. This technique has also been validated through implementation in a laboratory experiment where the flow in a 112 μm channel has been measured. This technique could be implemented in both macro- and micro-PIV experiments. Furthermore, this technique could be expanded by the use of a second camera and performed in stereo to yield fully 3D3C velocity vector field data with only two cameras. Alternatively in wall bounded flows, by using the continuity equation, one can recover out-of-plane velocity to achieve 3D3C measurements.