A simple calibration technique for stereoscopic particle image velocimetry

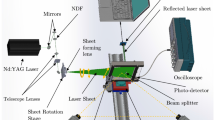
Abstract

A novel Stereo PIV technique, with improvements over other techniques, is presented. The key feature of the new technique is the direct measurement of calibration data at each point in space on the measurement grid, so that no interpolation is necessary. This is achieved through the use of a contiguous target which can be analysed using standard PIV processing software. The technique results in three-dimensional measurements of high accuracy with a significantly simpler calibration phase. This has the benefit of improving ease of use and reducing the time taken to obtain data. Thorough error analysis shows that while previously-described error trends are correct, additional facets of the technique can be optimised to allow highly accurate results. The new technique is rigorously validated here using pure translation and rotation test cases. Finally, the technique is used to measure a complex swirling flow within a cylindrical vessel.

1 Introduction

Stereo particle image velocimetry (SPIV) is now a well-established extension of traditional particle image velocimetry (PIV) (Arroyo and Greated 1991; Willert 1997; Prasad 2000). SPIV offers several advantages over standard or planar PIV in cases where measured flow fields are three-dimensional. These advantages include the improved accuracy of in-plane components of the velocity field due to removal of perspective error and the resolution of the out-of-plane components themselves. Recent extensions of SPIV include three-dimensional high speed scanning (Hori and Sakakibara 2004), dual-time SPIV for acceleration measurement (Perret et al. 2006), multi-plane SPIV (Schroder and Kompenhans 2004), and stereoscopic micro-PIV (Lindken 2006).

SPIV involves the reconstruction of a three-component velocity field in a two-dimensional plane using two velocity fields derived using PIV. This reconstruction process relies on both simple geometrical equations utilising basic information about the camera setup, and a complicated calibration step to relate information acquired on the image plane to events occurring in the object plane. The techniques, by which the inevitable distortion of the measurement field is taken into account and the two two-dimensional vector fields are reconstructed into a single three-dimensional vector field, can be categorised as two-dimensional calibration-based reconstruction, three-dimensional calibration-based reconstruction and geometric reconstruction (Prasad 2000).

Geometric reconstruction mathematically relates the parameters of image acquisition and the measured two-dimensional velocity fields through ray tracing to the derived three-dimensional vector field (Prasad and Adrian 1993). It has been argued that as parameters become more complex, the process of geometric reconstruction becomes exponentially more difficult.

Two-dimensional calibration is similar to geometric reconstruction in that it uses information relating to imaging parameters to perform the reconstruction. It differs in that the distortion field is derived from the calibration process, rather than calculating distortion directly from the imaging parameters. In this way, the correction for distortion and the reconstruction are separated into two distinct processes.

Three-dimensional calibration based techniques, such as those described by Soloff et al. (1997), are more commonly used than two-dimensional calibration. The main advantage of three-dimensional calibration is that no information regarding the geometric parameters of the stereoscopic image acquisition are required. Instead, a direct mapping function is derived between an object in three-dimensional space and its corresponding location in the image planes. The three-dimensional methods are similar to two-dimensional calibration techniques in that the distortion is corrected for by a calibration in the imaging plane. The difference lies in that they also involve calibration from the object plane to a number of parallel planes near the imaging plane. This additional information frees the technique from the requirement of information relating to the imaging geometry as this information is inferred in the additional calibrations (Prasad 2000; Prasad and Adrian 1993; Raffel et al. 1998; Soloff et al. 1997).

An interesting idea, central to the theme of this paper, was developed in Willert (1997) and further in Wieneke (2005). This idea is to utilise the cross correlation of the particle images to generate additional information regarding the relative camera positions and image deformations. This has the advantage of correcting for the errors caused by misalignment of the calibration target and the laser sheet. The disadvantages of this approach include further complication of the technique. Furthermore, any differences in image distortions caused by different camera positions will result in degradation of correlation between images. Wieneke (2005) tackle this problem by de-warping the images prior to this step, but this adds further complexity and computational effort.

Almost all two-dimensional and three-dimensional calibration techniques utilise a calibration target, which consists of a discrete number of markers displaced on a regular Cartesian grid (Lawson and Wu 1997b). Typically these targets contain in the order of 100 such markers, i.e. approximately a 10 × 10 grid. The authors believe that it is this limited approach that has largely dictated much of the development of these techniques. The images of the target are compared to the known positional layout of the target and the relative positions of all markers on the calibration target. The exact method of this varies depending on the PIV software being utilised but is largely based on the PIV algorithms themselves. For some software this even requires the practitioner to manually identify markers in an image and link them to a corresponding marker on the target. The uncertainty in identifying the position of these markers by use of PIV software is proportional to the size of these markers. The calibration data are then fitted by a method such as least squares fitting, (both linear and non-linear are used), to obtain general data applicable to the entire measurement region. The dependency of calibration techniques on precise knowledge of the target geometry introduces measurement error and further complicates the SPIV procedure.

2 New technique

The new calibration technique described in this paper is based on the same principles as previous two-dimensional calibration techniques but differs considerably in implementation. The main improvement offered by the new technique is that interpolation is not necessary at any stage of the calibration and reconstruction process. In other words, the calibration is performed on a 1:1 basis: each resultant three-dimensional vector is calculated in object space. Each pair of two-dimensional vectors is similarly interrogated from a region in object space that is determined by a process similar to calibration. Lawson and Wu (1997b) also used a contiguous target to obtain information for calibration purposes, but did not use their cross correlated results to directly obtain calibration vectors at each PIV window location.

A schematic diagram of the configuration and co-ordinate system used in this paper is shown in Fig. 1. A flow chart of the entire procedure is shown in Fig. 2. Unlike most two-dimensional calibration techniques, much of the analysis is completed using standard PIV interrogation, and the final reconstruction is a relatively simple process.

Fig. 1

Schematic diagram of generic stereo PIV configuration including the co-ordinate systems used in this paper. Shown on the figure are the X,Y and Z axes. The origin of the coordinate system is the point on the laser sheet plane center in the center of the imaged region of interest. Here an example of two cameras, denoted left (L) and right (R) for simplicity are shown. Also shown is the Scheimpflug configuration and the definition of the camera angles β_L, β_R and camera positions X _L, Z _L and X _R, Z _r. Also shown is the paraxial camera in its fixed position with β = 0

Fig. 2

Description of the new technique to yield three-dimensional vector fields using the analysis of target and flow images. Rhomboids represent input or output and rectangles represent processes. The five sets of input images are included. Also shown is the direct process resulting from the 1:1 mapping achieved by interrogating a contiguous target

A significant difference in methodology between the new technique and other two-dimensional calibration techniques is that a contiguous calibration target is utilised rather than a regular grid. Instead of comparing the target images with a priori knowledge, the target image is digitally compared with a second image acquired through paraxial imaging. This combination of a contiguous target and a reference paraxial calibration target image allows calibration data to be measured by any PIV interrogation software.

One example of a contiguous calibration target that can be successfully used for this technique is a sandblasted glass plate. The distortion of the random surface pattern produced by sandblasting is better correlated by typical PIV analysis software than a regular pattern. Indeed, sandblasted surface patterns have been used successfully in other distortion measurement imaging techniques involving cross correlation (Fouras et al. 2006). In that case, it was shown that sandblasted glass gave a remarkably high level of information, allowing very high resolution correlation measurements. Ideally, the reference plate is positioned in the camera field of view so that the test pattern aligns in such a way as to represent an artificial laser-illuminated particle field, i.e. at the same angle to the camera lens as the measurement plane. Back-illumination of the plate using diffuse white light sources positioned in line with the CCD cameras helps optimise the contrast in the images, and thus improves the PIV signal to noise ratio.

If the field of view in the horizontal (X) direction is the same for the angularly displaced camera images as it is for the paraxial image, then the field of view in the vertical (Y) direction will be larger in the paraxial image. Therefore, the paraxial image must be digitally stretched in the Y direction by a factor of 1/sin (β), where β is the camera displacement angle. Alternatively, the two angled camera images may be shrunk in the Y direction. Bi-cubic interpolation is an appropriate method for stretching or shrinking these images. It is then necessary but straightforward to crop the paraxial image in the Y direction so that the images are of the same size. When superimposed onto one another, the images of the reference plate from the angled perspective and the stretched paraxial perspective appear similar to Fig. 3. In the combined image, the magnification heterogeneity across the field of view is clearly visible, as is the point where the magnifications of the two images are matched.

Fig. 3

Superimposed stretched paraxial and left camera images of a sandblasted glass plate reference pattern

By selecting the paraxial calibration target image as the first image in the interrogation process, by ensuring that only sampling windows in the displaced images are shifted during any offset interrogation processes, and by performing the PIV interrogation process with exactly the same input parameters (e.g. sampling window offset, overlap, etc.), the resulting vector fields are in fact 1:1 vector maps of the distortion caused by the angular offset.

For example, the image pair shown in Fig. 3 can be used to derive a left-to-paraxial calibration field such as that shown in two-dimensional vector form in Fig. 4a. The vectors quantify the degree to which each regularly-spaced interrogation window on the paraxial image is distorted in the left image because of the angular offset. The shaded bands represent the distortion in the Y component. Solid contour lines denote regions of positive Y distortion while dashed contour lines denote regions of negative Y distortion. The edges of Fig. 4a have the greatest magnitude of distortion, which is representative of the fact that the greatest magnification difference between the angularly displaced and paraxial images occurs in these regions. The edge of the image plane nearest to the angularly displaced camera is on the left hand side, where the vectors point away from the center. Similarly, the vectors on the right hand side of Fig. 4a point toward the center of the image, as the right edge of the image plane is the furthest from the camera. It is worth noting that an additional stretching of the X component occurs across the entire field of view as the process takes into account any mismatch between the paraxial and displaced camera fields of view.

Fig. 4

Left-to-paraxial (a) and right-to-paraxial (b) distortion calibration field in two-dimensional vector form for β = 45°. The contour levels represent vertical (Y) distortion

A right-to-paraxial calibration vector field, corresponding to the same example, is presented in Fig. 4b. In this case, the near edge of the field of view is on the right hand side of the right camera image, and the far edge is on the left hand side. Theoretically, the expectation is that this calibration field should resemble a Y-axis reflection of the left-to-paraxial calibration field. While this is approximately the case, in reality there are subtle differences between the two fields caused by slight discrepancies in camera positioning and magnification. Herein lies a demonstration of one of the advantages of the improved calibration technique; that is, by measuring the distortions directly, the positional and magnification imprecision associated with the angularly displaced cameras is compensated for automatically.

When the PIV interrogation is performed to determine the two two-dimensional vector flow fields, the base position of each flow vector is offset by the corresponding vector at the same location on the calibration vector field. This results in all measurements being performed on the same grid in real space. Moreover, an added benefit is obtained whereby the distortion field can be differentiated to yield local magnification data, allowing velocity vectors to be corrected to this additional error of perspective. This differentiation can be performed to high accuracy using any advanced numerical differentiation technique, such as that described by Fouras and Soria (1998). This leaves just the straightforward, well-documented step of reconstructing the three-component vectors from matching pairs of two-component vectors measured at that same location (Lawson and Wu 1997a).

3 Error analysis

The equations for geometric reconstruction are simply derived using similar triangles or parametric equations. For the current analysis, we define the two cameras as camera A and B, with position co-ordinates (X _a , Y _a , Z _a ) and (X _b , Y _b , Z _b ), respectively. As the two cameras are typically positioned on the horizontal plane, Y _a and Y _b are assumed to be zero. The projected displacement vectors on camera A and B are also needed to derive the stereoscopic velocity field. We define these as ${\hat{x}_a, \hat{y}_a}$ and ${\hat{x}_b, \hat{y}_b},$ respectively.

The solution to the equations is defined as the reconstructed vector R with components Δx,Δy, and Δz. The solution for Δy is over-constrained and can be acquired just as easily in two different ways. Usually the average of the two solutions is used. The solutions for Δx and Δz are much more interesting than Δy and discussion here is limited to these components:

$$ \begin{aligned} \Delta x &= ((\hat{x}_a - X_a) \hat{x}_b Z_b + (\hat{x}_b - X_b) \hat{x}_a Z_a) / D_{1},\\ \Delta z &= (\hat{x}_a - \hat{x}_b)Z_a Z_b / D_{1}, \end{aligned} $$

(1)

where

$$D_{1} = (\hat{x}_a-X_a)Z_b + (\hat{x}_b-X_b)Z_a.$$

To calculate sensitivity of R to errors in the underlying PIV, we calculate ${{\bf R}^{\prime}(\hat{x}_{a}^{\prime}, \hat{x}_{b}^{\prime})}$ by substituting the following expressions into Eq. 1:

$$ \begin{aligned} \hat{x}_{a}^{\prime} &= \hat{x}_a + \varepsilon_{\hat{x}a},\\ \hat{x}_{b}^{\prime} &= \hat{x}_b + \varepsilon_{\hat{x}b}, \end{aligned} $$

(2)

where ${ \varepsilon_{\hat{x}a}}$ and ${\varepsilon_{\hat{x}b}}$ represent the errors in measuring the projected displacement vector.

We can then define ε as R′ − R or

$$ \begin{aligned} \varepsilon_x = & R_{x}^{\prime} - R_x,\\ \varepsilon_z = & R_{z}^{\prime} - R_z. \end{aligned} $$

(3)

To then simplify Eq. 3, we make the assumption that ${X_a, X_b, Z_a, Z_b, \hat{x}_a, \hat{x}_b > > \varepsilon_{\hat{x}a}, \varepsilon_{\hat{x}b}}.$ Using this assumption, we expand terms in Eq. 3 and then remove terms of least significance. This produces the equations:

$$ \begin{aligned} \varepsilon_x &= (\varepsilon_{\hat{x}a} X_b Z_a - \varepsilon_{\hat{x}b} X_a Z_b) / D_{4},\\ \varepsilon_z &= ((\varepsilon_{\hat{x}b} - \varepsilon_{\hat{x}a}) Z_a Z_b) / D_{4}, \end{aligned} $$

(4)

where

$$D_{4} = (X_b Z_a - X_a Z_b).$$

We define σ _x , σ _z , σ _a , σ _b to be the standard deviations of the random variables ${\varepsilon_x, \varepsilon_z, \varepsilon_{\hat{x}a},\varepsilon_{\hat{x}b}}.$

Of use is the variable σ_PIV which is used to represent the expected uncertainty in the PIV processing, taking into account all the conditions and qualities of the PIV process, but with a paraxial perspective. For consistency with previous work we also define σ _p , which is almost identical to σ_PIV but is related to the direct processing error not normalised for stereo angle β.

$$\begin{aligned} \sigma_{pa} &= \sigma_{\rm PIV}/\hbox{cos}(\beta_{a}),\\ \sigma_{pb} &= \sigma_{\rm PIV}/\hbox{cos}(\beta_{b}). \end{aligned}$$

(5)

Using the definition of the standard deviation, assuming that ${\varepsilon_{\hat{x}a}, \varepsilon_{\hat{x}b}}$ are independent random variables with standard deviation σ _pa , σ _pb , and converting to polar co-ordinates for convenience, we have:

$$ \begin{aligned} \sigma_{x} &= \sigma_{\rm PIV} \sqrt{(\sin^2(\beta_a)+ \sin^2(\beta_b))/ \sin^2(\beta_b - \beta_a)},\\ \sigma_{z} &= \sigma_{\rm PIV} \sqrt{(\cos^2(\beta_a)+ \cos^2(\beta_b))/ \sin^2(\beta_b - \beta_a)}. \end{aligned}$$

(6)

It is interesting to note that the radius terms from the polar equations cancel, leaving the expression only in terms of β _a , β _b . These general equations are easily solved for any geometry and allow us to solve for optimisation of errors. In Figs. 5 and 6, we present this information over the entire circle about the measurement volume.

Fig. 5

Error in reconstructed Δx (lateral) displacements expressed relative to the expected PIV for a paraxial camera measuring a 2D flow as a function of camera angles β _a and β _b measured in degrees

Fig. 6

Error in reconstructed Δz (out-of-plane) displacements expressed relative to the expected PIV for a paraxial camera measuring a 2D flow as a function of camera angles β _a and β _b measured in degrees

For Fig. 5, there are a few interesting observations. First, the minimum error, relative to paraxial camera PIV error, is ${1/\sqrt{2}}.$ Furthermore, it is clearly preferable to use a symmetric geometry with a small stereo angle to minimise this relative error in the reconstructed Δx component.

In Fig. 6, we see a pattern of sensitivity for the Δz component similar to, albeit asymmetrically out of phase with, the Δx sensitivity. We see the same minimum sensitivity level; it occurs with a symmetric camera geometry but at camera offset angles approaching 90°, which is not unexpected.

Figure 7 shows the combined sensitivity of both Δx and Δz components of the reconstructed vector. This combination is simply calculated as half of the sum of the two components. Two key points can be derived from this figure. First, it can be seen that the minimum of the average is not in fact ${1/\sqrt{2}},$ but 1.0. While the reconstruction allows increased accuracy due to an averaging process, the regions of high accuracy are out of phase and thus are suppressed in the averaged plot. Second, we see that the measurements least sensitive to error can theoretically be achieved at any mean stereo angle, as long as the two cameras are positioned orthogonal to one another. This expands on the previously reported finding by Lawson and Wu (1997a), that the best relative sensitivity for a symmetric configuration occurs when β = ±45°. It should be remembered, however, that when β is close to ±90°, the measurements would most likely suffer from additional higher order errors and in any case at such oblique measurement angles, other practical issues will make measurements difficult.

Fig. 7

Average of both the X and Z errors in reconstructed X displacements expressed relative to the expected PIV for a paraxial camera measuring a 2D flow. Note that the minimum value is 1.0, and lies on the line of β _a − β _b = 90°

Since most practitioners use symmetric camera geometries, it is appropriate to force these conditions on the above equations. The conditions of symmetry are:

$$ \begin{aligned} \sigma_{p} &= \sigma_{pa} = \sigma_{pb},\\ X_c &= X_a = -X_b,\\ Z_c &= Z_a = Z_b. \end{aligned} $$

(7)

This time we define σ _p as the PIV error relative to an angularly displaced camera rather than to a paraxial camera. This produces the familiar result found in Prasad and Adrian (1993) and Zang and Prasad (1997) of:

$$ \begin{aligned} \sigma_x &=\, \sigma_{\rm PIV}/ \left(\sqrt{2} \cos(\beta) \right) = \sigma_p/ \sqrt{2},\\ \sigma_z &= \sigma_{\rm PIV}/ \left(\sqrt{2} \sin(\beta) \right) =\, \sigma_p / \left (\sqrt{2} \tan(\beta) \right). \end{aligned} $$

(8)

We can use a similar approach to determine the sensitivity of the new technique to the practitioner’s ability to accurately measure the positions of the cameras relative to the measurement volume. This is particularly important as a means of validating the new technique, as unlike the technique of Soloff et al. (1997), the use of geometric reconstruction depends on the measurements of camera position. The sensitivity test can be undertaken by analysing the error in the reconstruction error caused by errors in X _a , X _b , Z _a and Z _B . Solving for the equivalent of Eq. 4 yields:

$$ \begin{aligned} \varepsilon_x = & ((\varepsilon_{xa} X_b + \varepsilon_{xb} X_a) Z_a Z_b\\ & \quad -(\varepsilon_{za} Z_b + \varepsilon_{zb} Z_a) X_a X_b)/D_{9},\\ \varepsilon_z = & (\varepsilon_{xa} Z_a Z_b^2 - \varepsilon_{xb} Z_b Z_a^2 \\ & \quad -\varepsilon_{za} X_a Z_b^2 - \varepsilon_{zb} X_b Z_a^2)/D_{9},\\ \end{aligned} $$

(9)

where

$$D_{9} = (X_a^2 Z_b^2 - 2 X_a X_b Z_a Z_b + X_b^2 Z_a^2)/(\hat{x}_a - \hat{x}_b).$$

These equations can be expressed in various ways to help the practitioner establish the sensitivity of the resolved stereo vector field to the accuracy of the measurements of camera positions, as a function of those camera positions. They could also be further expressed in statistical terms and for any geometry. Once again they are expressed here only for the symmetric case with the same assumptions for symmetry as in Eq. 7. We further assume that positional errors for X _a , X _b , Z _a and Z _b are equally represented by σ _m .

$$ \sigma_x = \sigma_z = \sigma_m \sqrt{X_c^2 + Z_c^2} (\hat{x}_a-\hat{x}_b)/ (2 \sqrt{2} X_c Z_c). $$

(10)

This solution is based on the assumption that ε _xa , ε _xb , ε _za and ε _zb are independent random variables. However, this is rarely the case. Most practitioners mount both stereo cameras on some form of support structure. Let us now consider the particular case whereby the structure used constrains the cameras so that they must lie on the projected stereo angle. This means that the positional error would be sensitive to the distance from the measurement volume R and not β.

Now we use polar co-ordinates, along with symmetry conditions on the errors as well as the camera co-ordinates. This produces the straightforward but interesting result of:

$$ \sigma_x = \sigma_z = 0.$$

(11)

This result is highly significant in that it implies that, to first order accuracy, the measurement accuracy of positions is of secondary importance, so long as the mechanism for holding the cameras in place constrains the cameras to lie on the angle β.

4 Translation test

The performance of the improved two-dimensional calibration technique was tested on a precision optical table (Melles-Griot, UK). Two Pixelfly CCD cameras (PCO, Germany) of 1,360 × 1,024 pixels resolution were installed on the table in an angular displacement configuration which included individual Scheimpflug devices. This popular camera configuration has been described previously (Zang and Prasad 1997; Prasad 2000). Separate experiments were undertaken to test the ability of the new system to measure object translation and rotation. The various test cases are listed in Table 1.

Table 1 List of test cases used for the validation of calibration technique

The translation experiments were carried out using two different camera displacement angles (β), as SPIV system performance often varies with β (Lawson and Wu 1997b). Camera angles of β = 45° (Case A) and β = 30° (Case B) were chosen, as these represent typical offsets that produce significant image distortion.

The test configuration for the translation experiments is illustrated schematically in Fig. 8. For these cases, the flow field was simulated by a sheet of paper printed with a pseudo-random pattern. This paper was held stationary between glass plates and affixed to a linear traverse constructed with a 1 mm lead screw (THK, Japan) and an 18:1 geared stepper motor (Oriental Motor, Japan). Alignment of the traverse at an angle β to the cameras was maintained by screwing all apparatus to the optical table. The object was positioned for each image using a micro-stepping, stepper motor controller (National Instruments, USA).

Fig. 8

Test configuration for the translation cases. Configuration is based on a test plate mounted on a PC controlled linear traverse illuminated by twin white light sources. Also shown are symmetric CCD cameras in the standard Scheimpflug configuration

Images were recorded at 101 positions with a small known displacement between each image. This allowed a flexible system of analysis. By integrating against different pairs, different length vectors were achieved. Frame 1 was compared with frame 2 and frame 2 with 3 and so on for a data set with displacement δx. Frame 1 was compared to frame 3 and 2 with 4 for a data set with displacement 2 δx. In this manner, the complete data set was used to develop 16 reliable data sets of increasing magnitude. Since image quality and other PIV acquisition and processing parameters were held constant, PIV errors were also held constant in absolute terms. By normalising each data set by the known displacement, 16 nearly identical data sets, with varying levels of PIV accuracy, were achieved.

After resolving the two displacement vector fields onto the object plane using the calibration fields shown in Fig. 4a, b, and then applying the basic three-dimensional reconstruction equations, the resultant vector field appeared, as expected, to have a consistent horizontal (Δx) component and zero vertical (Δy) or out-of-plane (Δz) component. Figure 9 represents probability density functions of the difference, ε, between the expected displacement and the measured displacement, for Case A and Case B, respectively. ε was found to vary between each vector component, as well as between Cases A and B. For Case A, with a displacement of 15δx, the standard deviation of the error, σ _R , in the resolved Δx component was 1.33 × 10⁻³ compared to a signal of unit value, whereas the standard deviations in the remaining components, Δy and Δz, were 1.11 × 10⁻³ and 1.40 × 10⁻³, respectively. For Case B, with the same displacement, σ _R was 1.15 × 10⁻³ for the Δx component, 0.87 × 10⁻³ for Δy, and 1.88 × 10⁻³ for Δz. The lower σ _R values corresponding to the Δx and Δy components in Case B may be attributable to the lower optical errors occurring when β = 30° than when β = 45° (Lawson and Wu 1997b). The larger discrepancy between Δx and Δz when β = 30° than when β = 45° is also consistent with the results of Eq. 8 and previously published error analyses (Lawson and Wu 1997b; Prasad 2000).

Fig. 9

Probability density function of error ε in the measured displacement components, for (left) the β = 45° translation case (Case A) and (right) for the β = 30°, translation case (Case B). The top plot shows the Δx component, the middle plot shows the Δy component and the lower plot shows the Δz component. The displacement between frames was equal to 15δx (≈33.95 px). The figure demonstrates the relative magnitudes of reconstructed displacement errors and their Gaussian nature

Overall, the histograms of error presented in Fig. 9 demonstrate the success of the technique in measuring linear translation. The error values are relatively small compared to the signal, which has been normalised so that δx is equal to one. Furthermore, the error distribution is unskewed. Any deviation from zero of the median ε value in the Δy or Δz components appears to be due to very minor movements of the displaced paper target in the vertical or out-of-plane directions. Similarly, any deviation of the median ε value from zero of the median ε value in the Δx component may be attributable to imprecision in the mechanical translation system.

As described above, the methodology undertaken to test the SPIV technique for translation cases allowed the level of PIV accuracy to be controlled. By varying the displacement of the target between images, 16 different values of σ _p , the standard deviation of the PIV processing error, were achievable. This facilitated a comparison between the standard deviation of the reconstructed stereo error σ _R , and σ _p . In this way it was possible to verify the performance of the system on the basis of the theoretical prediction of the ratio of σ _R on σ _p (see Eq. 8).

The symbols in Fig. 10 illustrates the measured relationship between σ _R and σ _p for cases A and B, respectively. The lines in each figure represent Eq. 8. For Case A, the lines corresponding to the σ _x component and the σ _z component are co-linear, as tan (β) in Eq. 8 reduces to 1. For both β, the data show good agreement with the predicted results in both components.

Fig. 10

Reconstructed vector field standard deviation (σ _R ) as a function of PIV processing error (σ _p ), for (left) the β = 30°, translation case (Case A) and (right) the β = 45°, translation case (Case B). open circle symbols denote the standard deviation of Δz (σ _z ) while open square symbols indicate the standard deviation of Δx (σ _x ). The line represents the theoretical prediction of Eq. 8

5 Rotation test

Test Cases C and D were undertaken under pure rotational conditions, with the displacement occurring in the Z direction. As with the translation test, the first stage of the procedure involved capturing paraxial and angled perspective images of a sandblasted glass plate aligned with the image plane, in order to derive the 1:1 calibration offset vector map.

The second stage of the test procedure involved placing a sandblasted glass test block on a turntable mechanism so that the front surface was aligned with the image plane. From this position, designated as 0°, the turntable was rotated in the counter-clockwise direction to a position of 0.50°, measured using a dial gauge to an accuracy of ±0.03°. An image was recorded on each CCD camera, and then the turntable was rotated in the clockwise direction to a position of −0.5°, where another set of images was recorded. This procedure ensured that the theoretical Δx and Δy values were 0 when comparing the stereoscopic displacement fields between the two positions. The rotation angle of θ = 1.0° in Case C provided an opportunity to test the SPIV reconstruction system under conditions involving large displacements, large displacement variations, and a large out-of-plane to in-plane displacement ratio. The procedure also involved a movement of the recorded plane off the focused object plane, thus testing the sensitivity of the two-dimensional calibration technique to slight out-of-focus effects. The test was repeated for Case D with a rotation angle θ = 0.5°. The test configuration for the rotation experiments is illustrated schematically in Fig. 11.

Fig. 11

Test configuration for the rotation cases. Configuration is based on a test plate mounted on a PC controlled turntable illuminated by twin white light sources. Also shown are symmetric CCD cameras in the standard Scheimpflug configuration

As illustrated by Fig. 12, the resultant three-component vector field accurately depicts solid body rotation. The scatter-plots in Fig. 13 show only the measured Δz components, and thus clearly demonstrate the ability of the technique to measure the out-of-plane component in both directions. For both Cases C and D, the rotation angle, determined by applying a linear regression to the Δz information, was found to match the expected θ value to an accuracy well within that of the dial gauge measurement. In both cases the R ² coefficient of the Δz regression line exceeded 0.99.

Fig. 12

Reconstructed three-dimensional test case vector field for θ = 1.0° (Case C). Shading indicates Δz component magnitude

Fig. 13

Reconstructed Δz component as a function of X, for the β = 45°, rotation cases. The different shaped symbols represent the two different solid body rotation angles, as denoted by the figure legend

The probability density functions for the three components are plotted in Fig. 14 for Case C. As the signal varies with X, the measurements have not been normalised, meaning that the ε values are greater than those presented in Fig. 9. As with Fig. 9, the ε probability density function is similar for the Δx and Δz components.

Fig. 14

Probability density function of error ε in the measured displacement components, for the β = 45°, θ = 1.0 rotation case (Case C). The top plot shows the Δx component, the middle plot shows the Δy component and the lower plot shows the Δz component

6 Measurement of a rotating flow

A complex rotating flow was measured as a final demonstration of the new technique. A cylindrical container was screwed onto the turntable setup used for the solid-body rotation test, in such a way that the rotating platform fit closely to the cylinder wall but was capable of independent rotation. As illustrated schematically in Fig. 15, a column of water of height, H, equal to 1.5 times the radius of the disk, R, was added to the cylinder. The disk was rotated at constant angular velocity (ω) using the micro-stepping controller. The camera angles used were ±45°, respectively. The Reynolds number of the flow, given by Re = ωR ²/ν, where ν is the kinematic viscosity, was equal to 1,200. The flow produced in a cylinder with a free-surface by a rotating disk was first observed by Spohn et al. (1993) and has recently been used to study potential bio-reactor applications (Dusting et al. 2006). At Re = 1,200, there are strong radial, axial and azimuthal velocity components, as well as significant spatial velocity variations across the vessel. As a result, the flow provides a good demonstration of the capabilities of the new technique.

Fig. 15

Experimental setup for the rotating flow, including co-ordinate system and the measured region of interest

For the SPIV measurements, silver-coated hollow glass spheres of 12 μm diameter (Potters Industries, USA) were seeded into the working fluid and illuminated using Nd:Yag lasers (Spectra-Physics, USA). The laser light sheet was aligned vertically with the meridional plane so that the recirculation pattern in the upper portion of the vessel could be captured. Calibration was undertaken by imaging a sandblasted glass plate and processing using the new technique, as described previously. The resulting normalised three-component vector field for the Re = 1,200 case is shown in Fig. 16. For the sake of clarity, every second vector has been omitted and only the right-hand side is shown. The in-plane vector field, shown in Fig. 17, contains excellent resolution of a reversed-flow vortex breakdown bubble located near the cylinder axis of symmetry, as well as the main meridional-plane recirculation. The corresponding azimuthal velocity (v _θ) distribution is shown in Fig. 18. The predominantly azimuthal flow produces a large out-of-plane component, meaning that it is likely that the left and right camera PIV vector fields have relatively high σ _p errors. Despite this, the three-component SPIV vector field was successfully captured by performing three-component reconstruction, thus illustrating the robustness of the new technique.

Fig. 16

Three-dimensional vector field for the rotating flow

Fig. 17

Meridional plane vector field for the rotating flow

Fig. 18

Distribution of azimuthal velocity component normalised by maximum disk speed for the rotating flow

7 Conclusions

A new calibration technique for Stereo PIV has been developed. The use of a contiguous target and PIV interrogation to derive the distortion map makes the process simple to implement, as much of the geometric analysis is no longer necessary. Furthermore, no interpolation is required since a common grid is used for both the distortion analysis and the flow analysis. Importantly, the calibration process also automatically takes into account any discrepancy between the field of view on the left and right camera images, thus reducing the sensitivity to camera misalignments, lens misalignments, or magnification differences.

The new system has been tested under conditions of pure translation and pure rotation. As part of this process, the system has been tested for the case where there is significant motion in the out-of-plane direction, as well as significant motion within the image plane. The system has also been evaluated at multiple camera displacement angles. In all cases, accurate measurement of the test sample motion was obtained in Δx, Δy, and Δz. Standard deviations of less than 0.2% of the signal were consistently achieved.

A thorough error analysis of the geometric reconstruction has been performed. The measured ratios of σ _x and σ _z to σ _p agree closely with the trends predicted by Prasad and Adrian (1993). The most accurate configuration for the measurement of Δx and Δz was determined to be a symmetric camera geometry, with small camera spacing for Δx and large camera spacing for Δz. The optimal configuration for overall measurement accuracy was found to be any geometry with a relative angle of 90° between cameras. Furthermore, it was found that under certain achievable circumstances, the error due to inaccurate measurement of camera geometry was zero. The level of measurement accuracy resulting from this new, simple technique may reduce the advantage in using more complicated SPIV techniques such as three-dimensional calibration.