Holographic method for site-resolved detection of a 2D array of ultracold atoms

Abstract

We propose a novel approach to site-resolved detection of a 2D gas of ultracold atoms in an optical lattice. A near-resonant laser beam is coherently scattered by the atomic array, and after passing a lens its interference pattern is holographically recorded by superimposing it with a reference laser beam on a CCD chip. Fourier transformation of the recorded intensity pattern reconstructs the atomic distribution in the lattice with single-site resolution. The holographic detection method requires only about two hundred scattered photons per atom in order to achieve a high reconstruction fidelity of 99.9 %. Therefore, additional cooling during detection might not be necessary even for light atomic elements such as lithium. Furthermore, first investigations suggest that small aberrations of the lens can be post-corrected in imaging processing.

1 Introduction

Ultracold atoms in optical lattices allow for investigating many-body physics in a very controlled way (see e.g., [1]). For such experiments, site-resolved detection of the exact atomic distribution in the lattice can be very advantageous and it has recently been demonstrated [2–7]. In these experiments, the fluorescence of illuminated atoms is detected using a high-resolution objective. During the imaging process, typically several thousand photons are scattered per atom. This leads to strong heating of the atoms, requiring additional cooling.

Alternative imaging techniques using the diffraction of a laser beam by an atomic ensemble have been demonstrated for the detection of cold atomic clouds [8–13]. However, these techniques have not been discussed either for single-particle resolution or for single-site detection.

Here, we propose to image an atomic array with high resolution by using a variation of the off-axis holography technique of Leith and Upatnieks [13, 14]. Two coherent laser beams are used to record the hologram of an illuminated atomic array. One acts as a probe beam and is coherently scattered by the atoms [15], while the other acts as a reference beam which bypasses the atoms. Both beams are superimposed to interfere and to generate the hologram which is recorded with a charge-coupled device (CCD) camera. An algorithm based on fast Fourier transformation reconstructs an image of the atomic array. The reference beam fulfills two purposes: On the one hand, it separates the holographic image from disturbing low-spatial frequency signals in the reconstruction. On the other hand, it strongly amplifies the atomic signal, as in spatial heterodyne detection [13]. This allows the use of a weak probe beam while keeping the signal high compared to detection noise. We estimate that for our scheme the number of scattered photons per atom can be small enough ($\approx$150 photons) such that single-site detection could be realized without additional cooling. Moreover, the scheme might open the path for multi-particle detection per lattice site, since the low photon flux reduces photoassociation.

The paper is organized as follows: Sect. 2 sketches the basic scheme of the holographic detection method. Section 3 reviews theoretical background on atom light interaction, and on optical signals. In Sect. 4, we present the results of numerical calculations for the concrete example of $^6\text {Li}$ atoms in an optical lattice. Furthermore, we discuss the conditions for which a successful reconstruction of an atomic distribution can be achieved, including noise, mechanical vibrations, and lens aberrations. Section 5 concludes with a short summary and an outlook.

2 Detection scheme

We discuss the proposal in terms of a concrete example. As depicted in Fig. 1, we consider an ensemble of $N_{{\text{A}}} = 50$ atoms distributed over a 2D lattice with $11 \times 11$ sites and a lattice constant of $a=1\,\upmu \hbox {m}$. Each site is either empty or occupied by one single atom. We assume the lattice potential to be deep enough such that tunneling between the lattice sites is negligible.

Fig. 1

Ensemble of $N_{{\text{A}}} = 50$ atoms, distributed over a 2D square lattice with lattice constant $a=1\,\upmu \hbox {m}$

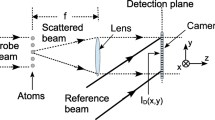
The overall setup for the detection method is shown in Fig. 2. A Gaussian laser beam, near-resonant to an optical atomic transition, is split into two beams, the probe and the reference beam. The probe beam propagates perpendicularly to the atomic layer and illuminates the atoms in the optical lattice. It has a diameter much larger than the spatial extent of the atomic sample, such that its electric field strength is approximately the same for all atoms.

The atoms are treated as Hertzian dipoles that coherently scatter the probe light. The scattered light is collimated by a diffraction-limited lens with a large numerical aperture and forms nearly perfect plane waves, which propagate toward the CCD detector. Since the spatial extent of the atomic sample is typically about three orders of magnitude smaller than the focal length f (Fig. 2 is not to scale!), the wave vectors of the plane waves are nearly parallel to the z direction (optical axis).

The non-scattered part of the probe beam is blocked by a small beam dump in the back focal plane of the lens. The reference beam bypasses the atomic layer and is superimposed with the collimated scattered light in the detection plane at an angle $\theta$. In order to keep $\theta$ small (see discussion in Sect. 4), the reference beam is transmitted through the same lens as the scattered probe light. For this purpose, it is focussed to a micrometer spot size in the front focal plane (at a sufficiently large distance to the atoms) and then collimated by the lens.

Fig. 2

Basic scheme of the holographic detection method. A probe beam illuminates the 2D array of atoms and the scattered light is collimated by a lens with focal length f. The scattered light is superimposed with a reference beam on the CCD detector which is placed at a distance d behind the back focal plane. A beam dump blocks the unscattered light

The overall intensity pattern is recorded by a CCD camera with a high dynamic range in order to resolve weak interference fringes on a high background signal. The pattern is subjected to a 2D Fourier transform (FT) [16] which directly yields the atomic distribution in the lattice. This step is analogous to classical holography where a readout wave reconstructs the original object, corresponding to the holograms Fourier transform [17].

3 Theoretical description

3.1 Coherent light scattering

We use a semiclassical model for the interaction of a single atom with a monochromatic coherent light field. Each atom acts as a quantum mechanical two-level system with transition frequency $\omega _0$. The atom is driven by a weak external laser field with frequency $\omega$. This leads to photon scattering with a rate [18]

$$R_{{\text{S}}} = {\frac{{\varGamma }}{2}}{\frac{I/I_{\text{sat}}}{1 + \left( 2{\varDelta }/{\varGamma }\right) ^2 + I/I_{{\text{sat}}}}} = {\frac{N_{{\text{ph}}}}{T_{\text{ac}}}},$$

(1)

where I denotes the incident intensity of the driving field, $I_{{\text{sat}}}$ the saturation intensity of the atomic transition, and ${\varDelta }= \omega - \omega _0$ the detuning between laser and transition frequency. ${\varGamma }$ is the linewidth of the atomic transition, and $N_{{\text{ph}}}$ the total number of scattered photons per atom within the acquisition time $T_{\text{ac}}$.

In general, the intensity $I_{\text{sc}}$ of the scattered light consists of both coherently and incoherently scattered parts. The coherent fraction of the scattered light $I_{\text{coh}}/I_{\text{sc}}$ is given by [18, 19]

$${\frac{{I}_{\text{coh}}}{{I_{\text{sc}}}}} = {\frac{1+ \left( 2{\varDelta }/{\varGamma }\right) ^2}{1 + \left( 2{\varDelta }/{\varGamma }\right) ^2 + I/I_{{\text{sat}}}}}.$$

(2)

A weak incident beam with large detuning will therefore yield mainly coherently scattered light. As a concrete example, choosing $I/I_{{\text{sat}}}< 1$ and ${\varDelta }= - {\varGamma }$ yields mostly coherent emission.

The probe beam as well as the reference beam ($\theta \approx 1^{\circ }, \phi =45^{\circ }$ see Eq. 9) are linearly polarized along the y direction. Treating the atoms as Hertzian dipoles, the electric field at position ${\mathbf{r}}= (x, y, z)$ in the far field, emitted by a single atom n at position ${\mathbf{r}}_n = (x_n,y_n,0)$, is given by

$$E_{{{\text{A}}}}({\mathbf{r}},{\mathbf{r}}_n) = E_{\text{A0}} {\frac{{\sqrt{(x-x_n)^2+z^2}}}{k\left| {\mathbf{r}}-{\mathbf{r}}_n\right| ^2}} {\text{e}}^{ik|{\mathbf{r}}-{\mathbf{r}}_n|}\,,$$

(3)

with the wave number $k = 2\pi /\lambda$. Integrating the corresponding intensity over the entire solid angle $4\pi$ relates $E_{\text{A0}}$ and the total number $N_{{\text{ph}}}$ of scattered photons per atom

$$E_{\text{A0}}^2 = \frac{3 k^2 \hbar \omega }{4\pi c \epsilon _0 T_{\text{ac}}}N_{{\text{ph}}}.$$

(4)

Here, c denotes the speed of light in vacuum and $\epsilon _0$ the permittivity of free space.

The wave emitted by the nth atom in the optical lattice is converted by the lens into a nearly perfect plane wave with wave vector

$$\mathbf {k}_n = \left( \begin{array}{c} k_{n,x} \\ k_{n,y} \\ k_{n,z} \end{array} \right) = \frac{k}{\sqrt{x_n^2 + y_n^2 + f^2}} \left( \begin{array}{c} -x_n \\ -y_n \\ f \end{array} \right) .$$

(5)

The field distribution of the plane wave in the detector plane $z=z_{\text{D}}$ reads

$$E_{{{\text{S}}},n}(x,y) = E_{\text{A0}} \, g_{{\text{A}}}(x,y)\, {\text{e}}^{i(x k_{n,x} + y k_{n,y} + \varphi _n)},$$

(6)

where $\varphi _n$ includes the constant term $z_{\text{D}} k_{n,z}$ and the phase shift acquired by the wave while passing through the lens.

The field envelope $g_{{\text{A}}}(x,y)$ is a slowly varying function which can be determined from Eq. (3). Since $f \gg |x_n|, |y_n|$, the propagation directions of all plane waves behind the lens are almost parallel to the z-axis and $g_{{\text{A}}}(x,y)$ is essentially independent of z. Therefore, we calculate $g_{{\text{A}}}(x,y)$ at the position of the lens. Setting $z=f$ in Eq. (3) and using the relation $|\mathbf {r}_n| \ll |\mathbf {r}|$ we obtain

$$g_{{\text{A}}}(x,y) \approx \frac{\sqrt{x^2+f^2}}{k(x^2+y^2+f^2)}{\varTheta }(r_{\text{l}}-\sqrt{x^2+y^2}).$$

(7)

The Heaviside function ${\varTheta }$ accounts for the finite size of the lens with radius $r_{\text{l}}$.

The electric field of the Gaussian-shaped reference beam at the detector reads

$$E_{{\text{R}}}(x,y) = E_{\text{R0}}\ g_{{\text{R}}}(x,y) {\text{e}}^{i(x k_{\text{R},x} + y k_{\text{R},y} + \varphi _{\text{R}})},$$

(8)

with the wave vector

$$\mathbf {k}_{\text{R}} = \left( \begin{array}{c} k_{\text{R},x} \\ k_{\text{R},y} \\ k_{\text{R},z} \end{array} \right) = k \left( \begin{array}{c} \sin \theta \cos \phi \\ \sin \theta \sin \phi \\ \cos \theta \end{array} \right).$$

(9)

For small $\theta$, the Gaussian field envelope $g_{\text{R}}(x,y)$ is given by

$$g_{\text{R}}(x,y) \approx {\text{e}}^{-(x^2+y^2)/w^2}{\varTheta }(r_{\text{l}}-\sqrt{x^2+y^2}),$$

(10)

with reference beam waist w.

3.2 Interference and Fourier transformation

The total electric field in the detector plane is obtained by adding up all individual fields. The corresponding intensity,

$$I_{\text{D}}(x,y) = \frac{1}{2}c\epsilon _0 \left| E_{{{\text{R}}}}(x,y) + \sum _{n} E_{{{\text{S}}},n}(x,y)\right| ^2 ,$$

(11)

can be written as a sum of three contributions

$$I_{\text{D}} = I_0 + I_{{\text{S}}} + I_{\text{RS}}.$$

(12)

The particle distribution is derived from the Fourier transform $F_{\text{D}}$ of the intensity profile $I_{\text{D}}$. $F_{\text{D}}$ decomposes into three parts, $F_{0}, F_{{\text{S}}}$, and $F_{\text{RS}}$. This is illustrated in the schematic plot in Fig. 3, which depicts a 1D cut through a 2D FT along the spatial frequency axis $\nu _x$ at $\nu _y = 0$. The illustration is consistent with the atomic distribution in Fig. 1 and presumes a wave vector $\mathbf {k}_{\text{R}}$ with $k_{\text{R},y} = 0$.

Fig. 3

1D cut through a schematic 2D FT along the spatial frequency axis $\nu _x$ at $\nu _y = 0$, illustrating the contributions of $F_{\mathrm{0}}, F_{{\text{S}}}$, and $F_{\text{RS}}$. The four peaks around $\nu _x \times \lambda f \approx$ 20 $\upmu$m reconstruct the positioning of the four atoms in Fig. 1 arranged along the $x_{{\text{A}}}$ axis at $y_{{\text{A}}} = 0$

The first contribution $I_0$ in Eq. (12) is a broad structureless intensity background

$$I_0 \propto E_{\text{R0}}^2 \ g^2_{{{\text{R}}}}(x,y) + N_{{\text{A}}} E_{\text{A0}}^2 \ g_{{\text{A}}}^2(x,y)$$

(13)

whose FT $F_{\text{0}}$ is represented by the large peak at the origin in Fig. 3. The width of the peak is determined by the inverse beam sizes $g_{\text{R}}$ and $g_A$. The second contribution

$$I_{{\text{S}}} \propto E_{\text{A0}}^2 \ g_{{\text{A}}}^2(x,y) \sum _{n>m} \cos [2\pi (\nu _{nmx} x + \nu _{nmy} y) + {\varDelta }\varphi _{nm}]$$

(14)

with ${\varDelta }\varphi _{nm} = \varphi _{n} - \varphi _{m}$ arises from the interference between the electric fields $E_{{{\text{S}}},n}$ emitted by the individual atoms in the optical lattice. Since $f \gg |x_n|, |y_n|$, the spatial frequencies $\nu _{nmx}$ and $\nu _{nmy}$ are approximately given by

$$\nu _{nmx} = \frac{x_m - x_n}{f\lambda },\quad \nu _{nmy} = \frac{y_m - y_n}{f\lambda },$$

(15)

where $(x_n,y_n)$ are the atomic positions in the optical lattice. Each pair of spatial frequencies $\nu _{nmx}, \nu _{nmy}$ gives rise to a well-defined peak in the FT close to the origin. The width of the peaks is again determined by the inverse of the collimated beam width $g_{\text{A}}$. The third term in Eq. (12),

$$\begin{aligned} I_{\text{RS}}&\propto E_{\text{R0}}E_{\text{A0}} \ g_{{{\text{R}}}}(x,y)\, g_{{\text{A}}}(x,y) \\ &\times \sum _{n} \cos [2\pi (\nu _{nx} x + \nu _{ny} y) + {\varDelta }\varphi _{\text{R}n}], \end{aligned}$$

(16)

arises from the interference of the scattered beams with the reference beam. Here, ${\varDelta }\varphi _{\text{R}n} = \varphi _{\text{R}} - \varphi _{n}$. The FT of $I_{\text{RS}}$, i.e., $F_{\text{RS}}$, can be conveniently used to extract the atomic distribution in the lattice. Apart from an overall constant factor $\lambda f$, the spatial frequencies $\nu _{nx}$ and $\nu _{ny}$ directly correspond to the coordinates $x_n$ and $y_n$ of each particle n.

$$\begin{aligned} \nu _{nx}&=\frac{x_n}{\lambda f} + \frac{\sin \theta \cos \phi }{\lambda }, \\ \nu _{ny}&=\frac{y_n}{\lambda f} + \frac{\sin \theta \sin \phi }{\lambda } \end{aligned}$$

(17)

The offsets, $\sin \theta \cos \phi / \lambda$ and $\sin \theta \sin \phi /\lambda$, can be tuned by adjusting the direction of the incident reference beam (see Eq. 9). As in spatial heterodyne detection, they are used to shift the peaks of the signal $F_{\text{RS}}$ away from the origin to separate them from the peaks of $F_{\text{0}}$ and $F_{{\text{S}}}$. Resolving Eq. (17) for the atomic coordinates $x_n$ and $y_n$ yields

$$\begin{aligned} x_n=\,& {} \lambda f \nu _{nx} - f \sin \theta \cos \phi , \\ y_n=\, & {} \lambda f \nu _{ny} - f \sin \theta \sin \phi . \end{aligned}$$

(18)

4 Numerical calculations

In this section, we present the results of our numerical calculations. First, we specify the used parameters and discuss the case of a noiseless detection. Then, we include detection noise and analyze its influence on the reconstruction fidelity. Finally, we compare our method with direct fluorescence detection, estimate its sensitivity to mechanical vibrations, and discuss lens aberrations.

4.1 Parameters and details

In the following, we consider an ensemble of $N_{{\text{A}}} = 50$ $^6\text {Li}$ atoms in a 2D lattice (see Fig. 1). The wavelength of the coherent probe and reference laser beams is set to $\lambda = 671$ nm, close to the $D_2$ transition of $^6\text {Li}$. The saturation intensity is $I_{{\text{sat}}}=2.54$ mW/cm$^{2}$ at a natural linewidth of ${\varGamma }=2\pi \times 5.87$ MHz. The focal length of the collimation lens is chosen to be $f = 7$ mm and the numerical aperture (NA) is 0.71, which matches typical parameters of a custom long-working-distance objective (see Fig. 2).

In the given case, we set the reference beam waist to $w=5$ mm (see Eq. 10). The illuminated area in the detection plane, which is located 70 mm away from the lens, has a radius of about 7 mm. In our simulations, we consider only a part of this area, namely a square section of 10$\times$10 mm$^2$. The CCD pixel size is assumed to be $A_{{{\text{p}}}}$ = $7\times 7\,\upmu$m$^2$, the quantum efficiency is set to $Q=0.8$. We choose an acquisition time $T_{\text{ac}}$ of 200 $\upmu$s. On the considered timescale, mechanical vibrations and particle tunneling inside the lattice can be neglected.

Two fundamental parameters are varied: the average number of photons $N_{{\text{ph}}}$ scattered by a single atom into the entire solid angle $4\pi$ within $T_{\text{ac}}$ and the total power $P_{{{\text{R}}}}$ of the reference beam. In the present study, we consider the ranges $100 \le N_{{\text{ph}}} \le 500$ and $10^{-8}\,{\text{W}} \le P_{{{\text{R}}}} \le 10^{-2}\,{\text{W}}$. Given an average number of scattered photons $N_{{\text{ph}}}$, the corresponding electric field strength $E_{\text{A0}}$ is obtained from Eq. (4). Using Eqs. (1) and (2), we verify that with these parameters we stay in the regime of mainly coherent emission.

4.2 Calculating the intensity pattern

We calculate the image captured by the CCD camera as follows. First, the intensity profile $I_{\text{D}}(x,y)$ in the considered section of the detection plane is calculated using Eq. (11). Then, the intensity $I_{\text{CCD}}(x_{\text{p}},y_{\text{p}})$ collected by a CCD pixel at position $(x_{\text{p}},y_{\text{p}})$ is obtained by averaging over all intensity contributions covered by the corresponding pixel area. In contrast to x and y, the coordinates $x_{\text{p}}$ and $y_{\text{p}}$ exhibit only discrete values. $I_{\text{CCD}}$ is converted into an integer number $N_{\text{D}}$ of nominally incident photons, ignoring for now photon shot noise,

$$N_{\text{D}}(x_{\text{p}},y_{\text{p}}) = {\text{round}}\left( \frac{I_{\text{CCD}}(x_{\text{p}},y_{\text{p}}) T_{\text{ac}} A_{{\text{p}}}}{\hbar \omega }\right).$$

(19)

The output signal of a CCD camera in counts is

$$N_{{\text{counts}}}(x_{\text{p}},y_{\text{p}}) = {\text{round}} \left( \frac{N_{\text{D}}(x_{\text{p}},y_{\text{p}}) Q}{\xi }\right),$$

(20)

where $\xi$ denotes the number of accumulated electrons per pixel that correspond to one count. It predefines the dynamic range of the CCD camera, which decreases with increasing $\xi$. In the calculations presented in Sect. 4, we use $\xi = 1$. For the considered parameters, however, values up to $\xi = 10$ yield almost the same results.

4.3 Calculations without noise

Let us start the discussion of our calculations by considering the idealized situation of absent noise. Furthermore, for the purpose of better illustration, we choose an example where the power of the reference laser is comparatively low ($P_{{\text{R}}}$ = $10^{-8}$ W). For this choice, interference fringes are clearly visible, since the ratio $I_{\text{RS}}/I_0$ is comparatively high.

Figure 4a shows a cut through the corresponding intensity profile $I_{\text{D}}(x,y)$ along the x-axis at y = 0 calculated with $N_{{\text{ph}}} = 500$.

Fig. 4

a 1D cut through the calculated 2D intensity profile $I_{\text{D}}(x,y)$ in the detection plane along the x-axis for y = 0. The intensity profile results from a superposition of the scattered probe beam and the broad Gaussian reference beam. An enlargement of the central part (inset) clearly reveals a sinusoidal interference pattern. For illustration purposes, a very low reference signal has been used in this model calculation, such that the interference fringes are clearly visible on the Gaussian background signal. b 2D intensity distribution in the detection plane without reference beam (false color image; blue: low, red: high intensity). It strongly resembles the diffraction pattern of a 2D square lattice where the zeroth and first-order peaks are located in the center and at the edges, respectively

The pronounced oscillations on top and at the tails of a Gaussian profile as well as weak oscillations in between arise from the interference between the scattered probe light and the Gaussian-shaped reference beam. Since the relevant information about the atom positions is stored in these interference fringes, the period length of the oscillations must be large enough to be resolved even after averaging intensity values within a pixel (see explanation above). We achieve this by using a small angle of incidence $\theta \approx 1^\circ$. This results in a sufficiently large period length of about 40 $\upmu \hbox {m}$ as revealed by the inset of Fig. 4a. The angle corresponds to a distance between the focus of the reference beam and the atomic ensemble of about 100 $\upmu \hbox {m}$ (see Fig. 2).

The emergence of the pronounced interference peaks at $0, \pm 4.5$ mm in Fig. 4a can be understood as follows. The light scattered by the rectangular array of atoms resembles the diffraction pattern of a perfect 2D square lattice, as depicted in Fig. 4b. The quickly oscillating intensity peaks in the center and at the edges in Fig. 4a are the corresponding zeroth and first-order diffraction peaks which interfere with the reference beam. The atomic array, however, is not perfect as a number of lattice sites are unoccupied. As a consequence, the intensity in between the major diffraction peaks is nonzero. This leads to the weak, but still clearly visible interference patterns in Fig. 4a between the strong oscillations in the middle and at the edges. The information about occupied lattice sites is contained in these oscillations. In order to resolve them, especially for a higher reference laser power, the CCD camera needs a large dynamic range (12 bit or better).

As explained in Sect. 3, the atomic positions in the lattice can be directly derived from a 2D FT of the intensity profile $I_{\text{D}}(x,y)$ or more precisely from a FT of $N_{{\text{counts}}}(x_{\text{p}},y_{\text{p}})$. An appropriately chosen section of such a FT is shown in Fig. 5, where the absolute values of the Fourier coefficients are displayed as a false color image.

Fig. 5

Section of the 2D FT yielding a perfectly reconstructed image of the atomic distribution in Fig. 1. The false color plot displays absolute values of the Fourier coefficients (blue: low, red: high FT amplitude). The simulation was performed without noise using the parameters $N_{{\text{ph}}} = 150$ and $P_{\text{R}} = 10^{-5}$ W

The coordinates $x_{{\text{A}}}$ and $y_{{\text{A}}}$ give the position within the atomic layer and are related to the spatial frequencies $\nu _x$ and $\nu _y$ of the FT by (see Eq. 18)

$$\begin{aligned} x_{{\text{A}}}= & {} \lambda f \nu _x - f \sin \theta \cos \phi , \\ y_{{\text{A}}}= & {} \lambda f \nu _y - f \sin \theta \sin \phi . \end{aligned}$$

(21)

The maxima in the 2D plot at $y_{{\text{A}}}=0$ correspond to the group of peaks labeled by $F_{\text{RS}}$ in the schematic 1D illustration of Fig. 3. In contrast to Fig. 4a, $N_{{\text{counts}}}(x_{\text{p}},y_{\text{p}})$ is calculated using $N_{{\text{ph}}} = 150$ and $P_{{\text{R}}}$ = $10^{-5}$ W. A comparison with Fig. 1 reveals that the atomic distribution is perfectly reconstructed.

4.4 Speckle and shot noise

Let us now turn to the realistic situation where the image acquired by the CCD camera is disturbed by different kinds of noise. These need to be taken into account to understand where the limits of the presented holographic detection method lie. In general, in an experiment there are several sources which decrease the fidelity of a detection. For a CCD camera, there are photon shot noise, readout noise, and dark counts which have to be taken into account. However, for the case of a relatively strong reference beam and thus of a high light intensity, the dominant detection noise is given by shot noise. Shot noise describes fluctuations in the number of detected photons and obeys a Poisson distribution. It is taken into account by replacing $N_{\text{D}}$, calculated from $I_{\text{CCD}}(x_{\text{p}},y_{\text{p}})$ in Eq. (19), by a Poisson-distributed variable with expectation value $N_{\text{D}}$.

Imperfections of the ideally Gaussian intensity profiles of the probe and reference beams will also have an effect on the reconstruction. Such corrugations can be caused by effects such as shortcomings in the quality of optical elements or weak stray reflections of the laser beams. The resulting intensity distribution typically shows high-frequency intensity fluctuations similar to laser speckle [20, 21]. If we assume the fluctuations to occur on a length scale of about 1 $\upmu \hbox {m}$ in the detection plane, this kind of noise adds the intensity $I_{\text{SP}}(x,y)$ to $I_{\text{D}}(x,y)$. It is known [20, 21] that this added noise has an exponentially decreasing probability as a function of $|I_{\text{SP}}|$

$$P_{\text{SP}}(I_{\text{SP}})\propto \exp \left( -\frac{|I_{\text{SP}}|}{\alpha I_{\text{D}}}\right).$$

(22)

From our own laboratory experience, we estimate that the typical amplitude of these fluctuations is on the level of about one percent. Therefore, we set $\alpha = 0.01$.

In order to take into account readout noise, we add an integer number ${\varDelta }N_{{\text{counts}}}(x_{\text{p}},y_{\text{p}})$ to $N_{{\text{counts}}}(x_{\text{p}},y_{\text{p}})$. This noise is obtained from a zero-centered normal distribution with a standard deviation of 3 counts (typical specification of a commercial electron multiplying CCD camera).

The combined effects of intensity averaging, noise, and photon counting (see Eq. 20) are illustrated in Fig. 6. It depicts a 1D cut through the CCD image $N_{{\text{counts}}}(x_{\text{p}},y_{\text{p}})$ along the $x_{\text{p}}$ axis for $-0.3\,{\text{mm}} \le x_{\text{p}} \le 0.3\,{\text{mm}}$ and $y_{\text{p}} = 0$, calculated with $N_{{\text{ph}}} = 150$ and $P_{\text{R}} = 10^{-5}$ W. In contrast to the inset of Fig. 4a, which displays the same x range, the interference pattern is now barely perceptible. The corresponding 2D FT is shown in Fig. 7.

Fig. 6

1D cut through the calculated CCD image $N_{{\text{counts}}}(x_{\text{p}},y_{\text{p}})$ along the $x_{\text{p}}$ axis at $y_{\text{p}} = 0$ including noise (red line/dots). The parameters used in the calculation are $N_{{\text{ph}}} = 150$ and $P_{\text{R}} = 10^{-5}$ W. The blue line depicts the undisturbed interference signal for comparison

Fig. 7

Example of a reconstructed image of the atomic distribution (2D FT of $N_{{\text{counts}}}(x_{\text{p}},y_{\text{p}}))$ taking into account speckle, shot, and readout noise (blue: low, red: high FT amplitude). The simulation was performed using the parameters $N_{{\text{ph}}}=150$ and $P_{\text{R}} = 10^{-5}$ W. For this example, our simple recognition algorithm (see text) yields a fidelity of 99.2 % to identify the occupation of an individual site

In contrast to Fig. 5, it is very noisy. However, we can still reconstruct the atomic distribution with a sufficiently high fidelity.

For this, we use the following simple algorithm. We normalize the reconstruction signal (absolute values of the Fourier coefficients) within the FT section depicted in Figs. 5 and 7. Next, we place the lattice grid on top as shown in Fig. 7. The normalized value at each grid point is compared to a threshold value. If the value lies (below) above the threshold, the lattice site is identified as (un)occupied. We define a fidelity as the percentage of correctly identified sites. An analysis of a variety of atomic arrays with different filling factors shows that for the investigated range of parameters $N_{{\text{ph}}}$ and $P_{{\text{R}}}$ a threshold value of 0.4 yields the highest fidelity.

The histogram in Fig. 8 displays the probability distribution of the normalized Fourier coefficients for $N_{{\text{ph}}} = 150$, $P_{\text{R}} = 10^{-5}$ W. It is obtained by averaging over the probability distributions of 1000 reconstructed images of the particle distribution of Fig. 1. The calculation includes a fixed speckle noise and randomly varying shot and readout noise. As shown by the red line in Fig. 9, the distribution resembles two overlapping Gaussians with a pronounced minimum at 0.4.

Fig. 8

Probability distribution of the normalized Fourier coefficients determined at the optical lattice sites (see Fig. 7). The histogram represents an average over 1000 probability distributions obtained for $N_{{\text{ph}}} = 150$, $P_{\text{R}} = 10^{-5}$ W, fixed speckle noise, and randomly varying shot noise. The dip at 0.4 coincides with the threshold value with highest reconstruction fidelity. The red solid curve are two partially overlapping Gaussians which are fitted to the histogram

In Fig. 9, the fidelity is plotted as a function of $P_{{\text{R}}}$ for different values of $N_{{\text{ph}}}$. Each data point is again obtained by averaging over the fidelities of 1000 reconstructed images, calculated with randomly varying shot and readout noise. For $N_{{\text{ph}}} \ge 150$ the fidelity reaches maximum values clearly exceeding 99.5 %, for $N_{{\text{ph}}} = 100$ (not shown) it is still nearly 98.5 %.

Depending on the range of $P_{{\text{R}}}$, the fidelity is limited by different kinds of noise. At low and high reference power, readout noise and speckle noise prevail, respectively. In both cases, the noise leads to a strong decline of the fidelity. In between, shot noise is dominant. The dependence of the fidelity on $P_{{\text{R}}}$ and $N_{{\text{ph}}}$ can be understood by the signal-to-noise ratio (SNR) of the interference fringes on the CCD camera. Neglecting atomic contributions to $I_0$ in Eq. (13), a rough estimate yields

$${\text{SNR}} \approx \frac{{I_{{{\text{RS}}}} }}{{\sqrt {I_{0} } }} \propto E_{{{\text{A}}0}} \propto \sqrt {N_{{{\text{ph}}}} }.$$

(23)

In the fraction $I_{\text{RS}}/\sqrt{I_{\text{0}}}$, the field amplitude $E_{\text{R0}}$ of the reference beam drops out and the SNR is independent of $P_{{\text{R}}}$. As a consequence, the fidelity features a plateau. The width of the plateau as well as the maximum fidelity decreases with decreasing $N_{{\text{ph}}}$. This can be explained by the proportionality of SNR to the atomic field amplitude $E_{\text{A0}}\propto \sqrt{N_{{\text{ph}}}}$. Above a critical value of $P_{{\text{R}}}$, marked by the dashed line in Fig. 9, the pixels near the center of the CCD camera saturate (assuming a dynamic range of 16 bit). Therefore, in practice the speckle-induced drop should be irrelevant.

Moreover, all effects leading to global laser intensity fluctuations do not disturb the interference signal, since they do not change the relative phase between atomic and reference signal.

Fig. 9

Fidelity as a function of $P_{\text{R}}$ for different average total numbers of scattered photons per atom $N_{{\text{ph}}}$. Each data point is obtained by averaging over the fidelities of 1000 reconstructed images (with fixed particle distribution), calculated with randomly varying shot and readout noise. Above a critical value of $P_{{\text{R}}}$, marked by the dashed line, the pixels near the center of a CCD camera with a dynamic range of 16 bit start to saturate

4.5 Comparison with fluorescence detection

As demonstrated in Fig. 9, the proposed detection scheme should yield fidelities higher than 99.5 % even for moderate numbers of scattered photons. This is achieved by means of the reference beam which amplifies the atomic diffraction signal. In contrast, the direct fluorescence detection method, e.g., used in [3–7], does not involve such a reference beam. During detection several thousands of photons are scattered by a single atom. As a disadvantageous consequence, the atoms are strongly heated and may hop between lattice sites even in the case of deep optical lattices (see e.g., [7]). Therefore, complex cooling techniques have to be applied.

To compare our scheme with the fluorescence detection, we estimate the particle heating. We assume that the particles are initially in the vibrational ground state $\vert v=0\rangle$ of a deep optical lattice with a depth of 2.5 mK and a Lamb–Dicke parameter of $\eta =0.23$ (see [22]). During detection, the particles scatter 150 photons per atom. The transition probability from $\vert v=n\rangle$ to $\vert v=n\pm 1\rangle$ for a single scattering event is given by $\eta ^2\left( n+1\right)$ and $\eta ^2n$, respectively. An estimate based on random walk yields that 99 % of the atoms end up at a vibrational state $\vert v_{\text{Final}}\le 24\rangle$. The excitation to higher vibrational states reduces the tunneling time of a particle inside the lattice. However, since the tunneling time of a particle in state $\vert v_{\text{Final}}=24\rangle$ is on the order of 1 ms, i.e., long compared to the acquisition time $T_{\text{ac}} = 200\,\upmu$s, tunneling can be neglected. This means that the heating due to light scattering should hardly influence the reconstruction fidelity. Therefore, our scheme might open the path to circumvent additional cooling during detection.

4.6 Mechanical vibrations

In terms of a technical issue of the proposed scheme, we need to take into account the sensitivity of the setup to mechanical vibrations. For this, we consider Eqs. (16) and (21). During the acquisition time, the relative phases ${\varDelta }\varphi _{{\text{R}n}}$ between reference and scattered laser fields may vary, leading to a blurring of the contrast of the interference fringes. A jitter $\delta \theta$ in the reference angle $\theta$ leads to a similar effect. In order to estimate the influence of the jitter, we rewrite $x_{{\text{A}}}$ in Eq. (21) for angles close to $\theta \approx 1^\circ$ (as used in our simulations) with $\phi = 45^\circ$ fixed:

$$x_{{\text{A}}} = \lambda f \nu _x - \frac{f}{\sqrt{2}} \theta.$$

(24)

A jitter $\delta \theta$ thus causes a blurring $\delta x = f \delta \theta /\sqrt{2}$ of the coordinates in the reconstruction. If we demand $\delta x \ll a$, the jitter has to be much smaller than $\sqrt{2}\times 1\,\upmu {\text{m}}/f \approx 200 \,\upmu$rad. This should not pose a problem since pointing stabilities of $10 \upmu$rad or better are typical in an optical laboratory environment. Furthermore, achieving fluctuations in the relative phase ${\varDelta }\varphi _{{\text{R}n}} \ll \pi$ is standard on an optical table.

4.7 Lens aberrations

Another technical issue of the holographic detection scheme is lens aberrations. In our scheme, a large NA lens collimates the emitted light of the atoms and the reference beam. Even for a high-quality lens the transmitted wavefront can be distorted by lens imperfections and aberrations.

To estimate such shortcomings, we perform a 1D calculation in the presence of small spherical aberration which results in a position-dependent tilt of the wave vectors $\mathbf {k}_{n}$ and $\mathbf {k}_{\text{R}}$ (see Eqs. 5, 9). We simulate the tilt in the detection plane by

Fig. 10

Distortion of the interference pattern due to spherical aberration and its correction. a Shown is a distorted 1D holographic interference pattern in the presence of spherical aberration (black curve). The atomic emitters are located 0, 2, 5 $\upmu \hbox {m}$ away from the optical axis. Using an appropriate mapping the interference pattern can be corrected (red curve). b Reconstruction of the particle distribution with (red) and without (black) correction. The positions of the atomic emitters are marked with arrows

$$\mathbf {k}_{n,{\text{R}}} \propto \left( \begin{array}{c} -x_{n,{\text{R}}} - \beta (x + 10\, x_{n,{\text{R}}})^3 \\ f \end{array} \right),$$

(25)

where the empirical parameter $\beta$ sets the influence of the spherical aberration and $x_{\text{R}}$ denotes the position of the reference beam in the front focal plane of the lens. The black curves in Fig. 10a, b show the interference fringes and the corresponding reconstruction, respectively, for a reference beam and three atoms at positions $x_n = 0, 2, 5\upmu$m. The aberration leads to an increase in the spatial frequency $\nu _{{\text{SF}}}(x)$ in the interference pattern with increasing distance x to the optical axis. As a result, the Fourier transform no longer yields a high-fidelity reconstruction (Fig. 10b). However, the effect of the aberration can be compensated with the help of an empirical nonlinear mapping which locally stretches the interference pattern such that it exhibits a constant $\nu _{{\text{SF}}}$ (red curve in Fig. 10a). The sharp peaks at $x_n = 0, 2, 5\upmu$m in Fig. 10b demonstrate that the atomic distribution can be successfully reconstructed in this way.

In order to derive an appropriate nonlinear mapping, we calculated the interference between the reference beam and a single point emitter at $x_n = 0\,\upmu$m in the presence of aberration and determined the dependence of $\nu _{{\text{SF}}}(x)$ on the position x. The mapping results from a comparison between $\nu _{{\text{SF}}}(x)$ and the known spatial frequency in the case of absent aberration. Although the correction is obtained only for a single point emitter, it successfully works even for a larger number of atoms.

We thus demonstrate a preliminary way to correct distorted interference patterns. Clearly, more general and sophisticated compensation algorithms can be developed which will turn the holographic detection scheme robust against aberrations of the lens. This might prove to be very useful in the future as it relaxes the required lens specifications for high-resolution imaging.

5 Conclusion

In conclusion, we propose a holographic scheme for site-resolved detection of a 2D gas of ultracold atoms in an optical lattice. We have discussed the method for the example of 50 lithium atoms in a square optical lattice, but it will also work for larger sample sizes, other atomic elements, or other lattice geometries. The method features a high detection fidelity (>99.5 $\%$) even for a low number of scattered photons per atom ($\approx$150) in the presence of detection noise and small lens aberration.

The low number of scattered photons might open the path for single-site detection without additional cooling. Moreover, it might allow for imaging multiple occupancy of a single lattice site.