Laser-induced incandescence from laser-heated silicon nanoparticles

Abstract

This work describes the application of temporally and spectrally resolved laser-induced incandescence to silicon nanoparticles synthesized in a microwave plasma reactor. Optical properties for bulk silicon presented in the literature were extended for nanostructured particles analyzed in this paper. Uncertainties of parameters in the evaporation submodel, as well as measurement noise, are incorporated into the inference process by Bayesian statistics. The inferred nanoparticle sizes agree with results from transmission electron microscopy, and the determined accommodation coefficient matches the values of the preceding study.

1 Introduction

Gas-phase synthesis is a promising route toward large-scale production of nanoparticles with high purity and specific properties [1, 2]. Silicon nanoparticles [3] have applications in photovoltaics, lithium-ion batteries [4], light emitters [5], and thermoelectrics [6]. The widespread use of these nanoparticles motivates the development of high throughput gas-phase synthesis techniques, which have been scaled up to pilot plant and production scale [7]. Developing these reactors requires instrumentation that can provide spatially and temporally resolved nanoparticle sizes and concentrations in order to understand the nanoparticle nucleation and growth within the reactors, and to ensure that the nanopowders produced by the reactors have the desired properties. Laser-based methods are particularly useful for measuring species concentrations [8], temperature [9], and nanoparticle size without requiring physical access and without perturbing the local physics and chemistry processes that underlie nanoparticle synthesis and growth.

Time-resolved laser-induced incandescence (TiRe-LII) is a well-studied diagnostic mainly used to recover soot/carbon black particle sizes and volume fractions in combustion-related applications [10–13]. In this technique, a laser pulse heats the nanoparticles within a sample volume of aerosol, and the resulting spectral incandescence is measured as the nanoparticles return to the ambient gas temperature. The incandescence magnitude indicates the volume fraction of the nanoparticles, while the incandescence decay rate and thus the variation in temperature over time indicates their primary particle-size distribution.

Interpreting TiRe-LII data requires a spectroscopic model that relates the measured instantaneous spectral intensity to the nanoparticle temperature, and a heat transfer model that relates the temperature decay to the nanoparticle size. Both models require knowledge of the radiative and other thermophysical properties of the nanoparticles. In the context of soot measurements, uncertainty in these properties places a severe constraint on the reliability of LII-inferred parameters. Soot is a highly complex material, usually of uncertain composition and (often heterogeneous) structure; consequently, the radiative and thermophysical properties of soot depend on its formation conditions (e.g., different types of fuels) and its temperature history (“young” vs. “mature” soot) [14, 15]. In contrast, the properties of inorganic particulates are more predictable and exhibit less variability. Synthesis processes that generate pure non-aggregated particles with narrow size distributions are therefore ideal for studying the spectroscopic and radiative properties, and the various processes involved in the laser heating and subsequent cooling of aerosolized nanoparticles. Once these processes are understood, LII measurements can be used to determine nanoparticle sizes within gas-phase reactors. Moreover, knowledge gained from studying this simple, well-characterized system can potentially be transferred to improve the reliability of LII measurements on more complex synthetic nanoaerosols, and potentially soot.

While LII has been applied to a range of synthetic metal and nonmetal nanoaerosols (see overview in [10]), to the best of our knowledge, the only previous attempt to characterize aerosolized silicon nanoparticles using TiRe-LII was a preliminary study by Sipkens et al. [16], who took in situ measurements on Si nanoparticles within a microwave reactor. In that work, nanoparticle incandescence was measured at two wavelengths using photomultiplier tubes equipped with narrow band-pass filters; the data were combined with published radiative properties for liquid silicon. These temperatures were then analyzed using a heat transfer model that included a thermal accommodation coefficient derived from molecular dynamics.

This paper presents important refinements on the preliminary study of Sipkens et al. [16]. LII measurements are taken on liquid Si nanoparticles synthesized within the same reactor type used in the previous study. While the previous work relied on spectral incandescence, we instead obtain spectrally and temporally resolved incandescence measurements using a streak camera–spectrometer combination. Emission spectra are interpreted using a Drude dispersion model, which is verified separately using extinction measurements taken through the aerosol using a halogen lamp and a spectrometer. A heat transfer model is then derived, which includes both evaporation and conduction heat transfer. Evaporation is particularly important for TiRe-LII on low-melting-point materials, but there is considerable uncertainty in the parameters in the evaporation submodel. A free-molecular heat conduction model is derived that considers a multicomponent bath gas.

Bayesian analysis is then used to infer probability densities for nanoparticle size and thermal accommodation coefficient, accounting for noise in the effective temperatures caused mainly by photonic shot noise as well as for uncertainties in the evaporation submodel. The recovered probability densities of d _p and α are consistent with previously published data [16]. The determined uncertainties represent the effect of uncertainties in published data and measurement noise.

2 Experimental apparatus

Silicon nanoparticles are generated within a microwave plasma reactor operating at 100 m bar, shown schematically in Fig. 1. Fresh gases (Ar/H₂) and silane (SiH₄) precursor are injected with 0.03/2/0.2 standard liter per minute (slm), respectively, through a nozzle directly below the center of the plasma region. Silane is decomposed by the plasma, and the resulting supersaturated Si vapor leads to nucleation and growth of silicon nanoparticles [4]. A swirling co-flow of Ar/H₂ with 6.6/0.5 slm constrains and stabilizes the generated particle stream into a ~1-mm-thick annulus with a diameter of 12.5 mm located 300 mm downstream of the plasma. More details of reactor layout and operation are provided in Refs. [16, 17].

Fig. 1

Left: schematics of the microwave plasma reactor. Middle: view of the particle stream during plasma synthesis (top) and TEM image of particles sampled 300 mm downstream of the plasma (bottom). Right: particle-size distribution inferred from TEM analysis of extracted nanoparticles [17]

Optical measurements are taken in situ via four quartz window ports (60 mm diameter) in an ISO flange (160 mm nominal diameter) cross piece mounted on top of the cylindrical segment housing the nozzle flange. At this location, incandescence from the silicon nanoparticles is visible to the unaided eye, a feature that will be used to estimate the nanoparticle and gas temperature from spectrally resolved emission measurements as described in the next section. In the same location, spectrally and time-resolved LII measurements were taken with a spatial resolution determined by the volume formed through the intersection of the heating laser beam, the particle cloud, and the imaged probe region. Within the particle-laden gas flow, the laser beam and the observation direction cross at 90°. Line-of-sight absorption (LOSA) measurements have also been taken with spectrally resolved detection of the particle-laden gas flow against broadband background illumination.

For additional ex situ evaluation of the particle-size distribution, a pneumatically actuated thermophoretic particle sampler [18] was inserted into the hot particle-laden gas stream for approximately 500 ms at the same height above the plasma. TEM analysis of the grids reveals single spherical particles with diameters of ~25 nm with a soft agglomeration, suggesting that they are isolated nanospheres within the aerosol (cf., Fig. 1).

2.1 Spectrally resolved line-of-sight attenuation measurements (LOSA)

For the measurement of the relative strength of broadband transmission/incandescence of visible light in the LOSA technique [19, 20], light from a 100-W halogen bulb is diffused through a frosted glass (Fig. 2, left). A lens system (f ₁ = 150 mm, f ₂ = 250 mm) images this diffuse light source to the location of the particle stream. At the exit port, a lens collects the transmitted light into an optical fiber, which is then focused onto the slit of an imaging spectrometer (Acton SP2015) connected to an EMCCD detector (Andor iXon DV887).

Fig. 2

Top view of the two relevant measurement setups. a Line-of-sight attenuation (LOSA): the light of a diffused white-light source is imaged to the measurement plane and then collected into an optical fiber. The emission spectrum is retrieved by a spectrometer/EMCCD combination. b Arrangement for laser-induced incandescence measurements. Here, the fundamental wavelength of the Nd:YAG laser is guided into the probe volume and shaped by a ceramic aperture. The incandescence light is focused on the spectrometer slit. The spectrally dispersed light is focused on the streak camera entrance slit. A CCD camera records the image that contains spectral and temporal information

Fig. 3

Silicon vapor pressure p ⁰_v as a function of temperature, using the Clausius–Clapeyron parameters in Table 1. The shaded region corresponds to the uncertainty reported by Tomooka et al. [34]

Fig. 4

Evaporation, conduction, and radiation heat transfer rates from a 30-nm-diameter silicon nanoparticle with α = 0.3, as a function of temperature

Fig. 5

a Results of the Drude model for the dielectric function for molten silicon match experimental values reported in the literature (ε_I < 0, ε_II > 0); b Q _abs,λ calculated using Drude theory assuming d _p = 30 nm matches line-of-sight extinction measurements

Fig. 6

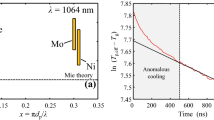
Streak camera pyrometry (F ₀ = 8 mJ/mm²). The time axis is adjusted to the peak incandescence at 500 nm. Estimates for T _p,k and C _k are found by fitting Eq. (5) to each row of pixels (spectrum k) corresponding to t _k . Variation in C _k with time (right y-axis) and the particle temperature (left y-axis)

2.2 Laser-induced incandescence measurements

The gas-borne silicon nanoparticles were heated using a 1064-nm pulsed Nd:YAG laser (Continuum, Powerlite 7000) operating in the 2–100 mJ/mm² fluence range. The trigger pulses for the flashlamp and the Q-switch as well as the trigger pulses for the streak camera are controlled by a pulse generator (Stanford Research Systems, DG645, pulse jitter below 50 ps). The temporal profile was analyzed for several flashlamp voltages with a fast photodiode (Thorlabs, DET10A, rise time 1 ns) attached to an oscilloscope (Tektronix, DPO70404C). While the temporal profile of the single laser pulses varies, the multi-pulse averaged temporal profile is Gaussian with a full width at half maximum (FWHM) ranging between 10 and 25 ns depending on the flashlamp voltage. This pulse length variation was incorporated into the LII evaluation for a more accurate heat transfer modeling.

As shown in Fig. 2b, the incandescence from the laser-heated nanoparticles was imaged using collection optics (collimation by f = 250 mm, f _# = 5, focusing by f = 200 mm, f _# = 4) onto a 2000-μm-wide entrance slit of an Acton SpectraPro SP 2300 imaging spectrometer (50 grooves/mm grating blazed for 600 nm; set to a center wavelength of 580 nm) that is connected to a Hamamatsu C10910 streak camera. The transmittance efficiency of the streak camera–spectrometer combination is calibrated using a halogen lamp mounted in an integrating sphere. The single streak camera images are corrupted by shot noise, which is reduced by averaging the signal from 1200 sequential laser shots. The laser is also subject to a temporal jitter of <2 ns, which was not resolvable due to the temporal resolution of the streak camera in this time range setting.

2.3 Influence of experimental parameters on the temperature determination

The determination of the time-resolved temperature of the particles relies on an exact representation of the signal intensity decay at various wavelengths. Therefore, the influence of the instrument function and the impact of the laser pulse length on the temperature measurement were studied. It was found that the laser pulse length affects the peak particle temperatures but does not influence the determination of size and accommodation coefficient, which are done using pyrometric temperatures measured after the laser pulse.

Temporal blurring of the highly dynamic signal due to the temporal instrument function can also affect the determination of peak temperatures. The temporal resolution of the streak camera in this experiment was 5 ns (as measured by comparing the measured laser pulse length of a streak camera image with the measurements by the photodiode). Monte Carlo simulations of artificial streak camera images using the known instrument function show only a minor (~3%) depression of peak temperature up to 4000 K within the initial 5–10 ns, which is below the measurement uncertainty of the noise-contaminated raw images. At later times, the instrument function does not affect the determined temperature. Therefore, temperature measurements are only analyzed starting from >20 ns after the peak temperature. At these times after the end of the laser pulse, laser heating does no longer occur; therefore, q _laser can be excluded from the heat transfer model.

3 Measurement theory

3.1 LII model

At any instant, the spectral intensity measured by the streak camera (Fig. 7) due to nanoparticle incandescence is given by [21]

$$J_{\lambda } \left( t \right) = \eta N_{\text{p}} \mathop \int \limits_{0}^{\infty } p\left( {d_{\text{p}} } \right)I_{{{\text{b}},\lambda }} \left[ {T_{p} \left( {t, d_{\text{p}} } \right)} \right]\frac{{\pi d_{\text{p}}^{2} }}{4}Q_{{{\text{abs}},\lambda }} \left( {d_{\text{p}} } \right) dd_{\text{p}} ,$$

(1)

where η is a calibration constant that depends on the depth of the measurement volume and the collection optics, N _p is the nanoparticle number density, p(d _p) is the probability density of nanoparticles having the diameter d _p, I _b,λ is the blackbody intensity at the particle temperature T _p, and Q _abs,λ is the spectral absorption cross section of the nanoparticles at the wavelength λ. (The absorption and emission efficiencies are equal through Kirchhoff’s law [22].) For narrow particle-size distributions (as is the case for the present Si synthesis process), Eq. (1) can be simplified to

$$J_{\lambda } \left( t \right) \cong \eta N_{\text{p}} I_{b,\lambda } \left[ {T_{\text{p}} \left( {t, d_{\text{p}} } \right)} \right]\frac{{\pi d_{\text{p}}^{2} }}{4}Q_{{{\text{abs,}}\lambda }} \left( {d_{\text{p}} } \right).$$

(2)

Fig. 7

Results of the time-resolved pyrometry measurements with the streak camera (F ₀ = 8 mJ/mm²): The plot on the right shows the fits (solid lines) of the measured incandescence spectra (symbols; rows on the streak image (left panel) marked with dashed lines) using Eq. (5). Measurement times (0, 50, and 100 ns after the laser pulse) correspond to those shown in Fig. 8

Equation (1) can also be used to model the incandescence from a polydisperse aerosol at short measurement times [21], in which case T _p is an effective nanoparticle temperature biased toward larger nanoparticles due to their more intense thermal emission (since they cool more slowly than smaller nanoparticles) and larger absorption cross section. A monodisperse size distribution will be assumed through the remainder of this analysis.

In most TiRe-LII experiments, the time-resolved spectral incandescence data are processed in two steps: First, Eqs. (1) and (2) are inverted to obtain a pyrometric temperature T _p(t) at each measurement time t. The pyrometric temperature decay is then used to infer the particle-size distribution and associated parameters. These steps require two models: a spectroscopic model for Q _abs,λ(t) to find T _p(t), and a heat transfer model to relate the temperature decay to the nanoparticle-size distribution.

3.2 Spectroscopic model

The expected particle diameter is much smaller than the detection wavelengths, and accordingly the governing Mie equations simplify to the Rayleigh approximation [22]

$$Q_{{{\text{abs}},\lambda }} \left( {d_{\text{p}} ,\lambda } \right) = \frac{{4\pi d_{\text{p}} }}{\lambda }\Im \left( {\frac{\varepsilon - 1}{\varepsilon + 2}} \right) = \frac{{4\pi d_{\text{p}} }}{\lambda } E(m),$$

(3)

where ε = ε _I + iε _II is the (wavelength-dependent) dielectric function and m = n + ik is the complex refractive index; the two parameters are related by ε _I = n ²-k ² and ε _II = 2nk. In this scenario, the spectroscopic model can be used to infer the particle temperature independent of the particle size, since d _p (along with N _p and other constants) can be included into the calibration coefficient η in Eq. (2) to yield

$$J_{\lambda } \left( t \right) = C_{k} \frac{{I_{b,\lambda } \left[ {T_{\text{p}} \left( {t,d_{\text{p}} } \right)} \right]}}{\lambda } \Im \left( {\frac{\varepsilon - 1}{\varepsilon + 2}} \right).$$

(4)

While the optical properties of soot are notoriously ill-defined and not amenable to a simple theoretical model [23, 24], those of liquid silicon can be accurately described using Drude theory (e.g., [25–27]). In the classical interpretation of Drude theory, conduction-band electrons accelerate due to Columbic forces imposed by the oscillating electromagnetic field, but their motion is damped due to collisions between electrons and a background of neutral ions and atoms. These collisions are the mechanism that couples the electromagnetic radiation to the internal energy of the liquid metal. According to this model,

$$\varepsilon_{I} = 1 - \frac{{\omega_{\text{p}}^{2} \tau^{2} }}{{\omega^{2} \tau^{2} + 1}},\quad \varepsilon_{II} = \frac{{\omega_{\text{p}}^{2} \tau }}{{\omega \left( {\omega^{2} \tau^{2} + 1} \right)}} ,$$

(5)

where ω = 2πν = 2πc ₀/λ is the angular frequency of the electromagnetic wave, ω_p is the plasma frequency of the electrons, and τ is the relaxation time, which is related to the collision frequency between electrons and atoms/ions. The plasma frequency is given by

$$\omega_{\text{p}} = \sqrt {\frac{{n_{{{\text{e}},liq}} e^{2} }}{{\varepsilon_{0} m_{\text{e}} }}}$$

(6)

where e and m _e are the charge and rest mass of an electron, ε ₀ is the vacuum permittivity, and n _e,liq is the electron number density within the liquid metal, which is found from the atomic number density assuming that each silicon atom contributes four valence electrons to the conduction band. The relaxation time can be inferred from the bulk electrical conductivity

$$\tau = \sqrt {\frac{{m_{e} \sigma_{\text{DC}} }}{{n_{e,liq} e^{2} }}} .$$

(7)

Following Kawamura et al. [27], the Drude parameters used in this study are obtained from Eqs. (6) and (7) using the density ρ [28] and the bulk resistivity σ_DC [29] of molten silicon at 1900 K, which is the highest temperature at which σ_DC has been measured. The resulting parameters ω_p = 2.64×10¹⁶ rad/s and τ = 2.10×10⁻¹⁶ s closely match the parameters Li and Fauchet [26] found by fitting Eq. (5) to ellipsometry measurements on molten silicon. (An extrapolation to 3000 K, assuming a linear model for σ_DC and MD-derived values of ρ [30], also gave similar parameters.)

The spectrally resolved LOSA data are obtained by sequentially acquiring four spectra. With the lamp on and the particles present, the intensity incident on the spectrometer I _t+e,λ consists of transmitted incident intensity, incandescence emitted by the silicon nanoparticles (heated within the plasma region of the reactor), and scattered light from the plasma. The intensity due to thermal emission from the nanoparticles, I _e,λ, is isolated by taking a measurement with the lamp off. (Subtracting these measurements also removes the dark current.) This measurement is normalized by the transmitted intensity through a transparent medium, which is made by subtracting the intensity measured with the lamp on and no particles, I _lamp,λ, and a dark signal measurement, I _dark,λ, made by covering the optical port of the spectrometer. The spectral opacity, κ_λ = K _abs,λ L, is found from the Beer–Lambert law by

$$\kappa_{\lambda } = - \ln \left( {\frac{{I_{\lambda } }}{{I_{\lambda ,0} }}} \right) = - \ln \left( {\frac{{I_{t + e,\lambda } - I_{e,\lambda } }}{{I_{{{\text{lamp}},\lambda }} - I_{{{\text{dark}},\lambda }} }}} \right)$$

(8)

where I _λ,0 and I _λ are the incident and transmitted intensities and K _abs,l is the path-averaged spectral extinction coefficient. Assuming that the nanoparticle sizes are homogenous, the local absorption coefficient is related to the nanoparticle absorption efficiency by K _abs,λ = N _p πd ² _p /4Q _abs,λ, where N _p is the local nanoparticle number density.

3.3 Heat transfer model

Upon laser heating in LII, the nanoparticle temperature found from the spectroscopy model is related to the nanoparticle-size distribution through a cooling model

$$\frac{{\pi d_{\text{p}}^{3} \left( t \right)}}{6}\rho c_{\text{p}} \frac{{dT_{\text{p}} }}{dt} = q_{\text{net}} \left( {t,T_{\text{p}} } \right) = q_{\text{abs}} \left( t \right) - q_{\text{evap}} \left( {T_{\text{p}} } \right) - q_{\text{cond}} \left( {T_{\text{p}} } \right) - q_{\text{rad}} \left( {T_{\text{p}} } \right) ,$$

(9)

where q _abs(t) is the laser absorption as a function of time, ρ [28] and c _p [31] are the density and the specific heat of liquid silicon, and q _evap, q _cond, and q _rad are the heat losses due to evaporation, conduction, and radiation. The nanoparticle mass and diameter also change due to evaporation

$$\frac{{dm_{\text{p}} }}{dt} = - m_{\text{evap}} = - m_{\text{v}} \frac{{q_{\text{evap}} }}{{\Delta H_{\text{v}} }},$$

(10)

where m _v is the molecular mass of the evaporated vapor and ΔH _v is the latent heat of vaporization in units of J/molecule. The instantaneous nanoparticle diameter is then found from

$$d_{\text{p}} \left( t \right) = \left\{ {\frac{{6 m_{\text{p}} \left( t \right)}}{{\pi \rho \left[ {T_{\text{p}} \left( t \right)} \right]}}} \right\}^{{\frac{1}{3}}} .$$

(11)

Nanoparticle heating due to absorption by the laser pulse is given by

$$q_{\text{abs}} \left( t \right) = F_{0} q\left( t \right)\frac{{\pi d_{\text{p}}^{2} }}{4}Q_{{{\text{abs}},\lambda_{\text{laser}} }} ,$$

(12)

where F ₀ is the laser fluence (J/m²), q(t) is the temporal profile of the laser pulse (s⁻¹), and Q_abs,λlaser is the nanoparticle absorption cross section, calculated using Eq. (3). As noted above, q(t) is modeled as a Gaussian function with a FWHM ranging between 10 and 20 ns depending on the fluence. This is representative of the profile found by averaging laser pulses, although the individual laser pulses have a non-Gaussian shape due to their modes (also see the Experimental section above).

Since for the current experimental conditions the nanoparticle diameter (~30 nm) is smaller than the molecular mean free path in the bath gas (>1 μm), evaporation and conduction heat transfer take place in the free-molecular regime. The evaporation heat transfer rate is given by

$$q_{\text{evap}} \left( t \right) = \pi d_{\text{p}}^{2} N_{\text{v}}^{''} \Delta H_{\text{v}} = \pi d_{\text{p}}^{2} \frac{{n_{\text{v}} v_{\text{th}} }}{4} \Delta H_{\text{v}} ,$$

(13)

where N _v″ is the number flux of evaporated molecules above the nanoparticle surface, the number density, and the mean thermal speed of the evaporated species are given by n _v = p _v/(k _B T _p) and v _th = [8k _B T _p/(πm _v)]^1/2, respectively, where p _v is the vapor pressure of the evaporated species, k _B is Boltzmann’s constant, and m _v is the molecular mass of the evaporating species. (The number flux, N _v″ = n _v v _th/4, is derived from kinetics theory assuming that the velocity component of evaporated atoms normal to the surface obeys a shifted Boltzmann distribution [32].) Equation (13) neglects recondensation of evaporated species, which is reasonable given the large surface energy of the laser-heated nanoparticles relative to the potential well depth between the silicon atoms and the nanoparticle surface. For a bulk material, the vapor pressure is related to the latent heat of vaporization through the Clausius–Clapeyron equation,

$$p_{\text{v}}^{0} = C_{1} \exp \left( { - \frac{{\Delta H_{\text{v}} }}{{k_{\text{B}} T_{\text{p}} }}} \right) ,$$

(14)

which assumes phase equilibrium between the liquid and the vapor on either side of the phase interface. In this work, we adopt a model recommended by Sevast’yanov et al. [33], who calculated the equilibrium vapor pressure of silicon from other thermodynamic properties in the literature. Vapor pressure is reported in base-10 logarithm,

$$\log_{10} \left( {p_{\text{v}}^{0} } \right) = C_{1} /T + C_{2}$$

(15)

with p ⁰_v is in units of Pascal, ΔH _v = −C ₁ln10 and A = exp[C₂ln(10)]. Sevast’yanov et al. recommend C ₁ = −20,567 K and C ₂ = 10.94 and observe that the vapor almost entirely consists of atomic silicon over the temperatures important to LII. This value of C ₁ corresponds to a latent heat of vaporization of 6.53×10⁻¹⁹ J/molecule, or 389 kJ/mol. Table 1 and Fig. 3 show that these values are consistent with tabulated vapor pressure data presented by Desai [31], and coefficients reported by Tomooka et al. [34], inferred from Knudsen effusion cell experiments. While Sevast’yanov do not directly provide uncertainties for their recommended C ₁ and C ₂ values, Tomooka et al. report approximately 5% uncertainties on their experimentally derived C ₁ and C ₂ values [35], which we will adopt for an uncertainty analysis in this paper. The gray-shaded area in Fig. 3 reveals considerable uncertainty in the reported values for C ₁ and C ₂, especially at higher nanoparticle temperatures.

Table 1 Comparison of Clausius–Clapeyron parameters for modeling the vapor pressure of Si

When modeling nanoparticle evaporation, Eq. (15) should be modified using the Kelvin equation to account for the increased surface energy caused by interface curvature

$$p_{\text{v}} = p_{\text{v}}^{0} \exp \left[ {\frac{{4\gamma (T_{\text{p}} )}}{{d_{\text{p}} \rho RT_{\text{p}} }}} \right] = C_{1} \exp \left[ { - \frac{1}{{k_{\text{B}} T_{\text{p}} }}\left( {\Delta H_{\text{v}} - \frac{4\gamma }{{nd_{\text{p}} }}} \right)} \right] ,$$

(16)

where the surface tension γ is taken from Ref. [36] and n is the number density of the liquid silicon.

Free-molecular heat conduction between the nanoparticle and the bath gas is given by

$$q_{\text{cond}} = \pi d_{\text{p}}^{2} N_{\text{g}} \langle E_{0} - E_{i} \rangle = \pi d_{\text{p}}^{2} \frac{{n_{\text{g}} v_{\text{th}} }}{4}\alpha \langle E_{0} - E_{i} \rangle_{\rm{max}} ,$$

(17)

where n _g = p _g/(k _B T _g) and v _th = [8k _B T _g/(πm _g)]^1/2 is the number density and the mean thermal speed in the equilibrium gas, and <E ₀₋ E _i  > is the average energy transfer when a gas molecule scatters from the nanoparticle surface. The latter quantity is usually written in terms of the maximum value allowed by the second law of thermodynamics, < E ₀₋ E _i  > _max = 2k _B(T _p− T _g) in the case of a monatomic gas, and α is the thermal accommodation coefficient. The bath-gas temperature is taken to be 1560 K, following the emission spectroscopy measurements described above and assuming that the nanoparticles are in thermal equilibrium with the bath gas at the measurement location before the laser pulse. Results from LIF thermometry using the SiO A–X (2,0) electronic band [37, 38] also support the assumed gas-phase temperature.

In the case of free-molecular conduction within a gas mixture, Eq. (17) can be written for each species, using the corresponding partial pressure and molecular mass to calculate the incident number flux of each gas-phase species, and also a separate thermal accommodation coefficient for each species. These equations can then be combined into a single equation

$$q_{\text{cond}} = \pi d_{\text{p}}^{2} \left( {N_{{{\text{g}},{\text{Ar}}}} \alpha_{\text{Ar}} + N_{{{\text{g}},{\text{H}}_{2} }} \alpha_{{{\text{H}}_{2} }} } \right)\left\langle {E_{0} - \left. {E_{i}}\right\rangle} _{\rm{max}} \right. = \pi d_{\text{p}}^{2} \left( {N_{{{\text{g}},{\text{Ar}}}} + N_{{{\text{g}},{\text{H}}_{2} }} } \right)\alpha_{\text{eff}} \left\langle {E_{0} - \left. {E_{i}} \right\rangle}_{\rm{max}} \right.,$$

(18)

where α_eff is an effective thermal accommodation coefficient for the gas mixture, representing the average of the thermal accommodation coefficients for Ar and H₂ weighted by the respective incident number fluxes. The atmosphere within the reactor used in this study consists of 93% Ar and 7% H₂, based on the metered flow rates of gas, along with trace amounts of SiH₄ that can be neglected in the heat transfer analysis. Assuming that the bath-gas temperature is 1600 K, the corresponding incident number fluxes for Ar and H₂ are 9.82×10²⁵ and 2.35×10²⁵ molecules/(m²s), respectively. While the gas consists of 7% H₂, this species accounts for 20% of the gas–surface collisions, due to the higher molecular speed of the H₂ molecules compared to the more massive Ar atoms.

Of all the parameters in the spectroscopy and heat transfer models, the thermal accommodation coefficient is subject to the greatest level of uncertainty; to the best of our knowledge, the only attempt to quantify α for LII measurements on silicon nanoparticles is by Sipkens et al. [16], who found α ≈ 0.35 for Si/Ar and α ≈ 0.11 for Si/He through molecular dynamics calculations. The latter value was used to model the thermal accommodation coefficient for Si/H₂, based on similar molecular masses of H₂ and He. Using this value, Sipkens et al. recovered nanoparticle-size parameters from TiRe-LII data that were consistent with the Sauter mean diameter inferred from BET analysis [16]. Using Eq. (18) and the conditions in the present reactor corresponds to an MD estimate of α _eff = 0.30. The accuracy of this parameter will be revisited later in this paper.

Finally, the heat transfer due to thermal radiation from a nanoparticle is given by

$$q_{\text{rad}} = 4\pi \mathop \int \limits_{0}^{\infty } \frac{{\pi d_{\text{p}}^{2} }}{4}Q_{{{\text{abs}},\lambda }} \left( {T_{\text{p}} } \right)I_{{{\text{b}},\lambda }} \left( {T_{\text{p}} } \right)d\lambda$$

(19)

Figure 4 shows the relative magnitudes of qevap, qcond, and qrad as a function of Tp, for dp = 30 nm, pg = 100 mbar, Tg = 1500 K, and α = 0.3. The results show that evaporation heat transfer dominates conduction at temperatures greater than 2300 K, while radiation heat transfer is negligible relative to qevap and qcond, and is neglected in the remainder of this paper.

4 Results and discussion

4.1 Optical properties of silicon nanoparticles

The spectroscopy model (Eq. 4) used in LII has often been validated for the respective materials system using line-of-sight attenuation (LOSA) measurements [19, 20]. We follow the same approach here for Si nanoparticles formed in the plasma flow.

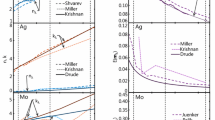
Figure 5a shows the ε_I and ε_II values required for Eq. (3) calculated by the Drude model (Eq. 5–7) in comparison with ellipsometry data reported in the literature [25, 39]. The optical properties of solid (dashed curves) and liquid silicon (solid curves) differ strongly because in the case of solid Si, the valence electrons are locked in covalent bonds while liquid silicon is metallic. At >400 nm, solid silicon can be modeled as a dielectric, having much smaller absorption cross sections compared to a similar-sized liquid Si nanoparticles. This strong variation in absorption and emission properties provides an option to observe the magnitude of crystallization in a nanoparticle-forming reactor. The demonstration will be part of future work.

Figure 5b shows the spectral opacity measured through the aerosol at 300 mm above the microwave antenna. The measured values match the calculated Q _abs,λ based on the Drude model for ε _λ and assuming liquid particles (Q _abs,λ ≫ Q _sca,λ within the Rayleigh regime (d _p ≪ λ) [22]). The good agreement verifies the calculation based on the Drude model. The data could not have been fitted with the absorption of solid silicon.

The temperature of the liquid nanoparticles at the same location was found to be 1559±3 K by fitting the incandescence portion of the signal (~I _e,λ − I _dark,λ) to Eq. (2), which is below the melting temperature of bulk silicon (1683 K [6]). While this may appear inconsistent with the Drude-like radiative properties of molten silicon, it is well known that the melting temperature for nanoparticles decreases with the particle size due to the contribution of the surface energy to the overall Gibbs free energy [6, 40]. Therefore, liquid silicon nanoparticles at 1559 K are plausible and consistent with recent experimental measurements [6]. Spectrally resolved emission measurements might therefore be suitable to determine the melting point of nanoparticle entities.

4.2 Time-resolved particle temperature measurements

As noted above, because the silicon nanoparticles absorb and emit thermal radiation in the Rayleigh regime, the spectroscopic model can be used to infer nanoparticle temperatures as well as the unknown constant C _k in Eq. (4) without direct knowledge of d _p. Time-resolved spectral measurements taken with the streak camera can therefore be used to determine the temporal variation in particle temperature even during evaporating conditions. For this purpose, the streak camera spectral range is set to 425–700 nm, with an equivalent pixel width of 0.4 ns; this range should include the peak incandescence for particle temperatures greater than 2900 K and is therefore well suited for pyrometry.

For LII measurements, the laser fluence of F ₀ = 8 mJ/mm² was chosen because at this value the peak temperature crosses the evaporation temperature (cf. Figure 8). This leads to a maximum LII intensity without significantly affecting the initial particle size during laser heating. Figure 6 shows the temperature decay and the constant C _k as a function of time.

Fig. 8

Simulated particle temperatures (lines) and pyrometrically measured values (symbols) as a function of laser fluence F ₀. The dashed line shows the boiling point of silicon at 100 mbar [33]. The maximum temperature increases linearly with fluence below 5 mJ/mm²/3000 K because the laser pulse energy is balanced by the sensible energy of the nanoparticle. Beyond this point, a larger fraction of the laser pulse energy is lost through evaporation. The short duration of the laser pulse results in superheating

Since the streak camera images contain approximately 350,000 pixels, a direct “all at once” regression between simulated and measured images is prohibitively time-consuming. Instead, we estimate [C _k , T _p(t _k )] at each measurement time by regressing Eq. (4) to the k ^th row of pixels. While one would expect C _k to be constant over the entire image, Fig. 6 shows that this parameter initially drops abruptly just after reaching the peak temperature and then approaches a constant value. This problem is discussed in Sect. 4.4.

The right graph in Fig. 7 shows the fit between the extracted experimental spectral profiles from the streak camera image (left panel) and simulated incandescence spectra at 0 (peak incandescence), 50, and 100 ns. Even though the experimental spectra show considerable noise, the simulated profiles closely match the experimental ones in all cases, even at the peak incandescence.

4.3 Analysis of peak temperatures

We compare the temperatures predicted with the full heat transfer model, Eq. (9), to those inferred from the streak camera spectra at various laser fluences. As noted above, the influence of the streak camera instrument function on the signal is most pronounced near the peak temperature, where the temporal variation of J _λ is highest. Accordingly, we compare the measured and modeled temperatures at t = 0 ns (peak streak image incandescence/modeled temperature), as well as 50 and 100 ns after the peak (cf., Figure 7). Figure 8 shows that the pyrometric temperature tracks the peak temperature. Both of these temperatures increase linearly with the laser fluence until approximately 8 mJ/mm², at which point T _p increases more slowly with increasing F ₀.

The transition from a linear to sublinear increase in T _p,max with F ₀ occurs near the boiling temperature of silicon. At temperatures below 3000 K, the peak nanoparticle temperature is determined largely by equating the change in sensible energy, left-hand side of Eq. (9), to q _laser, thus T _p,max increases linearly with F ₀. At higher temperatures, an increasing fraction of the laser heating is lost to q _evap, cf. Figure 4, which reduces dT _p,max/dF ₀. The nanoparticle temperatures exceed the boiling point of Si because the laser heating rate exceeds the evaporation rate, which is limited by the fraction of silicon atoms having energies that exceed the cohesive energy of the liquid state, ∝ exp[-ΔH _v/(k _B T _p)]. Consequently, the excess laser heating increases the sensible energy of the nanoparticle, which causes superheating.

4.4 Temporal variation of the scaling factor, C_k

As discussed above, the scaling factor, C _k, in Eq. (4) relates the detection measurement to the incandescence from the nanoparticles, and accounts for factors that include the nanoparticle volume fraction and the photoelectric efficiency of the detectors. Intriguingly, however, Fig. 6 shows that the scaling factor C _k is largest close to the laser pulse/peak temperature and then decays to a near constant value over approximately 50–100 ns. Further measurements at fluences ranging from 3 to 100 mJ/mm² reveal a rather complex fluence dependence: Below 5 mJ/mm², no change in C _k was observed (regime i), between 5 and 30 mJ/mm², a fast descending C _k after the laser pulse was measured (regime ii/Fig. 6), and above 30 mJ/mm², an ascending C _k after the laser pulse was measured (regime iii).

The most obvious explanation for a descending C _k after the laser pulse at high fluences (regime ii) is due to evaporation-induced loss of particle volume fraction. According to the evaporation model, at 8 mJ/mm² shown in Fig. 6, the evaporation of the nanomaterial is approximately 5% of the particle mass, which should correspond to a 5% decrease in the scaling factor during the evaporation phase, while we observe a reduction in C _k of almost 50%. Therefore, this phenomenon cannot be explained by evaporation alone.

Additional signal contributions from nonthermal origin (anomalous cooling, enhanced absorption, Bremsstrahlung [41, 42]) can impact the signal level during and shortly after the laser pulse. Variations in C _k with fluence could be evidence of the formation of a microplasma surrounding the nanoparticles, and inverse Bremsstrahlung heating due to the strong coupling of the laser and the plasma. One would expect that Bremsstrahlung from the plasma would contribute to the observed LII signal, and thus equate to a hypothetical aerosol having a larger nanoparticle volume fraction (and larger C _k) [42, 44]. In contrast to thermal particle radiation (I _thermal ~ σT ⁴_p ), Bremsstrahlung scales with I _{Bremsstrahlung} ~ T ^1/2_e [43] to the electron temperature. Above 5 mJ/mm² (regime ii), due to the square-root behavior of Bremsstrahlung, this process can significantly contribute to the measured signal intensity.

The increasing scaling factor after the laser pulse in regime iii can be attributed to the instrument response function described above, which results is a temporal blurring of the measured intensities. The finite instrument response function has the largest effect in cases of rapid temporal signal intensity variations at high laser fluences around the laser pulse/peak temperature. The nonlinear signal increase with temperature biases the derived mean temperature to higher values. In contrast, the lack of intensity at the lower temperature decreases the overall intensity, which results in an underestimation of the scaling factor for the mean intensity. For this work, we observed a reduction in the scaling factor C _k at the laser pulse due to blurring of the intensity profiles by an instrument function at the peak temperature for the high-fluence regime (iii). This indicates that the temporal resolution of the detector is too low at these fluences. A higher temporal resolution yields an almost constant C _k after the laser pulse but is not suitable for LII analysis.

For fluences above 30 mJ/mm², the increase in C _k after the laser pulse could be explained if the blurring by the instrument function exceeds the contribution from Bremsstrahlung. So far, it is not fully clarified which of the potential nonthermal effects causes this behavior. The possible formation of a microplasma enveloping the nanoparticle during laser heating, and its influence on the detected LII signal, is the focus of ongoing research.

4.5 Particle sizing through Bayesian inference

We next estimate the nanoparticle size, d _p, and thermal accommodation coefficient, α, from the pyrometrically inferred temperature decay using the heat transfer model defined above (Eq. (9)). It is important to acknowledge that noise in the pyrometric temperature data, as well as the uncertainties in the evaporation heat transfer model, means that many candidate solutions of [d _p,α] could explain the data with almost equal probability. Consequently, we calculate d _p and α using the Bayesian methodology; this technique allows for a statistically rigorous quantification of uncertainty attached to the inferred variables, and also permits incorporation of information known prior to the measurements to reduce this uncertainty.

The quantities of interest, x = [d _p,α]^T, and noisy pyrometric temperature data T = [T _p,₁,T _p,₂…,T _p, _N ]^T are treated as stochastic variables. Rather than treating the evaporation model parameters as deterministic, we also model them as stochastic variables that obey a distribution, θ = [C ₁,C ₂]^T. The variables in θ are called “nuisance parameters” because they are not the focus of the inference process but must also be inferred to properly account for uncertainty in the quantities of interest. These variables are related through Bayes’ equation

$$p\left( {{\mathbf{x}},{\varvec{\uptheta}}|{\mathbf{T}}} \right) = \frac{{p\left( {{\mathbf{T}}|{\mathbf{x}},{\varvec{\uptheta}}} \right)p_{\text{pr}} \left( {\mathbf{x}} \right)p_{\text{pr}} \left( {\varvec{\uptheta}} \right)}}{{p_{\text{pr}} \left( {\mathbf{T}} \right)}}$$

(20)

where p(x,θ|T) is the joint posterior probability density of x and θ conditional on the observed data in T, p(T|x,θ) is the likelihood of the observed data occurring for a hypothetical x, p _pr(x) = p _pr,dp(d _p) p _pr,α(α) and p _pr(θ) = p _pr,C1(C ₁) p _pr,C2(C ₂) are the joint prior probabilities of the parameters in x and θ based on the knowledge available about these parameters before the measurement, and p(T) is the evidence,

$$p\left( {\mathbf{T}} \right) = \mathop \int \mathop \int p\left( {{\mathbf{T}}|{\mathbf{x}},{\varvec{\uptheta}}} \right)p_{\text{pr}} \left( {\mathbf{x}} \right)p_{\text{pr}} \left( {\varvec{\uptheta}} \right)d{\mathbf{x}}d{\varvec{\uptheta}}$$

(21)

used to scale Eq. (20) so that it satisfies the law of total probability.

If the temperature measurements are independent at each measurement time and the noise is normally distributed, the likelihood is given by

$$p\left( {\varvec{T}|{\mathbf{x}},{\varvec{\uptheta}}} \right) \propto \exp \left\{ { - \mathop \sum \limits_{j = 1}^{Nt} \frac{{\left[ {T_{{{\text{p}},{\text{j}}}} - T_{\text{p}} \left( {\mathbf{x},\varvec{\uptheta} , t_{\text{j}} } \right)} \right]^{2} }}{{2\sigma_{{{\text{T}},j}}^{2} }}} \right\},$$

(22)

where T _p(x,θ,t _j ) are found by solving Eqs. (9) and (10) with the unknown particle size d _p and the first pyrometric temperature in T as initial conditions.

Finding the values of x and θ by minimizing the summation in Eq. (22), equivalent to naïve least-squares minimization, returns the maximum likelihood estimate [x,θ]_MLE, which is the most probable value [x,θ] based on the observed data. There are two key problems with using this estimate: (1) The measurement noise contaminating the data and the large number of degrees of freedom give p(T|x,θ) a flat topography surrounding the maximum likelihood estimate. Reporting a single point estimate only, therefore severely understates the uncertainty in these inferred parameters. (2) This process neglects additional information about x = [d _p,α]^T and, especially, θ = [C ₁,C ₂]^T known prior to the LII measurement, which can dramatically reduce the uncertainty in the inferred values.

This additional information is incorporated into the inference through the prior probabilities in Eq. (21). Specifically, by definition d _p > 0 and 0 ≤ α ≤ 1, which corresponds to

$$p_{{{\text{pr}},d{\text{p}}}} \left( {d_{\text{p}} } \right) \equiv \left\{ {\begin{array}{*{20}c} 1 & {d_{\text{p}} > 0} \\ 0 & {\text{otherwise}} \\ \end{array} } \right. \quad p_{{{\text{pr}},\alpha }} \left( \alpha \right) \equiv \left\{ {\begin{array}{*{20}c} 1 & {0 \le \alpha \le 1} \\ 0 & {\text{otherwise}} \\ \end{array} } \right..$$

(23)

In other words, values of d _p < 0 and α < 0 or α > 1 have zero probability. Priors for C ₁ and C ₂ are derived from values for these parameters reported in the literature, e.g., Refs. [31, 33–35]. Specifically, Gaussian prior densities for C ₁ and C ₂ are prescribed, centered on the parameters recommended by Sevast’yanov et al. [33] with standard deviations equation to 2.5% of the mean values (corresponding to a standard error of ±5%), based on experimental uncertainties reported by Tomooka et al. [34]. Modeling the C ₁ and C ₂ priors as normal distributions is consistent with the principle of maximum entropy [45] which states that the prior should only contain testable information, and is also mathematically convenient, since they can easily be incorporated into the likelihood function, Eq. (22), which is also normally distributed. These uncertainties roughly correspond to the shaded region shown in Fig. 3.

Maximizing p(x,θ|T) ∝ p(T|x,θ) p _pr(x) p _pr(θ) provides the maximum a posteriori (MAP) estimate, x _MAP, which is the most probable estimate for [d _p,α,C ₁,C ₂] considering both the observed temperature data and prior knowledge about the evaporation model parameters. The influence of the nuisance variables can be removed by integrating over their domain, leaving a 2D-marginalized posterior probability density

$$p\left( {{\mathbf{x}}|{\mathbf{T}}} \right) = \mathop \int \limits_{\varvec{\theta} }^{{}} p\left( {{\mathbf{x}},{\varvec{\uptheta}}|{\mathbf{T}}} \right)d{\varvec{\uptheta}} = \mathop \int \limits_{ - \infty }^{\infty } \mathop \int \limits_{ - \infty }^{\infty } p\left( {{\mathbf{x}},{\varvec{\uptheta}}|\mathbf{T}} \right)dC_{1} dC_{2} ,$$

(24)

which can then be marginalized into 1D probability densities for d _p and α,

$$p\left( {d_{\text{p}} |{\mathbf{T}}} \right) = \mathop \int \limits_{0}^{1} p\left( {{\mathbf{x}} |{\mathbf{T}}} \right){\text{d}}\alpha , p\left( {\alpha |{\mathbf{T}}} \right) = \mathop \int \limits_{0}^{\infty } p\left( {{\mathbf{x}} |{\mathbf{T}}} \right)dd_{\text{p}} .$$

(25)

Finally, these densities can be summarized by Bayesian credibility intervals (loosely interpreted as confidence regions) that contain a prescribed probability density, e.g., 90%.

An estimate of the measurement noise contaminating the pyrometric temperatures is needed to quantify the likelihood, Eq. (22). While this parameter can, in principle, be found from the variance of temperatures inferred from n independent streak images, we instead estimate σ _T,j from the residuals between the pyrometrically inferred temperatures and a smooth interpolating curve. The residuals are approximately equal in magnitude at all measurement times, and obey a normal distribution with a standard deviation of ~100 K.

The nanoparticle diameter and thermal accommodation coefficient are inferred from an LII measurement taken using a laser fluence of 8 mJ/mm². Figure 9 shows the pyrometric data, the modeled data corresponding to the MAP estimate, as well as the posterior density contours, p(x|T), and marginalized probabilities for d _p and α. The results show a MAP estimate of x _MAP = [20.6 nm, 0.33]^T, with 90% credibility intervals d _p,90%∈[0, 39 nm] and α_90% = [0, 0.65]. These credibility intervals can be interpreted to mean that the “true” values lie within the corresponding interval with 90% probability, in view of the noisy temperature and uncertainties in the evaporation model. These ambiguous results are not surprising, given that nanoparticle cooling is dominated by evaporation heat transfer (cf. Figure 4) over the recorded temperature range. The wide credibility intervals for d _p are due to uncertainty in the evaporation model, although this interval contains the primary particle sizes inferred from the TEM analysis, shown in Fig. 1. Significant uncertainty in the thermal accommodation coefficient is expected because the temperature decay is nearly independent of α. The MAP estimate for α is close to zero, which is unlikely since there should be considerable energy transfer when Ar and H₂ molecules scatter from the molten Si nanoparticle. Although this technique does not account for uncertainty in gas temperature and pressure, a parametric analysis showed that the inferred parameters were insensitive to variations in p _g and T _g, due to the dominance of evaporation during the relevant phase of particle cooling.

Fig. 9

Results of the Bayesian inference of dp and α, for a fluence of 8 mJ/mm2 using pyrometric temperatures starting from 15 ns after the peak incandescence. Contours denote marginalized posterior probabilities, plotted on a log scale. Top: An analysis of a single streak image gives a robust estimate of dp but not α because nanoparticle cooling is dominated by evaporation at these temperatures. Center: Combining the first streak image with a second one (with 1 μs delay) produces a more robust MAP estimate for the thermal accommodation coefficient since conduction heat transfer becomes more important at lower temperatures. Bottom: Analysis of dp and α neglecting the uncertainty of C1 and C2

We next consider a second set of available data made by patching together streak camera images recorded with a temporal offset of 1 μs. Bayesian analysis of these data, also shown in Fig. 9, gives a different MAP estimate, x _MAP = [25.1 nm, 0.19]^T, but nearly identical 90% credibility intervals, d _p90% ∈ [0, 43 nm] and α_90% ∈ [0, 0.35]. This result highlights that measurement data at longer cooling times provide little additional information about the particle size, but shift the MAP estimate of α toward a more physical value as the model becomes more sensitive to heat conduction. The credibility interval for the thermal accommodation coefficient almost contains the MD-inferred value of ~0.3 from Sipkens et al. [16].

Finally, the bottommost plot in Fig. 9 shows the posterior probability and credibility intervals obtained assuming fixed values for C ₁ and C ₂. This results in much narrower posterior densities for d _p and α, but this treatment does not reflect the true state of knowledge in the evaporation model, as indicated in Fig. 3. Consequently, neglecting this uncertainty would lead one to have more confidence in the recovered parameters than can be justified based on uncertainty in the evaporation model.

5 Conclusions

Time-resolved laser-induced incandescence (TiRe-LII) was used for the investigation of sizes d _p of gas-borne silicon nanoparticles in microwave-plasma-heated reactive flows. The quantitative interpretation of TiRe-LII signals requires the knowledge of spectroscopic properties of the laser-heated material as well as heat transfer models. Model parameters as well as underlying measurements are prone to uncertainties and experimental error. Knowing all these influences allows a statistical analysis by Bayesian inference that provides not only most likely values of the parameters of interest but also their uncertainties in terms of credible intervals.

The radiative properties of Si nanoparticles were characterized in situ using line-of-sight attenuation (LOSA) measurements. The data show strong evidence that the particles are liquid at the measurement location within the reactor, which is confirmed by the fact that the spectral transmittance can be explained using Drude theory that applies to metals, and that silicon metallizes upon melting. Based on this model, time-resolved particle temperatures were determined from spectrally and temporally resolved measurements of the LII signal using a streak camera system.

We subsequently presented a detailed heat transfer model that considered parametric uncertainty in the evaporation submodel, and a free-molecular heat conduction model that considers gas mixtures. The underlying thermophysical properties of liquid silicon show large uncertainties for the observed temperatures. Consequently, the nanoparticle sizes were calculated by a heat conduction model that was extended by Bayesian inference to the latent heat of evaporation ΔH as nuisance parameter with the published standard deviation. While preceding work neglected the uncertainty of these values which led to a strong underestimation of uncertainty, this work shows a rigorous inclusion of known uncertainties into the heat transfer model. This widens the credible intervals for d _p and α, but it accurately reflects the state of knowledge about these quantities in view of the uncertainty associated with the evaporation parameters.

More broadly, this work highlights the application of TiRe-LII to aerosols of synthetic nanoparticles, where thermophysical properties and their uncertainties are well documented. This enables a rigorous uncertainty analysis on the parameters of interest d _p, α, C ₁ and C ₂ by Bayesian inference. The strategy demonstrated here in case of silicon can be transferred to other inorganic nanoparticles as well as soot.

At higher fluences (>10 mJ/mm²), we start to observe line emissions which can be attributed to thermally excited monoatomic silicon atoms at 288 nm, which does not interfere with the temperature determination (450–700 nm). Ongoing research is focused on combining the atomic emission intensity with the evaporation submodel presented here to increase the significance of the evaporation-based parameters C ₁ and C ₂, and improve the robustness of the derived quantities. Ambiguity about the scaling factor C _k and its possible relationship to a microplasma are also a focus of ongoing research. This work presents a first assessment of processes causing the non-constant behavior of C _k and needs to be reviewed for future measurements and other material systems.