1 Introduction

Over half a century of research on nanotechnology [1] has contributed to rapid development in nanoresonators in terms of mass detection [2, 3], signal processing [4, 5] and energy collection [6,7,8]. In particular, carbon nanotube (CNT)-based resonators are praised for excellent performance originating from their high Young’s modulus and low density [9, 10]. These unique devices have enabled the application fields to be expanded. For instance, in Chaste’s work, these devices have represented a minimum mass resolution of 1.7 yg, which is at least two orders below other electromechanical systems [11, 12]. Such high mass sensitivity allows us to accurately monitor the absorption of naphthalene molecules that are used for expelling cockroaches. In addition, the quality factor of CNT is up to 5 million at 30 mK, offering new chances for optomechanical experiments in the quantum regime [9]. In gas detection, different gas atoms in the surrounding environment were distinguished through the velocity shift of impulse wave propagating in the CNT [13]. Moreover, with the help of pump excitation, parameter amplification and self-oscillation will be observed in the CNT resonator, contributing to the realization of ultralow force sensing [14]. Despite the successful application above, CNT also has disadvantages as a resonator material. Most significantly, it has poor frequency self-tuning and, therefore, requires strong external drives and complicated calculation models to control detection ranges and accuracy [15, 16]. The ideal resonator material should own high sensitivity, low dissipation and precise frequency self-tuning properties. It is, therefore, highly desirable to build a new structure to meet the abovementioned requirements.

Boron nitride nanotubes (BNNTs) offer a unique alternative to CNT as resonators with the piezoelectrically tunable property [17]. Especially, the coaxial heterostructure with core CNT sheathed by outer BNNT (CNT@BNNT), which was first fabricated in 2003 by packing C60 molecules in BNNT [18], shows more promise. In addition to Young’s modulus comparable to that of CNT and BNNT [19, 20], CNT@BNNT is fairly stable under terrible circumstances, such as squashed deformation and high temperature, which provides an excellent candidate for nanocables [21, 22]. Furthermore, benefiting from the complementary properties of CNT and BNNT, the conductive channel of CNT@BNNT remains independent and protected against any external perturbation [23]. Although the mechanical and electrical properties of CNT@BNNT have been thoroughly studied, their performance as resonators has not been notably probed so far. The resonant frequency of CNT@BNNT was demonstrated to decrease with the length increase in previous works [24, 25]. Yet, to date, little research has been done on the frequency and intrinsic dissipation self-tuning of CNT@BNNT. The application of the CNT@BNNT resonator is lacking in investigation as well.

Hence, in this work, we adopt molecular dynamics (MD) simulations to investigate piezoelectric tuning on the resonant frequency and intrinsic dissipation of (17,0) BNNT, (5,5) CNT, and the coaxial heterostructure of an inner (5,5) CNT and an outer (17,0) BNNT (CNT(5,5)@BNNT(17,0)) under a certain electric field range. During the vibration simulation, the resonant frequency and quality factor are largely calculated with the displacement of the center of mass (COM). Axial Stress and piezoelectric constant variation are additionally analyzed to further reveal the piezoelectric tuning mechanism and the distinction of tuning effect among three resonators. In the end, we evaluate the performance of CNT(5,5)@BNNT(17,0) in mass detection through mass resolution.

2 Computational methods

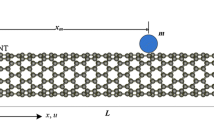
Figure 1 only shows the atomic structure of the bridged CNT(5,5)@BNNT(17,0)-based resonator owing to similar models of three bridged resonators. The distance between the inner and outer layer of the heterostructure is close to 3.4 Å, which is the most stable interlayer distance of the multi-walled nanotubes [26]. To accurately describe the interaction between atoms, the widely used adaptive intermolecular reactive empirical bond order (AIREBO) potential was chosen to describe the carbon–carbon interactions [27]. It is reported that the BNNT piezoelectric coefficient and the potential energy of boron nitride nanoribbons obtained by MD simulations using Tersoff potential agree well with those of the first-principle calculations [7, 17]. In addition, the deformation behaviors of an armchair BNNT under tensile strains have been successfully studied by Tersoff potential [28], so it is feasible to utilize the Tersoff potential to model the boron–nitrogen interactions [29]. As for the atomic interactions between layers, the 12–6 Lennard–Jones was used, given by the following equation:

$$\Phi_{ij} (r) = 4\mu \varepsilon \left[ {\left( {\frac{\sigma }{r}} \right)^{12} - \left( {\frac{\sigma }{r}} \right)^{6} } \right],$$
(1)

where μ is used to adjust the coupling strength between BNNT and CNT, ε is the well depth, σ is the equilibrium separation, and r is the distance between two paired atoms. The value of σ and ε in this work were chosen as εB-C = 5. 96 meV, εN-C = 3.69 meV, σB-C = 3.53 Å, σN-C = 3.35 Å [30, 31]. The electron distribution of the outer BNNT and inner CNT in the CNT(5,5)@BNNT(17,0) does not change significantly compared with that of the single tube [19], so the effective charges, similar to the single BNNT and CNT, were set as + 2.6e, − 2.6e and 0 for boron, nitrogen and carbon atoms, respectively [32]. The size of the simulation system was 37.5 Å × 37.5 Å × 118.6 Å with a fixed boundary condition in every direction.

Fig. 1
figure 1

Schematics of bridged CNT(5,5)@BNNT(17,0)-based resonator (two ends are fixed). The red arrow represents the initial displacement direction. Here the blue, pink, and gray balls represent the nitrogen, boron, and carbon atoms, respectively

Full size image

To calculate the resonant frequency of the structure, the following procedure was performed. First of all, the conjugate gradient method was used to minimize the system energy. Then, the optimized structure was relaxed in the NVT (constant number of particles, volume, and temperature) ensemble for 150 picoseconds (ps). To minimize the effects of thermal fluctuation, the Noose–Hoover thermostat [33] was utilized and the temperature was kept at room temperature 300 K. At the same time, the velocity Verlet algorithm was utilized to update the positions and velocities of atoms at a time step of 1 femtosecond (fs). Next, the atoms at both ends were fixed and a certain displacement along the positive Y-axis at the midpoint of the model was imposed. Meanwhile, the NVT ensemble was switched to the NVE (constant number of particles, volume, and energy) ensemble to maintain the conservation of system energy. To avoid geometric nonlinearity, the displacement distance did not exceed 2% of the total length. At last, the displacement load was removed and the displacements of the COM along the Y-axis were recorded for 500 ps. The resonant frequency of the structure was obtained by applying the fast Fourier transform method to the displacements. All the MD simulations were carried out using LAMMPS software [34].

3 Results and discussion

3.1 Piezoelectric tuning comparison

3.1.1 Resonant frequency

To characterize the piezoelectric tuning, the resonance process of three resonators is investigated under five different axial electric fields ranging from − 10 V/nm to 10 V/nm. The axial electric field is applied between the two fixed ends of resonators with a length of 10 nm, as shown in the inset of Fig. 2. It can be seen from Fig. 2 that on one hand, without the external electric field, the resonant frequency of (5,5) CNT about 198 GHz, is the smallest, while (17,0) BNNT presents the highest resonant frequency value of 276 GHz among the three resonators. These results reasonably agree with that calculated through the continuum model [35, 36]. On the other hand, enormous differences exist in the resonant frequency of three resonators under the axial electric field. It is found that both the resonant frequencies of (17,0) BNNT and CNT(5,5)@BNNT(17,0) increase linearly with the axial electric field varies from − 10 V/nm to 10 V/nm. The only discrepancy is that the increment of the resonant frequency of (17,0) BNNT is nearly up to 50 GHz, larger than that of CNT(5,5)@BNNT(17,0). In contrast, the resonant frequency of (5,5) CNT is not affected by the axial electric field and remains at 198 GHz, because CNT is a non-piezoelectric material.

Fig. 2
figure 2

Resonant frequency variation of (17,0) BNNT, (5,5) CNT, and CNT(5,5)@BNNT(17,0) with the axial electric field. The inset shows the bridged CNT(5,5)@BNNT(17,0)-based resonator subject to an axial electric field

Full size image

In the light of the piezoelectricity theory [37], for a zigzag BNNT, an axial electric field generates normal stress, known as residual stress. Thus, to further reveal the mechanism of piezoelectric tuning, we calculated the residual stress of (17,0) BNNT, (5,5) CNT, and CNT(5,5)@BNNT(17,0) under different axial electric fields. As is illustrated in Fig. 3, the residual stress of (17,0) BNNT is positively correlated with the axial electric field within the − 10 V/nm to 10 V/nm range, which implies that tensile deformation exists in the (17,0) BNNT under the positive electric field, and compressive deformation exists under the negative electric field. A similar phenomenon is still observed in CNT(5,5)@BNNT(17,0) though the variation range of its residual stress is smaller than that of (17,0) BNNT. However, regardless of the positive or negative electric field applied, the residual stress of (5,5) CNT is 0. According to the results that the residual stress varies with the axial electric field, it is supposed that the principle of piezoelectric tuning effects on the resonant frequency might be closely related to the axial deformation of these structures.

Fig. 3
figure 3

Residual stress of (17,0) BNNT, (5,5) CNT, and CNT(5,5)@BNNT(17,0) as a function of the axial electric field

Full size image

To verify the supposition, the resonant frequency variations of (17,0) BNNT and CNT(5,5)@BNNT(17,0) by applying the axial mechanical deformation are investigated and compared with the results obtained by applying the axial electric field. The resonant frequency under mechanical deformation is illustrated in Fig. 4a, which is largely identical to that obtained by applying the electric field. Specifically, the difference between resonant frequency under the same residual stress obtained by two methods, depicted in Fig. 4b, is not beyond 2 GHz, evidencing that the tuning effect of the axial electric field on the resonant frequency is mostly comparable to that of the mechanical deformation. Since the charged particles are subject to the axial electric field force, the axial mechanical deformation is generated in the resonator with two ends fixed. In addition, the deformation direction is supposed to depend on the atom types closest to the fixed ends. A simple example is that compared with our results, the (8,0) BNNT resonator studied in the previous work [17], owing to the opposite direction of resonator placement, shows an inverse deformation direction under the same axial electric field. According to Cao’s study [38], a critical buckling load is produced when both ends of a resonator are fixed without an axial electric field. The ratio of the axial load to the critical buckling load, positively correlated with the resonant frequency of structures, changes with the axial strain induced by the axial mechanical deformation and ultimately influences the resonant frequency of structures, consistent with the conclusion obtained by the spatial frame structure method [39].

Fig. 4
figure 4

a Resonant frequency versus different residual stress of (17,0) BNNT and CNT(5,5)@BNNT(17,0) under the axial mechanical deformation. b Comparison in the resonant frequency of (17,0) BNNT and CNT(5,5)@BNNT(17,0) with identical residual stress obtained by the axial deformation and the axial electric field, respectively

Full size image

Aside from the residual stress, the piezoelectric constant (e) that precisely measures the polarization of the piezoelectric body[40] is another significant index to be concerned with. Its value is calculated by [37] \(e = \left| {\frac{\partial \sigma }{{\partial E}}} \right|\), where σ is the residual stress, and E is the axial electric field. It is noted that e is the slope of the line in Fig. 3. The axial piezoelectric coefficient of the (17,0) BNNT is 0.162, consistent with the result in the previous molecular mechanics calculations[41]. In contrast, the axial piezoelectric coefficient of CNT(5,5)@BNNT(17,0) is 0.1, much lower than that of (17,0) BNNT. The discrepancy of the piezoelectric constant mainly results from the non-piezoelectric inner layer of CNT(5,5)@BNNT(17,0). The electric field force applied to CNT(5,5)@BNNT(17,0) is mainly the same as that to (17,0) BNNT due to the non-piezoelectric (5,5) CNT. Nevertheless, the volume of CNT(5,5)@BNNT(17,0), attributed to the carbon atoms in the inner layer, is larger than that of (17,0) BNNT, leading to the lower residual stress of CNT(5,5)@BNNT(17,0) under the same axial electric field. Finally, the piezoelectric coefficient of CNT(5,5)@BNNT(17,0), owing to the same electric field that applied in (17,0) BNNT, decreases as well.

3.1.2 Intrinsic dissipation

With the exception of resonant frequency, energy dissipation is another important indicator of resonators, generally characterized by the quality factor (\(Q\)). The low dissipation suggests the high quality factor. Here only the intrinsic dissipation is evaluated, while the external dissipation is out of our consideration. The root mean square (RMS) displacement of the COM is utilized to estimate the quality factor, since the thermal motion of atoms has been averaged without further post-processing [42]. It is noted that the decaying relationship between the RMS displacement and time, as shown in the red fitting curve of the inset of Fig. 5, is exponential (\(e^{ - \xi \omega t}\), where \(\xi\) is the damping ratio and \(\omega\) is the resonant angular frequency) under the assumption of vibration with nothing but one mode. Then the quality factor of the resonator is determined as \(Q = \frac{1}{2\xi }\). As delineated from Fig. 5, similar to the corresponding resonant frequency, the larger positive axial electric field contributes to the higher quality factor of (17,0) BNNT and CNT(5,5)@BNNT(17,0), whereas the larger negative axial electric field leads to the lower counterparts. On the contrary, the quality factor of (5,5) CNT, regardless of the change of the axial electric field, remains at 2049 [43].

Fig. 5
figure 5

Quality factors of three resonators plotted as a function of the axial electric field. The inset shows the RMS displacement of the COM of CNT(5,5)@BNNT(17,0) under no axial electric field. The red line is the fitting curve of the RMS displacement

Full size image

To further elucidate the principle of piezoelectric tuning on the intrinsic dissipation of (17,0) BNNT and CNT(5,5)@BNNT(17,0), the classic theory of energy dissipation is utilized. In general, thermoelastic damping is one of the main dissipation sources at room temperature [44]. According to the theory of heat conduction [45], the expression for thermoelastic damping of a resonator is given by

$$Q_{{{\text{TED}}}}^{ - 1} = \frac{1}{2\pi }\frac{\Delta Q}{W} = \frac{{{\text{Im}} \left\{ {k \cdot \int_{0}^{L} {EI\left( {\frac{{{\text{d}}^{{2}} Y_{0} (z)}}{{{\text{d}}z^{2} }}} \right)}^{{2}} {\text{d}}z} \right\}}}{{\left( {\int_{0}^{L} {EI\left( {\frac{{{\text{d}}^{{2}} Y_{0} (z)}}{{{\text{d}}z^{2} }}} \right)}^{{2}} {\text{d}}z + F\int_{0}^{L} {\left( {\frac{{{\text{d}}Y_{0} (z)}}{{{\text{d}}z}}} \right)}^{{2}} {\text{d}}z} \right)}},$$
(2)

where ΔQ is the energy dissipation within per vibration period, W is the maximum mechanical energy stored in the resonator, k is a constant related to the inherent properties of resonators, such as thermal expansion, Young’s modulus, and so on. \(\frac{1}{2}\int_{0}^{L} {EI\left( {\frac{{{\text{d}}^{{2}} Y_{0} (z)}}{{{\text{d}}z^{2} }}} \right)}^{{2}} {\text{d}}z\) is the strain energy induced by the buckling deformation, where E is Young’s modulus, I is the moment of inertia of the cross section, Y0(z) is the deflection of the resonator. \(\frac{1}{2}F\int_{0}^{L} {\left( {\frac{{{\text{d}}Y_{0} (z)}}{{{\text{d}}z}}} \right)}^{{2}} {\text{d}}z\) is the energy associated with the elongation of resonators, where F is the force applied in the axial direction. In this study, tension deformation is generated as the positive electric field is applied, increasing the energy related to the elongation of resonators. Since the strain energy caused by the bending deformation is hardly influenced by the elongation of the resonator, the maximum mechanical energy stored in the resonator, then increases as well. In the end, the energy dissipation arising from thermoelastic damping decreases. Commonly, aside from thermoelastic damping, phonon scattering is another intrinsic dissipation mechanism of resonators. Considering that the simulated length of CNT(5,5)@BNNT(17,0)-based resonator is much smaller than the mean free path of phonons, the phonon transmission is mainly dominated by ballistic transport without phonon scattering [46, 47]. Thus, the influence of phonon scattering on the intrinsic dissipation of CNT(5,5)@BNNT(17,0)-based resonator with this length could be ignored.

Notably, the quality factor under no electric field is obtained as 683 and 966 for (17,0) BNNT and CNT(5,5)@BNNT(17,0), respectively. Furthermore, the quality factors of (17,0) BNNT are all lower than that of CNT(5,5)@BNNT(17,0) under different axial electric fields. The improvement of the quality factor above is mainly attributed to interlayer binding strength and incommensurate interlayer lattice matching [48]. Since the vibration of (5,5) CNT decays more slowly than that of (17,0) BNNT, the RMS displacement of CNT(5,5)@BNNT(17,0), thanks to interlayer binding strength, decays more slowly than that of (17,0) BNNT, which indicates the less energy dissipation of CNT(5,5)@BNNT(17,0) than that of (17,0) BNNT. Moreover, it is noted that the interlayer binding strength, as well as the interlayer sliding resistance between incommensurate layers, is relatively lower than that between commensurate layers [49], which means the incommensurate interlayer lattice matching also contributes to reducing the energy dissipation of CNT(5,5)@BNNT(17,0). It is, therefore, feasible to place a CNT with the incommensurate interlayer lattice inside a BNNT for reducing the intrinsic dissipation of BNNT.

3.2 Mass resolution

It is, therefore, necessary to evaluate the performance of CNT(5,5)@BNNT(17,0)-based resonator as a mass sensor in the light of ultrahigh sensitivity that CNT-based resonators exhibit in mass detection. The simulation of mass sensors utilizes the idea of equivalent mass that the mass of attached external particles is uniformly distributed on some atoms around the deposited position [50]. The inset of Fig. 6b shows the model of the mass sensor. According to the theory of mass sensing, when the detected mass is much larger than the minimum detectable mass of the resonator, the resonant frequency as a function of the attached mass can be expressed as [12]

$$f_{m} = \tfrac{f}{{\sqrt {a \cdot m + 1} }},$$
(3)

where f is the natural frequency of the resonator, m indicates attached mass, fm represents the resonant frequency with attached mass and a is a constant obtained by fitting the simulation results.

Fig. 6
figure 6

a Resonant frequencies of CNT(5,5)@BNNT(17,0) as a function of the attached mass of the resonator. The points show the simulation results and the lines represent the fitting curves using Eq. (3). b Length-dependent mass resolution of CNT(5,5)@BNNT(17,0). The inset shows the bridged CNT(5,5)@BNNT(17,0)-based resonator for mass sensing

Full size image

The resonant frequency as a function of the mass attached to resonators with different lengths is shown in Fig. 6a. The resonant frequency is almost unchanged with the attached mass not exceeding 100 yg, whereas it declines sharply when the deposited mass goes beyond 1000 yg. Herein, the term mass resolution is employed to quantify the mass sensing performance of CNT(5,5)@BNNT(17,0)-based resonators, referring to the minimum mass detected at a certain frequency shift. For comparison and quantitative analysis, the frequency shift 2 GHz is selected to calculate the mass resolution of CNT(5,5)@BNNT(17,0)-based resonators in this study. After the constant a is gained using Eq. (3) to fitting the simulation results in Fig. 6a, the mass resolution could be obtained and the relationship between the mass resolution and sensor length is shown in Fig. 6b. The mass resolution of CNT(5,5)@BNNT(17,0)-based resonator with a length of 41.5 Å is 38.7 yg at room temperature, which means that it can detect the total mass of nearly 23 hydrogen atoms. It is reported that the mass resolution of (6,6) CNT-based resonator with the same length is approximately 25 yg at 1 K [51]. Considering the distinction in temperature, our results demonstrate that the CNT(5,5)@BNNT(17,0)-based resonator maintains the high mass sensitivity of the CNT-based resonator. Thus, the CNT(5,5)@BNNT(17,0)-based resonator not only has superb mass sensitivity which is not inferior to the CNT-based resonator but also the precise piezoelectrical tuning property that the CNT-based resonator lacks.

4 Conclusions

Based on a series of MD simulations, we have investigated the piezoelectric tuning on the resonant frequency and intrinsic dissipation of (17,0) BNNT, (5,5) CNT, and the corresponding heterostructure CNT(5,5)@BNNT(17,0) as well as the application of CNT(5,5)@BNNT(17,0) as a mass sensor. Just as expected, the resonant characteristics and intrinsic dissipation of (17,0) BNNT and CNT(5,5)@BNNT(17,0) are easy to be adjusted by applying the axial electric field, while that of (5,5) CNT remains constant. Further investigation reveals that applying an axial electric field leads to the axial deformation of (17,0) BNNT and CNT(5,5)@BNNT(17,0), which changes the proportion of the axial load to the critical buckling load and finally influences the resonance characteristics. Simultaneously, the maximum mechanical energy stored in the resonator change with the axial deformation, giving rise to the variation of intrinsic dissipation caused by thermoelastic damping. Furthermore, the intrinsic dissipation of CNT(5,5)@BNNT(17,0) is less than that of (17,0) BNNT by virtue of the interlayer binding strength and the incommensurate interlayer lattice matching. In mass detection, the CNT(5,5)@BNNT(17,0)-based resonator can detect the total mass of nearly 23 hydrogen atoms at room temperature, representing high mass sensitivity no less than that of the CNT-based resonator. Our study demonstrates that CNT(5,5)@BNNT(17,0), as an attractive piezoelectric resonator material, has a remarkable application prospect to satisfy certain frequency self-tuning and mass sensing conditions in the resonator industry.