A novel recursive multi-scale modeling for predicting the burst pressure of filament wound composite pressure vessels

Abstract

A novel recursive multi-scale modeling is developed for the purpose of predicting the burst pressure in filament wound composite pressure vessels. The modeling covers all scales of micro, meso and macro and the unavoidable imperfections associated with fiber arrangement during the filament winding process are taken into account. The modeling starts from the scale of micro where fiber spacing and fiber contiguity are simulated. Then at the scale of meso as an in-between scale, the influence of fiber-bundle undulation, crossovers and overlaps are captured. At the final scale of macro, the distribution of stress/strain on each layer is analyzed. After accomplishment of bottom-up modeling, a top-down modeling is implemented. The obtained stress/strain are downscaled from macro to meso and from meso to micro to extract individual stress components on fiber and resin. The failure occurrence is investigated using micro-failure criteria and progressive damage modeling. The recursive modeling procedure repeats till the complete failure of the vessel.

1 Introduction

Cleanness, high efficiency in comparison with fossil fuels, and rational cost are the main reasons that hydrogen energy has recently received much more attention among various eco-friendly energy sources from industrial sectors and academic community. Global warming concerns and the necessary requirements of avoiding greenhouse gas emission are the most important motivations for replacing fossil fuels with hydrogen. Various ways of storing hydrogen are polymer and composite foams [1], liquid storage tanks [2], metal hydrides [3] and gaseous high-pressure vessels [4]. Currently, the most prominent storage method of hydrogen for the purpose of commercial applications is recognized as high pressure gaseous hydrogen storage.

Excellent resistance to corrosion, high strength-/stiffness-to-weight ratio and more importantly prolonged service lifetime against cyclic loading are the unique characteristics of composite pressure vessels. Hence, the application of Type III and Type IV of composite pressure vessels is rapidly increasing in the field of high-pressure storage and transportation of hydrogen.

The cost reduction of hydrogen storage is a key issue for the economical and extensive deployment of hydrogen energy in large scale. This can be accomplished through the appropriate structural design of the composite vessels. The safe and at the same time inexpensive structural design of composite pressure vessels is in need of the proper understanding of its mechanical behavior.

The ultimate strength of a composite pressure vessel determined by failure pressure plays an essential role in the structural integrity of the vessel during service. Consequently, accurate prediction of the failure pressure in composite pressure vessels is viewed as the basic requirement of safe design.

Predicting the burst pressure of composite pressure vessels relying on computational modeling has been the main streamline of various studies. Since the burst pressure is associated with occurrence of last-play-failure, combining various failure criteria with material degradation rules in the form of progressive damage modeling (PDM) was the main core of some investigations [5,6,7,8,9,10,11,12,13,14,15]. A few studies have been performed to investigate the influence of manufacturing parameters consisting of fiber volume fraction, strength, fiber packing and winding angle on the burst pressure and thus stochastic modeling was conducted [16,17,18,19]. Among them, stochastic or probabilistic studies have performed capturing the influence of manufacturing-induced uncertainties on the burst pressure of composite pressure vessels [17, 18]. From the open literature, it is evident that less attention has been paid to the imperfections arisen from fiber distribution patterns in the filament winding process. Limited studies have focused on analyzing the influence of fiber distribution imperfections on the effective properties of filament wound vessels without predicting the burst pressure [20, 21].

2 Problem statement

The main objective of this research is to predict the burst pressure of a composite pressure vessels taking into account fiber crossovers, undulation and overlaps. For this purpose, a recursive multi-scale modeling is developed covering scales of micro, meso and macro. The effect of fiber packing and contiguity at micro-scale and the influence of fiber crossovers and undulation on the macro-scale stress are studied. Then, obtained stress at the level of laminate (macro-scale stress) are fed back into meso-scale and then to the micro-scale. Therefore, micro-stress components imposed on fiber and resin are extracted, separately. The failure of the pressure vessel is studied at the scale of micro using proper micro-level failure criteria.

Motivated by experimental observations carried out by Wang et al. [14, 15], the case study is performed on the Type-III composite over-wrapped pressure vessel (COPV) with Aluminum liner. The diameter of the COPV is 185 mm and the thickness of liner is 2.5 mm. The filament wound lay-up configuration of the vessel is [90/±12/±15/±19/90/±22/±27/±32/±38/90] and the fiber volume fraction was reported as 62%. Carbon fiber has elastic modulus of 277 GPa, Poisson's ratio of 0.3, tensile strength of 4150 MPa and compressive strength of 2075 MPa. The utilized epoxy resin has Young's modulus of 3 GPa and the Poisson's ratio of 0.4 with tensile and compressive strengths of 105 MPa and 241 MPa, respectively. COPV was subjected to the increasing internal pressure with the rate of 0.2 MPa/s and the burst pressure was observed as 95~98 MPa [17].

3 Developing recursive multi-scale modeling

The overall roadmap of the recursive multi-scale modeling for the purpose of predicting burst pressure of COPV capturing the imperfections associated with fiber distribution and winding patterns is shown in Fig. 1. The outputs of each scale are used as the input of the very next scale during a bottom-up approach and results of the stress analysis at each scale is used as the constraints of the preceding scale in a top-down procedure. The failure is examined at the scale of micro and thus it is required to extract the induced stress at this scale. If failure occurs at the scale of micro, the mechanical properties of fiber and resin are degraded properly based on continuum damage mechanics. Thus, the bottom-up and top-down modeling approaches are recursively repeated in an integrated framework till no load more loading can be tolerated by the COPV. The details of the employed strategy and utilized modeling are present in the proceeding sections.

Fig. 1

Overview of recursive multi-scale modeling

4 Bottom-up modeling

4.1 Micro-scale modeling

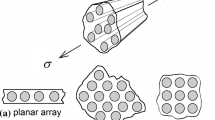
The modeling starts from the scale of micro by selecting proper representative volume element (RVE). For the purpose of capturing fiber spacing and fiber contiguity, those types of micro-scale RVEs containing multiple fibers are required to be chosen instead of the RVEs accommodating single fiber. The chosen micro-scale RVEs are schematically shown in Fig. 2. Commercial Abaqus FE package is employed to construct the FE models of the micro-scale RVEs. Solid elements are used and the dimensions of the FE models are chosen in a manner to resemble the same fiber volume fraction of the COPV chosen for case study (i.e. 62%). Perfect bonding is assumed between fiber and resin. Constructed FE models of the micro-scale RVE are subjected to the proper periodic boundary conditions (PBC) and loadings detailed in Appendix A. Thus, effective mechanical properties of the micro-scale RVE are extracted.

Fig. 2

Micro-scale RVEs accounting for fiber spacing and fiber contiguity

4.2 Meso-scale modeling

At the scale of meso, winding pattern is aimed to be considered. Designated by ±θ, the winding of each helical layer is accomplished through the numerous and certain numbers of circuits as shown in Fig. 3. Each circuit is also shaped by two successive passages of fiber bundles. The number of required winding circuits for completing a cross ply can be calculated using following formulation [20]:

$$ n = \frac{\pi D\cos \theta }{w} $$

(1)

where D is the diameters of the cylinder, w stands for the bandwidth of the fiber bundle and θ is the winding angle.

Fig. 3

Formation of fiber undulation during filament winding process

Reciprocal winding process of helical layers intrinsically induces fiber bundle crossovers and undulation. These geometrical imperfections have considerable effect on the effective properties of the layers. Undulations are formed as a consequence of fiber bundle intersections in the crossover regions.

Therefore, undulation appears because of fiber bundle overlaps in the crossover regions after two sequential passages of the fiber for the completion of a circuit. Introduced fiber undulation is not exclusively associated with filament winding process, but they also appear in woven and braided composites. Unfolding the filament wound tubes to a plane rectangle, a series of repetitive diamonds can be observed as shown in Fig. 3. The aforementioned diamonds can be viewed as a meso-scale repeated unit cell (RUC) addressing fiber bundle undulation.

The cross-section of the fiber bundle includes a rectangle with two wings at both ends based on the microscopic observations by Rousseau et al. [22] on the specimen cut from the filament wound cylinder. Depicted in Fig. 4, the shape of the end wings at assumed fiber strips can be described as below [20]:

$$ y = \frac{h}{2}\left[ {1 - \cos \left( {\frac{x}{b}\pi } \right)} \right] $$

(2)

Fig. 4

Fiber bundle cross section and meso-scale RUC

When two fiber bundles with the same orientation are placed adjacent to each other, wing parts will overlap. Thus, the effective bandwidth of the assumed fiber bundle shape is equivalent to 2a + b. Thus Eq. (1) is reformed as below:

$$ n = \frac{\pi \cos \theta }{{2a + b}}D $$

(3)

Thus, a, b, θ and n as four independent parameters describe the geometrical shape of the meso-scale RUC.

Indicated in Fig. 4, the meso-scale RUC is partitioned into three different types of constitutive blocks designated by A, B and C. These meso-blocks are specified as: (A) The crossovers with three layers, (B) the crossovers with four layers and (C) uniform segment without undulation [22]. Therefore, 3-D modeling of the RUC block is carried out through the following steps:

• 1) Creating meso-blocks A, B and C with the dimensions of a×b×2h, b×b×2h and a×a×2h

• 2) Defining the required numbers of each meso-blocks based on the number of winding circuit (i.e., n)

• 3) Positioning of each meso-block at the appropriate place in the meso-scale RUC

A computer code is written using Python to perform abovementioned tasks for any arbitrary winding angle.

Due to the complex configurations of the meso-blocks, especially types A and B, tetrahedral element is used for constructing the FE model of the meso-scale RUC. Extracted mechanical properties at the scale of micro (Sect. 4.1) are assigned to the fiber bundles in the meso-scale blocks as input data of the scale of meso. Constructed FE model for blocks A and B is shown in Fig. 5. Due to the periodic nature of the meso-scale RUC, its effective properties are obtained using periodic boundary conditions as detailed in Appendix B.

Fig. 5

Constructed FE models for meso-block types A and B

4.3 Macro-scale modeling

At the scale of macro, full-scale FE model of the investigated COPV is constructed. The liner of the COPV is constructed using cubic solid element (C3D8R) and presented stress-strain curve in Fig. 6 is considered as its constitutive behavior [15]. Composite overwrapped layers are built using continuum shell elements (SC8R) on the outer surface of the liner.

Fig. 6

Stress-strain curve of the Aluminum liner and constructed FE model of the COPV

Mechanical properties of each pair of helical layer are the outputs of performed analyses at the preceding scale of meso. The model is subjected to a uniform internal hydrostatic pressure. All degree-of-freedoms of a nipple node on one cap are fully restricted to avoid rigid body motion. A cut view of the constructed FE model of the COPV is provided in Fig. 6. The output of the macro-scale analysis is the distribution of stress/strain components for each ply.

5 Top-down modeling

Obtained stress/strain distributions at the uppermost scale of the macro in the bottom-up modeling are scaled down to extract micro-stress components on fiber and resin, separately. The applied stress to each layer is read as the output of the macro-scale FEA and applied to the FE model of the meso-scale RUC as boundary conditions. Thus, stress components in meso-scale RUC are extracted. Then, the meso-scale stress components are scaled down to the micro-scale to obtain the stress distribution on the micro-scale RVE. Inspired from the developed generalized method by Jin et al. [23], the stress components can be scaled down to micro-scale using below formulation:

$$ \sigma = M_{\sigma } \overline{\sigma } + A_{\sigma } \Delta T $$

(4)

where σ is micro-stress and $\overline{\sigma }$ is the stress at higher scale. $M_{\sigma }$ and $A_{\sigma }$ are stress magnification factors and thermal effect coefficients, respectively. $\Delta T$ also denotes temperature variations. For the purpose of this study, thermal variation is not considered and thus the second part of Eq. (4) is ignored. Stress magnification factors are formed as below [23]:

$$ M_{\sigma } = \left( {\begin{array}{*{20}c} {M_{11} } & {M_{12} } & {M_{13} } & {M_{14} } & 0 & 0 \\ {M_{21} } & {M_{22} } & {M_{23} } & {M_{24} } & 0 & 0 \\ {M_{31} } & {M_{32} } & {M_{33} } & {M_{34} } & 0 & 0 \\ {M_{41} } & {M_{42} } & {M_{43} } & {M_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {M_{55} } & {M_{56} } \\ 0 & 0 & 0 & 0 & {M_{65} } & {M_{66} } \\ \end{array} } \right) $$

(5)

For deriving the components of $M_{\sigma }$ matrix, one unity stress is applied to the FE model of the micro-scale RVE. In the meantime, others stress components are zero and proper boundary conditions are also applied for each case of loading. The details of applied boundary conditions and loading for obtaining the components of $M_{\sigma }$ matrix is outlined in Appendix C. After extracting $M_{\sigma }$ for each micro-scale RVE, then micro-stress components can be obtained using reduced form of Eq. (4). After obtaining the overall micro-stress distributions on micro-scale RVE, the average of individual micro-stress components acting on fiber and resin are obtained. It should be emphasized that the explained procedure for obtaining stress magnification factors is implemented once for each shape of micro-scale RVE and obtained components of $M_{\sigma }$ matrix is used in all stages.

Now, having in hand the micro-stress components acting on fiber and resin, the occurrence of failure at micro-scale is examined. The failure criteria for identifying failure initiation in fiber is used as below [24]:

$$ - C_{f} < \sigma_{f1} < T_{f} $$

(6)

where $C_{f}$ and $T_{f}$ stand for compressive and tensile strengths of fiber, respectively. $\sigma_{f1}$ denotes longitudinal stress in fiber.

Treating matrix as an isotropic material, the initiation of failure in matrix is identified using below failure criterion [24]:

$$ \frac{{\sigma_{\nu m}^{2} }}{{T_{m} C_{m} }} + \left( {\frac{1}{{T_{m} }} - \frac{1}{{C_{m} }}} \right)I_{1} = 1 $$

(7)

where C_m and T_m are compressive and tensile strengths of matrix. I₁ is also first stress invariant and σ_vm stands for von-misses stress in matrix at the scale of micro.

After occurrence of failure either in fiber or matrix, applying more loading is resulted in degradation of mechanical properties in the context of continuum damage mechanics [25]. The material degradation model is chosen as linear energy-based softening law as below [25]:

$$ G_{C} = \int\limits_{0}^{\infty } {\sigma_{eq} d\left( {\delta_{eq} } \right)} $$

(8)

where $\delta_{eq}$ and $\sigma_{eq}$ for fiber and resin are calculated using following formulations [25]:

$$ \left. {\delta_{eq} } \right|_{f} = l_{c} \varepsilon_{11} ,\left. {\sigma_{eq} } \right|_{f} = {{l_{c} \left( {\sigma_{11} \varepsilon_{11} } \right)} \mathord{\left/ {\vphantom {{l_{c} \left( {\sigma_{11} \varepsilon_{11} } \right)} {\left. {\delta_{eq} } \right|}}} \right. \kern-\nulldelimiterspace} {\left. {\delta_{eq} } \right|}}_{f} $$

(9)

$$ \left. {\delta_{eq} } \right|_{m} = l_{c} \sqrt {\varepsilon_{22}^{2} + \varepsilon_{12}^{2} + \varepsilon_{23}^{2} } ,\left. {\sigma_{eq} } \right|_{m} = {{l_{c} \left( {\sigma_{22} \varepsilon_{22} + \tau_{12} \varepsilon_{12} + \tau_{23} \varepsilon_{23} } \right)} \mathord{\left/ {\vphantom {{l_{c} \left( {\sigma_{22} \varepsilon_{22} + \tau_{12} \varepsilon_{12} + \tau_{23} \varepsilon_{23} } \right)} {\left. {\delta_{eq} } \right|_{m} }}} \right. \kern-\nulldelimiterspace} {\left. {\delta_{eq} } \right|_{m} }} $$

(10)

where l_c is characteristic length of the utilized element in Abaqus commercial FE package [25]. For fiber failure, the failure energy is taken as fracture toughness of composites along fiber, whilst for matrix failure, the failure energy is obtained using mixed-mode fracture energy as below [25]:

$$ G_{c} = G_{nc} + \left( {G_{sc} - G_{nc} } \right)\left( {\frac{{G_{s} }}{{G_{n} + G_{s} }}} \right)^{\eta } $$

(11)

where G_nc and G_sc stand for transverse normal toughness and transverse shear toughness, respectively. G_ns and G_sc are assumed as 0.28 and 0.79, respectively [15]. G_n and G_s are normal fracture toughness and shear fracture toughness, respectively and obtained using below formulations [26]:

$$ G_{n} = \frac{1}{2}\left( {\sigma_{22} \varepsilon_{22} } \right)l_{c} ,G_{s} = \frac{1}{2}\left( {\tau_{12} \varepsilon_{12} + \tau_{23} \varepsilon_{23} } \right)l_{c} $$

(12)

Finally, damage variables for fiber and resin are expressed as below [26]:

$$ d = 1 - \frac{{\delta_{eq}^{0} \left( {\delta_{eq}^{f} - \delta_{eq} } \right)}}{{\delta_{eq} \left( {\delta_{eq}^{f} - \delta_{eq}^{0} } \right)}}\quad \, \delta_{eq}^{0} \le \, \delta_{eq} \le \delta_{eq}^{f} \, $$

(13)

Inserting corresponding values for fiber and matrix in Eq. (8), damage variable for fiber (d_f) and resin (d_m) are obtained, accordingly. In Eq. (13), $\delta_{eq}^{0}$ is equivalent displacement at failure initiation and $\delta_{eq}^{f}$ is equivalent displacement at final failure. Thus, corresponding constitutive laws for fiber damage and matrix damage are mentioned in Fig. 7.

Fig. 7

Constitute laws for fiber (left) and matrix (right)

The constitutive laws for a cohesive zone can be categorized as initially elastic or initially rigid. For the case of initially elastic rules, the traction is zero at zero separation and then it increases with increasing separation till a maximum value and then it diminishes and approached to zero. In the case of initially rigid cohesive laws, the surfaces subjected to separation remain in contact till a critical traction is reached [27, 28]. Afterward, the traction decreases to zero with growing separation. In this specific study, initially elastic cohesive laws are employed.

After obtaining the damage variables associated with fiber and resin, the mechanical properties are degraded using below relation [26]:

$$ C_{d} = \left( {\begin{array}{*{20}c} {\left( {1 - d_{f} } \right)C_{11} } & {\left( {1 - d_{f} } \right)\left( {1 - d_{m} } \right)C_{12} } & {\left( {1 - d_{f} } \right)\left( {1 - d_{m} } \right)C_{13} } & 0 & 0 & 0 \\ {} & {\left( {1 - d_{m} } \right)C_{22} } & {\left( {1 - d_{m} } \right)C_{23} } & 0 & 0 & 0 \\ {} & {} & {\left( {1 - d_{m} } \right)C_{33} } & 0 & 0 & 0 \\ {} & {} & {} & {\left( {1 - d_{s} } \right)C_{44} } & 0 & 0 \\ {} & {sym} & {} & {} & {\left( {1 - d_{s} } \right)C_{55} } & 0 \\ {} & {} & {} & {} & {} & {\left( {1 - d_{s} } \right)C_{66} } \\ \end{array} } \right) $$

(14)

where d_f and d_m are obtained using Eq. (13) as independent damage variables, while d_s is obtained using below formulation [26]:

$$ d_{s} = 1 - \left( {1 - d_{f}^{{}} } \right)\left( {1 - d_{m}^{{}} } \right) $$

(15)

Some advanced multi-sale modeling techniques have been already developed for the purpose of predicting fracture of composites [29,30,31], however, in this article the developed recursive multi-scale modeling is categorized under the continuum damage mechanics framework.

6 Implementing recursive multi-scale modeling

The explained bottom-up modeling and top-down modeling are integrated in an unitized modeling using a written code with Python. The flowchart of the whole modeling procedure is provided in Fig. 8.

Fig. 8

Flowchart of the developed recursive multi-scale modeling

First of all, mechanical properties of the micro-scale RVE are extracted taking into account fiber contiguity and fiber spacing. The results of obtained mechanical properties through FE modeling of micro-scale RVEs in comparison with outputs of simple micromechanics rules are presented in Table 1. The comparison clearly shows the degree to which fiber contiguity and fiber spacing can affect the mechanical properties, since aforementioned phenomena are not considered using micromechanical rules at all. As it can be seen the maximum discrepancy of the results with micromechanics rule is associated with the micro-scale RVE with 65º-fiber arrangement. This specific micro-scale RVE and also the outputs of micromechanical rules are chosen for the remaining of the analysis. It should be pointed out that rule of mixture is used for obtaining longitudinal modulus and Poisson’s ratio, whilst Halpin-Tsai rule is employed for predicting shear modulus [32].

Table 1 Mechanical properties of the micro-scale RVEs

The obtained mechanical properties of the micro-scale RVE are fed as input data to the meso-scale RUC. Proper meso-scale RVEs are generated for each winding angle capturing fiber bundle overlap/undulation/crossovers as the effective parameters of meso-scale. Then, the effective properties of meso-scale RUC are extracted through FEA. Full-scale FE model of the COPV is constructed at the scale of macro. The COPV is subjected to internal pressure and induced stress are extracted. The obtained stress distributions at the scale of macro are downscaled to the scale of micro and the occurrence of failure is examined at the micro-scale. If no failure is experienced, the whole procedure repeats with increased internal pressure from the beginning. If failure is experienced, the mechanical properties of the microscale RVE are degraded accordingly and the modeling is restarted from the scale of micro. The whole procedure repeats several times till COPV cannot undergo any more loading implying on the complete failure.

Implementing the developed recursive multi-scale modeling, the burst pressure of the investigated COPV is obtained as 93.8~95.3 MPa which in excellent agreement with experimentally measured 95~98 MPa [15].

7 Conclusion

A novel multi-scale modeling is developed for predicting the burst pressure of filament wound composite pressure vessel taking into account manufacturing-induced inconsistencies. Unlike conventional multi-scale modeling where involved scales are proceeded in a one-way manner, the modeling takes place through recursive multi-scale modeling. The effect of fiber spacing and contiguity at micro-scale and the influence of fiber crossovers, undulation and overlaps on the macro-scale stress are studied. Then, obtained stress at the level of laminate (macro-scale stress) are fed back into meso-scale and then to the micro-scale. Therefore, micro-stress components imposed on fiber and resin are extracted, separately. The failure of the pressure vessel is studied at the scale of micro using proper micro-level failure criteria. The main reason of investigating failure at the scale of micro instead of using widely available macro-scale failure criteria is placed behind this fact that the influence of fiber undulation on the failure can be also taken into account during the progressive damage modeling process. The estimated outputs of this research not only agree perfectly with experimental observations, but also the developed modeling converges to the lower bound of experimental data rendering the approach as a conservative one. The results of this research imply on the significant importance of fiber arrangement as a local phenomenon on the global behavior of pressure vessel characterized by the burst pressure.

Appendices

Appendix A

Extracting mechanical properties of the micro-scale RVE

Applied boundary conditions to the micro-scale RVE for extracting its mechanical properties are presented in Table 2. The overall shape of the element and assumed dimensions are also shown in Fig. 9 for square-shaped RVE as an example.

Fig. 9

Square-shaped micro-scale RVE and its dimensions

Table 2 Applied loadings and periodic boundary conditions to the micro-scale RVE [33]

The average stress and strain are related together as below:

$$ \overline{{\sigma_{\alpha } }} = C_{\alpha \beta } \overline{\varepsilon }_{\beta } \left( {\alpha ,\beta = 1,\,...\,,6} \right) $$

(A1)

where C is the effective stiffness matrix of micro-scale RVE. The average of stress and strain are also defined as below:

$$ \overline{\sigma }_{\alpha } = \frac{1}{V}\int_{v}^{{}} {\sigma_{\alpha } dV} $$

(A2)

$$ \overline{\varepsilon }_{\beta } = \frac{1}{V}\int_{v}^{{}} {\mathop {\varepsilon_{\beta } }\limits^{{}} dV} $$

(A3)

where σ_α and ε_α are stress and strain of each element, respectively.

Applying PBC’s to the micro-scale RVE, just one of the strain components has unity value for each case while the others are all zero. Thus, for each case of loading mentioned in Table 2 we have [30]:

$$ C_{\alpha \beta } = \overline{\sigma }_{\alpha } = \frac{1}{V}\int_{v}^{{}} {\sigma_{\alpha } \left( {x_{1} ,x_{2} x_{3} } \right)dV} ,\overline{\varepsilon }_{\beta } = 1 $$

(A4)

Consequently, the components of $C_{\alpha \beta }$ will be obtained. Finally, inversing stiffness matrix ($C_{\alpha \beta }$), compliance matrix of the micro-scale RVE is obtained ($C_{\alpha \beta }^{ - 1} = S_{\alpha \beta }$) and then effective mechanical properties of the micro-scale RVE are obtained as below:

$$ \begin{gathered} \begin{array}{*{20}c} {E_{x} = \frac{1}{{S_{{11}} }}} & {\nu _{{xy}} = - \frac{{S_{{12}} }}{{S_{{11}} }}} & {G_{{xy}} = \frac{1}{{S_{{66}} }}} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {E_{y} = \frac{1}{{S_{{22}} }}} & {G_{{yz}} = \frac{1}{{S_{{44}} }}} \\ \end{array} \hfill \\ \end{gathered} $$

(A5)

Since YZ plane is considered as the plane of isotropy in Fig. 9, the final remaining mechanical property can be obtained using below formulation:

$$ G_{yz} = \frac{{E_{y} }}{{2(1 + \nu_{yz} )}} $$

(A6)

Appendix B

Extracting mechanical properties of meso-scale RUC

Suquet expressed the displacement field for a periodic array as below in accordance with tensorial notation [34]:

$$ u_{i} (x_{1} ,x_{2} ,x_{3} ) = \overline{\varepsilon }_{ik} x_{k} + u_{i}^{*} (x_{1} ,x_{2} ,x_{3} ) $$

(B1)

where $\overline{\varepsilon }_{ik}$ is the global strain applied to the periodic body, and x_k is the Cartesian coordinate. $u_{i}^{*} (x_{1} ,x_{2} ,x_{3} )$ is the periodic part of the deformation. The continuity condition of traction is also expressed as below:

$$ \sigma_{ij} \left( M \right)n_{j} \left( M \right) = - \sigma_{ij} \left( N \right)n_{j} \left( N \right) $$

(B2)

where M and N are an arbitrary pair of periodic points on the two opposite boundary surfaces and n_j is the components of the unit outward normal vector to the surfaces. The boundary conditions applied to the RUC can be expressed as displacement constraints enforcing the boundaries of the RUC being parallel before and after the deformation [35, 36]. On the boundary pair (C₁, C₃), for an arbitrary pair of periodic points M, N, we denote the displacement as u_i(M ϵ C₁)-u_i(N ϵ C₃)=u_i(C₁) - u_i(C₃). Thus, for opposite boundaries we have:

$$ \begin{gathered} u_{i}^{j + } = \overline{\varepsilon }_{ik} x_{k}^{j + } + u_{i}^{*} \hfill \\ u_{i}^{j - } = \overline{\varepsilon }_{ik} x_{k}^{j - } + u_{i}^{*} \hfill \\ \end{gathered} $$

(B3)

where j+ and j- denote a pair of opposite parallel boundaries in the RUC. Thus we have:

$$ u_{i}^{j + } - u_{i}^{j - } = \overline{\varepsilon }_{ik} (x_{k}^{j + } - x_{k}^{j - } ) = \overline{\varepsilon }_{ik} \Delta x_{k}^{j} $$

(B4)

Since, the boundaries are parallel pairs in the investigated RUC, $\Delta x_{k}^{j}$ is constant and hence we have:

$$ u_{i}^{j + } (x_{1} ,x_{2} ,x_{3} ) - u_{i}^{j - } (x_{1} ,x_{2} ,x_{3} ) = c_{i}^{j} $$

(B5)

where $c_{i}^{j}$ stands for mean extension/contradiction in the RUC. Eq. (B5) can be directly used as boundary conditions in FEA.

Applying mentioned displacement constraints, a unique solution is obtained in a displacement-based FEM and the traction continuity condition expressed by Eq. (B2) is automatically satisfied [37].

The average stress and strain over the volume V of the RUC can be written as:

$$ \begin{gathered} \overline{\sigma }_{ij} = \frac{1}{V}\int_{v}^{{}} {\sigma_{ij} dV = \frac{1}{V}\sum\limits_{k = 1}^{N} {\sigma_{ij}^{k} V^{k} (i,j = 1,2,3)} } \hfill \\ \overline{\varepsilon }_{ij} = \frac{1}{V}\int_{v}^{{}} {\mathop {\varepsilon_{ij} }\limits^{{}} dV = \frac{1}{V}\sum\limits_{k = 1}^{N} {\varepsilon_{ij}^{k} V^{k} (i,j = 1,2,3)} } \hfill \\ \end{gathered} $$

(B6)

where V^k is the volume of k^th element. N is also the total numbers of integration points in FE model of the RUC.

Finally, elastic relation between stress and strain is described as:

$$ \overline{\sigma }_{ij} = C_{ijkl} \overline{\varepsilon }_{ij} (i,j,k,l = 1,2,3) $$

(B7)

where C_ijkl is the effective stiffness of the RUC.

Thus, the effective properties of the RUC are extracted using abovementioned procedure.

Appendix C

Boundary conditions and loadings for obtaining micro-stress components

Applied boundary conditions and loadings to the micro-scale RVE for extracting micro-stress distribution based on meso-scale stress distribution are presented in Table 3. The overall shape of the element and assumed dimensions are the same as Fig. 9

Table 3 Applied loadings and periodic boundary conditions to the micro-scale RVE [20]

Reflected “C” in Table 3 implies on a certain value where the plane faces remain plane after deformation for the parallelograms [38].

A sample of stress distribution under different loadings and applied boundary conditions are shown in Fig. 10.

Fig. 10

Outputs of the FE analysis on the micro-scale RVE