Large magnetocaloric effect in La_0.75Ca_0.25–xNa_xMnO₃ (0 ≤ x ≤ 0.10) manganites

Abstract

We have studied the effect of a partial substitution of Ca²⁺ by Na⁺ on the structural, magnetic and magnetocaloric properties of the mixed valence perovskites ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{{{0}{\text{.25 - }}x}} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10), prepared by the flux method. X-ray diffraction studies revealed that our samples crystallize in the orthorhombic structure with a Pbnm space group. Rietveld analysis showed that MnO₆ octahedron has a little distortion and that θ_Mn–O–Mn bond angles increase with increasing Na⁺ content. The field cooled (FC) and zero field cooled (ZFC) magnetizations indicated that our samples have a paramagnetic-ferromagnetic phase transition, when decreasing temperature. A small deviation was observed between FC and ZFC curves. This deviation can be explained by the competition between the ferromagnetic and antiferromagnetic interactions, leading to a glassy behavior. The Curie temperature, T_C, increased from 268 K for x = 0 to 278 K for x = 0.10. The magnetizations isotherms of our compounds, with a second-order phase transition, were investigated. For the x = 0.10 sample, the maximum of the magnetic entropy change was found to be 3.15 and 6.44 J kg⁻¹ K⁻¹, under an applied magnetic field of 2 and 5 T, respectively. Moreover, it has important relative cooling power values of about 134.82 and 317.79 J kg⁻¹, under the same applied magnetic field. In addition, rescaled entropy data collapsed into the same curve, which indicates the universal behavior for the magnetocaloric effect (MCE) in our compounds. These materials could be potential candidates as working substances in magnetic refrigeration.

1 Introduction

In the recent years, synthesis of magnetic materials as a thin films and nanostructures has been investigated for various applications due to their unique structural, electrical and magnetic properties [1,2,3]. Perovskite manganites with the general formula ${\text{Ln}}{\kern 1pt}_{{{1 - }x}} {\text{MMnO}}_{{3}}$ (where Ln is a trivalent rare earth ion and M is a divalent ion such as alkaline elements) have been widely studied during the last few years. This is due to their important physical properties such as colossal magnetoresistance (CMR), metal–insulator transition, and charge/orbital ordering. These properties make perovskite manganites as the potential candidates especially for the refrigeration technology [4,5,6,7,8,9,10]. Furthermore, these materials have many advantages such as their small volume requirement, chemical stability, low production cost, and high efficiency. Indeed, they are environment friendly, which makes them very attractive to further scientific research. Currently, there are other materials belonging to the family of oxides, which have attracted the attention of researchers, they are more suitable for future technological domains such as ferrites with the structure of perovskite, spinel, and magnetoplumbite [11, 12]. We can mention that the hexaferrites are the strongest magnetic compounds with T_C ~ 740 K. This is the simplest type of all ferrites with a hexagonal structure. More than 90% of permanent magnets are produced all over the world based on these compounds. They have a ferrimagnetic structure and a total magnetic moment of 20 μB in the ground state. Moreover, the resonant frequency is determined by the frequency of natural ferromagnetic resonance. In addition, hexaferrites are physiologically harmless [13, 14]. In other hand, some works have been focused on the oxygen deficiency effect in manganites system, as important parameters that affect the magnetic properties. The oxygen non stoichiometry is very important for complex transition oxides and changes seriously the total magnetic moment and Curie point. It leads to the formation of a weak magnetic state such as spin glass and change some magnetic parameters [15,16,17].

The parent compound,${\text{LnMnO}}_{{3}}$, is an antiferromagnetic (AFM) insulator, in which only Mn³⁺ ions are present. It is characterized by a super exchange (SE) coupling between Mn³⁺ sites. Upon the substitution of a divalent ion (M), in the Ln site, a few Mn³⁺ with the electronic configuration $\left ( {3{\text{d}}^{4} ,{\text{t}}_{{{\text{2g}}}}^{3} \uparrow {\text{e}}_{{\text{g}}}^{1} \uparrow ,S = 2} \right)$ transform into Mn⁴⁺ ions with the electronic configuration $\left ( {{\text{3d}}^{{3}} {\text{,t}}_{{{\text{2g}}}}^{{3}} \uparrow {\text{e}}_{{\text{g}}}^{{0}} {,}\;S = {{3} \mathord{\left/ {\vphantom {{3} {2}}} \right. \kern-\nulldelimiterspace} {2}}} \right)$. During this transformation, the e_g electron becomes delocalized. The holes facilitate the charge transfer in the e_g band, which is highly hybridized with the oxygen 2p state. According to Hund’s rule, the charge transfer induces a ferromagnetic (FM) coupling between Mn³⁺ and Mn⁴⁺ ions. This coupling gives rise to a double-exchange transfer (DE) of spin-polarized electrons from Mn³⁺ to Mn⁴⁺ ions [18]. Generally, the substitution in Ln-sites controls the Mn³⁺/Mn⁴⁺ ratio in this type of material. In particular, Lanthanum manganites have attracted the attention of several researchers, thanks to the very rich phase diagram observed in ${\text{La}}_{{{1 - }x}} {\text{Ca}}_{x} {\text{MnO}}_{{3}}$ and ${\text{La}}_{1 - x} {\text{Sr}}_{x} {\text{MnO}}_{{3}}$ samples. Lanthanum manganites are characterized by multi-phase transitions, including: paramagnetic (PM)—insulator, PM—metallic, FM—insulator, FM—metallic, AFM—metallic, spin canted—insulator, charge-ordered, and canted AFM states, together with different variations of the critical temperatures [19,20,21].

Furthermore, upon the addition of Na to the ${\text{LaMnO}}_{{3}}$ sample, an amount (2x) of Mn³⁺ transform into Mn⁴⁺. Taking charge neutrality into account, the chemical formula can be defined as: ${\text{La}}_{1 - x}^{{3 + }} {\text{Na}}_{x}^ + \left ( {{\text{Mn}}_{1 - 2x}^{{3 + }} {\text{Mn}}_{2x}^{{4 + }} } \right){\text{O}}_{{3}}$. As a first interpretation, the substitution of La by a small amount of Na results in a large number of charge carriers, leading to an increase in the conductivity. In addition, the potential between the Na and the La ions increases although the ionic radii of La³⁺ and Na⁺ are comparable. This is due to the large valence difference between them. The study of the effect of the substitution of Na on lanthanum manganite may provide a better understanding of the CMR effect in these materials [22, 23]. There are several works that are interested on the divalent ions substituted manganites such as [24,25,26,27].They are focused on the studying of structural, magnetic, and electrical properties of perovskite materials, especially after the creation of oxygen vacancies.

Among the different studied manganites, ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{{{0}{\text{.25}}}} {\text{MnO}}_{{3}}$ sample has attracted exceptional interest in several recent works. This is due to its good physical properties. Yi et al. observed that the MR of ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{{{0}{\text{.25}}}} {\text{MnO}}_{{3}}$ sample is strengthened at low temperatures. This is due to the spin-polarized tunneling phenomena [28]. In addition, Pekala et al. observed that MR does not tend to zero at low temperatures, which confirms that grains size is fine [29]. Moreover, Guo et al. noted that this sample admits a large magnetic entropy change [30]. Thus, ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{{{0}{\text{.25}}}} {\text{MnO}}_{{3}}$ is one of the most widely studied manganite systems.

As a contribution to the investigation of manganite materials, we report here the study of the effect of Na substitution on the structural and magnetic properties and MCE effect of ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{{{0}{\text{.25}}}} {\text{MnO}}_{{3}}$ samples. There are several synthesis methods of magnetic materials, the usual methods such as sol–gel and solid-state reactions or the new process such as sol–gel auto combustion technique [31] and the citrate sol–gel method [32]. In our work, we choose to prepare our samples by flux method using sodium chloride (NaCl) as a flux.

In our work, we choose to prepare our samples by flux method using sodium chloride (NaCl) as a flux.

The advantages of NaCl solvents are the presence of a common anion and the insignificant incorporation of Na into the material to be synthesized at low temperature, which prevents the evaporation of Na. In our previous work [33], we detected the high doping effect of Na content on ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{{{0}{\text{.25}}}} {\text{MnO}}_{{3}}$ sample. In our present paper, we choose to test the low Na content effect and to compare it with our last results.

2 Experimental details

To produce a very high quality, homogenous, and nano-polycrystalline powder, ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) compounds were prepared by the flux method, using NaCl as a flux. All experimental details are stated in our last work [33]. The structure and phase purity of the prepared sample were determined by powder X-ray diffraction (XRD) at room temperature using a Panalytical X pert Pro-diffractometer with Cu-K_α radiation (λ = 1.5406 Å). Data for Rietveld refinement were collected in a 2θ range between 10° and 100° with a scanning step of 0.017 and a time step of 18 s. The structural analyses were carried out by the Rietveld method using the FULLPROF program [34]. The microstructure was studied by a scanning electron microscope (SEM) at room temperature using a Philips XL30. In addition, a semi-quantitative analysis was performed at 20 kV accelerating voltage using energy dispersive X-ray analyses (EDX).

Magnetizations (M) as a function of temperatures (T) were performed using an extraction magnetometer developed in Louis Neel Laboratory of Grenoble. Magnetization isotherms (M (µ₀H)) were measured in the range of 0–5 T fields, for different temperatures, around Curie temperature (T_C). M (µ₀H) measurements were corrected by a demagnetization factor, noted D, obtained from M (µ₀H) curves at low-fields linear response at a low-temperature region.

3 Results and discussions

3.1 X-ray diffraction study

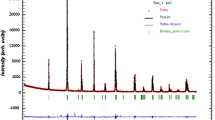
As a first step, we carried out XRD analysis to verify the crystal structure of the studied samples. Powder XRD patterns of ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) compounds, collected at room temperature, are plotted in Fig. 1. We note that our samples are of a single phase with a very small amount of Mn₃O₄, as found in recent works [33]. XRD data were carried out using Rietveld refinement [35]. Figure 2 exemplifies the Rietveld refinement of XRD profile for ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{{{0}{\text{.20}}}} {\text{Na}}_{{{0}{\text{.05}}}} {\text{MnO}}_{{3}}$ sample, with good agreement between the observed and the calculated profiles. This is due to the excellent goodness of χ². The analyzed data showed that our samples crystallize in the orthorhombic structure with Pbnm (Z = 4) space group no (62), in which the (La/Ca/Na) is at 4 (c) (x, y, 1/4) position, (Mn) at 4 (b) (1/2, 0, 0), O₁ at 4 (c) (x, y, 1/4), and O₂ at 8 (d) (x, y, z). On the other hand, in our previous work [33] for x = 0.15 and 0.20, we found that the x = 0.15 sample is a mixture of orthorhombic and rhombohedral structures with Pbnm and ${\text{R}}\overline{{3}} c$ space groups, respectively. While, the x = 0.20 sample is characterized by the rhombohedral structure with a ${\text{R}}\overline{{3}} {\text{c}}$ space group. We can remark that for the low doping rate, we can get the same space group (for x = 0, 0.05 and 0.1), followed by a change of crystallographic structure with the increase of doping rate (in the case of our previous work).

Fig. 1

XRD pattern of ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) samples at room temperature

Fig. 2

The observed and calculated solid line of XRD patterns of La_0.75Ca_0.2Na_0.05MnO₃ sample determined by Rietveld refinement. The vertical lines show the Bragg’s peak positions and the lowest curve shows the difference between the data and the calculation patterns. The inset shows the crystal structure of La_0.75Ca_0.20Na_0.05MnO₃

The unit cell and different fitting parameters of our samples are summarized in Table 1.

Table 1 Refined structural parameters determined from X-ray Rietveld refinement for ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) samples measured at room temperature

The relative amount of Mn₃O₄ was determined from XRD patterns of the samples by measuring the relative intensities of the major ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) and Mn₃O₄ peaks, using the following expression [36, 37]:

$${\text{Mn}}_{{3}} {\text{O}}_{{4}} (\% ) = 100 \times \frac{{I_{{{\text{Mn}}_{{3}} {\text{O}}_{{4}} }} }}{{I_{{{\text{Mn}}_{{3}} {\text{O}}_{{4}} }} + I_{{{\text{Pbnm}}}} }},$$

(1)

where $I_{{{\text{Mn}}_{{3}} {\text{O}}_{{4}} }}$ is the major Mn₃O₄ peak and $I_{{{\text{Pbnm}}}}$ is the major ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) peak. We found that the relative impurity amount of Mn₃O₄ is negligible and does not affect the physical properties.

Lattice distortions may be caused by Jahn–Teller effect inherent to the Mn³⁺ high spin state or the connecting pattern of MnO₆ octahedron leading to the formation of rhombohedral or orthorhombic lattice. Furthermore, the tolerance factor, T_G, is introduced to describe the ionic match between A and B site ions and to predict the distortion of the perovskite structure. This is defined by the following expression [38, 39]:

$$T_{{\text{G}}} { = }\frac{{\left\langle {r_{{{\kern 1pt} {\kern 1pt} \left ( {\text{La,Ca,Na}} \right)}} } \right\rangle + \left\langle {r_{{\text{O}}} } \right\rangle }}{{\sqrt {2} \left ( {\left\langle {r_{{{\text{Mn}}}} } \right\rangle + \left\langle {r_{{\text{O}}} } \right\rangle } \right)}}.$$

(2)

The manganese oxide compounds have a perovskite structure if their $T_{{\text{G}}}$ is in the range of 0.89 < T_G < 1.02 [40]. The obtained values of T_G for our samples are listed in Table 1. This confirms the stability of this structure.

From Table 1, we can remark that the unit cell volume increases with the increase in Na content. According to Shannon [41], the ionic radius of ($r_{{{\text{Na}}^ + }}$ = 1.24 Å) is higher than that of ($r_{{{\text{Ca}}^{{2 + }} }}$ = 1.18 Å). On the other hand, the average of ($r_{{{\text{Mn}}^{{3 + }} }}$ = 0.645 Å) is larger than that of ($r_{{{\text{Mn}}^{{4 + }} }}$ = 0.53 Å). Generally, the bigger ion at the substituted site can strengthen some Mn–O–Mn bond angle, which results in the decrease of the average Mn–O bond distance. This hypothesis was confirmed by the determination of Mn–O–Mn angles and Mn–O distances, using the Rietveld refinement (Table 1). It has been reported that the deformation of the MnO₆ octahedron may be responsible for the distortion in the perovskite structures. The crystal structure and MnO₆ octahedron of the sample (x = 0.05) were drawn using VESTA program [42] based on the refined atomic positions (shown in the inset of Fig. 2).

3.2 Morphological properties

The average crystallite sizes of ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) compounds were determined using Scherrer's formula after the evaluation of the most intense peak broadening and SEM. Scherrer's formula can be written as [43]:

$$D = \frac{K\lambda }{{\beta \cos (\theta )}},$$

(3)

where λ = 1.5406 Å is the wavelength for CuK_α radiation, θ is the diffraction angle of the most intense peak, K is the shape factor equal to 0.9, β is the full width at half maximum of the highest peak. The average crystallite sizes are listed in Table 2.

Table 2 Average crystallites sizes calculated by Scherrer’s formula and SEM

The morphological properties of our samples were studied using SEM (inset of Fig. 3, for x = 0.05 as an example). We can notice that our samples have polycrystalline characteristics. The average particle sizes were determined by ImageJ software [44] and calculated using Gaussian functions. From Table 2, the calculated grain sizes are larger than those calculated by Scherrer’s formula. This indicates that each particle is formed by several crystallites [45]. The influence of grain size on the peroveskite materials has been investigated by many researches. Mahesh et al. [46] have varied the grain size from 0.025 to 3.5 µm and they get a significant change in properties. They observe that when the grain size decreases, there is an enhancement in the low magnetoresistance temperature. There are many works that have been concentrated to understand the mechanism of inter-grain tunneling conduction such as Doroshev et al. [47] and Zhang et al. [48]. The average crystallite size of our samples is calculated from the XRD and SEM analyses. We can observe that the average increases as a function of Na content. In our work, we will discuss the effect of this slight grain size increase on the magnetic properties.

Fig. 3

EDX analysis for x = 0.05. a Shows the typical SEM and b shows the histogram of the distribution of particles size

To check the existence of all elements in our samples, EDX was performed at room temperature. Figure 3 represents the EDX spectrum, for x = 0.05 as an example. We can see clearly that La, Ca, Na, Mn, O elements are present, which indicates that there is no loss of any integrated element during the sintering process. The typical cationic composition for our samples is represented in Table 3.

Table 3 Results of EDX analysis

3.3 Magnetic study

To better understand the magnetic behavior of our samples, Fig. 4 shows the temperature dependence of FC and ZFC, under an applied field of 0.05 T in the temperature range of 5–330 K. It is clearly remarkable that our samples underwent a sharp magnetic transition from FM to PM state when increasing temperature. This behavior was remarked in our last work for x = 0.15 and 0.20 [33]. Also, we can see from this figure that the magnetization values, which were quite stable at temperatures below 230 K for x = 0, 235 K for x = 0.05, and 240 K for x = 0.10 began to decrease rapidly at T_C. A small divergence between FC and ZFC curves can be observed at the irreversibility temperature of 250 K for x = 0, 255 K for x = 0.05, and 260 K for x = 0.10. This phenomenon is observed in other magnetic materials [49,50,51], which is assigned to the existence of an isotropic field generated from FM clusters [50]. At low temperatures, a small peak was observed around 40 K. This confirms the presence of Mn₃O₄ secondary phase [52, 53]. T_C was calculated from d²M/d²T as a function of temperatures. From Fig. 4 (blue color), T_C values were found to be around 268, 270, and 278 K, respectively, for x = 0, x = 0.05, and x = 0.10. However, for x = 0.15 and 0.20, Tc values are equal to 301.5 and 300 k, respectively. We can conclude that when the doping rate increases, Tc approaches room temperature, which indicates that our samples are good candidates for the refrigeration domain. In our work, the substitution of Ca²⁺ by Na⁺ led to an increase of the Mn⁴⁺ content from 25 (x = 0) to 35% (x = 0.10). This is explained by the increase of <Mn–O–Mn> bond angle and the decrease of <Mn–O> bond distance. Therefore, the DE interactions were gradually strengthened, which resulted in the increase of FM character. This is not the case for x = 0.15 and 0.20 in which the increase of Mn⁴⁺ content above 40%, produced a decrease in the DE interaction and enhanced the SE interaction [54]. It is worth noting that all samples show a ferromagnetic behavior with close phase transition temperature. Their magnetization is strongly influenced by the grain size. It increases with the increase of grain size, which is due to the decrease of magnetically disordered states at the surface of grains. Therefore, the increase of particle size decreases the surface to volume ratio, thereby increasing the net magnetization. This is leading to increases the ferromagnetic transition temperature. Tc passed from 268 to 278 °C for our samples.

Fig. 4

The ZFC and FC magnetizations and d²M/dT² as function of temperatures for ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) samples, under a magnetic field of 0.05 T

The bandwidth is characterized by the overlap between Mn_3d and O_2p orbitals. It can be described empirically by the following expression [55]:

$$W_{{\text{b}}} \approx \frac{\cos w}{{{\kern 1pt} {\kern 1pt} d_{{\text{ (Mn - O)}}}^{{{3}{\text{.5}}}} }},$$

(4)

where $w{\kern 1pt} { = }{{1} \mathord{\left/ {\vphantom {{1} {2}}} \right. \kern-\nulldelimiterspace} {2}}\left ( {\pi - \left\langle {\text{Mn - O - Mn}} \right\rangle } \right)$ and d _(Mn–O) is the bond length. The calculated W_b values are tabulated in Table 1. We can remark that W_b is inversely proportional to Mn–O–Mn angle. This result is attributed to the increase of <ra>. It may be explained by the increase of the average grain size. These changes lead to a significant rise in the Curie temperature [56]. In addition, the substitution of Ca²+ by Na⁺ leads to the increase of the order effect. According to Trukhanov et al., an average grain size is inversely related to the surface tension forces' relative to the bulk elastic forces [57].

To comprehend the dynamics of spin, we have calculated the inverse of magnetic susceptibility as a function of temperature from the magnetization data (M (T)). In the high-temperature range, the susceptibility obeys the Curie–Weiss (CW) law, defined by:

$$\chi {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{C}{{T - {\kern 1pt} {\kern 1pt} \theta_{{\text{P}}} }},$$

(5)

where $\theta_{{\text{P}}}$ is the CW temperature and C is the Curie constant, defined by [58]:

$$C{\kern 1pt} {\kern 1pt} {\kern 1pt} { = }{\kern 1pt} {\kern 1pt} \frac{{{\text{N}}_{{\text{a}}} }}{{{3}k_{{\text{B}}} }}\mu_{{{\text{eff}}}}^{{2}} ,$$

(6)

where Na = 6.023 × 10^–23 mol⁻¹ is the number of Avogadro and k_B is Boltzmann’s constant.

The linear PM region was fitted using Eq.  (5). The obtained $\theta_{{\text{P}}}$ values are listed in Table 4. Noting that $\theta_{{\text{P}}}$ value can be negative, positive, or null according to whether the behavior, respectively, is AFM, FM, or PM. The positive value of $\theta_{{\text{P}}}$, in our case, indicates the presence of FM interactions between the spins. Also, we can note that the obtained values of $\theta_{{\text{P}}}$ are greater than those of T_C for each sample. This may be due to magnetic inhomogeneity above T_C. Thus, we have also calculated the experimental effective moment $\mu_{{{\text{eff}}}}^{{\exp}}$ using Eq.  (6) and the theoretical one ($\mu_{{{\text{eff}}}}^{{{\text{theo}}}}$) is calculated by:

$$\mu_{{{\text{eff}}}}^{{{\text{theo}}}} { = }\sqrt {{ (0}{\text{.75}} - x{)}\left[ {\mu_{{{\text{eff}}}} {\text{ (Mn}}^{{3 + }} {)}} \right]^{{2}} { + (0}{\text{.25}} + x{)}\left[ {\mu_{{{\text{eff}}}} {\text{ (Mn}}^{{4 + }} {)}} \right]^{{2}} } ,$$

(7)

where $\mu_{{{\text{eff}}}}^{{}} {\text{ (Mn}}^{{3 + }} {)}$ = 4.9 μ_B and $\mu_{{{\text{eff}}}}^{{}} {\text{ (Mn}}^{{4 + }} {)}$ = 3.87 μ_B [59].

Table 4 Some experimental values for ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) samples

The different calculated $\mu_{{{\text{eff}}}}^{{\exp}}$ and $\mu_{{{\text{eff}}}}^{{{\text{theo}}}}$ values are listed in Table 4. We can remark a difference between these two parameters. This may be attributed to FM correlations in PM region, which is probably caused by the formation of FM clusters [60]. Our results are comparable to those obtained in the literature [60, 61]. It is important to mention that the paramagnetic moment and the susceptibility (M/H) can be seen to be decreasing with the increase in the crystallite size. To better understand the magnetic properties of our samples, the hysteresis cycles M (µ₀H), at low temperature, were studied. Figure 5a, b displays M (µ₀H) at 10 K of the range of µ₀H =  ± 6 T, for x = 0.00 and 0.10 samples, as examples. From these figures, we can see a similar behavior with a small hysteresis loop. The insets of Fig. 5a, b display a zoomed portion of the low magnetic field region. We can see clearly that magnetization increased rapidly at a low applied field. Surprisingly, a sharp saturation was observed in which the M_S values were found to be 92.65 and 105.43 emu g⁻¹ for x = 0.00 and 0.10, respectively. This indicates the typical FM behavior. Additionally, we remarked that our samples have negligible values of the remnant magnetizations (M_r) and the coercive fields (µ₀H_C). µ₀H_C values were found to be 52 × 10^–4 and 19 × 10^–4 T, for x = 0.00 and 0.10, respectively. M_r values were found to be 2.30 and 1.40 emu g⁻¹ for x = 0.00 and 0.10, respectively. These three parameters change slightly with change in the grain size. The increase of the grain size led to the decreases of the total grain boundary and therefore, the movement of domains becomes easier inside the crystal leading to increase in Ms and decrease in H_C. Here, we can conclude that our samples have a soft FM behavior. These results make them good candidates for some technological applications such as reading and writing process in high density recording media or information storage [62]. In addition, x = 0.15 and 0.20 [33], have also negligible values. In which, M_S values were found to be 88.10 and 92.21 emu g⁻¹, µ₀H_C values were found to be 21 × 10^–4 and 16 × 10^–4 T, and M_r values were equal to 1.49 and 1.11 emu g⁻¹, for x = 0.15 and x = 0.20, respectively. Together with hysteresis loop studies, we measured magnetization as a function of the applied magnetic field around their FM–PM phase transition, as shown in the inset of Fig. 6 for our studied samples. At the low temperature region, we can see a rapid increase in the magnetization at the weak magnetic field region up to 1 T. Then, M (µ₀H) curves reached saturation as a result of increase in the magnetic field, indicating a typical FM state. This is caused by the complete alignment of the spins in our studied samples.

Fig. 5

Magnetic hysteresis cycles at T = 10 K of ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) samples. The insets show a zoom portion of the low magnetic field region

Fig. 6

M² vs. μ₀H/M plots, for ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) samples. Insets show M (µ₀H) curves at different temperatures

To get a deeper understanding of the nature of the magnetic phase transition for our samples, we derived the Arrott’s plots (M² vs. μ₀H/M) from M (μ₀H) (Fig. 6). According to Banerjee’s criterion [63, 64], if the slope of the curve is negative, the magnetic transition is of first order. Otherwise, it is of second order, which is the case in our study.

3.4 Magnetocaloric study

Magnetocaloric effect is an intrinsic property of magnetic materials. It represents their thermal response under the application or elimination of an external magnetic field. The coupling between the lattice and spin plays an important role, which leads to an additional magnetic entropy change near T_C and favors MCE. $- \Delta S_{{\text{M}}}$ allows one to verify whether a magnetic material may be considered as a good magnetic refrigerant or not. It can be calculated from the isothermal magnetization curves under different magnetic fields. According to the fundamentals of thermodynamics, $- \Delta S_{{\text{M}}}$ produced by the variation of the applied magnetic field from 0 to μ₀H_max, can be expressed by the following expression [65]:

$${\Delta }S_{{\text{M}}} { (}T{,}\mu_{{0}} H{)} = S_{{\text{M}}} { (}T{,}\mu_{{0}} H{)} - S_{{\text{M}}} { (}T,0) = \int\limits_{{0}}^{{\mu_{0} H_{\max } }} {\left ( {\frac{{\partial {\text{S}}}}{{\partial (\mu_{0} H)}}} \right)}_{T} d\left ( {\mu_{0} H} \right).$$

(8)

From Maxwell’s thermodynamics, a relationship between $- \Delta S_{{\text{M}}}$ and M is defined as:

$$\left ( {\frac{\partial S}{{\partial (\mu_{0} H)}}} \right)_{T} = \left ( {\frac{\partial M}{{\partial T}}} \right)_{{ (\mu_{0} H)}} .$$

(9)

Then, one can determine the following relation:

$$\Delta S_{{\text{M}}} (T,\mu_{0} H) = \int\limits_{0}^{{\mu_{0} H_{\max } }} {\left ( {\frac{\partial M}{{\partial T}}} \right)}_{{\mu_{0} H}} d\left ( {\mu_{0} H} \right).$$

(10)

Here µ₀H_max represents the maximum of the applied magnetic field [66].

Generally, to predict MCE, $- \Delta S_{{\text{M}}}$ is often determined by some different numerical calculations. The first approximation is a direct method, based on the M (T) measurement under different external magnetic fields. In the case of a small discrete field, $- \Delta S_{{\text{M}}}$ can be approximated as [67]:

$$\Delta S_{{\text{M}}} \left ( {\frac{{T_{1} + T_{2} }}{2}} \right) = \frac{1}{{T_{2} - T_{1} }}\left[ {\int\limits_{0}^{{\mu_{0} H_{\max } }} {M (T_{2} ,\mu_{0} H)d (\mu_{0} H) - \int\limits_{0}^{{\mu_{0} H_{\max } }} {M (T_{1} ,\mu_{0} H)d (\mu_{0} H)} } } \right].$$

(11)

The second one is based on M (µ₀H) measurement. To evaluate $- \Delta S_{{\text{M}}}$, one needs to use a numerical approximation to the integral in Eq.  (9). $- \Delta S_{{\text{M}}}$ can be written as [68]:

$$- \Delta S_{{\text{M}}} \left ( {T,\Delta (\mu_{0} H)} \right) = \sum {\frac{{M_{i + 1} (T_{i + 1} ,\mu_{0} H_{i + 1} ) - M_{i} (T_{i} ,\mu_{0} H_{i} )}}{{T_{i + 1} - T_{i} }}\Delta \mu_{0} H_{i} } ,$$

(12)

M_i and M_i+1 are the experimental magnetization values, respectively, at T_i and T_i+1, under an external magnetic field μ₀H_i [69].

In the following part of this work, we have used the first approximation to evaluate the variation of $- \Delta S_{{\text{M}}}$ as a function of temperature under an applied magnetic field. Figure 7 displays $- \Delta S_{{\text{M}}} \left ( T \right)$ for our samples. The obtained curves are similar to those obtained in other perovskite manganites [70, 71]. They have a positive sign in all studied temperatures, which confirms the FM behavior. Our studied samples exhibit $- \Delta S_{{\text{M}}}^{\max }$ of 6.25, 6.35, and 6.44 J kg⁻¹ K at a magnetic field of 5 T for x = 0, 0.05, and 0.10, respectively. On other hand, x = 0.20 sample exhibited a classical behavior of $- \Delta S_{{\text{M}}}$ with $- \Delta S_{{\text{M}}}^{\max }$ equal to 6.01 J kg⁻¹ K⁻¹. While, x = 0.15 indicated the coexistence of two peaks, which corresponds to two-Curie temperatures [33]. We can notice also, that for low Na content our samples x = 0, 0.05, and 0.10 exhibited high entropy values, better than x = 0.15 and 0.20. Here, it is important to mention that the magnetic entropy change was observed to increase with increase in the magnetic field and to be higher for the high grain size.

Fig. 7

$- \Delta S_{{\text{M}}}$ as function of temperatures at different magnetic fields, for ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) samples

In magnetic refrigeration, another useful parameter to quantify the efficiency of MC material is the relative cooling power (RCP). This latter refers to the heat transfer between the hot and cold reservoirs in the ideal refrigeration cycle. This parameter represents the area under $- \Delta S_{{\text{M}}}$ (T) curve. It is defined as [72,73,74]:

$${\text{RCP}}{\kern 1pt} = {\kern 1pt} {\kern 1pt} {\kern 1pt} - \Delta S_{{\text{M}}}^{\max } \left ( {T,\mu_{0} H} \right) \times \delta T_{{{\text{FWHM}}}} ,$$

(13)

where, $\delta T_{{{\text{FWHM}}}}$ is the full width at half maximum in $- \Delta S_{{\text{M}}}$ (T) curve.

Figure 8 shows the variation of $\delta T_{{{\text{FWHM}}}}$ and RCP as a function of the applied magnetic field at T_C for x = 0.10 as an example. A monotonous increase is seen in these parameters when increasing the applied magnetic field. This increase is due to the weakness of the effect of spin coupling that is less important when the applied magnetic field is high. Table 5 presents the obtained $- \Delta S_{{\text{M}}}^{\max }$ and RCP values for our samples together with those obtained in other magnetic materials. From this table, it is clear that our values are in agreement with those obtained in the literature. This makes our compounds potential candidates for magnetic refrigeration.

Fig. 8

RCP and δ_FWHM values vs. µ₀H, for x = 0.10 sample

Table 5 Summary of MC properties of ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) samples compared with other magnetic materials

The magnetization related change of the specific heat, $\Delta C_{{{\text{p}},\mu_{0} H}}$, is expressed as:

$$\Delta C_{{\text{p}}} \left ( {T,\mu_{0} H} \right) = C_{{\text{p}}} \left ( {T,\mu_{0} H} \right) - C_{{\text{p}}} \left ( {T,0} \right) = T\frac{{\partial \Delta S_{{\text{M}}} \left ( {T,\mu_{0} H} \right)}}{\partial T}.$$

(14)

Using this equation, we calculated $\Delta C_{{{\text{p}},\mu_{0} H}}$ as a function of temperature for our samples under different applied magnetic fields (Fig. 9). We can see that $\Delta C_{{{\text{p}},\mu_{0} H}}$ changed sharply around T_C, from a negative to a positive value, upon increasing temperatures [75, 76]. The sum of the two parts is the magnetic contribution to the total specific heat. This affects the heating or cooling power of magnetic refrigerators. $\Delta C_{{{\text{p}},\mu_{0} H}}$ data of a magnetic material are useful in the design of a refrigerator.

Fig. 9

−ΔCP as function of temperatures for ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) samples at different magnetic fields

To get better insights into MCE, Amaral [77, 78] proposed a theatrical modeling based on Landau’s theory of magnetic phase transition. Gibbs free energy can be developed as follows [77]:

$$G (T,M) = G_{0} + \frac{1}{2}A (T)M^{2} + \frac{1}{4}B (T)M^{4} + \frac{1}{6}C (T)M^{6} + \cdots - \mu_{0} HM,$$

(15)

where A (T), B (T), and C (T) are temperature-dependent parameters according to the thermal variation of the amplitude of the spin fluctuation known as Landau’s coefficients.

In the equilibrium condition, $\partial G/\partial M = 0$, the magnetic equation of state is derived as:

$$\frac{{\mu_{0} H}}{M} = A (T) + B (T)M^{2} + C (T)M^{4} .$$

(16)

Fitting Arrot’s plots by the last equation, the evolution of the best obtained values of Landau’s coefficients as function temperatures is shown in Fig. 10, for x = 0, under an applied field of 5 T as an example. According to Amaral et al. [77, 79], the nature of B (T) plays a fundamental role in investigating $- \Delta S_{{\text{M}}} \left ( {T,\mu_{0} H} \right)$. The inset of Fig. 10 indicates that B (T) is negative below T_C. However, it has a positive sign above T_C. The behavior of this curve is obtained in recent works [80, 81]. This suggests the second-order phase transition in our samples [82]. Therefore, using the differentiation of Gibbs free energy with respect to temperatures, we can determine $- \Delta S_{{\text{M}}} \left ( {T,\mu_{0} H} \right)$ theoretically by:

$$S_{{\text{M}}} (T,\mu_{0} H){\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} - \left ( {\frac{{\partial G\left ( {\mu_{0} H,T} \right)}}{\partial T}} \right)_{{\mu_{0} H}} = {\kern 1pt} {\kern 1pt} {\kern 1pt} - \frac{1}{2}\frac{\partial A}{{\partial T}}M^{2} - \frac{1}{4}\frac{\partial B}{{\partial T}}M^{4} - \frac{1}{6}\frac{\partial C}{{\partial T}}M^{6} .$$

(17)

Fig. 10

Experimental and calculated values of $- \Delta S_{{\text{M}}}$ as function of temperatures, under 5 T magnetic field for x = 0. The inset shows the Landau’s coefficients A (T) and B (T)

The theoretical $- \Delta S_{{\text{M}}} \left ( {T,\mu_{0} H} \right)$ is defined as:

$$\begin{aligned} \Delta S_{{\text{M}}} (T,\mu_{0} H){\kern 1pt} & = {\kern 1pt} {\kern 1pt} S_{{\text{M}}} \left ( {T,0} \right) - S_{{\text{M}}} \left ( {T,\mu_{0} H} \right)\;\; \\ & = {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \frac{1}{2}\;\frac{\partial A}{{\partial T}}\left ( {M_{0}^{2} - M^{2} } \right) - \frac{1}{4}\frac{\partial B}{{\partial T}}\left ( {M_{0}^{4} - M^{4} } \right) - \frac{1}{6}\frac{\partial C}{{\partial T}}\left ( {M_{0}^{6} - M^{6} } \right)\;. \\ \end{aligned}$$

(18)

The value of M₀ can be obtained by extrapolating M in the absence of a magnetic field. Figure 10 displays the variation of $- \Delta S_{{\text{M}}}$ as a function of temperatures under an applied magnetic field of 5 T, for x = 0 as an example. We can see that the theoretical and experimental curves are in good agreement, which suggests that the present model does not take into account the influence of the Jahn–Teller’s effect and exchange interactions on the magnetic properties of manganites [82].

3.5 Universal curve scaling analysis

Recently, Franco et al. have proposed a phenomenological universal curve for the applied magnetic field dependence of $- \Delta S_{{\text{M}}}$ [83]. This is based on normalizing all $- \Delta S_{{\text{M}}} \left ( {T,\mu_{0} H} \right)$ curves by the following expression:

$$\Delta S^{^{\prime}} = \Delta S_{{\text{M}}} (T,\mu_{0} H)/\Delta S_{{\text{M}}}^{\max } .$$

(19)

In addition, the temperature axis is differently rescaled above and below T_C, as expressed in:

$$\theta = \left\{ \begin{gathered} \frac{{T - T_{{\text{C}}} }}{{T_{{\text{C}}} - T_{{{\text{r}}_{{1}} }} }}\quad T < T_{{\text{C}}} \hfill \\ \frac{{T - T_{{\text{C}}} }}{{T_{{{\text{r}}_{{2}} }} - T_{{\text{C}}} }}\quad T > T_{{\text{C}}} \hfill \\ \end{gathered} \right.\quad ,$$

(20)

where $T_{{{\text{r}}_{{1,2}} }}$ are the temperatures of two reference points, corresponding to ${{ - \Delta S_{{\text{M}}}^{\max } } \mathord{\left/ {\vphantom {{ - \Delta S_{{\text{M}}}^{\max } } 2}} \right. \kern-\nulldelimiterspace} 2}$ (T_r1 < T_C and T_r2 > T_C). Figure 11 shows the variation of $\Delta S^{^{\prime}}$ as a function of $\theta$, under different magnetic fields, for ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) samples. We can see that all curves collapse on the same curve. This confirms the second-order phase transition for our samples [84].

Fig. 11

Universal behavior of $\Delta S^{\prime}\left ( \theta \right)$ curves at different magnetic fields, for ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) samples

On the other hand, the search for universal curves and scaling laws emerges in all fields of scientific research. We can see clearly that all the experimental curves collapse on one universal curve. The universal curve can be well fitted by Lorentz function:

$$\Delta S^{\prime} = \frac{a}{{b + (\theta - c)^{2} }}.$$

(21)

Generally, a, b, and c are free parameters. Taking into account the asymmetry of the plots, we can use two different sets of constants such as for T < T_C region, a = 0.952 ± 0.013, b = 0.954 ± 0.011, and c =  − 0.043 ± 0.007. While, for T > T_C state a = 0.537 ± 0.030; b = 0.539 ± 0.031; and c = 0.208 ± 0.019, for x = 0 as an example. According to Eq. 21, the different $- \Delta S_{{\text{M}}}^{\max }$, T_C, T_r1 and T_r2 values are obligatory to characterize $- \Delta S_{{\text{M}}}$. Once we have determined the parameters from the properties of these materials, we can determine $- \Delta S_{{\text{M}}}$ from $\Delta S^{\prime}$.

According to Oesterreicher et al. [85], the variation of $- \Delta S_{{\text{M}}}$ as a function of temperatures under different magnetic fields, for the magnetic materials with second-order phase transition around their T_C, follows an exponent power law:

$$\Delta S_{{\text{M}}} (T,\mu_{0} H) = a (T)\left ( {\mu_{0} H} \right)^{n} ,$$

(22)

where n is the critical exponent of the magnetic transition, defined as [86]:

$$n (T,\mu_{0} H) = \frac{{d\ln \left ( {\left| {\Delta S_{{\text{M}}} } \right|} \right)}}{{d\ln \left ( {\mu_{0} H} \right)}}.$$

(23)

Figure 12 shows the variation of n as a function of temperatures, for x = 0 sample as an example, under different applied fields. In the FM region, n is close to 1. Then, it increased to 2, in PM state. Moreover, it decreased moderately with increasing temperature and a minimum value around T_C. These results are observed in different magnetic materials [87,88,89,90].

Fig. 12

Temperature dependence of local exponent n measured, at different magnetic fields, for x = 0

4 Conclusion

To sum up, we chose to detect the effect of low Na content on the ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ sample. We prepared ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) using the flux method. Then, we studied their structural and magnetic properties and MCE. Rietveld refinement of XRD patterns shows that our samples crystallize in an orthorhombic structure with a Pbnm space group, at room temperature. Substituting Ca²⁺ by Na⁺ increased T_C from 268 to 278 K. This is accompanied by an increase of $- \Delta S_{{\text{M}}}$. Our samples have a second-order phase transition from FM to PM, upon increasing temperature. In addition, we found that $- \Delta S_{{\text{M}}}$ is in agreement with the theoretical one calculated using Landau’s theory. From x = 0.10, the composition shows the largest value of $- \Delta S_{{\text{M}}}^{\max }$ = 6.44 J kg⁻¹ K⁻¹ for μ₀H = 5 T in the series. Additionally, our samples exhibit high values of RCP = 198, 270.5, and 317.7 J k⁻¹ for x = 0, 0.05, 0.10, respectively. The magnetic entropy change was also characterized by one universal curve. This confirms that a second-order phase transition occurred. The obtained results indicate that ${\text{La}}_{{{0}{\text{.75}}}} {\text{Ca}}_{0.25 - x} {\text{Na}}_{x} {\text{MnO}}_{{3}}$ (0 ≤ x ≤ 0.10) samples could be considered as a promising material for magnetic refrigeration technology. The most important results, in our present work, were compared with our last work for different doping rates of 0.15 and 0.20.