Density functional investigation of structural, electronic, optical and thermodynamic properties of Zn_1−xBe_xO semiconductor

Abstract

Based on the first principles calculations using a full potential linearized augmented plane wave (FP-LAPW) method in the modified Becke–Johnson (mBJ) approximation, we calculated the electronic, optical and thermodynamic properties of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ for different Be concentrations ($0 \le x \le 1$). The calculated structure of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ for $x = 0.25, x = 0.5\;{\text{and}}\;x = 0.75$ was changed compared to the end structures ($x = 0\;{\text{and}}\;x = 1$) and passed from wurtzite to orthorhombic structures, while most of the previous works show that the structures of ZnO remained unchanged after doping with Be. Our result shows that the orthorhombic lattices have lower formation energies than wurtzite. The calculated band structures show an increase in energy bandgap with increasing Be concentrations and present a gap bowing close to 10 eV. The electronic structure was studied by oxygen k-edge X-ray emission (XES) and X-ray absorption (XAS). Moreover, the calculated absorption coefficient indicates that the ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ exhibit more interesting properties in UV region main absorption. The thermodynamic stability of these compounds has also been well studied and confirms well the previous experimental results. The calculations show that if the Be doping quantity increases, the doping system absorption spectrum blueshift becomes more significant, the energy loss peak moves towards the direction of high energy and the plasmon frequency $\omega_{\text{p}}$ become stronger in the case of BeO.

1 Introduction

The II–VI semiconductor compounds doped with Be have attracted great attention, because they are a promising technology for application in solar cells, blue and ultraviolet (UV) light-emitting devices, optoelectronic devices and highly sensitive UV detectors [1,2,3,4]. In the last years, several studies have been dedicated to investigating ZnBeO compounds. The importance of doping is to lie in adapting its electronic, optical and thermodynamic properties. The most important characteristics of doped semiconductor (DS) are their energy bandgap $E_{\text{g}}$, dielectric constants and thermodynamic parameters.

The effect of Be on ZnO has been studied experimentally. ZnBeO films are appealing for the following reasons [5]: first, the solubility of Be in ZnO can vary over the entire composition range from 0 to 100%, and there is no phase segregation between ZnO and BeO [6]. Second, BeO has a wide bandgap of 10.6 eV, allowing it to be modulated in a wide range from 3.4 to 10.6 eV [6].

In ZnBeO, an increase in energy bandgap and a large boing parameter are predicted and this conclusion is due to the large difference in lattice constants between ZnO and BeO [7]. The effect on lattice constants remains theoretically unclear, whereas an overall decrease is predicted from ZnO to BeO [7]. Furthermore, it was shown experimentally that lattice parameters decrease with increasing beryllium [6]. In this work, after doping (W) ZnO with 0. 25 and 0.75 Be concentrations, we have found that the initial (W) structure changed to orthorhombic with CmC2₁ structures. For doping with 0.5 concentration, we obtained an orthorhombic structure with Pmn2₁. All previous DFT calculations assumed that ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ crystallize in the (W) structure for all Be compositions. But, only one study confirmed our results and showed that orthorhombic structures obtained from (W) ZnO unit cell can exist for x = 0.25, 0.5 and 0.75 [8].

The purpose of this paper has not been exploited much. Introducing a few percent of beryllium at the zinc sites in ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ compound modifies the energy bandgap, dielectric constants, thermodynamic parameters and defect formation energy. As we know, although several works were devoted to the study of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$, X-ray emission and X-ray absorption spectra have not been experimentally investigated. In this work, we reported the results of energy bandgap, optical, thermodynamic constants and XSPEC calculations on ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$.

In the present work, we investigate the unexplored properties of ZnO semiconductors doped with Be and we also predict if they can be considered good candidates in optoelectronic investigations. Computational details are presented in Sect. 2. The results and discussion on all properties are reported in Sect. 3. A summary of results and conclusion are presented in Sect. 4.

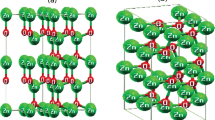
2 Computational details

Based on the DFT, the first principles calculations are performed using the LAPW method included in the WIEN2k package [9]. For the calculation of the electronic properties, we use the modified Becke–Johnson (mBJ) scheme [10] which yields a reasonable bandgap. In the present calculations, the convergence parameter, R_mtK_max was set to 8.0. The wave functions are expanded in the muffin-tin spheres to l_max = 12. For the expansion of charge density, we fixed $G_{\hbox{max} }$ up to 14 Ry. We use 72k-points in the irreducible Brillouin zone (IBZ) and the total energy was converged until it was less than 10⁻⁴ Ry. To investigate the optical properties, we use denser k-points. For this purpose, 120k-points were generated in the (IBZ). The ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ (x = 0.0, 0.25, 0.5, 0.75, 1.0) structures are obtained by construction of the 2 × 2 × 1 supercell from the wurtzite (W) supercell (${\text{P}}6_{3} {\text{mc}}$) which contains eight atoms per cell. For $x$ = 25% and 75%, one and three Zn atoms are replaced by Be atoms, respectively. After doping (W) ZnO with these Be compositions, we found that the initial (W) structure changed to the orthorhombic one (O) with ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ structure. For doping with 0.5 concentration, we also obtained an orthorhombic structure with ${\text{Pmn}}2_{1}$. All previous DFT calculations assumed that ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ crystallize in the (W) structure for all Be compositions. But, only one study confirmed our results and showed that the orthorhombic structures obtained from (W) ZnO unit cell can exist for x = 0.25, 0.5 and 0.75 [8].

3 Results and discussion

3.1 Structural properties and formation energies

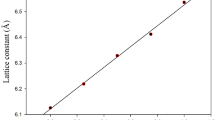
Both ZnO and BeO have an identical crystalline wurtzite structure with the same space group (P6₃mc). To obtain their optimized structure, we vary total energy versus (c/a) ratio which is calculated by fitting to the Birch–Murnaghan equation of states [11], as presented in Fig. 1.

Fig. 1

Variation of total energy versus (% c/a) ratio for BeO (a) and ZnO (b)

The optimized lattice constants with calculated bulk modulus B (GPa) and its pressure derivative B′ are listed in Table 1 with other theoretical and experiment results.

Table 1 Calculated lattice constants, bulk modulus (B) and pressure derivative of bulk modulus (B′) of the (W) structures of ZnO and BeO

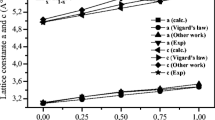
The ternary alloys ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ for x = 0.25, 0.5 and 0.75 have different structures depending on the Be compositions. For x = 0.25 and 0.75, Zn₃BeO₄ and ZnBe₃O₄ have orthorhombic unit cells with ${\text{CmC}}21$ structure, while for $x$ = 0.5, ZnBeO₂ has orthorhombic unit cell with ${\text{Pmn}}21$ structure. For this purpose, the structural properties of Zn₃BeO₄, ZnBeO₂ and ZnBe₃O₄ are investigated in the orthorhombic structure by varying total energy with respect to volume. Using the Birch–Murnaghan equation of states, we fit the calculated (E–V) results as shown in Fig. 2a–c.

Fig. 2

Variation of total energy versus volume for a $x$ = 25%, b $x$ = 50%, and c $x$ = 75%

The optimized lattice constants, the bulk modulus B and its first derivative B′ are summarized in Table 2 with other existing available values.

Table 2 Calculated lattice constants, bulk modulus (B) and pressure derivative of bulk modulus (B′), for different Be concentrations: $x$ = 25%, $x$ = 50%, and $x$ = 75%

On the other hand, the variation of the pressure as a function of volume has been also calculated for ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ as shown in Fig. 3a (for $x = 0.5$). The pressure–volume (P–V) curve is fitted to the Birch–Murnaghan equation of state [11] as shown in Eq. (1):

$$ P\left( V \right) = \frac{3}{2}B\left[ {\left( {\frac{{V_{0} }}{V}} \right)^{3/2} - \left( {\frac{{V_{0} }}{V}} \right)^{{\frac{3}{2}}} } \right] \times \left\{ {1 + \frac{3}{4}\left( {B^{\prime} - 4} \right)\left[ {\left( {\frac{{V_{0} }}{V}} \right)^{3/2} - 1} \right]B^{\prime}} \right\}. $$

(1)

Fig. 3

a Variations of the pressure versus volume and b lattice constants versus pressure (for $x$ = 50%)

The variations in lattice constants with the pressure between − 20 and 12 GPa are illustrated in Fig. 3b (for x = 50%). We noted that the lattice constants decrease with the increase in the pressure due to the increase in the strength of repulsion between atoms [12]. The structural evolution of alloys under pressure from first principles calculations was widely studied by Yang et al. [20]. In particular, authors mostly studied the effect of the pressure on lattice constants in intermetallic alloys and revealed the excellent properties of this kind of material.

To describe theoretically the relative stability and the site reference of the defect in the structure, one can calculate the defect formation energy within a supercell model at 0 K. For a given structure, ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ its formation energy can be determined by the following relation [2]:

$$ E_{\text{f}} \left( {{\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}} } \right) = E\left( {{\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}} } \right) - xE\left( {\text{BeO}} \right) - \left( {1 - x} \right)E\left( {\text{ZnO}} \right) $$

(2)

which can be rewritten as:

$$ E_{\text{form}} = E\left( {{\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}} } \right) - E\left( {\text{ZnO}} \right) - n\left( {E\left( {\text{BeO}} \right) - E\left( {\text{ZnO}} \right)} \right), $$

(3)

where $E\left( {{\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}} } \right)$ represent the total energy of the defect supercell, $E\left( {\text{ZnO}} \right)$ and $E\left( {\text{BeO}} \right)$ are the total energies of the supercell of the host without the defect containing equivalent number of atoms as that of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ defect supercell. The n is the number of Zn atoms removed and Be atoms added to the supercell of ZnO. Our results for defect formation energies of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ ($x$ = 0, 0.25, 0.5, 075 and 1) are listed in Table 3. From Table 3, it can be noted that the structures of substitutional Be in ZnO for $x$ = 0.25, 0.5 and 0.75 are more energetically favored than wurtzite structures. In addition, all calculated values of formation energy for ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ are negative which is in agreement with other studies. This result shows that ZnBeO alloys can be experimentally achievable.

Table 3 Calculated energies bandgaps (eV) and defect formation energies (eV) for different Be concentrations

3.2 Electronic properties and core-level spectroscopy

The bandgap energies of the end compounds ZnO and BeO and their alloys ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ for the two structures (wurtzite and orthorhombic) were obtained self-consistently using mBJ approximation. The choice of mBJ scheme is not arbitrary in this work. We used this approximation because it gives reliable results close to the experiment. Figure 4 presents the electronic band structures of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ for $x$ = 0, 0.25, 0.5, 075 and 1. All calculated electronic band structures present a direct bandgap that occurs between $\varGamma - \varGamma$ points. Table 3 listed calculated bandgaps with the available theoretical and experimental results.

Fig. 4

Calculated band structures of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ for different Be concentrations. a ZnO ($x$ = 0), b Zn₃BeO₄ ($x$ = 25%), c ZnBeO₂ ($x$ = 50%), d ZnBe₃O₄ ($x$ = 75%) and e BeO ($x$ = 100%)

The calculated values of energy gaps in the mBJ approximation presented in Table 3 are better than those calculated using other approximations such as PBE–GGA [21]. On the other hand, other approximations can be used which give results close to those achieved experimentally such as the on-site Coulomb interaction in which the correlated electron systems are described [22]. The results shown in Table 3 also indicated some deviation between the experiment’s results and the calculated ones, but the difference is not large. Some experimental results are available now and further investigation is needed to find a more accurate energy bandgap. We think that this difference may result from the large lattice constant difference between ZnO and BeO. Such problems will generate a large lattice mismatch if we want to obtain a large bandgap offset between ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ and ZnO. To solve such problems, Ryu et al. proved that a good lattice matching between ZnO and BeZnO can be achieved by adding an appropriate amount of Mg into the BeZnO alloy [4].

The bandgap variation according to the composition $x$ for the alloys ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ is plotted in Fig. 5. We show that $E_{\text{g}}$ varies non-linearly with $x$ and presents a gap bowing determined by fitting E_g with a second-order polynomial as:

$$ E_{\text{g}}^{\text{mBJ}} \left( {{\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}} } \right) = xE_{\text{g}} \left( {\text{BeO}} \right) + \left( {1 - x} \right)E_{\text{g}} \left( {\text{ZnO}} \right) - bx\left( {1 - x} \right), $$

(4)

where the parameter b refers to a bandgap bowing.

Fig. 5

Bandgap energy $E_{\text{g}}$ of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ versus the Be concentrations. The solid line is fit to Eq. (4) for a bowing parameter of 10 eV

After fitting, the calculations present $E_{\text{g}}^{\text{mBJ}}$ as follows:

$$ E_{\text{g}}^{\text{mBJ}} = 2.6 + 7.4x + 10x\left( {1 - x} \right). $$

(5)

The best fit of Eq. (4) gives b equal to 10 eV. The obtained bowing parameter b is larger than other theoretical results for ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ [23] because the mBJ approach was used in our calculations. Yu et al. found a value of about 6.32 using photocurrent spectroscopy [24]. The deviation from quadratic variation in the case of Zn₂Be₂O (x = 75%) is due to the fact that bulk modulus is high (526.466 GPa) than other alloys. This phenomenon corresponds to the volume deformation contribution to the bowing parameter and represents the relative response of the band structure to hydrostatic pressure, which arises in this case from the change of the individual equilibrium lattice constants.

To study the energy band variation, the energy band structures of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ along with the high symmetry points of the Brillouin zone are calculated at 0, 5, 9, 12 GPa for Be concentration $x = 0.5$ and are listed in Fig. 6. The main feature of Fig. 6 is the variation of the energy bandgap under pressure. Indeed, when the pressure increases, the conduction band moves towards high energies while the valence band remains almost unchanged. The effect of pressure on the energy band in the vicinity of fermi level has been well explained by Gao et al. [25] and Yang et al. [26].

Fig. 6

Energy band of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ for $x = 0.5$ at 0, 5, 9, 12 GPa, respectively

The variation of the energy bandgap as a function of the pressure is presented in Fig. 7. It is easy to observe that the energy bandgap increases by increasing pressure from 3.456 eV for 0 GPa to 3.585 eV for 12 GPa, which gives an increase in the value of the energy bandgap by 129 meV between low and high pressure.

Fig. 7

Bandgap energy $E_{\text{g}}$ of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ for $x = 0.5$ versus the pressure

To determine the contribution of the following atoms Zn-3d, Be-2s and O-2p in the calculated band structures, we calculated the total (TDOS) and partial (PDOS) densities of states for all concentrations of beryllium presented in Fig. 8. Our discussion focused only on $x = 0$ and $x = 0.75$. From PDOS ZnO ($x = 0$), the valence band between [− 5, 0] eV mainly originated from O-p states located at the upper part [− 2.3 to 0] eV and Zn-d orbitals at the lower valence band [− 5, − 2.3] eV.

Fig. 8

Total (TDOS) and partial (PDOS) density of states of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ for a $x = 0$, b $x$ = 1, c $x$ = 0.25, d $x$ = 0.5 and e $x$ = 0.75

As seen in Fig. 8e, the valence band region from − 4 to 0 eV can be divided into three energy regions. The first region between − 4 and − 3 eV consists mainly of Zn3d and O2p orbitals with the least contribution of Be-2s. Whereas, in the second region between − 3.1 and − 1.4, we can see that Zn-3d and O-2p states represent the mainly contribution with the least contribution of Be-2s and Zn-4s orbitals. Further, one could find that the Zn-d states and Be-s states are located at lower ranges than those of O-p and Be-s states, suggesting a stronger Be–Zn bond and weaker Be–O bond [27]. In the third region which represents the upper valence band from − 1.4 to 0 eV, the strongest contribution is due to the O-2p states with small contribution from Zn-3d and Be-s orbitals. The conduction band originated mainly from Be-s states with small contribution from O-2p and Zn-4s states. The contributions of Zn-d, Be-s and O-p states in valence band of ${\text{Zn}}_{0.25} {\text{Be}}_{0.75} {\text{O}}$ ($x = 0.75$) show a strong hybridization between Zn-d and O-p states with least hybridization between Zn-d/O-p and Be-s states.

The bonding feature and the charge transfer properties of ZnBeO, could be described by the evaluation of the electronic charge densities contour. In Fig. 9, we have plotted the charge density contour plot in (011) plane of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ for $x = 0.75$. The obtained charge density contour plot shows a mixed covalent and ionic character for the Zn–O and Be–O bonds. The contour plot shows a strong covalent bounding between Zn and O Sites and a partial ionic character of Be–O bonds. This is due to the strong-d hybridization between Zn and O atoms and also due to the electronegativity difference between Be and O atoms [27, 28].

Fig. 9

Charge density contour projected (100) for ${\text{Zn}}_{0.25} {\text{Be}}_{0.75} {\text{O}}$

In the present study, we used another procedure to exploit the electronic properties of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ alloys based on the core-level XES and XAS. The XAS and XES spectra were calculated using ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ supercells with a single O 1s electrons. To create a core hole for the photo-excitation process, O 1s electron is removed and then added to the account. The oxygen k-edge was calculated from the electronic structure using the XSPEC program included in Wien2k package. Figure 10 displays the calculated O k-edge XES and XAS spectra for Be-doped ZnO at different compositions $x$ ($x$ = 0, 0.25, 0.5, 0.75 and 1). The first observed peak in XAS spectra is attributed to a transition between the O2p core states to the unoccupied states of the conduction band. Hybridization takes place between the O2p and Zn-4s states with a contribution from the Be-p. In the high energy region, the spectrum is primarily attributed to hybridization between O-2p and Zn-4p states. X-ray emission spectra at the oxygen k edge spectra fundamentally arise from the mixed states O-2p and Zn-3d. To the best of our knowledge, no theoretical or experimental study has dealt with the XAS and XES spectra, so this work made the first predictions in this area.

Fig. 10

XAS (black line) and XES (red line) spectra of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$

3.3 Optical properties

Theoretical studies exist on the calculation of the optical properties of the ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ structures based on the DFT calculations considering that the ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ crystallizes in the wurtzite structure for all values of $x$ [5]. In the present work, we will study these alloys taking into account that the end compounds ZnO and BeO are in the wurtzite structure so they have two polarization directions (100) and (001), while for ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ ($x$ = 0.25, 0.5 and 0.75) we consider three polarization directions due to their orthorhombic CmC2₁ and Pmn2₁ structures. The study of the optical properties of materials is so important to know their possibility of being used them in optoelectronic devices. Optical properties are mostly based on the complex dielectric function given by:

$$ \varepsilon \left( \omega \right) = \varepsilon_{1} \left( \omega \right) + {\text{i}}\varepsilon_{2} \left( \omega \right), $$

$\varepsilon_{1}$ and $\varepsilon_{2}$ represent the real and imaginary parts of ε(ω), respectively. $\varepsilon_{2} \left( \omega \right)$ is obtained from the momentum matrix elements between the occupied and unoccupied states, while $\varepsilon_{1} \left( \omega \right)$ is determined from $\varepsilon_{2} \left( \omega \right)$ using the Kramers–Kronig relation. Absorption coefficient $\alpha \left( \omega \right)$, refractive index $n\left( \omega \right)$, extinction coefficient $k\left( \omega \right)$ and the energy loss function $L\left( \omega \right)$ are obtained from $\varepsilon_{1} \left( \omega \right)$ and $\varepsilon_{2} \left( \omega \right)$ [29, 30].

Figure 11 illustrates $\varepsilon_{1} \left( \omega \right)$ and $\varepsilon_{2} \left( \omega \right)$ as a functions of the photon energy up to 30 eV. The $\varepsilon_{2} \left( \omega \right)$ start at around 0.5 eV, 1 eV, 1.5 eV, 2.2 eV and 7.4 eV at $x$ = 0.0, 0.25, 0.50, 0.75 and 1.0 along all polarization directions. This starting critical point of $\varepsilon_{2} \left( \omega \right)$ moves towards higher energies when increasing the doping concentrations of the atom Be. The same result was obtained in Ref. [5]. It is noted also that ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ for $x$ = 0.50 has a strong absorption region which starts from around 2–25 eV along the three polarization directions. The anisotropic behavior is clearly presented in $\varepsilon_{2} \left( \omega \right)$ which reduced with increasing Be compositions. $\varepsilon_{2} \left( \omega \right)$ spectra present main peaks that appear at different photon energies. These peaks are related to the densities of states [31]. We restrict our analysis for $x = 0.75$. From Fig. 11b, $\varepsilon_{2} \left( \omega \right)$ spectra for $x = 0.75$ contains four prominent peaks located at 4.49 eV, 7.3 eV, 11.08 eV and 13.69 eV, respectively. The highest peak located at 11.08 eV is mainly due to the transition between O-p and Be-s States.

Fig. 11

Calculated $\varepsilon_{1} \left( \omega \right)$ (a) and $\varepsilon_{2} \left( \omega \right)$ (b) functions of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ alloys along polarization directions

The same feature of anisotropy discussed in $\varepsilon_{2} \left( \omega \right)$ is also observed for $\varepsilon_{1} \left( \omega \right)$ along different polarization directions. $\varepsilon_{1} \left( 0 \right)$ constitutes an important quantity derived from the $\varepsilon_{1} \left( \omega \right)$ curve which presents the zero frequency limit. The calculated $\varepsilon_{1} \left( 0 \right)$ of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ are listed in Table 4. We note that $\varepsilon_{1} \left( 0 \right)$ constants reduce with increasing Be concentrations.

Table 4 Static dielectric constant $\varepsilon_{1} (0)$ and refractive index $n(0)$ for ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$

Figure 12 presents the refractive index $n\left( \omega \right)$ and the extinction coefficient $k\left( \omega \right)$ of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ with different concentrations $x$. Table 5 listed the static refractive indexes along the three polarization directions. $n\left( 0 \right)$ and $\varepsilon_{1} \left( 0 \right)$ are related by the relation: $n\left( 0 \right) = \varepsilon_{1}^{1/2} \left( 0 \right)$. Table 5 shows that the calculated values of $n\left( 0 \right)$ obey to the relation mentioned above. From Fig. 12, it should also be noted that the extinction coefficient curves $k\left( \omega \right)$ has the same look as the imaginary parts of the dielectric function $\varepsilon_{2} \left( \omega \right)$.

Fig. 12

Calculated refractive index (a) and extinction coefficient (b) of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ alloys along polarization directions

Table 5 Positions of plasmon peaks appear in $L\left( \omega \right)$ and the plasmon frequency $\omega \left( p \right)$ for the three polarization directions

The most important feature observed in the energy loss function $L(\omega )$ spectra illustrated by Fig. 13 is the sharp peak which shifts towards higher energies with a growing composition $x$. These peaks are defined as the plasmon peaks, which described the plasma resonance [32]. We summarized the values of the plasmon frequency $\omega_{\text{p}}$ in Table 5. This can be determinated by the model of Penn [33] given by the expression:

$$ \varepsilon_{1} \left( 0 \right) \approx 1 + \left( {\frac{{\hbar \omega_{\text{p}} }}{{E_{\text{g}} }}} \right)^{2} . $$

(6)

Fig. 13

Energy loss spectrum L(ω) of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ alloys along polarisations directions

Another important optical parameter is the absorption coefficient $\alpha \left( \omega \right)$ which is studied for all alloys of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$. Figure 14 shows that the absorption region is reduced with increasing concentrations $x$. In addition, the absorption edge of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ shifts to higher energy side with increasing $x$. Moreover, the major part of absorption part is located at the ultraviolet region for all compositions.

Fig. 14

Absorption coefficient of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ alloys along polarisations directions

3.4 Thermodynamic properties

To evaluate thermodynamic description of alloys of the type A_1−xB_xX, the function for the Gibbs free energy of mixing $\Delta G^{\text{m}}$ can be determined using the following relation:

$$ \Delta G^{\text{m}} = \Delta H^{\text{m}} - T\Delta S^{\text{m}} $$

(7)

where $\Delta H^{\text{m}}$ and $\Delta S^{\text{m}}$ are the enthalpy and the entropy of mixing, respectively. T represents the absolute temperature. According to the model given by Emeljanova et al. [34], one can give $\Delta H^{\text{m}}$ and $\Delta S^{\text{m}}$ as:

$$ \Delta H^{\text{m}} = \varOmega x\left( {1 - x} \right);\quad \Delta S^{\text{m}} = - R\left[ {x\ln x + \left( {1 - x} \right)\ln \left( {1 - x} \right)} \right], $$

(8)

where Ω is the interaction parameter and R is the universal gas constant.

To obtain the interaction parameter Ω, we calculated the mixing enthalpy $\Delta H^{\text{m}}$ using the calculated total energies as:

$$ \Delta H^{\text{m}} = E_{{{\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}}} - \left( {1 - x} \right)E_{\text{ZnO}} - xE_{\text{BeO}} , $$

(9)

where $E_{{{\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}}}$, $E_{\text{ZnO}}$ and $E_{\text{BeO}}$ are the calculated total energies of the ternary alloys and the end compounds, respectively. Table 6 listed the calculated values of $\Delta H^{\text{m}}$ and Ω for Zn_1−xBe_xO. The average value of $\varOmega$ (Ω_av) in the range $0 \le x \le 1$ is estimated to be 94.575 K cal mol⁻¹. Lakel et al. found Ω_av = 16.445 K cal mol⁻¹ [5]. This difference is due essentially to the total energies of alloys which possess different structurees. It should be mentioned that ZnO-doped Be is considered thermodynamically stable and this can be justified by their negative enthalpy [35].

Table 6 Calculated enthalpy energy $\Delta H^{\text{m}}$ and interaction parameter $\varOmega$ of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ alloys

4 Conclusion

In the present study, first principles methods have been used to explore electronic, optical and thermodynamic properties of ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ compound. Our calculation reveals that after doping (W) ZnO with Be compositions, the initial (W) structure is changed to orthorhombic one (O) with ${\text{CmC}}2_{1}$ structure. For doping with 0.5 concentration, we also obtained an orthorhombic structure with ${\text{Pmn}}2_{1}$. The calculations demonstrate that orthorhombic structures, at given Be compositions, are energetically more favorable than the W structure. Moreover, all calculated values enthalpy and formation energy for ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ are negative which is in accordance with other results and shows that these alloys can be experimentally achievable.

Using the mBJ approximation, an improvement in the band structure parameters and reasonable bandgaps close to the experimental values is obtained. We found that doping ${\text{ZnO}}$ with different amounts of beryllium results in an enhancement of the energy bandgap, a blue shift of the optical absorption and more stability of thermodynamic parameters. This result demonstrates that ${\text{Zn}}_{1 - x} {\text{Be}}_{x} {\text{O}}$ could display a potential application for UV photon emitters and detectors.