1 Introduction

Indentation techniques are traditionally used to determine some mechanical characteristics of materials. Several decades ago the indentation techniques have been enriched by introducing by Kalei [29] depth-sensing micro/nanoindentation techniques (see also, [23] and references therein). The progress in development of depth-sensing micro/nanoindentation, see, e.g. reviews by Borodich and Keer [10], Bull [11], Chaudhri and Lim [14] and Borodich [6, 7], has made it possible to study various homogeneous materials in small volumes. These techniques were also applied to study mechanical properties of thin films and coated materials, i.e. sample/substrate systems that are inhomogeneous in the vertical direction. However, many artificial aggregates and natural materials such as rocks and coals are highly inhomogeneous at the micro/nanoscales, hence films of the materials are inhomogeneous in horizontal directions. One needs to use methods of rock mechanics and engineering geomechanics at underground developments to analyse stress–strain state of rock mass and opportunities for coal industry developments [28]. For this purpose, one needs in turn to know physical and mechanical properties of rocks and coals. These properties have been intensively studied (see, e.g. [37, 38]). Although the mechanical and other engineering properties of these inhomogeneous materials are dominated by their properties at the micro/nanoscale and structural features, they have been traditionally treated as homogeneous materials with relatively uniform mechanical properties. Only relatively, recently it was attempted to determine accurately by the depth-sensing indentation (DSNI) techniques the individual mechanical properties of components of cement pastes and other aggregates that are widely used in civil engineering applications. It was shown that the modern DSNI techniques allow the researchers to study the mechanical properties of various micro/nanoscale features of distinct constituents of various cementitious materials including synthetically prepared pure cement clinker phases and selected hydrate phases in well-hydrated cement pastes (see, e.g. [16, 17, 27, 40, 43, 45, 46] and references therein). There are a few recently published works that utilize the depth-sensing nanoindentation for inhomogeneous materials such as rocks [2, 47]. Although applications of DSNI techniques to coals were recently discussed by Kožušníková [32], solely microindentation techniques were employed and the specific features of the application of the nanoindentation techniques were not considered.

The reason for application of the nanoindentation techniques is the same for all these inhomogeneous materials: the materials are heterogeneous in all directions at the microscale and micromechanical properties have to be assessed separately for its individual constituents. On the other hand, the customarily used techniques of microindentation allow the researcher to characterize the relatively large components of materials. Hence, conventional microindentation techniques do not usually allow to get estimations of the properties for a specified small material components, and one can extract just statistically averaged properties of the materials. To the best of our knowledge, no results have been published on the application of modern nanoindentation techniques to coals. This paper is devoted to development of techniques for evaluation of mechanical properties of compounds of highly inhomogeneous materials such as rocks and coals from experimental data. It is shown how the values of the elastic contact modulus of specific components of materials may be quantified using the depth-sensing nanoindentation techniques. In our complementary paper, we have reported preliminary results for nanoindentation testing of the main groups of the coal-forming macerals [21]. Here, our focus is on procedures of preparation of proper samples and techniques for extraction of quantitative data from the nanoindentation tests.

The conventional DSNI techniques show the effective properties of the section/substrate system rather than the properties of the material, in particular the so-called effective (equivalent or composite) elastic modulus \(E^{*}_{\mathrm{eq}}\) is extracted, while the goal is to extract intrinsic mechanical properties of the material film \(E^{*}_{\mathrm{f}}\). The equivalent modulus can be generally expressed as [1, 36]

$$\begin{aligned} E^{*}_{\mathrm{eq}}=E^{*}_{\mathrm{s}} + \left(E^{*}_{\mathrm{f}}-E^{*}_{\mathrm{s}}\right)\Phi (x) \end{aligned}$$
(1)

or

$$\begin{aligned} E^{*}_{\mathrm{eq}}=E^{*}_{\mathrm{f}} + \left(E^{*}_{\mathrm{s}}-E^{*}_{\mathrm{f}}\right)\Psi (x) \end{aligned}$$
(2)

where \(\Phi (x)\) and \(\Psi (x)\) are some weight functions of relative penetration \(x\) that \(\Psi (x)=1-\Phi (x)\); \(\Psi (x)=0\) at \(x=0\) and \(\Psi (x)\rightarrow 0\) at very large depths. One needs to study these approaches to finding \(\Phi (x)\) or \(\Psi (x)\) functions because the thin sections (material films) are glued to the substrate and the glue thickness is approximately equal to the thickness of the section. The paper is organized as follows:

First some preliminary information concerning depth-sensing indentation (DSNI) is given. The popular approaches used for extraction of mechanical properties of materials from experimental data obtained by contact interactions are critically re-examined.

Then special features of the coal samples are described. It is argued that the depth-sensing nanoindentation methods are much more effective for studying the properties of compounds of microinhomogeneous materials (e.g. pure coal macerals) when compared to the currently used microindentation techniques. It is explained why the samples of the materials have to be prepared as very thin and very smooth sections, and it is argued that the depth-sensing nanoindentation techniques have to be integrated with transmitted light microscopy.

Finally, the approaches for extracting effective contact modulus of an inhomogeneous elastic layer attached to an elastic substrate are discussed. It is proposed to describe the sample/substrate system using the classic exponential weight function for the dependence of the equivalent elastic contact modulus on the depth of indentation. The proposed approach is demonstrated on application to the experimental data obtained by Berkovich nanoindentation with varying values of the relative penetration \(x\).

2 Experimental depth-sensing indentation techniques

2.1 Microindentation techniques

The hardness studies of materials have a long history (see a review by Borodich [6, 7]). There were several very important steps in the development of modern hardness techniques. Smith and Sandland [41] introduced a square-base diamond pyramid indenter (the Vickers indenter). Later Khrushchov and Berkovich [33, 34] introduced devices for microhardness testing of metals—the PMT-2 and the PMT-3—that are very similar to the Vickers indenters. They suggested also to use three-sided pyramidal indenters. In addition, Berkovich suggested using the same relation between the three-sided pyramidal indenter cross section area \(A\) at height \(h\) as the Vickers indenter has. In fact, \(A_{\mathrm{Vickers}} = 24.5h^2\), while \(A_{\mathrm{Berkovich}} = 24.56h^2\), i.e. \(A_{\mathrm{Vickers}} \approx A_{\mathrm{Berkovich}}\).

During the last 70 years or so, microindentation devices that combine an indentation system along with an optical microscope were used as an effective technique for determination of strength of coals and their microhardness. The state standards used in the Soviet Union and the standards that are currently valid in Russia and a number of the former Soviet Union (FSU) countries [25], assumes the use of the PMT-3 device for characterization of microhardness of many materials, including metals and hard coals. The same device is used to estimate microbrittleness of hard coals. As has been explained above, the PMT-3 device is based on the use of a diamond Vickers pyramid that produces a square imprint and the microhardness is calculated by the size of the imprints diagonal measured by the use of optical microscopy. The hardness \(H\) was defined originally as the ratio of the maximum indentation force to the area of the imprint after unloading

$$\begin{aligned} H=\frac{\hbox {Load}}{\hbox {Area of imprint}}. \end{aligned}$$

Hence, the Vickers microhardness value \(H_V\) is calculated as

$$\begin{aligned} H_V=\frac{2P\sin (\alpha /2)}{d^2} \end{aligned}$$

where \(d\) is the average of two measured diagonals of the imprint, \(P\) is the maximum load acting on the indenter, and \(\alpha\) is the angle between the sides of the pyramid sides at its apex [38]. For a Vickers pyramid \(\alpha = 136^{\circ }\) and, hence, \(H_V\) is calculated as

$$\begin{aligned} H_V=1.854\frac{P}{d^2}. \end{aligned}$$

The microbrittleness of minerals and coals is usually calculated using the idea introduced by Bernhardt [3] who showed that for any brittle material there exists such a critical load \(P_{\mathrm{cr}}\) that there is no cracking during microindentation of the material. This observation was employed for estimation of the microbrittleness of minerals and coals by calculating the number of imprints producing cracks in a group of 100 imprints of a sample [20, 38]. Although the microindentation tests show quite reliable results for determination of microbrittleness of coal samples, and these results may be used for estimation of crushability of coals, these tests do not provide reliable information for studying processes of sorption–desorption, localization of deformations, sorptional deformations and so on [18–20].

2.2 Depth-sensing indentation techniques

Depth-sensing indentation is the continuously monitoring of the \(P\)–\(h\) curve, where \(P\) is the applied load and \(h\) is the displacement (the approach of the distant points of the indenter and the sample). The DSNI techniques are widely used in materials science. Although, originally both depth-sensing nanoindenters introduced by Kalei [29] and atomic force microscopes (AFM) introduced by Binnig et al. [4] were based on the use of sharp pyramidal probes, currently the DSNI techniques with spherical probes (either at the tip of the indenter or attached to the end of the AFM cantilever beam) are also widely used (see [9] and references therein).

Evidently, the load–displacement diagram at loading reflects both elastic and plastic deformations of the material, while the unloading is normally taking place elastically. The boundary demarcating the elastic and plastic regions may only be estimated by numerical techniques, for example, by the finite element method. In the problems of probing of elastic isotropic materials, the effective (reduced) contact elastic modulus (\(E^{*}\) or \(E_{\mathrm{r}}\)) is usually estimated using either the unloading branch of the \(P\)–\(h\) curve, assuming that the material deforms elastically at unloading and employing the so-called BASh formula [12, 13]. They applied the elastic contact solution to unloading path of the load–displacement diagram assuming the non-homogeneity of the residual stress field in a sample after plastic deformation may be neglected and noted that the slope of the \(P\)–\(h\) curves for the Hertz-type contact between axisymmetric solids is

$$\begin{aligned} S=\frac{{\mathrm{d}}P}{{\mathrm{d}}h}= 2E^{*}a \end{aligned}$$
(3)

where the reduced elastic modulus is

$$\begin{aligned} \frac{1}{E^{*}}=\frac{1-(\nu ^+)^2}{E^+} + \frac{1-(\nu ^-)^2}{E^-} \end{aligned}$$
(4)

\(a\) is the contact radius, and \(E^{+}, E^{-}\) and \(\nu ^{+}, \nu ^{-}\) are the elastic moduli and the Poisson ratios for the material sample and the indenter respectively. If the indenter is rigid, i.e. \(E^{-}=\infty\) then \(E^{*} =E/(1-\nu ^{2})\) where \(E=E^{+}\) and \(\nu =\nu ^{+}\) are the elastic modulus and the Poisson ratio of the half space, respectively.

Then Bulychev et al. [12, 13] suggested to rewrite this exact relation (3) using an effective contact radius \(a=\sqrt{A/\pi }\)

$$\begin{aligned} S=\frac{{\mathrm{d}}P}{{\mathrm{d}}h}= \frac{2\sqrt{A}}{\sqrt{\pi }}E^{*} \end{aligned}$$
(5)

because the contact area \(A\) is \(A=\pi a^2\). Based on the examples they studied, they concluded: “an important practical property of the curve of the elastic unloading of the plastic imprint is the independence of its slope at the initial stage of the unloading from the character of the pressure distribution under the imprint” [13].

Combining (5) and (4), Bulychev et al. [13] suggested the following expression to estimate the Young modulus of tested material

$$\begin{aligned} E=\frac{1-\nu ^2}{2\sqrt{A}/(\sqrt{\pi }S)-e_2}, \quad e_2 = \frac{1-\nu _{\mathrm{ind}}^2}{E_{\mathrm{ind}}}. \end{aligned}$$
(6)

where \(E_{\mathrm{ind}}\) and \(\nu _{\mathrm{ind}}\) are the elastic constants of the indenter.

Finally, they argued that “the equations (5), (6) are applicable to both circular and square in plane shape of imprints” and they suggested to use (5) not only for axisymmetric punches but also for \(3D\) indenters. In fact, (5) is a semi-empirical approximation for an exact expression (3).

There are also alternative approaches based on depth-sensing techniques, e.g. the BG method [7, 8] that is based on the employment of models of adhesive contact. Using the inverse analysis of a stable part of an experimental load–displacement diagram obtained from the DSNI of a sphere into a sample, it may extract both the contact (reduced) modulus and the work of adhesion of the contacting pair from one experiment. The application of the BG method to experimental curves of homogeneous materials shows that the obtained estimations of the elastic modulus and work of adhesion have very small error even for rather contaminated data. Although the BG method is very robust to external noise and it is very fast, the method cannot be employed in its present form for extraction of mechanical characteristics of the components of such highly inhomogeneous materials as coals. On the other hand, although the former approach for determination of \(E^{*}\) based on the BASh formula has several drawbacks [6], it is generally accepted that the results obtained for bulk material samples have acceptable accuracy. In addition, the use of sharp nanoindenters looks very reasonable taken into account that some microcomponents of tested materials are very small.

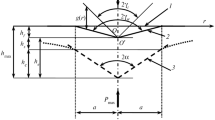
Note that if the Hertz-type theory is applied to a linear elastic solid then for a general power-law shaped indenter of degree \(d\) [the shape function \(f(r)= B_d(\theta ) r^{d}, B_{d}\) is the shape constant, and \(r, \theta\) are the polar coordinates], one has [5, 24]

$$\begin{aligned} P\propto h^{d/(d+1)} \end{aligned}$$
(7)

Hence, if assumes that the Hertz-type solutions are applied for analysis of the unloading branch [24] then there is a residual depth \(h_{\mathrm{r}}\) after unloading due to plastic deformation of the sample. Let us denote by \(h_{\mathrm{max}}\) the depth at of indentation at the maximum load \((P_{\mathrm{max}})\). To apply the Hertz-type contact solutions, one needs to shift the origin of the displacement axis by \(h_{\mathrm{r}}\). Thus, (7) should be written as

$$\begin{aligned} P\propto (h- h_{\mathrm{r}})^{d/(d+1)}. \end{aligned}$$
(8)

Taking a derivative of (8), one obtains an expression that is valid even for non-axisymmetric contact problems

$$\begin{aligned} \frac{{\mathrm{d}}P}{{\mathrm{d}}\delta } \propto \frac{d}{d+1}(h- h_{\mathrm{r}})^{-1/(d+1)}. \end{aligned}$$
(9)

Then neglecting the distortion of the surface due to plastic deformation, one obtains \(P \propto (h- h_{\mathrm{r}})^{2/3}\) or \(P=c(h- h_{\mathrm{r}})^{2/3}\) for a spherical indenter. Here constant \(c\) is defined as \(c=P_{\mathrm{max}} /(h_{\mathrm{max}}- h_{\mathrm{r}})^{2/3}\). For a pyramidal or conical indenter, one has \(P\propto (h- h_{\mathrm{r}})^{1/2}\).

Several practical approaches for evaluation of elastic modulus of material by nanoindentation were developed (see a review by Fischer-Cripps [23]). All these approaches are based on the use of the BASh relation (5). It is clear that in order to use (5), one needs to know the contact area. Practically it is very difficult to measure the contact area used in (5). If one considers an ideal Vickers indenter then the area of a horizontal cross section at the height \(h\) is \(A(h)=24.5h^2\). As it has been mentioned, the same relation is valid for an ideal Berkovich indenter. This relation was also used to approximate the contact area by some authors. However, if the material of a sample deforms elastically then the surface outside the contact region moves downwards along the \(z\) axis (like in the classic Hertz contact problem). In Materials Science, this behaviour is called sinking-in. If the material of a sample deforms plastically then the surface outside the contact region moves upwards along the \(z\) axis increasing the actual contact region. Indeed, the plastic deformations occur without changing the volume of the material and, therefore it goes up like an incompressible fluid during an immersion of a rigid body. The latter behaviour is called piling-up. Hence, fitting formulae for the contact area as a function of depth at unloading were introduced. It was suggested by Oliver and Pharr [42] to approximate the contact area under a Berkovich indenter that may have some imperfections by the following indenter area function

$$\begin{aligned} A(h)=24.5h^2+\sum _{i=0}^7 C_ih^{1/2^i} \end{aligned}$$
(10)

where \(C_i\) are fitting parameters. Oliver and Pharr [42] suggested also to approximate the unloading branch of the curve as

$$\begin{aligned} P=\alpha (h-h_{\mathrm{r}})^m \end{aligned}$$
(11)

where \(\alpha\) contains geometric constants and the elastic characteristics of both the sample and the indenter, and \(m\) is a power-law exponent that is related to the geometry of the indenter: for a flat-ended cylindrical punch, \(m=1\); for a paraboloid of revolution, \(m=1.5\), and for a cone, \(m=2\). One can note that after shifting the coordinate origin, the expression (11) will immediately follow from (8) and it is valid not only for axisymmetric indenters but also for non-axisymmetric indenters whose shapes are described by homogeneous functions of degree \(d\). Hence, it follows from (8) that \(m\) in (11) can be treated as \(m={(d+1)/d}\). Substituting \(d=\infty\) for a flat-ended cylindrical punch, \(d=1\) for a cone or a pyramidal indenter and \(d=2\) for a paraboloid, one obtains the corresponding values of \(m\) in the approximation (11). Thus, the approximation (11) may be explained as consisting of the shift of the coordinate origin of the \(P\)–\(h\) curve and the assumption that the indenter shape is described by a power-law function \(B_d(\theta ) r^d\) of degree \(d\).

2.3 Specific features of indentation tests of the inhomogeneous materials

Let us consider coals as an example of a natural inhomogeneous material. The heterogeneity of coals exists at many length scales from the nano to the macroscale. It defines specific features of the physical and mechanical properties of coals. Coals are composed of a number of distinct organic entities called macerals and some amount of inorganic substances along with internal pores and cracks. The organic part of coals contains from 65 to 95 % carbon depending on the degree of the coal metamorphism. The maceral composition of coals is defined by many factors such as specific features of the coalification processes, the nature of the initial plant material and the conditions of its accumulation and decomposition. It is customary to identify three basic groups of coal macerals: vitrinite, inertinite and liptinite. In each of these groups, it is also possible to allocate different submacerals. The vitrinite group macerals are glass-like materials where the original cellular plant structure has practically disappeared, while the liptinite macerals retain this structure. In other words, the microstructure of the liptinite group macerals includes the transformed remains of plants that include biochemically stable fragments of plant spores, cuticles, resins and suberin biopolymers. The inertinite group can be defined as fossilized charcoal.

It is not simple to separate coals into pure macerals. Indeed, coals are highly heterogeneous materials and the size of a specific maceral in a coal specimen is often smaller than the size of the imprint of the microhardness tester. Hence, microhardness tests usually show results not for a pure maceral but for a mixture of macerals, and there is normally a considerable scatter of the data obtained for the same sample. As a result, just the nominal hardness values of a tested coal sample obtained by averaging of 10–30 measurements, could be calculated. An extended review of the application of microindentation for evaluation of microhardness and microbrittleness of coals was given by Musyal [38]. It was found the following values for microhardness (H) of coals: (1) \(H = 60\)–200 \(\hbox {N/mm}^2\) for brown and low volatile coals; (2) \(H = 250\)–350 \(\hbox {N/mm}^2\) for high volatile coals; (3) \(H = 430\)–1,400 \(\hbox {N/mm}^2\) for anthracites [20, 38]. Later results of microhardness studies were published by many researchers (see, e.g. [18, 19, 26, 32], and references therein).

There are problems related to the use of the microindentation tests. The customarily used techniques of microindentation allow the researcher to characterize the relatively large components of materials (usually the characteristic size of the component region has to be over \(40 \, \upmu \hbox {m}\)), while micromechanical properties have to be assessed separately for its individual constituents at microscale. Although it is possible to evaluate microhardness of macerals of the vitrinite group in a reliable way, the microhardness indenters can barely be used to evaluate the microhardness of macerals of the inertinite group, and they cannot be used for measurements of the properties of macerals of the liptinite group due to the small size of these maceral inclusions. Further, the microindentation tests do not normally record the load–displacement curve, but rather they are based on the use of the plastic imprint in the sample. Hence, if the maximum load was very low then sometimes it is practically impossible to see the imprint due to low level of plastic deformations. On the other hand, if \(P_{\mathrm{max}}\) greater than \(P_{\mathrm{cr}}\) then there are some cracks in the sample. In addition, the elastic modulus of a tested material can be estimated using the BASh relation or its extensions that, in turn is based on the employment of the DSNI techniques. One cannot extract the elastic modulus using traditional microindentation techniques. Hence, we believe that the employment of the modern DSNI techniques is more preferable than the traditional microindentation techniques.

One of the problems that contribute to the difficulty in application of indentation techniques to natural inhomogeneous materials is the presence of numerous initial microcracks and voids. Microindentation tests of relatively thick coal samples are often influenced by the pores and cracks within the sample. Since coal samples prepared for microhardness testing are normally relatively thick, it was not possible to employ either transmission electronic microscopy (TEM) or atomic force microscopy (AFM) to enable detailed phase and crack distribution analysis. In addition, microindentation tests of relatively thick coal samples can produce imprints of quite distinctive appearance of inverse stepped pyramids that look like American pyramids or the pyramid of Djoser rather than the other more famous Egyptian pyramids. It is argued that to avoid the influence of the pores and cracks, the samples of the materials have to be prepared as very thin and very smooth sections. Note if the material has layered structure then the sample has to be prepared as a cross section of the layers.

Evidently, indentation techniques have to be accompanied by the use of microscopy techniques. Both reflected light and transmitted light techniques may be employed. Vitrinite varies from light brown to red colour in transmitted light, and it appears as pale grey in reflected light. The colours of the microcomponents of the inertinite group in reflected light microscopy vary from yellow to white, and they appear black in transmitted light. As a rule, there are rather sharp boundaries that separate macerals or submacerals. However, if one looks at a thin section of a coal sample in the reflected light then it is not very simple to recognize the distinct macerals. Indeed, the inertinite group macerals have black colour, and the vitrinite group macerals looks pale grey and the liptinite group macerals looks grey (Fig. 1). On the other hand, the boundaries between macerals can be clearly seen by examination of thin sections of coals in transmitted polarized light. The micro and nanoscale pores can be also clearly seen in the sample (Fig. 2). We have to emphasize that the transmitted light techniques may be employed only for thin sections of the materials.

Fig. 1
figure 1

A thin section of a coal sample in reflected light. Macerals of the inertinite, vitrinite and liptinite groups have black, pale grey and grey colours, respectively. The micro and nanoscale pores are also present in the sample

Full size image

For the first tests of coal thin sections, coals of the Donetsk and Kizel (Ural region) coal basins were chosen. Both types of coals consist of about 85–90 % of vitrinite, while the rest is presented by other marcerals and a small amount of inorganic substances. To prepare coal samples of \(25\times 25 \, \hbox {mm}\), they were glued to glass bases. The thickness of the glue layer was 12–15 \(\upmu \hbox {m}\). Using a RotoPol (Struers) polishing machine, the 13–14 \(\upmu \hbox {m}\) thick sections of coals were prepared at Laboratory of Physics and Chemistry of Coals, NUST MISiS. The sample surfaces were perpendicular to the coal layered structure. Typical transmitted light micrographs of the two types of coal are shown in Figs. 2 and 3. For reliable measurement of the properties of individual macerals, it is assumed that the structures are the same through the thickness of the section. However, local tilting of the layered structure may occur and this might affect the reliability of the indentation data.

Fig. 2
figure 2

A colour image of coal sample N5 (Kizel coal basin) in transmitted light (vitrinite has brown colour; inertinite is black; and liptinite is yellow). The relatively uniform vitrinite (brown) regions are relatively soft and viscoelastic, but the inertinite (mottled brown) areas are stiffer and show no viscoelasticity

Full size image
Fig. 3
figure 3

A colour image of coal sample N14 (Donetsk coal basin) in transmitted light (vitrinite has red colour; liptinite is orange; and inertinite is black). The maximum load of all nanoindentation tests was 10 mN

Full size image

Because the samples were very thin we were able to locate the indentations in clearly visible regions occupied by a specific maceral. The prepared samples were very smooth and allowed us to use the automated depth-sensing nanoindentation techniques available at Newcastle University in regions occupied by specific marcerals. The transmitted light microscopy was used to identify the co-ordinates of specific macerals to test, and these were located by a motorized stage and confirmed by reflected light microscopy in the nanoindentation system. Nanomechanical testing using a Hysitron TriboIndenter (Hysitron Inc., Minneapolis, MN) was performed at room temperature using a well-used three-sided pyramidal shaped Berkovich diamond indenter with a tip end radius of 250 nm.

Determination of mechanical properties of individual macerals was performed within a chosen \(100\times 100\) micron region. This enabled the consistency of the data to be checked and systematic errors due to maceral alignment and edge proximity to be assessed. The maximum load of all nanoindentation tests were 10 mN. The spacing between indents was \(10 \, \upmu \hbox {m}\) in a \(10\times 10\) array. With the large number of indentation test results at each location, it was possible to generate local maps of mechanical properties to identify trends in the data which reveal edge effects and give a statistically meaningful characterization of the tested region. Initially, the tests were done under open loop control using a triangular load function. However, in some experiments creep or viscoelasticity was observed even before the peak load of 1 mN was reached. The tests were then repeated using two different loading protocols: a trapezoidal load scheme with 2 s hold at 1 mN maximum load and a displacement control experiment to 400 nm maximum depth with 2 s hold at maximum depth. These experimental schemes as functions of time (a trapezoidal load function and the displacement control scheme) were used to assess the extent to which creep run-out occurs. For each indent, the contact modulus was calculated using the common Oliver–Pharr method.

2.4 Preliminary experimental results

Two samples from the Kizel (the sample N5 Fig. 2) and the Donetsk (the sample N14 Fig. 3) coal basins were chosen as representative samples for the initial tests. The coals of these basins have different stages of the coal metamorphism and coal genotypes. The above-described depth-sensing nanoindentation techniques have been applied to characterize macerals of these coals.

2.4.1 Sample N5

A colour image of coal sample N5 from the Kizel coal basin in transmitted light is presented in Fig. 2. The macerals have the following colours, respectively: vitrinite is brown; inertinite is black; and liptinite is yellow. For the region occupied by the vitrinite maceral of the sample N 5 (Kizel coal basins), the above-described triangular and trapezoidal loading protocols were used. There was no difference in the results obtained using the two different approaches within experimental error. A 13 nm increase in displacement during the hold period at peak load was observed, and the displacement does not stabilize in the 2 s hold, i.e. no creep run-out was observed. This behaviour may be caused by viscoelasticity of the vitrinite maceral. Both the hardness and modulus show no systematic variation across the region sampled in both cases. For the triangular load protocol, the average values of the contact modulus were measured as \(E^{*}_{\mathrm{eq}}= 5.48\pm 1.07 \, \hbox {GPa}\) and the hardness as \(H = 367\pm 105 \, \hbox {MPa}\). The trapezoidal load protocol, these values were measured as \(E^{*}_{\mathrm{eq}}= 5.31\pm 1.1 \, \hbox {GPa}\) and the hardness as \(H = 387\pm 134 \, \hbox {MPa}\). The mean contact depth under the \(P_{\mathrm{max}}=10\) mN was about 300 nm.

2.4.2 Sample N14

A colour image of coal sample N14 from the Donetsk coal basin in transmitted light is presented in Fig. 3. The macerals have the following colours, respectively: vitrinite is red, liptinite is orange or yellow, and inertinite is black. The average values of hardness for liptinite maceral and vitrinite maceral groups were \(408\pm 24 \, \hbox {MPa}\) and \(538\pm 61 \, \hbox {MPa}\) , respectively, the contact modulus for the same groups were \(4.57\pm 0.02 \, \hbox {GPa}\) and \(5.5\pm 0.3 \, \hbox {GPa}\) , respectively. There is no difference in the results obtained using the two different test protocols (with controlled load and displacement, respectively) within experimental error, however the displacement control data is slightly higher due to the larger contact depth.

3 Substrate effects

The above values of the effective contact modulus have been obtained by combination of the BASh equation (5) with the Oliver–Pharr approach (10) and (11). However, the measured values for the tested components cannot be considered as objective quantification of the material properties (see, e.g. [1, 15, 36]) , and the obtained numerical values can be used only for comparison between each other. This is due to the influence of the glue layer and the glass substrate. These caused some uncertainty in determination of the maceral contact modulus obtained as the BASh formula and the Oliver–Pharr approach were developed for a homogeneous elastic half space. Hence, the system can be considered as a film based on an elastic foundation. As Kerr [31] noted, the foundation is very often a rather complex medium; however, often the problem may be reduced to finding a relatively simple mathematical expression which should describe the response of the foundation at the contact region with a reasonable degree of accuracy.

3.1 Some elastic foundation models

Perhaps the simplest structural model of elastic foundation is the Fuss–Winkler foundation (the elastic spring mattress) that consists of independently working vertical springs. One can found a detailed critical review of this and many other elastic foundation models in the book by Kuznetsov [35]. In particular, he discussed in details the models proposed by Wieghardt [44] and by Filonenko-Borodich [22]. Then, he presented several possible extensions of the structural Fionenko-Borodich model. Kerr [31] presented another critical review of elastic foundation models and extended the discussion to the case of viscoelastic foundations.

The vertical displacement of an elastic foundation \(w(r)\) at point \(r\) due to pressure \(p(\xi )\) acting at the point \(\xi\) may be expressed as

$$\begin{aligned} w(x)=c\int p(\xi )K(x, \xi ) {\mathrm{d}}\xi \end{aligned}$$
(12)

where \(c\) is a constant that depends on the elastic properties of the foundation, and \(K\) the kernel of the integral equation [35]. Wieghardt [44] suggested to describe the kernel as an exponential function

$$\begin{aligned} K(x, \xi )=e^{-b|x-\xi |} \end{aligned}$$
(13)

where \(b\) is a constant depending on the elastic foundation because \(1/b\) represents the characteristic length of action of the elastic foundation. The idea of an exponentially decaying action of the elastic foundation may be used to describe the equivalent composite modulus by the relation (1).

3.1.1 Comment

As it was noted by Kuznetsov [35], Wieghardt did not suggested any structure for his model of an elastic foundation as did Fuss or Winkler. In fact, N. Fuss considered an elastic beam floating on the surface of an ideal liquid; using the beam theory of his teacher L. Euler, he wrote an equation for a beam on elastic foundation. Almost a century later, E. Winkler suggested to model an elastic foundation as mattress consisting of non-connected elastic springs with the spring constant \(k\). To achieve some degree of interaction between the spring elements, it was proposed by Filonenko-Borodich [22] to connect the top ends of the springs of the Fuss–Winkler foundation by a stretched elastic string (or membrane) subjected to a constant-tension field \(T\). The interaction of the spring elements is characterized by the intensity of the tension field \(T\) in the string. Denoting \(\omega ^2 = k/T\), it is easy to find (see, e.g. [35]) that the Filonenko-Borodich structural model loaded by a concentrated load at the coordinate origin leads to

$$\begin{aligned} w(x)=e^{-\omega x}/(2T\omega ) \end{aligned}$$

and this in turn leads to (12) with (13) where

$$\begin{aligned} c= (2T\omega )^{-1}, \quad b=\omega . \end{aligned}$$

3.1.2 Comment

The same Eq. (12) with an exponentially decaying kernel (13) can be derived using other elastic foundation models, e.g. the two-parameter Pasternak model and the Vlasov–Leontiev model (see, e.g. [31, 35]). However, one of the authors (FB) believes that the use of the Filonenko-Borodich model (1940) is more appropriate for many problems of nanomechanics to describe contact interactions between very soft materials whose behaviour is largely affected by the surface tension. However, this discussion is out the scope of the present paper.

3.2 The approximative approaches

Some approximations for the relation (1) were discussed in many papers including papers by Argatov and Sabina [1], Bull [11] and Menčík et al. [36]. In particular, it was suggested to represent \(\Phi\) as a linear function, i.e.

$$\begin{aligned} \Psi (x) =x,\quad x=a/t \end{aligned}$$
(14)

where \(t\) is the thickness of the film (the material section).

Another approach is based on the use an exponential function, i.e.

$$\begin{aligned} \Phi _1(x) =e^{-\alpha x},\quad x=a/t \end{aligned}$$
(15)

and, respectively

$$\begin{aligned} E^{*}_{\mathrm{eq}}=E^{*}_{\mathrm{s}} + (E^{*}_{\mathrm{f}}-E^{*}_{\mathrm{s}})e^{-\alpha x} \end{aligned}$$
(16)

These are many other approaches based on the relations (1) and (2) that we will not discuss here.

Fig. 4
figure 4

Experimental relation for sample N5 (Kizel coal basin) for equivalent reduced (contact) modulus versus depth of indentation. Comparison between vitrinite (red points) and inertinite (blue points) macerals

Full size image

One can see in Fig. 4 the values of the equivalent reduced (contact) modulus \(E^{*}_{\mathrm{eq}}\) for varying contact depths (the maximum indentation depth) calculated for tests on the above mentioned sample N5. The red points correspond to vitrinite maceral, while the blue points correspond to inertinite maceral. Because the thin section was glued to the substrate and the glue thickness was \(14 \, \upmu \hbox {m}\) that was equal to the thickness of the section \(t\), we need to use (1) taking into account \(E^{*}_{\mathrm{s}}=2 \,\hbox {GPa}\). As the first approximation, the sample/elastic foundation system has been described using the exponential weight function (16). Solving the inverse problem, one can find the values of \(\alpha\) and \(E^{*}_{\mathrm{f}}\). In particular it was found that (see Fig. 5)

$$\begin{aligned} E^{*}_{\mathrm{eq}}=2 + 19e^{-30 x} \end{aligned}$$

for vitrinite (red line)

$$\begin{aligned} E^{*}_{\mathrm{eq}}=2 + 25e^{-30 x} \end{aligned}$$

for inertinite (blue line). For the first sight, it looks strange that \(E_{\mathrm{f}}=21 \,\hbox {GPa}\) for vitrinite and \(E_{\mathrm{f}}=27 \,\hbox {GPa}\) for inertinite, while one can see in Fig. 2 that \(E^{*}_{\mathrm{eq}}= 3.2\pm 0.1\, \hbox {GPa}\) for vitrinite and \(E^{*}_{\mathrm{eq}}= 5.0\pm 0.4 \,\hbox {GPa}\) for inertinite. However, if one takes into account that these values were obtained for tests with \(h_{\mathrm{max}}\approx 300\,\upmu \hbox {m}\) then it is possible to see that Figs. 2 and 4 are in full agreement with each other. Comparing the detailed graphs (see Fig. 6) of the relation (16) for the equivalent modulus with the exponentially decaying weight function (\(t=14\, \upmu \hbox {m}, E_{\mathrm{S}}=2 \,\hbox {GPa}, \alpha = 30, E^{*}_{\mathrm{f}}= 21\,\hbox {GPa}\) and \(E^{*}_{\mathrm{f}}= 21\,\hbox {GPa}\) for vitrinite and inertinite macerals, respectively and Fig. 4), one can find that these values are in good agreement with the experimental data for a three-sided pyramidal shaped Berkovich diamond indenter.

Fig. 5
figure 5

Graph of the equivalent reduced (contact) modulus versus depth of indentation relation (16). Comparison between vitrinite (red line) and inertinite (blue line) macerals

Full size image

4 Conclusions

It is known that it is possible to predict the behaviour of a heterogeneous material at meso and macroscales using the methods of micromechanics of materials [30, 39]. However, despite the importance of knowledge about micromechanical properties of compounds, the information about the material properties of these components is often absent. Taking coals as an example of such an inhomogeneous materials, the experimental and numerical techniques for evaluation of mechanical properties of highly inhomogeneous materials are discussed.

Fig. 6
figure 6

A detailed \(E_{\mathrm{eq}}\)–\(h\) graphs for vitrinite (red line and \(E_{\mathrm{f}}=21\,\hbox {GPa}\)) and inertinite (blue line and \(E_{\mathrm{f}}=27\,\hbox {GPa}\)) macerals. The exponential relation (16) is used with \(t=14\,\upmu \hbox {m}, E_{\mathrm{S}}=2\,\hbox {GPa}\) and \(\alpha = 30\)

Full size image

It has been argued that the DSNI techniques have to be employed for testing material samples rather than the conventional microindentation. The main difference between the common microindentation and the modern DSNI techniques is that the former uses just one measurement of the plastic imprint of the sample, while the latter extracts information from the continuous diagrams obtained during loading and unloading of the indenter. Hence, depth-sensing nanoindentation can be applied to much smaller objects than used for microindentation tests. In addition, the modern techniques allow researchers to extract much more information about the mechanical behaviour of the tested material, in particular to extract the contact modulus of the contacting pair.

It has been explained why the samples of the materials have to be prepared as very thin and very smooth sections. Indeed, the use of such sections allow us to avoid the influence of the pores and cracks. In addition, transmitted light microscopy can be used, that in turn allows us to visualize the tested regions. With the large number of indentation test results at each location, it was possible to generate local maps of mechanical properties to identify trends in the data which reveal edge effects and give a statistically meaningful characterization of the tested region. For example, mechanical properties of individual macerals have been determined within chosen \(100\times 100\) micron regions. This enabled the consistency of the data to be checked and systematic errors due to maceral alignment and edge proximity to be assessed.

It has been demonstrated that the use of the modern nanoindentation techniques integrated with transmitted light microscopy is very effective for evaluation of elastic modulus of coal macerals. However, because the thin sections are glued to the substrate, the approximative approaches have to be used to extract the real elastic modulus of the tested material from the information about the relation of the equivalent modulus calculated for varying contact depth. The proposed approach is demonstrated on application to the experimental data obtained by Berkovich nanoindentation.