1 Introduction

Hydrogen storage systems for fuel cells in vehicles are required to store more than 5.5 wt% hydrogen, as proposed by the US Department of Energy (DOE) [1]. Many attempts have been made to achieve this target using physical or chemical methods [2]. Among the physical methods, hydrogen adsorption in carbon materials such as activated carbon and nanotubes has been extensively studied. These materials have various porous structures with low densities and high chemical stabilities. Early studies reported extremely high hydrogen storage capacity beyond the DOE target; however, it is now recognized that the hydrogen storage of carbon materials is less than 1 wt% at room temperature and 5 wt% at 77 K, even under high-pressure conditions [3–7].

Despite this limitation, Thomas [7] used experimental data to predict that carbon materials with pore widths of less than 7 Å can possibly have a storage density of over 5 wt% at 77 K. This prediction is based on the expectation that a reduction in the pore size increases the number of carbon atoms neighboring the adsorbed molecule, which strengthens the binding force as well as expands the surface area. For example, Cheng et al. [8] simulated hydrogen adsorption on single-walled carbon nanotubes at room temperature, and showed that the adsorption energy per hydrogen molecule could be increased from ∼60 to ∼100 meV by shrinking the diameter of the nanotube from ∼12 to ∼7 Å for the case of 3 wt% loading. The obtained energy is larger than the adsorption energies of typical activated carbon as measured by Bénard and Chahine [9] over wide ranges of temperature and pressure: 50–64 meV for the adsorption enthalpy and 47 meV for the adsorption energy. Bhatia and Myers [10] estimated that the adsorption enthalpy necessary to maximize the hydrogen storage/release under a mild condition was 150 meV, and Kuchta et al. [11] showed that a graphene slit with an 8 to 11 Å width could achieve the DOE target density if the adsorption energy was somehow increased to this value. These results suggest that nanoporous carbon can obtain larger hydrogen adsorption energy than typical carbon materials such as graphite and activated carbon; this is accomplished by a pore size reduced to ∼7 Å or less, and the DOE target density may be achieved if the adsorption energy reaches 150 meV.

Up to the present, many theoretical researches involved with the optimal pore size of the carbon nanotubes and carbon slits have been done using various methods [12–21]. Fan et al. [12] calculated the hydrogen binding energy of a single-walled carbon nanotube by a density functional method including dispersion interaction and showed that the binding energy inside the tube became larger than 200 meV when the diameter was 6–7 Å. Mpourmpakis et al. [13] studied the effect of the curvature of a nanotube on the binding energy using density functional theory and found that the most efficient adsorption outside the tube was observed at 3.2 Å from the surface. Cabria et al. [14, 15] found that the optimal pore size of the carbon slit to achieve the DOE target was 6–10 Å at 300 K and 10 MPa based on a thermodynamical model and molecular dynamics simulation including quantum effects. Wang and Johnson [16] carried out a path-integral dynamics calculation and showed that the carbon slit with 9 Å separation gave a large storage density close to the DOE target at 77 K and 5 MPa. Kowalczyk et al. [17] performed a path-integral Monte Carlo simulation and showed that the storage density in the slit exceeded the DOE target when the width was 6–10 Å at 77 K and 1 MPa. Deng et al. [18] proposed a method to increase the interlayer distance of the graphite by lithium doping and predicted by using Monte Carlo simulation that the DOE target was achieved when the separation was 8–10 Å. These researches reported large hydrogen storage beyond the experimental observations [3–7] with a somewhat broad range of the pore size; however, the lower limit of the pore size (6 Å) was almost in accord with that estimated by Thomas [7].

Previously, one of the authors prepared hydrogen-terminated graphenes (named ‘hydro-graphenes’) by the pyrolysis of some raw materials, and reported that the interlayer distance between these graphenes was varied from ∼3.8 to ∼4.2 Å by changing the pyrolysis temperature [22]. We also calculated the hydrogen binding energy of aromatic hydrocarbons by an ab initio molecular orbital method, and showed that the energy increased from 50 to 170 meV by adding lithium atoms and increased to 370 meV by adding beryllium atoms [23].

From the viewpoint of realizing a practical hydrogen storage system consisting of carbon nanopores, we need to know how the nanopore shape and size influence the hydrogen adsorption energy. For this purpose, a theoretical examination of hydrogen adsorption on well-characterized nanocarbons is a prerequisite. In this work, we evaluate the binding energy of a hydrogen molecule in nanocarbons having different shapes and sizes; these were a pair of coplanar disks, a hollow cylinder with open ends, and a hollow sphere with a circular window consisting of graphene sheets. Using the Lennard–Jones potential function, we derive an analytical expression for the binding energy as a function of the position of the hydrogen molecule and the size of the nanocarbon, and we determine the optimum shape and size of the nanocarbon that provides the deepest binding energy. The numerical values of the energies were calculated by adopting the parameters determined by a scattering experiment of a hydrogen molecule from the graphite surface [24].

2 Binding energy of a hydrogen molecule on a single graphene sheet

We begin by calculating the binding energy of a hydrogen molecule adsorbed on a single graphene sheet. We assume that the energy can be expressed as the sum of the pair potential between a hydrogen molecule and a carbon atom in the sheet. Using the Lennard–Jones potential function (V LJ) for this potential and assuming that the molecule is spherical, we can write the binding energy as

$$ W = \sum_{i} V_{\mathrm{LJ}} ( r_{i} ), $$
(1)

where r i denotes the distance between the hydrogen molecule and the ith carbon atom in the sheet. We use the 12–6 potential function for V LJ,

$$ V_{\mathrm{LJ}} ( r ) =4 \epsilon_{\mathrm{C}- \mathrm{H}_2} \biggl[ \biggl( \frac{\sigma_{\mathrm{C}\mbox{--}\mathrm{H}_2}}{r} \biggr)^{12} - \biggl( \frac{\sigma_{\mathrm{C}\mbox{--}\mathrm{H}_2}}{r} \biggr)^{6} \biggr]. $$
(2)

The main defect of this potential is the extremely steep increase of the repulsive part with the decrease of r. To improve this, the repulsive part may be replaced by an exponential function together with damping the attractive part [25, 26]. However, the 12–6 potential has the advantage of facilitating the calculation and its validity is not lost [25]. Actually, this function is used for evaluating the interaction between the hydrogen molecule and the carbon surface [16, 20, 24, 27, 28].

Assuming that the carbon atoms are continuously distributed in the sheet with a uniform density, the energy can be determined by integrating V LJ over the sheet,

$$ W= \rho_{\mathrm{s}} \int_{\sigma} V_{\mathrm{LJ}} ( r ) \,\mathrm{d} \sigma, $$
(3)

where ρ s and dσ denote the surface density of the carbon atoms and the surface element of the sheet, respectively. In the case of an infinite planar sheet, the energy is obtained as [27]

$$ W_{\mathrm{sg}} ( d ) = \frac{D_{\mathrm{sg}}}{3} \biggl[ 2 \biggl( \frac{d_{\mathrm{sg}}}{d} \biggr)^{10} - 5 \biggl( \frac{d_{\mathrm{sg}}}{d} \biggr)^{4} \biggr], $$
(4)

where d, d sg, and D sg denote the distance of the molecule from the sheet, the optimum distance, and the potential depth, respectively:

$$ d_{\mathrm{sg}} = \sigma_{\mathrm{C} \mbox{--} \mathrm{H}_2}, $$
(5)
$$ D_{\mathrm{sg}} = \frac{6}{5} \pi \epsilon_{\mathrm{C} \mbox{--} \mathrm{H}_2} \rho_{\mathrm{s}} \sigma_{\mathrm{C} \mbox{--} \mathrm{H}_2}^{2}. $$
(6)

In evaluating these quantities, the density of the graphene sheet was set to that of the graphite layer: ρ s=0.382 atoms/Å2. The Lennard–Jones parameters were taken from Mattera et al. [24], who performed a scattering experiment of a hydrogen molecule from the (0001) graphite surface. They fitted the experimental data to the 10–3 potential function derived by summing up the attractive part of Eq. (4) over the graphite layers so as to reproduce the energy eigenvalues obtained by the scattering experiment, and determined that \(\varepsilon_{\mathrm{C}\mbox{--}\mathrm{H}_{2}} = 3.89\) meV and . These values are close to those adopted in the Monte Carlo simulation by Nguyen et al. [28] derived from the Berthelot rule: \(\varepsilon_{\mathrm{C}\mbox{--}\mathrm{H}_{2}} = 2.76\)–3.66 meV and \(\sigma_{\mathrm{C}\mbox{--}\mathrm{H}_{2}} = 2.97\)–3.18 Å. The obtained 10–3 potential function well reproduces the eigenvalues from the bottom to the higher states; then, we consider that the potential function based on Eq. (3) is applicable to a wide range of the hydrogen position with adopting Mattera et al.’s parameters. Using these parameters, we obtained d sg=2.89 Å and D sg=46.8 meV, which are close to those obtained by the MP2 calculation using small hydrocarbon molecules [15, 23]. These parameters are very close to those for hydrogen binding on a bulk graphite surface (2.87 Å and 51.7 meV [24]). This indicates that the surface layer of the bulk graphite mainly contributes to the binding energy.

3 Binding energies of a hydrogen molecule adsorbed by nanocarbons

3.1 Geometries of nanocarbons examined

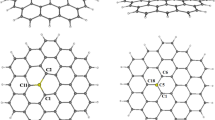
Here we examine hydrogen binding by nanocarbons having different shapes and sizes: a pair of coplanar disks, a hollow cylinder with open ends, and a truncated hollow sphere. We assume that these systems have the same density as the planar graphene sheet. Their structures are shown with coordinate axes in Fig. 1. The distance from the origin to the surface, given by d, represents half of the space between two disks, the radius of the cylinder, or the radius of the sphere. The radius of the disk, the length of the cylinder, and the radius of the section are denoted by R, 2L, and a, respectively. The hydrogen molecule is placed on the axis perpendicular or parallel to the surface. Its position is denoted by x 0 when it is on the x-axis.

Fig. 1
figure 1

Nanocarbons consisting of graphene sheets: (a) a pair of coplanar disks each with the same radius R, (b) a hollow cylinder with length 2L and open ends, (c) a hollow sphere truncated by a section with radius a. The distance from the origin to the surface is given by d for each system. The hydrogen molecule moves along the axis perpendicular or parallel to the surface. The position of the molecule is denoted by x 0 when it is on the x-axis

Full size image

3.2 A pair of infinite disks, a cylinder with infinite length, and a closed sphere

First we examine hydrogen binding by a pair of disks with infinite radius, a cylinder with infinite length, and a sphere without truncation. The hydrogen molecule is placed on the axis perpendicular to the surface (i.e. on the z-axis for the pair of disks and on the x- or y-axis for the cylinder). For each system, the binding energy of a hydrogen molecule is obtained in a closed form as

$$ W ( \xi_{0},d ) = \frac{D}{3} \biggl[ A ( {\xi_{0}} / {d} ) \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{10} - B ( { \xi_{0}} / {d} ) \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{4} \biggr], $$
(7)

where ξ 0 and D denote the position of the hydrogen molecule and the potential depth, respectively. The distance d e is the optimum distance of the surface from the origin that gives the lowest minimum of Eq. (7) when ξ 0=0. The parameters d e and D are characteristic for each system. The coefficients A and B are functions of ξ 0/d and they take different forms depending on the system.

To investigate the behavior of this potential curve, we treat the bound molecule as an oscillating particle near equilibrium. We expand W(ξ 0,d) to the fourth power of ξ 0,

$$\begin{aligned} W_{4} ( \xi_{0},d ) =& W ( 0, d ) + \frac{1}{2} W^{ ( 2 )} ( 0, d ) \xi_{0}^{2} \\ &{}+ \frac{1}{24} W^{ ( 4 )} ( 0, d ) \xi_{0}^{4} + \cdots \\ =& \frac{D}{3} \biggl\{ \biggl[ 2 \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{10} - 5 \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{4} \biggr] \\ &{}+ \frac{1}{2} \biggl[ a_{12} \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{12} - b_{6} \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{6} \biggr] \biggl( \frac{\xi_{0}}{ d_{\mathrm{e}}} \biggr)^{2} \\ &{}+ \frac{1}{24} \biggl[ a_{14} \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{14} - b_{8} \biggl( \frac{d_{\mathrm{e}}}{ d} \biggr)^{8} \biggr] \biggl( \frac{\xi_{0}}{d_{\mathrm{e}}} \biggr)^{4} \\ &{} + \cdots \biggr\}. \end{aligned}$$
(8)

This potential shows a single minimum at ξ 0=0 as long as W (2)(0,d) and W (4)(0,d) give positive values. In this situation, the energy bottom is given by W(0,d) and the deepest minimum (−D) is obtained when d=d e. As the distance d becomes larger than d e, the potential becomes shallow and shows a double minima when W (2)(0,d) becomes negative while W (4)(0,d) remains positive. The potential curve changes from a single well to a double minima at the critical distance where W (2)(0,d) becomes zero. The critical distance is given by

$$ d_{\mathrm{c}} = \biggl( \frac{a_{12}}{b_{6}} \biggr)^{1/6} d_{\mathrm{e}}. $$
(9)

When d<d c, the zero-point-corrected binding energy may be determined by the harmonic approximation if W (2)(0,d) is larger than W (4)(0,d),

$$ W_{0} ( d ) =W ( 0,d ) + n_{\mathrm{f}} \frac{\hbar\omega ( d )}{2}, $$
(10)

where n f denotes the vibrational degree of freedom; it is 1 for the pair of disks, 2 for the cylinder, and 3 for the sphere. The quantity ω(d) denotes the harmonic vibrational frequency at d. We are neglecting the motion of the graphene sheet because the mass of the carbon sheet is much larger than that of the hydrogen molecule; then, this is given by

$$ \omega ( d ) = \sqrt{\frac{W^{ ( 2 )} (0, d)}{ m_{\mathrm{H}_2}}}, $$
(11)

where \(m_{\mathrm{H}_{2}}\) denotes the mass of a hydrogen molecule.

At d=d c, the harmonic approximation breaks down because W (2)(0,d) vanishes. The energy of the particle moving in a quartic potential function can be estimated by the WKB approximation [29]. We can write the energy at d c using the form of a particle in a box,

$$ W_{0} ( d_{\mathrm{c}} ) =W ( 0, d_{\mathrm{c}} ) + n_{\mathrm{f}} \frac{\pi^{2} \hbar^{2}}{2 m_{\mathrm{H}_2} L_{\mathrm{a}}^{2}}, $$
(12)

where L a denotes the apparent potential width given by

$$ L_{\mathrm{a}} = \biggl[ \frac{\pi \varGamma (5/4)}{\varGamma (7/4)} \biggr]^{2/3} \biggl[ \frac{\hbar^{2}}{3m_{\mathrm{H}_2} W^{ ( 4 )} (0, d_{\mathrm{c}} )} \biggr]^{1/6}. $$
(13)

Precise treatments of the double-well potential can be found in Ref. [30].

Table 1 shows the magnitudes of D, d e, and d c measured respectively by D sg, d sg, and d e for each system. Since we neglect the interaction between two disks, D and d e of the disk pair are equal to 2D sg and d sg, respectively. We find that the potential depth becomes deeper in the curved system than it does in the planar one. A change in the graphene sheet from a planar shape to a curved shape increases the number of carbon atoms surrounding the adsorbed molecule and enhances both the repulsive and attractive forces acting on it. The repulsive force decreases more rapidly than the attractive force with an increase in d, so a deeper potential is obtained in the curved system than in the planar system if there is a small increase in d. We obtain D=3.39D sg with d e=1.09d sg for the cylinder and D=4.34D sg with d e=1.16d sg for the sphere. The value of d c decreases from 1.14d e to 1.10d e as the system changes from the disk pair to the sphere, since the attractive term in W (2)(0,d) is larger in the curved system than in the planar system. At d c, the bottom energy becomes −0.806D for the disk pair, −0.851D for the cylinder, and −0.883D for the sphere.

Table 1 Characteristic parameters of the hydrogen binding potential: D, the potential depth; d e, the optimum distance of the carbon surface from the origin; d c, the critical distance at which the potential changes from a single well to a double well. D sg and d sg are the potential depth and the optimum distance of a hydrogen molecule on a single graphene sheet, respectively. Approximate values are shown in square brackets
Full size table

Numerical values of D, d e, and d c are shown in Table 2 and were used to evaluate the minimum of the hydrogen binding potential given by Eq. (7). In Table 3, the values of the energy bottom W(0,d) and the energy with zero-point correction W 0(d) are shown when d=d e and d=d c. The value of W(0,d) of the disk pair is −94 meV when the disks are separated by 2d e (=5.87 Å). This separation is 1.7 times larger than the space between the graphite layers (3.35 Å). In actuality, these two disks attract each other at this separation, so a chemical modification is required to sustain this separation or the binding energy will be reduced by the work needed to separate them from their optimum distance. For the cylinder, the value of W(0,d) increases from −159 to −135 meV and W 0(d) increases from −133 to −129 meV when d increases from d e (=3.14 Å) to d c (=3.52 Å). The distance d c is close to the radius of the smallest carbon nanotube (∼3.5 Å). Among the structures, the sphere shows the deepest energies; its W(0,d) changes from −203 meV to −180 meV and its W 0(d) changes from –171 to –172 meV when d increases from d e (=3.37 Å) to d c (=3.71 Å). The radius of C60 (3.56 Å) is located in this range. For each system, the zero-point energy decreases with an increase of d due to the broadening of the potential width.

Table 2 The values of the potential depth (D), the optimum distance (d e), and the critical distance (d c)
Full size table
Table 3 The values of the hydrogen binding energies (in meV) at the equilibrium distance (d e) and the critical distance (d c) for the infinite or closed nanocarbons. W(0,d) is the energy bottom and W 0(d) is the energy with zero-point correction
Full size table

Figure 2 depicts the potential curve of the hydrogen binding given by Eq. (7) as d changes from 0.9d e to 2.5d e for each system. The boundaries of the system are located at ξ 0/d=±1. As mentioned above, a single minimum is found at ξ 0=0 when d is less than d c (∼1.1d e) in each system. This splits into two minima when d exceeds d c, and they approach −D sg as d goes to infinity. The potential width is wider in the curved system than in the planar system; therefore, the zero-point energy of the former becomes smaller than that of the latter. The minima outside the boundaries are shallower than those inside. The outside minima of the disk pair are close to −D sg irrespective of the size of d, because the molecule coming from the outside of the boundaries interacts effectively only with one of the two disks. On the other hand, the outside minima of the curved systems are higher than −D sg because the molecule bound on the outside of the curved surface is more distant from the carbon atoms than the one outside the planar surface. The minima become deeper with the increase of d and they approach −D sg when d goes to infinity.

Fig. 2
figure 2

The potential energy curves of the hydrogen molecule adsorbed by the nanocarbons: (a) a pair of coplanar disks with infinite radii, (b) a cylinder with infinite length, (c) a closed sphere

Full size image

3.3 A pair of finite disks, a cylinder with finite length, and an open sphere

Next we examine hydrogen binding by a pair of disks having the same radius R, by a cylinder with length 2L, and by a truncated sphere having a section with radius a. The hydrogen molecule is placed on the axis parallel to the surface for the disk pair and the cylinder, and on the axis perpendicular to the opening for the sphere. The potential energy curve for the hydrogen binding of each system is also obtained in a closed form as

$$\begin{aligned} W ( \xi_{0},d, \eta ) =& \frac{D}{3} \biggl[ A ( \xi_{0} / {d}, \eta / {d} ) \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{10} \\ &{}- B ( \xi_{0} / d, \eta / d ) \biggl( \frac{d_{\mathrm{e}}}{ d} \biggr)^{4} \biggr], \end{aligned}$$
(14)

where η stands for R, L, or a. The forms of D and d e are the same as those in Eq. (7).

For the disk pair and the cylinder, the energy bottom is located at the origin when d is close to d e; in other words, the potential remains a single well with respect to the axis perpendicular to the surface. In this case, the energy bottoms of these systems are given by

$$\begin{aligned} W ( 0,d,R ) =& \frac{D}{3} \biggl[ 2 \biggl( 1 - \frac{1}{ ( R^{2} / d^{2} +1 )^{5}} \biggr) \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{10} \\ &{}- 5 \biggl( 1 - \frac{1}{ ( R^{2} / d^{2} +1 )^{2}} \biggr) \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{4} \biggr] \end{aligned}$$
(15)

for the disk pair and

$$\begin{aligned} W ( 0,d,L ) =& \frac{D}{3} \biggl[ \frac{4}{\pi} \biggl( \tan^{- 1} ( L / d )+ \frac{L / d ( L^{8} / d^{8} + 490 L^{6} / {105 d^{6}} + {896 L^{4}} / {105 d^{4}} + {790 L^{2}} / 105 d^{2} + 965 / 315 )}{ ( L^{2} / d^{2} +1 )^{5}} \biggr) \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{10} \\ &{}- \frac{10}{\pi} \biggl( \mathrm{t} \mathrm{an}^{- 1} ( L / d ) + \frac{L / d ( L^{2} / d^{2} + 5 / 3 )}{ ( L^{2} / d^{2} +1 )^{2}} \biggr) \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{4} \biggr] \end{aligned}$$
(16)

for the cylinder. Each formula rapidly converges to the first term of Eq. (8) with an increase in R or L.

Figure 3 shows the potential curves for the finite disk pair and cylinder given by Eq. (14), with η changing from d to 3d when d=d e, or with η=3d when d=0.9d e. The molecule enters the system through the boundaries located at ξ 0=±η. When d=d e, each curve decreases monotonically to its minimum. In the case of η=d e, the bottom of the curve is considerably shallower than it is for the infinite system (−D): ∼−0.6D for the disk pair and ∼−0.9D for the cylinder. The energy bottom approaches −D when η exceeds 2d e. For the disk pair, the energy bottom becomes −0.934D when R=2d e and −0.983D when R=3d e; for the cylinder, it becomes −0.989D when L=2d e and −0.998D when L=3d e. For the case when d=0.9d e, the curve shows a maximum in the vicinity of each side of the boundaries, and its bottom is close to that of the infinite system when d=0.9d e.

Fig. 3
figure 3

The potential energy curves of the hydrogen molecule adsorbed by finite nanocarbons: (a) a pair of coplanar disks each with the same radius R, (b) a cylinder with length 2L

Full size image

The hydrogen binding energy of the truncated sphere is shown by expanding to the first power of z 0,

$$\begin{aligned} \ W ( z_{0},d,a ) =& \frac{D}{3} \biggl\{ \cos^{2} ( \theta_{a} / 2 ) \biggl[ 2 \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{10} - 5 \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{4} \biggr] \\ &{}- 6 \sin^{2} ( \theta_{a} / 2 ) \cos^{2} ( \theta_{a} / 2 ) \\ &{}\times\biggl[ 4 \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{11} - 5 \biggl( \frac{d_{\mathrm{e}}}{d} \biggr)^{5} \biggr] \frac{z_{0}}{ d_{\mathrm{e}}} + \cdots \biggr\}, \end{aligned}$$
(17)

where θ a (0<θ a <π) satisfies

$$ \sin \theta_{a} = \frac{a}{d}. $$
(18)

The second term in Eq. (17) shifts the equilibrium position of the molecule from the origin to a position on the z-axis depending on the size of d. The position moves from positive to negative when d passes (4/5)1/6 d e (∼0.963d e). The second term becomes very small when d≈d e; then, the energy bottom is approximately given by the first term of Eq. (17),

$$ W ( 0, d_{\mathrm{e}},a ) \approx - \cos^{2} ( \theta_{a} / 2 ) D. $$
(19)

This formula gives −0.933D at a=d e/2, −0.75D at a=31/2 d e/2, and −0.5D at a=d e.

Figure 4 shows the potential curves of the open spheres for different opening radii (a=d/2, 21/2/2d, 31/2/2d, and d) and as the sphere radius changes from d=0.9d e to 1.8d e. The molecule enters the sphere from the positive z-axis through the center of the opening located at z=dcosθ a . For a=d/2, the curve shows a shallow minimum in front of the opening, a maximum close to the opening, and a deep minimum near the origin when d ranges from 0.9 to 1.1d e. When d=d e, the values of the outside minimum, the maximum, and the deepest minimum are −0.145D (at z 0=1.55d), 36.2D (z 0=0.838d), and −0.934D (z 0=−0.011d), respectively. Further increases in d lower the barrier and lift the bottom, thereby splitting it into two asymmetrical minima. The lower minimum increases from −0.839D to −0.437D as its position moves from the vicinity of the origin (z 0=−0.103d) to the inner side of the sphere (z 0=−0.510d) when d increases from 1.1d e to 1.8d e.

Fig. 4
figure 4

The potential energy curves of the hydrogen molecule adsorbed by a sphere truncated by a section with radius a: (a) a=d/2, (b) a=21/2 d/2, (c) a=31/2 d/2, (d) a=d

Full size image

The increase in a lowers the barrier and lifts the bottom. When a=21/2 d/2, the values of the barrier and the bottom are 0.373D (z 0=0.677d) and −0.857D (z 0=−0.025d), respectively, when d=d e . The barrier diminishes and the bottom flattens near −0.435D (z 0=−0.510d) when d increases to 1.8d e. When a=31/2 d/2, the barrier is not observed in each curve. The bottom becomes shallower from −0.758D (z 0=−0.038d) to −0.433D (z 0=−0.510d) when d increases from d e to 1.8d e. When a=d, the bottom increases from −0.514D (z 0=−0.052d) to −0.421D (z 0=−0.511d) when d increases from d e to 1.8d e.

4 Summary

We examined hydrogen adsorption by nanocarbons consisting of graphene sheets. These include a pair of disks with radius R separated by 2d, a cylinder with radius d and length 2L, and a sphere with radius d truncated by a section with radius a. Using the 12–6 Lennard–Jones potential function for the pair interaction between a hydrogen molecule and a carbon atom, we obtained the binding energy of the molecule as a function of the molecule’s position and the size of the system. The energy is in the form of a 10–4 function with respect to 1/d and is characterized by the potential depth (D) and the optimum distance (d e) as the specific parameters for each system.

For infinite or closed systems, the lowest binding energies (−D) were obtained when the molecule rests at the center of the nanocarbon with d=d e. These energies were −94 meV (−78 meV with zero-point correction) for the disk pair with separation 5.87 Å, −158 meV (−133 meV) for the cylinder with diameter 6.28 Å, and −203 meV (−171 meV) for the sphere with diameter 6.74 Å. The energies were 2–4.3 times deeper than that of a single graphene sheet. The optimum separation between two disks was much larger than that of the graphite layers (3.35 Å). The optimum diameters of the cylinder and the sphere were slightly smaller than those of the smallest nanotube (∼7 Å) and C60 (7.12 Å). The bottom of the potential became shallow as d increased and changed from a single well to a double well at the critical distance (d c). At d c, the values of the bottom energy were −76 meV (−72 meV with zero-point correction) for the disk pair with separation 6.58 Å, −135 meV (−129 meV) for the cylinder with diameter 7.04 Å, and −180 meV (−172 meV) for the sphere with diameter 7.42 Å.

For the finite disk or cylinder, the energy bottom of each system approached that of the infinite system when its diameter (2R) or length (2L) increased to more than 2–3 times above its separation or diameter (2d). The binding energy of the finite disk pair with spacing 2d e amounted to more than −0.983D (−92 meV) when the diameters of both disks were larger than 6d e (17.3 Å). The binding energy of the finite cylinder with diameter 2d e amounted to more than −0.989D (−156 meV) when the length of the cylinder was greater than 4d e (12.6 Å).

For the truncated sphere, an enlargement of the opening lifted the energy bottom; however, it reduced the energy barrier for the incoming/outgoing molecule. For the sphere with diameter 2d e, the barrier and bottom were 0.373D (76 meV) and −0.857D (−174 meV), respectively, when the diameter of the opening was 1.41d e (4.76 Å). The barrier diminished and the bottom rose to −0.758D (−154 meV) when the diameter increased to 1.73d e (5.83 Å), and the bottom moved to −0.514D (−104 meV) when the diameter reached 2d e.

Finally, we conclude that the optimum spacing between graphene sheets for hydrogen adsorption is about 6–7 Å, and the adsorption energy can be increased to nearly 200 meV (170 meV with the zero-point correction) if the carbon atoms surrounding the molecule are arranged on a spherical surface. The number of carbon atoms on a spherical surface with density 0.382 atoms/Å2 is about 60 when the diameter is 7 Å. These obtained results are in accordance with the argument that carbon materials with a pore size of less than 7 Å can possibly achieve the DOE target density [7], and that the energy which allows hydrogen storage at mild conditions is 150 meV [10]. Actual nanocarbons cannot take a spherical shape but they may have polyhedral structures as fullerenes do. The experimental method of making an opening on C60 was previously established [31] and the hydrogen encapsulation into C60 has been demonstrated [32]. On the other hand, hydrogen adsorption between carbon polyhedrons is also necessary for increasing the storage density, so the shape and size of the cavity surrounded by these polyhedrons should be investigated. This subject is related to the space-filling problem by polyhedrons. Constructing a network of carbon polyhedrons suitable for hydrogen storage will be addressed in the future.