1 Introduction

Subsurface laser machining of dielectrics is a well-known technology with applications such as the formation of crystals [1], waveguides [2], gratings [3], and three-dimensional data storage [4]. The production of waveguides in silicon has also been demonstrated [5], despite that the location where the waveguides emerged could not yet be fully controlled. Subsurface laser machining of semiconductors is also of interest as a method of wafer dicing [6].

Wafer dicing is the process to cut wafers into small separate components. Thin wafers and mems devices present significant challenges to the saw dicing process, due to issues with cracking and/or contamination [7]. An additional challenge is the dicing of small dies. When dicing wafers containing smaller devices, while keeping the width of the dicing streets constant, a relatively large wafer area is lost due to the dicing process. A potential solution to these issues is to dice from the inside out [6]. That is, by creating laser-induced subsurface modifications. This dicing method consists of two steps. First, a laser beam is tightly focused inside a wafer, producing modifications which weaken the wafer mechanically in the bulk. Secondly, an external force is applied. This step separates the wafer along the planes with the laser-induced modifications.

To produce subsurface modifications, a large number of processing parameters have to be optimized. Therefore, there is a need for modeling. One-dimensional numerical models have been successfully used to simulate surface melting of silicon [8–14]. A model for nanosecond subsurface modification of silicon has been published [6, 15], which is based on the assumption that absorbed laser energy is instantaneously converted into lattice heat in the silicon. This model takes into account the temperature dependence of the interband absorption coefficient of silicon and the resulting thermal runaway. However, elevated concentrations of free carriers due to interband absorption of photons and physical optics were not included.

A model for 1300-nm femtosecond laser pulses focused inside silicon has recently been published [16], which simulates the generation of free carriers in detail, by combining a two-temperature model with the finite difference time domain method. However, this model does not deal with material properties at elevated lattice temperatures, as it is aimed at explaining transmission measurements on a femtosecond timescale and not at predicting phase transformations.

The model developed in the current research combines laser beam propagation in the bulk, a two-temperature model including a variable density of free carriers, and material data at high lattice temperatures. It is aimed at enabling parameter studies of subsurface material damage in silicon, covering a broad range of process conditions.

2 Numerical model

2.1 Two-temperature model

A two-temperature model (ttm) accounts for the fact that the energy of photo-excited electrons is not instantaneously converted into lattice heat [17]. Moreover, in the case of a semiconductor, additional free carriers are generated during the laser pulse, due to electrons moving from the valence to the conduction band when absorbing photons. To model these phenomena, a conservation equation has to be solved for each of the following distributions in the material: (1) the density of free carriers, (2) the lattice temperature, and (3) the electron temperature.

2.1.1 Density of free carriers

The material is considered to remain locally charge-neutral, i.e., the electrons and holes will not move independently from each other. This is a reasonable assumption, as charge separation generates a counteracting electric field, preventing significant differences between the electron and hole currents [8]. This leads to the following conservation law for the electron–hole pairs:

$$ \frac{\partial N}{\partial t}+\nabla\cdot \mathbf {q}_{N}=Q_{N}, $$
(1)

in which N denotes the density of electron–hole pairs, q N the current and Q N the source term. The latter includes generation and recombination of electron–hole pairs. The current is given by q N =−k N ∇N [8], where k N is the ambipolar diffusivity. The influence of the Seebeck effect and spatial variations in the band gap were neglected. The ambipolar diffusivity based on the Einstein relation is given by [18]:

$$ k_{N}=\frac{k_{e}\mu_{h}+k_{h}\mu_{e}}{\mu_{e}+\mu_{h}}=\frac{2k_{B}T_{l}}{e}\frac{\mu_{e}\mu_{h}}{\mu_{e}+\mu_{h}}, $$
(2)

where k is the diffusivity, μ the mobility, k B the Boltzmann constant, T l the lattice temperature, and e the elementary charge. The subscripts e and h refer to the electrons and holes, respectively.

2.1.2 Lattice temperature

The conservation of lattice heat is given by the usual heat equation:

$$ \rho c_{\mathrm{app}}\frac{\partial T_{l}}{\partial t}+\nabla\cdot \mathbf {q}_{l}=\gamma (T_{e}-T_{l} ), $$
(3)

in which ρ denotes the density, c app the apparent lattice specific heat capacity, q l the lattice heat flux and γ the electron–phonon coupling coefficient. The latent heat of fusion is accounted for in the apparent heat capacity [19]:

$$ c_{\mathrm{app}=}\begin{cases} (\int_{T_{s}}^{T_{f}}c_{p}\,dT_{l}+L )/2\Delta T & T_{s}<T_{l}<T_{f},\\ c_{p} & \mathrm{otherwise}, \end{cases} $$
(4)

where c p is the specific heat capacity and L the latent heat. Further, ΔT represents a mushy temperature interval to model the solid–liquid transition. The solid and fluid temperatures are defined respectively as: T s =T m −ΔT and T f =T m +ΔT, with T m the melting temperature. Supercooling of the melt was not considered, as the current model is aimed at predicting where the liquid phase has been reached in the material (see Sect. 3.1). The only source of lattice heat originates from the electron–phonon coupling. The flux q l is described by Fourier’s law: q l =−k l ∇T l , with k l the thermal conductivity of the lattice.

2.1.3 Electron temperature

To derive the conservation equation for the electron temperature, first a conservation equation for the total energy density U of the electron–hole pairs has to be defined. This energy density is the sum of the kinetic and band gap energy of the electron–hole pairs [8], which reads

$$ U=E_{\mathrm{kinetic}}+E_{\mathrm{bandgap}}=3k_{B}T_{e}N+E_{g}N, $$
(5)

where E g is the band gap energy. The kinetic energy is assumed to show a Boltzmann distribution. Since high carrier densities, as a result of the laser–material interaction, are accompanied by high electron temperatures, the electron–hole plasma will not be highly degenerate [8]. The specific heat capacity of the electron–hole pairs C e then reads

$$ C_{e}=\frac{\partial U}{\partial T_{e}}\bigg\rvert _{N}=3k_{B}N. $$
(6)

The conservation equation for the electronic energy is

$$ \frac{\partial U}{\partial t}+\nabla\cdot \mathbf {W}=Q_{e}-\gamma (T_{e}-T_{l} ), $$
(7)

with W the electronic heat flux and Q e the source term representing all absorbed laser energy. To obtain a conservation equation for the electron temperature, Eqs. (1), (5) and (6) are substituted into Eq. (7) to yield

(8)

The electronic heat flux W consists of two terms [8]. The first term is the electron–hole current q n multiplied by the sum of the band gap and the Peltier coefficient. The second term is the electronic thermal conduction q e . That is, W=q n (E g +4k B T e )+q e . Like the lattice heat flux, the electronic thermal conduction q e is described by Fourier’s law: q e =−k e ∇T e , where k e is the electronic thermal conductivity, which follows from the Wiedemann–Franz law [20]: \(k_{e}=2k_{B}^{2}T_{e}N (\mu_{e}+\mu_{h} )/e\).

2.2 Source terms

Next, the source terms Q N , γ and Q e in Eqs. (1), (3) and (8) respectively will be derived. For the electron–phonon coupling a relaxation-time model was used [8], which implies that γ=C e /τ e . Here τ e is the electron–phonon relaxation time which reads τ e =τ 0(1+(N/N crit)2) [21], where τ 0 is the carrier density independent relaxation time and N crit the critical carrier density for screening of the electron–phonon coupling to occur.

Next, the carrier density source term Q N in Eq. (1) is derived. Each single- or two-photon absorption event creates a free carrier which is described by Q N-laser=αI/E photon+βI 2/(2E photon), with α the interband absorption coefficient, β the two-photon absorption coefficient, I the laser radiation intensity and E photon the photon energy. It is noted that α is strongly temperature-dependent in an indirect band gap semiconductor like silicon.

The Auger recombination process is dominant in silicon, at the high carrier densities that are encountered during laser–material interaction [22]. Therefore, radiative recombination [23], Shockley–Read–Hall recombination [24], and surface recombination [25] were neglected. During Auger recombination, the recombination energy is transferred to a free carrier. As an electron, a hole and another free carrier are involved, this process can be expressed using a third-order function [22]: Q N-Auger=γ 3 N 3, where γ 3 denotes the Auger recombination coefficient.

Additionally, impact ionization, which is a process that uses energy from free carriers to generate additional carriers [26], can occur at high electron temperatures and carrier densities. It is described by Q N-impact=δN [8], where δ is the impact ionization coefficient. The complete source term of the free carrier distribution is then given by Q N =Q N-laser−Q N-Auger+Q N-impact.

Finally, a source term Q e is required for Eq. (8), describing the electron temperature. This term includes all energy absorbed from the laser: Q e =αI+βI 2+σNI, where σ is the free carrier cross section.

2.3 Beam propagation

A laser beam with a Gaussian power density distribution was selected for the simulations. The beam quality factor M 2 was used to describe small deviations from a Gaussian beam [27]. The beam was assumed to be paraxial. Even when focusing with high numerical aperture (NA) objectives, this assumption will generally hold inside silicon. Due to its high refractive index, the rays are refracted away from the surface normal at the air–silicon interface. Details of high NA focusing objectives, such as the cover correction, are not modeled. It is assumed that a practical optical system provides a Gaussian beam shape, in the area of interest near the focus. Some inaccuracies in the simulations are expected at the location where the wave hits the outer region of the strongly absorbing laser-heated volume below the surface. In this region, the wave amplitude will show high gradients in propagation direction. Due to the paraxial approximation, the second-order derivative of the wave amplitude in propagation direction is neglected.

Two different approaches to model the propagation of the beam have been evaluated, to find the best balance between accuracy and computational performance. One is based on solving the paraxial Helmholtz equation and another on shape-invariant propagation. As the pulse durations that are of interest are significantly longer than the time it takes for the laser light to travel through a thin wafer, the intensity profile was considered to be steady state during a time step. Then, for the next time step, the intensity profile is recomputed based on the new instantaneous laser power and material properties.

The intensity was reduced by a factor R at the air–silicon interface to account for surface reflections. Back reflections at the bottom of the silicon wafer were neglected, as they do not have an appreciable effect on the intensity near the focus.

The scalar paraxial Helmholtz equation, when factoring out a carrier wave of the form \(e^{-jk_{0}z}\) from the field, is given by:

$$ \frac{\partial}{\partial z}\tilde{u}=\frac{1}{2jk_{0}}\nabla_{\bot}^{2} \tilde{u}+\frac{k_{0}}{2j} \biggl(\frac{n^{2}}{n_{0}^{2}}-1 \biggr)\tilde{u}, $$
(9)

where \(\tilde{u}\) is the wave amplitude, j the imaginary unit, \(\nabla_{\bot}^{2}\) the transverse Laplace operator, \(k_{0}=\frac{2\pi n_{0}}{\lambda}\) the real reference wavenumber, n 0 the real reference refractive index and n is the complex refractive index. The intensity follows from \(I=\vert \tilde{u}\vert ^{2}\). Since the beam was assumed to be paraxial, its absorption is given by

$$ -\frac{\partial I}{\partial z}=\alpha I+\beta I^{2}+\sigma NI. $$
(10)

Then ℑ(n) in Eq. (9) can be set accordingly, to obtain the correct attenuation corresponding to the non-linear absorption. ℜ(n) was based on data on its dependence on temperature [28], carrier density [29] and intensity due to the Kerr effect [30].

The optical model based on the paraxial Helmholtz equation was compared with a simplified approach, which assumes the propagation of the beam to be shape invariant, following the envelope of a Gaussian beam. The shape-invariant convergence or divergence of the beam was implemented numerically by interpolating the intensity profile and subsequently integrating and scaling it to maintain energy conservation, both by applying monotonicity preserving cubic Hermite splines [31]. In this case, the absorption was modeled by reducing the intensity in-between the interpolation steps, to take the non-linear absorption corresponding to a small step in propagation direction into account.

The shape-invariant method was found to produce similar results to solving the paraxial Helmholtz equation. When comparing the lengths of the subsurface modifications along the optical axis, obtained from both methods, the shape-invariant method predicts modifications that are up to two micrometers shorter for a pulse energy of 1 μJ. Reference lengths of the modifications can be found in Figs. 3 and 4. The reason the shape-invariant method performs well is because the beam remains Gaussian, at most of the trajectory inside the silicon, until it hits a thin absorption front caused by a thermal runaway, where almost all non-linear absorption is concentrated (see Sect. 3.2). Because the current work is focused on parameter studies that require the evaluation of many different process conditions, the shape-invariant propagation method was selected, as it has a high computational efficiency.

2.4 Numerical solver, boundary conditions and material properties

Due to the symmetry of the incident laser beam, an axisymmetric computational domain was used. The domain was chosen sufficiently large, such that the material at the outer radius remains near equilibrium within the simulated time. Moreover, the flux through the symmetry axis should be equal to zero. Additionally, surface recombination, radiative losses and convective losses were neglected. This results in the following Neumann boundary condition for all edges of the lattice temperature, electron temperature and carrier density distributions: ∇u(x,t)⋅n=0 ∀x∈∂Ω, where u is the value of the distribution, which is a function of the location x and time t; n is the outer normal to the edges ∂Ω of the computational domain Ω. For both the lattice and electron temperature, the initial temperature, at t=0, was set to the ambient temperature: T l (x,0)=T e (x,0)=T amb. For the carrier density, the initial density, at t=0, was set equal to the equilibrium density at ambient temperature, as given in [26].

Equations (1), (3) and (8) were solved with the MSC.Marc finite element solver. Convergence checks were performed for the mesh size, the time step and the maximum residual allowed in the iterative solver. Equation (9) was solved with the explicit finite difference beam propagation method [32].

The material that was selected for the simulations is intrinsic monocrystalline silicon, the parameters that were used are listed in Table 1.

Table 1 Values of the parameters used in the numerical simulations
Full size table

3 Simulation results

3.1 Damage mechanism

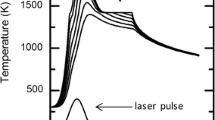
An example of the simulated maximum lattice temperatures that were reached during or after the pulse is shown in Fig. 1. A time interval of four times the full duration at half maximum (fdhm) of the laser power was simulated, with the peak intensity located halfway during the simulation. The gray area in Fig. 1 indicates the region in which the silicon has reached the liquid phase. The corresponding temperature contour is slightly above the melting point due to the mushy interval where the latent heat was modeled (see Sect. 2.1.2).

Fig. 1
figure 1

Contour plot of maximum lattice temperatures [K]. Wavelength: 1064 nm, focus depth: 100 μm, NA = 0.7, M 2=1.3, pulse energy: 2 μJ, pulse duration (fdhm): 50 ns

Full size image

The predicted size of the area that has reached the liquid phase during or after the pulse has been verified to be an accurate indicator for surface damage of monocrystalline silicon wafers, induced by pico- and nanosecond pulses [8–14]. The damage is a result of the rapid resolidification that occurs, which prevents the silicon from regaining its nearly defect-free monocrystalline structure. The same damage criterion has been applied when simulating subsurface modifications, since similar high cooling rates are expected when a subsurface liquid volume is surrounded by cold material. For femtosecond pulses, the mechanism of ultra-fast melting has also been proposed [42]. Since the conditions where the laser light absorption can be concentrated in the intended volume were found to be limited to the pico- to nanosecond range, this phenomenon does not have to be considered.

3.2 Parameter study

To obtain the required parameters to produce subsurface modifications, a parameter study was performed using the model. The laser beam was focused at a depth of 100 μm below the silicon surface, inside a 160-μm thick wafer. Both the temporal and the spatial profile of the laser beam were Gaussian, with the 1/e 2 radius of the beam filling the cone corresponding to a numerical aperture of 0.7.

Three parameters were varied during the simulations: the pulse energy, the wavelength and the pulse duration. Two different strategies to produce bulk modifications in silicon were analyzed by model simulations: one based on single-photon absorption at a wavelength of 1064 nm and another based on two-photon absorption at a wavelength of 1300 nm.

The single-photon absorption strategy consists of selecting a photon energy close to the band gap, such that a low but not negligible amount of single-photon interband absorption occurs at room temperature. The absorption should be low enough to allow the beam to reach the focus location, without too much absorption in the preceding beam path. However, the absorption should be high enough to slowly start heating the focal volume, where the laser power is to be concentrated. The strong temperature dependence of the interband absorption coefficient will ensure that a thermal runaway is triggered around the focus, moving towards the incident beam. An example of the lattice temperature in the focus as a function of time is shown in Fig. 2. Note that the thermal runaway in the focus is triggered before the peak power of the pulse has been reached. Soon after the start of the thermal runaway, the temperatures start to drop, as the laser energy is absorbed closer to the surface, instead of in the focus.

Fig. 2
figure 2

Lattice temperature in the focus and laser power as a function of time. Wavelength: 1064 nm, focus depth: 100 μm, NA = 0.7, M 2=1.3, pulse energy: 2 μJ, pulse duration (fdhm): 50 ns

Full size image

For the two-photon absorption strategy, the photon energy should be sufficiently below the band gap energy, such that the single-photon interband absorption at room temperature is negligible. By ensuring that only the intensity in the focus is high enough to trigger two-photon absorption, the laser energy can be selectively absorbed in a small volume in and around the focus.

Both the single- and two-photon strategies profit from the fact that interband absorption generates free carriers that will enhance the absorption at a later stage of the pulse. For both strategies, the length of the subsurface modification along the optical axis was calculated, as a function of the pulse duration and pulse energy (see Figs. 3 and 4). According to the simulation results, both the single- and two-photon strategies are suitable for the production of subsurface modifications in silicon. The optimal pulse duration for λ=1064 nm (between 10−9 and 5×10−8 s) is longer than for λ=1300 nm (between 10−10 and 10−9 s).

Fig. 3
figure 3

Subsurface modification length as a function of pulse duration and pulse energy. Wavelength: 1064 nm, focus depth: 100 μm, NA=0.7, M 2=1.3

Full size image
Fig. 4
figure 4

Subsurface modification length as a function of pulse duration and pulse energy. Wavelength: 1300 nm, focus depth: 100 μm, NA=0.7, M 2=1.3

Full size image

An advantage of the single-photon strategy is that it performs well with nanosecond pulses with a wavelength of 1064 nm, that can be generated with a common Nd:YAG laser source. However, losses due to interband absorption will occur throughout the beam path. When using the two-photon approach, at a wavelength of 1300 nm, linear absorption at room temperature will be negligible. Consequently, absorption at low intensities will only be due to free carriers. This allows for better confinement of the laser energy absorption compared with the single-photon approach. Therefore, for low to moderate doping concentrations, the two-photon approach is expected to be advantageous for the processing of wafers with a thickness of more than several hundred micrometers.

3.3 Boundaries of the process window

For the pulse energies considered during the parameter study, only a limited range of pulse durations results in a subsurface modification (see Figs. 3 and 4). To study the causes of the boundaries of the process window, simulations have been run while disabling several physical phenomena, such as single-, two-photon and free carrier absorption and the diffusion of heat and free carriers. Two-photon absorption and diffusion were found to determine the process window for the pulse duration (see Fig. 5).

Fig. 5
figure 5

Subsurface modification length as a function of pulse duration. Wavelength: 1064 nm, focus depth: 100 μm, NA=0.7, M 2=1.3, pulse energy: 2 μJ

Full size image

According to the simulation results, the upper limit for the pulse duration, to form a modification, is related to two phenomena. First, for λ=1300 nm, the intensities, when applying long pulses, are insufficient for two-photon absorption. Secondly, for both wavelengths, diffusion of heat and free carriers away from the focus limits the ability to selectively generate high temperatures near or in the focus.

The lower limit for the pulse duration is due to the onset of two-photon absorption of laser energy above the focus. The laser pulse needs to contain enough energy to melt a small subsurface volume. If the laser pulse is too short, while keeping the pulse energy at the required minimum level, the laser intensity above the focus exceeds the threshold for two-photon absorption. This results in a dense electron–hole plasma above the focus, causing unwanted free carrier absorption. Simulations that use the paraxial Helmholtz equation for the beam propagation, including refractive index gradients, suggest an additional negative effect of this plasma. Since the refractive index decreases with increasing carrier density towards the center of the beam, defocusing of the beam occurs before it reaches the intended focus location.

If a pulse duration is selected that is too short to produce a subsurface modification, eventually a surface modification will be produced, if the pulse energy is increased beyond the upper limit of the parameter study.

4 Comparison of model with experimental results

The performance of the model has been verified by comparing simulation results with experimental data on surface (see Sect. 4.1) and subsurface (see Sect. 4.2) modifications.

4.1 Surface modifications

The performance of the model has first been verified with experimental data on surface damage thresholds. The data were taken from literature on damage observed by optical microscopy or reflectivity measurements for picosecond [43], 10 ns [44, 45], 30 ns [46] and 40 ns pulses [13], all at wavelengths ranging from 1060 to 1064 nm. The temporal profile of these pulses was assumed to be Gaussian.

The results of the comparison of the model with experimental data are presented in Fig. 6. The error bars show, if available, the combined ranges of 0 to 100 percent damage probability, compiled from the references stated above. The data markers indicate the midpoint of this range. Uncertainties in the pulse duration are not shown. When comparing the numerical results with the experimental data, a good agreement is observed.

Fig. 6
figure 6

Comparison of experimental (circles) and simulated (triangles) surface damage thresholds. Wavelength: 1064 nm

Full size image

4.2 Subsurface modifications

In an earlier study, a first series of experiments to produce subsurface modifications was performed, using three laser sources with pulse durations of 6.6 ps, 8 ns and 170 ns [47]. Their peak wavelengths were 1030, 1064 and 1062 nm, respectively. To assess the effect of the difference in wavelength between the picosecond and nanosecond sources, the 1064 nm simulations have been repeated with a wavelength of 1030 nm for a pulse energy of 2 μJ [47]. It was found that there is only a minor impact on the size of the modifications: the 1030 nm wavelength results in subsurface modifications that are approximately 2 μm smaller compared to the 1064 nm wavelength.

The laser pulses were focused in the bulk of 160-μm thick double-sided polished p-type silicon wafers, with a resistivity of 10.3 Ω cm. This resistivity is sufficiently high to obtain behavior that is consistent with the simulations for intrinsic silicon. The focusing objectives that were used are Leica 11 101 666 and 11 101 887 infrared microscope objectives with a numerical aperture of 0.7 and a cover correction adapted to the focus depth.

Both the 8 ns and 170 ns pulses were successful in generating subsurface modifications in silicon, as observed by infrared transmission microscopy. No modifications were found for the 6.6 ps pulses. This experimental observation is in agreement with the results presented in Fig. 3. Additionally, a comparison was made between the experimental and simulated lengths of the modifications along the optical axis, as a function of pulse energy (see Fig. 7). A fairly good agreement between the simulated modification shapes and the experimental results was observed. Within the range of pulse energies shown in Fig. 7, the experimental and simulated modification lengths were within 3 μm of each other.

Fig. 7
figure 7

Simulated and experimental modification lengths as a function of pulse energy. Wavelength: 1062 nm, pulse duration (fdhm, Gaussian temporal profile): 170 ns, focus depth: 130 μm, M 2=1.1

Full size image

The experimental data on subsurface modifications that were used for the comparison with numerical results are obtained by measurements after dicing. Whether the dicing process influences the features observed on the cleavage plane is a subject of future research. Further details about the experiments can be found in [47].

5 Discussion and conclusions

A model was developed to simulate the production of pulsed-laser–induced subsurface modifications in silicon. The numerical model was validated with experimental data on surface as well as subsurface modifications. A good agreement between the simulations and the experimental results was observed, in terms of the dependence of the modification shape on the pulse duration and pulse energy.

It was found that both single- and two-photon absorption can be used to produce subsurface modifications in silicon, by simulating laser pulses with a wavelength of 1064 and 1300 nm. The single-photon approach benefits from silicon being an indirect band gap semiconductor, with a strongly temperature-dependent interband absorption coefficient. This offers the possibility to trigger a thermal runaway. The two-photon approach results in less absorption at low light intensities. Therefore, it is expected to be better suited for the manufacturing of subsurface modifications at a depth of more than several hundred micrometers below the surface. For both wavelengths, a compromise has to be found between unwanted diffusion of heat and free carriers when extending the pulse duration and the formation of a too dense electron-hole plasma above the focus when using sub-nanosecond pulses.

The experimental data sets, on which the material parameters are based, rarely cover the full range of temperatures and carrier densities that are encountered during laser-material interaction. Consequently, the accuracy of many parameters is unknown, making it hard to reliably estimate the uncertainties in the simulations. Therefore, future experimental work is needed to obtain a more extensive data set for the validation and improvement of the numerical model.

When working near the lower boundaries of the process windows for the pulse duration, refractive index gradients occur above the focus, due to elevated temperatures and carrier densities. This effect has not been taken into account during the parameter studies. Therefore, it is recommended to use the simulated process windows (see Figs. 3 and 4) with caution.

Finally, in the current model, the material that has reached the liquid phase is considered to remain in a modified state after resolidification, due to the high cooling rates that will occur in a melt that is surrounded by cold material. Future work is required to analyze and predict the material structure of the subsurface modifications after resolidification.