Efficient and Accurate KAM Tori Construction for the Dissipative Spin–Orbit Problem Using a Map Reduction

Abstract

We consider the dissipative spin–orbit problem in Celestial Mechanics, which describes the rotational motion of a triaxial satellite moving on a Keplerian orbit subject to tidal forcing and drift. Our goal is to construct quasi-periodic solutions with fixed frequency, satisfying appropriate conditions. With the goal of applying rigorous KAM theory, we compute such quasi-periodic solutions with very high precision. To this end, we have developed a very efficient algorithm. The first step is to compute very accurately the return map to a surface of section (using a high-order Taylor’s method with extended precision). Then, we find an invariant curve for the return map using recent algorithms that take advantage of the geometric features of the problem. This method is based on a rapidly convergent Newton’s method which is guaranteed to converge if the initial error is small enough. So, it is very suitable for a continuation algorithm. The resulting algorithm is quite efficient. We only need to deal with a one-dimensional function. If this function is discretized in N points, the algorithm requires $O(N \log N)$ operations and O(N) storage. The most costly step (the numerical integration of the equation along a turn) is trivial to parallelize. The main goal of the paper is to present the algorithms, implementation details and several sample results of runs. We also present both a rigorous and a numerical comparison of the results of averaged and not averaged models.

1 Introduction

The construction of invariant structures in Celestial Mechanics and Astrodynamics has become of great importance in recent times, both for theoretical reasons and for the practical design of space missions. At present, many space missions are based on the determination of periodic and quasi-periodic orbits. Some notable examples of periodic/quasi-periodic orbits used in mission design are Lyapunov, Lissajous and halo orbits (see, e.g., Celletti et al. 2015; Gómez and Mondelo 2001; Jorba and Masdemont 1999).

The existence and persistence of quasi-periodic orbits were developed by KAM theory (Kolmogorov 1979; Arnol’d 1963; Moser 1962). Making KAM theory into a practical tool is an ongoing and rapidly progressing area, which applies to models of increasing complexity; it also leads to applications and has uncovered new mathematical phenomena.

With these motivations, this work develops a method for the construction of invariant tori in a concrete model of interest in Celestial Mechanics, namely the dissipative spin–orbit problem (see Sect. 2), which describes the rotation about its center of an oblate moon orbiting a planet and subject to tidal forces. Our goal is to develop a method to compute quasi-periodic solutions in the spin–orbit problem. As it is well known, quasi-periodic orbits can be described geometrically as invariant tori on which the motion is conjugate to a rigid rotation. Hence, we will use indistinctly the names quasi-periodic solution and invariant (rotational) torus.

1.1 Overview of the method

The method we develop starts by constructing a surface of section and a return map to it. The invariant tori for the flow correspond to invariant tori for the return map. We show that these return maps for the spin–orbit problem have the remarkable property that they transform the symplectic form into a multiple of itself. These maps are called conformally symplectic systems and enjoy several remarkable properties that lie at the root of a KAM theory and efficient algorithms (see Sect. 4.1).

To find the invariant torus of the map, we follow the approach in Calleja et al. (2013a) and formulate a functional equation for the drift parameter and for the embedding of the torus, whose solutions are obtained formulating a quasi-Newton method that, given an approximate solution of the functional equation, produces another one with a quadratically small reminder. The quasi-Newton method in Calleja et al. (2013a) takes advantage of the conformally symplectic geometric property.

The results of Calleja et al. (2013a) guarantee that the method converges (as a double exponential, as Newton’s methods) if the initial error is small enough (compared to some readily computable condition numbers).

The theorem in Calleja et al. (2013a) also shows that the difference between the true solution and the initial approximation is controlled by the error of the invariance equation, see Eq. (26). Results of this form are called a posteriori theorems in numerical analysis. We also note that one of the consequences of the work in Calleja et al. (2013a) is a local uniqueness for the solutions of (26), except for composition for a rotation. This lack of uniqueness comes from the freedom on the choice of coordinates in the parameterization, but the geometric object and the drift parameter are locally unique.

Since the iterative method converges for small enough error, it will be used as the basis of a continuation method in parameters, which is guaranteed to converge until the assumptions in the theorem fail. Indeed, arguments in Calleja and de la Llave (2010) show that the method can be used as a practical way to compute the breakdown of the torus (see Calleja and Celletti 2010 for an implementation to conformally symplectic maps). Note that the method is backed up by theorems and guaranteed to reach to the boundary of validity of the theorem, if given enough computational resources.

In this paper, we will implement the method with extended arithmetic precision, motivated by the fact that the size of the error needed to apply the a posteriori theorem is typically smaller than what can be obtained in double precision. With modern programming techniques, writing extended precision programs is not much more time consuming than using standard arithmetic. Of course, there is a penalty in speed, but since the algorithm is so efficient, one can still run comfortably even with extended precisions in today’s desktop machines (see Sect. 5.5 for details on timings and resources). Of course, in continuations, it is also possible to run the first iterations in double precision till the error is dominated by the double precision round-off and then run the final iterations in extended precision.

We have also used jet transport in order to get automatically the (first order) variational flow with respect to initial conditions and parameters. In Calleja et al. (2020b), we use the jet transport to get high-order variational flows following the results in Gimeno et al. (2021).

Finally, we have taken advantage of some modern advances such as multicore machines and multithreading given, for instance, continuation iterations in around 1 min when the initial guess is small enough. We did not explore other advanced architectures such as GPU, whose application in Celestial Mechanics is an interesting challenge. Some work on a simpler problem is in Kumar et al. (2021).

1.2 Efficiency and accuracy of the method

The use of return maps is very economical and natural. In the study of invariant tori for differential equations, it is standard to separate the directions along the flow and the transversal directions.

On the one hand, the torus remains very smooth along the directions of the flow for all values of the perturbation parameter. The flow in these directions can just be reduced to the well-studied problem of computing solutions of ODEs, and in fact, there are many different algorithms suitable in different conditions.

On the other hand, the computation of the torus in the directions of the section is a much more complicated problem, since it requires KAM theory and the tori along these directions are much less regular; indeed, for large enough values of the perturbation, the tori may disappear. Nevertheless, even for values of the perturbation parameter where the tori do not exist, the solutions of the differential equations can be comfortably computed.

By dividing the problem into the KAM part for maps and the propagation to the return section, we reduce significantly the difficulty of the KAM part, since the tori have lower dimension. The computation of the return map is more complicated, but it is easily parallelizable and there are many studies on optimizing it. Hence, the breakup ends being rather advantageous. As indicated above, the methodologies of the two parts are very different and each of them can be fine-tuned separately.

The KAM part for maps is well documented in Calleja et al. (2013a); the algorithm therein applies quasi-Newton corrections and takes advantage of several identities related to the fact that the map is conformally symplectic.

The number of explicit steps of the KAM iterative procedure is about a dozen, see Algorithm 5.4. All the elementary steps are well-structured vector operations that are primitives in modern languages or libraries, so that they are not too cumbersome to program.

Quite remarkably, all the steps are diagonal either in a grid representation of the function or in a Fourier representation. Of course, we can switch from one representation to the other using FFT. Hence, for a function discretized in N modes, the quadratically convergent method requires only O(N) storage and $O(N \log N)$ operations. Note that, in modern computers, the vector operations and the FFT are highly optimized, with specialized hardware.

These KAM algorithms have been implemented for maps given by explicit simple formulas (Calleja and Celletti 2010; Calleja and Figueras 2012; Calleja et al. 2020). In theory, the only thing that one would need to do is to use the return map of the ODE (and its variational equations) in place of the explicit formulas. However, as we report in Calleja et al. (2020a), in contrast with the explicit formulas that have few important harmonics, the return maps have many more relevant harmonics; this requires some adaptations and the phenomena observed are different.

1.2.1 Relation with other methods

The methods of computing invariant tori based on normal form theory require working with functions with as many variables as the phase space, see Stefanelli and Locatelli (2012, 2015). In contrast, our methods require to manipulate only functions with as many variables as the dimension of the tori of the map. Reducing the number of variables in the unknown function is very important, since the number of operations needed to manipulate a function grows exponentially (with a large exponent) with the number of variables. Some recent papers that are also using return maps in Celestial Mechanics are, for instance, Haro and Mondelo (2021) (full-dimensional tori in Hamiltonian systems) and Kumar et al. (2021) (whiskered tori, their stable and unstable manifolds and their intersections in Hamiltonian systems).

It is interesting to compare the methods developed here to Olikara (2016), which uses a discretization of the tori without separating the tori and the flow directions. If the torus is discretized in N points, this method requires $O(N^2)$ storage and $O(N^3)$ operations. Notice that N points in 2-D tori give more or less the same precision as $N^{\frac{1}{2}}$ in 1-D tori.

A curious remark is that the linearization of the invariance Eq. (26) has a spectrum lying in circles as shown by Mather (1968) (see Adomaitis et al. 2007; Haro 2002 for numerical experimentations), so that the Arnold–Krylov methods, successful in other models (Sánchez et al. 2010), do not work very well. The method we use can be understood as saying that, using geometric identities, we get the linearized equations to become constants. (This phenomenon is called automatic reducibility.)

One improvement in continuation methods, after an expensive effort in one step, is that one can compute inverses (Moser 1973; Hald 1975) or diagonalizations (Haro and de la Llave 2006; Jorba and Olmedo 2009), perturbatively. These methods require to store O(N) storage, and the perturbative calculations still require $O(N \log N)$ operations even if the constants improve.

1.3 The model

We have implemented our results to the so-called dissipative spin–orbit model (Celletti 2010). In this section, we will review the physical bases of the model as well as formulate several variants [so-called time-dependent friction (8) and averaged friction (9)]. These models will be analyzed (numerically and rigorously) in subsequent sections.

The spin–orbit model describes the rotational motion of a triaxial non-rigid satellite whose center of mass moves along an elliptic Keplerian orbit around a central planet. The spin-axis of the satellite is assumed to be perpendicular to the orbital plane and coinciding with the shortest physical axis. The rotation angle of the satellite is the angle between the longest axis of the satellite and a fixed direction, e.g., the periapsis line.

The motion of the rotation angle satisfies a second-order differential equation depending periodically on time, through the orbital elements describing the osculating position of the center of mass of the satellite; such equation depends on two parameters, namely the orbital eccentricity and the equatorial flattening of the satellite. The model equations include a dissipative term due to the non-rigidity of the satellite, since the rotation gives rise to tides that dissipate energy and generate a torque. We adopt the model of Peale (2005) in which the tidal torque is proportional to the angular velocity with a time-periodic coefficient. The dissipative term depends on two parameters: the orbital eccentricity and the dissipative factor, which is determined by the physical features of the satellite.

For typical bodies of the solar system, e.g., the Moon and many others among the biggest satellites, the force induced by the dissipation is much smaller than the conservative part, so that dissipation can be ignored in the description over short times. Nevertheless, since the dissipative forces have consequences that accumulate over time, they are very important in the description of long-term effects.

In the applied literature, it is very common to use a simplified version of the tidal torque that can be obtained by averaging the dissipation over time (Celletti and Chierchia 2009; Celletti and Lhotka 2014; Correia et al. 2004), so that the tidal torque becomes proportional to the derivative of the rotation angle.

One of the advantages of the method in this paper is that it provides a rather general rigorous justification of the averaging method for quasi-periodic solutions. The basic idea is very simple: Using standard averaging methods, we control the $2\pi$-time map and, then, the effect of changing the map is controlled by the a posteriori theorem (see Appendix A). For the spin–orbit problem, we also provide another justification that applies to all solutions.

Our formalism provides also rigorous estimates on the validity of the averaging approximation. Standard averaging theory can give estimates on the difference between the return maps in the averaged model and the true model. (Notice that the time of flights in return maps is about 1, so that controlling the averaging method to order 1 is very standard.) Then, we can use the a posteriori format of the KAM theory in Calleja et al. (2013a) to obtain estimates on the difference between the KAM tori and the drift parameters in the averaged and non-averaged cases. This result may look surprising, since one obtains control on solutions (and drift) for very long times. Besides this very general perturbative argument, in Appendix A we present some elementary arguments that, taking advantage of the structure of the system, obtain non-perturbative results.

We conclude by mentioning that the current work has several consequences: In Calleja et al. (2020b), we study the quantitative verification of a posteriori theorems and the quantitative condition numbers, while in Calleja et al. (2020a) we explore numerically the boundary of validity of KAM theory and uncover several phenomena that deserve further mathematical investigation. We hope that this paper (and the companions Calleja et al. 2020b and Calleja et al. 2020a) can stimulate further research, for example, turning the estimates in Calleja et al. (2020b) into rigorous computer-assisted proofs, studying higher-dimensional models, incorporating more advanced computer architectures and explaining the phenomena at breakdown.

1.4 Organization of this paper

This work is organized as follows. In Sect. 2, we present the spin–orbit model with tidal torque. The numerical formulation of the spin–orbit problem is given in Sect. 3, while the spin–orbit map is derived in Sect. 4. The algorithm for the construction of invariant attractors and its applications is presented in Sect. 5. Finally, some conclusions are given in Sect. 6.

2 The spin–orbit problem with tidal torque

Consider the motion of a rigid body, say a satellite ${\mathcal {S}}$, with a triaxial structure, rotating around an internal spin-axis and, at the same time, orbiting under the gravitational influence of a point-mass perturber, say a planet ${\mathcal {P}}$. A simple model that describes the coupling between the rotation and the revolution of the satellite goes under the name of spin–orbit problem, which has been extensively studied in the literature in different contexts (see, e.g., Beletsky 2001; Celletti 1990b, a; Correia et al. 2004; Wisdom et al. May 1984). This model is based on some assumptions that we are going to formulate as follows. Let ${\mathcal {A}}< {\mathcal {B}} < {\mathcal {C}}$ denote the principal moments of inertia of the satellite ${\mathcal {S}}$; then, we assume that:

H1.:

The satellite ${\mathcal {S}}$ moves on an elliptic Keplerian orbit with semimajor axis a and eccentricity $e$, and with the planet ${\mathcal {P}}$ in one focus;

H2.:

The spin-axis of the satellite coincides with the smallest physical axis of the ellipsoid, namely the axis with associated moment of inertia ${\mathcal {C}}$;

H3.:

The spin-axis is assumed to be perpendicular to the orbital plane;

H4.:

The satellite ${\mathcal {S}}$ is affected by a tidal torque, since it is assumed to be non-rigid.

We adopt the units of measure of time such that the orbital period, say $T_{orb}$, is equal to $2\pi$, which implies that the mean motion $n=2\pi /T_{orb}$ is equal to one.

We define the equatorial ellipticity as the parameter $\varepsilon >0$ given by

$$\begin{aligned} \varepsilon = \frac{3}{2} \frac{{\mathcal {B}}-{\mathcal {A}}}{{\mathcal {C}}}\ , \end{aligned}$$

(1)

which is a measure of the oblateness of the satellite. When $\varepsilon = 0$, then ${\mathcal {A}}={\mathcal {B}}$ which means that the satellite is symmetric in the equatorial plane and, because of (H3), it coincides with the orbital plane.

We consider the perturber ${\mathcal {P}}$ at the origin of an inertial reference frame with the horizontal axis coinciding with the direction of the semimajor axis. It is convenient to identify the orbital plane with the complex plane ${\mathbb {C}}$. The location of the center of mass of the rigid body ${\mathcal {S}}$ with respect to the perturber ${\mathcal {P}}$ is given, in exponential form, by $r \exp (\mathtt {i}f) \in {\mathbb {C}}$, where $r > 0$ and f are real functions depending on the time t and they represent, respectively, the instantaneous orbital radius and the true anomaly of the Keplerian orbits. Indeed, over time, r and f describe an ellipse of eccentricity $e\in [0,1)$, semimajor axis a and focus at the origin, see Fig. 1.

Given that the mean motion n has been normalized to one, then the mean anomaly coincides with the time t. By Kepler’s equation (Celletti 2010), we have the following relation between the eccentric anomaly u and the time:

$$\begin{aligned} t = u - e\sin u\ . \end{aligned}$$

(2)

The expressions which relate r and f with the eccentric anomaly (and hence with time through (2)) are given by

$$\begin{aligned} r&= a(1 - e\cos u)\ , \end{aligned}$$

(3)

$$\begin{aligned} r \exp (\mathtt {i}f)&= a(\cos u - e+ \mathtt {i}\sqrt{1 - e^2} \sin u)\ . \end{aligned}$$

(4)

Notice that we are assuming in (4) that for $t=0$, $f(0) = u(0) = 0$, and consequently, $f(\pi ) = u(\pi ) = \pi$ when $t = \pi$. We also recall the following relations between the Keplerian elements that will be useful in the following:

$$\begin{aligned} \cos f = \frac{\cos u - e}{1 - e\cos u} \qquad \text {and} \qquad \sin f = \frac{\sqrt{1 - e^2} \sin u}{1 - e\cos u}\ . \end{aligned}$$

(5)

As for the rotational motion, let x be the angle formed by the direction of the largest physical axis, which belongs to the orbital plane, due to the assumptions (H2) and (H3), with the horizontal (or semimajor) axis a.

If we neglect dissipative forces, the equation of motion which gives the dependence of x on time is given by the following expression (Celletti 2010) to which we refer as the conservative spin–orbit equation:

$$\begin{aligned} \frac{\mathrm{d}^2x(t)}{\mathrm{d}t^2} + \varepsilon \biggl (\frac{a}{r(t)}\biggr )^3 \sin \bigl (2 x(t) - 2f(t)\bigr ) = 0\ , \end{aligned}$$

(6)

where $\varepsilon > 0$ is given in (1), $r(t)=r(u(t);e)$ in (3), $f(t)=f(u(t);e)$ in (5), and where u is related to t through (2).

Fig. 1

The spin–orbit problem: A triaxial satellite ${\mathcal {S}}$ moves around a planet ${\mathcal {P}}$ on an elliptic orbit with semimajor axis a and eccentricity e. The position of the barycenter of ${\mathcal {S}}$ is given by the orbital radius r and the true anomaly f. The rotational angle is denoted by x

If we now assume that the satellite is not rigid, then we must consider a tidal torque, say ${\mathcal {T}}_d$, that acts on the satellite. According to Macdonald (1964), Peale (2005), we can write the tidal torque as a linear function of the velocity:

$$\begin{aligned} {\mathcal {T}} _d \biggl (\frac{\mathrm{d}x(t)}{\mathrm{d}t}, t\biggr ) = - \eta \biggl (\frac{a}{r(t)}\biggr )^6 \biggl (\frac{\mathrm{d}x(t)}{\mathrm{d}t} - \frac{\mathrm{d} f(t)}{\mathrm{d}t} \biggr )\ , \end{aligned}$$

(7)

where $\eta > 0$ is named the dissipative constant. Since we are interested in astronomical applications, we specify that $\eta$ depends on the physical and orbital features of the body and takes the form

$$\begin{aligned} \eta = 3n\ \frac{k_2}{\xi Q} \biggl (\frac{R_e}{a}\biggr )^3 \frac{M}{m}\ , \end{aligned}$$

where $k_2$ is the second degree potential Love number (depending on the structure of the body), Q is the so-called quality factor (which compares the frequency of oscillation of the system to the rate of dissipation of energy), $\xi$ is a structure constant such that $C=\xi mR_e^2$, $R_e$ is the equatorial radius, M is the mass of the central body ${\mathcal {P}}$, and m is the mass of the satellite ${\mathcal {S}}$. Astronomical observations suggest that for bodies like the Moon or Mercury the dissipative constant $\eta$ is of the order of $10^{-8}$.

The dynamics including the tidal torque is then described by the following equation to which we refer as the dissipative spin–orbit equation:

$$\begin{aligned} \frac{\mathrm{d}^2x(t)}{\mathrm{d}t^2} + \varepsilon \biggl (\frac{a}{r(t)}\biggr )^3 \sin \bigl (2 x(t) - 2f(t)\bigr ) = - \eta \biggl (\frac{a}{r(t)}\biggr )^6 \biggl (\frac{\mathrm{d}x(t)}{\mathrm{d}t} - \frac{\mathrm{d} f}{\mathrm{d}t} \biggr )\ . \end{aligned}$$

(8)

The expression for the tidal torque can be simplified by assuming (as in Peale (2005), Correia et al. (2004)) that the dynamics is essentially ruled by the average $\overline{{\mathcal {T}}}_d$ of the tidal torque over one orbital period, which can be written as

$$\begin{aligned} \overline{{\mathcal {T}}}_d \biggl (\frac{\mathrm{d}x}{\mathrm{d}t} \biggr ) = -\eta \biggl ({\bar{L}}(e)\frac{\mathrm{d}x}{\mathrm{d}t} -{\bar{N}}(e)\biggr ) \ , \end{aligned}$$

(9)

where (compare with Peale 2005)

$$\begin{aligned} \begin{aligned} {\bar{L}}(e)&\equiv {1\over {(1-e^2)^{9/2}}} \biggl (1+3e^2+{3\over 8}e^4 \biggr ) \ , \\ {\bar{N}}(e)&\equiv \frac{1}{(1-e^2)^6} \biggl (1+{{15}\over 2}e^2+{{45}\over 8}e^4+ {5\over {16}}e^6 \biggr )\ . \end{aligned} \end{aligned}$$

When considering the averaged tidal torque, one is led to study the following equation of motion to which we refer as the averaged dissipative spin–orbit equation:

$$\begin{aligned} \frac{\mathrm{d}^2x(t)}{\mathrm{d}t^2} + \varepsilon \biggl ({a\over r(t)}\biggr )^3 \sin \bigl (2x(t)-2f(t) \bigr ) = -\eta \biggl (\bar{L}(e)\frac{\mathrm{d}x(t)}{\mathrm{d}t}-{\bar{N}}(e)\biggr )\ . \end{aligned}$$

(10)

Note that in this model, we consider the average of the tidal forces, but do not average the conservative forces (see Appendix A). This is justified because, as indicated before, in practical problems, the dissipative forces are much smaller than the conservative ones.

Remarks 2.1

• (i) The parameter $\varepsilon$ in (1) is zero only in the case of an equatorial symmetry with ${\mathcal {A}} = {\mathcal {B}}$. In that case, the equation of motion (6) is trivially integrable.

• (ii) When $e=0$, the orbit is circular and therefore $r = a$ and $f = t + t _0$. Also, in this case the equation of motion (6) is integrable.

• (iii) Equation (6) is associated with the following one-dimensional, time-dependent Hamiltonian function:

  $$\begin{aligned} {\mathcal {H}}(y,x,t) = \frac{y^2}{2} - \frac{\varepsilon }{2} \Big (\frac{a}{r(t)}\Big )^3 \cos (2x - 2f(t))\ . \end{aligned}$$

  (11)

• (iv) Equations (6), (8) and (10) are defined in a phase space which is a subset of $[0,2\pi )\times {\mathbb {R}}$. Such a phase space can be endowed with the standard scalar product and a symplectic form $\Omega$, which in our case is just the two-dimensional area in phase space. Even if in two-dimensional phase spaces the area (volume) is the same as the symplectic manifold, in systems with N degrees of freedom ($N > 1$) the preservation of the two-form $\Omega$ is much more stringent than the preservation of the 2N-dimensional volume.

3 Numerical version of the spin–orbit problem

To get a numerical representation of the ordinary differential Eq. (8) (equivalently (6) or (10)), it is convenient to express the equation in terms either of the eccentric anomaly u or the mean anomaly which coincides with t. Although there is a clear bijection between t and u through (2), it seems reasonable to redefine everything in terms of the eccentric anomaly u due to the expressions of r in (3) and f in (4). The procedure to get the equation of motion with u as independent variable is the following.

The expression of f in (5) is given easily in terms of u (and $e$). Let $s(x)=s(x;u,e)$ be the function defined as $s(x;u,e):=\sin (2x(t)-2f(t))$, where the dependence on u, $e$ enters through f. Using trigonometric identities, we have an explicit expression in terms of u and $e$ for the sinus in (8):

$$\begin{aligned} s(x; u, e) = \sin (2x) (2\cos ^2 f-1) - \cos (2x)2\cos f \sin f\ . \end{aligned}$$

(12)

Note here the useful relation for the derivatives of s, c:

$$\begin{aligned} \begin{aligned}&\frac{\partial s}{\partial x}(x; u, e) = 2c(x; u, e) \ , \\&\frac{\partial c}{\partial x}(x; u, e) = -2 s (x; u, e) \ , \end{aligned} \end{aligned}$$

(13)

where

$$\begin{aligned} c(x) = c(x; u, e) :=\cos (2x) (2\cos ^2 f-1) + \sin (2x)2\cos f \sin f\ . \end{aligned}$$

(14)

The time change given by (2) leads to

$$\begin{aligned} \frac{\mathrm{d} f}{\mathrm{d}t} = \left( \frac{a}{r}\right) ^2 \sqrt{1 - e^2}\ . \end{aligned}$$

As a consequence, Eq. (8) can be expressed in terms of the independent variable u as

$$\begin{aligned} \frac{\mathrm{d}^2 \beta (u)}{\mathrm{d}u ^2} - \frac{\mathrm{d}\beta (u)}{\mathrm{d}u} \frac{a}{r(u)} e\sin u + \varepsilon \frac{a}{r(u)} s(\beta ) = - \eta \biggl (\frac{a}{r(u)}\biggr )^5 \biggl (\frac{\mathrm{d}\beta (u)}{\mathrm{d}u} - \frac{a}{r(u)} \sqrt{1 - e^2}\biggr ) \end{aligned}$$

(15)

with r defined in (3) and $s(\beta ) :=s(\beta ; u, e)$ given in (12).¹

Note that the introduction of u as independent variable implies a non-constant deformation in the angular component. More precisely, if $y(t) = \frac{\mathrm{d}x(t)}{\mathrm{d}t}$, defining

$$\begin{aligned} \beta (u) :=x (u - e\sin u)\ , \end{aligned}$$

(16)

we obtain

$$\begin{aligned} \gamma (u) :=\frac{\mathrm{d}\beta (u)}{d u} = \frac{r(u)}{a}y(u - e\sin u)\ . \end{aligned}$$

The ODE system (15) can now be integrated by any classical numerical integrator (Hairer et al. 1993) without having to solve the Kepler’s Eq. (2) at each integration step. In the following sections, we will use a Taylor’s integrator (Jorba and Zou 2005a) that we briefly recall for self-consistency in Appendix B. We have used Taylor’s method because it can produce solutions with high accuracy (say $10^{-30}$), since it can easily increase the orders of the Taylor’s expansions in order to provide good enough trajectory values. These integrators are also used to produce rigorous enclosures (Berz and Makino 1998). Both features seem to be important toward the goal of producing computer-assisted proofs (progress toward this goal will be reported in Calleja et al. (2020b)) or in the study of phenomena at breakdown that require delicate calculations not easy to make convincing. (Progress toward this goal will be reported in Calleja et al. (2020a).)

Even if not directly used in the present paper, we report in Appendix C the variational equations associated with (15). The variational equations with respect to coordinates and parameters can be used for different purposes (see Calleja et al. 2020b, a), e.g., to compute the parameterization of invariant structures, to get estimates based on the derivative of the flow, to compute chaos indicators like the Fast Lyapunov Indicator (Froeschlé et al. 1997).

4 The conformally symplectic spin–orbit map

In this section, we introduce the notion of conformally symplectic systems (Sect. 4.1), we reduce the study of the spin–orbit problem to a discrete map (Sect. 4.2) and we provide an explicit expression of the conformally symplectic factor (Sect. 4.3).

4.1 Conformally symplectic systems

Conformally symplectic systems are dissipative systems that enjoy the remarkable property that they transform the symplectic form into a multiple of itself.

The formal definition for 2n-dimensional discrete and continuous systems is the following.

Let ${\mathcal {M}} = U\times {\mathbb {T}}^n$ be the phase space with $U\subseteq {\mathbb {R}}^n$ an open and simply connected domain with smooth boundary. We endow the phase space ${\mathcal {M}}$ with the standard scalar product and a symplectic form $\Omega$, represented by a matrix J at the point ${{\underline{z}}}$ acting on vectors ${{\underline{u}}},{{\underline{v}}}\in {\mathbb {R}}^{2n}$ as $\Omega _{{\underline{z}}}({{\underline{u}}}, {{\underline{v}}}) = ({{\underline{u}}}, J({{\underline{z}}}){{\underline{v}}})$.

For the spin–orbit model, the symplectic form $\Omega$ is represented by the constant matrix J which takes the form

$$\begin{aligned} J = \begin{pmatrix} 0 &{} 1 \\ -1 &{} 0 \end{pmatrix}\ . \end{aligned}$$

(17)

Definition 4.1

A diffeomorphism f on ${\mathcal {M}}$ is conformally symplectic if, and only if, there exists a function $\lambda :{\mathcal {M}}\rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} f^* \Omega = \lambda \Omega \ , \end{aligned}$$

(18)

where $f^*$ denotes the pull-back of f (i.e., $f^*\Omega = \Omega \circ f$) and $\lambda$ is called the conformal factor.

In the following, we will consider a family $f _\mu :{\mathcal M}\rightarrow {{\mathcal {M}}}$ of mappings and we will call $\mu \in {{\mathbb {R}}}$ the drift parameter. Correspondingly, we will replace (18) by

$$\begin{aligned} f_\mu ^* \Omega = \lambda \Omega \ . \end{aligned}$$

We notice that for $\lambda =1$, we recover the symplectic case. Moreover, as remarked in Calleja et al. (2013a), for $n=1$ any diffeomorphism is conformally symplectic with a conformal factor that might depend on the coordinates; in particular, when $\Omega$ is the standard area, one has either $\lambda (x)=|\det (Df _\mu (x))|$ or $\lambda (x)=-|\det (D f _\mu (x))|$. When $n\ge 2$, it follows that $\lambda$ is a constant (see, e.g., Banyaga 2002; Calleja et al. 2013a).

Definition 4.1 extends to continuous systems by the use of the Lie derivative.

Definition 4.2

We say that a vector field X is a conformally symplectic flow if, and only if, denoting by $L _X$ the Lie derivative, there exists a function $\mu :{\mathbb {R}}^{2n} \rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} L_X\Omega = \mu \Omega \ . \end{aligned}$$

(19)

Denoting by $\Phi _{t _0}^t$ the flow at time t of the vector field X from the initial time $t _0$, we observe that (19) implies that

$$\begin{aligned} (\Phi _{t _0}^t)^*\Omega =e^{\mu (t - t _0)} \Omega \ . \end{aligned}$$

In our applications, we will consider a family of vector fields $X _\sigma$ depending on a drift parameter $\sigma \in {\mathbb {R}}$ and we will replace (19) by

$$\begin{aligned} L_{X _\sigma }\Omega = \mu \Omega \ . \end{aligned}$$

In our applications, we will also have to consider time-dependent vector fields. A time-dependent vector field X(t) is conformally symplectic when $L_{X(t) }\Omega = \mu (t) \Omega$. It is not difficult to show that $\Phi _a^b$, the diffeomorphism which takes initial conditions at time a to the position at time b (hence $\Phi _a^c = \Phi _b^c \circ \Phi _a^b$), satisfies

$$\begin{aligned} (\Phi _a^b)^*\Omega = e^{\int _a^b \mu (s) \, \mathrm{d}s} \Omega \ . \end{aligned}$$

(20)

Note that (20) implies that if X(t) is periodic of period T, the conformal factor of $\Phi _a^{a+T}$ is independent of a and it is equal to the conformal factor of a vector field with a constant ${\bar{\mu }} = \frac{1}{T} \int _a^{a+T} \mu (s) \, \mathrm{d}s$. This will be useful in the justification of averaging (see Appendix A).

The spin–orbit models described by (8) and (10) are both conformally symplectic. Let us start to show that the averaged system (10) is conformally symplectic. We write (10) as the first-order system

$$\begin{aligned} \dot{x}&= y\\ \dot{y}&= -\varepsilon \Big (\frac{a}{r}\Big )^3\ \sin (2x-2f)-\mu (\dot{x}-\upsilon )\ , \end{aligned}$$

where $\mu = \eta {\bar{L}}(e)$ and $\upsilon = \frac{\bar{N}(e)}{{\bar{L}}(e)}$. Hence, $\mu$ is the conformal factor and $\upsilon$ is the drift parameter. Denoting by $i_X$ the interior product and recalling that $\Omega =\mathrm{d}y\wedge \mathrm{d}x$, we have

$$\begin{aligned} i_X\Omega =\dot{y} \mathrm{d}x-\dot{x} \mathrm{d}y=\Big [-\mu (y-\upsilon )-\varepsilon \Big (\frac{a}{r}\Big )^3\ \sin (2x-2f)\Big ]\, \mathrm{d}x-y\, \mathrm{d}y\ . \end{aligned}$$

Then, we have

$$\begin{aligned} \mathrm{d}(i_X\Omega )=-\mu \, \mathrm{d}y\wedge \mathrm{d}x=-\mu \Omega \ . \end{aligned}$$

Since

$$\begin{aligned} L_X\Omega =i_X\, \mathrm{d}\Omega +\mathrm{d}(i_X\Omega )=\mathrm{d}(i_X\Omega )\ , \end{aligned}$$

we conclude that

$$\begin{aligned} L_X\Omega =-\mu \Omega \ . \end{aligned}$$

A similar computation shows that the model described by (8) is conformally symplectic.

4.2 The spin–orbit map

We introduce the Poincaré map associated with (8) or (10), which allows one to reduce the continuous spin–orbit problem to a discrete system. We denote by $G _e$ the flow at time $2\pi$ in the independent variable u associated with the equation of motion (15) in the coordinates $(\beta ,\gamma )$:

$$\begin{aligned} G _e(\beta _0,\gamma _0)= \begin{pmatrix} \beta (2\pi ;\beta _0,\gamma _0,e) \\ \gamma (2\pi ;\beta _0,\gamma _0,e) \end{pmatrix} \end{aligned}$$

(21)

with $\beta (2\pi ;\beta _0,\gamma _0,e)$ and $\gamma (2\pi ; \beta _0,\gamma _0,e)$ denoting the solution at $u=2\pi$ with initial conditions $(\beta _0,\gamma _0)$ at $u = 0$. If we set $G _e= (G^{(1)} _e, G^{(2)} _e)$, then the Poincaré map associated with (15) is

$$\begin{aligned} {{\bar{\beta }}}&= G^{(1)}_e(\beta ,\gamma ) \\ {{\bar{\gamma }}}&= G^{(2)}_e(\beta ,\gamma )\ . \end{aligned}$$

The Poincaré map $P_e$ at time $t = 2\pi$ associated with (8) is then given by the conjugacy

$$\begin{aligned} P _e=\Psi _e^{-1}\circ G _e\circ \Psi _e\end{aligned}$$

(22)

with the (time) change of coordinates from $(x,y)/(2\pi )$ to $(\beta , \gamma )$ given by

$$\begin{aligned} \Psi _e= 2\pi \ \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1-e\end{pmatrix}\ . \end{aligned}$$

(23)

Using the map $G _e$ is very advantageous in numerical implementation because this allows us to avoid to dealing with the Kepler’s Eq. (2). On the other hand, the map $P _e$ is appropriate for physical interpretations, and the close and explicit relation among them (22) allows to choose the most advantageous one for the task at hand.

4.3 The conformally symplectic factor

Our next task is to find an explicit form for the conformally symplectic factor $\lambda$ of the Poincaré map associated with (8) or equivalently (15).

By the Jacobi–Liouville theorem, the determinant of the differential of the Poincaré map is obtained by integrating the trace of the Jacobian matrix associated with (8). Since the determinant and the trace of a matrix are invariant under a change of basis, their values are the same if we compute the system (15) via the Jacobian with elements $a_{ij}$ given by

$$\begin{aligned} \begin{aligned} a _{11}&= 0,&a _{21}&= -2\varepsilon \frac{a}{r(u)}c(\beta ;u,e) \ , \\ a _{12}&= 1,&a _{22}&= e\frac{a}{r(u)} \sin u - \eta \biggl (\frac{a}{r(u)}\biggr )^5\ . \end{aligned} \end{aligned}$$

This leads to the following expression for the conformal factor:

$$\begin{aligned} \lambda = \exp \left( \int _0^{2\pi } \left( e\frac{a}{r(u)}\sin u - \eta \left( \frac{a}{r(u)}\right) ^5 \right) \, \mathrm{d}u \right) \ . \end{aligned}$$

(24)

It is remarkable that the integral in (24) can be computed analytically in terms of $\eta$ and $e$. To this end, we need the following preliminary result.

Lemma 4.3

If $e\in [0, 1)$ and $r = a (1 - e\cos u)$, then

$$\begin{aligned} \int _0^{2\pi } \left( \frac{a}{r(u)}\right) ^5 \, \mathrm{d}u = \pi \frac{3e^4 +24 e^2 +8}{4 (1 - e^2)^{9/2}}\ . \end{aligned}$$

Proof

Since $e\in [0,1)$, then $(\frac{a}{r})^5$ has no poles in the unit circle. By the change of variables $z = \exp (\mathtt {i}u)$ and a straightforward application of the residue theorem, we obtain:

$$\begin{aligned} \int _0^{2\pi } \biggl (\frac{a}{r(u)} \biggr )^5 \, \mathrm{d}u = 2 \pi \sum _{\begin{array}{c} w \text { sing.} \\ |w |< 1 \end{array}} {{\,\mathrm{Res}\,}}\biggl (\frac{2^5z^5}{(2z-ez^2-e)^5}, w\biggr )\ , \end{aligned}$$

where ${{\,\mathrm{Res}\,}}$ denotes the residue of a holomorphic function. To compute the residue, we need to evaluate the poles $\alpha _\pm$ which are given by $\alpha _\pm = e^{-1}(1 \pm \sqrt{1 - e^2})$. Since $|\alpha _- | < 1$, then by an explicit computation, we get:

$$\begin{aligned} \int _0 ^{2\pi } \biggl (\frac{a}{r(u)} \biggr )^5\, \mathrm{d}u&= 2 \pi \frac{1}{4!} \lim _{z \rightarrow \alpha _-} \frac{\mathrm{d}^4}{\mathrm{d}z^4} (\frac{-2^5z^4}{e^5(z-\alpha _+)^5}) \\&= 2\pi \lim _{z \rightarrow \alpha _-}\frac{32 \left( \alpha _+^4+16 \alpha _+^3 z+36 \alpha _+^2 z^2+16 \alpha _+ z^3+z^4\right) }{e^5 (\alpha _+-z)^9} \\&= \pi \frac{3 e^4+24 e^2+8}{4 \left( 1-e^2\right) ^{9/2}}. \end{aligned}$$

$\square$

The above result leads to the following corollary, which gives an explicit form of the conformal factor of the spin–orbit model described by (8).

Corollary 4.4

The conformally symplectic factor of the $2\pi$-time map of the spin–orbit problem with tidal torque given by the system (8) has the following expression:

$$\begin{aligned} \lambda = \exp \biggr (-\eta \pi \frac{3 e^4+24 e^2+8}{4 \left( 1-e^2\right) ^{9/2}}\biggl )\ . \end{aligned}$$

Remarks 4.5

• (i) Note that the result in Corollary 4.4 is also valid under the change of time given in (2). This means that the $2\pi$-time map associated with the system (15) has the same symplectic factor, since the determinant is invariant under a change of basis.

• (ii) The conformally symplectic factor $\lambda$ can be either contractive, expansive or neutral. The value $\lambda$ has a clear dynamical interpretation: At each $2\pi$-interval of time, the values move $\lambda$ far away from unity. We remark that in this work we are interested to the contractive case, namely $\eta > 0$.

5 The computation of invariant attractors

We consider the model described by Eq. (8), and we provide an algorithm (see Sect. 5.1) for the construction of KAM invariant attractors. The algorithm relies on the fact that, starting from an initial approximate solution, one can construct a better approximate solution. A possible choice for the initial approximate solution is presented in Sect. 5.2. A validation of the goodness of the solution is considered in Sect. 5.3, which provides some accuracy tests. The construction of the invariant attractors through the implementation of the algorithm described in Sect. 5.1 requires some technical procedures, precisely multiple precision arithmetic (see Appendix D) and parallel computing (see Sect. 5.5). Examples of the application of Algorithm 5.4 are given in Sect. 5.6.

5.1 An algorithm for constructing invariant attractors

Invariant attractors for the map $P_e$ defined in (22) associated with the dissipative spin–orbit Eq. (8) can be obtained by implementing an efficient algorithm based on Newton’s method; this algorithm is also used to give a rigorous proof of invariant tori through KAM theorem, see Calleja et al. (2020b), as well as to give accurate bounds on the breakdown threshold, see Calleja et al. (2020a).

To introduce the algorithm, we need to fix the frequency $\omega$, that we are going to choose sufficiently irrational, see Definition 5.1, and we need to introduce invariant KAM attractors, see Definition 5.2.

Definition 5.1

The number $\omega \in {\mathbb {R}}$ is said Diophantine of class $\tau$ and constant $\nu$ for $\tau \ge 1$, $\nu >0$, and briefly denoted as $\omega \in {\mathcal {D}}(\nu , \tau )$, if the following inequality holds:

$$\begin{aligned} |\omega \ k-q|^{-1}\le \nu ^{-1}|k|^\tau \end{aligned}$$

(25)

for $q\in {\mathbb {Z}}$, $k\in {\mathbb {Z}}\backslash \{0\}$.

We remark that the sets of Diophantine numbers as in Definition 5.1 are such that their union over $\nu >0$ has full Lebesgue measure in ${\mathbb {R}}$.

Next, we define as follows an invariant attractor with frequency $\omega$ satisfying (25).

Definition 5.2

Let $P _e:{\mathcal {M}}\rightarrow {\mathcal {M}}$ be a family of conformally symplectic maps defined on a symplectic manifold ${\mathcal {M}}\subset {\mathbb {T}}\times {\mathbb {R}}$ and depending on the drift parameter $e$. A KAM attractor with frequency $\omega$ is an invariant torus described by an embedding $K _p :{\mathbb {T}}\rightarrow {\mathcal {M}}$ and a drift parameter $e_p$, satisfying the following invariant equation for $\theta \in {\mathbb {T}}$:

$$\begin{aligned} P_{e_p}\circ K_p(\theta ) = K_p(\theta +\omega )\ . \end{aligned}$$

(26)

We will often write (26) in the form

$$\begin{aligned} P_{e_p}\circ K_p = K_p\circ T_\omega \ , \end{aligned}$$

where $T_\omega$ denotes the shift function by $\omega$, i.e., $T _\omega (\theta ) = \theta + \omega$.

The solutions of the invariance Eq. (26) are unique up to a shift. For all real $\alpha$, if ${\hat{K}} _p(\theta ) :=K _p(\theta + \alpha )$, then $({\hat{K}} _p, e_p)$ is also a solution of (26). Note that all these solutions parameterize the same geometric object. In Calleja et al. (2013a), there is a simple argument showing that this is the only source of lack of local uniqueness.

We remark that the link between the parameterization of the return map and that of the continuous system is detailed in Appendix E.

Remark 5.3

It is easy to see—even in the integrable case—that to obtain an attractor with a specific frequency, we need to adjust the drift parameter.

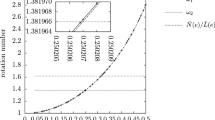
Hence, repeating the calculation several times, we obtain the drift as a function of the frequency. One can invert this—one-dimensional—function and obtain the frequency as a function of the drift, so that the two are mathematically equivalent, see Fig. 2.

For astronomers, the frequency is directly observed and it is natural to think of using the measurements of the frequency to obtain values of the drift.

Theoretical physicists may prefer that the values of the drift are known and that one predicts the frequency.

Both points of view are mathematically equivalent modulo inverting a 1-D function. In astronomy, since there is little a priori information on the values of the elastic properties of the satellites, it seems more natural to study the drift as function of the frequency. On other physical applications, where the values of the model are known from the start, the other point of view may be preferable.

One small technical problem (that can be solved) is that the function is not defined for all values of the frequency. The theory only establishes for a set of large measure. Repeatedly, not all the values of the drift parameter lead to a system that has a rotational attractor.

The starting point of the iterative process in the spin–orbit problem is then $(K,e)$, an approximate solution of the invariance equation (26),

$$\begin{aligned} P_e\circ K(\theta ) - K(\theta +\omega )=E(\theta )\ , \end{aligned}$$

(27)

where the “error” E is thought of as small. (Making precise the notion of small will require the introduction of norms.)

Algorithm 5.4 takes the pair $(K , e)$ and produces another approximate solution $({{\tilde{K}}},{\tilde{e}})$, which satisfies (26) up to an error whose norm is quadratically smaller with respect to E. (Again, making all this precise requires introducing norms.)

We note that all the steps are rather explicit operations taking derivatives, shifting and performing algebraic operations. The most delicate steps are 8, 12, which involve solving cohomology equations and step 9 which involves solving a $2 \times 2$ linear equation. The assumption of invertibility of this explicit $2\times 2$ matrix is a non-degeneracy assumption that takes the place of the classical twist condition.

Algorithm 5.4 is based on that described in Calleja et al. (2013a) and adapted for the spin–orbit problem. Even if, for the sake of simplicity, we only present the algebraic operations in the recipe, in Calleja et al. (2013a) there are geometric interpretations that motivate the steps.

Algorithm 5.4

(Newton’s method for finding a torus in the spin–orbit problem)

$\star$:

Inputs: J as in (17), $\omega$ a fixed frequency, an initial embedding $K:{\mathbb {T}} \rightarrow {\mathbb {T}} \times {\mathbb {R}}$, access to the $2\pi$-time flow map $G _e$ of (15) for fixed values $\varepsilon$ and $\eta$, change of coordinates depending on $e$, $\Psi _e\equiv 2\pi \left( {\begin{matrix} 1 &{} 0 \\ 0 &{} 1-e\end{matrix}} \right)$, and conformally symplectic map $P _e\equiv \Psi ^{-1} _e\circ G _e\circ \Psi _e$.

$\star$:

Output: New K and $e$ satisfying the invariance Eq. (26) up to a given tolerance.

$\star$:

Notation: If A is defined in ${\mathbb {T}}$, ${\overline{A}} :=\int _{{\mathbb {T}}} A$ and $A^0 :=A - {\overline{A}}$.

1.:

$E \leftarrow P _ e\circ K - K \circ T _\omega$,

$E _1 \leftarrow E _1 - \mathtt {round}(E _1)$.

2.:

$\alpha \leftarrow D K$.

3.:

$N \leftarrow (\alpha ^t \alpha ) ^{-1}$.

4.:

$M \leftarrow \begin{bmatrix} \alpha&J ^{-1} \alpha N \end{bmatrix}$.

5.:

${\widetilde{E}} \leftarrow (M ^{-1}\circ T _\omega ) E$.

6.:

$\lambda$ from Corollary 4.4.

7.:

$P \leftarrow \alpha N$,

$S \leftarrow (P \circ T _\omega )^t D P _ e\circ K J ^{-1} P$,

${\widetilde{A}} \leftarrow M ^{-1} \circ T _\omega D _eP _e\circ K$.

8.:

$(B _a)^0$ solving $\lambda (B _a) ^0 - (B _a)^0 \circ T _ \omega = - ({\widetilde{E}} _2)^0$,

$(B _b)^0$ solving $\lambda (B _b) ^0 - (B _b)^0 \circ T _ \omega = - ({\widetilde{A}} _2)^0$.

9.:

Find ${\overline{W}} _2$, $\sigma$ solving the linear system

$$\begin{aligned} \begin{pmatrix} \overline{S} &{} \overline{S(B _b)^0} + \overline{{\widetilde{A}} _1} \\ \lambda - 1 &{} \overline{{\widetilde{A}} _2} \end{pmatrix} \begin{pmatrix} {\overline{W}} _2 \\ \sigma \end{pmatrix} = \begin{pmatrix} - \overline{{\widetilde{E}} _1} - \overline{S(B _a)^0} \\ - \overline{{\widetilde{E}} _2} \end{pmatrix}\ . \end{aligned}$$

10.:

$(W _2)^0 \leftarrow (B _a)^0 + \sigma (B _b)^0$.

11.:

$W _2 \leftarrow (W _2)^0 + \overline{W}_2$.

12.:

$(W _1)^0$ solving $(W _1) ^0 - (W _1)^0 \circ T _ \omega = - (S W _2)^0 - ({\widetilde{E}} _1)^0 - ({\widetilde{A}} _1)^0 \sigma$.

13.:

$K \leftarrow K + M W$,

$e\leftarrow e+ \sigma$.

Algorithm 5.4 needs some practical remarks:

• Because of the periodicity condition $K (\theta + 1) = K (\theta ) + \left( {\begin{matrix} 1 \\ 0 \end{matrix}} \right)$, one can always define the periodic map ${\widetilde{K}}(\theta ) :=K(\theta ) - \left( {\begin{matrix} \theta \\ 0 \end{matrix}} \right)$ which, generically, admits a Fourier series. Then, one obtains that

  $$\begin{aligned} K\circ T _\omega = {\widetilde{K}} \circ T _\omega + \left( {\begin{matrix} \omega \\ 0 \end{matrix}} \right) . \end{aligned}$$

• The function E in step 1 must perform the subtraction in the first component in ${\mathbb {T}}$. For a numerical implementation that can be fulfilled by the assignment $E _ 1 \leftarrow E _1 - \mathtt {round}(E _1)$, where $\mathtt {round}$ returns the nearest integer value of its argument. Such a function is commonly provided in almost all programming languages.

• The matrix M in step 4 is unimodular, which allows to get an easy inverse matrix expression.

• The quantities $D P _e$ and $D _eP _e$ in step 7 are needed to compute the directional variational flow of $\Phi$, which can be done automatically using the explanations in Section C.1.

• The stopping criterion is either that $\Vert E\Vert$ or $\max \{ \Vert MW \Vert , | \sigma |\}$ is smaller than a prefixed tolerance.

A common numerical representation for periodic mappings is a Fourier series in the inputs $K_1$ and $K _2$, which gives us a representation of $K\equiv (K _1, K _2)$. In such a representation, we can use the Fourier transform, or its numerical version via fast Fourier transform (FFT) algorithm.

Therefore, any periodic mapping, say f, admits two representations, namely in points (or table of values) and in Fourier coefficients. The first one is just the values $(\check{f}_k) _{k = 0}^{n-1}$ of the mapping in an equispaced mesh in [0, 1) of size n. The second one is obtained by the inverse of the fast Fourier transform (IFFT), denoted by $({\widehat{f}} _k) _{k = 0}^{n-1}$. Notice that because the function is assumed to be real-valued, the two representations can have the same size, i.e., n real values.

Depending on the step in Algorithm 5.4, it may be better to use one representation or the other. For instance, $P _e\circ K$ in 1 and $D P _e\circ K$, $D _eP _e\circ K$ in 7 are better when K is in a table of values, although an ODE version of (8) in terms of Fourier coefficients can be considered.

On the other hand, the composition with $T _\omega$ and the solution of the cohomological equations in 8 and 12 are easier if K is in Fourier series. Indeed, these equations can be solved in Fourier coefficients, using the following result whose proof is straightforward.

Lemma 5.5

Let $\eta (\theta ) = \sum _k \eta _k \exp (2\pi \mathtt {i}k \cdot \theta )$, and let $\omega$ be irrational. Then:

• (i) If $\eta _0 = 0$, then $\phi \circ T _\omega - \phi = \eta$ has solution $\phi (\theta ) = \sum _k \phi _k \exp (2\pi \mathtt {i}k \cdot \theta )$ with

  $$\begin{aligned} \phi _k = {\left\{ \begin{array}{ll} \frac{\eta _k}{\exp (2\pi \mathtt {i}k \cdot \omega ) - 1} &{} \text {if } k \ne 0, \\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

• (ii) If $\lambda$ is not a root of unit, then $\phi \circ T _\omega - \lambda \phi = \eta$ has solution with coefficients

  $$\begin{aligned} \phi _k = \frac{\eta _k}{\exp (2\pi \mathtt {i}k \cdot \omega ) - \lambda } \ . \end{aligned}$$

5.2 Initial approximation of the invariant curve

Repeated application of the Newton’s method from Algorithm 5.4 produces a very accurate solution provided that one can get a good enough initial approximation. In this section, we address the problem of producing such an initial approximation. Although the methods are rather general, we are going to give the results for the cases of study in this paper. We select the following two frequencies with good Diophantine conditions belonging to the class ${\mathcal {D}}( \frac{2}{3-\sqrt{5}}, 1)$, see Definition 5.1:

$$\begin{aligned} \omega _1&= \gamma _g^+ \end{aligned}$$

(28)

and

$$\begin{aligned} \omega _2&= 1 + \frac{1}{2 + \gamma _g^-} \ , \end{aligned}$$

(29)

where we define $\gamma _g^\pm = \frac{\sqrt{5}\pm 1}{2}$.

One method to provide an initial approximation is, of course, to continue from an integrable case that can be solved explicitly. Another method is to do an easy calculation of an approximate torus. Since the system is dissipative, the torus, if it exists, will be an attractor.

5.2.1 A continuation method from the integrable case

Let us start to analyze the averaged problem for which we look for the drift starting from the integrable case. Fix the frequency $\omega$ and set $\varepsilon =0$ in (10); then, the drift $e$ can be chosen so that

$$\begin{aligned} \frac{{\bar{N}}(e)}{{\bar{L}}(e)} = \omega \ . \end{aligned}$$

The above equation provides the eccentricity as a function of the frequency. In fact, as noticed in Celletti and Chierchia (2009), for $\eta \ne 0$ the solution of (10) can be written as

$$\begin{aligned} x(t) = x(0) + \frac{{\bar{N}}(e)}{{\bar{L}}(e)} t + \frac{1-\exp ({-\eta t})}{\eta }\ \biggl (\dot{x}(0) - \frac{\bar{N}(e)}{{\bar{L}}(e)}\biggr )\ , \end{aligned}$$

which shows that $\dot{x}=\frac{{\bar{N}}(e)}{{\bar{L}}(e)}$ is a global attractor for the unperturbed, purely dissipative case $\varepsilon =0$. Setting $y=\dot{x}$, we can select as initial starting condition

$$\begin{aligned} x(0) = 0 \qquad \text {and} \qquad y(0)={{{\bar{N}}(e)}\over {{\bar{L}}(e)}}\ . \end{aligned}$$

(30)

We remark that, despite the use of the averaged version of the spin–orbit problem given in (10), to approximate an initial guess of the eccentricity in terms of the frequency, we can also use the non-averaged spin–orbit problem (8) to provide an approximated eccentricity, see Sect. 5.2.2.

5.2.2 Direct iteration

We propose a method different from Sect. 5.2.1, which takes advantage of the fact that the torus, if it exists, is an attractor. We do not need to consider the average equation and we can start from the model (8). Hence, we start by selecting a set of points at random; after a transient number of iterations (e.g., choose the transient as the inverse of the dissipation multiplied by a convenient safety factor), we expect that the orbit is close to the attractor. Then, we assess whether indeed this orbit has a rotation number.

Since not all the attractors of dissipative maps are rotational orbits, not all of them should have a rotation number. Of course, there may be situations where the orbit is a chaotic attractor that happens to have a rotation number.

Given the importance of the rotation number, there are quite a number of algorithms to compute it, e.g., Laskar et al. (1992), Athanassopoulos (1998), Laskar (1999), Alsedà et al. (2000), Laskar (1999), Seara and Villanueva (2006), Gómez et al. (2010a), Gómez et al. (2010b), Sánchez et al. (2010). We have used the method in Das et al. (2017) which speeds the convergence to the rotation number. We will present more details of the calculation in Calleja et al. (2020b). We note that the method in Das et al. (2017) gives a very good indication of the existence of an invariant circle. In Das et al. (2017), it is shown that if there is a smooth invariant circle, the convergence of the method to a rotation number is very fast. Hence, the fast convergence of the algorithm is a reasonably good evidence of the existence of a rotational torus. Of course, the convergence of the Newton’s method started in this guess is a much stronger validation of the correctness of the guess.

Figure 2 compares the two approaches explained here and in Sect. 5.2.1. The first one is straightforward, since it consists in plotting the function ${\bar{N}}(e)/{\bar{L}}(e)$ in terms of the eccentricity $e$. The second one requires a little bit more effort, since it needs to numerically integrate (8) to compute the rotation number.

Fig. 2

Eccentricity versus the rotation number denoted by + of the system (8) with $\varepsilon = 10^{-4}$ and $\eta =10^{-5}$. Frequencies as in (28) and (29). The small window is just a zoom-in near to $\omega _2$ which shows that the averaged quantity ${\bar{N}}(e) /{\bar{L}}(e)$ approaches the non-averaged rotation number

5.2.3 Initial approximation for the embedding

Once we have fixed an initial guess for the eccentricity and an initial starting point, we can proceed to get an initial guess of the embedding K which is needed as input in Algorithm 5.4. To this end, we first perform a preliminary transient of iterations of $G _e$, defined in (21), at the initial point $\Psi _e(x(0), y(0)/(2\pi ))$, with (x(0), y(0)) given in (30). After that, we can follow the steps in Algorithm 5.6 to get the initial guess for K for Algorithm 5.4.

Algorithm 5.6

(Invariant curve approximation)

$\star$:

Inputs: Points $(\beta _k, \gamma _k)_{k=0}^{n-1}\subset [0,2\pi ) \times {\mathbb {R}}$ from iteration of the $2\pi$-time Poincaré map of (15) with parameter values $\varepsilon , \eta$, and $e$ and number of Lagrange interpolation points $2j\in {\mathbb {N}}$.

$\star$:

Output: Initial embedding K for Algorithm 5.4 with a given mesh size $n _\theta$.

1.:

Sort $(\beta _{i _k}, \gamma _{i _k}) _{k =0}^{n-1}$ such that $\beta _{i _ 1} \le \cdots \le \beta _{i _n}$.

2.:

Mesh ${{\overline{\beta }}} _k = 2\pi k / n _\theta$ with $k = 0, \dotsc , n _\theta -1$.

3.:

For each $k = 0, \dotsc , n _\theta - 1$, let ${{\overline{\gamma }}} _k$ be the Lagrange interpolation centered at $(\beta _{i _k},\gamma _{i _k})$ with 2j points $\gamma _{i _{k}-j \pmod n},\dotsc , \gamma _{i _ {k}+j \pmod n}$ and their respective abscissae.

4.:

Return the table of values $K \equiv (\Psi _e^{-1} ({{\overline{\beta }}} _k, {{\overline{\gamma }}} _k)) _{k=0}^{n_\theta -1}$ with $\Psi _e$ from (23).

5.3 Accuracy tests

We are now looking for $K :{\mathbb {T}} \rightarrow {\mathbb {T}} \times {\mathbb {R}}$ and the parameter $e$ so that the invariance Eq. (26) is verified, for $P _e$ given in (22) and a fixed frequency $\omega$ like in (28) or (29).

In this process, we have three main sources of error that affect the result.

$(\mathbf{E1})$:

The error of the invariance condition on the table of values. This error is controlled by the Newton’s procedure.

$(\mathbf{E2})$:

The error on the integration. This error is controlled by the numerical integrator when we request absolute and relative tolerances.

$(\mathbf{E3})$:

The error in the discretization. To control this source of errors, we need first to estimate it, and then to be able to change the mesh when the error is too large.

Let us address the error coming from (E3). Let ${\mathcal {A}} \subset {\mathbb {T}}$ be the set of points corresponding to the table of values used in the algorithm. In the case of a Fourier representation of size $n _\theta$, then ${\mathcal {A}} = \{k / n_\theta \}_{k = 0}^{n_\theta -1}$ is an equispaced mesh of [0, 1). After some iterations of the Newton’s Algorithm 5.4, we obtain a set of values $\{K (\theta _i)\} _{\theta _i \in {\mathcal {A}}}$ and an eccentricity $e$ satisfying the invariance equation in a mesh

$$\begin{aligned} \max _{\theta _i \in {\mathcal {A}}} \Vert P _{e} \circ K (\theta _i) - K (\theta _i + \omega ) \Vert < \delta \ , \end{aligned}$$

(31)

where $\delta$ is a fixed tolerance, e.g., $\approx 10^{-11}$ in double precision. Note that we are not fixing the norm in (31) which typically can be the sup-norm, the analytic norm, etc.

Let us now define $\delta ^*$ as

$$\begin{aligned} \delta ^*= \max _{\theta \in {\mathbb {T}}} \Vert P _{e} \circ K (\theta ) - K (\theta + \omega ) \Vert \ . \end{aligned}$$

The computation of $\delta ^*$ is in general difficult, and we suggest two standard heuristic alternatives.

The first option is very fast: It consists in looking at the norm of some of the “last” Fourier coefficients and using it as an estimate for the truncation error of the series. Once the Newton’s iteration has converged on a given mesh, we check the size of these coefficients. If one of them is larger than a prescribed threshold, we assume that the interpolation error is too big, and we increase the number of Fourier modes in the direction of these large coefficients.

The second option is to evaluate the error in (31) on a set of values $\widetilde{{\mathcal {A}}} \subset {\mathbb {T}}$ different from ${\mathcal {A}}$. One can use a thinner set $\widetilde{{\mathcal {A}}}$ to produce a better estimate of the invariance $\delta ^*$. This procedure can be computationally expensive. An easier alternative is to consider $\widetilde{{\mathcal {A}}}$ with the same number of points as ${\mathcal {A}}$. For instance,

$$\begin{aligned} \widetilde{{\mathcal {A}}} = {\mathcal {A}} + \upsilon \end{aligned}$$

with $\upsilon$ equal to one half of the distance between points of ${\mathcal {A}}$ in the direction $\theta _i \in {\mathcal {A}}$. In the Fourier case, $\widetilde{{\mathcal {A}}} = \{(k + 0.5) / n _\theta \} _{k = 0}^{n _\theta - 1}$ should be enough.

Hence, we have a new mesh $\widetilde{{\mathcal {A}}}$ which is interlaced with the initial mesh ${\mathcal {A}}$. Then, we check that

$$\begin{aligned} \max _{\theta _i \in \widetilde{{\mathcal {A}}} } \Vert P _{e} \circ K (\theta _i) - K (\theta _i + \omega ) \Vert < \delta \ . \end{aligned}$$

(32)

If this test is not satisfied, we add more Fourier coefficients and we go back to the Newton’s iteration given by Algorithm 5.4. If the test is satisfied, we can either stop and accept the solution or check it again with a thinner mesh.

The key is then to avoid checking with thinner meshes during the computation as much as possible, because it is too costly, and to do just a single check at the end to ensure the accuracy.

5.4 Implementation of the algorithm

Once Algorithm 5.4 is coded so that it becomes a sequence of arithmetic operations (and transcendental functions), it is almost easy to make it run in extended precision arithmetic, see Appendix D.

There are, however, some caveats:

• One loses the hardware support.

• The hardware optimized libraries have to be replaced by hand coded libraries. Notably, one cannot use BLAS, LAPACK, or FFTW and they have to be substituted by explicit algorithms. We have used our own implementations.

• In iterative processes, one has to choose the stopping criteria appropriately. As standard, one writes the stopping criteria as a power of Machine epsilon.

• For us, the most important point is that, in order to achieve high accuracy of the ODE integration with a reasonable step in a reasonable amount of time, one needs a high-order method.

  We have used the Taylor’s method, which is based on computing the Taylor’s expansion of the solution of the equation to a very high order, see Appendix B.

  The paper Jorba and Zou (2005a) presents a very general purpose generator of Taylor’s integrators based on automatic differentiation. If one specifies (in a very simple format) a differential equation, the program taylor (supplied and documented in Jorba and Zou (2005a)) generates automatically an efficient Taylor solver written in C. The user can select whether this Taylor solver uses standard arithmetic or extended precision arithmetic (either GMP or MPFR). It is important that Taylor’s methods can work well with different versions of the arithmetic.

  One important product of the Taylor’s integrator (Gimeno et al. 2021) is that we obtain very efficient solvers of the variational equations. We will report on them in Appendix C, since they are a natural extension of the Taylor’s integrator. We note that we will not use them in the numerical experiments of this paper, but we will use them in Calleja et al. (2020b). We remark that in mission design, they appear in the method of differential corrections.

5.4.1 Using profilers to detect bottlenecks

The computation of invariant tori with the Newton method that we propose is remarkably fast when the initial guess is good enough. However, the continuation to the breakdown requires to increase the Fourier modes and then the computational cost will increase in proportion.

The key step in a continuation process is the correction of the solution for the new parameter values which are being continued. In our case, it is the Newton step. We have used a C profiler in a single continuation step with multiprecision of 55 digits to realize which are the most CPU-time-consuming parts. We did it for different values of $\varepsilon \in \{10^{-4}, 2\cdot 10^{-4}\}$, $\eta \in \{10^{-3}, 10^{-6}\}$, $\omega \in \{\omega _1, \omega _2\}$, and $N \in \{128,256\}$ number of Fourier modes getting, in all of them, similar results.

In average, around 98.1% was dedicated to the Newton step correction; inside this step around 97.6% was for the evaluation of the ODE (and its variationals) in the ODE integrator and the correction of the integration stepsize. Inside of it, around 31% was for the addition of jet transport elements, 25% for multiplication, 18% for assignments, and 6.5% for scalar multiplications.

As a consequence, we conclude that the FFT, the solvers of cohomological equations and the shiftings in Algorithm 5.4 are irrelevant in terms of CPU-time as well as the memory allocation. The second conclusion is that the ODE integration is the crucial part. This fact will be exploited and detailed in Sect. 5.5.

5.5 Parallelization

There are several operations in Algorithm 5.4 that are fully independent to each other, such as those steps which are done in a table of values of $\theta$ and the solution of the cohomological equations using Lemma 5.5.

The use of a profiler shows that the main bottleneck, in terms of CPU-time usage, is the ODE integration involved in $P _e$, given in (22), and its first-order directional derivatives.

A simple concurrent parallelization for each of the different numerical integrations (previously ensuring that there is non-shared memory between the threads) shows an evident speedup with respect to non-concurrent versions. In our case, we run the code with multiprecision arithmetic, in particular with MPFR, and we must be sure that each of the parallelized parts work correctly with the multiprecision. In the case of MPFR, we must initialize the precision and the rounding mode for each of the different CPUs.

Figure 3 shows the non-parallel execution times and the speedups of Algorithm 5.4 using the initial guess from Algorithm 5.6 with $\eta = 10^{-6}$, $\varepsilon =10^{-4}$, 135 digits of precision and different number of modes in the Fourier representation. The figure was done in an Intel Xeon Gold 5220 CPU at 2.20GHz with 18 CPUs with hyperthreading which simulates 36 CPUs.

Note that the non-parallel data in Fig. 3 are extremely well fit by

$$\begin{aligned} T = 0.430018N + 4.75918\ , \end{aligned}$$

where T denotes the CPU time in seconds and N the Fourier representation size. This means that the single core time scales behave (in practice) linearly with the size of the problem. The logarithmic correction appearing in the theory of the FFT does not seem to be observable which is due to the fact that the FFT is not the main problem in the performance of our method. Of course, this is significantly better than the $N^3$ of Newton’s methods based on inverting matrices.

Algorithm 5.4 also accepts other concurrent computations such as the FFT algorithm or the solution of the cohomology equations in steps 8 and 12. The latter did not show an important speedup, presumably because the time spent in these calculations is not so important overall. (The number of points needed is not so large, due to our reduction to 1-D.)

Fig. 3

On the left: timings not using parallelization and fit of the times changing the number of Fourier modes. On the right: Speedup by a parallel ODE integration in step 7 of Algorithm 5.4 for different number of threads and different number of Fourier modes

5.6 A practical implementation of Algorithm 5.4

As an example of the implementation of Algorithm 5.4, we provide in Fig. 4 the construction of the invariant attractors for (8) with a small dissipation, say $\eta =10^{-6}$, and frequencies given by (28) and (29). Figure 5 gives the results for a higher dissipation, namely $\eta =10^{-3}$.

Both figures show different invariant attractors when the perturbative parameter $\varepsilon$ changes by using a standard continuation procedure with interpolation. At each of these continuation steps with respect to $\varepsilon$, we apply Algorithm 5.4 with a tolerance $10^{-35}$, which refines the embedding $K_\varepsilon$ and the eccentricity $e_\varepsilon$, and we also check the accuracy, see Sect. 5.3, to ensure that the numerical solution is accurate enough.

Additionally, we perform an extra refinement at each continuation step to ensure that the plots in Figs. 4 and 5 make the value of x in the range $[0,2\pi )$. More precisely, if $({{\tilde{K}}} _\varepsilon , e_\varepsilon )$ is the output of Algorithm 5.4, then we assign $K _\varepsilon \leftarrow {{\tilde{K}}} _\varepsilon$ with $K _\varepsilon ^1(0) = 0$. That is, we apply a shift $\alpha$ on ${{\tilde{K}}} _\varepsilon$ with $\alpha$ so that the first component of ${{\tilde{K}}} _\varepsilon$ at 0 is zero.

Fig. 4

Invariant attractor of (8) with a fixed dissipation $\eta =10^{-6}$ after a continuation w.r.t. the perturbative parameter $\varepsilon$. On the left, the frequency $\omega$ is like in (29) and on the right as in (28)

Fig. 5

Invariant attractor of (8) with a fixed dissipation $\eta =10^{-3}$ after a continuation w.r.t. the perturbative parameter $\varepsilon$. On the left, the frequency $\omega$ is like in (29) and on the right as in (28)

The results shown in Fig. 4 give evidence of the effectiveness of the method of constructing invariant attractors, using the reduction to a map and the implementation of Algorithm 5.4.

5.7 An empirical comparison between the model with time-dependent friction (8) and the average friction (10)

In this section, we present a comparison between the numerical results in the model with time-dependent dissipation (8) and the model with the averaged dissipation (10). In Appendix A, we present two rigorous justifications of the averaging procedure.

In Fig. 6, we plot the difference between the drift parameters (namely the eccentricities) of the full and averaged models for the tori with frequencies $\omega _1$ and $\omega _2$; such difference is small, say of the order of $10^{-7}$, even for parameter values close to breakdown. We also note that the y-axis in Fig. 6 is just the difference (without absolute value) which means that $e > e _{avg}$ at each of the $\varepsilon$ values.

Fig. 6

Difference of the eccentricities of the tori using the averaged (10) and the non-averaged (8) spin–orbit model in the case of dissipation $\eta =10^{-6}$ and for the two frequencies of interest $\omega _1$ in (28) on the left and $\omega _2$ in (29) on the right

5.8 Comment for double precision accuracy

The computation with multiprecision is already fast enough thanks to the quadratic convergence of our method. The use of multiprecision allows to get tori of arbitrary accuracy, and in particular, it helps to reach values of the parameter close to the breakdown. These calculations can be used to identify mathematical patterns close to breakdown and to use KAM theory. However, we can also perform double or even float precision computations for values that are not close to the breakdown. As one expects, the required time to converge using the Newton process presented in this paper, see Algorithm 5.4, is smaller than in multiprecision, paying the price of accuracy.

The first reason for this speed is because we request less accuracy—around $10^{-14}$ for double precision—which makes the algorithm converge in fewer iterations. The second reason is that we avoid the possible overhead of using a software package, such as MPFR, and we can then exploit the hardware optimizations provided by compilers.

After adapting our code to run with double precision, we detect that the values of $\varepsilon$ for which our method still converges are around $7.8\times 10^{-3}$ which is far from the $\varepsilon \sim 10^{-2}$ using more accuracy, the speedup of the parallelization strategy, see Sect. 5.5, behaves similarly, and the time of a continuation step (with one CPU) decreases. It still depends on the number of Fourier modes, and some example of values is reported in Table 1.

Table 1 Example of time T (in seconds) of a continuation step using double precision, N Fourier modes, no parallelism, $\eta = 10^{-3}$, $\omega$ as in (28), Newton’s tolerance $10^{-14}$, and integration tolerance $10^{-16}$. The data fit extremely well with $T = 0.00884 N + 0.0561$

In certain problems, it may be worth optimizing the speed (at the price of accuracy and programming time). In such cases where speed is the most important consideration, it may be worth taking advantage of modern computer architectures such as GPUs. (The very structured nature of our algorithm makes it a tantalizing possibility.) We encourage these (or any other) developments on the methods presented here.

6 Conclusions

There are several important features of the method developed in this paper for the construction of invariant tori using the return map; we highlight below some of these features.

• The method only requires dealing with functions of a low number of variables.

• The iterative step to construct the tori is quadratically convergent.

• The operation count and the operation requirements are low.

• The most costly step (integration of the equations) is very easy to parallelize efficiently. Many other steps of the algorithm involve vector operations, Fourier transforms, which also can take advantage of modern computers but here with less impact in the performance.

• The method is well adapted to the rather anisotropic regularity of KAM tori and, in the smooth direction, takes advantage of the developments in integration of ODEs.

• The method is reliable, since it is backed by rigorous a posteriori theorems.

• The condition numbers required are evaluated in the approximate solution and do not involve global assumptions on the flow such as twist.

• From the theoretical point of view, the a posteriori theorems give a justification of other heuristic methods that produce approximate solutions including asymptotic expansions and averaging methods.

Appendices

Appendix A. Justification of averaging methods

In this section, we study the relation between the time dependent spin–orbit model (8) and the model (9) in which the dissipation is averaged.

Superficially, the relation between the two models and their attractors seems to be problematic even in the perturbative regime, since the existence of quasi-periodic solutions makes assertions for all the time and conventional averaging methods make assertions only for times which are inverse powers of the perturbation.

We will present two arguments showing that, indeed for the problem of the existence of quasi-periodic tori, the averaging method produces an accurate result. The first argument (Section A.1) will apply to very general models, but will produce results for KAM tori. The second method (Section A.2) will be very specific for the spin–orbit problem but will provide information for all orbits.

We note, however, that our method produces not only a rigorous estimate on the error of the averaging method, but also suggests other approximations that are more accurate than the usual procedure of averaging only the dissipation (see Section A.2). Our results show that, if besides averaging the dissipation, one changes slightly the conservative forces (we give explicit formulas), one gets results that are more accurate than just averaging the friction.

In this section, we will consider a differential equation of the form

$$\begin{aligned} \frac{\mathrm{d}^2 x(t)}{\mathrm{d}t^2} + a(t) \frac{\mathrm{d} x(t)}{\mathrm{d}t} + F(x(t),t) = 0\ . \end{aligned}$$

(33)

In the perturbative case, we will have that there is a small parameter in the time dependence $a(t) = \mu \alpha (t)$.

1.1 A.1. Perturbative arguments based on a posteriori theorems

We first observe that the key to our result is the study of the time-one map of the vector field.

If the return maps of two vector fields are close (in a smooth enough norm) and they satisfy the non-degeneracy conditions, the solutions of the invariance Eq. (26) for the two systems are close.

To detail this remark, let us consider two Poincaré maps $P_e^{(A)}$ and $P_e^{(C)}$, depending on a drift term e and satisfying some non-degeneracy conditions; for example, we can take $P_e^{(A)}$ as the Poincaré map of the averaged system and $P_e^{(C)}$ as the Poincaré map of the complete, non-averaged system.

Let $(K_A,e_A)$ be an approximate solution of the invariance equation as in (27) with a small error term $E_A$:

$$\begin{aligned} P_{e_A}^{(A)}\circ K_A(\theta )-K_A(\theta +\omega )=E_A(\theta )\ . \end{aligned}$$

Assume that the maps $P_e^{(C)}$, $P_e^{(A)}$ are close (in a suitable norm); then $(K_A,e_A)$ is an approximate solution for $P_e^{(C)}$; in fact, we have that

$$\begin{aligned}&P_{e_A}^{(C)}\circ K_A(\theta )-K_A(\theta +\omega )\\&\quad =(P_{e_A}^{(C)}-P_{e_A}^{(A)})\circ K_A(\theta )+P_{e_A}^{(A)}\circ K_A(\theta )-K_A(\theta +\omega )\nonumber \\&\quad =(P_{e_A}^{(C)}-P_{e_A}^{(A)})\circ K_A(\theta )+E_A(\theta )\equiv E_C(\theta ) \end{aligned}$$

with $E_C$ small. Using the KAM theory given in Calleja et al. (2013a), there exists $(K_C,e_C)$ such that

$$\begin{aligned} P_{e_C}^{(C)}\circ K_C(\theta )-K_C(\theta +\omega )=0\ ; \end{aligned}$$

besides, the results in Calleja et al. (2013a) show that $K_C$ is close to $K_A$ and $e_C$ is close to $e_A$.

The importance of this remark is that to obtain the distance of the maps, we only need to estimate the difference between the evolution for a time $2 \pi$. In the perturbative regime, when the oscillation is of size $\mu$, controlling the distance between the solution of the averaged and non-averaged systems is well within the reach of standard averaging methods (Jack 1980; Sanders et al. 2007) (which deal well with times $O(\mu ^{-1})$, much larger than $2 \pi$).

1.2 A.2. Non-perturbative arguments based on elementary scaling of variables and of time

In this section, we present a completely elementary (non-perturbative) technique to justify the averaging method.

We just observe that if x satisfies (33), then, for any nonzero (smooth) function $\gamma (t)$, the function y(t) defined by $x(t) = \gamma (t)y(t)$ satisfies:

$$\begin{aligned} \gamma (t) \frac{\mathrm{d}^2 y(t)}{\mathrm{d}t^2} +( 2 \gamma '(t) + a(t) \gamma (t) ) \frac{\mathrm{d} y(t)}{\mathrm{d}t} + (\gamma ''(t) + a(t) \gamma '(t) ) y(t) + F(\gamma (t) y(t),t) = 0\ . \end{aligned}$$

(34)

Let $\bar{a}$ be the average value of a(t); if we choose

$$\begin{aligned} \gamma (t) = \exp \biggl ( -\frac{1}{2} \int _0^t ( a(s) - \bar{a}) \, \mathrm{d}s \biggr )\ , \end{aligned}$$

(35)

which is a periodic function, Eq. (34) becomes:

$$\begin{aligned} \frac{\mathrm{d}^2 y(t)}{\mathrm{d}t^2} +\bar{a} \frac{\mathrm{d} y(t)}{\mathrm{d}t} + G(y(t),t) = 0\ , \end{aligned}$$

(36)

where

$$\begin{aligned} G(y,t) :=\frac{ \gamma ''(t) + a(t) \gamma '(t)}{\gamma (t)} y + {1\over {\gamma (t)}} F(\gamma (t) y,t)\ . \end{aligned}$$

(37)

Hence, the function y satisfies the equation with an average dissipation (and a different F). Notice that $\gamma (0) = \gamma (2 \pi ) = 1$, so that

$$\begin{aligned} \begin{aligned} x (0)&= y(0) \gamma (0)\\ x(2 \pi )&= y(2 \pi ) \gamma (2\pi )\\ y'(0)&= x'(0) + \frac{1}{2}(a(0) - \bar{a}) x(0)\\ y'(2\pi )&= x'(2\pi ) + \frac{1}{2}(a(2\pi ) - \bar{a}) x(2\pi )\ . \end{aligned} \end{aligned}$$

(38)

We can think of (38) as a change of variables in phase space from $(x,x')$ to $(y, y')$. The return map for the averaged Eq. (36) in the variables $(y,y')$ is equivalent to the original problem.

Hence, we can read off the original return map as the return map of the averaged equation under a change of variables.

Note that, as standard in the averaging method, the relation between the averaged equations and the true ones is mainly a change of variables and a modification to the equations. Note, that in our very simple equations, the equivalence is exact.

In the perturbative case, we obtain that $\gamma = 1 + O(\varepsilon )$ and that the function G in (37) satisfies $G - F = O(\varepsilon )$; also the change of variables between $(x,x')$ and $(y, y')$ is $O(\varepsilon )$ close to the identity.

Our treatment shows that models with average dissipation should involve also a change of variables and a modification of the forces.

Appendix B. Taylor’s integration methods

Taylor’s method is one of the most common numerical integration techniques of an initial value problem of an ordinary differential equation of the form

$$\begin{aligned} \begin{aligned} \dot{z}&= F(z,t), \\ z(t _0)&= z _0\ . \end{aligned} \end{aligned}$$

(39)

The Taylor’s method is competitive, in speed and accuracy, with respect to other standards methods. The main drawback is that the Taylor’s method is an explicit method, so it has all limitations of these kind of schemes; for example, it is non-appropriate for stiff systems.

The idea behind the Taylor’s method is very simple. Given the initial condition $z (t _0) = z _0$, the value $z (t _1)$, with $t _1 = t _0 + h$, is approximated by the Taylor series of z(t) at $t = t _0$. The Taylor series is truncated up to an order, say N, to try to ensure the absolute/relative tolerances requested during the numerical integration. Therefore, to get the solution $z_1$ at time $t=t_1$ from the solution $z_0$ at time $t=t_0$ we consider the expression

$$\begin{aligned} z_1=z_1+z_0^{[1]}h+z_0^{[2]}h^2+ \cdots +z_0^{[N]}h^N\ , \end{aligned}$$

(40)

where $z_0^{[k]}$, $k=1, \dotsc ,N$, represents the normalized derivative at order k computed at $t_0$, i.e.,

$$\begin{aligned} z_0^{[k]}={1\over {k!}}\ {{\mathrm{d}^kz}\over {\mathrm{d}t^k}}(t_0)\ . \end{aligned}$$

Using the coefficients of the Taylor’s expansion in (40), one can estimate the range of h where the Taylor series is valid (up to a tolerance). This fact makes the Taylor’s method suitable for multiprecision arithmetic.

The computation of the derivatives might be a difficult task, which can be lightened by using automatic differentiation (see, for instance, Rall and Corliss 1996; Griewank and Walther 2008), thus providing very efficient implementations of Taylor’s method as illustrated in to which we refer for full details. We recall that automatic differentiation provides a recursive computation of operations on polynomials, which implies the manipulation of formal power series.

We also mention that jet transport (see Appendix F), namely automatic differentiation with respect to initial data and parameters, can be used in Taylor’s method to approximate the high-order variational flow as it has been proved in Gimeno et al. (2021).

Appendix C. Variational equations for the spin–orbit problem

In this section, we provide the formulae for the computation of the variational equations with respect to coordinates and parameters, motivated by the fact that—even if not used in the present paper—they are useful in different contexts, like the parameterization of invariant objects, estimates based on derivatives of the flow, computation of chaos indicators.

1.1 C.1 Variational equations

The variation with respect to the initial conditions of (15) involves the Jacobian whose elements are given by

$$\begin{aligned} \begin{aligned} a _{11}&= 0,&a _{21}&= -2\varepsilon \frac{a}{r(u;e)}c(\beta ;u,e), \\ a _{12}&= 1,&a _{22}&= e\frac{a}{r(u;e)} \sin u - \eta \left( \frac{a}{r(u;e)}\right) ^5 \end{aligned} \end{aligned}$$

(41)

with $c(\beta ;u,e)$ defined in (14).

The variations with respect to the initial conditions for the system (15) or for the system (8) are not the same, although some properties such as the determinant or the eigenvalues of the $2\pi$-time map are preserved. The explicit relation between the two variations is given by

$$\begin{aligned} \begin{aligned} \frac{\partial x}{\partial x _0}(t)&= \frac{\partial \beta }{\partial \beta _0}(u),&\frac{\partial x}{\partial y _0}(t)&= \frac{\partial \beta }{\partial \gamma _0}(u) (1 - e\cos u _0) , \\ \frac{\partial y}{\partial x _0}(t)&= \frac{\partial \gamma }{\partial \beta _0}(u) \frac{1}{1 - e\cos u},&\frac{\partial y}{\partial y _0}(t)&= \frac{\partial \gamma }{\partial \gamma _0}(u) \frac{1 -e\cos u _0}{1 - e\cos u}\ , \end{aligned} \end{aligned}$$

(42)

where $(x _0, y _0 ) = (\beta _0, \gamma _0/(1 - e\cos u _0))$. The relation (42) must be interpreted as follows: After the integration of (15) and its first variational equations, which uses the terms in (41), from time $u _0$ to u and with initial condition $(\beta _0, \gamma _0) \in [0, 2\pi ) \times {\mathbb {R}}$, then the variation with respect to the initial condition $(x _0, y _0)$ in (8) from the initial time $t _0 = u _0-e\sin u _0$ to the final time $t = u - e\sin u$ is given by the relations in (42).

Note that (42) is simplified when $u _0 = 0$ and $u = 2\pi$.

1.2 C.2. Variational equations with respect to the parameters

The variational equations with respect to the parameters $\varepsilon$ and $\eta$ of the system (15) are quite straightforward as well as their relations in terms of the variables (x, y). They are given by the following expressions:

$$\begin{aligned} \frac{\partial x}{\partial \bigstar } (t) = \frac{\partial \beta }{\partial \bigstar }(u) \text { and } \frac{\partial y}{\partial \bigstar } (t) = \frac{\partial \gamma }{\partial \bigstar }(u) \frac{a}{r}, \qquad \bigstar \in \{\varepsilon , \eta \}\ . \end{aligned}$$

(43)

However, the case for the parameter $e$ in (15) requires a little bit more of work and its relation with respect to the coordinates (x, y) also involves more terms which we make explicit below:

$$\begin{aligned} \begin{aligned} \frac{\partial x}{\partial e}(t)&= \begin{aligned}&\frac{\partial \beta }{\partial e}(u) - \frac{\partial \beta }{\partial \gamma _0}(u) \frac{\gamma _0 \cos u _0}{1 - e\cos u _0} + \gamma (u)\frac{a}{r} \sin u\\&+ \bigg [\frac{\partial \beta }{\partial u _0}(u) + \frac{\partial \beta }{\partial \gamma _0}(u) \frac{\gamma _0 e\sin u _0}{1 - e\cos u _0}\biggr ]\frac{\sin u _0}{1 - e\cos u _0}\ , \end{aligned} \\ \frac{\partial y}{\partial e}(t)&= \begin{aligned}&\frac{\partial \gamma }{\partial e}(u) \frac{a}{r} + \gamma (u)(\frac{a}{r})^2\cos u - \frac{\partial \gamma }{\partial \gamma _0}(u) \frac{a}{r} \frac{\gamma _0 \cos u _0}{1 - e\cos u _0}\\&+ \biggl [ \frac{\partial \gamma }{\partial u}(u) - \gamma (u) \frac{a}{r}e\sin u \biggr ](\frac{a}{r})^2 \sin u \\&+\biggl [ \frac{\partial \gamma }{\partial u _0}(u) + \frac{\partial \gamma }{\partial \gamma _0}(u) \frac{a}{r} \frac{\gamma _0 e\sin u _0}{1 - e\cos u _0} \biggr ] \frac{\sin u _0}{1 - e\cos u _0}\ . \end{aligned} \end{aligned} \end{aligned}$$

(44)

Note that (44) is simplified when $u _0 = 0$ and $u = 2\pi$.

1.3 C.3. High-order variational equations

In many cases, the first-order variational equations are straightforward and one can explicitly write them down in the numerical integrator. However, high-order variational equations are cumbersome and the use of jet transport becomes highly recommended, see Gimeno et al. (2021). The jet transport is also useful in the study of other structures such as stable manifolds (which will not be considered here).

Jet transport uses automatic differentiation (see Griewank and Walther 2008), which manipulates multivariate polynomials to carry out the truncated Taylor’s approximation containing (in the case of jet transport) the higher-order variational flow, see Gimeno et al. (2021) for a precise formulation. We also refer to Appendix B for a discussion of a polynomial manipulator up to degree 2.

In the case of the spin–orbit problem given by (15), the polynomial manipulator must at least contain the sum, product, sine, cosine, and power operations. All of them have explicit recurrence expressions (Knuth et al. 1997; Haro et al. 2016). By the use of the polynomial manipulator, expressions such as (44) for higher orders are automatically obtained.

Appendix D. Different models of computer arithmetic

Algorithm 5.4 can be implemented with multiprecision arithmetic. The idea is that there are different models of computer arithmetic implementation. It is very easy to switch between different models using features of modern languages such as overloading.

We recall that computers deal only with representable numbers, which are just a (finite) subset of the real numbers and whose elements have the form

$$\begin{aligned} \pm m \cdot \beta ^{e-t}\ , \end{aligned}$$

(45)

where $m \in [0, \beta ^{t}-1]$ is an integer called mantissa, $\beta$ is the base or radix (typically $\beta = 2$), t is a positive integer denoting the precision, and $s\in [s_{min}, s_{max}]$ is also an integer called the exponent. Typical values in the double precision arithmetic following the IEEE 754 standard² are $\beta = 2$, $t=53$, $s _{min} = -1021$, and $s _{max} = 1024$.

Performing arithmetic operations on representable numbers very often yields numbers that are not representable. Sometimes, the results are in the middle of representable numbers, and then, one assigns the result to one of the neighboring numbers. This is called rounding. There are several rules that are in common use: rounding to nearest, rounding down, rounding up, rounding toward zero, rounding away to zero. There are operations that yield a number that is far from any representable number (e.g., adding the largest representable number to itself). One usually represents those as Inf. Of course, one needs to have rules on how to deal with Inf (e.g., does one distinguish between positive/negative infinity). Finally, there operations that do not make sense, such as division by zero.

In the IEEE 754 standard, it is specified that there is a so-called control word. The bits of the control word specify the rounding modes and how to treat infinity.

Finally, we just note that, when the result of two numbers is very close to zero, rounding leads to a great loss of precision. IEEE 754 has introduced also the denormalized numbers which make the gaps near zero smaller, even if they require specialized rules to be handled.

We also note that the IEEE 754 standard specifies the calculations of some transcendental functions subject to the same rules of rounding.

Nowadays, the IEEE 754 standard is implemented in hardware. Both in CPUs and in many GPUs, many important libraries (BLAS/ATLAS, FFTW3) take advantage of the availability of hardware and obtain advantages in speed. Having very reliable rounding modes that satisfy identities allows to improve also the accuracy. For example, there are algorithms that sum a sequence of numbers with a round-off error independent of the length of the sequence to be summed. One can also use interval arithmetic that provides rigorous estimates of the arithmetic operations.

Nowadays, there exist libraries that provide the same capabilities indicated above (representable numbers of the standard form, rounding modes, etc.), but with a number of digits that can be selected at run time, for example, MPFR Fousse et al. (2007) (which is the one we have used) or some other.

Using modern programming techniques such as overloading, it is not difficult to write versions of our programs for the arithmetic using the hardware or in MPFR and select the precision.

It is important to remark that in a parallel scenario, one must be sure that the global variables used in these libraries are initialized in each of the different threads. In particular, in the MPFR case, one needs to initialize the precision and the rounding for each of the threads; otherwise, the output will differ from the non-parallel version.

Appendix E. Link between the parameterization of a torus using maps or flows

As indicated in Sect. 1.2, the calculation of a torus in a time section is more efficient than computing the torus in the whole flow of the differential equation since it needs less storage and it reduces the problem in one dimension.

However, for some applications the torus for flows is needed. In such cases, we can reconstruct the torus for flows using the torus that was computed for maps. Another option is computing directly the torus for flows with a specific algorithm, such as the one in Calleja et al. (2013a) for symplectic flows.

If one wants to compute directly the torus for flows without using the one computed for maps, it will be, in general, more computationally challenging since it introduces another layer of discretization and therefore a new error source. In the spin–orbit case (8), the differential equation is periodic, and to provide a general recipe for time-periodic conformally symplectic systems, we can consider a parameter family of ODEs with time-periodic vector field of period T, that is, $X _\mu :{\mathbb {R}}^{2n} \times (T\cdot {\mathbb {T}}) \rightarrow {\mathbb {R}}^{2n}$ such that

$$\begin{aligned} \dot{x} = X_\mu (x,t) \ , \end{aligned}$$

(46)

and for all x and t, $X_\mu (x, t + T) = X_\mu (x,t)$.

A parameterization of a torus by the flow of (46) requires to seek a drift parameter $\mu$ and an embedding $W:{\mathbb {T}}^n\times (T \cdot {\mathbb {T}}) \rightarrow {\mathbb {R}}^{2n}$ (in our case $n = 1$) in such a way that for a fixed $\theta _0 \in {\mathbb {T}}$, related to the initial integration time, $W( \theta _0 + \frac{1}{T} \omega t, t)$ is a solution of (46), namely

$$\begin{aligned} \left( (1/T)\omega \partial _\theta + \partial _t \right) W( \theta , t) = X_\mu ( W(\theta ,t), t)\ . \end{aligned}$$

(47)

Equation (47) is called invariance equation of the torus for conformally symplectic flows, and it is the equation that the algorithm in Calleja et al. (2013a) addresses taking advantage of the conformally symplectic structure.

On the other hand, W can be reconstructed in terms of the computed torus for maps by taking a point in the torus and propagating the flow with respect to time. These trajectories give the torus for flows.

More explicitly, recall that Algorithm 5.4, which is based on the one in Calleja et al. (2013a), produces $K:{\mathbb {T}}^n \rightarrow {\mathbb {R}}^{2n}$ and $\mu$ in such a way that $F_\mu \circ K(\theta ) = K(\theta + \omega )$. Here, $F_\mu$ denotes the map that, given initial conditions at time $t=0$, associates the value of the solution of (46) at time $t=T$. The general recipe to produce W and $\mu$ out of the results of Algorithm 5.4 consists in:

• Set the computed drift parameter $\mu$ for the flow case as well.

• Set

  $$\begin{aligned} W(\theta , t ) = \Phi _t( K(\theta - (1/T) \omega t ) )\ , \end{aligned}$$

  where $\Phi _t$ is the map that gives the time t solution of (46) from the initial at time $t=0$. Note that since the equation is non-autonomous, the initial time matters.

Then, we have that

$$\begin{aligned} \partial _t W(\theta , t )= & {} \frac{\partial }{\partial t } \Phi _{t} ( K(\theta - (1/T) \omega t) ) \nonumber \\= & {} X_\mu ( K(\theta - (1/T) \omega t), t) - (1/T) \omega \partial _\theta W(\theta , t)\ . \end{aligned}$$

(48)

Hence, moving to the other side, we obtain that W satisfies the differential Eq. (47). Furthermore, the embedding W is periodic of period T in the t variable. We have $W(\theta ,0) = \Phi _0( K(\theta ) ) = K(\theta )$ and, because of the invariance equation satisfied by K, we also have that $W(\theta , T) = \Phi _T( K(\theta - \omega ) ) = K(\theta )$.

In practice, once we have K, we can construct the W satisfying (48) by integrating the initial conditions in a grid of points in $\theta$. Note that the calculation is easily parallelizable. The integrations corresponding to each initial condition can be associated with a thread. (Other more sophisticated parallelization methods are also possible, of course.)

In the case of the spin–orbit problem, we can be more explicit, taking into account the explicit formulas for the time dependence. That is, the drift parameter now is the eccentricity $e$, we use the Kepler’s relation t(u) in (2), and the conjugacy flow is defined by

$$\begin{aligned} \Psi _e(u) = 2 \pi \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 - e\cos u \end{pmatrix} \ , \end{aligned}$$

that at $u = 2\pi$ coincides with $\Psi _e$ in (23). Then, we end up to the invariance equation

$$\begin{aligned} \Phi _{t(u)} (\Psi _e(0) W(\theta ; 0)) = \Psi _e(u) W (\theta + \omega t(u) / (2\pi ); t(u)), \quad \forall \, u \in 2\pi {\mathbb {T}}\text { and } \theta \in {\mathbb {T}}\ . \end{aligned}$$

The idea is that $W(\theta , t)$ is in the variable $(x,y)/(2\pi )$, then by the conjugacy we change to $(\beta , \gamma )$ to integrate the flow in the variable u, and finally, we go back to the variable t where the $\omega$ has a physical interpretation.

Appendix F. A goodness test for jet transport

Let $\dot{x} = f(t,x)$ an ODE in ${\mathbb {R}}^d$ with flow denoted by $\varphi (t; x)$. The test consists in running three integrations with two different integrators.

First, we run $x _0 + s$ with an integrator with jet transport of order, say N, up to a time, say 1. The output is the jet y(s) of order N.

Second, we choose a unitary vector v and a scalar h (typically small, say $h=10^{-7}$), and we define the quantity

$$\begin{aligned} c _h = \Vert y(h) - \varphi (1; x _0 + hv) \Vert \ , \end{aligned}$$

which is expected to behave as $c _h \approx c h ^{N+1}$ for some $c > 0$.

The third and last run is to repeat the second one, but now with h/2 to get the quantity $c _{h/2}$.

Finally, it must happen that

$$\begin{aligned} \frac{c _h}{c _{h/2}} \approx 2 ^{N+1}. \end{aligned}$$

(49)

Therefore, the test is successful when $\log _2(c _{h}/c _{h/2}) \approx N+1$, being N the order of jets in the first integration.

Notice that (49) may suffer loss of precision if h is too small. Therefore, one needs to choose a suitable h by systematically trying several choices.