On the Geometry of Discrete Contact Mechanics

Abstract

In this paper, we continue the construction of variational integrators adapted to contact geometry started in Vermeeren et al. (J Phys A 52(44):445206, 2019), in particular, we introduce a discrete Herglotz Principle and the corresponding discrete Herglotz Equations for a discrete Lagrangian in the contact setting. This allows us to develop convenient numerical integrators for contact Lagrangian systems that are conformally contact by construction. The existence of an exact Lagrangian function is also discussed.

1 Introduction

Contact Hamiltonian and Lagrangian systems have deserved a lot of attention in recent years Bravetti (2017, 2018) or de León and Lainz Valcázar (2019b). One of the most relevant features of contact dynamics is the absence of conservative properties contrarily to the conservative character of the energy in symplectic dynamics; indeed, we have a dissipative behavior. This fact suggests that contact geometry may be the appropriate framework to model many physical and mathematical problems with dissipation we find in thermodynamics, statistical physics, quantum mechanics (Ciaglia et al. 2018), gravity or control theory, among many others. Consequently, it becomes an important necessity to develop numerical methods adapted to the contact setting for applications in the above mentioned subjects. The idea is to develop geometric integrators, that is, numerical methods for differential equations which preserve geometric properties like contact structure, symmetries, configuration space. This preservation of structural properties is often desirable to achieve correct qualitative behavior and long time stability (Hairer et al. 2010; Sanz-Serna and Calvo 1994; Blanes and Casas 2016).

As far as we know, the first attempt to develop geometric integrators for the contact case is in the paper (Vermeeren et al. 2019) (see also Bravetti et al. 2020), where the authors present geometric numerical integrators for contact flows that stem from a discretization of Herglotz variational principle.

Our goal in the current paper is to go further in the discrete description of contact dynamics, so we will mention some of the new and relevant results that the reader can find in the next pages. Instead of deriving the discrete Herglotz equations by an heuristic argument, they are directly obtained from a clear discrete variational principle. In addition, to develop the discrete algorithm we use the natural discretization $Q \times Q \times {\mathbb {R}}$, which preserves all the contact geometry flavor.

Another relevant point is the discussion of the existence of an exact discrete Lagrangian function (Marsden and West 2001; Patrick and Cuell 2009), which will lead us to define the contact exponential map and prove its existence. This construction is essential to develop a complete theory of variational error analysis for contact Lagrangian systems.

Finally, we consider a discrete version of the infinitesimal symmetries discussed in de León and Valcázar (2020) and Gaset et al. (2020), jointly with the corresponding dissipated quantities.

The paper is structured as follows. Section 2 is devoted to a quick review of contact Hamiltonian and Lagrangian systems in the continuous setting. In particular, we recall the Herglotz variational principle, since it will be the motivation to develop the corresponding discrete version. Section 3 is devoted to construct the discrete version of contact Lagrangian dynamics for a discrete Lagrangian $L_d : Q \times Q \times {\mathbb {R}} \rightarrow {\mathbb {R}}$, where Q is the configuration manifold. We consider the discrete Herglotz principle to obtain the so-called discrete Herglotz equations. The Legendre transformations $F^{-}L_d$ and $F^{+}L_d$ are defined, and consequently the discrete flow (at the Lagrangian and Hamiltonian levels); the main result is that the discrete flow is a conformal contactomorphism. In Sect. 4 we define the contact exponential map for the Herglotz vector field and prove that it is a local diffeomorphism. This result permits to study the existence of an exact Lagrangian function. Finally, we consider several examples to illustrate our theoretical developments.

2 Continuous Contact Mechanics

2.1 Contact Manifolds and Hamiltonian Systems

In this section we will recall the main definitions and results on the theory of contact manifolds and Hamiltonian system. See de León and Lainz Valcázar (2019a) for a more detailed overview.

A contact manifold $(M,\eta )$ is an $(2n+1)$-dimensional manifold with a contact form $\eta$ (Libermann and Marle 1987). That is, $\eta$ is a 1-form on M such that $\eta \wedge {\mathrm {d}}\eta ^n$ is a volume form. This type of manifolds have a distinguished vector field: the so-called Reeb vector field ${\mathcal {R}}$, which is the unique vector field that satisfies:

$$\begin{aligned} i_{{\mathcal {R}}} {\mathrm {d}}\eta = 0, \quad \eta ({\mathcal {R}})=1. \end{aligned}$$

(1)

On a contact manifold $(M,\eta )$, we define the following isomorphism of vector bundles:

$$\begin{aligned} \begin{aligned} \flat : \quad&TM\longrightarrow & {} T^* M,\\&\quad v\longmapsto & {} i_{v}{\mathrm {d}}\eta + \eta (v)\eta . \end{aligned} \end{aligned}$$

(2)

Notice that $\flat ({\mathcal {R}}) = \eta$.

There is a Darboux theorem for contact manifolds. In a neighborhood of each point in M one can find local coordinates $(q^i, p_i, z)$ such that

$$\begin{aligned} \eta = {\mathrm {d}}z - p_i {\mathrm {d}}q^i. \end{aligned}$$

(3)

In these coordinates, we have

$$\begin{aligned} {\mathcal {R}}= \frac{\partial }{\partial z}. \end{aligned}$$

(4)

An example of a contact manifold is $T^*Q\times {\mathbb {R}}$. Here, the contact form is given by

$$\begin{aligned} \eta _Q = {\mathrm {d}}z - \theta _Q = {\mathrm {d}}z - p_i {\mathrm {d}}q^i, \end{aligned}$$

(5)

where $\theta _Q$ is pullback the tautological 1-form of $T^*Q$, $(q^i,p_i)$ are natural coordinates on $T^*Q$ and z is the ${\mathbb {R}}$-coordinate.

We say that a (local) diffeomorphism between two contact manifolds $F:(M,\eta ) \rightarrow (N,\tau )$ is a (local) contactomorphism if $F^* \tau = \eta$. We say that F is a (local) conformal contactomorphism if $F^* \ker \tau = \ker \eta$ or, equivalently, $F^* \tau = \sigma \eta$, where $\sigma : M \rightarrow {\mathbb {R}}\setminus \{0\}$ is the conformal factor.

We say that a vector field X on M is an infinitesimal (conformal) contactomorphism if its flow $F_t$ consists of (conformal) contactomorphisms.

From the general identity, where $F_t$ is a flow and X is its infinitesimal generator

$$\begin{aligned} \frac{\partial }{\partial t} F_t^* \eta = F_t^* {\mathcal {L}}_{X} \eta , \end{aligned}$$

(6)

we deduce that X is an infinitesimal contactomorphism if and only if

$$\begin{aligned} {\mathcal {L}}_{X} \eta = 0. \end{aligned}$$

(7)

Furthermore, X is a conformal contactomorphism if and only if

$$\begin{aligned} {\mathcal {L}}_{X} \eta = a \eta , \end{aligned}$$

(8)

for some $a:M\rightarrow {\mathbb {R}}$. The function a is related to the conformal factors $\sigma _t$ of the conformal contactomorphisms $F_t$ by

$$\begin{aligned} \sigma _t (x)= \exp \left( \int _0^t a(F_\tau (x)) {\mathrm {d}}\tau \right) . \end{aligned}$$

(9)

Given a smooth function $f:M\rightarrow {\mathbb {R}}$, its Hamiltonian vector field $X_f$ is given by

$$\begin{aligned} \flat (X_f) = {\mathrm {d}}f - (f + {\mathcal {R}}(f)) \eta . \end{aligned}$$

(10)

A vector field X is the Hamiltonian vector field of some function f if and only if it is an infinitesimal conformal contactomorphism. In that case $X=X_f$ for $f = - \eta (X)$. Moreover, ${\mathcal {L}}_{X} \eta = - {\mathcal {R}}(f) \eta$. Hence X is an infinitesimal contactomorphism if and only if $X = X_f$ for some function f such that ${\mathcal {R}}(f) = 0$.

We call the triple $(M, \eta , H)$ a contact Hamiltonian system, where $(M,\eta )$ is a contact manifold and $H:M \rightarrow {\mathbb {R}}$ is the Hamiltonian function.

In contrast to their symplectic counterpart, contact Hamiltonian vector fields do not preserve the Hamiltonian. In fact

$$\begin{aligned} X_H(H) = -{\mathcal {R}}(H) H. \end{aligned}$$

(11)

2.2 Contact Lagrangian systems

Now we review the Lagrangian picture of contact systems. In de León and Lainz Valcázar (2019b) we give a more comprehensive description which also covers the case of singular Lagrangians.

Let Q be an n-dimensional configuration manifold and consider the extended phase space $TQ \times {\mathbb {R}}$ and a Lagrangian function $L:TQ\times {\mathbb {R}}\rightarrow {\mathbb {R}}$. In this paper, we will assume that the Lagrangian is regular, that is, the Hessian matrix with respect to the velocities $(W_{ij})$ is regular where

$$\begin{aligned} W_{ij} = \frac{\partial ^2 L}{\partial {\dot{q}}^i \partial {\dot{q}}^j }, \end{aligned}$$

(12)

and $(q^i, {\dot{q}}^i,z)$ are bundle coordinates for $TQ \times {\mathbb {R}}$. Equivalently, L is regular if and only if the one-form

$$\begin{aligned} \eta _L = {\mathrm {d}}z - \theta _L \end{aligned}$$

(13)

is a contact form. Here,

$$\begin{aligned} \theta _L&= S^* ({\mathrm {d}}L) = \frac{\partial L}{\partial \dot{q}^i} {\mathrm {d}}{q}^i, \end{aligned}$$

(14)

where S is the canonical vertical endomorphism $S:TTQ \rightarrow TTQ$ extended to $TQ \times {\mathbb {R}}$, that is, in local $TQ \times {\mathbb {R}}$ bundle coordinates,

$$\begin{aligned} S = {\mathrm {d}}q^i \otimes \frac{\partial }{\partial {\dot{q}}^i}. \end{aligned}$$

(15)

The energy of the system is defined by

$$\begin{aligned} E_L = \Delta (L) - L = {\dot{q}}^i \frac{\partial L}{\partial {\dot{q}}^i} - L, \end{aligned}$$

(16)

where $\Delta$ is the Liouville vector field on TQ extended to $TQ\times {\mathbb {R}}$ in the natural way.

The Reeb vector field of $\eta _L$, which we will denoted by ${\mathcal {R}}_L$ is given by

$$\begin{aligned} {\mathcal {R}}_L = \frac{\partial }{\partial z} - (W^{ij}) \frac{\partial ^2 L}{\partial {\dot{q}}^i \partial z} \frac{\partial }{\partial {\dot{q}}^j}, \end{aligned}$$

(17)

where $(W^{ij})$ is the inverse of the Hessian matrix with respect to the velocities $(W_{ij})$ (Eq. (12)).

The Hamiltonian vector field of the energy $E_L$ will be denoted $\xi _L = X_{E_L}$, hence

$$\begin{aligned} \flat _L(\xi _L) = {\mathrm {d}}E_L - ({\mathcal {R}}_L(E_L)+E_L)\eta _L, \end{aligned}$$

(18)

where $\flat _L(v) = i_{v} {\mathrm {d}}\eta _L + \eta _L (v) \eta _L$ is the isomorphism defined in Eq. (17) for this particular contact structure.

$\xi _L$ is a second-order differential equation (SODE) (that is, $S(\xi _L) = \Delta$) and its solutions are just the ones of the Herglotz equations (also called generalized Euler–Lagrange equations) for L (see de León and Lainz Valcázar 2019b):

$$\begin{aligned} \frac{{\mathrm {d}}}{{\mathrm {d}}t} \left( {\frac{\partial L}{\partial {\dot{q}}^i}}\right) - \frac{\partial L}{\partial q^i} = \frac{\partial L}{\partial {\dot{q}}^i} \frac{\partial L}{\partial z}. \end{aligned}$$

(19)

There exists a Legendre transformation for contact Lagrangian systems. Given the vector bundle $TQ\times {\mathbb {R}}\rightarrow Q \times {\mathbb {R}}$, one can consider the fiber derivative ${\mathbb {F}}L$ of $L:TQ \times {\mathbb {R}}\rightarrow {\mathbb {R}}$, which has the following coordinate expression in natural coordinates:

$$\begin{aligned} \begin{aligned} {\mathbb {F}}L:TQ \times {\mathbb {R}}&\rightarrow T^*Q \times {\mathbb {R}}\\ (q^i,{\dot{q}}^i,z)&\mapsto \left( q^i, \frac{\partial L}{\partial {\dot{q}}^i},z\right) . \end{aligned} \end{aligned}$$

(20)

If we consider the contact structure $\eta _Q$ (5) on $T^*Q \times {\mathbb {R}}$, and $\eta _L$ on $TQ\times {\mathbb {R}}$ then ${\mathbb {F}}L$ is a local contactomorphism.

In the case that ${\mathbb {F}}L$ is a global contactomorphism, then we say that L is hyperregular. In this situation, we can define a Hamiltonian $H:T^*Q\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ such that $E_L = H \circ {\mathbb {F}}L$ and the Lagrangian and Hamiltonian dynamics are ${\mathbb {F}}L$-related, that is, ${\mathbb {F}}L_* \xi _L = X_H$.

2.2.1 Herglotz Variational Principle

Equations (19) can be derived from a modified variational principle (Herglotz 1930). In contrast to the symplectic case, the action is not a definite integral. The contact action is the value at the endpoint of solution to a non-autonomous ODE.

In de León and Lainz Valcázar (2019b) we defined the action on the space of curves with fixed endpoints. However, for our purposes here it is more convenient to define the action on the space of all curves and all initial conditions and then restrict it to the appropriate submanifold.

Let $\Omega$ be the (infinite dimensional) manifold of curves on Q, $c:[0,1]\rightarrow Q$. We denote by $\Omega (q_0, q_1) \subseteq \Omega$, where $q_0,q_1 \in Q$, the submanifold whose elements are the smooth curves $c \in \Omega$ such that $c(0)=q_0$, $c(1)=q_1$. The tangent space of $\Omega$ at a curve c is given by vector fields over c. In the case of $T_c \Omega (q_0,q_1)$, the vector fields over c vanish a the endpoints. That is,

$$\begin{aligned} T_c \Omega&= \{ \delta v \in {\mathcal {C}}^\infty ([0,1] \rightarrow TQ) \mid \tau _Q \circ \delta v = c\}, \end{aligned}$$

(21)

$$\begin{aligned} T_c \Omega (q_0,q_1)&= \{ \delta c \in T_c \Omega \mid \delta c(0)=0, \, \delta c(1)=0 \}. \end{aligned}$$

(22)

We define the operator

$$\begin{aligned} {\mathcal {Z}}:\Omega \times {\mathbb {R}}\rightarrow {\mathcal {C}}^\infty ([0,1] \rightarrow {\mathbb {R}}), \end{aligned}$$

(23)

which assigns to each curve and initial condition $(c,z_0)$ the curve ${\mathcal {Z}}_{z_0}(c)$ that solves the following ODE:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{{\mathrm {d}}{\mathcal {Z}}_{z_0}(c)}{{\mathrm {d}}t} &{}= L(c, {\dot{c}}, {\mathcal {Z}}_{z_0}(c)),\\ {\mathcal {Z}}_{z_0}(c)(0) &{}= z_0. \end{array}\right. \end{aligned}$$

(24)

Now we define the contact action functional as the map which assigns to each curve c and initial condition $z_0$, the solution to the previous ODE evaluated at the endpoint:

$$\begin{aligned} \begin{aligned} {\mathcal {A}}: \Omega \times {\mathbb {R}}&\rightarrow {\mathbb {R}},\\ (c,z_0)&\mapsto {\mathcal {Z}}_{z_0}(c)(1). \end{aligned} \end{aligned}$$

(25)

When restricted to $\Omega (q_0,q_1)\times \{z_0\}$, the critical points of ${\mathcal {A}}$ are the solutions to Herglotz equation. More precisely,

Theorem 2.1

(Herglotz variational principle) Let $L: TQ \times {\mathbb {R}}\rightarrow {\mathbb {R}}$ be a Lagrangian function and let $c\in \Omega (q_0, q_1)$ and $z_0 \in {\mathbb {R}}$. Then, $(c,{\dot{c}}, {\mathcal {Z}}_{z_0}(c))$ satisfies the Herglotz equations (19) if and only if c is a critical point of ${\mathcal {A}}_{z_0}\vert _{\Omega (q_0, q_1)}$.

Although it is not strictly necessary for this proof we will compute $T{\mathcal {Z}}$ in order to compare with the discrete case. The variational principle follows from the expression of $T_{\delta c} {\mathcal {A}}_{z_0} = T_{\delta c} {\mathcal {Z}}_{z_0} (1)$.

Lemma 2.2

The tangent map to the operator ${\mathcal {Z}}$ defined in (24) is given by

$$\begin{aligned} \begin{aligned}&T_{(c, z_0)} {\mathcal {Z}} (\delta c, {\dot{z}})(t) = \frac{{\dot{z}}}{\sigma (t)} + \delta {c}^i(t) \frac{\partial L}{\partial {\dot{q}}^i}(\chi (t)) \\&\quad + \frac{1}{\sigma (t)} \int _0^t {\delta c} ^i(\tau ) \sigma (\tau ) \left( \frac{\partial L}{\partial q^i}(\chi (\tau )) - \frac{{\mathrm {d}}}{{\mathrm {d}}\tau } \frac{\partial L}{\partial {\dot{q}}^i}(\chi (\tau ))+ \frac{\partial L}{\partial {\dot{q}}^i}(\chi (\tau )) \frac{\partial L}{\partial z}(\chi (\tau )) \right) {\mathrm {d}}\tau , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \sigma (t) = \exp \left( {-\int _0^t \frac{\partial L}{\partial z}(\chi (\tau )) {\mathrm {d}}\tau }\right) > 0. \end{aligned}$$

(26)

Proof

Let $c \in \Omega (q_0, q_1)$ be a curve and consider some tangent vector $\delta c \in T_c \Omega$. We will first compute the partial derivative with respect to c by fixing $z_0\in {\mathbb {R}}$, and then we will fix the curve and compute the partial derivative with respect to the initial condition $z_0$. In order to simplify the notation, let $\chi =(c,{\dot{c}}, {\mathcal {Z}}_{z_0}(c))$ and put $\psi = T_c {\mathcal {Z}}_{z_0}(\delta c)$.

Consider a curve $c_\lambda \in \Omega$ (that is, a smoothly parametrized family of curves) such that

$$\begin{aligned} \delta c={\frac{{\mathrm {d}}c_\lambda }{{\mathrm {d}}\lambda }}\Big \vert _{\lambda =0} \end{aligned}$$

Since ${\mathcal {Z}}_{z_0}(c_\lambda )(0)=z_0$ for all $\lambda$, then $\psi (0)=0$.

We compute the derivative of $\psi$ by interchanging the order of the derivatives using the ODE defining ${\mathcal {Z}}$:

$$\begin{aligned} {\dot{\psi }}(t)&= {\frac{{\mathrm {d}}}{{\mathrm {d}}\lambda }\frac{{\mathrm {d}}}{{\mathrm {d}}t} {\mathcal {Z}}_{z_0}(c_\lambda (t))}\vert _{\lambda =0} \\&= \frac{{\mathrm {d}}}{{\mathrm {d}}\lambda }{L(c_\lambda (t), {\dot{c}}_\lambda (t),{\mathcal {Z}}(c_\lambda )(t))}\vert _{\lambda =0} \\&= \frac{\partial L}{\partial q^i}(\chi (t)) {\delta c} ^i(t) + \frac{\partial L}{\partial {\dot{q}}^i}(\chi (t)) {\delta {\dot{c}}}^i(t) + \frac{\partial L}{\partial z}(\chi (t)) \psi (t). \end{aligned}$$

Hence, the function $\psi$ is the solution to the ODE above. Using that $\psi (0)=0$, we can solve the Cauchy problem and obtain

$$\begin{aligned} \psi (t) = \frac{1}{\sigma (t)} \int _0^t \sigma (\tau ) \left( { \frac{\partial L}{\partial q^i}(\chi (\tau )) {\delta c} ^i(\tau ) + \frac{\partial L}{\partial {\dot{q}}^i}(\chi (\tau )) {\delta {\dot{c}}}^i(\tau ) } \right) {\mathrm {d}}\tau , \end{aligned}$$

(27)

where

$$\begin{aligned} \sigma (t) = \exp \left( {-\int _0^t \frac{\partial L}{\partial z}(\chi (\tau )) {\mathrm {d}}\tau }\right) > 0. \end{aligned}$$

(28)

Integrating by parts we get the following expression

$$\begin{aligned} \begin{aligned} \psi (t)&= \delta {c}^i(t) \frac{\partial L}{\partial {\dot{q}}^i}(\chi (t)) \\&\quad + \frac{1}{\sigma (t)} \int _0^t {\delta c}^i (\tau ) \left( \sigma (\tau ) \frac{\partial L}{\partial q^i}(\chi (\tau )) - \frac{{\mathrm {d}}}{{\mathrm {d}}\tau } \left( \sigma (\tau )\frac{\partial L}{\partial {\dot{q}}^i}(\chi (\tau ))\right) \right) {\mathrm {d}}\tau \\&= \delta {c}^i(t) \frac{\partial L}{\partial {\dot{q}}^i}(\chi (t)) \\&\quad + \frac{1}{\sigma (t)} \int _0^t {\delta c} ^i(\tau ) \sigma (\tau ) \left( \frac{\partial L}{\partial q^i}(\chi (\tau )) - \frac{{\mathrm {d}}}{{\mathrm {d}}\tau } \frac{\partial L}{\partial {\dot{q}}^i}(\chi (\tau )) \right. \\&\quad \left. + \frac{\partial L}{\partial {\dot{q}}^i}(\chi (\tau )) \frac{\partial L}{\partial z}(\chi (\tau )) \right) {\mathrm {d}}\tau . \end{aligned} \end{aligned}$$

Now we compute the partial derivative with respect to the initial condition $z_0$. We interchange the order of the derivatives

$$\begin{aligned} \frac{{\mathrm {d}}}{{\mathrm {d}}t} \frac{\partial {\mathcal {Z}}_{z_0}(c)}{\partial z_0} = \frac{\partial L}{\partial z} (c,{\dot{c}}, {\mathcal {Z}}(c)) \frac{\partial {\mathcal {Z}}_{z_0}(c)}{\partial z_0} \end{aligned}$$

(29)

If we solve for $\frac{\partial {\mathcal {Z}}_{z_0}(c)}{\partial z_0}$ the ODE above using that $\frac{\partial {\mathcal {Z}}_{z_0}(c)}{\partial z_0}(0)=1$, we notice that

$$\begin{aligned} \frac{\partial {\mathcal {Z}}_{z_0}(c)}{\partial z_0}(t) = \exp \left( {\int _0^t \frac{\partial L}{\partial z}(\chi (\tau )) {\mathrm {d}}\tau }\right) = \frac{1}{\sigma (t)} , \end{aligned}$$

(30)

where $\sigma$ is defined in (26). $\square$

2.2.2 Symmetries and Dissipated Quantities on Contact Lagrangian Systems

As explained in Gaset et al. (2020) and de León and Valcázar (2020), given a symmetry on a contact system, one does not obtain a conserved quantity, but a quantity f that dissipates at the same rate as the Hamiltonian.

Given a contact Hamiltonian system $(M,\eta , H)$, we say that a quantity $f:M\rightarrow {\mathbb {R}}$ is dissipated if

$$\begin{aligned} {\mathcal {L}}_{X_H} f = -{\mathcal {R}}(H) f, \end{aligned}$$

(31)

or, equivalently,

$$\begin{aligned} {\phi _t}^*(f) = \sigma _t, \end{aligned}$$

(32)

where $\phi$ is the flow of $X_H$ and $\sigma _t$, its conformal factor.

Notice that the quotient of two dissipated quantities (if it is well defined) is a conserved quantity.

We end this section by stating a Noether theorem in this setting, which provides a link between symmetries of the Lagrangian and conserved quantities.

Let $L:TQ \times {\mathbb {R}}\rightarrow {\mathbb {R}}$ be a regular Lagrangian. Let G be a Lie group acting on Q

$$\begin{aligned} \Phi : G\times Q \rightarrow Q. \end{aligned}$$

(33)

We defined the lifted action as

$$\begin{aligned} {\tilde{\Phi }}: G\times TQ\times {\mathbb {R}}\rightarrow TQ\times {\mathbb {R}}, \end{aligned}$$

(34)

given by ${\tilde{\Phi }}(g, v_q, z) = (T_q\Phi (v_q), z)$ where $v_q\in T_qQ$. We denote by $\xi _{TQ\times {\mathbb {R}}}$ to the vector field on $TQ\times {\mathbb {R}}$ which is the infinitesimal generator by the lifted action of an element $\xi$ of the Lie algebra ${\mathfrak {g}}$ of G.

We define the momentum map $J_L$:

$$\begin{aligned} \begin{aligned} J_L: TQ \times {\mathbb {R}}&\rightarrow {\mathfrak {g}}^*,\\ \langle J_L(v_q,z), \xi \rangle&= - \eta _L(\xi _{TQ \times {\mathbb {R}}}). \end{aligned} \end{aligned}$$

(35)

and we define ${\hat{J}}(\xi ): TQ\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ by ${\hat{J}}(\xi )(v_q, z) =\langle J_L(v_q,z), \xi \rangle$.

Then we have the following (de León and Valcázar 2020, Section 4.1)

Theorem 2.3

Let the lifted action ${\tilde{\Phi }}$ preserve the Lagrangian L, then ${\tilde{\Phi }}$ acts by contactomorphisms on $(TQ\times {\mathbb {R}},\eta _L,E_L)$ and ${\hat{J}}(\xi )$ is a dissipated quantity for every $\xi \in {\mathfrak {g}}$.

3 Discrete Contact Mechanics

In this section, we will extend the approach to discrete mechanics as in Marsden and West (2001) to the case of contact dynamics (see also Vermeeren et al. 2019).

Let $L_{d}:Q\times Q \times {\mathbb {R}}\rightarrow {\mathbb {R}}$ be a discrete Lagrangian function. In our point of view $Q\times Q \times {\mathbb {R}}$ will be the discrete space corresponding to the manifold $TQ\times {\mathbb {R}}$, where continuous contact Lagrangian mechanics takes place. We fix a time-step $h>0$, on which $L_{d}$ depends, though we will omit this explicit dependence.

For each $N \in {\mathbb {N}}$, let us define the discrete path space as the space containing sequences on Q with length $N+1$, i.e.,

$$\begin{aligned} {\mathcal {C}}_{d}^{N}(Q)=\{ (q_{0},q_{1}, \ldots , q_{N} ) | q_{k}\in Q,\ k=0,\ldots , N \}. \end{aligned}$$

The set ${\mathcal {C}}_{d}^{N}(Q)$ is a manifold and it is canonically identified with the product space $Q^{N+1}$.

To each $q_{d}\in {\mathcal {C}}_{d}^{N}(Q)$ and each $z_{0}\in {\mathbb {R}}$ we will associate another sequence $(z_{k})\in {\mathbb {R}}^{N+1}$ defined by

$$\begin{aligned} z_{k+1}-z_{k}=L_{d}(q_{k},q_{k+1},z_{k}), \quad k=0,\ldots , N-1. \end{aligned}$$

(36)

In the sequel, for each $1\leqslant k \leqslant N$, we will denote by ${\mathcal {Z}}_{k}$ the function ${\mathcal {Z}}_{k}:Q \times Q \times {\mathbb {R}}\longrightarrow {\mathbb {R}}$

$$\begin{aligned} {\mathcal {Z}}_{k}(q_{k-1},q_{k},z_{k-1})=z_{k-1}+L_{d}(q_{k-1},q_{k},z_{k-1}). \end{aligned}$$

We define the contact discrete action to be the functional that for each point $q_{d}\in {\mathcal {C}}_{d}^{N}(Q)$ and each real number $z_{0}$ returns as output the real number $z_{N}$ obtained recursively from (36), i.e.,

$$\begin{aligned} \begin{aligned} {\mathcal {A}}_{d}: \ {\mathcal {C}}_{d}^{N}(Q)\times {\mathbb {R}}&\longrightarrow {\mathbb {R}}\\ (q_{d},z_{0})&\mapsto z_{N}. \end{aligned} \end{aligned}$$

(37)

A variation of a sequence $q_{d}\in {\mathcal {C}}_{d}^{N}(Q)$ is a curve ${\widetilde{q}}_{d}:(-\epsilon ,\epsilon )\rightarrow {\mathcal {C}}_{d}^{N}(Q)$ satisfying ${\widetilde{q}}_{d}(0)=q_{d}$. Given such a variation, we will define its infinitesimal variation by

$$\begin{aligned} \delta q_{d} := \left. \frac{{\mathrm {d}}}{{\mathrm {d}}\epsilon }\right| _{\epsilon =0} {\widetilde{q}}_{d}(\epsilon )=(\delta q_{0}, \ldots , \delta q_{N}), \end{aligned}$$

where $\delta q_{k}:=\left. \frac{{\mathrm {d}}}{{\mathrm {d}}\epsilon }\right| _{\epsilon =0} \widetilde{q}_{k} (\epsilon )$.

Proposition 3.1

Let $L_{d}$ be a smooth discrete Lagrangian. Then, if we fix $z_0\in {\mathbb {R}}$, we obtain the functional

$$\begin{aligned} \begin{aligned} {\mathcal {A}}_{d,z_{0}}: \ {\mathcal {C}}_{d}^{N}(Q)&\longrightarrow {\mathbb {R}}\\ q_{d}&\mapsto {\mathcal {A}}_{d}(q_{d},z_{0}). \end{aligned} \end{aligned}$$

The differential of the functional ${\mathcal {A}}_{d,z_{0}}$ is the following

$$\begin{aligned} \begin{aligned} {\mathrm {d}}{\mathcal {A}}_{d,z_{0}}(q_{d})&= \sigma _{N}\cdot \cdot \cdot \sigma _{2}\frac{\partial {\mathcal {Z}}_{1}}{\partial q_{0}}(q_{0},q_{1},z_{0}){\mathrm {d}}q_{0} \\&\quad +\sum _{k=1}^{N-1} \prod _{j=k+2}^{N}\sigma _{j}\cdot \left( \frac{\partial {\mathcal {Z}}_{k+1}}{\partial q_{k}}+\frac{\partial {\mathcal {Z}}_{k+1}}{\partial z_{k}}\frac{\partial {\mathcal {Z}}_{k}}{\partial q_{k}} \right) {\mathrm {d}}q_{k} \\&\quad +\frac{\partial {\mathcal {Z}}_{N}}{\partial q_{N}}(q_{N-1},q_{N},z_{N-1}){\mathrm {d}}q_{N}, \end{aligned} \end{aligned}$$

(38)

where we are using the identification of ${\mathcal {C}}_{d}^{N}(Q)$ with $Q^{N+1}$ and for each $1 \leqslant j\leqslant N$

$$\begin{aligned} \sigma _{j}=\frac{\partial {\mathcal {Z}}_{j}}{\partial z_{j-1}}(q_{j-1},q_{j},z_{j-1}). \end{aligned}$$

Proof

Using the identification of ${\mathcal {C}}_{d}^{N}(Q)$ with $Q^{N+1}$, note that the discrete action may be rewritten as

$$\begin{aligned} {\mathcal {A}}_{d,z_{0}}(q_{d})={\mathcal {Z}}_{N}(q_{N-1},q_{N},{\mathcal {Z}}_{N-1}(q_{N-2},q_{N-1},{\mathcal {Z}}_{N-2}(...{\mathcal {Z}}_{1}(q_{0},q_{1},z_{0})...)). \end{aligned}$$

Using that

$$\begin{aligned} {\mathrm {d}}{\mathcal {A}}_{d,z_{0}}(q_{d})=\frac{\partial {\mathcal {A}}_{d,z_{0}}}{\partial q_{0}} {\mathrm {d}}q_{0}+\sum _{k=1}^{N-1}\frac{\partial {\mathcal {A}}_{d,z_{0}}}{\partial q_{k}} {\mathrm {d}}q_{k}+\frac{\partial {\mathcal {A}}_{d,z_{0}}}{\partial q_{N}} {\mathrm {d}}q_{N}. \end{aligned}$$

and applying the chain rule, we deduce that

$$\begin{aligned} \frac{\partial {\mathcal {A}}_{d,z_{0}}}{\partial q_{0}}=\frac{\partial {\mathcal {Z}}_{N}}{\partial z_{N-1}}\cdot \cdot \cdot \frac{\partial {\mathcal {Z}}_{2}}{\partial z_{1}}\frac{\partial {\mathcal {Z}}_{1}}{\partial q_{0}}, \end{aligned}$$

since the function ${\mathcal {Z}}_{1}$ is the only one that depends on $q_{0}$ among all the N functions ${\mathcal {Z}}_{k}$. It is also clear that

$$\begin{aligned} \frac{\partial {\mathcal {A}}_{d,z_{0}}}{\partial q_{N}}=\frac{\partial {\mathcal {Z}}_{N}}{\partial q_{N}}, \end{aligned}$$

since none of the functions ${\mathcal {Z}}_{k}$ depend on $q_{N}$ except the function ${\mathcal {Z}}_{N}$. Finally if $1\leqslant k \leqslant N-1$ we have that

$$\begin{aligned} \frac{\partial {\mathcal {A}}_{d,z_{0}}}{\partial q_{k}}=\frac{\partial {\mathcal {Z}}_{N}}{\partial z_{N-1}}\cdot \cdot \cdot \frac{\partial {\mathcal {Z}}_{k+2}}{\partial z_{k+1}}\left( \frac{\partial {\mathcal {Z}}_{k+1}}{\partial q_{k}}+\frac{\partial {\mathcal {Z}}_{k+1}}{\partial z_{k}}\frac{\partial {\mathcal {Z}}_{k}}{\partial q_{k}}\right) , \end{aligned}$$

where we applied the chain rule and the fact that the functions ${\mathcal {Z}}_{k+1}$ and ${\mathcal {Z}}_{k}$ are the only ones that depend on $q_{k}$. Hence, we finished the proof. $\square$

Remark 3.2

Let us see the special case $N=2$, where we can directly compute the differential of the action:

Let $L_{d}$ be a smooth discrete Lagrangian. In the case where $N=2$, the differential of the discrete action function satisfies:

$$\begin{aligned} \begin{aligned}&{\mathrm {d}}{\mathcal {A}}_{d,z_{0}} = \left( D_{1}L_{d} (q_{1},q_{2},z_{1})+(1+D_{z}L_{d}(q_{1},q_{2},z_{1}) D_{2}L_{d}(q_{0},q_{1},z_{0}) \right) {\mathrm {d}}q_{1} \\&\quad \ + D_{2}L_{d}(q_{1},q_{2},z_{1}) {\mathrm {d}}q_{2} + (1+D_{z}L_{d}(q_{1},q_{2},z_{1}))D_{1}L_{d}(q_{0},q_{1},z_{0}) {\mathrm {d}}q_{0}. \end{aligned} \end{aligned}$$

(39)

Definition 3.3

(Discrete Herglotz Principle) Given $z_{0}\in {\mathbb {R}}$, a discrete path $q_{d}=(q_{0},\ldots , q_{N})$ in ${\mathcal {C}}_{d}^{N}(Q)$ is said to satisfy the Discrete Herglotz Principle if $q_{d}$ is a critical value of the discrete action functional ${\mathcal {A}}_{d,z_{0}}$ among all paths in ${\mathcal {C}}_{d}^{N}(Q)$ with fixed end points $q_{0},q_{N}$.

We will now obtain as a sufficient and necessary condition for a path to satisfy the discrete Herglotz principle, a set of equations called Discrete Herglotz equations (Vermeeren et al. 2019).

Theorem 3.4

Let $L_{d}$ be a discrete Lagrangian function such that $1+D_{z}L_{d}$ is non-vanishing everywhere. Given $z_{0}\in {\mathbb {R}}$, a discrete path $q_{d}\in {\mathcal {C}}_{d}^{N}(Q)$ satisfies the discrete Herglotz principle if and only if it satisfies

$$\begin{aligned} \begin{aligned}&D_{1}L_{d} (q_{k},q_{k+1},z_{k})+(1+D_{z}L_{d}(q_{k},q_{k+1},z_{k})) D_{2}L_{d}(q_{k-1},q_{k},z_{k-1})=0,\\&z_{k}-z_{k-1}=L_{d}(q_{k-1},q_{k},z_{k-1}), \end{aligned} \end{aligned}$$

(40)

for $k=1,\ldots ,N-1$.

Proof

Let $q_{d}(\epsilon )$ be a variation of $q_{d}\in {\mathcal {C}}_{d}^{N}(Q)$ with fixed end-points $q_{0}$ and $q_{N}$. Then $q_{d}$ is a critical value of the discrete action functional if and only if

$$\begin{aligned} \left. \frac{{\mathrm {d}}}{{\mathrm {d}}\epsilon }\right| _{\epsilon =0}({\mathcal {A}}_{d,z_{0}}(q_{d}(\epsilon )))={\mathrm {d}}{\mathcal {A}}_{d,z_{0}}(\delta q_{d})=0. \end{aligned}$$

By (38) the last expression is equivalent to

$$\begin{aligned} \sum _{k=1}^{N-1} \prod _{j=k+2}^{N} \sigma _{j}\cdot \left( \frac{\partial {\mathcal {Z}}_{k+1}}{\partial q_{k}}+\frac{\partial {\mathcal {Z}}_{k+1}}{\partial z_{k}}\frac{\partial {\mathcal {Z}}_{k}}{\partial q_{k}} \right) \delta q_{k} = 0. \end{aligned}$$

Since the infinitesimal variations $\delta q_{k}$, $1\le k\le N-1$, are arbitrary we deduce

$$\begin{aligned} \prod _{j=k+2}^{N} \sigma _{j}\cdot \left( \frac{\partial {\mathcal {Z}}_{k+1}}{\partial q_{k}}+\frac{\partial {\mathcal {Z}}_{k+1}}{\partial z_{k}}\frac{\partial {\mathcal {Z}}_{k}}{\partial q_{k}} \right) = 0. \end{aligned}$$

Note that,

$$\begin{aligned} \sigma _{j}=\frac{\partial {\mathcal {Z}}_{j}}{\partial z_{j-1}}(q_{j-1},q_{j},z_{j-1})=1+D_{z}L_{d}(q_{j-1},q_{j},z_{j-1}) \end{aligned}$$

is non-vanishing by hypothesis and

$$\begin{aligned} \frac{\partial {\mathcal {Z}}_{k+1}}{\partial q_{k}}+\frac{\partial {\mathcal {Z}}_{k+1}}{\partial z_{k}}\frac{\partial {\mathcal {Z}}_{k}}{\partial q_{k}}= D_{1}L_{d}(q_{k},q_{k+1},z_{k})+\sigma _{k+1}D_{2}L_{d}(q_{k-1},q_{k},z_{k-1}), \end{aligned}$$

from where the result follows. $\square$

Remark 3.5

The discrete principle introduced in Vermeeren et al. (2019) is just the condition

$$\begin{aligned} \frac{\partial {\mathcal {Z}}_{k+1}}{\partial q_{k}}+\frac{\partial {\mathcal {Z}}_{k+1}}{\partial z_{k}}\frac{\partial {\mathcal {Z}}_{k}}{\partial q_{k}}=0, \end{aligned}$$

afer rewriting it in our notation. For discrete Lagrangian functions where $1+D_{z}L_{d}$ is non-vanishing, the condition above is equivalent to the Herglotz discrete principle.

3.1 Discrete Lagrangian Flows and Discrete Legendre Transforms

Given a discrete contact Lagrangian $L_{d}$, if $1+D_{z}L_{d}(q_0,q_1,z_0)$ does not vanish, we can define two maps called discrete Legendre transforms: ${\mathbb {F}}^{\pm }L_{d}:Q \times Q \times {\mathbb {R}}\rightarrow T^{*}Q \times {\mathbb {R}}$

$$\begin{aligned} \begin{aligned}&{\mathbb {F}}^{+}L_{d}(q_0,q_1,z_0)=(q_{1},D_{2}L_{d}(q_0,q_1,z_0),z_{0}+L_d(q_0, q_1, z_0)) \\&{\mathbb {F}}^{-}L_{d}(q_0,q_1,z_0)=\left( q_{0},-\frac{D_{1}L_{d}(q_0,q_1,z_0)}{1+D_{z}L_{d}(q_0,q_1,z_0)},z_{0} \right) . \end{aligned} \end{aligned}$$

(41)

Lemma 3.6

${\mathbb {F}}^{+}L_{d}$ is a local diffeomorphism if and only if ${\mathbb {F}}^- L_d$ is a local diffeomorphism.

Proof

It is a direct consequence of the implicit function theorem. $\square$

The Legendre transforms allow us to rewrite discrete Herglotz equations (40) as a momentum matching equations as in Marsden and West (2001). Indeed, provided $1+D_{z}L_{d}(q_0,q_1,z_0)$ is not zero, we may write

$$\begin{aligned} {\mathbb {F}}^{+}L_{d}(q_0,q_1,z_0)={\mathbb {F}}^{-}L_{d}(q_1,q_2,z_1). \end{aligned}$$

(42)

Inspired by the following theorem, we say that a discrete contact Lagrangian is regular if the function $1+D_{z}L_{d}(q_0,q_1,z_0)$ does not vanish and its negative discrete Legendre transform ${\mathbb {F}}^{-}L_{d}$ is a local diffeomorphism. Thus, we have the following theorem

Theorem 3.7

Suppose that the discrete Lagrangian $L_{d}:Q\times Q \times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is regular. Then there is a well-defined discrete Lagrangian flow $\Phi _{d}:Q\times Q\times {\mathbb {R}}\rightarrow Q\times Q \times {\mathbb {R}}$ for the discrete Herglotz equations. Moreover $\Phi _{d}$ is a local diffeomorphism given by

$$\begin{aligned} \Phi _{d}=({\mathbb {F}}^{-}L_{d})^{-1}\circ {\mathbb {F}}^{+}L_{d}. \end{aligned}$$

Proof

Consider the points $(q_0, q_1, z_0)\in Q\times Q\times {\mathbb {R}}$ and $(q_1, q_2, z_1)\in Q\times Q\times {\mathbb {R}}$ satisfying Eq.  (42). If ${\mathbb {F}}^{-}L_{d}$ is a local diffeomorphism, then the map defined by

$$\begin{aligned} \Phi _{d}=({\mathbb {F}}^{-}L_{d})^{-1}\circ {\mathbb {F}}^{+}L_{d} \end{aligned}$$

is also a local diffeomorphism and satisfies

$$\begin{aligned} \Phi _d (q_0, q_1, z_0) =(q_1, q_2, z_1), \end{aligned}$$

showing that it is the discrete Lagrangian flow for discrete Herglotz equations. $\square$

The discrete Legendre transforms also allow us to define an associated discrete Hamiltonian flow on $T^{*}Q\times {\mathbb {R}}$. Indeed, considering a regular discrete Lagrangian function $L_{d}$, let $\widetilde{\Phi _{d}}:T^{*}Q\times {\mathbb {R}}\rightarrow T^{*}Q\times {\mathbb {R}}$ be defined by

$$\begin{aligned} \widetilde{\Phi _{d}}={\mathbb {F}}^{+}L_{d}\circ \Phi _{d} \circ ({\mathbb {F}}^{+}L_{d})^{-1}. \end{aligned}$$

(43)

It is not difficult to show that the discrete Hamiltonian flow admits the alternative expressions

$$\begin{aligned} \widetilde{\Phi _{d}}={\mathbb {F}}^{-}L_{d}\circ \Phi _{d} \circ ({\mathbb {F}}^{-}L_{d})^{-1} \qquad \hbox {or}\qquad \widetilde{\Phi _{d}}={\mathbb {F}}^{+}L_{d}\circ ({\mathbb {F}}^{-}L_{d})^{-1}. \end{aligned}$$

(44)

(45)

We may define the one-forms

$$\begin{aligned} \eta ^{+}=({\mathbb {F}}^{+}L_{d})^{*}\eta , \quad \eta ^{-}=({\mathbb {F}}^{-}L_{d})^{*}\eta , \end{aligned}$$

(46)

where $\eta$ is the canonical contact form on $T^{*}Q\times {\mathbb {R}}$. These are contact forms on $Q\times Q \times {\mathbb {R}}$. If we chose natural coordinates $(q^{i},p_{i},z)$ on $T^{*}Q\times {\mathbb {R}}$ where $\eta ={\mathrm {d}}z-p_{i}{\mathrm {d}}q^{i}$, the discrete 1-forms may be locally written as the pullback

$$\begin{aligned} \begin{aligned} \eta ^{+}&={\mathrm {d}}z_{0}+{\mathrm {d}}L_d(q_{0},q_{1},z_{0})-D_{2}L_{d}(q_{0},q_{1},z_{0}){\mathrm {d}}q_{1}, \\ \eta ^{-}&={\mathrm {d}}z_{0}+\frac{D_{1}L_{d}(q_0,q_1,z_0)}{1+D_{z}L_{d}(q_0,q_1,z_0)}{\mathrm {d}}q_{0}, \end{aligned} \end{aligned}$$

(47)

by the corresponding discrete Legendre transform. The one-form $\eta ^{+}$ is further simplified to

$$\begin{aligned} \eta ^{+}=(1+D_{z}L_{d}(q_{0},q_{1},z_{0})){\mathrm {d}}z_{0}+D_{1}L_{d}(q_{0},q_{1},z_{0}){\mathrm {d}}q_{0}. \end{aligned}$$

(48)

Given a discrete Lagrangian $L_{d}$, let $\sigma _{d}:Q\times Q\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ be the smooth function given by

$$\begin{aligned} \sigma _{d}(q_0,q_1,z_0)=1+D_{z}L_{d}(q_0,q_1,z_0) \end{aligned}$$

then we have that:

Lemma 3.8

The discrete contact forms $\eta ^{\pm }$ satisfy

• (i) $\eta ^{+}=\sigma _{d} \cdot \eta ^{-}$;

• (ii) $(\Phi _{d})^{*}\eta ^{-}=\eta ^{+}$.

Proof

For the first item, observe that (48) is equivalent to

$$\begin{aligned} \eta ^{+}=(1+D_{z}L_{d}(q_{0},q_{1},z_{0}))\eta ^{-}. \end{aligned}$$

For the second one, note that

$$\begin{aligned} (\Phi _{d})^{*}\eta ^{-}= (\Phi _{d})^{*}\circ ({\mathbb {F}}^{-}L_{d})^{*}\eta =({\mathbb {F}}^{-}L_{d}\circ \Phi _{d})^{*}\eta =({\mathbb {F}}^{+}L_{d})^{*}\eta \end{aligned}$$

by applying Theorem 3.7. $\square$

As a consequence of the last Lemma we have the following theorem:

Theorem 3.9

Let $L_{d}$ be a regular discrete Lagrangian function. The discrete flow $\Phi _{d}$ associated to $L_{d}$ is a conformal contactomorphism with respect to both contact structures $\eta ^{\pm }$. In particular, it satisfies

$$\begin{aligned} (\Phi _{d})^{*}\eta ^{+}=(\sigma _{d} \circ \Phi _{d})\cdot \eta ^{+}, \quad (\Phi _{d})^{*}\eta ^{-}=\sigma _{d} \cdot \eta ^{-} \end{aligned}$$

(49)

Likewise, the discrete Hamiltonian flow $\widetilde{\Phi _{d}}$ is also a conformal contactomorphism satisfying

$$\begin{aligned} (\widetilde{\Phi _{d}})^{*}\eta =(\sigma _{d} \circ ({\mathbb {F}}^{-}L_{d})^{-1}) \cdot \eta . \end{aligned}$$

(50)

Proof

The first two claims are trivial consequences of Lemma 3.8. Indeed, combining the two statements of the Lemma we get

$$\begin{aligned} (\Phi _{d})^{*}\eta ^{-}=\sigma _{d} \cdot \eta ^{-}. \end{aligned}$$

Then, also

$$\begin{aligned} (\Phi _{d})^{*}\eta ^{+}=(\Phi _{d})^{*}(\sigma _{d} \cdot \eta ^{-})=(\sigma _{d} \circ \Phi _{d}) \cdot (\Phi _{d})^{*}\eta ^{-}=(\sigma _{d} \circ \Phi _{d}) \cdot \eta ^{+}. \end{aligned}$$

As for the last equation, observing that the discrete Hamiltonian flow satisfies $\widetilde{\Phi _{d}}={\mathbb {F}}^{+}L_{d}\circ \Phi _{d} \circ ({\mathbb {F}}^{+}L_{d})^{-1}$ by definition, then

$$\begin{aligned} \begin{aligned} (\widetilde{\Phi _{d}})^{*}\eta&= (({\mathbb {F}}^{+}L_{d})^{-1})^{*} \circ (\Phi _{d})^{*} \eta ^{+}=(({\mathbb {F}}^{+}L_{d})^{-1})^{*}((\sigma _{d} \circ \Phi _{d}) \cdot \eta ^{+}) \\&= (\sigma _{d} \circ \Phi _{d}\circ ({\mathbb {F}}^{+}L_{d})^{-1}) \cdot (({\mathbb {F}}^{+}L_{d})^{-1})^{*}\eta ^{+}, \end{aligned} \end{aligned}$$

where the last equality comes from the properties of the pullback. Since we have that

$$\begin{aligned} \Phi _{d}\circ ({\mathbb {F}}^{+}L_{d})^{-1}=({\mathbb {F}}^{-}L_{d})^{-1} \quad \text {and} \quad (({\mathbb {F}}^{+}L_{d})^{-1})^{*}\eta ^{+}=\eta , \end{aligned}$$

the desired result follows.

Moreover, since the discrete Lagrangian function $L_{d}$ is regular, the function $\sigma _{d}$ does not vanish. Hence, the discrete flows $\Phi _{d}$ and $\widetilde{\Phi _{d}}$ are conformal contact. $\square$

3.2 Discrete Symmetries and Dissipated Quantities

Let G be a Lie group acting on Q through the map $\Phi :G\times Q\rightarrow Q$. We define the lifted action on $Q\times Q \times {\mathbb {R}}$ to be the diagonal action on $Q\times Q$ and the identity on ${\mathbb {R}}$, so that

$$\begin{aligned} {\widetilde{\Phi }}:G\times Q\times Q\times {\mathbb {R}}\rightarrow Q\times Q\times {\mathbb {R}}, \quad {\widetilde{\Phi }}_{g}(q_{0},q_{1},z_{0})=(\Phi _{g}(q_{0}),\Phi _{g}(q_{1}),z_{0}). \end{aligned}$$

Let us denote by $\xi _{Q}\in {\mathfrak {X}}(Q)$ the infinitesimal generator associated to a Lie algebra element $\xi \in {{\mathfrak {g}}}$ and by ${\widetilde{\xi }}\in {\mathfrak {X}}(Q\times Q\times {\mathbb {R}})$ the corresponding infinitesimal generator on $Q\times Q\times {\mathbb {R}}$.

Notice that, since $\text {pr}_{3}(\Phi _{g}(q_{0},q_{1},z_{0}))=z_{0}$ is constant for all $g\in G$, where $\text {pr}_{3}:Q\times Q\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is the projection onto the third factor, then we have that

$$\begin{aligned} T_{(q_{0},q_{1},z_{0})}\text {pr}_{3}({\widetilde{\xi }}(q_{0},q_{1},z_{0}))=0. \end{aligned}$$

In fact, the infinitesimal generator may be identified with

$$\begin{aligned} {\widetilde{\xi }}(q_{0},q_{1},z_{0})=(\xi _{Q}(q_{0}),\xi _{Q}(q_{1}),0_{z_{0}})\in T_{q_{0}}Q\times T_{q_{1}}Q\times T_{z_{0}}{\mathbb {R}}, \end{aligned}$$

(51)

where $0:{\mathbb {R}}\rightarrow T{\mathbb {R}}$ is the zero section of $T{\mathbb {R}}$.

Lemma 3.10

If $L_{d}:Q\times Q\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is an invariant discrete Lagrangian function, i.e., $L_{d}\circ {\widetilde{\Phi }}_{g}=L_{d}$ for all $g\in G$, then it satisfies the equation

$$\begin{aligned} D_{1}L_{d}(q_{0},q_{1},z_{0})\xi _{Q}(q_{0})+D_{2}L_{d}(q_{0},q_{1},z_{0})\xi _{Q}(q_{1})=0. \end{aligned}$$

(52)

Proof

Since the discrete Lagrangian function is invariant for the lifted action, it satisfies

$$\begin{aligned} \langle {\mathrm {d}}L_{d}(q_{0},q_{1},z_{0}), {\widetilde{\xi }}(q_{0},q_{1},z_{0})\rangle =0, \ \forall (q_{0},q_{1},z_{0})\in Q\times Q\times {\mathbb {R}}. \end{aligned}$$

Then using Eq. (51), one immediately gets the desired expression. $\square$

Now consider the discrete momentum map $J_{d}$ given by

$$\begin{aligned} \begin{aligned} J_{d}: Q\times Q \times {\mathbb {R}}&\rightarrow {\mathfrak {g}}^*,\\ \langle J_{d}(q_{0},q_{1},z_{0}), \xi \rangle&= \langle \eta ^{-}, {\widetilde{\xi }}(q_{0},q_{1},z_{0})\rangle . \end{aligned} \end{aligned}$$

(53)

Theorem 3.11

Let $L_{d}$ be an invariant discrete Lagrangian function for the lifted action ${\widetilde{\Phi }}$. Then ${\widetilde{\Phi }}$ acts by contactomorphisms on $Q\times Q\times {\mathbb {R}}$ and the function ${\hat{J}}_{d}(\xi ):Q\times Q\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ given by

$$\begin{aligned} {\hat{J}}_{d}(\xi )(q_{0},q_{1},z_{0})=\langle J_{d}(q_{0},q_{1},z_{0}), \xi \rangle \end{aligned}$$

is dissipated along the discrete flow of Herglotz equations in the sense that

$$\begin{aligned} {\hat{J}}_{d}(\xi )(\Phi _{d} (q_{0},q_{1},z_{0}))= \sigma _{d}(q_{0},q_{1},z_{0}) {\hat{J}}_{d}(\xi )(q_{0},q_{1},z_{0}), \end{aligned}$$

where $\sigma _{d}(q_{0},q_{1},z_{0})=1+D_{z}L_{d}(q_{0},q_{1},z_{0})$.

Proof

The fact that ${\widetilde{\Phi }}$ acts by contactomorphisms is immediately checked by computing the pullback of either the 1-forms $\eta ^{\pm }$:

$$\begin{aligned} ({\widetilde{\Phi }}_{g})^{*}\eta ^{\pm }= \eta ^{\pm }. \end{aligned}$$

Indeed, it is a direct consequence of the G-invariance of $L_d$. Following a similar proof as in Subsection 1.3.3 in Marsden and West (2001) (where the authors show that, in the symplectic context, G-invariance implies that the action map preserves the discrete Lagrangian one-forms), we differentiate the equality $L_{d}\circ {\widetilde{\Phi }}_{g}=L_{d}$ with respect to $z_{0}$ and obtain

$$\begin{aligned} D_{z}L_{d} ({\widetilde{\Phi }}_{g}(q_{0},q_{1},z_{0}))=D_{z}L_{d}(q_{0},q_{1},z_{0}), \end{aligned}$$

while differentiation with respect to $q_{0}$ implies

$$\begin{aligned} ({\widetilde{\Phi }}_{g})^{*}(D_{1}L_{d}(q_{0},q_{1},z_{0}) {\mathrm {d}}q_{0})=D_{1}L_{d}(q_{0},q_{1},z_{0}) {\mathrm {d}}q_{0}. \end{aligned}$$

Then, from the local expressions (47) and (48) and noting that $({\widetilde{\Phi }}_{g})^{*} {\mathrm {d}}z_{0}={\mathrm {d}}z_{0}$, the result follows.

In order to simplify the notation, let $P_{0}=(q_{0},q_{1},z_{0})$ and $P_{1}=\Phi _{d} (q_{0},q_{1},z_{0})$. By definition we have that

$$\begin{aligned} {\hat{J}}_{d}(\xi )(P_{1})=\langle \eta ^{-}(P_{1}), {\widetilde{\xi }}(P_{1})\rangle . \end{aligned}$$

Now applying the definition of $\eta ^{-}$ and Eq. (51) we get

$$\begin{aligned} {\hat{J}}_{d}(\xi )(P_{1})=\frac{1}{\sigma _{d}(P_{1})}\langle D_{1}L_{d}(P_{1}), \xi _{Q}(q_{1})\rangle . \end{aligned}$$

Using the discrete Herglotz equations, the right-hand side reduces to

$$\begin{aligned} {\hat{J}}_{d}(\xi )(P_{1})=-\langle D_{2}L_{d}(P_{0}),\xi _{Q}(q_{1})\rangle . \end{aligned}$$

From the infinitesimal symmetry formula in Eq. (52), we deduce

$$\begin{aligned} {\hat{J}}_{d}(\xi )(P_{1})=\langle D_{1}L_{d}(P_{0}), \xi _{Q}(q_{0})\rangle . \end{aligned}$$

Now inserting $\sigma _{d}(P_{0})$ so that

$$\begin{aligned} {\hat{J}}_{d}(\xi )(P_{1})=\sigma _{d}(P_{0}) \langle \frac{D_{1}L_{d}(P_{0})}{\sigma _{d}(P_{0})},\xi _{Q}(q_{0})\rangle , \end{aligned}$$

we deduce

$$\begin{aligned} {\hat{J}}_{d}(\xi )(P_{1})=\sigma _{d}(P_{0})\langle \eta ^{-}(P_{0}),{\widetilde{\xi }}(P_{0})\rangle \end{aligned}$$

and so we have proved that

$$\begin{aligned} {\hat{J}}_{d}(\xi )(P_{1})=\sigma _{d}(P_{0}) {\hat{J}}_{d}(\xi )(P_{0}). \end{aligned}$$

$\square$

4 Exact Discrete Lagrangian for Contact Systems

4.1 The Contact Exponential Map

Given a contact regular Lagrangian $L:TQ\times {\mathbb {R}}\rightarrow {\mathbb {R}}$, consider the corresponding Lagrangian vector field $\xi _{L}$ and denote its flow by $\phi _{t}^{\xi _{L}}$.

Define the open subset $U_{h}$ of $TQ\times {\mathbb {R}}$ given by

$$\begin{aligned} U_{h}=\{(q_{0},{\dot{q}}_{0},z_{0})\in TQ \times {\mathbb {R}}\ | \ \phi _{t}^{\xi _{L}} \ \text {is defined for} \ t\in [0,h]\} \end{aligned}$$

and let the contact exponential map be defined by

$$\begin{aligned} \begin{aligned}&\text {exp}_{h}^{\xi _{L}}: \, U_{h} \subseteq TQ \times {\mathbb {R}}\rightarrow Q \times Q \times {\mathbb {R}}\\&\qquad (q_{0},{\dot{q}}_{0},z_{0})\mapsto (q_{0},q_{1},z_{0}), \end{aligned} \end{aligned}$$

(54)

where $q_{1}=p_{Q}\circ \phi _{h}^{\xi _{L}}(q_{0},{\dot{q}}_{0},z_{0})$ and $p_{Q}:TQ\times {\mathbb {R}}\rightarrow Q$ is the projection onto Q given by $p_{Q}(v_{q},z)=q$ for $v_{q}\in T_{q} Q$.

We will prove that the contact exponential map is a local diffeomorphism, using the fact that the non-holonomic exponential map, i.e., the exponential map of a non-holonomic system is a local embedding (see Anahory Simoes et al. 2020; Marrero et al. 2016). This recent result is a consequence from the analogous fact that the exponential map for arbitrary SODE vector fields is a local diffeomorphism and from classical analytical results in boundary values problems for second-order differential equations (cf. Chapter XII, Part II in Hartman 2002).

Indeed, to every regular contact system, one can associate a non-holonomic Lagrangian system on $T(Q\times {\mathbb {R}})$ with nonlinear constraints.

Consider the singular Lagrangian function

$$\begin{aligned} \widetilde{L}:T(Q\times {\mathbb {R}}) \rightarrow {\mathbb {R}}, \quad \widetilde{L}=L\circ \pi , \end{aligned}$$

(55)

where $\pi :T(Q\times {\mathbb {R}}) \rightarrow TQ\times {\mathbb {R}}$ is a projection onto $TQ\times {\mathbb {R}}$. Also, we take the nonlinear constraints

$$\begin{aligned} M_{L}=\{ (q,z,{\dot{q}},{\dot{z}})\in T(Q\times {\mathbb {R}}) \ | \ {\dot{z}}=L(q,{\dot{q}},z) \}. \end{aligned}$$

(56)

Observe that $M_{L}$ is the zero level set of the real-valued function $\Phi :T(Q\times {\mathbb {R}}) \rightarrow {\mathbb {R}}$ given by $\Phi (q,z,{\dot{q}},{\dot{z}})={\dot{z}}-L(q,{\dot{q}},z)$.

The pair $(\widetilde{L},M_{L})$ forms a Lagrangian non-holonomic system with nonlinear constraints determined by the submanifold $M_{L}$ and dynamics given by Chetaev’s principle (see Bloch 2015; de León and de Diego 1996 and references therein). According to this principle the equations of motion are

$$\begin{aligned} \begin{aligned}&\frac{{\mathrm {d}}}{{\mathrm {d}}t}\left( \frac{\partial \widetilde{L}}{\partial {\dot{q}}^{i}} \right) - \frac{\partial \widetilde{L}}{\partial q^{i}}=\lambda \frac{\partial \Phi }{\partial {\dot{q}}^{i}} \\&\frac{{\mathrm {d}}}{{\mathrm {d}}t}\left( \frac{\partial \widetilde{L}}{\partial {\dot{z}}} \right) - \frac{\partial \widetilde{L}}{\partial z}=\lambda \frac{\partial \Phi }{\partial {\dot{z}}} \\&\Phi (q^{i},z,{\dot{q}}^{i},{\dot{z}})=0, \end{aligned} \end{aligned}$$

(57)

with Lagrange multiplier $\lambda$. As $\widetilde{L}$ does not depend on ${\dot{z}}$ it is straightforward to check that the Lagrange multiplier is just

$$\begin{aligned} \lambda =-\frac{\partial L}{\partial z} \end{aligned}$$

and that Eq. (57) are equivalent to the Herglotz equations for L.

Moreover, since L is regular, we can define a SODE vector field $\Gamma _{(\widetilde{L},M_{L})}$ $\in {\mathfrak {X}}(M_{L})$ as the unique vector field on $M_{L}$ whose integral curves satisfy Eq. (57). Hence, we deduce

$$\begin{aligned} T\pi (\Gamma _{(\widetilde{L},M_{L})})=\xi _{L}\circ \pi . \end{aligned}$$

(58)

Let us denote the flow of the vector field $\Gamma _{(\widetilde{L},M_{L})}$ by $\phi _{t}^{\Gamma _{(\widetilde{L},M_{L})}}:M_{L}\rightarrow M_{L}$.

Consider now the submanifold of ${\mathcal {M}}_{L}$ given by

$$\begin{aligned} M_{L,h}=\{(q_{0},{\dot{q}}_{0},z_{0},{\dot{z}}_{0})\in T(Q \times {\mathbb {R}}) \ | \ \phi _{t}^{\Gamma _{(\widetilde{L},M_{L})}} \ \text {is defined for} \ t\in [0,h]\}. \end{aligned}$$

We define the non-holonomic exponential map to be

$$\begin{aligned} \begin{aligned} \text {exp}_{h}^{\Gamma _{(\widetilde{L},M_{L})}}: \ M_{L,h}\subseteq \ M_{L}&\longrightarrow (Q \times {\mathbb {R}}) \times (Q \times {\mathbb {R}}) \\ (q_{0},z_{0},{\dot{q}}_{0},{\dot{z}}_{0})&\mapsto (q_{0},z_{0},q_{1},z_{1}), \end{aligned} \end{aligned}$$

(59)

where $(q_{1},z_{1})=\tau _{Q\times {\mathbb {R}}}\circ \phi _{h}^{\Gamma _{(\widetilde{L},M_{L})}}(q_{0},z_{0},{\dot{q}}_{0},{\dot{z}}_{0})$, with $\tau _{Q\times {\mathbb {R}}}:T(Q\times {\mathbb {R}}) \rightarrow Q\times {\mathbb {R}}$ the tangent bundle projection.

In Anahory Simoes et al. (2020) the authors prove that there is an open subset $N_{h}\subseteq M_{L,h}$ such that the non-holonomic exponential map $\text {exp}_{h}^{\Gamma _{(\widetilde{L},M_{L})}}|_{N_{h}}$ is a smooth embedding and, hence, a diffeomorphism into its image, which we will denote by $M_{d}$.

Theorem 4.1

There exists a sufficiently small $h>0$ and an open set $V_{h}\subseteq U_{h}$ such that the contact exponential map $\text {exp}_{h}^{\xi _{L}}|_{V_{h}}$ is a diffeomorphism.

Proof

Let us consider the non-holonomic system $(\widetilde{L},M_{L})$ defined previously.

According to Eq. (58), the vector fields $\xi _{L}$ and $\Gamma _{(\widetilde{L},M_{L})}$ are $\pi$-related therefore, its flows satisfy

$$\begin{aligned} \pi \circ \phi _{t}^{\Gamma _{(\widetilde{L},M_{L})}}=\phi _{t}^{\xi _{L}} \circ \pi . \end{aligned}$$

We remark that $\pi |_{M_{L}}$ is a diffeomorphism, since $M_{L}$ is diffeomorphic to the graph of the Lagrangian function L. As such, we can also write

$$\begin{aligned} \phi _{t}^{\Gamma _{(\widetilde{L},M_{L})}}=(\pi |_{M_{L}})^{-1} \circ \phi _{t}^{\xi _{L}} \circ \pi |_{M_{L}}. \end{aligned}$$

Thus, we can write the non-holonomic exponential map in terms of the contact dynamics in the following way

$$\begin{aligned} \text {exp}_{h}^{\Gamma _{(\widetilde{L},M_{L})}}(q_{0},z_{0},{\dot{q}}_{0},{\dot{z}}_{0})=(q_{0},z_{0},q_{1},z_{1}), \end{aligned}$$

with $(q_{1},z_{1})=\tau _{Q\times {\mathbb {R}}}\circ (\pi |_{M_{L}})^{-1} \circ \phi _{h}^{\xi _{L}} \circ \pi |_{M_{L}}(q_{0},z_{0},{\dot{q}}_{0},{\dot{z}}_{0})$ where ${\dot{z}}_0=L(q_0, {\dot{q}}_0, z_0)$.

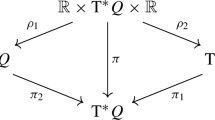
Also note that $\tau _{Q\times {\mathbb {R}}}\circ (\pi |_{M_{L}})^{-1}=p_{Q\times {\mathbb {R}}}$, where

$$\begin{aligned} p_{Q\times {\mathbb {R}}}:TQ\times {\mathbb {R}}\rightarrow Q\times {\mathbb {R}}, \quad p_{Q\times {\mathbb {R}}}(v_{q},z)=(q,z). \end{aligned}$$

In Diagram (60) we show the different projections we can define on the manifolds involved in this section.

(60)

With these projections we can also write the contact exponential map as

$$\begin{aligned} \text {exp}_{h}^{\xi _{L}}(q_{0},{\dot{q}}_{0},z_{0})=(q_{0},q_{1},z_{0}), \end{aligned}$$

with $q_{1}=\text {pr}_{1}\circ p_{Q\times {\mathbb {R}}} \circ \phi _{h}^{\xi _{L}} (q_{0},{\dot{q}}_{0},z_{0})$. Hence, we can write it as

$$\begin{aligned} \text {exp}_{h}^{\xi _{L}} = \widetilde{\text {pr}}_{1} \circ \text {exp}_{h}^{\Gamma _{(\widetilde{L},M_{L})}}\circ (\pi |_{M_{L}})^{-1}, \end{aligned}$$

(61)

with

$$\begin{aligned} \begin{aligned} \widetilde{\text {pr}}_{1}:(Q\times {\mathbb {R}}) \times (Q \times {\mathbb {R}})&\longrightarrow Q \times Q \times {\mathbb {R}}\\ (q_{0},z_{0},q_{1},z_{1})&\mapsto (q_{0}, \text {pr}_{1}(q_{1},z_{1}),z_{0}). \end{aligned} \end{aligned}$$

Therefore, if $\widetilde{\text {pr}}_{1}|_{M_{d}}$ is a local diffeomorphism then, by Eq. (61), the contact exponential map $\text {exp}_{h}^{\xi _{L}}|_{V_{h}}$ is a diffeomorphism if we choose

$$\begin{aligned} V_{h}=\pi |_{M_{L}}(N_{h}), \end{aligned}$$

where $N_{h}$ is the open subset where $\text {exp}_{h}^{\Gamma _{(\widetilde{L},M_{L})}}|_{N_{h}}$ is an embedding.

We are going to prove in the next Lemma that $\widetilde{\text {pr}}_{1}|_{M_{d}}$ is a local diffeomorphism. $\square$

Lemma 4.2

Using the same notation as in the previous theorem, $\widetilde{\text {pr}}_{1}|_{M_{d}}$ is a local diffeomorphism.

Proof

All we must prove is that $\widetilde{\text {pr}}_{1}|_{M_{d}}$ is a local submersion (immersion) since, by dimensional reasons, this forces $\widetilde{\text {pr}}_{1}|_{M_{d}}$ to be also a local immersion (submersion).

Let $x\in M_{d}$. Any vector in the kernel of $T_{x}\widetilde{\text {pr}}_{1}|_{M_{d}}$ must be the tangent vector of a curve of the form

$$\begin{aligned} Z(s)=(q_{0},z_{0},q_{1},w \cdot s)\in M_{d}, \quad w\in {\mathbb {R}}. \end{aligned}$$

Let $\gamma _{s}(t)=\phi _{t}^{\Gamma _{(\widetilde{L},M_{L})}}\circ (\text {exp}_{h}^{\Gamma _{(\widetilde{L},M_{L})}})^{-1}(Z(s))$. For each fixed value of s, this is an integral curve of $\Gamma _{(\widetilde{L},M_{L})}$ satisfying

$$\begin{aligned} \tau _{Q\times {\mathbb {R}}} \circ \gamma _{s}(0)=(q_{0},z_{0}), \quad \tau _{Q\times {\mathbb {R}}} \circ \gamma _{s}(h)=(q_{1},w \cdot s). \end{aligned}$$

Moreover, note that the projection of $\gamma _{s}(t)$ to $TQ\times {\mathbb {R}}$, i.e., the curve $\pi \circ \gamma _{s}(t)$ is an integral curve of $\xi _{L}$ with endpoints $q_{0}$ and $q_{1}$ for each fixed value of s and so $\pi \circ \gamma _{0}(t)$ must satisfy Herglotz’ principle. Note that the action over the curves $\pi \circ \gamma _{s}(t)$ is given by

$$\begin{aligned} {\mathcal {A}}(p_{Q}\circ \pi \circ \gamma _{s}(t))=p_{{\mathbb {R}}} \circ \pi \circ \gamma _{s}(h)=w \cdot s, \end{aligned}$$

where $p_{{\mathbb {R}}}:TQ\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is the projection onto the second factor.

Therefore, $p_{Q}\circ \pi \circ \gamma _{0}(t)$ is a critical value of the action if and only if $w=0$. Therefore, $T_{x}\widetilde{\text {pr}}_{1}|_{M_{d}}$ is trivial and $\widetilde{\text {pr}}_{1}|_{M_{d}}$ must be a local diffeomorphism in a neighbourhood of each point. $\square$

Since the contact exponential map is a local diffeomorphism we can define a local inverse called the exact retraction and denote it by $R_{h}^{e-}:Q \times Q \times {\mathbb {R}}\rightarrow TQ \times {\mathbb {R}}$. We will also use its translation by the flow

$$\begin{aligned} R_{h}^{e+}:Q \times Q \times {\mathbb {R}}\rightarrow TQ \times {\mathbb {R}}, \quad R_{h}^{e+}:=\phi _{h}^{\xi _{L}}\circ R_{h}^{e-}. \end{aligned}$$

4.2 The exact discrete Lagrangian Function

Consider the function $L_{h}^{e}: Q \times Q \times {\mathbb {R}}\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} L_{h}^{e} (q_{0},q_{1},z_{0})=\int _{0}^{h} L\circ \phi _{t}^{\xi _{L}}\circ R_{h}^{e-}(q_{0},q_{1},z_{0}) {\mathrm {d}}t \end{aligned}$$

(62)

is called the exact discrete Lagrangian function.

We will need the following classical result in the proof of the next theorem: the solution of the first-order linear equation ${\dot{y}}=a(t)+\frac{{\mathrm {d}}b}{{\mathrm {d}}t}(t)y$ with $b(0)=0$ is

$$\begin{aligned} y(t)=e^{b(t)}\left( \int _{0}^{t} a(s)e^{-b(s)} \ {\mathrm {d}}s + y(0) \right) . \end{aligned}$$

(63)

Theorem 4.3

The Legendre transforms of a regular Lagrangian $L:TQ\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ are related to the discrete Legendre transforms of the corresponding exact discrete Lagrangian $L_{h}^{e}:Q\times Q\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ in the following way

$$\begin{aligned} {\mathbb {F}}^{+}L_{h}^{e}={\mathbb {F}}L\circ R_{h}^{e+}, \quad {\mathbb {F}}^{-}L_{h}^{e}={\mathbb {F}}L\circ R_{h}^{e-}. \end{aligned}$$

(64)

Proof

We will prove in local computations that the derivatives of the exact discrete Lagrangian function satisfy

$$\begin{aligned} \begin{aligned}&D_{1} L_{h}^{e} (q_{0},q_{1},z_{0}) = -\frac{\partial L}{\partial {\dot{q}}}(q_{0},{\dot{q}}_{0},z_{0})e^{b(h)}; \\&D_{2} L_{h}^{e} (q_{0},q_{1},z_{0}) = \frac{\partial L}{\partial {\dot{q}}}(q_{1},{\dot{q}}_{1},z_{1}); \\&D_{z} L_{h}^{e} (q_{0},q_{1},z_{0}) = e^{b(h)}-1. \end{aligned} \end{aligned}$$

(65)

where

$$\begin{aligned} \begin{aligned}&(q_{0},{\dot{q}}_{0},z_{0})=R_{h}^{e-}(q_{0},q_{1},z_{0}), \quad (q_{1},{\dot{q}}_{1},z_{1})= \phi _{h}^{\xi _{L}}\circ R_{h}^{e-}(q_{0},q_{1},z_{0}), \\&\text {and} \quad b(t)=\int _{0}^{t} \frac{\partial L}{\partial z}(\phi _{s}^{\xi _{L}}\circ R_{h}^{e-}(q_{0},q_{1},z_{0})) \ {\mathrm {d}}s. \end{aligned} \end{aligned}$$

(66)

Then, from the definition of Legendre transform in (20) and discrete Legendre transforms in (41), the result follows immediately.

To simplify the notation in the proof we will use the notation $\gamma _{0,1}(t)=(q_{0,1}(t),{\dot{q}}_{0,1}(t),z_{0,1}(t)):=\phi _{t}^{\xi _{L}}\circ R_{h}^{e-}(q_{0},q_{1},z_{0})$. Under this convention we will have

$$\begin{aligned} L_{h}^{e} (q_{0},q_{1},z_{0})=\int _{0}^{h} L(\gamma _{0,1}(t)) {\mathrm {d}}t. \end{aligned}$$

Note first that any variation of the exact discrete Lagrangian will take the form

$$\begin{aligned} \begin{aligned}&\delta L_{h}^{e} (q_{0},q_{1},z_{0}) = {\left. \frac{{\mathrm {d}}}{{\mathrm {d}}\varepsilon } \right| _{\varepsilon =0}L_{h}^{e}({\tilde{q}}_{0}(\varepsilon ),{\tilde{q}}_{1}(\varepsilon ),{\tilde{z}}_{0}(\varepsilon ))} \\&\quad =\int _{0}^{h}\frac{\partial L}{\partial q}(\gamma _{0,1}(t))\delta q_{0,1} +\frac{\partial L}{\partial {\dot{q}}}(\gamma _{0,1}(t))\delta {\dot{q}}_{0,1}+\frac{\partial L}{\partial z}(\gamma _{0,1}(t))\delta z_{0,1} \ {\mathrm {d}}t. \end{aligned} \end{aligned}$$

(67)

Since $\gamma _{0,1}(t)$ is a solution of Euler–Lagrange equations, it satisfies

$$\begin{aligned} {\dot{z}}_{0,1}=L(q_{0,1}(t),{\dot{q}}_{0,1}(t),z_{0,1}(t)). \end{aligned}$$

Therefore, any variation of $z_{0,1}$ satisfies the variational equation

$$\begin{aligned} \delta {\dot{z}}_{0,1}=\frac{\partial L}{\partial q}(\gamma _{0,1}(t))\delta q_{0,1} +\frac{\partial L}{\partial {\dot{q}}}(\gamma _{0,1}(t))\delta {\dot{q}}_{0,1}+\frac{\partial L}{\partial z}(\gamma _{0,1}(t))\delta z_{0,1}. \end{aligned}$$

(68)

Hence, any variation of the exact discrete Lagrangian reduces to

$$\begin{aligned} \delta L_{h}^{e} (q_{0},q_{1},z_{0}) = \delta z_{0,1}(h)-\delta z_{0,1}(0). \end{aligned}$$

(69)

Moreover, we can solve the function $\delta z_{0,1}$ explicitly, by solving the differential Eq. (68)

$$\begin{aligned} \delta z_{0,1}(h)=e^{b(h)}\left( \int _{0}^{h} a(s)e^{-b(s)} \ {\mathrm {d}}s + \delta z_{0,1}(0) \right) , \end{aligned}$$

(70)

with

$$\begin{aligned} \begin{aligned} b(t)&= \int _{0}^{t} \frac{\partial L}{\partial z}(\gamma _{0,1}(s)) \ {\mathrm {d}}s, \\ a(t)&= \frac{\partial L}{\partial q}(\gamma _{0,1}(t))\delta q_{0,1} +\frac{\partial L}{\partial {\dot{q}}}(\gamma _{0,1}(t))\delta {\dot{q}}_{0,1}. \end{aligned} \end{aligned}$$

Let us compute the integration in the expression of $\delta z_{0,1}$:

$$\begin{aligned} \begin{aligned} \int _{0}^{h} a(s)e^{-b(s)} \ {\mathrm {d}}s&= \int _{0}^{h} \left( \frac{\partial L}{\partial q}\delta q_{0,1} +\frac{\partial L}{\partial {\dot{q}}}\delta {\dot{q}}_{0,1} \right) e^{-b(t)} \ {\mathrm {d}}t \\&= \int _{0}^{h} \left( \frac{\partial L}{\partial q} - \frac{d}{dt}\frac{\partial L}{\partial {\dot{q}}}+\frac{\partial L}{\partial {\dot{q}}}\frac{\partial L}{\partial z}\right) \delta q_{0,1} e^{-b(t)} \ {\mathrm {d}}t \\&\quad + \frac{\partial L}{\partial {\dot{q}}}(\gamma _{0,1}(h))e^{-b(h)}\delta q_{0,1}(h)-\frac{\partial L}{\partial {\dot{q}}}(\gamma _{0,1}(0))\delta q_{0,1}(0), \end{aligned} \end{aligned}$$

where we are using integration by parts. Note that the term between brackets is zero, since we are over solutions of Euler–Lagrange equations. Therefore,

$$\begin{aligned} \delta z_{0,1}(h)=\frac{\partial L}{\partial {\dot{q}}}(\gamma _{0,1}(h))\delta q_{0,1}(h)-\frac{\partial L}{\partial {\dot{q}}}(\gamma _{0,1}(0))e^{b(h)}\delta q_{0,1}(0) + e^{b(h)}\delta z_{0,1}(0).\qquad \end{aligned}$$

(71)

Note that the differentials of the discrete Lagrangian $D_{1}L_{h}^{e}$, $D_{2}L_{h}^{e}$ and $D_{z} L_{h}^{e}$ are instances of particular variations. Therefore, we have that

$$\begin{aligned} \begin{aligned} D_{1} L_{h}^{e}(q_{0},q_{1},z_{0})&= \left( \frac{\partial L}{\partial {\dot{q}}}(\gamma _{0,1}(h))\frac{\partial q_{0,1}(h)}{\partial q_{0}^{i}} -\frac{\partial L}{\partial {\dot{q}}}(\gamma _{0,1}(0))e^{b(h)}\frac{\partial q_{0,1}(0)}{\partial q_{0}^{i}} \right. \\&\quad \left. + (e^{b(h)}-1)\frac{\partial z_{0,1}(0)}{\partial q_{0}^{i}} \right) {\mathrm {d}}q_{0}^{i}\\&= -\frac{\partial L}{\partial {\dot{q}}^{i}}(\gamma _{0,1}(0))e^{b(h)}{\mathrm {d}}q_{0}^{i}, \end{aligned} \end{aligned}$$

(72)

since $q_{0,1}(h)\equiv q_{1}$ and so its derivative with respect to $q_{0}$ vanishes, $q_{0,1}(0)\equiv q_{0}$ and so its derivative with respect to $q_{0}$ is the identity and, finally, $z_{0,1}(0)\equiv z_{0}$ does not depend upon $q_{0}$. Likewise, the next derivative follows from applying similar arguments. Indeed, we have that

$$\begin{aligned} \begin{aligned} D_{2} L_{h}^{e}(q_{0},q_{1},z_{0})&= \left( \frac{\partial L}{\partial {\dot{q}}}(\gamma _{0,1}(h))\frac{\partial q_{0,1}(h)}{\partial q_{1}^{i}} -\frac{\partial L}{\partial {\dot{q}}}(\gamma _{0,1}(0))e^{b(h)}\frac{\partial q_{0,1}(0)}{\partial q_{1}^{i}} \right. \\&\quad \left. + (e^{b(h)}-1)\frac{\partial z_{0,1}(0)}{\partial q_{1}^{i}} \right) {\mathrm {d}}q_{1}^{i}\\&= \frac{\partial L}{\partial {\dot{q}}^{i}}(\gamma _{0,1}(h)){\mathrm {d}}q_{1}^{i}. \end{aligned} \end{aligned}$$

(73)

Analogously, we also deduce

$$\begin{aligned} \begin{aligned} D_{z} L_{h}^{e}(q_{0},q_{1},z_{0})&= \left( \frac{\partial L}{\partial {\dot{q}}}(\gamma _{0,1}(h))\frac{\partial q_{0,1}(h)}{\partial z_{0}} -\frac{\partial L}{\partial {\dot{q}}}(\gamma _{0,1}(0))e^{b(h)}\frac{\partial q_{0,1}(0)}{\partial z_{0}} \right. \\&\quad \left. + (e^{b(h)}-1)\frac{\partial z_{0,1}(0)}{\partial z_{0}} \right) {\mathrm {d}}z_{0}\\&= (e^{b(h)}-1){\mathrm {d}}z_{0}. \end{aligned} \end{aligned}$$

(74)

Now, the result follows by the definition of the discrete Legendre transforms. $\square$

The commutativity of the following diagram summarizes the statement of the previous theorem

(75)

Now, we are going to relate the continuous contact Lagrangian flow with its discrete counterpart, when we take as discrete Lagrangian the corresponding exact discrete Lagrangian.

Theorem 4.4

Take a regular Lagrangian $L:TQ\rightarrow {\mathbb {R}}$ and fix a time step $h>0$. Then we have that:

• 1. $L_{h}^{e}$ is a regular discrete Lagrangian function;

• 2. If H is the Hamiltonian function corresponding to L introduced at the end of Sect. 2.2 and $\phi _{t}^{X_{H}}$ is its contact Hamiltonian flow, we have that

  $$\begin{aligned} {\mathbb {F}}^{+} L_{h}^{e}=\phi _{h}^{X_{H}}\circ {\mathbb {F}}^{-} L_{h}^{e}. \end{aligned}$$

  (76)

• 3. If $(q,z):[0,Nh]\rightarrow Q\times {\mathbb {R}}$ is a solution of the Herglotz equations, then it is related to the solution of the discrete Herglotz equations $\{ (q_{0},z_{0}),(q_{1},z_{1}),\ldots ,(q_{N},z_{N}) \}$ for the corresponding exact discrete Lagrangian with (q(0), q(h), z(0)) as initial conditions in the following way:

  $$\begin{aligned} q_{k}=q(kh), \quad z_{k}=z(kh) \quad \text {for} \ k=0,\ldots , N. \end{aligned}$$

  (77)

Proof

Item 1. is a consequence of the previous theorem, since ${\mathbb {F}}^{-}L_{h}^{e}$ is a composition of two local diffeomorphisms it is itself a local diffeomorphism. Item 2. comes from unwinding the definitions:

$$\begin{aligned} {\mathbb {F}}^{+} L_{h}^{e}={\mathbb {F}}L \circ R^{e+}_{h}={\mathbb {F}}L \circ \phi _{h}^{\Gamma _{L}}\circ R^{e-}_{h}=\phi _{h}^{X_{H}}\circ {\mathbb {F}}L\circ R^{e-}_{h}=\phi _{h}^{X_{H}}\circ {\mathbb {F}}^{-} L_{h}^{e}. \end{aligned}$$

For item 3., it is not hard to show that

$$\begin{aligned} {\mathbb {F}}^{+} L_{h}^{e}={\mathbb {F}}^{-} L_{h}^{e} \circ (\text {exp}_{h}^{\xi _{L}}\circ \phi _{h}^{\xi _{L}}\circ R_{h}^{e-}). \end{aligned}$$

Moreover, for every $k=1,\ldots ,N-1$, since the curves q and z are solution of the Herglotz equations, we have that

$$\begin{aligned} \text {exp}_{h}^{\xi _{L}}\circ \phi _{h}^{\xi _{L}}\circ R_{h}^{e-}(q(k-1),q(k),z(k-1))=(q(k),q(k+1),z(k)). \end{aligned}$$

Hence,

$$\begin{aligned} {\mathbb {F}}^{+} L_{h}^{e}(q(k-1),q(k),z(k-1))={\mathbb {F}}^{-} L_{h}^{e}(q(k),q(k+1),z(k)) \end{aligned}$$

so that $\{ (q_{0},z_{0}),(q_{1},z_{1}),\ldots ,(q_{N},z_{N}) \}$ given by (77) satisfy the discrete Herglotz equations. $\square$

5 Numerical Examples

Given a mechanical contact Lagrangian with a euclidean metric and a potential function $V:Q\rightarrow {\mathbb {R}}$ of the type

$$\begin{aligned} L(q,{\dot{q}},z)=\frac{1}{2}{\dot{q}}^{2}-V(q)+\gamma z, \quad (q,{\dot{q}},z)\in TQ\times {\mathbb {R}}, \quad \gamma < 0. \end{aligned}$$

one usually approximates the exact discrete Lagrangian associated to L by means of a quadrature rule. Note that the restriction of $\gamma$ to negative values is necessary to model dissipative dynamics, though we could define the integrator for any value of $\gamma \in {\mathbb {R}}$. If we use the middle point rule to approximate the positions, i.e., $q\approx \frac{q_{1}+q_{0}}{2}$, one may define the discrete Lagrangian $L_{d}:Q\times Q\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ in the following way

$$\begin{aligned} L_{d}(q_{0},q_{1},z_{0})=\frac{1}{2h}(q_{1}-q_{0})^{2}-hV\left( \frac{q_{1}+q_{0}}{2}\right) +h\gamma z_{0}. \end{aligned}$$

We remark that the value of h should be chosen small enough so that the function $\sigma _{d}$ does not vanish anywhere. In this case, the discrete Herglotz equations are of the type

$$\begin{aligned} \begin{aligned}&\frac{q_{1}-q_{0}}{h}-\frac{h}{2}\frac{\partial V}{\partial q}\left( \frac{q_{1}+q_{0}}{2}\right) =\frac{1}{(1+h\gamma )}\left( \frac{q_{2}-q_{1}}{h}+\frac{h}{2}\frac{\partial V}{\partial q}\left( \frac{q_{2}+q_{1}}{2}\right) \right) \\&z_{1}=L_{d}(q_{0},q_{1},z_{0})=\frac{1}{2h}(q_{1}-q_{0})^{2}-hV\left( \frac{q_{1}+q_{0}}{2}\right) +(h\gamma +1) z_{0} \end{aligned} \end{aligned}$$

Example 1

The free single particle contact Lagrangian is

$$\begin{aligned} L(q,{\dot{q}},z)=\frac{1}{2}{\dot{q}}^{2}+\gamma z, \quad (q,{\dot{q}},z)\in TQ\times {\mathbb {R}}. \end{aligned}$$

A simple discretization of this Lagrangian would be

$$\begin{aligned} L_{d}(q_{0},q_{1},z_{0})=\frac{1}{2h}(q_{1}-q_{0})^{2}+h\gamma z_{0}. \end{aligned}$$

(78)

Then, choosing h small enough so that the function $\sigma _{d}$ is non-vanishing, the discrete Herglotz equations for $L_{d}$ are locally given by

$$\begin{aligned} \begin{aligned}&\frac{q_{1}-q_{0}}{h}=\frac{q_{2}-q_{1}}{h(1+h\gamma )} \quad \Rightarrow \quad q_{2}=(h\gamma +2)q_{1}-(h\gamma +1)q_{0} \\&z_{1}=\frac{1}{2h}(q_{1}-q_{0})^{2}+(h\gamma +1) z_{0} \end{aligned} \end{aligned}$$

The discrete flow obtained by solving these equations is plotted in Fig. 1.

In this case, one can also compute the exact discrete Lagrangian and solve the exact dynamics.

$$\begin{aligned} L_{h}^{e}(q_{0},q_{1},z_{0}) = \frac{\gamma \left( q_{1}- q_{0}\right) ^{2} e^{\gamma h}}{2 e^{\gamma h} - 2} - z_{0} \left( e^{\gamma h} - 1\right) . \end{aligned}$$

(79)

Fig. 1

Position q and z and logarithm of the discrete Hamiltonian $H\circ {\mathbb {F}}^- L_d$ for a free particle, computed by solving the discrete Herglotz equations for the discrete Lagrangian (78) (continuous line) and the exact dynamics (dashed line), for $\gamma = -0.05$ and the time-step $h = 0.5$. The initial conditions are $q_{0} = 1$, $q_{1} = 2$ and $z_0 = 0$

Example 2

The damped harmonic oscillator is described by the Lagrangian

$$\begin{aligned} L(q,{\dot{q}},z)=\frac{1}{2}{\dot{q}}^{2}-\frac{1}{2}q^{2}+\gamma z, \quad (q,{\dot{q}},z)\in TQ\times {\mathbb {R}}. \end{aligned}$$

Using a middle point discretization, i.e., $q\approx \frac{q_{1}+q_{0}}{2}$, one may define the discrete Lagrangian

$$\begin{aligned} L_{d}(q_{0},q_{1},z_{0})=\frac{1}{2h}(q_{1}-q_{0})^{2}-\frac{h}{8}(q_{1}+q_{0})^{2}+h\gamma z_{0}. \end{aligned}$$

(80)

In this case, after choosing h small enough, the discrete Herglotz equations hold

$$\begin{aligned} \begin{aligned}&\frac{q_{1}-q_{0}}{h}-\frac{h}{4}(q_{1}+q_{0})=\frac{1}{(1+h\gamma )}\left( \frac{q_{2}-q_{1}}{h}+\frac{h}{4}(q_{2}+q_{1})\right) \\&z_{1}=\frac{1}{2h}(q_{1}-q_{0})^{2}-\frac{h}{8}(q_{1}+q_{0})^{2}+(h\gamma +1) z_{0}, \end{aligned} \end{aligned}$$

which can be solved explicitly for $q_{2}$

$$\begin{aligned} q_{2}=-\frac{(h^{3}\gamma +4h\gamma +h^{2}+4)q_{0}+(h^{3}\gamma -4h\gamma +2h^{2}-8)q_{1}}{h^{2}+4}. \end{aligned}$$

The discrete flow obtained by solving these equations is plotted in Fig. 2.

In this case, the exact discrete Lagrangian and the exact discrete dynamics can be computed with the aid of a Computer Algebra system, but the analytic expressions are complicated, so we only include their graph in Fig. 2.

Fig. 2

Position q and z and logarithm of the discrete Hamiltonian $H\circ {\mathbb {F}}^- L_d$ for a harmonic oscillator, computed by solving the discrete Herglotz equations on the discrete Lagrangian (80) (continuous line) and the exact dynamics (dashed line), for $\gamma =- 0.05$ and the time-step $h = 0.5$. The initial conditions are $q_{0} = 1$, $q_{1} = 2$ and $z_0 = 0$

6 Conclusions and Future Work

In this paper, we went deeper in the geometry of discrete contact mechanics following, as a starting point, the results by Vermeeren et al. (2019). We have done a detailed study of the discrete Herglotz principle and its geometric properties, including the discrete Legendre transforms and the associated discrete Lagrangian and Hamiltonian flows. Moreover, we have analyzed the existence of dissipated quantities related with symmetries of the system and the construction of the exact discrete Lagrangian function giving the correspondence between the discrete and continuous system.

In future work, we will study the variational error analysis allowing us to estimate the error order of the proposed methods just from the error of approximation of the exact discrete Lagrangian function, that is, how well the discrete Lagrangian function matches the exact discrete Lagrangian function (Marsden and West 2001; Patrick and Cuell 2009). Moreover, we will introduce higher-order methods for contact Lagrangian systems extending the theory of Morse functions to Legendrian submanifolds (see Libermann and Marle 1987; Barbero Liñán et al. 2019; Ferraro et al. 2017). For instance, this theory will give a complete geometric explanation of other possible discretizations of the phase space, as for instance, the one used by Vermeeren et al which is $Q \times Q \times {\mathbb {R}}^2$ instead of $Q\times Q\times {\mathbb {R}}$.