1 Introduction

Extracting dynamical models and their main characteristics from time series data is a recurring problem in many areas of science and engineering. In the particularly popular approach of Markovian models, the future evolution of the system, e.g., state \({\mathbf {x}}_{t+\tau }\), only depends on the current state \({\mathbf {x}}_{t}\), where t is the time step and \(\tau \) is the delay or lag time. Markovian models are easier to analyze than models with explicit memory terms. They are justified by the fact that many physical processes—including both deterministic and stochastic processes—are inherently Markovian. Even when only a subset of the variables in which the system is Markovian are observed, a variety of physics and engineering processes have been shown to be accurately modeled by Markovian models on sufficiently long observation lag times \(\tau \). Examples include molecular dynamics (Chodera and Noé 2014; Prinz et al. 2011), wireless communications (Konrad et al. 2001; Ma et al. 2001) and fluid dynamics (Mezić 2013; Froyland et al. 2016).

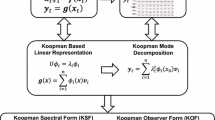
In the past decades, a collection of closely related Markov modeling methods were developed in different fields, including Markov state models (MSMs) (Schütte et al. 1999; Prinz et al. 2011; Bowman et al. 2014), Markov transition models (Wu and Noé 2015), Ulam’s Galerkin method (Dellnitz et al. 2001; Bollt and Santitissadeekorn 2013; Froyland et al. 2014), blind-source separation (Molgedey and Schuster 1994; Ziehe and Müller 1998), the variational approach of conformation dynamics (VAC) (Noé and Nüske 2013; Nüske et al. 2014), time-lagged independent component analysis (TICA) (Perez-Hernandez et al. 2013; Schwantes and Pande 2013), dynamic mode decomposition (DMD) (Rowley et al. 2009; Schmid 2010; Tu et al. 2014), extended dynamic mode decomposition (EDMD) (Williams et al. 2015a), variational Koopman models (Hao et al. 2017), variational diffusion maps (Boninsegna et al. 2015), sparse identification of nonlinear dynamics (Brunton et al. 2016b) and corresponding kernel embeddings (Harmeling et al. 2003; Song et al. 2013; Schwantes and Pande 2015) and tensor formulations (Nüske et al. 2016; Klus and Schütte 2015). All these models approximate the Markov dynamics at a lag time \(\tau \) by a linear model in the following form:

$$\begin{aligned} {\mathbb {E}}\left[ {\mathbf {g}}({\mathbf {x}}_{t+\tau })\right] = {\mathbf {K}}^{\top }{\mathbb {E}}\left[ {\mathbf {f}}({\mathbf {x}}_{t})\right] . \end{aligned}$$
(1)

Here \({\mathbf {f}}({\mathbf {x}})=(f_{1}({\mathbf {x}}),f_{2}({\mathbf {x}}),\ldots )^{\top }\) and \({\mathbf {g}}({\mathbf {x}})=(g_{1}({\mathbf {x}}),g_{2}({\mathbf {x}}),\ldots )^{\top }\) are feature transformations that transform the state variables \({\mathbf {x}}\) into the feature space in which the dynamics are approximately linear. \({\mathbb {E}}\) denotes an expectation value over time that accounts for stochasticity in the dynamics and can be omitted for deterministic dynamical systems. In some methods, such as DMD, the feature transformation is an identity transformation: \({\mathbf {f}}\left( {\mathbf {x}}\right) ={\mathbf {g}}\left( {\mathbf {x}}\right) ={\mathbf {x}}\)—and then Eq. (1) defines a linear dynamical system in the original state variables. If \({{\mathbf {{f}}}}\) and \({\mathbf {g}}\) are indicator functions that partition \(\varOmega \) into substates, such that \(f_{i}\left( {\mathbf {x}}\right) =g_{i}\left( {\mathbf {x}}\right) =1\) if \({\mathbf {x}}\in A_{i}\) and 0 otherwise, Eq. (1) is the propagation law of an MSM, or equivalently of Ulam’s Galerkin method, as the expectation values \({\mathbb {E}}\left[ {\mathbf {f}}({\mathbf {x}}_{t})\right] \) and \({\mathbb {E}}\left[ {\mathbf {g}}({\mathbf {x}}_{t+\tau })\right] \) represent the vector of probabilities to be in any substate at times t and \(t+\tau \), and \(K_{ij}\) is the probability to transition from set \(A_{i}\) to set \(A_{j}\) in time \(\tau \). In general, (1) can be interpreted as a finite-rank approximation of the so-called Koopman operator (Koopman 1931; Mezić 2005), which governs the time evolution of observables of the system state and can fully characterize the Markovian dynamics. As shown in Korda and Mezić (2018), this approximation becomes exact in the limit of infinitely sized feature transformations with \({\mathbf {f}}={\mathbf {g}}\), and a similar conclusion can also be obtained when \({\mathbf {f}},{\mathbf {g}}\) are infinite-dimensional feature functions deduced from a characteristic kernel (Song et al. 2013).

A direct method to estimate the matrix \({\mathbf {K}}\) from data is to solve the linear regression problem \({\mathbf {g}}({\mathbf {x}}_{t+\tau })\approx {\mathbf {K}}^{\top }{\mathbf {f}}({\mathbf {x}}_{t})\), which facilitates the use of regularized solution methods, such as the LASSO method (Tibshirani 1996). Alternatively, feature functions \({\mathbf {f}}\) and \({\mathbf {g}}\) that allow Eq. (1) to have a probabilistic interpretation (e.g., in MSMs), \({\mathbf {K}}\) can be estimated by a maximum likelihood or Bayesian method (Prinz et al. 2011; Noé 2008).

However, as yet, it is still unclear what are the optimal choices for \({\mathbf {f}}\)and \({\mathbf {g}}\)—either given a fixed dimension or a fixed amount of data. Notice that this problem cannot be solved by minimizing the regression error of Eq. (1), because a regression error of zero can be trivially achieved by choosing a completely uninformative model with \({\mathbf {f}}\left( {\mathbf {x}}\right) \equiv {\mathbf {g}}\left( {\mathbf {x}}\right) \equiv 1\) and \({\mathbf {K}}=1\). An approach that can be applied to deterministic systems and for stochastic systems with additive white noise is to set \({\mathbf {g}}\left( {\mathbf {x}}\right) ={\mathbf {x}}\), and then choose \({\mathbf {f}}\) as the transformation with smallest modeling error (Brunton et al. 2016a, b).

A more general approach is to optimize the dominant spectrum of the Koopman operator. At long timescales, the dynamics of the system are usually dominated by the Koopman eigenfunctions of the Koopman operator with large eigenvalues. If the dynamics obey detailed balance, those eigenvalues are real-valued, and the variational approach for reversible Markov processes can be applied that has made great progress in the field of molecular dynamics (Noé and Nüske 2013; Nüske et al. 2014). In such processes, the smallest modeling error of (1) is achieved by setting \({\mathbf {f}}={\mathbf {g}}\) equal to the corresponding eigenfunctions. Noé and Nüske (2013) describes a general approach to approximate the unknown eigenfunction from time series data of a reversible Markov process: Given a set of orthogonal candidate functions, \({\mathbf {f}}\), it can be shown that their time-autocorrelations are lower bounds to the corresponding Koopman eigenvalues, and are equal to them exactly if, and only if \({\mathbf {f}}\) are equal to the Koopman eigenfunctions. This approach provides a variational score, such as the sum of estimated eigenvalues (the Rayleigh trace), that can be optimized to approximate the eigenfunctions. If \({\mathbf {f}}\) is defined by a linear superposition of a given set of basis functions, then the optimal coefficients are found equivalently by either maximizing the variational score, or minimizing the regression error in the feature space as done in EDMD (Williams et al. 2015a)—see Hao et al. (2017). However, the regression error cannot be used to select the form and the number of basis functions themselves, whereas the variational score can. When working with a finite dataset, however, it is important to avoid overfitting, and to this end a cross-validation method has been proposed to compute variational scores that take the statistical error into account (McGibbon and Pande 2015). Such cross-validated variational scores can be used to determine the size and type of the function classes and the other hyper-parameters of the dynamicalmodel.

While this approach is extremely powerful for stationary and data and reversible Markov processes, almost all real-world dynamical processes and time series thereof are irreversible and often even nonstationary. In this paper, we introduce a variational approach for Markov processes (VAMP) that can be employed to optimize parameters and hyper-parameters of arbitrary Markov processes. VAMP is based on the singular value decomposition of the Koopman operator, which overcomes the limited usefulness of the eigenvalue decomposition of time-irreversible and nonstationary processes. We first show that the approximation error of the Koopman operator deduced from the linear model (1) can be minimized by setting \({\mathbf {f}}\) and \({\mathbf {g}}\) to be the top left and right singular functions of the Koopman operator. Then, by using the variational description of singular components, a class of variational scores, VAMP-r for \(r=1,2,\ldots \), are proposed to measure the similarity between the estimated singular functions and the true ones. Maximization of any of these variational scores leads to optimal model parameters and is algorithmically identical to Canonical Correlation Analysis (CCA) between the featurized time-lagged pair of variables \({\mathbf {x}}_{t}\) and \({\mathbf {x}}_{t+\tau }\). This approach can also be employed to learn the feature transformations by nonlinear function approximators, such as deep neural networks. Furthermore, we establish a relationship between the VAMP-2 score and the approximation error of the dynamical model with respect to the true Koopman operator. We show that this approximation error can be practically computed up to a constant, and define its negative as the VAMP-E score. Finally, we demonstrate that optimizing the VAMP-E score in a cross-validation framework leads to an optimal choice of hyper-parameters.

2 Theory

2.1 Koopman Analysis of Dynamical Systems and Its Singular Value Decomposition

The Koopman operator \({\mathcal {K}}_{\tau }\) of a Markov process is a linear operator defined by

$$\begin{aligned} {\mathcal {K}}_{\tau }g({\mathbf {x}})\triangleq {\mathbb {E}} \left[ g({\mathbf {x}}_{t+\tau })\mid {\mathbf {x}}_{t}= {\mathbf {x}}\right] . \end{aligned}$$
(2)

For given \({\mathbf {x}}_{t}\), the Koopman operator can be used to compute the conditional expected value of an arbitrary observable g at time \(t+\tau \). For the special choice that g is the Dirac delta function \(\delta _{{\mathbf {y}}}\) centered at \({\mathbf {y}}\), application of the Koopman operator evaluates the transition density of the dynamics, \({\mathcal {K}}_{\tau }\delta _{{\mathbf {y}}}({\mathbf {x}})={\mathbb {P}}({\mathbf {x}}_{t+\tau }={\mathbf {y}}|{\mathbf {x}}_{t}={\mathbf {x}})\) (see Appendix A.3). Thus, the Koopman operator is a complete description of the dynamical properties of a Markovian system. For convenience of analysis, we consider here \({\mathcal {K}}_{\tau }\) as a mapping from \({\mathcal {L}}_{\rho _{1}}^{2}=\left\{ g|\left\langle g,g\right\rangle _{\rho _{1}}<\infty \right\} \) to \({\mathcal {L}}_{\rho _{0}}^{2}=\left\{ f|\left\langle f,f\right\rangle _{\rho _{0}}<\infty \right\} \), where \(\rho _{0}\) and \(\rho _{1}\) are empirical distributions of \({\mathbf {x}}_{t}\) and \({\mathbf {x}}_{t+\tau }\) of all transition pairs \(\{({\mathbf {x}}_{t},{\mathbf {x}}_{t+\tau })\}\) occurring in the given time series (see Appendix A.1), and the inner products are defined by

$$\begin{aligned} \left\langle f,g\right\rangle _{\rho _{0}}=\int f\left( {\mathbf {x}}\right) g\left( {\mathbf {x}}\right) \rho _{0} \left( {\mathbf {x}}\right) \mathrm {d}{\mathbf {x}},\quad \left\langle f,g\right\rangle _{\rho _{1}}=\int f\left( {\mathbf {x}}\right) g\left( {\mathbf {x}}\right) \rho _{1} \left( {\mathbf {x}}\right) \mathrm {d}{\mathbf {x}}. \end{aligned}$$
(3)

How is the finite-dimensional linear model (1) related to the Koopman operator description? Let us consider \({\mathbf {f}}({\mathbf {x}}_{t})\) to be a sufficient statistics for \({\mathbf {x}}_{t}\), and let \({\mathbf {g}}\) be a dictionary of observables, then the value of an arbitrary observable h in the subspace of \({\mathbf {g}}\), i.e., \(h={\mathbf {c}}^{\top }{\mathbf {g}}\), with some coefficients \({\mathbf {c}}\), can be predicted from \({\mathbf {x}}_{t}\) as \({\mathbb {E}}\left[ h({\mathbf {x}}_{t+\tau })|{\mathbf {x}}_{t}\right] ={\mathbf {c}}^{\top }{\mathbf {K}}^{\top }{\mathbf {f}}({\mathbf {x}}_{t})\). This implies that Eq. (1) is an algebraic representation of the projection of the Koopman operator onto the subspace spanned by functions \({\mathbf {f}}\) and \({\mathbf {g}}\), and the matrix \({\mathbf {K}}\) is therefore called the Koopman matrix. Combining this insight with the generalized Eckart–Young Theorem (Hsing and Eubank 2015) leads to our first result, namely what is the optimal choice of functions \({\mathbf {f}}\) and \({\mathbf {g}}\):

Theorem 1

Optimal approximation of Koopman operator. If \({\mathcal {K}}_{\tau }\) is a Hilbert–Schmidt operator between the separable Hilbert spaces \({\mathcal {L}}_{\rho _{1}}^{2}\) and \({\mathcal {L}}_{\rho _{0}}^{2}\), the linear model (1) with the smallest modeling error in Hilbert–Schmidt norm is given by \({\mathbf {f}}=(\psi _{1},\ldots ,\psi _{k})^{\top }\), \({\mathbf {g}}=(\phi _{1},\ldots ,\phi _{k})^{\top }\) and \({\mathbf {K}}=\mathrm {diag}(\sigma _{1},\ldots ,\sigma _{k})\), i.e.,

$$\begin{aligned} {\mathbb {E}}\left[ \phi _{i}({\mathbf {x}}_{t+\tau })\right] =\sigma _{i}{ \mathbb {E}}\left[ \psi _{i}({\mathbf {x}}_{t})\right] ,\quad \mathrm{for}\; i=1,\ldots ,k \end{aligned}$$
(4)

under the constraint \(\mathrm {dim}({\mathbf {f}}),\mathrm {dim}({\mathbf {g}})\le k\), and the projected Koopman operator deduced from (4) is

$$\begin{aligned} \hat{{\mathcal {K}}}_{\tau }g=\sum _{i=1}^{k}\sigma _{i}\left\langle g,\phi _{i}\right\rangle _{\rho _{1}}\psi _{i}, \end{aligned}$$
(5)

where the singular value \(\sigma _{i}>0\) is the square root of the \(i\hbox {th}\) largest eigenvalue of \({\mathcal {K}}_{\tau }^{*}{\mathcal {K}}_{\tau }\) or \({\mathcal {K}}_{\tau }{\mathcal {K}}_{\tau }^{*}\), the left and right singular function \(\psi _{i},\phi _{i}\) are the ith eigenfunctions of \({\mathcal {K}}_{\tau }^{*}{\mathcal {K}}_{\tau }\) and \({\mathcal {K}}_{\tau }{\mathcal {K}}_{\tau }^{*}\) with

$$\begin{aligned} \left\langle \psi _{i},\psi _{j}\right\rangle _{\rho _{0}}=1_{i=j},\quad \left\langle \phi _{i},\phi _{j}\right\rangle _{\rho _{1}}=1_{i=j}, \end{aligned}$$
(6)

and the first singular component is always given by \((\sigma _{1},\phi _{1},\psi _{1})=(1,\mathbb {1},\mathbb {1})\) with \(\mathbb {1}\left( {\mathbf {x}}\right) \equiv 1\).

Proof

See Appendix A.2. \(\square \)

This theorem is universal for Markov processes, and the major assumption is that the Koopman operator is Hilbert–Schmidt, which is required for the existences of the singular value decomposition (SVD) of \({\mathcal {K}}_{\tau }\) and the finite Hilbert–Schmidt norm \(\Vert {\mathcal {K}}_{\tau }\Vert _{\mathrm {HS}}\). Appendix A.4 provides two sufficient conditions for the assumption. However, it is worth noting that the Koopman operators of deterministic systems are not Hilbert–Schmidt or even compact in usual cases (see Appendix A.5), and thus all conclusions and methods in this paper are not applicable to deterministic systems.

In addition, we prove in Appendix A.3 that \(\Vert \hat{{\mathcal {K}}}_{\tau }-{\mathcal {K}}_{\tau }\Vert _{\mathrm {HS}}\) is equal to a weighted \({\mathcal {L}}^{2}\) error of the transition density, which provides a more meaningful interpretation of the modeling error in Hilbert–Schmidt norm.

Fig. 1
figure 1

Analysis results of the dynamical system (7) with lag time \(\tau =1\). a A typical simulation trajectory. b Transition density \({\mathbb {P}}(x_{t+1}|x_{t})\). c The singular values. d The first three nontrivial left and right singular functions. [The first singular component is \((\sigma _{1},\phi _{1},\psi _{1})=(1,\mathbb {1},\mathbb {1})\).] e Approximate transition densities obtained from the projected Koopman operator \(\hat{{\mathcal {K}}}_{\tau }\) consisting of first k singular components defined by (5) for \(k=2,3,4\), where the relative error is calculated as \(\Vert \hat{{\mathcal {K}}}_{\tau }-{\mathcal {K}}_{\tau }\Vert _{\mathrm {HS}}/\Vert {\mathcal {K}}_{\tau }\Vert _{\mathrm {HS}}\)

Full size image

Example 1

Consider a one-dimensional dynamical system

$$\begin{aligned} x_{t+1}=\frac{x_{t}}{2}+\frac{7x_{t}}{1+0.12x_{t}^{2}}+6\cos x_{t}+\sqrt{10}u_{t} \end{aligned}$$
(7)

evolving in the state space \([-20,20]\), where \(u_{t}\) is a standard Gaussian white noise zero mean and unit variance (see Appendix K.1 for details on the numerical simulations and analysis). This system has two metastable states with the boundary close to \(x=0\) as shown in Fig. 1a, and the singular components are summarized in Fig. 1c, d. As shown in the figures, the sign structures of the second left and right singular functions clearly indicate the metastable states, and the third and forth singular functions provide more detailed information on the dynamics. An accurate estimate of the transition density can be obtained by combining the first four singular components, and the corresponding relative approximation error of the Koopman operator is only \(6.6\%\) (see Fig. 1b, e). In addition, we utilize the finite-rank approximate Koopman operators to predict the time evolution of the distribution of \(x_{t}\) for \(t=1,\ldots ,256\) with the initial state \(x_{0}=12\), and a small error can also be achieved when the rank is only 4 as displayed in Fig. 2, where

$$\begin{aligned} \mathrm {error}=\sum _{t=1}^{256}\int \rho _{1}(x_{t})^{-1} \left( \hat{{\mathbb {P}}}(x_{t}|x_{0})- {\mathbb {P}}(x_{t}|x_{0})\right) ^{2}\mathrm {d}x_{t} \end{aligned}$$
(8)

is the cumulative kinetic distance (Noé and Clementi 2015) between the transition density \({\mathbb {P}}(x_{t}|x_{0})\) and its estimate \(\hat{{\mathbb {P}}}(x_{t}|x_{0})\), and \(\rho _{1}\) is the stationary distribution.

Fig. 2
figure 2

Probability density of state \(x_{t}\) predicted by a the full model and b the projected Koopman operator \(\hat{{\mathcal {K}}}_{\tau }\) with rank \(k=2,3,4\), where the initial state is \(x_{0}=-12\)

Full size image

There are other formalisms to describe Markovian dynamics, for example, the Markov propagator or the weighted Markov propagator, also called transfer operator (Schütte et al. 1999). These propagators are commonly used for modeling physical processes such as molecular dynamics, and describe the evolution of probability densities instead of observables. We show in Appendix B that all conclusions in this paper can be equivalently established by interpreting \((\sigma _{i},\rho _{1}\phi _{i},\rho _{0}\psi _{i})\) as the singular components of the Markov propagator.

2.2 Variational Principle for Markov Processes

In order to allow the optimal model (4) to be estimated from data, we develop a variational principle for the approximation of singular values and singular functions of Markov processes.

According to the Rayleigh variational principle of singular values, the first singular component maximizes the generalized Rayleigh quotient of \({\mathcal {K}}_{\tau }\) as

$$\begin{aligned} (\psi _{1},\phi _{1})=\arg \max _{f,g}\frac{\left\langle f,{\mathcal {K}}_{\tau }g\right\rangle _{\rho _{0}}}{\sqrt{\left\langle f,f\right\rangle _{\rho _{0}}\cdot \left\langle g,g\right\rangle _{\rho _{1}}}} \end{aligned}$$
(9)

and the maximal value of the generalized Rayleigh quotient is equal to the first singular value \(\sigma _{1}=\left\langle \psi _{1},\,{\mathcal {K}}_{\tau }\phi _{1}\right\rangle _{\rho _{0}}\). For the \(i\hbox {th}\) singular component with \(i>1\), we have

$$\begin{aligned} (\psi _{i},\phi _{i})=\arg \max _{f,g}\frac{\left\langle f,{\mathcal {K}}_{\tau }g\right\rangle _{\rho _{0}}}{\sqrt{\left\langle f,f\right\rangle _{\rho _{0}}\cdot \left\langle g,g\right\rangle _{\rho _{1}}}} \end{aligned}$$
(10)

under constraints

$$\begin{aligned} \left\langle f,\psi _{j}\right\rangle _{\rho _{0}}=\left\langle g,\phi _{j}\right\rangle _{\rho _{1}}=0,\quad \forall j=1,\ldots ,i-1 \end{aligned}$$
(11)

and the maximal value is equal to \(\sigma _{i}=\left\langle \psi _{i},\,{\mathcal {K}}_{\tau }\phi _{i}\right\rangle _{\rho _{0}}\). These insights can be summarized by the following variational theorem for seeking all top k singular components simultaneously:

Theorem 2

VAMP variational principle. The k dominant singular components of a Koopman operator are the solution of the following maximization problem:

$$\begin{aligned} \sum _{i=1}^{k}\sigma _{i}^{r}&=\max _{{\mathbf {f}},{\mathbf {g}}}{\mathcal {R}}_{r}\left[ {\mathbf {f}},{\mathbf {g}}\right] ,\nonumber \\ s.t.&\left\langle f_{i},f_{j}\right\rangle _{\rho _{0}}=1_{i=j},\nonumber \\&\left\langle g_{i},g_{j}\right\rangle _{\rho _{1}}=1_{i=j}, \end{aligned}$$
(12)

where \(r\ge 1\) can be any positive integer. The maximal value is achieved by the singular functions \(f_{i}=\psi _{i}\) and \(g_{i}=\phi _{i}\) and

$$\begin{aligned} {\mathcal {R}}_{r}\left[ {\mathbf {f}},{\mathbf {g}}\right] =\sum _{i=1}^{k}\left\langle f_{i},{\mathcal {K}}_{\tau }g_{i}\right\rangle _{\rho _{0}}^{r} \end{aligned}$$
(13)

is called the VAMP-r score of \({\mathbf {f}}\) and \({\mathbf {g}}\).

Proof

See Appendix C. \(\square \)

This theorem generalizes Proposition 2 in Froyland (2013) where only the case of \(k=2\) is considered. It is important to note that this theorem has direct implications for the data-driven estimation of dynamical models. For \(r=1\), \({\mathcal {R}}_{r}\left[ {\mathbf {f}},{\mathbf {g}}\right] \) is actually the time correlation between \({\mathbf {f}}({\mathbf {x}}_{t})\) and \({\mathbf {g}}({\mathbf {x}}_{t+\tau })\) since \(\left\langle f_{i},{\mathcal {K}}_{\tau }g_{i}\right\rangle _{\rho _{0}}={\mathbb {E}}_{t}[f_{i}({\mathbf {x}}_{t})g_{i}({\mathbf {x}}_{t+\tau })]\) and \({\mathbb {E}}_{t}[\cdot ]\) denotes the expectation value over all transition pairs \((x_{t},x_{t+\tau })\) in the time series. Hence the maximization of VAMP-r is analogous to the problem of seeking orthonormal transformations of \({\mathbf {x}}_{t}\) and \({\mathbf {x}}_{t+\tau }\) with maximal time-correlations, and we can thus utilize the canonical correlation analysis (CCA) algorithm (Hardoon et al. 2004) in order to estimate the singular components from data.

2.3 Comparison with Related Analysis Approaches

The SVD of the Koopman operator is equivalent to the eigenvalue decomposition when the Markov process is time-reversible and stationary with \(\rho _{0}=\rho _{1}\), and therefore the variational principle presented here is a generalization of that developed for reversible conformation dynamics (Noé and Nüske 2013; Nüske et al. 2014). Specifically, VAMP-1 maximizes the Rayleigh trace, i.e., the sum of the estimated eigenvalues (Noé and Nüske 2013; McGibbon and Pande 2015), and VAMP-2 maximizes the kinetic variance introduced in Noé and Clementi (2015). See Appendix D for a detailed derivation of the reversible variational principle from the VAMP variational principle. For irreversible Markov processes, the singular functions can provide low-dimensional embeddings of kinetic distances between states like eigenfunctions of reversible processes (Paul et al. 2018). Furthermore, the coherent sets of nonstationary Markov processes, which are the generalization of metastable states, can be identified from dominant singular functions (Koltai et al. 2018).

The dynamics of an irreversible Markov process can also be analyzed through solving the eigenvalue problem \({\mathcal {K}}_{\tau }g=\lambda g\) [see, e.g., Williams et al. (2015a, b), Klus et al. (2015),Klus and Schütte (2015)], and the eigenfunctions form an invariant subspace of the Koopman operator for multiple lag times since the eigenvalue problem satisfies

$$\begin{aligned} {\mathcal {K}}_{\tau }g=\lambda g\Rightarrow {\mathcal {K}}_{n\tau }g=\lambda ^{n}g,\quad \forall n\ge 1. \end{aligned}$$
(14)

However, as far as we know, there is no variational principle for approximate eigenfunctions of irreversible Markov processes, and it is difficult to evaluate errors of projections of Koopman operators to the invariant subspaces. The SVD-based analysis approach overcomes the above problems and yields the optimal finite-rank approximate models. The major limitation of this approach comes from the fact that the singular functions are dependent on the choice of the lag time and the optimality of model (4) holds only for a fixed \(\tau \). The optimization and error analysis of Koopman models for multiple lag times will be studied in our future work.

3 Estimation Algorithms

We introduce algorithms to estimate optimal dynamical models from time series data. We make the Ansatz to represent the feature functions \({\mathbf {f}}\) and \({\mathbf {g}}\) as linear combinations of basis functions \(\varvec{\chi }_{0}=(\chi _{0,1},\chi _{0,2},\ldots )^{\top }\) and \(\varvec{\chi }_{1}=(\chi _{1,1},\chi _{1,2},\ldots )^{\top }\):

$$\begin{aligned} {\mathbf {f}}&={\mathbf {U}}^{\top }\varvec{\chi }_{0},\nonumber \\ {\mathbf {g}}&={\mathbf {V}}^{\top }\varvec{\chi }_{1}. \end{aligned}$$
(15)

Here, \({\mathbf {U}}\) and \({\mathbf {V}}\) are matrices of size \(m\times k\) and \(m^{\prime }\times k\), i.e., we are trying to approximate k singular components by linearly combining m and \(m^{\prime }\) basis functions. For the sake of generality we have assumed that \({\mathbf {f}}\) and \({\mathbf {g}}\) are represented by different basis sets. However, in practice one can justify using a single basis set the joint set \(\varvec{\chi }^{\top }=(\varvec{\chi }_{0}^{\top },\varvec{\chi }_{1}^{\top })\) as an Ansatz for both \({\mathbf {f}}\) and \({\mathbf {g}}\). Please note that despite the linear Ansatz (15), the feature functions may be strongly nonlinear in the system’s state variables \({\mathbf {x}}\), thus we are not restricting the generality of the functions \({\mathbf {f}}\) and \({\mathbf {g}}\) that can be represented. In this section, we consider three problems: (i) optimizing \({\mathbf {U}}\) and \({\mathbf {V}}\), (ii) optimizing \(\varvec{\chi }_{0}\) and \(\varvec{\chi }_{1}\) and (iii) assessing the quality of the resulting dynamical model.

For convenience of notation, we denote by \({\mathbf {C}}_{00},{\mathbf {C}}_{11},{\mathbf {C}}_{01}\) the covariance matrices and time-lagged covariance matrices of basis functions, which can be computed from a trajectory \(\{x_{1},\ldots ,x_{T}\}\) by

$$\begin{aligned} {\mathbf {C}}_{00}\triangleq & {} {\mathbb {E}}_{t}\left[ \varvec{\chi }_{0}\left( {\mathbf {x}}_{t}\right) \varvec{\chi }_{0}\left( {\mathbf {x}}_{t}\right) ^{\top }\right] \approx \frac{1}{T-\tau }\sum _{t=1}^{T-\tau }\varvec{\chi }_{0}\left( {\mathbf {x}}_{t}\right) \varvec{\chi }_{0}\left( {\mathbf {x}}_{t}\right) ^{\top }, \end{aligned}$$
(16)
$$\begin{aligned} {\mathbf {C}}_{11}\triangleq & {} {\mathbb {E}}_{t}\left[ \varvec{\chi }_{1}\left( {\mathbf {x}}_{t+\tau }\right) \varvec{\chi }_{1}\left( {\mathbf {x}}_{t+\tau }\right) ^{\top }\right] \approx \frac{1}{T-\tau }\sum _{t=1+\tau }^{T}\varvec{\chi }_{1}\left( {\mathbf {x}}_{t}\right) \varvec{\chi }_{1}\left( {\mathbf {x}}_{t}\right) ^{\top }, \end{aligned}$$
(17)
$$\begin{aligned} {\mathbf {C}}_{01}\triangleq & {} {\mathbb {E}}_{t}\left[ \varvec{\chi }_{0}\left( {\mathbf {x}}_{t}\right) \varvec{\chi }_{1}\left( {\mathbf {x}}_{t+\tau }\right) ^{\top }\right] \approx \frac{1}{T-\tau }\sum _{t=1}^{T-\tau }\varvec{\chi }_{0}\left( {\mathbf {x}}_{t}\right) \varvec{\chi }_{1}\left( {\mathbf {x}}_{t+\tau }\right) ^{\top }. \end{aligned}$$
(18)

If there are multiple trajectories, the covariance matrices can be computed in the same manner by averaging over all trajectories. Instead of the direct estimators (16–18), more elaborated estimation methods such as regularization methods (Tibshirani 1996) and reweighting estimators (Hao et al. 2017) may be used.

3.1 Feature TCCA: Finding the Best Linear Model in a Given Feature Space

We first propose a solution for the problem of finding the optimal parameter matrices \({\mathbf {U}}\) and \({\mathbf {V}}\) given that the basis functions \(\varvec{\chi }_{0}\) and \(\varvec{\chi }_{1}\) are known. Substituting the linear Ansatz (15) into the VAMP variational principle shows that \({\mathbf {U}}\) and \({\mathbf {V}}\) can be computed as the solutions of the maximization problem:

$$\begin{aligned} \max _{{\mathbf {U}},{\mathbf {V}}}&{\mathcal {R}}_{r}({\mathbf {U}},{\mathbf {V}})\nonumber \\ \mathrm {s.t.}&{\mathbf {U}}^{\top }{\mathbf {C}}_{00}{\mathbf {U}}={\mathbf {I}}\nonumber \\&{\mathbf {V}}^{\top }{\mathbf {C}}_{11}{\mathbf {V}}={\mathbf {I}}, \end{aligned}$$
(19)

where

$$\begin{aligned} {\mathcal {R}}_{r}({\mathbf {U}},{\mathbf {V}})=\sum _{i=1}^{k}\left( {\mathbf {u}}_{i}^{\top }{\mathbf {C}}_{01}{\mathbf {v}}_{i}\right) ^{r} \end{aligned}$$
(20)

is a matrix representation of VAMP-r score, and \({\mathbf {u}}_{i}\) and \({\mathbf {v}}_{i}\) are the ith columns of \({\mathbf {U}}\) and \({\mathbf {V}}\). This problem can be solved by applying linear CCA (Hardoon et al. 2004) in the feature spaces defined by the basis sets \(\varvec{\chi }_{0}({\mathbf {x}}_{t})\) and \(\varvec{\chi }_{1}({\mathbf {x}}_{t+\tau })\), and the same solution will be obtained for any other choice of r. (See Appendices E.1 and E.2 for more detailed proof and analysis.) The resulting algorithm for finding the best linear model is a CCA in feature space, applied on time-lagged data. Hence we briefly call this algorithm feature TCCA:

  1. 1.

    Compute covariance matrices \({\mathbf {C}}_{00},{\mathbf {C}}_{01},{\mathbf {C}}_{11}\) via (16–18).

  2. 2.

    Perform the truncated SVD

    $$\begin{aligned} \bar{{\mathbf {K}}}={\mathbf {C}}_{00}^{-\frac{1}{2}}{\mathbf {C}}_{01}{ \mathbf {C}}_{11}^{-\frac{1}{2}}\approx {\mathbf {U}}^{\prime }{ \mathbf {K}}{\mathbf {V}}^{\prime \top }, \end{aligned}$$

    where \(\bar{{\mathbf {K}}}\) is the Koopman matrix for the normalized basis functions \({\mathbf {C}}_{00}^{-\frac{1}{2}}\varvec{\chi }_{0}\) and \({\mathbf {C}}_{11}^{-\frac{1}{2}}\varvec{\chi }_{1}\), \({\mathbf {K}}=\mathrm {diag}(K_{11},\ldots ,K_{kk})\) is a diagonal matrix of the first k singular values that approximate the true singular values \(\sigma _{1},\ldots ,\sigma _{k}\), and \({\mathbf {U}}^{\prime }\) and \({\mathbf {V}}^{\prime }\) consist of the k corresponding left and right singular vectors respectively.

  3. 3.

    Compute \({\mathbf {U}}={\mathbf {C}}_{00}^{-\frac{1}{2}}{\mathbf {U}}^{\prime }\) and \({\mathbf {V}}={\mathbf {C}}_{11}^{-\frac{1}{2}}{\mathbf {V}}^{\prime }\).

  4. 4.

    Output the linear model (1) with \(K_{ii}\), \(f_{i}={\mathbf {u}}_{i}^{\top }\varvec{\chi }_{0}\) and \(g_{i}={\mathbf {v}}_{i}^{\top }\varvec{\chi }_{1}\) being the estimates of the ith singular value, left singular function and right singular function of the Koopman operator.

Please note that this pseudocode is given only for illustrative purposes and cannot be executed literally if \({\mathbf {C}}_{00}\) and \({\mathbf {C}}_{11}\) do not have full rank, i.e., are not invertible. To handle this problem, we ensure that the basis functions are linearly independent by applying a decorrelation (whitening) transformation that ensures that \({\mathbf {C}}_{00}\) and \({\mathbf {C}}_{11}\) will both have full rank. We then add the constant function \(\mathbb {1}\left( x\right) \equiv 1\) to the decorrelated basis sets to ensure that \(\mathbb {1}\) belongs to the subspaces spanned by \(\varvec{\chi }_{0}\) and by \(\varvec{\chi }_{1}\). It can be shown that the singular values given by the feature TCCA algorithm with these numerical modifications are bounded by 1, and the first estimated singular component is exactly \((K_{11},f_{1},g_{1})=(1,\mathbb {1},\mathbb {1})\) even in the presence of statistical noise and modeling error—see Appendix F.1 for details.

In the case of \(k=\mathrm {dim}(\varvec{\chi }_{0})=\mathrm {dim}(\varvec{\chi }_{1})\) and full rank \({\mathbf {C}}_{00},{\mathbf {C}}_{11}\), the output of the feature TCCA can be equivalently written as

$$\begin{aligned}&{\mathbb {E}}\left[ {\mathbf {V}}^{\top }\varvec{\chi }_{1} \left( {\mathbf {x}}_{t+\tau }\right) \right] ={\mathbf {K}}^{\top }{\mathbb {E}} \left[ {\mathbf {U}}^{\top }\varvec{\chi }_{0} \left( {\mathbf {x}}_{t}\right) \right] \nonumber \\&\quad \Rightarrow {\mathbb {E}}\left[ \varvec{\chi }_{1} \left( {\mathbf {x}}_{t+\tau }\right) \right] ={\mathbf {K}}_{\chi }^{\top }{ \mathbb {E}}\left[ \varvec{\chi }_{0}\left( {\mathbf {x}}_{t}\right) \right] \end{aligned}$$
(21)

where

$$\begin{aligned} {\mathbf {K}}_{\chi }= & {} {\mathbf {U}}{\mathbf {K}}{\mathbf {V}}^{-1}\nonumber \\= & {} {\mathbf {C}}_{00}^{-1}{\mathbf {C}}_{01} \end{aligned}$$
(22)

is equal to the least square solution to the regression problem \(\varvec{\chi }_{1}\left( {\mathbf {x}}_{t+\tau }\right) \approx {\mathbf {K}}_{\chi }^{\top }\varvec{\chi }_{0}\left( {\mathbf {x}}_{t}\right) \). Note that if we further assume that \(\varvec{\chi }_{0}=\varvec{\chi }_{1}\), (21) is identical to the linear model of EDMD. Thus, the feature TCCA can be seen as a generalization of EDMD that can provide approximate Markov models for different basis \(\varvec{\chi }_{0}\) and \(\varvec{\chi }_{1}\). More discussion on the relationship between the two methods is provided in Appendix G.

3.2 Nonlinear TCCA: Optimizing the Basis Functions

We now extend feature TCCA to a more flexible representation of the transformation functions \({\mathbf {f}}\) and \({\mathbf {g}}\) by optimizing the basis functions themselves:

$$\begin{aligned} {\mathbf {f}}\left( {\mathbf {x}}\right)&={\mathbf {U}}^{\top }\varvec{\chi }_{0}\left( {\mathbf {x}};{\mathbf {w}}\right) ,\nonumber \\ {\mathbf {g}}\left( {\mathbf {x}}\right)&={\mathbf {V}}^{\top }\varvec{\chi }_{1}\left( {\mathbf {x}};{\mathbf {w}}\right) . \end{aligned}$$
(23)

Here, \({\mathbf {w}}\) represents a set of parameters that determines the form of the basis functions. As a simple example, consider \({\mathbf {w}}\) to represent the mean vectors and covariance matrices of a Gaussian basis set. However, \(\varvec{\chi }_{0}\left( {\mathbf {x}};{\mathbf {w}}\right) \) and \(\varvec{\chi }_{1}\left( {\mathbf {x}};{\mathbf {w}}\right) \) can also represent very complex and nonlinear learning structures, such as neural networks and decision trees.

The parameters \({\mathbf {w}}\) could conceptually be determined together with the linear expansion coefficients \({\mathbf {U}},{\mathbf {V}}\) by solving (19) with \({\mathbf {C}}_{00}\), \({\mathbf {C}}_{11}\), \({\mathbf {C}}_{01}\) treated as functions of \({\mathbf {w}}\), but this method is not practical due to the nonlinear equality constraints are involved. In practice, we can set k to be \(\min \{\mathrm {dim}\left( \varvec{\chi }_{0}\right) ,\mathrm {dim}\left( \varvec{\chi }_{1}\right) \}\), i.e., the largest number of singular components that can be approximated given the basis set. Then the maximal VAMP-r score for a fixed \({\mathbf {w}}\) can be represented as

$$\begin{aligned} \max _{{\mathbf {U}},{\mathbf {V}}}{\mathcal {R}}_{r}=\left\| {\mathbf {C}}_{00}\left( {\mathbf {w}}\right) ^{-\frac{1}{2}}{\mathbf {C}}_{01}\left( {\mathbf {w}}\right) {\mathbf {C}}_{11}\left( {\mathbf {w}}\right) ^{-\frac{1}{2}}\right\| _{r}^{r}, \end{aligned}$$
(24)

which can also be interpreted as the sum over the r’th power of all singular values of the projected Koopman operator on subspaces of \(\varvec{\chi }_{0},\varvec{\chi }_{1}\) (see Eq. (80) in Appendix E.1 and Eq. (84) in Appendix E.2). Here \(\left\| {\mathbf {A}}\right\| _{r}\) denotes the r-Schatten norm of matrix \({\mathbf {A}}\), which is the \(\ell ^{r}\) norm of singular values of \({\mathbf {A}}\), and \(\left\| {\mathbf {A}}\right\| _{2}\) equals the Frobenius norm of \({\mathbf {A}}\). The parameters \({\mathbf {w}}\) can be optimized without computing \({\mathbf {U}}\) and \({\mathbf {V}}\) explicitly. Using these ideas, nonlinear TCCA can be performed as follows:

  1. 1.

    Compute \({\mathbf {w}}^{*}=\arg \max _{{\mathbf {w}}}\left\| {\mathbf {C}}_{00}\left( {\mathbf {w}}\right) ^{-\frac{1}{2}}{\mathbf {C}}_{01}\left( {\mathbf {w}}\right) {\mathbf {C}}_{11}\left( {\mathbf {w}}\right) ^{-\frac{1}{2}}\right\| _{r}^{r}\) by gradient descent or other nonlinear optimization methods.

  2. 2.

    Approximate the Koopman singular values and singular functions using the feature TCCA algorithm with basis sets \(\varvec{\chi }_{0}\left( {\mathbf {x}};{\mathbf {w}}^{*}\right) \) and \(\varvec{\chi }_{1}\left( {\mathbf {x}};{\mathbf {w}}^{*}\right) \).

Unlike the estimated singular components generated by the feature TCCA, the estimation results of the nonlinear TCCA do generally depend on the value of r. (An example is given in Appendix E.3, where the VAMP scores can be analytically computed.) We suggest to set \(r=2\) in applications for the direct relationship between the VAMP-2 score and the approximation error of Koopman operators and the convenience of cross-validation (see below). The details of the nonlinear TCCA, including the optimization algorithm and regularization, are beyond the scope of this paper. Appendix F.2 provides a brief description of the implementation, and related work based on kernel methods and deep networks can be found in Andrew et al. (2013) and Mardt et al. (2018).

Example 2

Let us consider the stochastic system described in Example 1 again. We generate 10 simulation trajectories of length 500 and approximate the dominant singular components by the feature TCCA. Here, the basis functions are

$$\begin{aligned} \chi _{0,i}(x)=\chi _{1,i}(x)=1_{\frac{40\cdot (i-1)}{m}-20\le x\le \frac{40\cdot i}{m}-20},\quad \text { for }i=1,\ldots ,m, \end{aligned}$$
(25)

which define a partition of the domain \([-20,20]\) into \(m=33\) disjoint intervals. In other words, the approximation is performed based on an MSM with 33 discrete states. Estimation results are given in Fig. 3a, where the discretization errors arising from indicator basis functions are clearly shown. For comparison, we also implement the nonlinear TCCA algorithm with radial basis functions

$$\begin{aligned} \chi _{0,i}(x;w)=\chi _{1,i}(x;w)=\frac{\exp \left( -w\left( x-c_{i} \right) ^{2}\right) }{\sum _{j=1}^{m}\exp \left( -w\left( x-c_{j}\right) ^{2} \right) } \end{aligned}$$
(26)

with smoothing parameter \(w\ge 0\), where \(c_{i}=\frac{40\cdot (i-0.5)}{m}-20\) for \(i=1,\ldots ,m\) are uniformly distributed in \([-20,20]\). Notice that the basis functions given in (25) are a specific case of the radial basis functions with \(w=\infty \), and it is therefore possible to achieve better approximation by optimizing w. As can be seen from Fig. 3b, the nonlinear TCCA provides more accurate estimates of singular functions and singular values (see Appendix K.1 for more details). In addition, both feature TCCA and nonlinear TCCA underestimate the dominant singular values as stated by the variational principle.

Fig. 3
figure 3

Estimated singular components of the system in Example 1, where dash lines represent true singular functions, and the estimation errors of singular functions are defined as \(\delta \psi _{i}=\int \left( f_{i}(x)-\psi _{i}(x)\right) ^{2}\rho _{0}(x)\mathrm {d}x\), \(\delta \phi _{i}=\int \left( g_{i}(x)-\phi _{i}(x)\right) ^{2}\rho _{1}(x)\mathrm {d}x\) with \(\rho _{0}=\rho _{1}\) being the stationary distribution. a Estimates provided by feature TCCA with basis functions (25). b Estimates provided by nonlinear TCCA with basis functions (26)

Full size image

The nonlinear TCCA is similar to the EDMD with dictionary learning (EDMD-DL) (Li et al. 2017), where the feature transformations are optimized by minimizing the regression error of (1). The major advantages of the nonlinear TCCA over EDMD-DL are: First, the uninformative model with zero regression error can be systematically excluded without any extra constraints on features. Second, the optimization objective is directly related to the approximation error of the Koopman operator (see Sect. 3.3). Some recent methods extend EDMD-DL for modeling Koopman operators of deterministic systems (Takeishi et al. 2017; Lusch et al. 2018; Otto and Rowley 2019), and solve the first problem by using the prediction error between the observed \(x_{t}\) and that predicted by the low-dimensional model. But they cannot be applied to stochastic Koopman operators of Markov processes directly.

3.3 Error Analysis

According to (5), both feature TCCA and nonlinear TCCA lead to a rank k approximation

$$\begin{aligned} \hat{{\mathcal {K}}}_{\tau }g=\sum _{i=1}^{k}K_{ii}\left\langle g,g_{i}\right\rangle _{\rho _{1}}f_{i}=\sum _{i=1}^{k}K_{ii}\left\langle g,{\mathbf {v}}_{i}^{\top }\varvec{\chi }_{1}\right\rangle _{\rho _{1}}{\mathbf {u}}_{i}^{\top }\varvec{\chi }_{0} \end{aligned}$$
(27)

to \({\mathcal {K}}_{\tau }\). We consider here the approximation error of (27) in a general case where \({\mathbf {f}}={\mathbf {U}}^{\top }\varvec{\chi }_{0}\) and \({\mathbf {g}}={\mathbf {V}}^{\top }\varvec{\chi }_{1}\) may not satisfy the orthonormal constraints due to statistical noise and numerical errors. After a few steps of derivation, the approximation error can be expressed as

$$\begin{aligned} \left\| \hat{{\mathcal {K}}}_{\tau }-{\mathcal {K}}_{\tau }\right\| _{\mathrm {HS}}^{2}=-{\mathcal {R}}_{E}[{\mathbf {K}},{\mathbf {f}},{\mathbf {g}}]+\left\| {\mathcal {K}}_{\tau }\right\| _{\mathrm {HS}}^{2} \end{aligned}$$
(28)

with

$$\begin{aligned} {\mathcal {R}}_{E}[{\mathbf {K}},{\mathbf {f}},{\mathbf {g}}]=2\sum _{i}K_{ii}\left\langle f_{i},{\mathcal {K}}_{\tau }g_{i}\right\rangle _{\rho _{0}}-\sum _{i,j}K_{ii}K_{jj}\left\langle f_{i},f_{j}\right\rangle _{\rho _{0}}\left\langle g_{i},g_{j}\right\rangle _{\rho _{1}}. \end{aligned}$$
(29)

Remarkably, this error decomposes into a unknown constant part (the square of Hilbert–Schmidt norm of \({\mathcal {K}}_{\tau }\)), and a model-dependent part \({\mathcal {R}}_{E}\) that can be entirely estimated from data by its matrix representation:

$$\begin{aligned} {\mathcal {R}}_{E}({\mathbf {K}},{\mathbf {U}},{\mathbf {V}})=\mathrm {tr} \left[ 2{\mathbf {K}}{\mathbf {U}}^{\top }{\mathbf {C}}_{01}{\mathbf {V}}-{ \mathbf {K}}{\mathbf {U}}^{\top }{\mathbf {C}}_{00}{\mathbf {U}}{\mathbf {K}}{ \mathbf {V}}^{\top }{\mathbf {C}}_{11}{\mathbf {V}}\right] . \end{aligned}$$
(30)

\({\mathcal {R}}_{E}\), is thus a score that can be used alternatively to the VAMP-r scores, and we call \({\mathcal {R}}_{E}\) VAMP-E score. It can be proved that the maximization of \({\mathcal {R}}_{E}\) is equivalent to maximization of \({\mathcal {R}}_{2}\) in feature TCCA or nonlinear TCCA. However, these scores will behave differently in terms of hyper-parameter optimization (see Sect. 4.1). Proofs and analysis are given in Appendix H.

4 Model Validation

4.1 Cross-Validation for Hyper-parameter Optimization

For a data-driven estimation of dynamical models, either using feature TCCA or nonlinear TCCA, we have to strike a balance between the modeling or discretization error and the statistical or overfitting error. The choice of number and type of basis functions is critical for both. If basis sets are very small and not flexible enough to capture singular functions, the approximation results may be inaccurate with large biases. We can improve the variational score and reduce the modeling error by larger and more flexible basis sets. But too complicated basis sets will produce unstable estimates with large statistical variances, and in particular poor predictions on data that has not been used in the estimation process—this problem is known as overfitting in the machine learning community. A popular way to achieve the balance between the statistical bias and variance are resampling methods, including bootstrap and cross-validation (Friedman et al. 2001). They iteratively fit a model in a training set, which are sampled from the data with or without replacement, and validate the model in the complementary dataset. Alternatively, there are also Bayesian hyper-parameter optimization methods. See Arlot and Celisse (2010) and Snoek et al. (2012) for an overview. Here, we will focus on cross-validation and describe how to use the VAMP scores in this and similar resampling frameworks.

Let \(\varvec{\theta }\) be hyper-parameters in feature TCCA or nonlinear TCCA that need to be specified. For example, \(\varvec{\theta }\) includes the number and functional form of basis functions used in feature TCCA, or the architecture and connectivity of a neural network used for nonlinear TCCA. Generally speaking, different values of \(\varvec{\theta }\) correspond to different dynamical models that we want to rank, and these models may be of completely different types. The cross-validation of \(\varvec{\theta }\) can be performed as follows:

  1. 1.

    Separate the available trajectories into J disjoint folds \({\mathcal {D}}_{1},\ldots ,{\mathcal {D}}_{J}\) with approximately equal size. If there are only a small number of long trajectories, we can divide each trajectory into blocks of length L with \(\tau <L\ll T\) and create folds based on the blocks. This defines a number of J training sets, with training set j consisting of all data except the jth fold, \({\mathcal {D}}_{j}^{\mathrm {train}}=\cup _{l\ne j}{\mathcal {D}}_{l}\), and the jth fold used as test set \({\mathcal {D}}_{j}^{\mathrm {test}}={\mathcal {D}}_{j}\).

  2. 2.

    For each hyper-parameter set \(\varvec{\theta }\):

    1. (a)

      For \(j=1,\ldots ,J:\)

      1. i.

        Train on \({\mathcal {D}}_{j}^{\mathrm {train}}\)n: training set \({\mathcal {D}}_{j}^{\mathrm {train}}\), construct the best k-dimensional linear model consisting of \(({\mathbf {K}},{\mathbf {U}}^{\top }\varvec{\chi }_{0},{\mathbf {V}}^{\top }\varvec{\chi }_{1})\) by applying the feature TCCA or nonlinear TCCA with hyper-parameters \(\varvec{\theta }\)

      2. ii.

        Validate on \({\mathcal {D}}_{\mathrm {test}}\): measure the performance of the estimated singular components by a score

        $$\begin{aligned} \mathrm {CV}_{j}\left( \varvec{\theta }\right) =\mathrm {CV}\left( {\mathbf {K}},{\mathbf {U}},{\mathbf {V}}|{\mathcal {D}}_{\mathrm {test}}\right) \end{aligned}$$
        (31)
    2. (b)

      Compute cross-validation score

      $$\begin{aligned} \mathrm {MCV}\left( \varvec{\theta }\right) = \frac{1}{J}\sum _{j=1}^{J}\mathrm {CV}_{j}\left( \varvec{\theta }\right) \end{aligned}$$
      (32)
  3. 3.

    Select model/hyper-parameter set with maximal \(\mathrm {MCV}\left( \varvec{\theta }\right) \).

The key to the above procedure is how to evaluate the estimated singular components for given test set. It is worth pointing out that we cannot simply define the validation score directly as the VAMP-r score of estimated singular functions for the test data, because the singular functions obtained from training data are usually not orthonormal with respect to the test data.

A feasible way is to utilize the subspace variational score as proposed for reversible Markov processes in McGibbon and Pande (2015). For VAMP-r this score becomes:

$$\begin{aligned} \mathrm {CV}\left( {\mathbf {K}},{\mathbf {U}},{\mathbf {V}}|{\mathcal {D}}_{ \mathrm {test}}\right)= & {} {\mathcal {R}}_{r}^{\mathrm {space}}\left( { \mathbf {U}},{\mathbf {V}}|{\mathcal {D}}_{\mathrm {test}}\right) \nonumber \\= & {} \left\| \left( {\mathbf {U}}^{\top }{\mathbf {C}}_{00}^{ \mathrm {test}}{\mathbf {U}}\right) ^{-\frac{1}{2}}\left( {\mathbf {U}}^{\top }{ \mathbf {C}}_{01}^{\mathrm {test}}{\mathbf {V}}\right) \left( { \mathbf {V}}^{\top }{\mathbf {C}}_{11}^{\mathrm {test}}{\mathbf {V}} \right) ^{-\frac{1}{2}}\right\| _{r}^{r}, \end{aligned}$$
(33)

where \({\mathcal {R}}_{r}^{\mathrm {space}}\) measures the consistency between the singular subspace and the estimated one without the constraint of orthonormality. However, this scheme suffers from the following limitations in practical applications: Firstly, the value of k must be chosen a priori and kept fixed during the cross-validation procedure, which implies that models with a different number of singular components cannot be compared by the validation scores. Secondly, computation of the validation score possibly suffers from numerical instability. (See Appendix I for detailed analysis.)

We suggest in this paper to perform the cross-validation based on the approximation error of Koopman operators. According to conclusions in Sect. 3.3, feature TCCA and VAMP-2 base nonlinear TCCA both maximize the VAMP-E score \({\mathcal {R}}_{E}\left( {\mathbf {K}},{\mathbf {U}},{\mathbf {V}}|{\mathcal {D}}_{\mathrm {train}}\right) \) for a given training set \({\mathcal {D}}_{\mathrm {train}}\).

Therefore, we can score the performance of estimated singular components on the test set by

$$\begin{aligned} \mathrm {CV}\left( {\mathbf {K}},{\mathbf {U}},{\mathbf {V}}|{\mathcal {D}}_{ \mathrm {test}}\right) ={\mathcal {R}}_{E}\left( {\mathbf {K}},{\mathbf {U}},{ \mathbf {V}}|{\mathcal {D}}_{\mathrm {test}}\right) . \end{aligned}$$
(34)

In contrast with the validation score (33) deduced from the subspace VAMP-r score, the validation score defined by (34) allows us to choose k according to practical requirements: If we are only interested in a small number of dominant singular components, we can select a fixed value of k. If we want to evaluate the statistical performance of the approximate model consisting of all available estimated singular components as in the EDMD method, we can set \(k=\min \{\mathrm {dim}(\varvec{\chi }_{0}),\mathrm {dim}(\varvec{\chi }_{1})\}\). We can even view k as a hyper-parameter and select a suitable rank of the model via cross-validation. Another advantage of the VAMP-E based validation score is that it does not involve any inverse operation of matrices and can be stably computed.

It is worth pointing out that a validation score is proposed Kurebayashi et al. (2016) for cross-validation of kernel DMD based on the analysis of approximation error of transition densities, which has a similar form to that of VAMP-E. The theoretical and empirical comparisons between the two scores will be performed in our future work.

Example 3

We consider here the choice of the basis function number m for the nonlinear TCCA in Example 2. We use five fold cross-validation with the VAMP-E score to compare different values of m. While the average score computed by training sets keeps increasing with m, both the cross-validation score and the exact VAMP-E score achieve their maximum value at \(m=33\) as in Example 2 (see Fig. 4a). The optimality can also be demonstrated by comparing Figs. 3b and 4b. A much smaller basis set with \(m=13\) yields large errors in the approximation of singular functions. When \(m=250\), the estimation of singular functions suffers from overfitting and the estimated singular value is even larger than the true value due to the statistical noise.

Fig. 4
figure 4

Cross-validation for modeling the system in Example 1. a Cross-validated VAMP-E scores for the choice of the number of basis functions m. The black line indicates the exact VAMP-E score calculated according to the true model. Using cross-validation we compute the average VAMP-E scores computed from the training sets (blue) and the test sets (red). b Estimated \(\psi _{2}\) and \(\phi _{2}\) obtained by the nonlinear TCCA with \(m=13\) and 250 (Color figure online)

Full size image

4.2 Chapman–Kolmogorov Test for Choice of Lag Times

Besides hyper-parameters mentioned in above, the lag time \(\tau \) is also an essential parameter especially for time-continuous Markov processes. If \(\tau \rightarrow 0\), the \({\mathcal {K}}_{\tau }\) is usually close to the identity operator and cannot be accurately approximated by a low-rank model, whereas a too high value of \(\tau \) can cause the loss of kinetic information in data since \({\mathbb {P}}({\mathbf {x}}_{t+\tau }|{\mathbf {x}}_{t})\) is approximately independent of \({\mathbf {x}}_{t}\) in the case of ergodic processes. However, the variational approach presented in this paper is based on analysis of the approximation error of the Koopman operator for a fixed \(\tau \), so we cannot compare models with different lag times and choose \(\tau \) by the VAMP scores.

In order to address this problem, the Chapman–Kolmogorov test can be used, which is common in building Markov state models (Prinz et al. 2011). Let us consider the covariance

$$\begin{aligned} \mathrm {cov}(f,g;n\tau )\triangleq & {} \left\langle f,{\mathcal {K}}_{n\tau }g\right\rangle _{\rho _{0}(n\tau )}\nonumber \\= & {} {\mathbb {E}}_{{\mathbf {x}}_{t}\sim \rho _{0}(n\tau )}\left[ f({\mathbf {x}}_{t})g({\mathbf {x}}_{t+n\tau })\right] \end{aligned}$$
(35)

between observables f and g of lag time \(n\tau \), which can be estimated from data as

$$\begin{aligned} \mathrm {cov}^{\mathrm {emp}}(f,g;n\tau )=\frac{1}{T-n\tau } \sum _{t=1}^{T-n\tau }f\left( {\mathbf {x}}_{t}\right) g \left( {\mathbf {x}}_{t+n\tau }\right) ^{\top }, \end{aligned}$$
(36)

where \(\rho _{0}(n\tau )\) is the empirical distribution of the simulation data excluding \(\{x_{t}|t>T-n\tau \}\). If our methods provide an ideal Markov model of lag time \(\tau \), the Koopman operator \({\mathcal {K}}_{n\tau }\) can be approximated by \(\hat{{\mathcal {K}}}_{\tau }^{n}\), and the covariance can also be predicted as

$$\begin{aligned} \mathrm {cov}^{\mathrm {pred}}(f,g;n\tau )= & {} \left\langle f,\hat{{\mathcal {K}}}_{\tau }^{n}g\right\rangle _{\rho _{0}(n\tau )}\nonumber \\= & {} {\mathbb {E}}_{{\mathbf {x}}_{t}\sim \rho _{0}(n\tau )}\left[ f({\mathbf {x}}_{t})\varvec{\chi }_{0}({\mathbf {x}}_{t})^{\top }\right] \nonumber \\&\cdot {\mathbf {U}}{\mathbf {R}}^{n-1}{\mathbf {K}}{\mathbf {V}}^{\top }\nonumber \\&\cdot {\mathbb {E}}_{{\mathbf {x}}_{t}\sim \rho _{1}}\left[ \varvec{\chi }_{1}({\mathbf {x}}_{t})g({\mathbf {x}}_{t})\right] \end{aligned}$$
(37)

(see Appendix J), where

$$\begin{aligned} {\mathbf {R}}={\mathbf {K}}\cdot {\mathbb {E}}_{{\mathbf {x}}_{t} \sim \rho _{1}}\left[ {\mathbf {g}}({\mathbf {x}}_{t})^{\top }{\mathbf {f}}({ \mathbf {x}}_{t})\right] . \end{aligned}$$
(38)

Therefore, the lag time \(\tau \) can be selected according to the following criteria in applications: (i) The lag time is smaller than the timescale that we are interested in. (ii) The equation

$$\begin{aligned} \mathrm {cov}^{\mathrm {pred}}(f,g;n\tau )=\mathrm {cov}^{\mathrm {emp}}(f,g;n\tau ) \end{aligned}$$
(39)

holds approximately for multiple observables f, g and lag times \(n\tau \). In this paper, we simply set f, g to be the estimated leading singular functions since they dominate the dynamics of the Markov process.

5 Numerical Examples

5.1 Double-Gyre System

Let’s consider a stochastic double-gyre system defined by:

$$\begin{aligned} \mathrm {d}x_{t}= & {} -\pi \,A\,\sin (\pi \,x_{t})\,\cos (\pi \,y_{t})\,\mathrm {d}t+ \varepsilon \sqrt{x_{t}/4+1}\,\mathrm {d}{\mathbf {W}}_{t,1},\nonumber \\ \mathrm {d}y_{t}= & {} \phantom {-}\pi \,A\,\cos (\pi \,x_{t})\,\sin (\pi \,y_{t})\,\mathrm {d}t+\varepsilon \, \mathrm {d}{\mathbf {W}}_{t,2}, \end{aligned}$$
(40)

where \({\mathbf {W}}_{t,1}\) and \({\mathbf {W}}_{t,2}\) are two independent standard Wiener processes. The dynamics are defined on the domain \([0,2]\times [0,1]\) with reflecting boundary. For \(\varepsilon =0\), it can be seen from the flow field depicted in Fig. 5a that there is no transport between the left half and the right half of the domain and both subdomains are invariant sets with measure \(\frac{1}{2}\) (Froyland and Padberg 2009; Froyland and Padberg-Gehle 2014). For \(\varepsilon >0\), there is a small amount of transport due to diffusion and the subdomains are almost invariant. Here we used the parameters \(A=0.25\), \(\epsilon =0.1\), and lag time \(\tau =2\) in analysis and simulations. The first two nontrivial singular components are shown in Fig. 5c, where the two almost invariant sets are clearly visible in \(\psi _{2},\phi _{2}\) and \(\psi _{3},\phi _{3}\) are associated with the rotational kinetics within the almost invariant sets.

We generate 10 trajectories of length 4 with step size 0.02, and perform modeling by nonlinear TCCA with basis functions

$$\begin{aligned} \chi _{0,i}(x,y;w)=\chi _{1,i}(x,y;w)=\frac{\exp \left( -w\left\| (x,y)^{\top }-{\mathbf {c}}_{i}\right\| ^{2}\right) }{\sum _{j=1}^{m}\exp \left( -w\left\| (x,y)^{\top }-{\mathbf {c}}_{j}\right\| ^{2}\right) },\quad \text {for }i=1,\ldots ,m \end{aligned}$$
(41)

where \({\mathbf {c}}_{1},\ldots ,{\mathbf {c}}_{m}\) are cluster centers given by k-means algorithm, and the smoothing parameter w is determined via maximizing the VAMP-2 score given in (24) (see Appendix K.2 for more details of numerical computations). The size of basis set \(m=37\) is selected by the VAMP-E based cross-validation proposed in 4.1 with 5 folds (see Fig. 5b), and it can be observed from Fig. 5c–e that the leading singular components are accurately estimated. In contrast, as shown in Fig. 5f, g, a much small value of m leads to significant approximation errors of singular components, while for a much larger value, the estimates are obviously influenced by statistical noise. Figure 6 illustrates that the Koopman operator estimated by nonlinear TCCA can successfully predict the long-time evolution of the distribution of the state. The Chapman–Kolmogorov test results are displayed in Fig. 7, which confirm that \(\tau =2\) is a suitable choice of the lag time.

Fig. 5
figure 5

Modeling of the double-gyre system (40). a Flow field of the system, where the arrows represent directions and magnitudes of \((\mathrm {d}x_{t},\mathrm {d}y_{t})\) with \(\epsilon =0\). b VAMP-E scores of estimated models obtained from the train sets, test sets and true model respectively. The largest MCV on test sets and exact VAMP-E score are both achieved with \(m=37\) basis functions. c The true singular values and estimated ones given by the nonlinear TCCA with \(m=37\). d The first two nontrivial singular components. e–g The estimated singular components obtained by the nonlinear TCCA with \(m=37\), 5 and 200

Full size image
Fig. 6
figure 6

Probability density of state \((x_{t},y_{t})\) of the double-gyre system predicted by a the full simulation model and b the estimated Koopman operator obtained by the nonlinear TCCA with \(m=37\), 5 and 200, where the initial state is \((x_{0},y_{0})=(1.48,0.8)\)

Full size image
Fig. 7
figure 7

Chapman–Kolmogorov test for modeling the double-gyre system by nonlinear TCCA with a\(\tau =2\) and b\(\tau =0.1\). The number of basis functions \(m=37\) for both cases, \(\mathrm {cov}_{i}(n\tau )=\mathrm {cov}({\hat{\psi }}_{i},{\hat{\phi }}_{i};n\tau )\) is the time-lagged covariance between \({\hat{\psi }}_{i},{\hat{\phi }}_{i}\) as defined in (35), and \({\hat{\psi }}_{i},{\hat{\phi }}_{i}\) are the ith singular functions estimated with \(\tau =2\). Blue lines indicate empirical covariances directly calculated from data, red lines indicate the predicted values given by \(\hat{{\mathcal {K}}}_{\tau }\) as in (37), and error bars represent standard deviations calculated from 100 bootstrapping replicates of simulation data (Color figure online)

Full size image
Fig. 8
figure 8

Modeling of the stochastic Lorenz system (42). a Flow field of the system, where the arrows represent the mean directions of \((\mathrm {d}x_{t},\mathrm {d}y_{t},\mathrm {d}z_{t})\). (b) A typical trajectory with \(\epsilon =0.3\) generated by the Euler–Maruyama scheme, which is colored according to time (from blue to red). c The first two nontrivial singular components computed by nonlinear TCCA. d Chapman–Kolmogorov test results for \(\tau =0.75\), where \(\mathrm {cov}_{i}(n\tau )=\mathrm {cov}({\hat{\psi }}_{i},{\hat{\phi }}_{i};n\tau )\), where error bars represent standard deviations calculated from 100 bootstrapping replicates of simulation data (Color figure online)

Full size image

5.2 Stochastic Lorenz System

As the last example, we investigate the stochastic Lorenz system which obeys the following stochastic differential equation:

$$\begin{aligned} \mathrm {d}x_{t}= & {} s(y-x)\,\mathrm {d}t+\epsilon x_{t}\,\mathrm {d}{\mathbf {W}}_{t,1},\nonumber \\ \mathrm {d}y_{t}= & {} (rx_{t}-y_{t}-x_{t}z_{t})\,\mathrm {d}t+\varepsilon y_{t}\,\mathrm {d}{\mathbf {W}}_{t,2},\nonumber \\ \mathrm {d}z_{t}= & {} (-bz_{t}+x_{t}y_{t})\,\mathrm {d}t+\varepsilon z_{t}\,\mathrm {d}{\mathbf {W}}_{t,2}, \end{aligned}$$
(42)

with parameters \(s=10\), \(r=28\) and \(b=8/3\). The deterministic Lorenz system with \(\epsilon =0\) is known to exhibit chaotic behavior (Sparrow 1982) with a strange attractor characterized by two lobes as illustrated in Fig. 8a. We generate 20 trajectories of length 25 with \(\epsilon =0.3\) by using the Euler–Maruyama scheme with step size 0.005, and one of them is shown in Fig. 8b. As stated in Chekroun et al. (2011), all the trajectories move around the deterministic attractor with small random perturbations and switch between the two lobes.

Fig. 9
figure 9

Modeling of the stochastic Lorenz system (42) in the space of \(\varvec{\eta }_{t}\). a Plots of a typical trajectory in spaces of \((\eta _{t}^{1},\eta _{t}^{2},\eta _{t}^{3})\) and \((\eta _{t}^{4},\eta _{t}^{5},\eta _{t}^{6})\), which are colored according to time (from blue to red). Force field of the system. b The projected singular functions in the space of \((x_{t},y_{t},z_{t})\) computed by nonlinear TCCA. c The singular values estimated from trajectories of \((x_{t},y_{t},z_{t})\in {\mathbb {R}}^{3}\) and \((\eta _{t}^{1},\ldots ,\eta _{t}^{6})\in {\mathbb {R}}^{6}\) (Color figure online)

Full size image

The leading singular components computed from the simulation data by the nonlinear TCCA are summarized in Fig. 8c, where the lag time \(\tau =0.75\) is determined via the Chapman–Kolmogorov test (see Fig. 8d), \(\varvec{\chi }_{0}=\varvec{\chi }_{1}\) consist of m normalized radial basis functions similar to those used in Sect. 5.1, and the selection of m is also implemented by 5-fold cross-validation. According to the patterns of the singular functions, the stochastic Lorenz system can be coarse-grained into a simplified model which transitions between four macrostates corresponding to inner and outer basins of the two attractor lobes. In particular, the sign boundary of \(\psi _{1}\) closely matches that between the almost invariant sets of the Lorenz flow (Froyland and Padberg 2009).

Next, we map the simulation data to a higher dimensional space via the nonlinear transformation \(\varvec{\eta }_{t}=\varvec{\eta }(x_{t},y_{t},z_{t})\) defined by

$$\begin{aligned} \begin{array}{lll} \eta _{t}^{1}=\left( \frac{z_{t}}{50}+\frac{1}{2}\right) \cos \left( \frac{\pi x_{t}}{30}+\frac{z_{t}}{50}-1\right) , &{} &{} \eta _{t}^{2}=\left( \frac{z_{t}}{50}+\frac{1}{2}\right) \sin \left( \frac{\pi x_{t}}{30}+\frac{z_{t}}{50}-1\right) ,\\ \eta _{t}^{3}=\left( \frac{z_{t}}{50}+\frac{1}{2}\right) \cos \left( \frac{\pi y_{t}}{30}+\frac{z_{t}}{50}-1\right) , &{} &{} \eta _{t}^{4}=\left( \frac{z_{t}}{50}+\frac{1}{2}\right) \sin \left( \frac{\pi y_{t}}{30}+\frac{z_{t}}{50}-1\right) ,\\ \eta _{t}^{5}=\cos \frac{\pi \left( x_{t}+y_{t}\right) }{40}, &{} &{} \eta _{t}^{6}=\cos \frac{\pi \left( x_{t}-y_{t}\right) }{40}. \end{array} \end{aligned}$$
(43)

Figure 9a plots the transformed points of the illustrative trajectory in Fig. 8b. We utilize the nonlinear TCCA to compute the singular components in the space of \(\varvec{\eta }_{t}=(\eta _{t}^{1},\ldots ,\eta _{t}^{6})\) by assuming that the available observable is \(\varvec{\eta }_{t}\) instead of \((x_{t},y_{t},z_{t})\), show in Fig. 9b the projections of the singular functions back on the three-dimensional space

$$\begin{aligned} \psi _{i}^{\mathrm {proj}}(x_{t},y_{t},z_{t})=\psi _{i}( \varvec{\eta }(x_{t},y_{t},z_{t})),\quad \phi _{i}^{ \mathrm {proj}}(x_{t},y_{t},z_{t})=\phi _{i}( \varvec{\eta }(x_{t},y_{t},z_{t})), \end{aligned}$$
(44)

and compares the singular values estimated from trajectories of \((x_{t},y_{t},z_{t})\) and \((\eta _{t}^{1},\ldots ,\eta _{t}^{6})\). It can be seen the projected leading singular components are almost the same as those directly computed from the three-dimensional data, which illustrates the transformation invariance of VAMP. Notice it is straightforward to prove that the exact \(\psi _{i}^{\mathrm {proj}}\) and \(\phi _{i}^{\mathrm {proj}}\) are the solution to the variational problem (12) in the space of \((x_{t},y_{t},z_{t})^{\top }\) if there is an inverse mapping \(\varvec{\eta }^{-1}\) with \(\varvec{\eta }^{-1}(\varvec{\eta }(x_{t},y_{t},z_{t}))\equiv (x_{t},y_{t},z_{t})\).

6 Conclusion

The linearized coarse-grained models of Markov systems are commonly used in a broad range of fields, such as power systems, fluid mechanics and molecular dynamics. Although the models were developed independently in different communities, the VAMP proposed in this paper provides a general framework for analysis of them, and the modeling accuracy can be quantitatively evaluated by the VAMP-r and VAMP-E scores. Moreover, a set of data-driven methods, including feature TCCA, nonlinear TCCA and VAMP-E based cross-validation, are developed to achieve optimal modeling for given finite model dimensions and finite data sets.

The major challenge in real-world applications of VAMP is how to overcome the curse of dimensionality and solve the variational problem effectively and efficiently for high-dimensional systems. One feasible way of addressing this challenge is to approximate singular components by deep neural networks, which yields the concept of VAMPnet (Mardt et al. 2018). The optimal models can therefore be obtained by deep learning techniques. Another possible way is to utilize tensor decomposition based approximation approaches. Some tensor analysis methods have been presented based on the reversible variational principle and EDMD (Nüske et al. 2016; Klus and Schütte 2015; Klus et al. 2018), and it is worth studying more general variational tensor method within the framework of VAMP in future.

One drawback of the methods developed in this paper is that the resulting models are possibly not valid probabilistic models with nonnegative transition densities if only the operator error is considered, and the probability-preserving modeling method requires further investigations. Moreover, the applications of VAMP to detection of metastable states (Deuflhard and Weber 2005), coherent sets (Froyland and Padberg-Gehle 2014) and dominant cycles (Conrad et al. 2016) will also be explored in nextsteps.