Periodic Solution and Stationary Distribution of Stochastic Predator–Prey Models with Higher-Order Perturbation

Abstract

In this paper, two stochastic predator–prey models with general functional response and higher-order perturbation are proposed and investigated. For the nonautonomous periodic case of the system, by using Khasminskii’s theory of periodic solution, we show that the system admits a nontrivial positive T-periodic solution. For the system disturbed by both white and telegraph noises, sufficient conditions for positive recurrence and the existence of an ergodic stationary distribution to the solutions are established. The existence of stationary distribution implies stochastic weak stability to some extent.

1 Introduction

Recently, the dynamics of predator–prey models have been extensively studied due to their theoretical and practical significance and the investigation of the predator–prey system has long been and will continue to be one of the most interesting hot topics in both ecology and mathematical biology (see e.g. Jia and Xue 2016; Xu et al. 2016; Freedman 1980). The deterministic predator–prey model with general functional response can be expressed as follows

$$\begin{aligned} \left\{ \begin{array}{llll} \frac{\mathrm{d}x}{\mathrm{d}t}=r_{1}x\left( 1-\frac{x}{K}\right) -f(x)y,\\ \frac{\mathrm{d}y}{\mathrm{d}t}=y[-r_{2}-ay+mf(x)], \end{array} \right. \end{aligned}$$

(1.1)

where $x=x(t)$ and $y=y(t)$ represent the biomass densities of the prey and predator at time t, respectively, the parameter $r_{1}$ is the intrinsic growth rate of the prey in the absence of the predator, $r_{2}$ is the death rate of the predator in the absence of the prey, K is the environmental carrying capacity of the prey, a is the density-dependent coefficient of the predator, m denotes the conversion rate of eaten prey into new predator and f is a nonlinear functional response function. The parameters involved in system (1.1) are assumed to be positive constants. The functional response function $f:\mathbb {R}_{+}\rightarrow \mathbb {R}_{+}$ is generally assumed to satisfy

However, as far as we know, both environmental fluctuations and demographic randomness are important components in an ecosystem (see e.g. Gard 1984, 1986). May (2001) has revealed that due to continuous fluctuations in the environment, the birth rates, death rates, carrying capacities, competition coefficients and other parameters involved in the system should exhibit random fluctuation to a greater or lesser extent. Hence, the deterministic predator–prey model has some limitations to predict the future dynamics accurately and the stochastic one can make it (see e.g. Zhao and Yuan 2016; Liu et al. 2016; Zhang et al. 2015). Motivated by this, in this paper, we introduce the higher-order perturbation into system (1.1) because the random perturbation may be dependent on square of variables x and y, respectively and hence we obtain the following stochastic predator–prey model with higher-order perturbation

$$\begin{aligned} \left\{ \begin{array}{llll} \text {d}x=\bigg [r_{1}x\bigg (1-\displaystyle \frac{x}{K}\bigg )-f(x)y\bigg ]\mathrm{d}t+\sigma _{11}x\mathrm{d}B_{11}(t)+\sigma _{12}x^{2}\mathrm{d}B_{12}(t),\\ \mathrm{d}y=y[-r_{2}-ay+mf(x)]\mathrm{d}t+\sigma _{21}y\mathrm{d}B_{21}(t)+\sigma _{22}y^{2}\mathrm{d}B_{22}(t), \end{array} \right. \end{aligned}$$

(1.2)

where $B_{ij}(t)$ are mutually independent standard Brownian motions, $\sigma _{ij}^{2}>0$ are the intensities of the white noise, $i,j=1,2$.

For biological reality, we assume that f(x) satisfies $H_{1}$ and $H_{2}$. Again, for the sake of clarity, we make two further classifications of assumptions for the generic nature

Note that the function f includes some special functional responses.

• (i) Lotka–Volterra type or Holling type I:

  $$\begin{aligned} f(x)=nx, \end{aligned}$$

where $n>0$ is a constant.

• (ii) Holling type II:

  $$\begin{aligned} f(x)=\frac{nx}{a+x}, \end{aligned}$$

where $n>0$ and $a>0$ are constants and a is called the half-saturation constant.

• (iii) Generalized Holling type III or sigmoidal:

  $$\begin{aligned} f(x)=\frac{nx^{2}}{ax^{2}+bx+1}, \end{aligned}$$

where n and a are positive constants and b is a constant. When $b=0$, it is the so-called Holling type III response function. When $b>-2\sqrt{a}$ (so that $ax^{2}+bx+1>0$ for all $x\ge 0$), it is called the generalized Holling type III or sigmoidal functional response.

• (iv) Generalized Holling type IV or Monod-Haldane:

  $$\begin{aligned} f(x)=\frac{nx}{ax^{2}+bx+1}, \end{aligned}$$

where n and a are positive constants and b is a constant. When $b=0$, it is called the Holling type IV functional response.

There are still some other types of functional response such as:

$$\begin{aligned} f(x)= & {} 1-e^{-\lambda x}, \lambda >0~(\text {IvIev functional response}), \\ f(x)= & {} \arctan x. \end{aligned}$$

On the other hand, it is well known that biological populations encounter fluctuations that occur in a more or less periodic fashion, due to the seasonal effects of weather condition, food supplies, mating habits, individual lifecycle, hunting and harvesting, etc., the birth rate, the death rate of the population and other parameters will exhibit a more or less periodicity. Hence, it is interesting to investigate the dynamics of population models with periodic environmental changes. However, to the best of our knowledge, there has been no result related periodic solutions of predator–prey models with higher-order perturbation. In this paper, corresponding to system (1.2), we shall consider the following nonautonomous periodic system

$$\begin{aligned} \left\{ \begin{array}{llll} \mathrm{d}x=\bigg [r_{1}(t)x\bigg (1-\displaystyle \frac{x}{K}\bigg )-f(x)y\bigg ]\mathrm{d}t+\sigma _{11}(t)x\mathrm{d}B_{11}(t)+\sigma _{12}(t)x^{2}\mathrm{d}B_{12}(t),\\ \mathrm{d}y=y[-r_{2}(t)-a(t)y+m(t)f(x)]\mathrm{d}t+\sigma _{21}(t)y\mathrm{d}B_{21}(t)+\sigma _{22}(t)y^{2}\mathrm{d}B_{22}(t), \end{array} \right. \nonumber \\ \end{aligned}$$

(1.3)

where the parameter functions $r_{i}(t)$, a(t), m(t) and $\sigma _{ij}(t)$ are positive and continuous functions of period T and T is a positive constant, $i,j=1,2$. One aim of this paper is to establish sufficient conditions for the existence of nontrivial positive periodic solutions to system (1.3).

Besides the white noise, predator–prey models may be disturbed by the colored noise, namely the telegraph noise which can make the system switch from one environmental regime to another (Luo and Mao 2007). Now we take a further step by considering the telegraph noise (Luo and Mao 2007; Takeuchi et al. 2006). The telegraph noise can be illustrated as a switching between two or more environmental regimes which differ by factors such as humidity and temperature (Du et al. 2004; Slatkin 1978). For example, the growth rate for some fish in dry season will be much different from it in rainy season. The switching between environmental regimes is often memoryless and the waiting time for the next switch follows the exponential distribution (Settati and Lahrouz 2014). Thus, the regime switching can be modeled by a continuous time Markov chain $(r(t))_{t\ge 0}$ taking values in a finite state space $\mathbb {S}=\{1,\ldots ,N\}$. Hence system (1.2) with regime switching takes the following form

$$\begin{aligned} \left\{ \begin{array}{llll} \mathrm{d}x\!=\!\bigg [r_{1}(r(t))x\bigg (1\!-\!\displaystyle \frac{x}{K}\bigg )\!-\!f(x)y\bigg ]\mathrm{d}t+\sigma _{11}(r(t))x\mathrm{d}B_{11}(t)\\ \quad \qquad +\,\sigma _{12}(r(t))x^{2}\mathrm{d}B_{12}(t),\\ \mathrm{d}y=y[-r_{2}(r(t))-a(r(t))y+m(r(t))f(x)]\mathrm{d}t +\sigma _{21}(r(t))y\mathrm{d}B_{21}(t)\\ \qquad \qquad +\,\sigma _{22}(r(t))y^{2}\mathrm{d}B_{22}(t). \end{array} \right. \end{aligned}$$

(1.4)

Since stochastic system (1.4) is perturbed by higher-order perturbation under regime switching, the existence of ergodic stationary distribution is an important question. However, to the best of our knowledge, there has been no result related this. In the present paper, we attempt to do some work in this field to fill the gap. The theory we used is developed by Zhu and Yin (2007). This method has been utilized by many authors (see e.g. Settati and Lahrouz 2014; Li et al. 2011; Zu et al. 2015). Studying such a problem is meaningful and challenging. The key difficulty is how to construct a suitable stochastic Lyapunov function and a bounded domain which is a subset of $\mathbb {R}_{+}^{2}=\{x=(x_{1},x_{2})\in \mathbb {R}^{2}:x_{i}>0,i=1,2\}$. Thus, the other aim of this paper is to establish sufficient conditions for the existence of an ergodic stationary distribution of solutions to the model (1.4).

The organization of this paper is as follows. In Sect. 2, we shall recall some fundamental theory and present two theorems concerning the existence and uniqueness of global positive solutions to systems (1.3) and (1.4), respectively. In Sect. 3, for the system (1.3), we show that system (1.3) has a nontrivial positive T-periodic solution. In Sect. 4, for the system (1.4), we establish sufficient conditions for positive recurrence and the existence of an ergodic stationary distribution to the solutions. Finally, some concluding remarks are presented to end this paper.

2 Preliminaries

In this section, we shall introduce some notations and lemmas which will be used later.

Throughout this paper, unless otherwise specified, let $(\Omega ,\mathcal {F},\{\mathcal {F}_{t}\}_{t\ge 0},\mathbb {P})$ be a complete probability space with a filtration $\{\mathcal {F}_{t}\}_{t\ge 0}$ satisfying the usual conditions (i.e., it is increasing and right continuous while $\mathcal {F}_{0}$ contains all $\mathbb {P}$-null sets) and let $B_{ij}(t)$ be mutually independent standard Brownian motions defined on the complete probability space, $i,j=1,2$. Denote $\mathbb {R}_{+}^{n}=\{(x_{1},\ldots ,x_{n})\in \mathbb {R}^{n}:x_{i}>0,i=1,\ldots ,n\}$ and $Z^{n\times n}=\{A=(a_{ij})_{n\times n}:a_{ij}\le 0,i\not =j\}$. Let r(t), $t\ge 0$ be a right-continuous Markov chain on the probability space $(\Omega ,\mathcal {F},\{\mathcal {F}_{t}\}_{t\ge 0},\mathbb {P})$ taking values in a finite state space $\mathbb {S}=\{1,\ldots ,N\}$. For any vector $g=(g(1),\ldots ,g(N))$, let $\hat{g}=\min _{k\in \mathbb {S}}\{g(k)\}$ and $\breve{g}=\max _{k\in \mathbb {S}}\{g(k)\}$. If f is an integrable function on $[0,+\infty )$, define $\langle f\rangle _{T}=\frac{1}{T}\int _{0}^{T}f(s)\mathrm{d}s$. If f is a bounded function on $[0,+\infty )$, define $f^{u}=\sup _{t\in [0,+\infty )}f(t)$, $f^{l}=\inf _{t\in [0,+\infty )}f(t)$. Assume that the generator $\varGamma =(\upgamma _{ij})_{N\times N}$ of the Markov chain is given by

$$\begin{aligned} \mathbb {P}\{r(t+\Delta t)=j|r(t)=i\}=\left\{ \begin{array}{ll} \upgamma _{ij}\Delta t+o(\Delta t), &{} \quad \hbox {if}~i\not =j,\\ 1+\upgamma _{ii}\Delta t+o(\Delta t),&{} \quad \hbox {if}~i=j, \end{array}\right. \end{aligned}$$

where $\Delta t>0$, $\upgamma _{ij}\ge 0$ is the transition rate from i to j if $i\not =j$, while $\sum _{i=1}^{N}\upgamma _{ij}=0$. In this paper, we assume that $\upgamma _{ij}>0$ for $i\not =j$. Suppose further that the Markov chain r(t) is irreducible, which implies that Markov chain r(t) has a unique stationary distribution $\pi =(\pi _{1},\ldots ,\pi _{N})$ which can be determined by the equation

$$\begin{aligned} \pi \varGamma =0 \end{aligned}$$

subject to

$$\begin{aligned} \sum _{h=1}^{N}\pi _{h}=1~\text {and}~\pi _{h}>0~\text {for any} ~h\in \mathbb {S}. \end{aligned}$$

We assume that Brownian motions $B_{ij}(\cdot )$ are independent of the Markov chain $r(\cdot )$, $r_{i}(k)$, a(k), m(k) and $\sigma _{ij}(k)$ are all positive constants for each $k\in \mathbb {S}$, $i,j=1,2$.

For the sake of convenience, we introduce some results concerning periodic Markov processes. For more details, we refer the reader to Khasminskii (2012).

Definition 2.1

A stochastic process $\xi (t)=\xi (t,\omega )$ $(-\infty<t<+\infty )$ is said to be periodic with period T if for every finite sequence of numbers $t_{1},\ldots ,t_{n}$ the joint distributions of random variables $\xi (t_{1}+h),\ldots ,\xi (t_{n}+h)$ are independent of h; here $h=kT$, $k=\pm 1,\pm 2,\ldots$

Khasminskii (2012) showed that a Markov process z(t) is T-periodic if and only if its transition probability function is T-periodic and the function $\mathbb {P}_{0}(t,A)=\mathbb {P}\{X(t)\in A\}$ satisfies the equation

$$\begin{aligned} \mathbb {P}_{0}(s,A)=\int _{\mathbb {R}^{d}}\mathbb {P}_{0}(s,dz)\mathbb {P}(s,z,s+T,A)\equiv \mathbb {P}_{0}(s+T,A), \end{aligned}$$

here $A\in \mathcal {B}$ and $\mathcal {B}$ is a $\sigma$-algebra.

Consider the following equation

$$\begin{aligned} X(t)=X(t_{0})+\int _{t_{0}}^{t}b(s,X(s))\mathrm{d}s+\sum _{r=1}^{k}\int _{t_{0}}^{t}\sigma _{r}(s,X(s))\mathrm{d}B_{r}(s),\quad X\in \mathbb {R}^{d}, \end{aligned}$$

(2.1)

where the vectors b(s, z), $\sigma _{1}(s,z),\ldots ,\sigma _{k}(s,z)$ $(s\in [t_{0},T],z\in \mathbb {R}^{d})$ are continuous functions of (s, z) and satisfy the following conditions

$$\begin{aligned}&|b(s,z)-b(s,\bar{z})|+\sum _{r=1}^{k}|\sigma _{r}(s,z)-\sigma _{r}(s,\bar{z})|\le B|z-\bar{z}|,\nonumber \\&|b(s,z)| +\sum _{r=1}^{k}|\sigma _{r}(s,z)|\le B(1+|z|), \end{aligned}$$

(2.2)

in every cylinder $I\times U$, where B is a constant and I is a subset of $\mathbb {R}_{+}$. Let $C^{2}$ denote the family of functions on $I\times U$ which are twice continuously differentiable with respect to $z_{1},\ldots ,z_{d}$ and continuously differentiable with respect to t.

Lemma 2.1

Suppose that the coefficients of (2.1) are T-periodic in t and satisfy the condition (2.2) in every cylinder $I\times U$, and suppose further that there exists a function $V(t,z)\in C^{2}$ in $I\times U$ which is T-periodic in t and satisfies the following conditions:

$$\begin{aligned} \mathrm{(i)}~\inf _{|z|>r}V(t,z)\rightarrow \infty ~\mathrm{as}~r\rightarrow \infty ;\end{aligned}$$

(2.3)

$$\begin{aligned} \mathrm{(ii)}~LV(t,z)\le -1~\mathrm{on the outside of some compact set}, \end{aligned}$$

(2.4)

where the operator L is defined by

$$\begin{aligned} L=\displaystyle \frac{\partial }{\partial t}+\sum _{i=1}^{d}b_{i}(t,z)\frac{\partial }{\partial z_{i}}+\frac{1}{2}\sum _{i,j=1}^{d}a_{ij}(t,z)\frac{\partial ^{2}}{\partial z_{i}\partial z_{j}},\quad a_{ij}=\sum _{r=1}^{k}\sigma _{r}^{i}(t,z)\sigma _{r}^{j}(t,z). \end{aligned}$$

Then there exists a solution of (2.1) which is a T-periodic Markov process.

The Lemma 2.1 has been proved by Khasminskii in his monograph (Khasminskii 2012), Chapter 3, p. 80. Readers can refer to this book for details.

Remark 2.1

According to the proof of Lemma 2.1, the linear growth condition is only used to guarantee the existence and uniqueness of the solution to Eq. (2.1).

Now we are in the position to give some results on the stationary distribution for stochastic differential equations under regime switching. For more details, we refer the reader to Zhu and Yin (2007). Let (X(t), r(t)) be the diffusion process described by the following equation

$$\begin{aligned} \mathrm{d}X(t)=b(X(t),r(t))\mathrm{d}t+\sigma (X(t),r(t))\mathrm{d}B(t),\quad X(0)=x_{0},\quad r(0)=r, \end{aligned}$$

(2.5)

where $B(\cdot )$ and $r(\cdot )$ are the d-dimensional Brownian motion and the right-continuous Markov chain in the above discussion, respectively, and $b(\cdot ,\cdot ):\mathbb {R}^{n}\times \mathbb {S}\rightarrow \mathbb {R}^{n}$, $\sigma (\cdot ,\cdot ):\mathbb {R}^{n}\times \mathbb {S}\rightarrow \mathbb {R}^{n\times d}$ satisfying $\sigma (x,k)\sigma ^{T}(x,k)=(d_{ij}(x,k))$. For each $k\in \mathbb {S}$, let $V(\cdot ,k)$ be any twice continuously differentiable function, the operator L can be defined by

$$\begin{aligned} LV(x,k)=\displaystyle \sum _{i=1}^{n}b_{i}(x,k)\frac{\partial V(x,k)}{\partial x_{i}}+\frac{1}{2}\sum _{i,j=1}^{n}d_{ij}(x,k) \frac{\partial ^{2}V(x,k)}{\partial x_{i}\partial x_{j}}+\sum _{l=1}^{N}\gamma _{kl}V(x,l). \end{aligned}$$

The following lemma gives a criterion for the ergodic stationary distribution of the solution (X(t), r(t)) to system (2.5).

Lemma 2.2

(Zhu and Yin 2007) If the following conditions are satisfied:

• (i) $\gamma _{ij}>0$ for any $i\not =j$;

• (ii) for each $k\in \mathbb {S}$, $D(x,k)=(d_{ij}(x,k))$ is symmetric and satisfies

  $$\begin{aligned} \varrho |\zeta |^{2}\le \langle D(x,k)\zeta ,\zeta \rangle \le \varrho ^{-1}|\zeta |^{2}~\mathrm{for all}~\zeta \in \mathbb {R}^{n}, \end{aligned}$$

  with some constant $\varrho \in (0,1]$ for all $x\in \mathbb {R}^{n}$;

• (iii) there exists a nonempty open set $\mathcal {D}$ with compact closure, satisfying that, for each $k\in \mathbb {S}$ there is a nonnegative function $V(\cdot ,k):\mathcal {D}^{C}\rightarrow \mathbb {R}$ such that $V(\cdot ,k)$ is twice continuously differentiable and that for some $\alpha >0$,

  $$\begin{aligned} LV(x,k)\le -\alpha ~\mathrm{for~any}~(x,k)\in \mathcal {D}^{C}\times \mathbb {S}, \end{aligned}$$

  then (X(t), r(t)) of system (2.5) is ergodic and positive recurrent. That is to say, there exists a unique stationary distribution $\mu (\cdot ,\cdot )$ such that for any Borel measurable function $f(\cdot ,\cdot ):\mathbb {R}^{n}\times \mathbb {S}\rightarrow \mathbb {R}$ satisfying

  $$\begin{aligned} \sum _{k=1}^{N}\int _{\mathbb {R}^{n}}|f(x,k)|\mu (\mathrm{d}x,k)<+\infty , \end{aligned}$$

  we have

  $$\begin{aligned} \mathbb {P}\bigg \{\lim _{t\rightarrow +\infty }\frac{1}{t}\int _{0}^{t}f(X(s),r(s))\mathrm{d}s=\sum _{k=1}^{N}\int _{\mathbb {R}^{n}}f(x,k)\mu (\mathrm{d}x,k)\bigg \}=1. \end{aligned}$$

Under the above assumptions of f(x) and using the same method as in Li et al. (2011), we can obtain that stochastic systems (1.3) and (1.4) has a unique global positive solution, respectively. Since the proofs are standard, we present the following two theorems concerning the existence and uniqueness of global positive solutions for stochastic systems (1.3) and (1.4) without proof.

Theorem 2.1

For any given initial value $(x(0),y(0))\in \mathbb {R}_{+}^{2}$, the stochastic system (1.3) has a unique solution (x(t), y(t)) on $t\ge 0$ and the solution will remain in $\mathbb {R}_{+}^{2}$ with probability one, that is to say, $(x(t),y(t))\in \mathbb {R}_{+}^{2}$ for all $t\ge 0$ almost surely (a.s.).

Theorem 2.2

For any given initial value $(x(0),y(0),r(0))\in \mathbb {R}_{+}^{2}\times \mathbb {S}$, there exists a unique solution (x(t), y(t), r(t)) of the stochastic system (1.4) on $t\ge 0$ and the solution will remain in $\mathbb {R}_{+}^{2}\times \mathbb {S}$ with probability one, namely, $(x(t),y(t),r(t))\in \mathbb {R}_{+}^{2}\times \mathbb {S}$ for all $t\ge 0$ almost surely (a.s.).

3 Existence of Nontrivial Positive T-Periodic Solution of System (1.3)

In this section, we shall show that system (1.3) admits a nontrivial positive T-periodic solution. We first give the following assumption.

and d is a positive constant satisfying the condition of Theorem 3.1.

Theorem 3.1

Let Assumptions $(H_1)$–$(H_5)$ hold, if $r_{1}^{l}>K^{2}(\sigma _{12}^{2})^{u}$ and there is a constant d such that the following condition holds

$$\begin{aligned} d>\max \left\{ 0,\left( \frac{c(t)r_{1}(t)-\frac{Kc_{2}m(t)}{2}}{r_{1}(t)-K^{2}\sigma _{12}^{2}(t)}\right) ^{u}\right\} , \end{aligned}$$

where

$$\begin{aligned} c(t)=\frac{f'(K)\int _{t}^{t+T}e^{\int _{s}^{t}r_{1}(\tau )d\tau }m(s)\mathrm{d}s}{1-e^{-\int _{0}^{T}r_{1}(\tau )d\tau }}. \end{aligned}$$

then system (1.3) admits a nontrivial positive T-periodic solution.

Remark 3.1

It is easy to check that c(t) is a T-periodic function and satisfies the following equation

$$\begin{aligned} c'(t)-r_{1}(t)c(t)+f'(K)m(t)=0. \end{aligned}$$

Proof

In view of Theorem 2.1, one can see that for any initial value $(x(0),y(0))\in \mathbb {R}_{+}^{2}$, system (1.3) has a unique global positive solution (x(t), y(t)), so we can take $\mathbb {R}_{+}^{2}$ as the whole space. It is clear that coefficients of system (1.3) satisfy the condition (2.2). By Lemma 2.1, in order to prove Theorem 3.1, it suffices to find a $C^{2}$-function V(t, x) which is T-periodic in t and a closed set $U\subset \mathbb {R}_{+}^{2}$ such that (2.3) and (2.4) hold.

Define a $C^{2}$-function

$$\begin{aligned} V(t,x,y)= & {} M[-\ln y-c(t)x+d\left( x-K-K\ln \frac{x}{K}\right) +\frac{(\sigma _{22}^{2})^{u}}{2a^{l}}y\\&+\,\frac{a^{u}+Kc_{1}d}{r_{2}^{l}}y+Kc(t) -\omega (t)]+x^{p}+y^{p}, \end{aligned}$$

where $0<p<1$ is a constant and $M>0$ is a constant satisfying $-M\langle \lambda \rangle _{T}+f_{1}^{u}+f_{2}^{u}\le -2$, the functions $f_{1}$, $f_{2}$ and T-periodic functions $\omega \in C^{1}(\mathbb {R}_{+};\mathbb {R})$ will be determined later. It is easy to check that V(t, x, y) is T-periodic in t and satisfies (2.3).

Next, we shall find a closed set $U\subset \mathbb {R}_{+}^{2}$ such that $LV(t,x,y)\le -1$ for any $(x,y)\in \mathbb {R}_{+}^{2}{\setminus } U$. Denote $V_{1}(x,y)=-\ln y-c(t)x+d(x-K-K\ln \frac{x}{K})+\frac{(\sigma _{22}^{2})^{u}}{2a^{l}}y+\frac{a^{u}+Kc_{1}d}{r_{2}^{l}}y+Kc(t)$, $V_{2}(x,y)=x^{p}+y^{p}$. Applying the Itô’s formula (Mao and Yuan 2006) to $V_{1}(x,y)$, one can get that

$$\begin{aligned} LV_{1}= & {} -m(t)f(x)+r_{2}(t)+\frac{\sigma _{21}^{2}(t)}{2}+a(t)y+\frac{\sigma _{22}^{2}(t)}{2}y^{2}\\&-\,c'(t)(x-K+K)-c(t)r_{1}(t)x\left( 1-\frac{x}{K}\right) \\&+\,c(t)f(x)y +d\left( -\frac{r_{1}(t)}{K}(x-K)^{2}-f(x)y+K\frac{f(x)}{x}y\right. \\&\left. +\,\frac{K}{2}\sigma _{11}^{2}(t)+\frac{K}{2}\sigma _{12}^{2}(t) (x-K+K)^{2}\right) \\&-\,\frac{(\sigma _{22}^{2})^{u}}{2a^{l}}r_{2}(t)y -\frac{(\sigma _{22}^{2})^{u}}{2a^{l}}a(t)y^{2}+\frac{(\sigma _{22}^{2})^{u}}{2a^{l}}m(t)f(x)y \\&-\,\frac{(a^{u}+Kc_{1}d) }{r_{2}^{l}}r_{2}(t)y-\frac{a(t)(a^{u}+Kc_{1}d)}{r_{2}^{l}}y^{2}\\&+\,\frac{m(t)(a^{u}+Kc_{1}d)}{r_{2}^{l}}f(x)y+Kc'(t)\\= & {} -m(t)f(x)+r_{2}(t)+\frac{\sigma _{21}^{2}(t)}{2}+a(t)y+\frac{1}{2}\left( \sigma _{22}^{2}(t)\right. \\&\left. -\,\frac{(\sigma _{22}^{2})^{u} a(t)}{a^{l}}\right) y^{2}-c'(t)(x-K)-c(t)r_{1}(t)\\&\times \,x\left( 1-\frac{x}{K}\right) +c(t)f(x)y+d\left( -\frac{r_{1}(t)}{K}(x-K)^{2} \right. \\ \end{aligned}$$

$$\begin{aligned}&-\,f(x)y+K\frac{f(x)}{x}y+\frac{K}{2}\sigma _{11}^{2}(t)+ \frac{K}{2}\sigma _{12}^{2}(t)(x\\&\left. -\,K+K)^{2}\right) -\frac{(\sigma _{22}^{2})^{u}}{2a^{l}}r_{2}(t)y +\frac{(\sigma _{22}^{2})^{u}}{2a^{l}}m(t)f(x)y \\&-\,\frac{(a^{u}+Kc_{1}d) }{r_{2}^{l}}r_{2}(t)y-\frac{a(t)(a^{u}+Kc_{1}d)}{r_{2}^{l}}y^{2}\\&+\,\frac{m(t)(a^{u}+Kc_{1}d)}{r_{2}^{l}}f(x)y\\\le & {} -m(t)f(x)+r_{2}(t)+\frac{\sigma _{21}^{2}(t)}{2}+a(t)y-c'(t)(x-K)\\&-\,c(t)r_{1}(t)x(1-\frac{x}{K})+c(t)f(x)y \\&+\,d(-\frac{r_{1}(t)}{K}(x-K)^{2} +Kc_{1}y+\frac{K}{2}\sigma _{11}^{2}(t)\\&+\,K\sigma _{12}^{2}(t)(x-K)^{2}+K^{3}\sigma _{12}^{2}(t))+\frac{m(t)(\sigma _{22} ^{2})^{u}}{2a^{l}}f(x)y\\&-\,\frac{(a^{u}+Kc_{1}d)}{r_{2}^{l}}r_{2}(t)y+\frac{m(t)(a^{u}+Kc_{1}d)}{r_{2}^{l}}f(x)y\\\le & {} -f(K)m(t)+r_{2}(t)+\frac{\sigma _{21}^{2}(t)}{2}+\frac{Kd\sigma _{11}^{2}(t)}{2}\\&+\,K^{3}d\sigma _{12}^{2}(t) +\Big [-m(t)f(x)+f(K)m(t)\\&-\,c'(t)(x-K)+\frac{c(t)r_{1}(t)}{K}x(x-K)-\frac{dr_{1}(t)}{K}(x-K)^{2}\\&+\,Kd\sigma _{12}^{2}(t)(x-K)^{2}\Big ]+[c(t)+\frac{m(t)( \sigma _{22}^{2})^{u}}{2a^{l}}\\&+\,\frac{m(t)(a^{u}+Kc_{1}d)}{r_{2}^{l}}]f(x)y\\= & {} -f(K)m(t)+r_{2}(t)+\frac{\sigma _{21}^{2}(t)}{2}+\frac{Kd\sigma _{11}^{2}(t)}{2}\\&+\,K^{3}d\sigma _{12}^{2}(t)+F(x,t) +\left[ c(t)+\frac{m(t)(a^{u}+Kc_{1}d)}{r_{2}^{l}}\right. \\&\left. +\,\frac{m(t)(\sigma _{22}^{2})^{u}}{2a^{l}}\right] f(x)y, \end{aligned}$$

where

$$\begin{aligned} F(x,t)= & {} -m(t)f(x)+f(K)m(t)-c'(t)(x-K)\\&+\,\frac{c(t)r_{1}(t)}{K}x(x-K)-\frac{dr_{1}(t)}{K}(x-K)^{2}\\&+\,Kd\sigma _{12}^{2} (t)(x-K)^{2} \end{aligned}$$

and in the first inequality, we have used the fact $(a+b)^{2}\le 2a^{2}+2b^{2}$ for any $a,b\in \mathbb {R}$. Then

$$\begin{aligned} \frac{\partial F(x,t)}{\partial x}= & {} -m(t)f'(x)-c'(t)+\frac{c(t)r_{1}(t)}{K}(2x-K) \\&-\,\frac{2dr_{1}(t)}{K}(x-K)+2Kd\sigma _{12}^{2}(t)(x-K),\\ \frac{\partial ^{2}F(x,t)}{\partial x^{2}}= & {} -m(t)f''(x)+\frac{2c(t)r_{1}(t)}{K} -\frac{2dr_{1}(t)}{K}+2Kd\sigma _{12}^{2}(t). \end{aligned}$$

Let

$$\begin{aligned} \frac{\partial F(x,t)}{\partial x}\bigg |_{x=K}=0, \end{aligned}$$

we have

$$\begin{aligned} c'(t)-r_{1}(t)c(t)+f'(K)m(t)=0. \end{aligned}$$

On the other hand, we have

$$\begin{aligned} \frac{\partial ^{2}F(x,t)}{\partial x^{2}}\le -m(t)c_{2}+\frac{2c(t)r_{1}(t)}{K}-d(\frac{2r_{1}(t)}{K}-2K\sigma _{12}^{2}(t))<0, \end{aligned}$$

where the inequality holds due to the Assumption $(H_{4})$ and the condition of Theorem 3.1. Then we have

$$\begin{aligned} F(x,t)\le F(K,t)=0. \end{aligned}$$

Hence

$$\begin{aligned} LV_{1}\le & {} -f(K)m(t)+r_{2}(t)+\frac{\sigma _{21}^{2}(t)}{2}+\frac{Kd\sigma _{11}^{2}(t)}{2}+K^{3}d\sigma _{12}^{2}(t) \nonumber \\&+\,[c(t)+\frac{m(t)(a^{u}+Kc_{1}d)}{r_{2}^{l}}+\frac{m(t)(\sigma _{22}^{2})^{u}}{2a^{l}}] c_{1}xy \nonumber \\= & {} -\lambda (t)+[c(t)+\frac{m(t)(a^{u}+Kc_{1}d)}{r_{2}^{l}}+\frac{m(t)(\sigma _{22}^{2})^{u}}{2a^{l}}]c_{1}xy, \end{aligned}$$

(3.1)

where

$$\begin{aligned} \lambda (t)=f(K)m(t)-r_{2}(t)-\frac{\sigma _{21}^{2}(t)}{2}-\frac{Kd\sigma _{11}^{2}(t)}{2}-K^{3}d\sigma _{12}^{2}(t). \end{aligned}$$

Define the T-periodic function $\omega (t)$ satisfying

$$\begin{aligned} \omega '(t)=\lambda (t)-\langle \lambda \rangle _{T}. \end{aligned}$$

(3.2)

Then combining (3.1) and (3.2), we obtain

$$\begin{aligned} L(V_{1}+\omega (t))\le -\langle \lambda \rangle _{T}+\bigg [c^{u}+\frac{m^{u}(a^{u}+Kc_{1}d)}{r_{2}^{l}}+\frac{m^ {u}(\sigma _{22}^{2})^{u}}{2a^{l}}\bigg ]c_{1}xy. \end{aligned}$$

(3.3)

Furthermore, we get

$$\begin{aligned} LV_{2}= & {} px^{p-1}\left[ r_{1}(t)x\left( 1-\frac{x}{K}\right) -f(x)y\right] +\frac{p(p-1)}{2}\sigma _{11}^{2}(t)x^{p} \nonumber \\&+\,\frac{p(p-1)}{2}\sigma _ {12}^{2}(t)x^{p+2}+py^{p}[-r_{2}(t)-a(t)y \nonumber \\&+\,m(t)f(x)] +\frac{p(p-1)}{2}\sigma _{21}^{2}(t)y^{p}+\frac{p(p-1)}{2}\sigma _{22}^{2}(t)y^{p+2} \nonumber \\\le & {} -\frac{p(1-p)}{2}(\sigma _{12}^{2})^{l}x^{p+2}+pr_{1}^{u}x^{p}-\frac{p(1-p)}{2}(\sigma _{22}^{2})^{l}y^{p+2} \nonumber \\&-\,pr_{2}^{l}y^{p}+pc_{1}m^{u}xy^{p}. \end{aligned}$$

(3.4)

Combining (3.3) and (3.4), one can obtain that

$$\begin{aligned} LV= & {} MLV_{1}+LV_{2}\\\le & {} M\left\{ -\langle \lambda \rangle _{T}+\left[ c^{u}+\frac{m^{u}(a^{u}+Kc_{1}d)}{r_{2}^{l}} +\frac{m^{u}(\sigma _{22}^{2})^{u}}{2a^{l}}\right] c_{1}xy\right\} \\&-\,\frac{p(1-p)}{2}(\sigma _{12}^{2})^{l}x^{p+2}+pr_{1}^{u}x^{p}-\frac{p(1-p)}{2}(\sigma _{22}^{2})^{l}y^{p+2}\\&-\,pr_{2}^{l}y^{p}+pc_{1}m^{u}xy^{p}\\= & {} f_{1}(x)+f_{2}(y)+M\left\{ -\langle \lambda \rangle _{T} +\left[ c^{u}+\frac{m^{u}(a^{u}+Kc_{1}d)}{r_{2}^{l}}\right. \right. \\&\left. \left. +\,\frac{m^{u}(\sigma _{22}^{2})^{u}}{2a^{l}}\right] c_{1}xy\right\} +pc_{1}m^{u}xy^{p}, \end{aligned}$$

where

$$\begin{aligned} f_{1}(x)=-\frac{p(1-p)}{2}(\sigma _{12}^{2})^{l}x^{p+2}+pr_{1}^{u}x^{p} \end{aligned}$$

and

$$\begin{aligned} f_{2}(y)=-\frac{p(1-p)}{2}(\sigma _{22}^{2})^{l}y^{p+2}-pr_{2}^{l}y^{p}. \end{aligned}$$

Denote

$$\begin{aligned} G(x,y)= & {} f_{1}(x)+f_{2}(y)+M\{-\langle \lambda \rangle _{T}+\left[ c^{u}+\frac{m^{u}(a^{u}+Kc_{1}d)}{r_{2}^{l}}\right. \\&\left. +\,\frac{m^{u}(\sigma _{22}^{2})^{u}}{2a^{l}}\right] c_{1}xy\} +pc_{1}m^{u}xy^{p}. \end{aligned}$$

Then

$$\begin{aligned} G(x,y)\le \left\{ \begin{array}{llll} G(+\infty ,y)\rightarrow -\infty ,~\hbox {as}~x\rightarrow +\infty ,\\ G(x,+\infty )\rightarrow -\infty ,~\hbox {as}~y\rightarrow +\infty ,\\ f_{1}^{u}+f_{2}^{u}-M\langle \lambda \rangle _{T}\le -2,~\hbox {as}~x\rightarrow 0^{+}~\hbox {or}~y\rightarrow 0^{+}. \end{array} \right. \end{aligned}$$

Thus we can take $0<\epsilon <1$ sufficiently small such that

$$\begin{aligned} LV(t,x,y)\le -1~\hbox {for any}~(x,y)\in \mathbb {R}_{+}^{2}{\setminus } U, \end{aligned}$$

where $U=[\epsilon ,\frac{1}{\epsilon }]\times [\epsilon ,\frac{1}{\epsilon }]$. Therefore (2.4) in Lemma 2.1 is also satisfied. In view of Lemma 2.1, one can see that system (1.3) has a nontrivial positive T-periodic solution. This completes the proof. $\square$

4 Positive Recurrence and Ergodic Properties of System (1.4)

In this section, we shall establish sufficient conditions for positive recurrence and the existence of an ergodic stationary distribution of system (1.4). Positive recurrence and the existence of an ergodic stationary distribution in the context of predator–prey systems mean that the predator and prey species can be persistent and coexistent in the long term. Firstly, motivated by Remark 3.1, we shall present a lemma as follows.

Lemma 4.1

The following linear equation

$$\begin{aligned} f'(K)m(k)-r_{1}(k)c(k)+\sum _{l\in \mathbb {S}}\gamma _{kl}c(l)=0 \end{aligned}$$

(4.1)

has a solution $(c(1),\ldots ,c(N))^{T}$.

Proof

System (1.4) can be rewritten in the following form

$$\begin{aligned} AC=D, \end{aligned}$$

(4.2)

where $C\in \mathbb {R}^{N}$, $D=(f'(K)m(1),\ldots ,f'(K)m(N))^{T}$ and

$$\begin{aligned} \begin{array}{llll} A=\left[ \begin{array}{cccc} r_{1}(1)-\gamma _{11}&{}\quad -\gamma _{12}&{}\quad \cdots &{}\quad -\gamma _{1N}\\ -\gamma _{21}&{}\quad r_{1}(2)-\gamma _{22}&{}\quad \cdots &{}\quad -\gamma _{2N}\\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ -\gamma _{N1}&{}\quad -\gamma _{N2}&{}\quad \cdots &{}\quad r_{1}(N)-\gamma _{NN} \end{array}\right] .\end{array} \end{aligned}$$

Obviously, $A\in Z^{N\times N}$. For each $k=1,\ldots ,N$, consider the leading principal submatrix

$$\begin{aligned} \begin{array}{llll} A_{k}=\left[ \begin{array}{cccc} r_{1}(1)-\gamma _{11}&{}\quad -\gamma _{12}&{}\quad \cdots &{}\quad -\gamma _{1k}\\ -\gamma _{21}&{}\quad r_{1}(2)-\gamma _{22}&{}\quad \cdots &{}\quad -\gamma _{2k}\\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ -\gamma _{k1}&{}\quad -\gamma _{k2}&{}\quad \cdots &{}\quad r_{1}(k)-\gamma _{kk} \end{array}\right] .\end{array} \end{aligned}$$

Clearly, $A_{k}\in Z^{k\times k}$. Additionally each row of submatrix $A_{k}$ has the sum

$$\begin{aligned} r_{1}(i)-\sum _{j=1}^{k}\gamma _{ij}=r_{1}(i)+\sum _{j=k+1}^{N}\gamma _{ij}\ge r_{1}(i)>0,\quad i=1,\ldots ,k. \end{aligned}$$

Following Lemma 5.3 in Mao and Yuan (2006), we have $det A_{k}>0$, $k=1,\ldots ,N$. That is to say, we have shown that all the leading principal minors of A are positive. Using Theorem 2.10 in Mao and Yuan (2006) leads to that A is a nonsingular M-matrix and for the vector $D\in \mathbb {R}^{N}$, the linear Equation (4.2) has a solution $C=(c(1),\ldots ,c(N))^{T}$. This completes the proof. $\square$

Moreover, we need the following assumption.

and $d_{1}$ is a positive constant satisfying the condition of Theorem 4.1.

Theorem 4.1

Let Assumptions $(H_1)$–$(H_4)$ and $(H_6)$ hold, if $\hat{r}_{1}>K^{2}\breve{\sigma }_{12}^{2}$ and there exists a constant $d_{1}$ such that the following condition holds

$$\begin{aligned} \begin{array}{llll} d_{1}>\max \Big \{0,\max _{k\in \mathbb {S}}\Big \{\frac{c(k)r_{1}(k)-\frac{Kc_{2}m(k)}{2}}{r_{1}(k)-K^{2}\sigma _{12}^{ 2}(k)}\Big \}\Big \}, \end{array} \end{aligned}$$

where c(k) is the solution of Eq. (4.1), then for any given initial value $(x(0),y(0),r(0))\in \mathbb {R}_{+}^{2}\times \mathbb {S}$, the solution (x(t), y(t), r(t)) of system (1.4) is positive recurrent and has a unique ergodic stationary distribution $\mu (\cdot ,\cdot )$ in $\mathbb {R}_{+}^{2}\times \mathbb {S}$.

Proof

In order to prove Theorem 4.1, it suffices to verify conditions (i), (ii) and (iii) in Lemma 2.2 hold. Assumption $\gamma _{ij}>0$ for $i\not =j$ in Sect. 2 shows that the condition (i) holds. Now we prove the condition (ii). It is easy to see that

$$\begin{aligned} \sum _{i,j=1}^{2}a_{ij}(x,y,k)\zeta _{i}\zeta _{j}= & {} \left( \begin{array}{ccccc} \sigma _{11}(k)x\zeta _{1}&\quad \sigma _{12}(k)x^{2}\zeta _{1}&\quad \sigma _{21}(k)y\zeta _{2}&\quad \sigma _{22}(k)y^{2}\zeta _{2} \end{array}\right) \left( \begin{array}{ccccc} \sigma _{11}(k)x\zeta _{1}\\ \sigma _{12}(k)x^{2}\zeta _{1}\\ \sigma _{21}(k)y\zeta _{2}\\ \sigma _{22}(k)y^{2}\zeta _{2} \end{array}\right) \\= & {} (\sigma _{11}^{2}(k)x^{2}+\sigma _{12}^{2}(k)x^{4}) \zeta _{1}^{2}+(\sigma _{21}^{2}(k)y^{2}+\sigma _{22}^{2}(k)y^{4})\zeta _{2}^{2}\\\ge & {} M_{1}\Vert \zeta \Vert ^{2}~\hbox {for any } (x,y,k)\in \mathcal {D}^{C}\times \mathbb {S},\quad \zeta =(\zeta _{1},\zeta _{2})\in \mathbb {R} ^{2}, \end{aligned}$$

where $M_{1}=\min \{\sigma _{11}^{2}(k)x^{2}+\sigma _{12}^{2}(k)x^{4},\sigma _{21}^{2}(k)y^{2}+\sigma _{22}^{2}(k)y^{4}\}$. This implies that the condition (ii) in Lemma 2.2 is satisfied.

Now we are in the position to verify the condition (iii) in Lemma 2.2.Define a $C^{2}$-function $V:\mathbb {R}_{+}^{2}\times \mathbb {S}\rightarrow \mathbb {R}$ as follows

$$\begin{aligned} V(x,y,k)= & {} P\left[ -\ln y-c(k)x+d_{1}\left( x-K-K\ln \frac{x}{K}\right) +\frac{\breve{\sigma }_{22}^{2}}{2\hat{a}}y\right. \\&\left. +\,\frac{\breve{a}+Kc_{1}d_{1}}{\hat{r}_ {2}}y+Kc(k)-\omega _{k}\right] +x^{p}+y^{p}, \end{aligned}$$

where $0<p<1$ is a constant and $P>0$ is a constant satisfying $-P\lambda +g_{1}^{u}+g_{2}^{u}\le -2$, and functions $g_{1}$, $g_{2}$ are similar to functions $f_{1}$ and $f_{2}$ in the proof of Theorem 3.1, $\omega :=(\omega _{1},\ldots ,\omega _{N})^{T}$ will be determined later. It is not difficult to check that there is a unique minimum value point $(x_{0}(k),y_{0}(k),k)$ of V(x, y, k).

Define a nonnegative $C^{2}$-function

$$\begin{aligned} \hat{V}(x,y,k)= & {} V(x,y,k)-V(x_{0}(k),y_{0}(k),k)\\= & {} P \left[ -\ln y-c(k)x+d_{1}\left( x-K-K\ln \frac{x}{K}\right) +\frac{\breve{\sigma }_{22}^{2}}{2\hat{a}}y\right. \\&\left. +\,\frac{\breve{a}+Kc_{1}d_{1}}{\hat{r}_ {2}}y+Kc(k)-\omega _{k}\right] +x^{p}+y^{p}\\&-\,V(x_{0}(k),y_{0}(k),k). \end{aligned}$$

Denote $V_{1}=-\ln y-c(k)x+d_{1}(x-K-K\ln \frac{x}{K})+\frac{\breve{\sigma }_{22}^{2}}{2\hat{a}}y+\frac{\breve{a}+Kc_{1}d_{1}}{\hat{r}_ {2}}y+Kc(k)-\omega _{k}$, $V_{2}=x^{p}+y^{p}-V(x_{0}(k),y_{0}(k),k)$. An application of the generalized Itô’s formula (Mao and Yuan 2006) to $V_{1}(x,y,k)$, we have

$$\begin{aligned} LV_{1}= & {} -m(k)f(x)+r_{2}(k)+\frac{\sigma _{21}^{2}(k)}{2}+a(k)y+\frac{\sigma _{22}^{2}(k)}{2}y^{2}\\&-\,c(k)r_{1}(k)x\left( 1-\frac{x}{K}\right) +c(k)f(x)y \\&-\,\sum _{l\in \mathbb {S}}\gamma _{kl}c(l)(x-K+K) +d_{1}\left( -\frac{r_{1}(k)}{K}(x-K)^{2}\right. \\&-\,f(x)y+K\frac{f(x)}{x}y+\frac{K}{2}\sigma _{11}^{2}(k) +\frac{K}{2}\sigma _{12}^{2}(k)\\&\left. \times \,(x-K+K)^{2}\right) -\frac{\breve{\sigma }_{22}^{2}}{2\hat{a}}r_{2}(k)y-\frac{\breve{\sigma }_{22}^{2}}{2\hat{a}}a(k) y^{2}+\frac{\breve{\sigma }_{22}^{2}}{2\hat{a}}m(k)f(x)y\\&-\,\frac{\breve{a}+Kc_{1}d_{1}}{\hat{r}_{2}}r_{2}(k)y-\frac{\breve{a}+Kc_{1}d_{1}}{\hat{ r}_{2}}a(k)y^{2}\\&+\,\frac{m(k)(\breve{a}+Kc_{1}d_{1})}{\hat{r}_{2}}f(x)y+K\sum _{l\in \mathbb {S}}\gamma _{kl}c(l)-\sum _{l\in \mathbb {S}} \gamma _{kl}\omega _{l}\\= & {} -m(k)f(x)+r_{2}(k)+\frac{\sigma _{21}^{2}(k)}{2}+a(k)y+\frac{1}{2} \left( \sigma _{22}^{2}(k)-\frac{\breve{\sigma }_{22}^{2}a(k)}{\hat{a}}\right) y^{2}\\&-\,c(k)r_{1}(k)x\left( 1-\frac{x}{K}\right) +c(k)f(x)y \\&-\,\sum _{l\in \mathbb {S}}\gamma _{kl}c(l)(x-K) +d_{1}\left( -\frac{r_{1}(k)}{K}(x-K)^{2}\right. \\&-\,f(x)y+K\frac{f(x)}{x}y+\frac{K}{2}\sigma _{11}^{2}(k)+\frac{K}{2}\sigma _{12}^{2 }(k)\\&\left. \times \,(x-K+K)^{2}\right) -\frac{\breve{\sigma }_{22}^{2}}{2\hat{a}}r_{2}(k)y+\frac{\breve{\sigma } _{22}^{2}}{2\hat{a}}m(k)f(x)y\\&-\,\frac{\breve{a}+Kc_{1}d_{1}}{\hat{r}_{2}}r_{2}(k)y-\frac{\breve{a}+Kc_{1}d_{1}}{\hat{r}_{2}}a(k)y^{2}\\&+\,\frac{m(k)(\breve{a}+Kc_{1}d_{1})}{\hat{r}_{2}}f(x)y-\sum _{l\in \mathbb {S}}\gamma _{kl}\omega _{l}\\\le & {} -m(k)f(x)+r_{2}(k)+\frac{\sigma _{21}^{2}(k)}{2}+a(k)y-c(k)r_{1}(k) x\left( 1-\frac{x}{K}\right) \\&+\,c(k)f(x)y-\sum _{l\in \mathbb {S}}\gamma _{kl}c(l)(x-K)\\&+\,d_{1}\left( -\frac{r_{1}(k)}{K}(x-K)^{2}+Kc_{1}y+\frac{K}{2}\sigma _{11}^{2}(k)\right. \\&+\,K\sigma _{12}^{2}(k)(x-K)^{2}\\&\left. +\,K^{3}\sigma _ {12}^{2}(k)\right) +\frac{\breve{m}\breve{\sigma }_{22}^{2}}{2\hat{a}}f(x)y\\&-\,\frac{\breve{a}+Kc_{1}d_{1}}{\hat{r}_{2}}r_{2}(k)y+\frac{m(k)(\breve{a}+Kc_{1}d_{1})}{\hat{r}_{2}}f(x)y-\sum _{l\in \mathbb {S}}\gamma _{kl}\omega _{l}\\\le & {} -f(K)m(k)+r_{2}(k)+\frac{\sigma _{21}^{2}(k)}{2}+ \frac{Kd_{1}\sigma _{11}^{2}(k)}{2}\\&+\,K^{3}d_{1}\sigma _{12}^{2}(k) +\left[ -m(k)f(x)+f(K)m(k)\right. \\&+\,\frac{c(k)r_{1}(k)}{K}x(x-K)-\frac{d_{1}r_{1}(k)}{K}(x-K)^{2}\\&\left. +\,Kd_{1}\sigma _{12}^{2}(k)(x-K)^{2}-\sum _{l\in \mathbb { S}}\gamma _{kl}c(l)(x-K)\right] \\&+\,\left( \breve{c}+\frac{\breve{m}\breve{\sigma }_{22}^{2}}{2\hat{a}}+\frac{\breve{m}(\breve{a}+Kc_{1}d_{1})}{\hat{r}_{2} }\right) f(x)y-\sum _{l\in \mathbb {S}}\gamma _{kl}\omega _{l}\\= & {} -f(K)m(k)+r_{2}(k)+ \frac{\sigma _{21}^{2}(k)}{2}+\frac{Kd_{1}\sigma _{11}^{2}(k)}{2}\\&+\,K^{3}d_{1}\sigma _{12}^{2}(k)- \sum _{l\in \mathbb {S}}\gamma _{kl}\omega _{l}+F(x,k)\\&+\,\left( \breve{c}+\frac{\breve{m}\breve{\sigma }_{22}^{2}}{2\hat{a}}+\frac{\breve{m}(\breve{a}+Kc_{1}d_{1})}{\hat{r}_{2}}\right) f(x)y, \end{aligned}$$

where

$$\begin{aligned} F(x,k)= & {} -m(k)f(x)+f(K)m(k)+\frac{c(k)r_{1}(k)}{K}x(x-K)\\&-\,\frac{d_{1}r_{1}(k)}{K}(x-K)^{2}+Kd_{1}\sigma _{12}^{2}(k)(x -K)^{2}\\&-\,\sum _{l\in \mathbb {S}}\gamma _{kl}c(l)(x-K) \end{aligned}$$

and in the first inequality, we have used the fact $(a+b)^{2}\le 2a^{2}+2b^{2}$ for any $a,b\in \mathbb {R}$. Then

$$\begin{aligned} \frac{\partial F(x,k)}{\partial x}= & {} -m(k)f'(x)+\frac{c(k)r_{1}(k)}{K}(2x-K)-\frac{2d_{1}r_{1}(k)}{K}(x-K)\\&+\,2Kd_{1}\sigma _{12}^{2}(k)(x-K)-\sum _{l\in \mathbb {S}}\gamma _{kl}c(l),\\ \frac{\partial ^{2}F(x,k)}{\partial x^{2}}= & {} -m(k)f''(x)+\frac{2c(k)r_{1}(k)}{K}-\frac{2d_{1}r_{1}(k)}{K}+2Kd_{1}\sigma _{12}^{2}(k). \end{aligned}$$

Let

$$\begin{aligned} \frac{\partial F(x,k)}{\partial x}|_{x=K}=0, \end{aligned}$$

we get

$$\begin{aligned} \sum _{l\in \mathbb {S}}\gamma _{kl}c(l)=-f'(K)m(k)+r_{1}(k)c(k). \end{aligned}$$

On the other hand, we obtain

$$\begin{aligned} \frac{\partial ^{2}F(x,k)}{\partial x^{2}}\le -m(k)c_{2}+\frac{2c(k)r_{1}(k)}{K}-d_{1}(\frac{2r_{1}(k)}{K}-2K\sigma _{12}^{2}(k))<0, \end{aligned}$$

where the inequality holds due to the Assumption $(H_{4})$ and the condition of Theorem 4.1. Therefore

$$\begin{aligned} F(x,k)\le F(K,k)=0. \end{aligned}$$

Thus

$$\begin{aligned} LV_{1}\le & {} -f(K)m(k)+r_{2}(k)+\frac{\sigma _{21}^{2}(k)}{2}+\frac{Kd_{1}\sigma _{11}^{2}(k)}{2}+K^{3}d_{1}\sigma _{12} ^{2}(k) \nonumber \\&+\,\left( \breve{c}+\frac{\breve{m}\breve{\sigma }_{22}^{2}}{2\hat{a}}+\frac{\breve{m}(\breve{a}+Kc_{1}d_{1})}{\hat{ r}_{2}}\right) c_{1}xy \nonumber \\&-\,\sum _{l\in \mathbb {S}}\gamma _{kl}\omega _{l} \nonumber \\= & {} -\lambda _{k}+\left( \breve{c}+\frac{\breve{m}\breve{\sigma }_{22}^{2}}{2\hat{a}}+\frac{\breve{m}(\breve{a}+Kc_{1}d_{1})}{\hat{r}_{2}}\right) c_{1}xy-\sum _{l\in \mathbb {S}}\gamma _{kl}\omega _{l}, \end{aligned}$$

(4.3)

where

$$\begin{aligned} \lambda _{k}=f(K)m(k)-r_{2}(k)-\frac{\sigma _{21}^{2}(k)}{2}-\frac{Kd_{1}\sigma _{11}^{2}(k)}{2}-K^{3}d_{1}\sigma _{12} ^{2}(k). \end{aligned}$$

Since the generator matrix $\varGamma$ is irreducible, let $\omega =(\omega _{1},\ldots ,\omega _{N})^{T}$ be the solution of the following Poisson system (see Khasminskii et al. 2007, Lemma 2.3)

$$\begin{aligned} \varGamma \omega =\sum _{h=1}^{N}\pi _{h}\lambda _{h}{} \mathbf{1}-\lambda , \end{aligned}$$

where $\lambda =(\lambda _{1},\ldots ,\lambda _{N})^{T}$. This implies that

$$\begin{aligned} \sum _{l\in \mathbb {S}}\gamma _{kl}\omega _{l}+\lambda _{k}=\sum _{k\in \mathbb {S}}\pi _{k}\lambda _{k}=\lambda . \end{aligned}$$

Substituting this equality into (4.3) gives

$$\begin{aligned} LV_{1}=-\lambda +(\breve{c}+\frac{\breve{m}\breve{\sigma }_{22}^{2}}{2\hat{a}}+\frac{\breve{m}(\breve{a}+Kc_{1}d_{1}) }{\hat{r}_{2}})c_{1}xy. \end{aligned}$$

Following the proof of the remainder of Theorem 3.1, we can obtain that the solution (x(t), y(t), r(t)) of system (1.4) is positive recurrent and has a unique ergodic stationary distribution $\mu (\cdot ,\cdot )$ in $\mathbb {R}_{+}^{2}\times \mathbb {S}$. This completes the proof. $\square$

Remark 4.1

Assume that system (1.4) is disturbed only by the white noise, then the linear equation (4.1) has a unique solution $c=\frac{mf'(K)}{r_{1}}$. And the conditions in Theorem 4.1 become $\sigma _{12}^{2}<\frac{r_{1}}{K^{2}}$ and $d>\max \Big \{0,\frac{mf'(K)-\frac{mKc_{2}}{2}}{r_{1}-K^{2}\sigma _{12}^{2}}\Big \}$. In other words, if these conditions hold, then for any initial value $(x(0),y(0))\in \mathbb {R}_{+}^{2}$, the solution (x(t), y(t)) of system (1.2) admits a unique ergodic stationary distribution $\mu (\cdot )$ in $\mathbb {R}_{+}^{2}$.

Remark 4.2

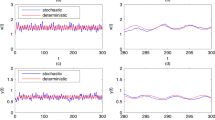
From Theorems 3.1 and 4.1, one can find that if the intensities of the noises are small, then the ergodicity and periodic solution imply that the predator and prey species can be persistent and coexistent in the long term. Moreover, the existence of stationary distribution implies stochastic weak stability to some extent.

5 Concluding Remarks

This paper is concerned with two stochastic predator–prey models with general functional response and higher-order perturbation. For the system (1.3) with periodic coefficients, by using Khasminskii’s theory of periodic solution, we show that system (1.3) has a nontrivial positive T-periodic solution. For the system (1.4) disturbed by both white and telegraph noises, we establish sufficient conditions for positive recurrence and the existence of an ergodic stationary distribution to the solutions. The existence of stationary distribution implies stochastic weak stability to some extent.

Some interesting topics deserve further investigation. On the one hand, one may propose some more realistic but complex models, such as considering the effects of impulsive perturbations on systems (1.3) and (1.4), respectively. On the other hand, it is interesting to introduce some other environmental noises into systems (1.3) and (1.4), such as Lévy noise, Poisson noise and so on and study some other dynamical properties of these systems. We leave these cases as our future work.