1 Introduction

The most fundamental property of turbulent dynamical systems, which distinguish them from all other problems of applied mathematics, is the presence of persistent instabilities over a large number of modes. From the dynamics point of view these instabilities are always balanced by a nonlinear energy transfer mechanism which acts both as a stabilizing factor for the unstable modes (of the linearized dynamics) but also as a supplier of energy for the stable modes (Sapsis and Majda 2013b), leading to broad energy spectra. From the modeling or uncertainty quantification (UQ) point of view the presence of internal instabilities naturally leads to growth of any uncertainties present in the modeling equations, initial conditions, or external forcing. Moreover, this synergistic activity of unstable modes, nonlinear energy transfer mechanisms, and stable modes presents important modeling difficulties since all the above components are equally crucial for a correct description of the turbulent dynamics.

Therefore, by the very nature of turbulent dynamical systems it is hard to capture this elegant balance through a reduced-set of modes. Nevertheless there are a large number of applications where the dynamics ‘live’ in a low-dimensional space (e.g. flows with a laminar character having a very small number of instabilities) and for these systems it is efficient to perform order reduction. Schemes based on this approach are essentially relying on the projection of the original system into a ‘suitable’ set of modes. These are chosen according to empirical criteria such as energy-based proper orthogonal decomposition (POD) (see for example Sirovich 1987; Holmes et al. 1996), linear-operator-theoretic model reduction methods, such as the balanced POD (Lall et al. 2002; Ma et al. 2010), and more recently dynamically orthogonal (DO) field equations that follow from the original system equation (Sapsis and Lermusiaux 2009; Sapsis 2013).

The effect of the projection on the linearized dynamics may not allow for the correct modeling of all the instabilities involved in the case where the modes are not sufficient in number or appropriately chosen. The same limitations hold for the modeling of intrinsically irreducible linearized dynamics (such as non-normal dynamics—see Sect. 4.1 in Sapsis and Majda 2013a) or even dynamical components, which despite the fact that they do not interact with other modes, their energy is important for the correct modeling (see Sect. 4.2.1—case II in Sapsis and Majda 2013a). A blended approach based on the quasilinear Gaussian (QG) closure and DO equations was developed in Sapsis and Majda (2013a) to resolve the misleading modeling of the linear dynamics due to the order reduction. In this case a reduced-order DO approach was used just for the modeling of the nonlinear fluxes while the linear dynamics where modeled completely. The developed QG-DO method performed very well in systems with stable mean and important nonlinear energy fluxes where the system energy (or the attractors finite size) was caused mainly due to the external stochastic forcing.

It turns out however, that a reduced-order modeling approach even at the level of nonlinear energy fluxes is not sufficient to approximate adequately the synergistic activity of unstable, stable, and nonlinear dynamics in a turbulent system. A first step towards this direction was the development of the modified quasilinear Gaussian closure (MQG) scheme (Sapsis and Majda 2013b). Through a second-order statistical framework the collective effect of the non-Gaussian statistics or nonlinear dynamics is quantified in the energy transfer level using second-order steady-state information. Subsequently this nonlinear energy transfer mechanism is represented and coupled to the original linear dynamics. In contrast to other second-order schemes (e.g. mean square models (DelSole 2004; Majda and Harlim 2012)) MQG not only recovers the correct steady-state statistics but it does this by correctly modeling the energy flow between different dynamical components (or different locations of the spectrum). This leads to very good performance of the UQ scheme even in transient regimes where the energy and number of instabilities are much different than the statistical steady state used to diagnose the energy fluxes.

Despite its very good performance MQG is ‘tied’ to the steady-state statistics for which it is tuned. Therefore in extremely different excitation scenarios with spatially non-homogeneous or even localized action some discrepancies may occur. This is because, even though the MQG nonlinear energy fluxes are complete or full-order (i.e. they model the energy transfers over the full set of a complete basis rather than a reduced one), they may not be able to model a specific dynamical scenario which is not present in the dynamics used to diagnose the nonlinear fluxes. Such a scenario can be, for example, injection of energy in high wavenumbers causing reverse flow of energy to large scale modes. In addition MQG can provide only second-order statistical information.

The goal of the present work is the improvement of the MQG scheme in extreme excitation scenarios that ‘push’ the system into very different dynamical regimes from those for which the MQG nonlinear fluxes have been tuned. To achieve this goal we will develop a blended framework of inexpensive, full-space, second-order UQ schemes (such as MQG) with high-order statistical models (such as the Fokker–Planck equation or Monte-Carlo simulation) in reduced-order subspaces (in the present work these will be DO subspaces). This is a particularly challenging task given the contradictory character of the two ingredient methods (MQG and DO). The coupling will be performed at the level of the energy fluxes by correcting the MQG fluxes using higher-order statistical information from a DO reduced-order subspace for which the nonlinear dynamics are modeled explicitly. On the other hand we will use the inexpensive second-order statistical model to maintain the correct energy content inside the DO subspace by modifying the reduced-order equation so that it implicitly takes into account the interactions of the subspace dynamics with the dynamics lying outside of it. We will prove that this two-way coupling integrates naturally the two methods resulting in pure improvement relative to the MQG method.

The structure of the paper is as follows. In Sect. 2 we present and analyze the dynamics of two paradigm systems with persistently unstable dynamics: the unstable triad and the Lorenz-96 system. We illustrate how the nonlinear energy fluxes are connected with non-Gaussian statistics and based on this connection we explain why order-reduction techniques will not be able to describe the correct dynamics (see Sapsis and Majda 2013a for more discussion). In Sect. 3 we illustrate the limitations of blended methods that perform reduction at the level of energy fluxes such as QG-DO method. In Sect. 4 we present the MQG-DO method and we show how the coupling approach results in a natural blending of the two methodologies that leads to monotonic improvement with respect to the number of modes for which the full statistics are resolved. Finally, in Sect. 5 we illustrate the advantages of the new blended approach in a variety of time-dependent and time-independent examples exhibiting a strongly unstable character.

2 Dynamical Systems with Unstable Mean

We will focus on the development of blended UQ techniques in order to describe the stochastic attractor (i.e. the set of all feasible states of a given system under given initial conditions and/or stochastic excitation) of systems with persistently unstable mean. These are systems whose linearized dynamics are associated with an important number of positive Lyapunov exponents and therefore the careful and precise consideration of the nonlinear terms is crucial in order to avoid blowup or severe underestimation of energy in the UQ scheme (Sapsis and Majda 2013b). By blended UQ techniques we refer to coupled schemes that model a large set of modes through second-order statistics and a selected set of modes through higher-order statistics.

This is a particularly challenging task given that our analysis will rely on the blending of two methodologies with completely opposing natures: one relying on the expensive statistical modeling of the dynamics in a low-dimensional subspace, and the other on the second-order (i.e. inexpensive) statistical modeling of the dynamics in the full space.

The generic system formulation on which our analysis and illustrations will be based is given by the quadratic system

$$ \frac{\mathrm {d}\mathbf{u}}{\mathrm {d}t}= [ L+D ] \mathbf{u}+B ( \mathbf{u,u} ) +\mathbf{F} ( t ) +\dot{W}_{k} ( t;\omega ) \sigma_{k} ( t ) $$
(1)

acting on \(\mathbf{u}\in\mathbb{R}^{N}\). In the above equation and for what follows repeated indices will indicate summation. In some cases the limits of summation will be given explicitly to emphasize the range of the index.

In the above equation we have:

  • L, being a skew-symmetric linear operator representing the β-effect of Earth’s curvature, topology etc. and satisfying,

    $$L^{\ast}=-L. $$

  • D being a negative definite symmetric operator,

    $$D^{\ast}=D, $$

    representing dissipative processes such as surface drag, radiative damping, viscosity, etc.

The quadratic operator \(B ( \mathbf{u,u} ) \) conserves the energy by itself so that it satisfies

$$B ( \mathbf{u,u} )\cdot\mathbf{u}=0. $$

Finally, \(\mathbf{F} ( t ) +\dot{W}_{k} ( t;\omega ) \sigma_{k} ( t ) \) represents the effect of external forcing, which we will assume that it can be split into a mean component F(t) and a stochastic component with white noise characteristics. In what follows we give the basic set-up for the exact statistical formulas which will be used in this paper.

We use a finite-dimensional representation of the stochastic field consisting of a fixed-in-time, N-dimensional, orthonormal basis

$$\mathbf{u} ( t ) =\bar{\mathbf{u}} ( t ) + Z_{i} (t;\omega ) \mathbf{v}_{i}, $$

where \(\bar{\mathbf{u}} ( t ) = \langle \mathbf{u} ( t ) \rangle \) represents the ensemble average of the response, i.e. the mean field, and Z i (t;ω) are stochastic processes. Note that the ensemble average is taken over the random argument ω which represents randomness in the initial conditions, and/or the stochastic excitation.

The mean field equation is given by

$$ \frac{\mathrm {d}\bar{\mathbf{u}}}{\mathrm {d}t}= [ L+D ] \bar{\mathbf{u}}+ B (\bar{\mathbf{u}},\bar{\mathbf{u}} ) +R_{ij}B ( \mathbf{v}_{i}, \mathbf{v}_{j} ) +\mathbf{F}, $$
(2)

where R=〈ZZ ∗〉 is the covariance matrix. Moreover the random component of the solution, u′=Z i (t;ω)v i satisfies

$$ \frac{\mathrm {d}\mathbf{u}^{\prime}}{ \mathrm {d}t}= [ L+D ] \mathbf{u}^{\prime} +B \bigl( \bar{\mathbf{u}},\mathbf{u}^{\prime} \bigr) +B \bigl( \mathbf{u}^{\prime} ,\bar{\mathbf{u}} \bigr) +B \bigl( \mathbf{u}^{\prime} ,\mathbf{u}^{\prime} \bigr) -R_{jk}B ( \mathbf{v}_{j},\mathbf{v}_{k} ) +\dot{W}_{k} ( t;\omega ) \sigma _{k} ( t ). $$
(3)

By projecting the above equation to each basis element v i we obtain

$$\begin{aligned} \frac{\mathrm {d}Z_{i}}{\mathrm {d}t} =&Z_{j} \bigl( [ L+D ] \mathbf{v}_{j}+B ( \bar{\mathbf{u}},\mathbf{v}_{j} ) +B ( \mathbf{v}_{j},\bar{\mathbf{u}} ) \bigr)\cdot\mathbf{v}_{i}+ \bigl( B \bigl( \mathbf{u}^{\prime},\mathbf{u}^{\prime} \bigr) -R_{jk}B ( \mathbf{v}_{j},\mathbf{v}_{k} ) \bigr)\cdot\mathbf{v}_{i}\\ &{}+\dot{W} _{k}\sigma_{k}\cdot \mathbf{v}_{i}. \end{aligned}$$

From the last equation we directly obtain the evolution of the covariance matrix R

$$ \frac{\mathrm {d}R}{\mathrm {d}t}=L_{v}R+RL_{v}^{\ast}+Q_{F}+Q_{\sigma}, $$
(4)

where we have:

(i) the linear dynamics operator expressing energy transfers between the mean field and the stochastic modes (effect due to B), as well as energy dissipation (effect due to D) and non-normal dynamics (effect due to L)

$$ \{ L_{v} \} _{ij}= \bigl( [ L+D ] \mathbf{v}_{j}+B ( \bar{\mathbf{u}},\mathbf{v}_{j} ) +B (\mathbf{v}_{j},\bar{\mathbf{u}} ) \bigr) \cdot\mathbf{v}_{i}; $$
(5)

(ii) the positive definite operator expressing energy transfer due to the external stochastic forcing

$$ \{ Q_{\sigma} \} _{ij}= ( \mathbf{v}_{i}\cdot \sigma_{k} ) ( \sigma_{k}\cdot\mathbf{v}_{j} ) ; $$
(6)

(iii) as well as the energy flux between different modes due to non-Gaussian statistics (or nonlinear terms) modeled through third-order moments

$$ Q_{F}=\overline{Z_{m}Z_{n}Z_{j}}B (\mathbf{v}_{m},\mathbf{v}_{n} ) \cdot\mathbf{v}_{i}+ \overline{Z_{m}Z_{n}Z_{i}}B ( \mathbf{v}_{m},\mathbf{v}_{n} ) \cdot \mathbf{v}_{j}. $$
(7)

The last term involves higher-order statistics and therefore suitable closure assumptions need to be made in order to set up a UQ scheme. The modeling of the nonlinear energy fluxes Q F based on a blended MQG and DO approach will be the main focus of this work.

We note that the energy conservation property of the quadratic operator B is inherited by the matrix Q F since

$$ \mathrm{Tr} [ Q_{F} ] =2\overline{Z_{m}Z_{n}Z_{i}}B ( \mathbf{v}_{m},\mathbf{v}_{n} ) \cdot\mathbf{v}_{i}=2B \bigl( \mathbf{u}^{\prime},\mathbf{u}^{\prime} \bigr) \cdot\mathbf{u}^{\prime}=0. $$
(8)

The above exact statistical equations will be the starting point for the approximation schemes that we will present and develop below. To illustrate and validate the developed UQ scheme we will consider two specific systems that belong to the general formulation (1) and mimic various mechanisms of turbulent dynamics. These will be the triad system in an unstable configuration, and the Lorenz-96 system under extreme time-space dependent excitation. In what follows we will give a detailed description of those examples as well as an analysis of the statistics and the associated energy transfers.

2.1 Unstable Triad System

The first example that we consider is a simple but nevertheless instructive model, namely the triad system. This is a three-dimensional system with a quadratic part that is both divergence free and energy preserving. In the standard formulation the linear part consists of a dissipative operator that is negative-definite and a skew-symmetric operator. The nonlinear coupling in triad systems is generic of nonlinear coupling between any three modes in larger systems with quadratic nonlinearities (Majda et al. 1999, 2001, 2002). We can think of this ‘toy’ problem as a ‘poor-mans’ approach to a full fluid system where the nonlinear terms, dissipation, and skew-symmetric part represent, respectively, the advection terms, the viscous dissipation, and the Coriolis effect while the stochastic noise represents the nonlinear interactions with other modes in a crude fashion.

In this standard formulation the mean is stable and the finite size of the stochastic attractor is by the external stochastic forcing. In this context the performance of the blended reduced-subspace algorithm based on the quasilinear Gaussian closure combined with dynamically orthogonal subspace reduction (QG-DO UQ scheme) has been proven to be very satisfactory (Sapsis and Majda 2013a). However, in a turbulent system a fundamental factor is the internal system instabilities that make the mean unstable over various directions in phase space as is typical for anisotropic fully turbulent systems.

To examine this case we will modify the standard triad system configuration by imposing negative damping to one of the degrees of freedom creating a strong, persistent instability that makes the role of the external stochastic excitation to be of secondary importance. In particular the system that we consider is a three-dimensional special case of the generic quadratic system (1) given by

$$\begin{aligned} \mathrm {d}u_{1} & = ( -\gamma_{1}u_{1}+ \lambda_{12}u_{2}+\lambda_{13}u_{3} +\beta_{1}u_{3}u_{2}+F_{1} )\,\mathrm {d}t+ \sigma_{1}\,\mathrm {d}W_{1}, \end{aligned}$$
(9a)
$$\begin{aligned} \mathrm {d}u_{2} & = ( -\gamma_{2}u_{2}- \lambda_{12}u_{1}+\lambda_{23}u_{3}+\beta_{2}u_{1}u_{3}+F_{2} )\,\mathrm {d}t+ \sigma_{2}\,\mathrm {d}W_{2}, \end{aligned}$$
(9b)
$$\begin{aligned} \mathrm {d}u_{3} & = ( -\gamma_{3}u_{3}- \lambda_{13}u_{1}-\lambda_{23}u_{2}+\beta_{3}u_{2}u_{1}+F_{3} )\,\mathrm {d}t+ \sigma_{3}\,\mathrm {d}W_{3}, \end{aligned}$$
(9c)

with β 1+β 2+β 3=0. To obtain an unstable configuration in the steady state we choose negative damping for u 1 (the unstable mode) and positive for u 2 and u 3: γ 1=−0.4, γ 2=γ 3=2. We choose strong nonlinear coupling β 1=2, β 2=β 3=−1, and weak external noise σ 1=0.25, σ 2=σ 3=0.79 since the energy of the system comes primarily from the instability of the first mode. The nonlinear coefficients are chosen to rapidly transfer energy from u 1 to u 2,u 3 with β 1 having the opposite sign of β 2,β 3 (Majda et al. 1999, 2001, 2002). We also choose constant external forcing for the second and third degree of freedom, F 2=−1, F 3=1, to achieve non-zero steady-state values for u 2 and u 3. This is essential for these modes to be active causing energy to flow towards them from u 1 so that the system will achieve a finite-energy steady state and u 1 will not blow up. The linear instability is always dominant for u 1 so we set F 1=0. Finally, we also add a skew symmetric component: λ 12=0.03, λ 13=0.06, and λ 23=−0.09.

To study the dynamical properties of this system we perform a Monte-Carlo simulation with 105 ensemble members which is sufficiently large to guarantee convergence of the third-order statistics (this parameter will be used for all the Monte-Carlo simulations that follow and involve the triad system). The statistical equilibrium of this system relies exclusively on the strong energy transfer (due to nonlinear mechanisms) from the unstable modes to the stable ones. In Fig. 1 (subplots a and d) we present the time series for the mean and variance for the three degrees of freedom showing clearly that u 1 is the dominant one. The time series for the third-order central moments responsible for nonlinear energy transfer,

$$M_{ijk}= \bigl\langle ( u_{i}-\bar{u}_{i} ) ( u_{j}-\bar {u}_{j} ) ( u_{k}- \bar{u}_{k} ) \bigr\rangle , $$

where 〈⋅〉 denotes averaging over the probability measure, are presented in subplot b for the first mode. These plots clearly indicate that there is a continuous energy transfer from the first mode that balances its unstable character. The latter is expressed through the eigenvalues of the linearized dynamics operator L v given by (5) and shown in subplot c. The strong third-order moments (causing the strong nonlinear energy transfers) are in full agreement with the deformed shape of the stochastic attractor illustrated in subplots e (through a low-value contour of the probability density function that contains most of the probability) and f (through two-dimensional scatter diagrams).

Fig. 1
figure 1

Triad system with one unstable direction: (a) time series for the mean of u; (b) time-series for the third-order central moments of u involving the unstable mode; (c) real part of the linearized dynamics \(L_{v} ( \bar{\mathbf{u}} ) \) eigenvalues; (d) time series for the variance of the three DOF and the trace of the covariance matrix; (e) a low-probability contour of the full pdf (\(\{ \mathbf{u|}f_{\mathbf{u}} ( \mathbf{u} ) =10^{-6} \} \)) in steady state. This surface bounds the major part of the probability measure; (f) 2D scatter plots in steady state

Full size image

Despite its low dimensionality the unstable triad example is a challenging case to validate and assess the performance of a blended UQ algorithm since the equilibrium relies on a very sensitive balance of nonlinear energy transfers (or equivalently third-order moments) and unstable dynamics. This connection has to be modeled very carefully in the UQ scheme in order to obtain meaningful results.

2.2 Lorenz-96 System

The second system that we study is the Lorenz-96 system (L-96), which is the simplest paradigm of a complex turbulent dynamical systems possessing properties found in realistic turbulent systems such as a linearly unstable mean state, important energy spanning the whole spectrum, a large number of persistent instabilities, and strong nonlinear energy transfers between modes. It is widely used as a test model for algorithms for prediction, filtering, and low-frequency climate response (Lorenz 1996; Lorenz and Emanuel 1998; Majda et al. 2005, 2010; Majda and Harlim 2012) Therefore, L-96 is a perfect candidate both to illustrate the limitations of existing UQ schemes but also to validate the derived UQ model (Sapsis and Majda 2013b).

The L-96 model is a discrete periodic system described by the equations

$$ \frac{\mathrm {d}u_{i}}{\mathrm {d}t}=u_{i-1} ( u_{i+1}-u_{i-2} ) -u_{i}+F_{i},\quad i=0,\ldots,J-1, $$
(10)

with J=40 and with F i the deterministic forcing. We can easily observe that the energy conservation property for the quadratic part is satisfied (i.e. \(B\mathbf{ ( \mathbf{u},\mathbf{u} )\cdot u=0}\)) and the negative definite part has the diagonal form D=−I.

The model is designed to mimic baroclinic turbulence in the midlatitude atmosphere with the effects of energy conserving nonlinear advection and dissipation represented by the first two terms in (10). For sufficiently strong forcing values such as F=6,8 or 16 the L-96 is a prototype turbulent dynamical system which exhibits features of weakly chaotic dynamics (F i =6), strong chaotic dynamics (F i =8), and turbulent dynamics (F i =16) (cf. Fig. 2—first row). Similarly with the triad system we will first study the dynamical properties of this system by performing Monte-Carlo simulations. We use 5×104 ensemble members which is sufficiently large to guarantee convergence of the third-order statistics (this parameter will be used for all the Monte-Carlo simulations that follow and involve the Lorenz-96 system).

Fig. 2
figure 2

The three different dynamical regimes for the Lorenz-96 system. Spatiotemporal patterns (first row); steady-state spectrum (second row). Third-order central moments between principal modes. Only the significant moments are plotted (i.e. larger than 15 % of the maximum) and are colored according to their magnitude and sign (third row). Captured percentage of the total nonlinear fluxes Q F using the s most energetic modes (blue solid curve), captured percentage of energy using s modes (red solid curve), and the normalized energy of each mode with respect to the maximum energy (red dashed curve) (Color figure online)

Full size image

In the L-96 system the external noise is zero, and therefore we have no such contribution in Eq. (4), i.e. Q σ =0. Thus, uncertainty can only build-up from the unstable modes of the linearized dynamics—described by \(L_{v} ( \bar{\mathbf{u}} ) \). Moreover, by observing the statistical steady-state spectrum of the response (Fig. 2—second row) we notice that energy spans all the wavenumbers, both stable and unstable; a clear indication that energy is continuously transferred through the nonlinear fluxes Q F caused by important third-order moments.

To obtain a more intuitive picture of the energy transfers between different dynamical components we project the statistical steady-state solution (obtained through Monte-Carlo simulation) to the empirical orthogonal function (EOF or POD) basis consisting of Fourier modes in the translation invariant system (Majda et al. 2005). In particular let u ∞ denote the statistical steady-state solution in physical space for the L-96. We choose as a base v i the EOF modes that satisfy

$$\mathbf{C}_{uu}\mathbf{v}_{j}=\sigma_{j}^{2} \mathbf{v}_{j},\quad j=1,\ldots,J, $$

where \(\mathbf{C}_{uu}= \langle ( \mathbf{u}_{\infty} -\bar{\mathbf{u}}_{\infty} ) ( \mathbf{u}_{\infty} -\bar{\mathbf{u}}_{\infty} ) ^{\ast} \rangle \) is the covariance matrix in physical space. We arrange the EOF modes, in descending order with respect to their energy, i.e. \(\sigma_{1}^{2}\geq\sigma_{2}^{2}\geq\cdots\geq\sigma _{J}^{2}\) and we represent the steady-state solution as

$$\mathbf{u}_{\infty}=\bar{\mathbf{u}}_{\infty}+Z_{\infty i} ( \omega ) \mathbf{v}_{i}. $$

After projecting the statistical steady-state solution to the EOF base we consider the third-order statistics

$$M_{ijk}= \langle Z_{\infty i}Z_{\infty j}Z_{\infty k} \rangle . $$

This 3-tensor provides information about the energy exchanges between different dynamical components (that represent different energy part of the spectrum) occurring in the form of triad interactions. In Fig. 2—third row we present contours that include moments which are, in magnitude, 15 % or larger than the maximum M ijk . In other words for each forcing value we present the contour |M ijk |=0.15max ijk M ijk . The coloring is according to the value of the contained moments i.e. red for negative moments and blue for positive moments.

Even for the smallest value of F from those that we consider, we can clearly observe that the dominant nonlinear interactions occur in the form of triad energy exchanges involving very high energy modes and very low energy modes. This property reveals the challenge behind the precise modeling of the nonlinear fluxes Q F since any attempt to ignore very low-energy dynamical components will have a dramatic impact on the energy transfer properties. This property is more pronounced as we go to more intense forcing.

The above property is also confirmed if we consider directly the nonlinear energy fluxes computed using only a few high-energy modes. In particular we saw that the nonlinear energy fluxes are given in terms of the third-order moments through Eq. (7). The partially modeled nonlinear energy fluxes (based only on the first s≤J modes) will be given by

$$ Q_{F,s}=\sum_{n=1}^{s}\sum _{m=1}^{s} \bigl( M_{mnj}B ( \mathbf{v}_{m},\mathbf{v}_{n} )\cdot \mathbf{v}_{i}+M_{mni}B ( \mathbf{v}_{m},\mathbf{v}_{n} ) \cdot\mathbf{v}_{j} \bigr). $$
(11)

In Fig. 2—fourth row we present what percentage of the nonlinear energy transfer terms is captured when we consider the s-most energetic modes. In particular for each s we present the ratio \(q ( s ) =\frac{\max_{i,j}Q_{F,s}}{\max_{i,j}Q_{F}}\) (blue solid curve) together with the normalized energy of the modes (red dashed curve) and their cumulative energy (red solid curve). We observe that retaining the 14 most energetic modes (corresponding to more than 50 % of the system energy) will not allow capturing more than 1–2 % of the total nonlinear energy fluxes. Even, if we consider more modes this percentage increases very slowly.

Our recent MQG scheme (Sapsis and Majda 2013b) is able to alleviate this problematic behavior by directly modeling the fluxes Q F in the second-order level using a given statistical steady state (over which it is tuned). However, the scope of the present work is to model the strong variations of the nonlinear energy fluxes (using third-order statistics) caused by strong modifications of the conditions under which the MQG scheme has been tuned, i.e. to develop a UQ scheme that will be able to perform satisfactory in extreme conditions very far away from the tuned MQG spectrum.

3 Limitations of Existing UQ Methodologies for Turbulent Systems

In this section we will provide an overview of existing UQ algorithms emphasizing their advantages and limitations for turbulent systems. In particular we will study the performance of UQ methods in turbulent systems with strong energy variations (over time) based

(i) on the reduced-order modeling of the nonlinear fluxes Q F using dynamical orthogonality subspaces (QG-DO method Sapsis and Majda 2013a), and

(ii) on the modified quasilinear Gaussian (MQG) closure method (Sapsis and Majda 2013b) tuned over a specific energy level (i.e. a specific statistical steady state).

3.1 Reduced-Order Modeling of the Dynamics of the Nonlinear Fluxes (QG-DO Method)

Order-reduction techniques for UQ are based on the assumption that the modes that carry small amounts of energy do not have important influence on the global dynamics of the stochastic system. Based on this assumption order reduction may be performed either on the complete dynamics (e.g. DO or POD equations) or just on the computation of the nonlinear fluxes Q F (QG-DO method). The advantages of the latter method over standard reduction techniques have analyzed in detail in Sapsis and Majda (2013a) and they are primarily related with the adequate modeling of

(i) non-normal dynamics which otherwise may be ignored, and

(ii) linear processes that contribute to the state covariance that plays an important role to the computation of the mean (Eq. (2)).

Although in some systems this may indeed be the case, there are situations where this assumption does not hold, such as the systems presented in the previous section, where many low-energy modes act as nonlinear channels of energy that either transfer or dissipate important amounts of energy and therefore their effect has to be considered in the UQ scheme. Here we illustrate these limitations by applying the QG-DO methodology to the unstable triad and the L-96 system.

We proceed by recalling the QG-DO UQ scheme (see Sapsis and Majda 2013a for details). As mentioned previously, it is based on the reduced-order modeling of the nonlinear fluxes using statistical information from a low-dimensional subspace (called the DO subspace). The solution inside this s-dimensional subspace is represented as

$$\mathbf{u} ( t ) =\bar{\mathbf{u}} ( t ) + \sum_{i=1}^{s} Y_{i} ( t;\omega ) \mathbf{e}_{i} ( t ), $$

where e i (t), i=1,…,s, are time-dependent modes and s≪N is the reduction order. The modes and the stochastic coefficients evolve according to the DO condition (Sapsis and Lermusiaux 2009). In particular the equations for the QG-DO scheme are as follows.

  • Equation for the mean

    The equation for the mean is obtained by averaging the original system equation (i.e. Eq. (2))

    $$ \frac{\mathrm {d}\bar{\mathbf{u}}}{\mathrm {d}t}= [ L+D ] \bar{\mathbf{u}}+ B{ (\bar{\mathbf{u}},\bar{\mathbf{u}} ) +}R_{ij}B ( \mathbf{v}_{i}, \mathbf{v}_{j} ) +\mathbf{F}. $$
    (12)

  • Equation for the stochastic coefficients and the modes

    Both the stochastic coefficients and the modes evolve according to the DO equations. The coefficients equations are obtained by a direct Galerkin projection and the DO condition

    $$\begin{aligned} \frac{\mathrm {d}Y_{i}}{\mathrm {d}t} & =Y_{m} \bigl( [ L+D ] \mathbf{e} _{m}+B ( \bar{\mathbf{u}},\mathbf{e}_{m} ) +B ( \mathbf{e}_{m},\bar{\mathbf{u}} ) \bigr) \cdot \mathbf{e}_{i} \\ &\quad {} + ( Y_{m}Y_{n}-C_{mn} ) B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \cdot \mathbf{e}_{i}+\dot{W}_{k}\sigma_{k}\cdot \mathbf{e}_{i}. \end{aligned}$$
    (13)

    Moreover, the modes evolve according to the equation obtained by stochastic projection of the original equation to the DO coefficients

    $$\begin{aligned} \frac{\partial\mathbf{e}_{i}}{\partial t} & = [ L+D ] \mathbf{e}_{i}+B ( \bar{\mathbf{u}},\mathbf{e}_{i} ) +B ( \mathbf{e}_{i},\bar{\mathbf{u}} ) +B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \langle Y_{k}Y_{m}Y_{n} \rangle C_{ik}^{-1} \\ & \quad {}-\mathbf{e}_{j} \bigl( [ L+D ] \mathbf{e}_{i}+B ( \bar{\mathbf{u}},\mathbf{e}_{i} ) +B ( \mathbf{e}_{i},\bar{\mathbf{u}} ) +B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \langle Y_{k}Y_{m}Y_{n} \rangle C_{ik}^{-1} \bigr)\cdot\mathbf{e}_{j}. \end{aligned}$$
    (14)

  • Equation for the covariance

    The equation for the covariance will be the exact equation (4) with approximated nonlinear fluxes

    $$\frac{\mathrm {d}R}{\mathrm {d}t}=L_{v}R+RL_{v}^{\ast}+Q_{F,s}+Q_{\sigma}, $$

    where the nonlinear fluxes are computed using reduced-order information from the DO subspace

    $$ Q_{F,s}= \langle Y_{m}Y_{n}Y_{k} \rangle \bigl( B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \cdot \mathbf{v}_{i} \bigr) ( \mathbf{v}_{j}\cdot\mathbf{e}_{k} ) + \langle Y_{m}Y_{n}Y_{k}\rangle \bigl( B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \cdot \mathbf{v}_{j} \bigr) ( \mathbf{v}_{i}\cdot\mathbf{e}_{k}). $$
    (15)

    The last expression is obtained by computing the nonlinear fluxes inside the subspace and project those back to the full N-dimensional space.

The QG-DO UQ method provides dramatic improvement compared with the standard Galerkin order-reduction methods (Sapsis and Majda 2013a). However, in systems with large number of instabilities, if s is not large enough to capture the complete nonlinear energy fluxes, the QG-DO scheme will not be able to equilibrate to the correct amount of energy leading to (i) either severe underestimation of energy to sufficiently low levels where the modeled part of the fluxes can balance the corresponding (for this energy level) number of instabilities, or (ii) to blowup of the solution due to instabilities which are not balanced by negative nonlinear fluxes. The above two scenarios have been analyzed previously in the context of completely absent modeling of the nonlinear fluxes Q F =0 (quasilinear Gaussian closure) (Sapsis and Majda 2013b).

In Fig. 5 (upper plots) we compare the performance of the QG-DO algorithm (using s=2) with direct Monte-Carlo simulation in the unstable triad system presented in the previous section. As we described previously, the two low-energy modes act as energy channels and therefore by ignoring one of them we do not allow the UQ scheme to reach a statistical equilibrium creating important discrepancies both to the mean and the variance.

For L-96 the problems are even more important since in this case we know a priori (using the results of Fig. 2) that for s≤14 the captured portion of the nonlinear fluxes is close to zero and thus the QG-DO scheme behaves essentially like the QG closure with poor behavior documented and explained in Sapsis and Majda (2013b). To this end we increase the number of modes to s=26, corresponding (according to Fig. 2) to a captured portion of the nonlinear fluxes greater than 50 % and to a captured portion of total energy by the subspace that is greater than 80 % (for F=8). The results are presented in Fig. 3 for constant forcing in space and time: F=8. We observe that there is an important underestimation of the energy of the mean—a feature caused by the misleading modeling of the nonlinear fluxes that cannot balance the number of instabilities occurring at the correct energy level. We also observe that there is essentially zero improvement compared with the DO method since the main cause of the failure is not misleading modeling of linear processes but rather insufficient modeling of the nonlinear mechanisms.

Fig. 3
figure 3

Misleading performance of QG-DO and DO method for the Lorenz-96 system with F=8. In both cases a large number of modes is employed (s=26)

Full size image

3.2 Modified Quasilinear Gaussian (MQG) Method

In the MQG closure the modeling of the nonlinear fluxes is done by using statistical steady-state information for a given set of forcing and system parameters (Sapsis and Majda 2013b). In particular we consider the first two moment equations (2) and (4) associated with the original system with respect to an orthogonal, fixed basis v i . In the statistical steady state the nonlinear fluxes Q F will satisfy the relation

$$ L_{v} ( \bar{\mathbf{u}}_{\infty} ) R_{\infty}+R_{\infty}L_{v}^{\ast} ( \bar{\mathbf{u}}_{\infty} ) +Q_{\sigma}+Q_{F\infty }=0. $$
(16)

We split the empirical fluxes into a positive semi-definite part \(Q_{F\infty }^{+}\) and a negative semi-definite part \(Q_{F\infty}^{-}\):

$$Q_{F\infty}=Q_{F\infty}^{-}+Q_{F\infty}^{+}. $$

Note that the empirical fluxes must satisfy for every time instant the conservative property of B which in the above context is expressed by the constraint:

$$ \mathrm{Tr} [ Q_{F} ] =0\Rightarrow \mathrm{Tr} \bigl[ Q_{F}^{+} \bigr] =-\mathrm{Tr} \bigl[ Q_{F}^{-} \bigr] . $$
(17)

The positive fluxes \(Q_{F}^{+}\) indicate the energy being ‘fed’ on the stable modes in the form of external stochastic noise. On the other hand the negative fluxes \(Q_{F}^{-}\) should act directly on the positive part of the L v -spectrum, effectively stabilizing the unstable modes. To achieve this we choose to represent the negative fluxes as additional damping

$$Q_{F}^{-} ( R ) =N_{\infty}R+RN_{\infty}^{\ast}$$

with N ∞ determined by solving the equation

$$Q_{F\infty}^{-}=N_{\infty}R_{\infty}+R_{\infty}N_{\infty}^{\ast},$$

which has as a unique solution:

$$N_{\infty}=\frac{1}{2}Q_{F\infty}^{-}R_{\infty}^{-1}. $$

In addition, as explained in detail in Sapsis and Majda (2013b) we add a small amount of damping and noise to improve the marginal stability which otherwise occurs in the steady state. Moreover, we scale the fluxes with a suitable functional (here we use the square-root of the total energy) in order to achieve the best possible accuracy in the timescales of the system and the transient response. This will give the final MQG closure scheme:

$$\begin{aligned} &\frac{\mathrm {d}\bar{\mathbf{u}}}{\mathrm {d}t}= [ L+D ] \bar{\mathbf{u}}+ B (\bar{\mathbf{u}},\bar{\mathbf{u}} ) +R_{ij}B ( \mathbf{v}_{i}, \mathbf{v}_{j} ) +\mathbf{F}, \end{aligned}$$
(18a)
$$\begin{aligned} &\frac{\mathrm {d}R}{\mathrm {d}t}=L_{v}R+RL_{v}^{\ast}+NR+RN^{\ast}+Q_{F}^{+}+Q_{\sigma}, \end{aligned}$$
(18b)
$$\begin{aligned} & N=\frac{1}{2}\frac{f ( R ) }{f ( R_{\infty} ) } \bigl( Q_{F\infty}^{-}-qI \bigr) R_{\infty}^{-1}\quad \text{and}\quad Q_{F} ^{+}=-\frac{\mathrm{Tr} [ Q_{F}^{-} ] }{\mathrm{Tr} [ Q_{F\infty}^{+} ] } \bigl( Q_{F\infty}^{+}+qI \bigr) , \\ \end{aligned}$$
(18c)

with q=q s λ max[Q F∞] and \(f ( R ) =\sqrt{\mathrm{Tr} ( R ) }\). The last formulation guarantees the conservation property (17) on every time-instant.

In the MQG closure the modeling of the nonlinear fluxes occurs in the second-order level and therefore no statistical information for higher-order moments is required to be computed or measured. Essentially, we are using the steady information to determine the magnitude (for each degree of freedom) of the minimum amount of additional damping and additional noise required to approximate the effect of the nonlinear energy transfer terms. This additional damping will balance the linear, persistent instabilities while the additional noise will ‘feed’ the stable modes with energy.

The MQG closure presents remarkable performance even under forcing conditions that ‘push’ the system to energetic regimes which are very far from the tuning regime (Sapsis and Majda 2013b). However, for forcing conditions which are strongly inhomogeneous in space and create local, in space, instabilities the additional damping and noise \(N,Q_{F}^{+}\) (which have been computed for homogeneous conditions) may fail to capture the correct energy transfers. Here we measure the performance of the MQG closure scheme through the L-96 system with a strongly time-space dependent forcing given by

$$ F_{i} ( t ) =F+2F\sin \biggl( a\frac{3i}{10}-\frac{3t}{20} \biggr) \sin \biggl( a\frac{3i}{2}+\frac{3t}{4}+\pi \biggr) ,\quad 0\leq i\leq39, $$
(19)

where F=8 and the nonlinear fluxes have been tuned based on the F=8 steady state. Note that there are large inhomogeneous changes in the forcing magnitude compared to the tuning value for any a. In Fig. 4 we observe that for a=0 and a=0.2, i.e. zero or slow spatial variation of the forcing but large changes in magnitude, the MQG algorithm has very good performance on capturing first- and second-order moments. For much faster spatial variation of the forcing (a=1) MQG is unable to adequately model the energy transfers. Therefore, despite its very good performance for homogeneous or close-to-homogeneous conditions, MQG may have important discrepancies in the case of strongly inhomogeneous excitations (Fig. 4). Modeling such inhomogeneous responses will be the goal of the next section where the nonlinear fluxes will be modeled by combining ideas from reduced-order subspaces with the MQG approach.

Fig. 4
figure 4

Comparison of MQG UQ scheme (solid line) with Monte Carlo (dashed line) in L-96 for different spatial dependence of the forcing F i (t) (Eq. (19)). First row: a=0—no spatial dependence; second row: a=0.2—weak spatial dependence; third row: a=1—strong spatial dependence. The tuning of the fluxes has been made using steady-state statistics that correspond to constant forcing F=8

Full size image

4 A Blended Approach Based on MQG and Subspace Generated Nonlinear Fluxes (MQG-DO Method)

We saw that MQG has the most robust behavior in UQ of turbulent systems, compared with all the other UQ methodologies. However, for strong forcing or variation of system parameters additional instabilities may be introduced which cannot be modeled appropriately by the MQG fluxes. For this case we introduce a blended approach where the MQG fluxes will be improved through a reduced-subspace model which will run over a DO basis. The reduced-order model that runs inside the subspace has also to take into account the energy fluxes coming from the nonlinear processes outside the subspace. To this end, we will have a two-way coupling between MQG and DO where

(i) the nonlinear fluxes of the MQG model will be corrected using higher-order stochastic information from the subspace, while

(ii) the evolution of the dynamics inside the subspace will take into account the nonlinear fluxes occurring due to the nonlinear interactions between the subspace modes and the orthogonal (to the subspace) modes, a feature that is captured by the MQG fluxes.

We will use a double representation for the solution. Similarly with the QG-DO method, we will represent the solution (i) using a fixed, high-dimensional basis

$$\mathbf{u}_{\mathrm{MQG}} ( t ) =\bar{\mathbf{u}} ( t ) + \sum_{i=1}^{N} Z_{i} ( t;\omega ) \mathbf{v}_{i} $$

and (ii) a time-dependent, low dimensional basis

$$\mathbf{u}_{\mathrm{DO}} ( t ) =\bar{\mathbf{u}} ( t ) + \sum _{i=1}^{s} Y_{i} ( t;\omega ) \mathbf{e}_{i} ( t ) $$

to represent the dynamics within a reduced-order subspace V S =span[e i (t)]. We require the two solutions to have the same mean and also to be identical inside the subspace. This is expressed by the condition

$$\mathbf{u}_{\mathrm{DO}} ( t ) \cdot\mathbf{e}_{i} ( t ) = \mathbf{u}_{\mathrm{MQG}} ( t ) \cdot\mathbf{e}_{i} ( t ),\quad \text{for}\ i=1,\ldots,s, $$

or equivalently,

$$ \sum_{j=1}^{N} Z_{j} \mathbf{v}_{j}\cdot\mathbf{e}_{i}=Y_{i}, $$
(20)

which gives the consistency condition between the high dimensional covariance (R=〈ZZ ∗〉) and the reduced-order covariance (C YY =〈YY ∗〉):

$$ C_{YY}=P^{\ast}RP,\quad \text{where}\ \mathbb{R}^{N\times s}\ni P_{ji}=\mathbf{v}_{j}\cdot\mathbf{e}_{i}. $$
(21)

Note that for the case where the stochastic coefficients are independent, identically, distributed stochastic processes the equality (20) implies directly Gaussian statistics for the coefficients (Marcinkiewicz 1938). This is consistent with the developed framework since for the case of independent, identically, distributed stochastic coefficients the nonlinear fluxes (which depend on the third-order moments) vanish identically and therefore we have linear dynamics which result in Gaussian statistics.

The MQG-DO UQ scheme is developed as follows.

Mean Field Equation

The mean field equation that we will employ is that one that takes into account the high-dimensional covariance information—expressed through the covariance R. This is Eq. (2) rewritten here for convenience

$$ \frac{\mathrm {d}\bar{\mathbf{u}}}{\mathrm {d}t}= [ L+D ] \bar{\mathbf{u}}+ B (\bar{\mathbf{u}},\bar{\mathbf{u}} ) +R_{ij}B ( \mathbf{v}_{i}, \mathbf{v}_{j} ) +\mathbf{F}. $$
(22)

Evolution of the Covariance Matrix R

We recall the second-order moment equation (Eq. (4))

$$\frac{\mathrm {d}R}{\mathrm {d}t}=L_{v}R+RL_{v}^{\ast}+Q_{F}+Q_{\sigma}. $$

In the MQG approach we represent the nonlinear fluxes Q F , using steady-state information, through a positive definite (external noise) and negative definite (minimum additional dissipation) part. In the QG-DO this is done using higher-order statistical information inside the subspace. In this blended MQG-DO approach we will combine these ideas by using MQG fluxes but improving those (since they rely on steady-state information) by correcting them using higher-order statistical information from the low dimensional subspace V S . In particular from the MQG nonlinear fluxes we will

(i) subtract the steady-state nonlinear fluxes \(Q_{V_{S},\infty}\) that correspond to the subspace V S , and

(ii) we will add the corresponding fluxes computed using the high-order statistics of the subspace which also include transient dynamics information:

$$ Q_{F}=Q_{\mathrm{MQG}}+Q_{V_{S}}-Q_{V_{S},\infty}, $$
(23)

where \(Q_{\mathrm{MQG}}=NR+RN^{\ast}+Q_{F}^{+}\) (see Eq. (18c)). This correction of the nonlinear fluxes (i.e. \(Q_{V_{S}}\) instead of \(Q_{V_{S},\infty}\)) will be able to take into account important transient, and spatially non-homogeneous effects. To this end the evolution equation for the full covariance will take the form

$$ \frac{\mathrm {d}R}{\mathrm {d}t}=L_{v}R+RL_{v}^{\ast}+Q_{\sigma}+Q_{V_{S}}+Q_{\mathrm{MQG}} -Q_{V_{S},\infty}. $$
(24)

The next step is to write down explicit formulas for the fluxes \(Q_{V_{S}}\) and \(Q_{V_{S},\infty}\). The energy flux in the reduced-order subspace will be given by

$$Q_{V_{S}}= \langle Y_{m}Y_{n}Y_{k} \rangle \bigl[ \bigl( B ( \mathbf{e}_{m},\mathbf{e}_{n} )\cdot \mathbf{v}_{i} \bigr) ( \mathbf{v}_{j}\cdot\mathbf{e}_{k} ) + \bigl( B ( \mathbf{e} _{m},\mathbf{e}_{n} ) \cdot\mathbf{v}_{j} \bigr) ( \mathbf{v}_{i}\cdot \mathbf{e}_{k} ) \bigr]. $$

This is the nonlinear flux matrix inside the subspace projected back to the high dimensional basis. The above fluxes also sum up to zero since V S ⊂span i [v i ] and therefore e m =(v q ⋅e m )v q . Thus we will have

$$\begin{aligned} \mathrm{Tr} [ Q_{V_{S}} ] & =2 \langle Y_{m}Y_{n}Y_{k} \rangle \bigl( B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \cdot \mathbf{v}_{p} \bigr) ( \mathbf{v}_{p}\cdot\mathbf{e}_{k} ) \\ & =2 \langle Y_{m}Y_{n}Y_{k} \rangle \bigl( B ( \mathbf{e} _{m},\mathbf{e}_{n} )\cdot \mathbf{e}_{k} \bigr) =0. \end{aligned}$$

To represent the steady-state nonlinear fluxes within the subspace we use the steady-state skewness (assumed to be known) suitably rescaled with the current variance of the system:

$$ Q_{V_{S},\infty}=\mu_{mnk,\infty}\sqrt{ \bigl\langle Y_{m}^{2} \bigr\rangle \bigl\langle Y_{n}^{2} \bigr\rangle \bigl\langle Y_{k}^{2} \bigr\rangle } \bigl[ \bigl( B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \cdot \mathbf{v}_{i} \bigr) ( \mathbf{v}_{j}\cdot \mathbf{e}_{k} ) + \bigl( B ( \mathbf{e}_{m} ,\mathbf{e}_{n} ) \cdot\mathbf{v}_{j} \bigr) ( \mathbf{v}_{i}\cdot\mathbf{e}_{k} ) \bigr],\vphantom{\Bigg|} $$
(25)

where the steady-state skewness coefficients are given by

$$\mu_{mnk,\infty}=\frac{ \langle Y_{m,\infty}Y_{n,\infty}Y_{k,\infty } \rangle }{\sqrt{ \langle Y_{m,\infty}^{2} \rangle \langle Y_{n,\infty}^{2} \rangle \langle Y_{k,\infty}^{2} \rangle }}, \quad \text{with}\ Y_{m,\infty}= ( \mathbf{u}_{\infty }-\bar{\mathbf{u}}_{\infty} )\cdot \mathbf{e}_{m} ( t ) . $$

We emphasize that the time-dependence in the skewness coefficients μ mnk,∞ comes only through the time-dependent modes. Additionally, we have by construction

$$\mathrm{Tr} [ Q_{\mathrm{MQG}} ] = \mathrm{Tr} [ Q_{V_{S}} ] =\mathrm{Tr} [ Q_{V_{S},\infty} ] =0. $$

Therefore, the nonlinear flux formulation (23) is consistent with the energy conservation property of the nonlinear operator B. Equation (24) expresses the first level of coupling, i.e. the influence of the DO subspace dynamics on the evolution of the high-dimensional covariance.

Evolution of the DO Stochastic Subspace

The evolution of the DO basis will be done using the standard DO equations for the basis (Sapsis and Lermusiaux 2009)

$$\begin{aligned} \frac{\partial\mathbf{e}_{i}}{\partial t} & = [ L+D ] \mathbf{e}_{i}+B ( \bar{\mathbf{u}},\mathbf{e}_{i} ) +B ( \mathbf{e}_{i},\bar{\mathbf{u}} ) +B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \langle Y_{k}Y_{m}Y_{n} \rangle C_{ik}^{-1} \\ &\quad {} -\mathbf{e}_{j} \bigl( [ L+D ] \mathbf{e}_{i}+B ( \bar{\mathbf{u}},\mathbf{e}_{i} ) +B ( \mathbf{e}_{i}, \bar{\mathbf{u}} ) +B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \langle Y_{k}Y_{m}Y_{n} \rangle C_{ik}^{-1} \bigr)\cdot\mathbf{e}_{j}. \end{aligned}$$
(26)

Reduced-order stochastic dynamics

The last step of our scheme is the formulation of a reduced-order dynamical system inside the time-dependent subspace. This will be formulated by minimally modifying the standard reduced-order model (obtained by Galerkin projection to the DO basis, i.e. Eq. (13)) so that the subspace covariance (expressed through the coefficients Y) is energetically consistent with the covariance of the coefficients Z (consistency condition (21)). Differentiating Eq. (21) gives

$$ \frac{\mathrm {d}C_{YY}}{\mathrm {d}t}=P^{\ast}\frac{\mathrm {d}R}{\mathrm {d}t}P+\dot{P}^{\ast}RP+P^{\ast}R \dot{P} $$
(27)

(where \(\frac{\mathrm {d}R}{\mathrm {d}t}\) is known, given by Eq. (24)). This is the consistency constraint expressed in differential form.

On the other hand for the evolution of the dynamics inside the subspace we consider the standard Galerkin projection model with an additional damping matrix \(N_{C}\in \mathbb{R}^{s\times s}\) and noise term \(Q_{C}^{1/2}\in \mathbb{R}^{s\times s}\) that will represent the nonlinear interactions between modes of the subspace and the modes outside of it. With this ansatz we will have the reduced-order dynamical system

$$\begin{aligned} \frac{\mathrm {d}Y_{i}}{\mathrm {d}t} =& \bigl( \bigl( P^{\ast}L_{v}P \bigr) _{im}+N_{C,im}\bigr) Y_{m}+ ( Y_{m}Y_{n}-C_{YY,mn} ) B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \cdot\mathbf{e}_{i}+ \dot{W}_{m}Q_{C,im}^{1/2} \\ &{}+\dot {W}_{k} \sigma_{k}\cdot\mathbf{e}_{i}. \end{aligned}$$
(28)

In the above equation all the quantities are known except for the pair N C and Q C . This will be determined by using the differential constraint (27). In particular we formulate the second-order equation for the covariance C YY by using Eq. (28):

$$ \frac{\mathrm {d}C_{YY}}{\mathrm {d}t}= \bigl( P^{\ast}L_{v}P+N_{C} \bigr) C_{YY}+C_{YY} \bigl( P^{\ast}L_{v}P+N_{C} \bigr) ^{\ast}+Q_{C}+P^{\ast}Q_{\sigma}P+P^{\ast }Q_{V_{S}}P. $$
(29)

From the covariance consistency condition (Eqs. (21), (27)) and the evolution equation for R (Eq. (24)) we have

$$\frac{\mathrm {d}C_{YY}}{\mathrm {d}t}=P^{\ast} \bigl( L_{v}R+RL_{v}^{\ast}+Q_{\sigma}+Q_{V_{S}}+Q_{\mathrm{MQG}}-Q_{V_{S},\infty} \bigr) P+\dot{P}^{\ast}RP+P^{\ast}R\dot{P}.$$

By equating the two right hand sides of the last two equations we obtain (also taking into account that C YY =P ∗ RP)

$$\begin{aligned} & N_{C} \bigl( P^{\ast}RP \bigr) + \bigl( P^{\ast}RP \bigr) N_{C}^{\ast }+Q_{C} \\ &\quad =P^{\ast}L_{v} \bigl[ I-PP^{\ast} \bigr] RP+P^{\ast}R \bigl[ I-PP^{\ast } \bigr] L_{v}^{\ast}P+P^{\ast}Q_{\mathrm{MQG}}P-P^{\ast}Q_{V_{S},\infty}P \\ &\qquad{}+ \dot {P}^{\ast}RP+P^{\ast}R\dot{P}. \end{aligned}$$
(30)

We recall that \(Q_{\mathrm{MQG}}=NR+RN^{\ast}+Q_{F}^{+}\) and we choose the positive definite matrix Q C as follows:

$$ Q_{C}=P^{\ast}Q_{F}^{+}P, $$
(31)

which is always possible since \(Q_{F}^{+}\) is by construction positive definite. Then Eq. (30) takes the form

$$\begin{aligned} & N_{C} \bigl( P^{\ast}RP \bigr) + \bigl( P^{\ast}RP \bigr) N_{C}^{\ast} \\ & \quad =P^{\ast} \bigl( L_{v} \bigl[ I-PP^{\ast} \bigr] +N \bigr) RP+P^{\ast }R \bigl( \bigl[ I-PP^{\ast} \bigr] +N^{\ast} \bigr) L_{v}^{\ast}P-P^{\ast }Q_{V_{S},\infty}P\\ &\qquad{}+ \dot{P}^{\ast}RP+P^{\ast}R\dot{P}. \end{aligned}$$

From this we obtain N C

$$\begin{aligned} N_{C} =&\frac{1}{2} \bigl[ P^{\ast} \bigl( \bigl( L_{v} \bigl[ I-PP^{\ast } \bigr] +N \bigr) R+R \bigl( \bigl[ I-PP^{\ast} \bigr] L_{v}^{\ast }+N^{\ast} \bigr) -Q_{V_{S},\infty} \bigr) P \\ &{}+\dot{P}^{\ast}RP+P^{\ast}R \dot{P} \bigr] \bigl( P^{\ast}RP \bigr) ^{-1} . \end{aligned}$$
(32)

With the above construction it is guaranteed that the dynamics inside the subspace will always contain the correct second-order information (correct energy) by taking into account the nonlinear energy fluxes due to the nonlinear interactions with the dynamics outside the subspace. The above construction can also be seen as a generalized Galerkin projection that takes into account available information for the dynamics which are not spanned by the employed basis. Equations (31) and (32) express the second level of coupling between MQG and DO, i.e. the influence of the MQG fluxes on the reduced-order dynamics. This completes the set of equations for the MQG-DO UQ scheme.

For s=0, MQG-DO is simplified to the standard MQG scheme while for s=N we recover the original equation. For s=1 the dynamics in the DO subspace become linear since B(e 1,e 1)⋅e 1=0. Therefore we expect Gaussian statistics for the stochastic coefficient Y 1. In this case the nonlinear fluxes \(Q_{V_{S}}\) generated by the subspace will vanish since \(\langle Y_{1}^{3} \rangle =0\). On the other hand, the steady-state fluxes \(Q_{V_{S},\infty}\) that we subtract will be non-zero since μ 111,∞ is based on exact statistics. Thus, for s=1 we expect inferior performance compared with MQG.

Note that although Eq. (28) can be formulated as a Fokker–Planck equation for the probability density function f Y of the coefficients Y i , this transport equation will not have a standard form since its coefficients will depend on the quantities \(\bar{\mathbf{u}},R\), and P which are essentially driven by integrals of f Y through the rest of the MQG-DO equations. Therefore, there will be a non-local dependence of the coefficients that govern f Y , on f Y . To this end the equation governing the pdf f Y can be seen as infinite-dimensional approximation of the full Kramers–Moyal expansion (Kramers 1940; Moyal 1949). The infinite-dimensional character is due to the fact that only quantities connected with statistical moments (i.e. integrals of f Y ) show-up in the coefficients of Eq. (28). We emphasize that only second or infinite-order approximations of the full Kramers–Moyal expansion are meaningful (Pawula 1967).

4.1 Consistency of the MQG-DO with the Exact Steady-State Statistics

Here we will prove that the MQG-DO UQ method will result in the correct steady-state statistics. Essentially, we will need to prove that the steady state of the MQG-DO scheme is compatible with the exact steady-state statistics. First we observe that

$$\begin{aligned} Q_{V_{S}}\vert _{\mathbf{Y}_{\infty}} & = \langle Y_{m\infty}Y_{n\infty}Y_{k\infty} \rangle \bigl[ \bigl( B ( \mathbf{e}_{m},\mathbf{e}_{n} )\cdot \mathbf{v}_{i} \bigr) ( \mathbf{v}_{j}\cdot\mathbf{e}_{k} ) + \bigl( B ( \mathbf{e} _{m},\mathbf{e}_{n} ) \cdot\mathbf{v}_{j} \bigr) ( \mathbf{v} _{i}\cdot \mathbf{e}_{k} ) \bigr] \\ & =\mu_{mnk,\infty}\sqrt{ \bigl\langle Y_{m\infty}^{2} \bigr\rangle \bigl\langle Y_{n\infty}^{2} \bigr\rangle \bigl \langle Y_{k\infty}^{2} \bigr\rangle } \bigl[ \bigl( B ( \mathbf{e}_{m},\mathbf{e} _{n} ) \cdot \mathbf{v}_{i} \bigr) ( \mathbf{v}_{j}\cdot\mathbf{e} _{k} )\\ &\quad{} + \bigl( B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \cdot\mathbf{v}_{j} \bigr) ( \mathbf{v}_{i}\cdot \mathbf{e}_{k} ) \bigr] \\ & =Q_{V_{S},\infty}. \end{aligned}$$

We will also have

$$\begin{aligned} \frac{\mathrm {d}R}{\mathrm {d}t}\bigg\vert _{\bar{\mathbf{u}}_{\infty},R_{\infty},\mathbf{Y}_{\infty}} & =L_{v} ( \bar{\mathbf{u}}_{\infty} ) R_{\infty}+R_{\infty}L_{v}^{\ast} ( \bar{\mathbf{u}}_{\infty} ) -\lim_{t\rightarrow\infty}Q_{V_{S}}+Q_{\mathrm{MQG}}+Q_{V_{S},\infty}+Q_{\sigma} \\ & =L_{v} ( \bar{\mathbf{u}}_{\infty} ) R_{\infty}+R_{\infty}L_{v}^{\ast} ( \bar{\mathbf{u}}_{\infty} ) +Q_{\mathrm{MQG}}+Q_{\sigma}=0, \end{aligned}$$

where the last equation vanishes by the construction of the MQG nonlinear fluxes Q MQG.

Next, we consider the equation for the coefficients (28). By construction the covariance of the coefficients satisfies Eq. (27). Therefore, assuming that the subspace has converged to a steady state, i.e. \(\dot{P}=0\ \)we obtain that for Y=Y ∞, \(\bar{\mathbf{u}}=\bar{\mathbf{u}}_{\infty }\), R=R ∞

$$\frac{\mathrm {d}C_{YY}}{\mathrm {d}t}\bigg\vert _{\bar{\mathbf{u}}_{\infty},R_{\infty},\mathbf{Y}_{\infty}}=0. $$

The mean equation is trivially satisfied. Thus, the MQG-DO model is indeed consistent (up to second order), by construction, with the correct steady-state information.

4.2 Summary of the MQG-DO Equations

Here we present a summary of the blended MQG-DO method for the convenience of the reader.

Equation for mean and covariance

$$ \begin{aligned} \frac{\mathrm {d}\bar{\mathbf{u}}}{\mathrm {d}t} & = [ L+D ] \bar{\mathbf{u}} +B ( \bar{\mathbf{u}},\bar{\mathbf{u}} ) + R_{ij}B ( \mathbf{v}_{i},\mathbf{v}_{j} ) +\mathbf{F}, \\ \frac{\mathrm {d}R}{\mathrm {d}t} & =L_{v}R+RL_{v}^{\ast}+Q_{\sigma}+Q_{V_{S}}+Q_{\mathrm{MQG}} -Q_{V_{S},\infty}, \end{aligned} $$
(33)

where

$$\begin{aligned} &Q_{\mathrm{MQG}}=NR+RN^{\ast}+Q_{F}^{+}, \\ &N=\frac{1}{2}\frac{f ( R ) }{f ( R_{\infty} ) } \bigl( Q_{F\infty}^{-}-qI \bigr) R_{\infty}^{-1}\quad \text{and}\quad Q_{F}^{+}=-\frac{\mathrm{Tr} [ Q_{F}^{-} ] }{\mathrm{Tr} [ Q_{F\infty}^{+} ] } \bigl( Q_{F\infty}^{+}+qI \bigr), \\ &Q_{F\infty}^{-}+Q_{F\infty}^{+}=Q_{F\infty}=-L_{v} ( \bar{\mathbf{u}}_{\infty} ) R_{\infty}-R_{\infty}L_{v}^{\ast} ( \bar{\mathbf{u}}_{\infty} ) -Q_{\sigma}, \\ &q=q_{s}\lambda_{\max} [ Q_{F\infty} ]\quad \text{and}\quad f ( R ) =\sqrt{\mathrm{Tr} ( R ) }, \end{aligned}$$

and

$$\begin{aligned} &Q_{V_{S}} = \langle Y_{m}Y_{n}Y_{k} \rangle \bigl[ \bigl( B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \cdot \mathbf{v}_{i} \bigr) ( \mathbf{v}_{j}\cdot\mathbf{e}_{k} ) + \bigl( B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \cdot\mathbf{v}_{j} \bigr) ( \mathbf{v}_{i}\cdot \mathbf{e}_{k} ) \bigr], \\ &Q_{V_{S},\infty} = \langle Y_{m\infty}Y_{n\infty}Y_{k\infty } \rangle \bigl[ \bigl( B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \cdot \mathbf{v}_{i} \bigr) ( \mathbf{v}_{j}\cdot\mathbf{e}_{k} ) + \bigl( B ( \mathbf{e}_{m},\mathbf{e}_{n} )\cdot \mathbf{v}_{j} \bigr) ( \mathbf{v}_{i}\cdot\mathbf{e}_{k} ) \bigr] . \end{aligned}$$

Equation for the subspace basis

$$\begin{aligned} \frac{\partial\mathbf{e}_{i}}{\partial t} & = [ L+D ] \mathbf{e}_{i}+B ( \bar{\mathbf{u}},\mathbf{e}_{i} ) +B ( \mathbf{e}_{i},\bar{\mathbf{u}} ) +B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \langle Y_{k}Y_{m}Y_{n} \rangle C_{ik}^{-1} \\ &\quad {} -\mathbf{e}_{j} \bigl( [ L+D ] \mathbf{e}_{i}+B ( \bar{\mathbf{u}},\mathbf{e}_{i} ) +B ( \mathbf{e}_{i},\bar{\mathbf{u}} ) +B ( \mathbf{e}_{m},\mathbf{e}_{n} ) \langle Y_{k}Y_{m}Y_{n} \rangle C_{ik}^{-1} \bigr)\cdot\mathbf{e}_{j}. \end{aligned}$$
(34)

Equation for the subspace dynamics

$$\begin{aligned} \frac{\mathrm {d}Y_{i}}{\mathrm {d}t} =& \bigl( \bigl( P^{\ast}L_{v}P \bigr) _{im}+N_{C,im}\bigr) Y_{m}+ ( Y_{m}Y_{n}-C_{YY,mn} ) B ( \mathbf{e}_{m},\mathbf{e}_{n} )\cdot \mathbf{e}_{i}+ \dot{W}_{m}Q_{C,im}^{1/2} \\ &{}+\dot {W}_{k} \sigma_{k}\cdot\mathbf{e}_{i}, \end{aligned}$$
(35)

where P ij =v i ⋅e j and

$$\begin{aligned} &N_{C}=\frac{1}{2} \bigl[ P^{\ast} \bigl( \bigl( L_{v} \bigl[ I-PP^{\ast } \bigr] +N \bigr) R+R \bigl( \bigl[ I-PP^{\ast} \bigr] L_{v}^{\ast }+N^{\ast} \bigr) -Q_{V_{S},\infty} \bigr) P\\ &\hphantom{N_{C}=} {}+\dot{P}^{\ast}RP+P^{\ast}R \dot{P} \bigr] \bigl( P^{\ast}RP \bigr) ^{-1}, \\ &Q_{C}=P^{\ast}Q_{F}^{+}P. \end{aligned}$$

4.2.1 Numerical Implementation and Computational Cost of the MQG-DO Scheme

The numerical implementation of the MQG-DO scheme is as follows:

(i) Computation of the current third-order statistics inside the subspace and subsequent computation of the subspace nonlinear fluxes \(Q_{V_{S}}\), \(Q_{V_{S,\infty}}\) (s-dimensional computation).

(ii) Evolution of the DO modes with a first-order Euler method (s-dimensional computation).

(iii) With fixed nonlinear fluxes from step (i) we evolve the nonlinear equations (33) for a numerical time step using a fourth-order Runge–Kutta method (N-dimensional computation).

(iv) We compute the matrices N C and Q C using the evolved values of R and \(\bar{\mathbf{u}}\) from the previous step (s-dimensional computation).

(v) We evolve the stochastic coefficients Y i for a numerical time step using a fourth-order Runge–Kutta method on Eq. (35) with fixed matrices N C and Q C given by the previous step (s-dimensional computation).

(vi) We perform orthonormalization of the DO modes and the stochastic coefficients to avoid numerical errors according to the procedure described in Ueckermann et al. (2013) (Sect. 5.2) (s-dimensional computation).

The computational cost associated with the MQG-DO method as well as a comparison with Monte-Carlo, MQG, and DO methods is presented in Table 1. The extra cost associated with the MQG-DO method, compared with standard DO reduction, is the evolution of the covariance matrix R. On the other hand in the MQG framework we do have to evolve the covariance matrix R but we do not need to solve a stochastic differential equation.

Table 1 Computational cost associated with the MC, DO, MQG, and blended methods
Full size table

4.2.2 Dimensionality of the Subspace

The dimensionality of the DO subspace (as well as adaptive criteria for its modification) has been discussed in the context of low-complexity fluid flows in Sapsis and Lermusiaux (2012). In the present framework the dimensionality of the subspace can be chosen based on the contribution of the nonlinear energy fluxes produced by this subspace to the overall energy transfers.

In particular, the estimation of the subspace dimensionality s can be made a priori (i.e. before performing any MQG-DO computation) using steady-state statistics obtained through (sufficiently long) time averaging of a single realization. Based on first- and second-order statistics we can estimate through Eq. (16) the matrix of nonlinear energy fluxes in steady state i.e., the nonlinear energy transfers due to the dynamical interplay of the complete basis. We can then estimate what part of these nonlinear energy transfers is modeled by the s most energetic modes (in steady state). The s most energetic modes can be obtained through second-order statistics while the nonlinear energy fluxes that correspond to these modes can be computed using expression (25) and third-order statistics. Through this approach we can construct diagrams showing the relative contribution of a specific number of modes to the overall energy fluxes (similar to those presented in Fig. 2—last row) and obtain a priori estimates about what would be the expected influence of s modes to the nonlinear energy fluxes.

5 Application of MQG-DO to Systems with Unstable Dynamics

Here we apply the new blended algorithm to the two unstable systems presented previously. We will consider for each system two configurations:

(i) a case with constant parameters where the system reaches the steady state which has been used to tune the MQG fluxes, and

(ii) a case where we have explicit time-dependence to the system/forcing parameters. This time dependence is chosen so that it ‘pushes’ the system away from the energetic regime for which the steady-state statistics have been computed by introducing additional instabilities.

5.1 Triad System with Unstable Mean State

5.1.1 Steady-State Dynamics

The first case that we consider is the triad system in the unstable configuration presented in Sect. 2.1. In Fig. 5 we compare the performance of the MQG-DO with direct Monte-Carlo simulation and with other UQ methods (MQG and QG-DO). Note that the performance of the QG-DO UQ scheme for the constant forcing case has been discussed already in Sect. 3.1 and it will not be considered here. For MQG we observe that even though it recovers very well the steady-state performance it presents some discrepancies during the transient regime, especially in the variance. On the other hand MQG-DO with two modes is able to resolve much more effectively the transient dynamics while it still maintains the very good performance of MQG in the steady state. In addition, through MQG-DO we are able to recover the full non-Gaussian steady-state statistics inside the DO subspace which compare favorably with the exact ones (Fig. 5). This is due to the fact that the fluxes are partially resolved explicitly.

Fig. 5
figure 5

Triad system in an unstable configuration with constant forcing/parameters resolved with various UQ methods. The mean and the variance are plotted. In the lower plots a comparison is given between the pdf inside the subspace computed with MQG-DO and direct Monte Carlo

Full size image

5.1.2 Time Dependent Forcing

To illustrate more clearly the advantages of the MQG-DO method we consider a case where both the forcing and the system parameters fluctuate over time. Their fluctuations are chosen so that the system moves between dynamical regimes of zero, one, and two instabilities. Note that the steady-state statistics are chosen based on the response of the previous (constant-parameters) configuration where only one instability is present. In particular the triad system that we consider has the form

$$\begin{aligned} \mathrm {d}u_{1} & = ( -\gamma_{1}u_{1}+ \lambda_{12}u_{2}+\lambda_{13}u_{3}+\beta_{1}u_{3}u_{2}+g_{1} )\,\mathrm {d}t+ \bigl( \sigma_{1}+f^{2} ( \sigma_{T1}- \sigma_{1} ) \bigr)\,\mathrm {d}W_{1}, \\ \mathrm {d}u_{2} & = ( -\gamma_{2}u_{2}- \lambda_{12}u_{1}+\lambda_{23}u_{3}+\beta_{2}u_{1}u_{3}+g_{2} ) \,\mathrm {d}t+ \bigl( \sigma_{2}+f^{2} ( \sigma_{T2}- \sigma_{2} ) \bigr)\,\mathrm {d}W_{2}, \\ \mathrm {d}u_{3} & = ( -\gamma_{3}u_{3}- \lambda_{13}u_{1}-\lambda_{23}u_{2}+\beta_{3}u_{2}u_{1}+g_{3} )\,\mathrm {d}t+ \bigl( \sigma_{3}+f^{2} ( \sigma_{T3}- \sigma_{3} ) \bigr)\,\mathrm {d}W_{3}, \end{aligned}$$

where the system parameters remain as in Sect. 2.1 and g 1,g 2,g 3, and f are functions of time. Moreover, we choose the new additional parameters for the noise as \(\sigma_{Ti}=\frac{3}{5}\sigma_{i}\) so that important variations in the noise intensity occur. We consider two cases for the time dependent functions: a time-periodic and one with random time dependence. For the periodic case we choose

$$g_{1} ( t ) =0,\quad g_{2} ( t ) =-1+0.5\sin \frac{\pi t}{2},\quad g_{3} ( t ) =1+0.2\cos \frac{\pi t}{2},\quad f ( t ) =1.3\sin \frac{\pi t}{2}, $$

and as we observe in Fig. 6 (lower-left subplot) the system oscillates between a stable and an unstable regime with one instability. The blended MQG-DO method (s=2) recovers very well both the periodic attractor and the initial transient regime in terms of the first- and second-order statistics. MQG does very well for the mean but it cannot track the second-order statistics very effectively. This is due to the fact that MQG has been tuned for a dynamical regime with one unstable direction and, as the results indicate, the correct nonlinear fluxes are not effectively represented in the fully stable regime. This is also the case for QG-DO where nonlinear fluxes are partially represented through the non-Gaussian statistics inside the DO subspace. By comparing QG-DO and MQG we can conclude that for unstable systems it is more effective to use a complete (full-order) model of the nonlinear fluxes based on steady-state statistics which may refer to a different energy/dynamical regime rather than model the nonlinear fluxes using an explicit approach such as QG-DO which gives an incomplete (reduced-order) representation of the nonlinear dynamics and creates important discrepancies.

Fig. 6
figure 6

Triad system with time dependent parameters and forcing. The system oscillates between a stable and an unstable regime. The performance of MQG-DO algorithm is compared with Monte Carlo and other UQ methods

Full size image

In the case with random time-dependence we have the functions g i given by

$$\mathbf{g} ( t ) =\left ( \begin{array} [c]{c}0\\ -1\\ 1 \end{array} \right ) +g ( t ) \left ( \begin{array} [c]{c}1\\ 1\\ 1 \end{array} \right ) \quad \text{where}\ \mathrm {d}g=-\frac{1}{4}g+0.4\sqrt{ \frac{1}{2}}\,\mathrm {d}W_{g} ( t;\omega ), $$

and the noise intensity is also controlled by an Ornstein–Uhlenbeck (OU) process

$$\mathrm {d}f=-\frac{1}{4}f+0.7\sqrt{\frac{1}{2}}\,\mathrm {d}W_{f} ( t;\omega ) . $$

In Fig. 6 (lower-right subplot) we show the resulted evolution of the eigenvalues for the linearized dynamics. The transition involves fully stable and unstable regimes with one and two instabilities. From Fig. 6 (second plot on the right column) we observe the explosion of variance occurring right after the system passes very briefly through the regime with two instabilities (t∼7.5). MQG-DO (s=2) is able to track very effectively this unstable transition while QG-DO and MQG overestimate the system variance since they cannot model the correct nonlinear fluxes during the subsequent stable phase. Similarly with the periodic case MQG performs very well for the estimation of the mean given its extremely inexpensive computational character. When we compare MQG with QG-DO we can make similar conclusions with the periodic case, i.e. that an empirical, but nevertheless complete (full-order) model, of the nonlinear fluxes (such as MQG) performs much better than a scheme that explicitly models the nonlinear fluxes through a reduced-order approach.

5.2 Lorenz-96 with Time-Space Dependent Forcing

The second application where we illustrate and validate MQG-DO method is the Lorenz-96 system presented in Sect. 2.2. Similarly with the triad system we will consider two cases:

(i) constant parameters where a statistical steady state is reached, and

(ii) strongly time-space dependent forcing.

5.2.1 Steady-State Dynamics

For this constant parameters case we choose F=8 and we use the second-order statistics describing the statistical steady state to obtain the MQG nonlinear fluxes. Then we resolve the transient problem in order to examine how well the blended MQG-DO method does on capturing the transient dynamics, the steady-state spectrum, and also recovering the higher-order statistical structures inside the subspace. Based on the study of the nonlinear energy fluxes that we presented previously (Fig. 2), we obtain an estimate of the maximum improvement on the nonlinear fluxes, by resolving s modes within the DO subspace. For example we can immediately conclude that if s<15 the impact of the DO correction to the MQG nonlinear fluxes will be less than 2–3 % and in this case the statistics inside the subspace are essentially driven by the MQG component. In order to achieve two way coupling we choose s=26 so that we have equal orders of contribution between the MQG and the DO component.

Note that due to the special geometry of the triad interactions occurring in the Lorenz-96 system the problem is particularly hard. In more realistic turbulent systems we do not expect the very low-energy modes to directly interact with the largest energy modes. In this case we rather expect strong triad interactions between high and intermediate energy modes and subsequent flow of energy through the inertial scales to the dissipations scales.

In Fig. 7 we present the performance of the MQG-DO scheme with s=26 modes. The recovery of the correct spectrum indicates that the two-level coupling between MQG and DO occurs naturally without causing important discrepancies. This is also suggested by the higher-order statistics in steady state. In particular in the lower plots of Fig. 7 we present the third-order moments in steady state, M ijk =〈Y ∞i Y ∞j Y ∞k 〉, as those are computed with MQG-DO and with direct Monte Carlo. In particular, we plot only the moments that have values for which |M ijk |>0.15max ijk M ijk and we color those according to their values. Through these results we can clearly see that the third-order moments inside the subspace are recovered very effectively even though a full Monte-Carlo scheme is run only for the DO dynamics inside the subspace.

Fig. 7
figure 7

Lorenz-96 system for F=8 resolved with MQG-DO method and s=26. The time series for the mean, the spectrum, and the third-order central moments within the subspace are shown and compared with direct Monte Carlo. The plotting of the third-order moments follows the same technique as used in Fig. 2

Full size image

5.2.2 Time-Space Dependent Forcing

Here we consider the strongly forced Lorenz-96 presented in Sect. 3.2 in the extreme regime where the MQG scheme fails to performs UQ adequately. In particular we consider the forcing given by Eq. (19) with a=1. The spatiotemporal pattern of the excitation is shown in Fig. 8 (upper-left subplot). Under the effect of this excitation we inject energy directly to the high-wavenumber modes and an important portion of it is transferred back to the small-wavenumber modes. MQG is not capable to model adequately this energy transfer since it has been calibrated in a completely different dynamical regime where such energy transfers do not occur. To this end, as we can observe in the MQG spectrum of Fig. 8, energy is overestimated in the high-wavenumber modes while the low-wavenumber modes have smaller energy than the Monte-Carlo simulation.

Fig. 8
figure 8

Lorenz-96 system with extreme time and space dependent forcing. The performance of MQG and MQG-DO methods (for various s) is shown and compared with Monte Carlo in terms of the spectrum, the energy of the mean, and the total stochastic energy

Full size image

On the other hand, MQG-DO directly models an important part of the nonlinear energy fluxes. As we observe in Fig. 9 the DO modes localize exactly in the locations where the high-frequency forcing is active. The non-Gaussian statistics in the stochastic subspace explicitly model the nonlinear fluxes from the high-wavenumber modes to the low-wavenumber modes. However, as explained previously, due to the peculiarity of the nonlinear interactions in Lorenz-96, we need an important number modes in order to have an effective correction of the MQG nonlinear fluxes (which do not take into account the time-space character of the external excitation). Therefore for s=14 the improvement is minimal and is restricted in the low-wavenumber modes of the spectrum. For a larger subspace (s=20) things are improved more but still the large-wavenumber modes do not carry completely the correct amount of energy to the low-energy modes. This is achieved when s=26 where the obtained spectrum has very good agreement with the exact spectrum. Note that some minor discrepancies are expected since still we do not resolve the full nonlinear energy fluxes and an important portion of them is based on steady-state information.

Fig. 9
figure 9

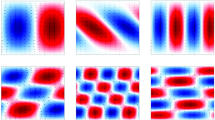
Upper plot: localization of the energy spanned by the DO modes \(\{ \mathbf{e}_{j} \} _{j=1}^{26}\) expressed through the grid point energy density \({\protect\sum_{m,n=1}^{26}}C_{YY,mn}e_{mk}e_{nk}\) for t=8 and s=26 (blue bold curve); the forcing F j (t) for t=8 (red solid curve) plotted together with the large scale modulation envelope of the forcing. Lower plot: the first three modes e 1, e 2, and e 3 for t=8 (Color figure online)

Full size image

In Fig. 8 we also present the time series for the energy of the mean and the trace of the covariance. We can immediately conclude the monotonic convergence to the Monte-Carlo statistics as the number of modes is increasing. This is another manifestation of the natural coupling between the MQG and the DO components that results in pure improvement of the MQG. Finally, in Fig. 10 we present the third-order moments inside the subspace as those are computed for t=8 using the MQG-DO scheme and a direct Monte-Carlo simulation. We emphasize that these results refer to a transient problem and even though the agreement is not in the point-wise sense we still have a very satisfactory estimation of the nonlinear interactions inside the subspace.

Fig. 10
figure 10

Comparison of third-order central-moments for Lorenz-96 subjected to extreme excitation. The moments inside the subspace are shown (for t=8) computed with MQG-DO (s=26) and Monte Carlo. The visualization follows the same technique as used in Fig. 2

Full size image

6 Conclusions and Future Directions

We have presented a blending framework between inexpensive, full-space, second-order methods based on diagnostic nonlinear energy fluxes from a steady-state (MQG) and high-statistical-order methods for reduced-order subspaces (DO). The coupling of these two methodologies presents particular challenges due to the contradictory nature of the two ingredients. Based on energy fluxes arguments we establish a two-way coupling by

(i) correcting the MQG nonlinear energy fluxes using non-Gaussian statistical information from the DO subspace, and

(ii) correct the reduced-order dynamics inside the subspace so that the interactions with dynamical components outside the subspace are fully taken into account.

With this blended MQG-DO method we prove that

(i) the steady-state statistics are still recovered correctly (as it happens in the MQG method), and

(ii) we obtain a pure improvement compared with the MQG method, which increases monotonically as the number of modes, whose full statistics are modeled, increases. We illustrate the blended approach in two unstable systems (where MQG and order-reduction approaches fail to approximate correctly) under extreme excitation scenarios involving localized forcing and energy injected in high-wavenumber modes. The results indicate that the MQG-DO method is able to recover the correct evolution of the spectrum and the mean (second-order statistics) over the full dimensionality of the system, but also approximate satisfactorily the higher-order statistics within the stochastic subspace. Future work includes the application of the above framework in realistic turbulent systems using a combination of DO and carefully chosen, fixed modes. Also, the above methodology has great potential for the correct quantification of non-Gaussian statistics and in particular extreme events for specific modes of interest (e.g. extreme waves in the ocean, etc.).