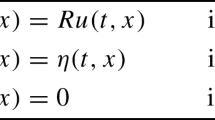1 Introduction

The goal of this paper is to develop, from a geometric point of view, numerical methods for optimal control of Lagrangian mechanical systems. Our approach employs the theory of discrete mechanics and variational integrators (Marsden and West 2001) to derive both an integrator for the dynamics and an optimal control algorithm in a unified manner. This is accomplished through the discretization of the Lagrange–d’Alembert variational principle on manifolds. An integrator for the mechanics is derived using a standard Lagrangian function and virtual work done by control forces, while control optimality conditions are derived using a special Lagrangian defined on a higher dimensional space which encodes the dynamics and a desired cost function. The resulting integration and optimization schemes are symplectic and respect the state-space structure and momentum evolution. These qualities are associated with favorable numerical properties which motivate the development of practical algorithms that can be applied to robotic or aerospace vehicles.

The proposed framework is general and applies to unconstrained systems, as well as systems with symmetries, underactuation, and nonholonomic constraints. In particular, our construction is appropriate for controlled Lagrangian systems that evolve on a general tangent bundle TQ with associated discrete state space Q×Q, where Q is a differentiable manifold (Marsden and West 2001; Ober-Blöbaum et al. 2011). We also focus on systems evolving on a Lie group G (Bloch et al. 2009; Bobenko and Suris 1999; Hussein et al. 2006; Kobilarov and Marsden 2011; Lee et al. 2006; Marsden et al. 1999) and consider the underactuated case (Kobilarov and Marsden 2011) applicable for rigid body systems. Finally, the theory extends to the more general principal bundle setting with discrete analog Q×Q×G (or more generally (Q×Q)/G) assuming that the action of a Lie group G of symmetry leaves the control system invariant (Cortés 2002; Ferraro et al. 2008; Kobilarov et al. 2010; Leok 2004).

The main idea is the following: we take an approximation of the Lagrange–d’Alembert principle for forced Lagrangian systems, which models control inputs and external forces such as gravity or drag. The formulation permits piecewise continuous control forces that can be encountered in practical applications. We observe that the discrete equations of motion for these types of systems are interpreted as the discrete Euler–Lagrange equations of a new Lagrangian defined in an augmented discrete phase space. Next, we apply discrete variational calculus techniques to derive the discrete optimality conditions. After this, we recover two sequences of discrete controls modeling a piecewise control trajectory.

Additionally, we show how to derive the equations for various reduced systems. We specifically develop numerical methods for systems on Lie groups that lead to practical algorithm implementation. One such example system—an underactuated underwater vehicle—is used to illustrate the developed methodology. The resulting algorithm is simple to implement and has the ability to quickly converge to a solution which is close to the optimal solution and to the true system dynamics. We also extend our techniques to more general reduced systems like optimal control problems in trivial principal bundles, and we show how to introduce nonholonomic constraints in our framework.

This work provides several contributions. First, it formulates and derives numerical methods for dynamics integration and optimal control of mechanical systems in a unified discrete variational setting. Performing the optimization (via trajectory variations) in an enlarged phase space then naturally enables the treatment of general systems on either vector spaces or principal bundles with Lie group symmetries and subject to underactuation, nonholonomic constraints, and discontinuous control inputs. Second, the paper details a nonlinear root-finding algorithm for the optimal control problem between two given initial and final states that is surprisingly easy to construct since it is implemented similarly to an integrator with the addition of a boundary reconstruction condition. Finally, the geometric preservation properties of the optimal control solutions, such as symplectic-momentum preservation in the standard case or Poisson bracket and momentum preservation for reduced systems, are automatically guaranteed using the results in Marsden and West (2001), Marrero et al. (2006).

The developed optimization methods inherit the backward error analysis properties of standard variational integrators. Yet, while backward error analysis explains the long-time properties of standard integrators, its significance in the context of optimal control problems with finite horizon and fixed final boundary state requires further study. In addition, while symplecticity is linked to favorable behavior in dynamics time stepping, the symplecticity of the higher dimensional optimal control system is likely to have further implications that remain to be studied. Finally, as with any other local optimization method for nonlinear systems, the proposed approach does not have global convergence guarantees.

The paper is organized as follows. Section 2 introduces variational integrators. Section 3 formulates optimal control problems for Lagrangian systems defined on tangent bundles, in continuous and discrete settings, and for both fully and underactuated systems. A simple control problem for a mechanical Lagrangian on ℝn illustrates these developments. In Sect. 4, discrete mechanics on Lie groups is introduced. Specifically, discrete Euler–Poincaré equations and their Hamiltonian version, the discrete Lie–Poisson equations, are obtained. Sections 5 and 6 develop the discretization procedure and the numerical aspects of the proposed approach. The developed algorithm is illustrated with an application to an unmanned underwater vehicle evolving on SE(3). Finally, Sect. 7 deals with reduced systems on a trivial principal bundle, using nonholonomic mechanics.

2 Discrete Mechanics and Variational Integrators

Let Q be an n-dimensional differentiable manifold with local coordinates (q i), 1≤i≤n. Denote by TQ its tangent bundle with induced coordinates \((q^{i}, \dot{q}^{i})\). Given a Lagrangian function L:TQ→ℝ the Euler–Lagrange equations are

$$ \frac{\mathrm{d}}{\mathrm{d}t} \biggl(\frac{\partial L}{\partial\dot{q}^i} \biggr)- \frac{\partial L}{\partial q^i}=0, \quad1\leq i\leq n. $$
(1)

These equations are a system of implicit second order differential equations. In the sequel, we will assume that the Lagrangian is regular, that is, the matrix \((\frac{\partial^{2} L}{\partial\dot{q}^{i} \partial\dot{q}^{j}})\) is nonsingular. It is well known that the origin of these equations is variational (see Abraham and Marsden 1978; Marsden and Ratiu 1999).

Variational integrators retain this variational character and also some of the key geometric properties of the continuous system, such as symplecticity and momentum conservation (see Hairer et al. 2002 and references therein). In the following we will summarize the main features of this type of numerical integrator (Marsden and West 2001). A discrete Lagrangian is a map L d :Q×Q→ℝ, which may be considered as an approximation of the integral action defined by a continuous Lagrangian L:TQ→ℝ: \(L_{\mathrm{d}}(q_{0}, q_{1})\approx\int^{h}_{0} L(q(t), \dot{q}(t))\,\mathrm{d}t\), where q(t) is a solution of the Euler–Lagrange equations for L, and where q(0)=q 0 and q(h)=q 1 and h>0 is sufficiently small.

Remark 2.1

The Cartesian product Q×Q is equipped with an interesting differential structure, termed a Lie groupoid, which allows the extension of variational calculus to various settings (see Marrero et al. 2006 for more details).

Define the action sum S d:Q N+1→ℝ, corresponding to the Lagrangian L d by \(S_{\mathrm{d}}=\sum_{k=1}^{N} L_{\mathrm{d}}(q_{k-1}, q_{k})\), where q k ∈Q for 0≤k≤N, and N is the number of steps. The discrete variational principle states that the solutions of the discrete system determined by L d must extremize the action sum given fixed endpoints q 0 and q N . By extremizing S d over q k , 1≤k≤N−1, we obtain the system of difference equations

$$ D_1L_{\mathrm{d}}( q_k, q_{k+1})+D_2L_{\mathrm{d}}( q_{k-1}, q_{k})=0, $$
(2)

or, in coordinates,

$$\frac{\partial L_{\mathrm{d}}}{\partial x^i}(q_k, q_{k+1})+\frac{\partial L_{\mathrm{d}}}{\partial y^i}(q_{k-1}, q_{k})=0, $$

where 1≤i≤n, 1≤k≤N−1, and x,y denote the n-first and n-second variables of the function L, respectively.

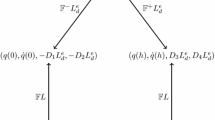
These equations are usually called the discrete Euler–Lagrange equations. Under some regularity hypotheses (the matrix (D 12 L d(q k ,q k+1)) is regular), it is possible to define a (local) discrete flow \(\varUpsilon_{L_{\mathrm{d}}}\colon Q\times Q\to Q\times Q\), by \(\varUpsilon_{L_{\mathrm{d}}}(q_{k-1}, q_{k})=(q_{k}, q_{k+1})\) from (2). Define the discrete Legendre transformations associated to L d as

and the discrete Poincaré–Cartan 2-form \(\omega_{\mathrm{d}}=(\mathbb {F}^{+}L_{\mathrm{d}})^{*}\omega _{Q}=(\mathbb{F}^{-}L_{\mathrm{d}})^{*}\omega_{Q}\), where ω Q is the canonical symplectic form on T ∗ Q. The discrete algorithm determined by \(\varUpsilon_{L_{\mathrm{d}}}\) preserves the symplectic form ω d, i.e., \(\varUpsilon_{L_{\mathrm{d}}}^{*}\omega_{\mathrm{d}}=\omega_{\mathrm{d}}\). Moreover, if the discrete Lagrangian is invariant under the diagonal action of a Lie group G, then the discrete momentum map \(J_{\mathrm{d}}\colon Q\times Q \to{\mathfrak{g}}^{*}\) defined by

$$\bigl\langle J_{\mathrm{d}}(q_k, q_{k+1}), \xi\bigr\rangle= \bigl\langle D_2L_{\mathrm{d}}(q_k, q_{k+1}), \xi_Q(q_{k+1})\bigr\rangle $$

is preserved by the discrete flow. Therefore, these integrators are symplectic-momentum preserving. Here, ξ Q denotes the fundamental vector field determined by \(\xi\in{\mathfrak{g}}\), where \({\mathfrak{g}}\) is the Lie algebra of G. (See Marsden and West 2001 for more details.)

3 Discrete Optimal Control on Tangent Bundles

Consider a mechanical system whose configuration space is an n-dimensional differentiable manifold Q and whose dynamics is determined by a Lagrangian L:TQ→ℝ. The control forces are modeled as a mapping f:TQ×U→T ∗ Q, where \(f(v_{q}, u)\in T_{q}^{*}Q\), v q ∈T q Q, and u∈U, where U is the control space. Observe that this last definition also covers configuration- and velocity-dependent forces such as dissipation or friction (see Ober-Blöbaum et al. 2011). For greater generality we consider control variables that are only piecewise continuous to account for impulsive controls.

The motion of the mechanical system is described by applying the principle of Lagrange–D’Alembert, which requires that the solutions q(t)∈Q must satisfy

$$ \delta\int^T_0 L\bigl(q(t), \dot{q}(t)\bigr)\, \mathrm{d}t + \int^T_0 f \bigl(q(t), \dot{q}(t), u(t)\bigr)\delta q(t)\,\mathrm{d}t=0, $$
(3)

where \((q,\dot{q})\) are the local coordinates of TQ and where we consider arbitrary variations δq∈T q(t) Q with δq(0)=0 and δq(T)=0 (since we are prescribing fixed initial and final conditions \((q(0), \dot{q}(0))\) and \((q(T), \dot{q}(T))\)).

Given that we are considering an optimal control problem, the forces f must be chosen, if they exist, as the ones that extremize the cost functional

$$ \int_0^T C\bigl(q(t), \dot{q}(t), u(t)\bigr)\, \mathrm{d}t, $$
(4)

where C:TQ×U→ℝ.

The optimal equations of motion can now be derived using the Pontryagin maximum principle. Generally, it is not possible to explicitly integrate these equations; consequently, it is necessary to apply a numerical method. In this work, using discrete variational techniques, we will first discretize the Lagrange–d’Alembert principle and then the cost functional. We obtain a numerical method that preserves some geometric features of the original continuous system, as we will see in the sequel.

To discretize this problem, we replace the tangent space TQ by the Cartesian product Q×Q and the continuous curves by sequences q 0,q 1,…,q N (we are using N steps, with time step h fixed, so that t k =kh and Nh=T). The discrete Lagrangian L d:Q×Q→ℝ is constructed as an approximation of the action integral in a single time step (see Marsden and West 2001), that is,

$$L_{\mathrm{d}}(q_k, q_{k+1})\approx\int _{kh}^{(k+1)h}L\bigl(q(t), \dot{q}(t)\bigr)\,\mathrm{d}t. $$

We choose the following discretization for the external forces: \(f^{\pm }_{k}:Q\times Q\times U\rightarrow T^{*}Q\), where U⊂ℝm, m≤n, such that

Observe that, as mentioned above, we have introduced the discrete controls as two different sequences, \(\{u_{k}^{-}\}\) and \(\{ u_{k}^{+}\}\). In the notation followed throughout this paper, the time interval [kh,(k+1)h] is referred to as the k-th interval, while the controls immediately before and after time t k+1=(k+1)h are denoted by \(u_{k}^{+}\) and \(u_{k+1}^{-}\), respectively. This choice allows us to model piecewise continuous controls, admitting discrete jumps at every time t k . The notation is also depicted in the following figure:

figure a

Moreover, we have that

where \((f^{-}_{k}(q_{k}, q_{k+1}, u_{k}^{-}), f^{+}_{k}(q_{k}, q_{k+1}, u_{k}^{+}))\in T_{q_{k}}^{*}Q\times T_{q_{k+1}}^{*}Q\) (see Marsden and West 2001).

Therefore, we derive a discrete version of the Lagrange–D’Alembert principle given in (3):

$$\delta\sum_{k=0}^{N-1}L_{\mathrm{d}}(q_k, q_{k+1}) +\sum_{k=0}^{N-1} \bigl(f^{-}_{k}\bigl(q_k, q_{k+1}, u_{k}^{-}\bigr)\delta q_k+f^+_{k} \bigl(q_k, q_{k+1}, u_{k}^{+}\bigr) \delta q_{k+1} \bigr)=0, $$

for all variations {δq k } k=0,…,N with \(\delta q_{k}\in T_{q_{k}}Q\) such that δq 0=δq N =0. From this principle it is easy to derive the system of difference equations:

(5)

where k=1,…,N−1. Equations (5) are called the forced discrete Euler–Lagrange equations (see Ober-Blöbaum et al. 2011).

We can also approximate the cost functional (4) in a single time step h by

$$C_{\mathrm{d}}\bigl(q_k, u_k^-, q_{k+1}, u_{k}^+\bigr) \approx\int_{kh}^{(k+1)h}C \bigl(q(t), \dot{q}(t), u(t)\bigr)\,\mathrm{d}t, $$

yielding the discrete cost functional

$$\sum_{k=0}^{N-1}C_{\mathrm{d}} \bigl(q_k, u_k^-, q_{k+1}, u_{k}^+ \bigr). $$

Observe that C d:Q×U×Q×U→ℝ.

3.1 Fully Actuated Systems

In this section we assume the following condition.

Definition 3.1

(Fully Actuated Discrete System)

The discrete mechanical control system is fully actuated if the mappings

are both diffeomorphisms.

Define the momenta

(6)
(7)

Since both \(f^{\pm}_{k}|_{(q_{k},q_{k+1})}\) are diffeomorphisms, we can express \(u_{k}^{\pm}\) in terms of (q k ,p k ,q k+1,p k+1) using (6) and (7). Next, we define a new Lagrangian \(\mathcal{L}_{\mathrm{d}}: T^{*}Q\times T^{*}Q\rightarrow \mathbb{R}\) by

(8)

The system is fully actuated; consequently, the Lagrangian \({\mathcal{L}}_{\mathrm{d}}\) is well defined on the entire discrete space T ∗ Q×T ∗ Q.

Now the discrete phase space is the Cartesian product T ∗ Q×T ∗ Q of two copies of the cotangent bundle. The definition (6), (7) gives us a matching of momenta (see Marsden and West 2001), which automatically implies

$$D_2L_{\mathrm{d}}(q_{k-1}, q_{k})+f^+_{k-1} \bigl(q_{k-1}, q_{k}, u_{k-1}^{+} \bigr)=-D_1L_{\mathrm{d}}(q_k, q_{k+1})-f^-_{k} \bigl(q_k, q_{k+1}, u_{k}^{-}\bigr), $$

k=1,…,N−1, which are the forced discrete Euler–Lagrange equations (5). In other words, the matching condition enforces that the momentum at time k should be the same when evaluated from the lower interval [k−1,k] or the upper interval [k,k+1]. Consequently, along a solution curve there is a unique momentum at each time t k , which can be called p k .

The discrete Euler–Lagrange equations of motion for the Lagrangian \({\mathcal{L}}_{\mathrm{d}}: T^{*}Q\times T^{*}Q\rightarrow\mathbb{R}\) are

(9)
(10)

Assuming the regularity of the matrix

$$\left( \begin{array}{@{}c@{\quad}c@{}} D_{13}{\mathcal{L}}_{\mathrm{d}}&D_{14}{\mathcal{L}}_{\mathrm{d}}\\ D_{23}{\mathcal{L}}_{\mathrm{d}}&D_{24}{\mathcal{L}}_{\mathrm{d}} \end{array} \right), $$

and then applying the implicit Function theorem, the two discrete Legendre transformations

are local diffeomorphisms. In many cases, such as if Q is a vector space, it may be that both discrete Legendre transformations are global diffeomorphisms. In that case we say that \({\mathcal{L}}_{\mathrm{d}}\) is hyperregular and can define the discrete Hamiltonian map \(\tilde{F}_{\mathrm{d}}\doteq\mathbb{F}^{+}{\mathcal{L}}_{\mathrm{d}}\circ (\mathbb{F}^{-}{\mathcal{L}}_{\mathrm{d}})^{-1}: T^{*}(T^{*}Q)\longrightarrow T^{*}(T^{*}Q)\). From the standard properties of discrete variational calculus (Marsden and West 2001), we deduce that the discrete Hamiltonian map will preserve the canonical symplectic form on T ∗(T ∗ Q) and the canonical momentum maps in the case of invariance of \({\mathcal{L}}_{\mathrm{d}}\) by a Lie group of symmetries (see the following subsections for further discussions).

In summary, we have obtained the discrete equations of motion for a fully actuated mechanical optimal control problem as the discrete Euler–Lagrange equations for a Lagrangian defined on the product of two copies of the cotangent bundle and derive its preservation properties.

3.2 Example: Optimal Control Problem for a Mechanical Lagrangian with Configuration Space ℝn

Consider the case Q=ℝn and assume that M is an n×n constant and symmetric matrix. The mechanical Lagrangian L:ℝ2n→ℝ is defined by \(L(x,\dot{x})=\frac{1}{2}\dot{x}^{T}M\dot{x}-V(x)\), where V:ℝn→ℝ is the potential function and x∈ℝ. The system is fully actuated and there exist no velocity constraints. The optimal control problem is typically given in terms of boundary conditions \((x(0),\dot{x}(0))\) and \(( x(T),\dot{x}(T))\) for a given final time T. Note that in the continuous setting we can define the momentum by the continuous Legendre transformation \(\mathbb{F}L:TQ\rightarrow T^{*}Q\), \((q,\dot{q})\mapsto(q,p)\): \(p=\frac{\partial L}{\partial\dot{x}}\), i.e., \(p(t)=\dot{x}^{T}(t)\,M\). In consequence, we can also define boundary constraints in the phase space: \((x(0),p(0)=\dot{x}(0)^{T}\,M)\) and \((x(T), p(T)=\dot{x}(T)^{T}\,M)\).

We employ a trapezoidal discretization for the Lagrangian (see Hairer et al. 2002), that is, \(L_{\mathrm{d}}(x_{k},x_{k+1})=\frac{h}{2}\,L(x_{k},\frac {x_{k+1}-x_{k}}{h})+\frac{h}{2}\,L(x_{k+1},\frac{x_{k+1}-x_{k}}{h})\) where, as above, h is the fixed time step and x 1,x 2,…,x N is a sequence of elements on ℝn. The discrete Lagrangian then becomes

$$L_{\mathrm{d}}(x_{k},x_{k+1})=\frac {1}{2h}(x_{k+1}-x_{k})^{T}M(x_{k+1}-x_{k})- \frac{h}{2}\bigl( V(x_{k})+V(x_{k+1})\bigr). $$

The control forces are \(f_{k}^{-}(x_{k},x_{k+1},u_{k}^{-})\in T_{x_{k}}^{*}\mathbb{R}^{n}\) and \(f_{k}^{+}(x_{k},x_{k+1},u_{k}^{+})\in T_{x_{k+1}}^{*}\mathbb{R}^{n}\). For clarity, we will fix the control forces in the following manner: \(f^{\pm}(x_{k},x_{k+1},u_{k}^{\pm})=u_{k}^{\pm}\). Using (6) and (7) it is straightforward to obtain the associated momenta p k and p k+1, namely,

Let \(C_{\mathrm{d}}=\frac{h}{4}\sum_{k=0}^{N-1} [(u_{k}^{-})^{2}+(u_{k}^{+})^{2}]\) be a discrete approximation of the cost function. Consequently, the Lagrangian over T ∗ℝn×T ∗ℝn is

where V x represents the derivative of V with respect to the variable x. Applying (9) and (10) to \(\mathcal{L}_{\mathrm{d}}\) we obtain the following equations:

(11)
(12)

where both sets of equations are defined for k=1,…,N−1. Note that it is possible to remove the dependence on p k in (12). However, we prefer to keep it to stress that the discrete variational Euler–Lagrange equations (9) and (10) are defined in T ∗ Q×T ∗ Q (T ∗ℝn×T ∗ℝn in the particular case we are considering in this example).

Expressions (11) and (12) give 2(N−1)n equations for the 2(N+1)n unknowns \(\{x_{k}\}_{k=0}^{N}\), \(\{p_{k}\}_{k=0}^{N}\). The boundary conditions

contribute 4n extra equations that convert (11) and (12) in a nonlinear root-finding problem of 2(N+1)n and the same amount of unknowns.

3.3 Underactuated Systems

In this section, we examine the case of underactuated systems defined as follows.

Definition 3.2

(Underactuated Discrete System)

A discrete mechanical control system is underactuated if the mappings

are both embeddings.

Under this hypothesis we deduce that \({\mathcal{M}}^{-}_{(q_{k},q_{k+1})}=f^{-}_{k}|_{(q_{k}, q_{k+1})}(U)\), \({\mathcal{M}}^{+}_{(q_{k},q_{k+1})}= f^{+}_{k}|_{(q_{k}, q_{k+1})}(U)\) are submanifolds of \(T^{*}_{q_{k}}Q\) and \(T^{*}_{q_{k+1}}Q\), respectively. Therefore, \(f^{\pm}_{k}|_{(q_{k}, q_{k+1})}\) are diffeomorphisms onto its image. Moreover, \(\dim {\mathcal{M}}^{-}_{(q_{k},q_{k+1})}= \dim{\mathcal{M}}^{+}_{(q_{k},q_{k+1})}=\dim U\).

The set of admissible forces is restricted to the space \({\mathcal{M}}^{-}_{(q_{k},q_{k+1})}\times{\mathcal{M}}^{+}_{(q_{k},q_{k+1})}\subset T_{q_{k}}^{*}Q\times T_{q_{k+1}}^{*}Q\). As a consequence, the set of admissible momenta defined in (6) and (7) satisfy

Thus, the Lagrangian function defined in (8) is restricted to these points only. It is then necessary to apply constrained variational calculus typically performed by means of constraint functions \(\varPhi^{-}_{\alpha},\varPhi^{+}_{\alpha}: T^{*}Q\times T^{*}Q\to\mathbb{R}\), 1≤α≤n−dimU. Therefore, the solutions of the optimal control problem are now viewed as the solutions of the discrete constrained problem determined by an extended Lagrangian \({\mathcal{L}}_{\mathrm{d}}\) and the constraints \(\varPhi^{\pm}_{\alpha}\). Since \(f^{\pm}|_{(q_{k},q_{k+1})}\) are embeddings, as established in definition (3.2), the number of constraints is determined by n minus the dimension of U. Note that the total number of constraints, \(\varPhi^{\pm}_{\alpha}\), is therefore 2(n−dimU).

To solve this problem we introduce Lagrange multipliers \((\lambda_{k}^{-})^{\alpha},(\lambda_{k}^{+})^{\alpha}\) and consider discrete variational calculus using the augmented Lagrangian

Observe that, even though the constraints are functions of the Cartesian product of two copies of the cotangent bundle, i.e., \(\varPhi _{\alpha}^{\pm}:T^{*}Q\times T^{*}Q\rightarrow\mathbb{R}\), \(\varPhi _{\alpha}^{-}\) does not depend on p k+1, nor \(\varPhi_{\alpha}^{+}\) on p k . The discrete Euler–Lagrange equations give us the solutions of the underactuated problem.

Typically, the underactuated systems appear in an affine way, that is,

where \(A_{k}^{-}(q_{k}, q_{k+1})\in T^{*}_{q_{k}}Q\), \(A_{k}^{+}(q_{k}, q_{k+1})\in T^{*}_{q_{k+1}}Q\). Moreover, \(B^{-}_{k}(q_{k}, q_{k+1})\in\mbox{Lin}(U, T_{q_{k}}^{*}Q)\) and \(B^{+}_{k}(q_{k}, q_{k+1})\in\mbox{Lin}(U, T_{q_{k+1}}^{*}Q)\) are linear maps (we assume that U is a vector space and Lin(E 1,E 2) is the set of all linear maps between E 1 and E 2). In consequence, \(B^{-}_{k}(q_{k}, q_{k+1})(u_{k}^{-})\in T^{*}_{q_{k}}Q\) and \(B^{+}_{k}(q_{k}, q_{k+1})(u_{k}^{+})\in T^{*}_{q_{k+1}}Q\).

Then the constraints are deduced using the compatibility conditions:

which imply constraints in (q k ,q k+1,p k ) and (q k ,q k+1,p k+1), respectively. Furthermore, the fact that \(f_{k}^{\pm}|_{(q_{k},q_{k+1})}\) are both embeddings implies that \(\operatorname{rank}B^{-}_{k}=\operatorname{rank}B^{+}_{k}=\dim U\).

Since we are dealing with a discrete constrained variational problem, the geometric preservation properties are deduced by directly applying the results in Marrero et al. (2011).

4 Discrete Optimal Control on Lie Groups

The case when the configuration space is a Lie group G is studied next. Variational integrators for such systems were developed in Marsden et al. (1999b), Bobenko and Suris (1999), and the corresponding discrete variational optimal control problems were studied in Lee et al. (2006), Bloch et al. (2009), Kobilarov and Marsden (2011), Burnett et al. (2011). Our approach, employing the developments in Kobilarov and Marsden (2011), is to reduce the second order Euler–Lagrange equations on G to first order equations on the Lie algebra \(\mathfrak{g}\) and to perform optimization in this reduced unconstrained space.

Following the developments in Sect. 2, assume that the Lagrangian defined by L d:G×G→ℝ is invariant, so that

$$L_{\mathrm{d}}(g_k, g_{k+1})=L_{\mathrm{d}}( \bar{g}g_k, \bar{g}g_{k+1}) $$

for any element \(\bar{g}\in G\) and (g k ,g k+1)∈G×G. According to this, we can define a reduced Lagrangian l d:G→ℝ by

$$l_{\mathrm{d}}(W_k)=L_{\mathrm{d}}\bigl(e, g_{k}^{-1} g_{k+1}\bigr), $$

where \(W_{k}=g_{k}^{-1}g_{k+1}\) and e is the identity of the Lie group G.

The reduced action sum is given by

$$\begin{array} {rrcl} S_{\mathrm{d}}:& G^{N-1}&\rightarrow& \mathbb{R} \\ &(W_0, \ldots, W_{N-1})&\longmapsto& \displaystyle\sum _{k=0}^{N-1}l_{\mathrm{d}}(W_k). \end{array} $$

Taking variations of S d and noting that

$$\delta W_k = -g^{-1}_k(\delta g_k) g^{-1}_k g_{k+1} + g_k^{-1} \delta g_{k+1} = -\eta_k W_k + W_{k} \eta_{k+1}, $$

where \(\eta_{k} = g_{k}^{-1}\delta g_{k}\), we obtain the discrete Euler–Poincaré equations

$$\bigl(r_{_{W_{k}}}^*\,\mathrm{d}l_{\mathrm{d}}\bigr) (W_k) - \bigl(l_{_{W_{k-1}}}^*\,\mathrm{d}l_{\mathrm{d}}\bigr) (W_{k-1}) = 0, \quad k = 1,\ldots, N-1, $$

where l:G×G→G and r:G×G→G are, respectively, the left and the right translations of the group (see also Bobenko and Suris 1999).

If we denote \(\mu_{k}=(r_{_{W_{k}}}^{*}\,\mathrm{d}l_{\mathrm{d}})(W_{k})\), then the discrete Euler–Poincaré equations are rewritten as

$$ \mu_{k+1}=\mathrm{Ad}^*_{_{W_{k}}}\mu_k, $$
(13)

where \(\mathrm{Ad}:G\times\mathfrak{g}\rightarrow\mathfrak{g}\) is the adjoint action of G on \(\mathfrak{g}\). Typically, these equations are known as the discrete Lie–Poisson equations (see Bobenko and Suris 1999; Marsden et al. 1999a, 1999b).

Consider a mechanical system determined by a Lagrangian \(l: {\mathfrak{g}}\rightarrow\mathbb{R}\), where \({\mathfrak{g}}\) is the Lie algebra of a Lie group G, which also is an n-dimensional vector space. The continuous external forces are defined as follows: \(f: {\mathfrak{g}}\times U\rightarrow{\mathfrak{g}}^{*}\). The motion of the mechanical system is described by applying the following principle:

$$ \delta\int^T_0 l\bigl(\xi(t)\bigr) \,\mathrm{d}t + \int^T_0 \bigl\langle f\bigl( \xi(t), u(t)\bigr),\eta (t)\bigr\rangle\,\mathrm{d}t=0, $$
(14)

for all variations δξ(t) of the form \(\delta\xi(t)=\dot {\eta }(t)+[\xi(t), \eta(t)]\), where η(t) is an arbitrary curve on the Lie algebra with η(0)=0 and η(T)=0 (see Marsden and Ratiu 1999). In addition, 〈⋅,⋅〉 is the natural pairing between \(\mathfrak{g}\) and \(\mathfrak{g}^{*}\). These equations give us the controlled Euler–Poincaré equations:

$$\frac{\mathrm{d}}{\mathrm{d}t} \biggl( \frac{\delta l}{\delta\xi} \biggr)= \mathrm{ad}^*_{\xi } \biggl( \frac{\delta l}{\delta\xi} \biggr)+f, $$

where ad ξ η=[ξ,η].

The optimal control problem consists of minimizing a given cost functional:

$$ \int_0^T C\bigl(\xi(t), u(t) \bigr)\,\mathrm{d}t, $$
(15)

where \(C: {\mathfrak{g}}\times U\longrightarrow\mathbb{R}\).

Now, we consider the associated discrete problem. First we replace the Lie algebra \({\mathfrak{g}}\) by the Lie group G and the continuous curves by sequences W 0,W 1,…,W N (since the Lie algebra is the infinitesimal version of a Lie group, its proper discretization is consequently that Lie group Marsden et al. 1999b; Marsden and West 2001).

The discrete Lagrangian l d:G→ℝ is constructed as an approximation of the action integral, that is,

$$l_{\mathrm{d}}(W_k)\approx\int_{kh}^{(k+1)h}l \bigl(\xi(t)\bigr)\,\mathrm{d}t. $$

Let define the discrete external forces in the following way: \(f^{\pm }_{k}:G\times U\rightarrow\mathfrak{g}^{*}\), where U⊂ℝm for \(m\leq n=\dim\mathfrak{g}\). Consequently,

$$\bigl\langle f^-_{k}\bigl(W_k,u_{k}^{-} \bigr),\eta_k\bigr\rangle+\bigl\langle f^+_{k} \bigl(W_k,u_{k}^{+}\bigr), \eta_{k+1}\bigr \rangle\approx\int_{kh}^{(k+1)h}\bigl\langle f\bigl( \xi(t), u(t)\bigr),\eta (t)\bigr\rangle\,\mathrm{d}t, $$

where \((f^{-}_{k}(W_{k},u_{k}^{-}), f^{+}_{k}(W_{k},u_{k}^{+}))\in{\mathfrak{g}}^{*}\times{\mathfrak{g}}^{*}\) and \(\eta_{k}\in{\frak{g}}\), for all k. In addition, η 0=η N =0 and 〈⋅,⋅〉 is the natural pairing between \(\mathfrak{g}\) and \(\mathfrak{g}^{*}\).

For simplicity we will sometimes omit the dependence on G×U of both \(f^{+}_{k}\) and \(f^{-}_{k}\).

Taking all of this into account, we derive a discrete version of the Lagrange–D’Alembert principle for Lie groups:

$$ \delta\sum_{k=0}^{N-1}l_{\mathrm{d}}(W_k)+ \sum_{k=0}^{N-1} \bigl(\bigl\langle f^-_{k},\eta_k\bigr\rangle+\bigl\langle f^+_{k}, \eta_{k+1}\bigr\rangle \bigr)=0, $$
(16)

for all variations {δW k } k=0,…,N−1 verifying the relation δW k =−η k W k +W k η k+1 with {η k } k=1,…,N−1 an arbitrary sequence of elements of \({\frak{g}}\) which satisfies η 0,η N =0 (see Lee et al. 2006; Kobilarov and Marsden 2011).

From this principle it is easy to derive the system of difference equations:

$$ l_{_{W_{k-1}}}^* \,\mathrm{d} l_{\mathrm{d}} (W_{k-1})-r_{_{W_{k}}}^* \,\mathrm{d}l_{\mathrm{d}}(W_{k}) +f^+_{k-1} \bigl(W_{k-1}, u_{k-1}^+\bigr)+f^-_{k} \bigl(W_k, u_k^-\bigr)=0, $$
(17)

for k=1,…,N−1; these are called the controlled discrete Euler–Poincaré equations.

The cost functional (15) is approximated by

$$ C_{\mathrm{d}}\bigl(u_k^-, W_k, u^+_k\bigr)\approx\int_{kh}^{(k+1)h}C\bigl( \xi(t), u(t)\bigr)\, \mathrm{d}t, $$
(18)

yielding the discrete cost functional:

$$ \mathcal{J}=\sum_{k=0}^{N-1}C_{\mathrm{d}} \bigl(u_k^-, W_k , u_{k}^+\bigr). $$
(19)

Observe that now C d:U×G×U→ℝ.

4.1 Fully Actuated Systems

In the fully actuated case the mappings \(f^{\pm}_{k}|_{W}: U\to {\mathfrak{g}}^{*}\) defined by \(f^{\pm}_{k}|_{_{W}}(u)=f^{\pm}_{k}(W, u)\) are diffeomorphisms for all W∈G; therefore, we can construct the Lagrangian \({\mathcal{L}}_{\mathrm{d}}: {\mathfrak{g}}^{*}\times G\times {\mathfrak{g}}^{*}\longrightarrow\mathbb{R}\) by

(20)

where the variables \(\nu_{k},\nu_{k+1}\in\mathfrak{g}^{*}\) are defined by

$$ \begin{array} {@{}l} \nu_k=r_{W_{k}}^*\, \mathrm{d}l_{\mathrm{d}}(W_{k})-f^-_{k}\bigl(W_k, u_k^-\bigr), \\[3mm] \nu_{k+1}=l_{W_{k}}^*\,\mathrm{d}l_{\mathrm{d}}(W_{k})+f^+_{k} \bigl(W_k, u_k^+\bigr). \end{array} $$
(21)

The discrete phase space \({\mathfrak{g}}^{*}\times G\times{\mathfrak{g}}^{*}\) is now a mixture of two copies of the Lie algebra \(\mathfrak {g}^{*}\) and a Lie group G. This is also an example of a Lie groupoid (Marrero et al. 2006).

The discrete optimal control problem defined in (16) and (18) has been reduced to a Lagrangian one, with Lagrangian function \(\mathcal{L}_{\mathrm{d}}:{\mathfrak{g}}^{*}\times G\times{\mathfrak{g}}^{*}\rightarrow\mathbb{R}\). Thus, we are able to apply discrete variational calculus to obtain the discrete equations of motion in the phase space \({\mathfrak{g}}^{*}\times G\times{\mathfrak{g}}^{*}\).

Let us show how to derive these equations from a variational point of view (see Marrero et al. 2006 for further details). Define first the discrete action sum

$$\mathcal{S}_{\mathrm{d}}= \sum_{k=0}^{N-1} \mathcal{L}_{\mathrm{d}} (\nu_k, W_k , \nu_{k+1}). $$

Consider sequences of the type {(ν k ,W k ,ν k+1)} k=0,…,N−1 with boundary conditions ν 0,ν N and the composition \(\bar{W}=W_{0}W_{1}\cdots W_{N-2}W_{N-1}\) fixed. Therefore, an arbitrary variation of this sequence has the form

$$\bigl\{\nu_k(\epsilon),h^{-1}_k( \epsilon)W_k h_{k+1}(\epsilon), \nu_{k+1}(\epsilon) \bigr\}_{k=0, \ldots, N-1}, $$

with ϵ∈(−δ,δ)∈ℝ (both ϵ and δ>0 are real parameters) and ν 0(ϵ)=ν 0, ν k (0)=ν k , ν N (ϵ)=ν N , h k (ϵ)∈G, and h 0(ϵ)=h N (ϵ)=e, for all ϵ. Additionally, h k (0)=e for all k.

The critical points of the discrete action sum subjected to the previous boundary conditions are characterized by

Taking derivatives, we obtain

where \({\mathcal{L}}_{\mathrm{d}}|_{(W)}: {\mathfrak{g}}^{*}\times {\mathfrak{g}}^{*}\to\mathbb{R}\) and \({\mathcal{L}}_{\mathrm{d}}|_{(\nu, \nu ')}: G\to\mathbb{R}\) are defined by \({\mathcal{L}}_{\mathrm{d}}|_{(W)}(\nu, \nu ')={\mathcal{L}}_{\mathrm{d}}|_{(\nu, \nu')}(W)= {\mathcal{L}}_{\mathrm{d}}(\nu, W, \nu')\), where W∈G and \(\nu, \nu'\in{\mathfrak{g}}^{*}\). Since δh k (which is defined as \(\frac{\mathrm{d}h_{k}}{\mathrm{d}\epsilon }|_{\epsilon=0}\)) and δν k (which is defined as \(\frac{\mathrm{d} \nu _{k}}{\mathrm{d}\epsilon}|_{\epsilon=0}\)), k=1,…,N−1 are arbitrary, we deduce the following discrete equations of motion:

$$ \begin{array} {@{}rcl} l_{_{W_{k-1}}}^* \,\mathrm{d} { \mathcal{L}}_{\mathrm{d}} |_{(\nu_{k-1}, \nu _{k})}(W_{k-1})-r_{_{W_{k}}}^*\, \mathrm{d} {\mathcal{L}}_{\mathrm{d}} |_{(\nu _k, \nu _{k+1})}(W_{k})&=&0, \\[2mm] D_2{\mathcal{L}}_{\mathrm{d}} |_{(W_{k-1})}(\nu_{k-1}, \nu_{k})+D_1{\mathcal{L}}_{\mathrm{d}} |_{(W_{k})}( \nu_k, \nu_{k+1})&=&0, \end{array} $$
(22)

for k=1,…,N−1. Similarly to Sect. 3.1 we obtain the control inputs \(u_{k}^{-}\) and \(u_{k}^{+}\) using (21).

Define the following discrete Legendre transformations:

$$\begin{array} {@{}rcl} \mathbb{F}^- {\mathcal{L}}_{\mathrm{d}}: { \mathfrak{g}}^*\times G\times{\mathfrak{g}}^*&\longrightarrow& {\mathfrak{g}}^*\times T^*{\mathfrak{g}}^*, \\[1mm] (\nu_{k-1}, W_{k-1}, \nu_k)&\longmapsto& \bigl(r_{_{W_{k-1}}}^*\,\mathrm{d} {\mathcal{L}}_{\mathrm{d}} |_{(\nu_{k-1}, \nu_{k})}(W_{k-1}), -D_1{\mathcal{L}}_{\mathrm{d}} |_{(W_{k-1})}(\nu_{k-1}, \nu_{k})\bigr), \end{array} $$

and

$$\begin{array}{@{}rcl} \mathbb{F}^+ {\mathcal{L}}_{\mathrm{d}}: { \mathfrak{g}}^*\times G\times{\mathfrak{g}}^*&\longrightarrow& {\mathfrak{g}}^*\times T^*{\mathfrak{g}}^*, \\[1mm] \ (\nu_{k-1}, W_{k-1}, \nu_k)&\longmapsto& (l_{_{W_{k-1}}}^*\, \mathrm{d} {\mathcal{L}}_{\mathrm{d}} |_{(\nu_{k-1}, \nu_{k})}(W_{k-1}), D_2{\mathcal{L}}_{\mathrm{d}} |_{(W_{k-1})}(\nu_{k-1}, \nu_{k}). \end{array} $$

These relationships implicitly define the discrete Hamiltonian evolution operator

$$\begin{array}{@{}rcl} \bar{\gamma}_{{\mathcal{L}}_{\mathrm{d}}}: {\mathfrak{g}}^* \times T^*{\mathfrak{g}}^*&\longrightarrow& {\mathfrak{g}}^*\times T^*{\mathfrak{g}}^*, \\[1mm] \bigl(r_{_{W_{k-1}}}^*\,\mathrm{d} {\mathcal{L}}_{\mathrm{d}} |_{(\nu_{k-1}, \nu_{k})}, -D_1{\mathcal{L}}_{\mathrm{d}} |_{(W_{k-1})}\bigr)&\longmapsto& \bigl(l_{_{W_{k-1}}}^*\, \mathrm{d} {\mathcal{L}}_{\mathrm{d}} |_{(\nu_{k-1}, \nu_{k})}, D_2{\mathcal{L}}_{\mathrm{d}} |_{(W_{k-1})}\bigr), \end{array} $$

which verifies

$$\bar{\gamma}_{{\mathcal{L}}_{\mathrm{d}}}^*\{ F, G\}_{{\mathfrak{g}}^*\times T^*{\mathfrak{g}}^*}=\bigl\{\bar{ \gamma}_{{\mathcal{L}}_{\mathrm{d}}}^* F,\bar{\gamma }_{{\mathcal{L}}_{\mathrm{d}}}^* G\bigr\}_{{\mathfrak{g}}^*\times T^*{\mathfrak{g}}^*}. $$

The Poisson bracket is specified in canonical coordinates (z i ,y i ,p i) on \({\mathfrak{g}}^{*}\times T^{*}{\mathfrak{g}}^{*}\) by

where \({\mathcal{C}}^{k}_{ij}\) are the structure constants of the Lie algebra \({\mathfrak{g}}\) fixed a basis {e i }, \(1\leq i\leq\dim {\mathfrak{g}}\). Here, we denote by z i and y i the induced coordinates on \({\mathfrak{g}}^{*}\), and by (y i ,p i ) the coordinates on \(T^{*}{\mathfrak{g}}^{*}\).

4.2 Underactuated Systems

The underactuated case can now be considered by adding constraints. Similarly to Sect. 3.3 underactuation restricts the control forces to lie in a subspace spanned by vectors {e s} of the basis {e s,e σ} of \({\mathfrak{g}}^{*}\), where {s,σ}=1,…,n. Then

where \(a^{-}_{k}(W_{k}), a^{+}_{k}(W_{k})\in{\mathfrak{g}}^{*}\) and \((b^{-}_{k}(W_{k},u_{k}^{-}))_{s}, (b^{+}_{k}(W_{k},u_{k}^{+}))_{s} \in\mathbb{R}\), for all s. Additionally, the embedding condition implies that \(\operatorname{rank} b_{k}^{-}=\operatorname{rank}b_{k}^{+}=\dim U\). Then, taking the dual basis {e s ,e σ }, we induce the following constraints:

(23a)
(23b)

Observe in (23a), (23b), that, even though the constraints are functions \(\varPhi_{\sigma}^{\pm}:\mathfrak{g}^{*}\times G\times\mathfrak {g}^{*}\rightarrow\mathbb{R}\), \(\varPhi_{\sigma}^{-}\) does not depend on ν k+1, nor \(\varPhi_{\sigma }^{+}\) on ν k . Once we have defined the constraints, we can implement the Lagrangian multiplier rule in order to solve the underactuated problem. Namely, we define the extended Lagrangian as

(24)

Defining the discrete action sum

$$\mathcal{S}_{\mathrm{d}}^{\mathrm{under}}=\sum_{k=0}^{N-1} \tilde {\mathcal{L}}_{\mathrm{d}}\bigl(\nu_k, \lambda_k^{-}, W_k , \nu_{k+1}, \lambda_k^{+}\bigr), $$

we obtain the underactuated discrete equations of motion

$$ \begin{array} {@{}l} l_{_{W_{k-1}}}^{*}\,\mathrm{d} \mathcal{L}_{\mathrm{d}} |_{(\nu_{k-1},\nu _k)}(W_{k-1})-r_{_{W_{k-1}}}^{*} \,\mathrm{d}\mathcal{L}_{\mathrm{d}} |_{(\nu_{k},\nu _{k+1})} (W_{k}) \\[2mm] \quad{}+l_{_{W_{k-1}}}^{*}\bigl(\bigl(\lambda_{k-1}^{-} \bigr)^{\sigma}\,\mathrm{d}\varPhi^{-}_{\sigma} |_{(\nu_{k-1},\nu_k)}( W_{k-1})+\bigl(\lambda_{k-1}^{+} \bigr)^{\sigma}\,\mathrm{d} \varPhi^{+}_{\sigma} |_{(\nu_{k-1},\nu_k)}( W_{k-1})\bigr) \\[2mm] \quad{}-r_{_{W_{k-1}}}^{*}\bigl(\bigl(\lambda_{k}^{-} \bigr)^{\sigma}\, \mathrm{d}\varPhi^{-}_{\sigma } |_{(\nu_{k},\nu_{k+1})}( W_{k})+\bigl(\lambda_{k}^{+} \bigr)^{\sigma}\, \mathrm{d}\varPhi^{+}_{\sigma} |_{(\nu_{k},\nu_{k+1})}( W_{k})\bigr)=0, \\[2mm] D_{2}\mathcal{L}_{\mathrm{d}} |_{(W_{k-1})}(\nu_{k-1}, \nu_k) + D_{1} \mathcal{L}_{\mathrm{d}} |_{(W_{k})} ( \nu_{k},\nu_{k+1}) + \bigl[\bigl(\lambda_{k-1}^{+} \bigr)^{\sigma}- \bigl(\lambda_{k}^{-} \bigr)^{\sigma} \bigr]e_{\sigma} = 0, \\[2mm] \varPhi^{-}_{\sigma}(\nu_k, W_k , \nu_{k+1})=0, \\[2mm] \varPhi^{+}_{\sigma}(\nu_k, W_k , \nu_{k+1})=0, \end{array} $$
(25)

where the subscripts (W k−1), (W k ), (ν k−1,ν k ), (ν k ,ν k+1) denote variables that are fixed.

5 Numerical Methods for Systems on Lie Groups

We now put the discrete optimal control equations (22) and (25) into a form suitable for algorithmic implementation. The numerical methods are constructed using the following guidelines:

  1. (1)

    good approximation of the dynamics and optimality,

  2. (2)

    avoidance of issues with local coordinates,

  3. (3)

    guarantee of numerical robustness and convergence,

  4. (4)

    numerical efficiency.

The algorithm developed in this section will be derived from a trapezoidal quadrature and will approximate the dynamics and optimality conditions to at least second order (Marsden and West 2001) (requirement 1). We will also satisfy requirement 2 for systems on Lie groups by lifting the optimization to the Lie algebra through a retraction map that will be defined in this section. The resulting algorithms are numerically robust in the sense that there are no issues with coordinate singularities and the dynamics and optimality conditions remain close to their continuous counterparts even at big time steps. Yet, as with any other nonlinear optimization scheme, it is difficult to formally claim that the algorithm will always converge (requirement 3). Nevertheless, in practice there are only isolated cases for underactuated systems that fail to converge. A remedy for such cases has been suggested in Kobilarov and Marsden (2011). In general, the resulting algorithms require a small number of iterations, e.g., between 10 and 20 to converge (requirement 4).

Note that the discrete mechanics approach provides an accurate approximation of the dynamics associated with its momentum and symplectic form (or Poisson bracket) preservation and good energy behavior. However, long-time stability becomes less important for optimal control problems with short time horizon T. Yet, the notion of symplectic optimality conditions for two-point boundary value problems likely has deeper implications, e.g., related to the region of attraction and numerical stability of the associated root-finding numerical procedure. Such directions are not explored in this work and require further study.

The optimization variables W k are regarded as small displacements on the Lie group. Thus, it is possible to express each term through a Lie algebra element that can be regarded as the averaged velocity of this displacement. This is accomplished using a retraction map \(\tau: {\mathfrak{g}}\to G\) which is an analytic local diffeomorphism around the identity such that τ(ξ)τ(−ξ)=e, where \(\xi\in\mathfrak{g}\). Two standard choices for τ are employed in this work: the exponential map and the Cayley map.

Regarding ξ as a velocity, we set the discrete Lagrangian l d:G→ℝ to

$$l_{\mathrm{d}}(W_k)=hl(\xi_k), $$

where \(\xi_{k}=\tau^{-1}(g_{k}^{-1}g_{k+1})/h=\tau^{-1}(W_{k})/h\). The difference \(g_{k}^{-1}\,g_{k+1}\in G\), which is an element of a nonlinear space, can now be represented by the vector ξ k in order to enable unconstrained optimization in the linear space \(\mathfrak{g}\) for optimal control purposes.

The variational principle will now be expressed in terms of the chosen map τ. The resulting discrete mechanics will thus involve the derivatives of the map, which we define next (see also Bou-Rabee and Marsden 2009; Iserles et al. 2005; Kobilarov 2008; Kobilarov and Marsden 2011).

Definition 5.1

Given a map \(\tau:\mathfrak{g}\rightarrow G\), its right trivialized tangent \(\mathrm{d}\tau_{\xi}:\mathfrak{g}\rightarrow \mathfrak {g}\) and its inverse \(\mathrm{d}\tau_{\xi}^{-1}:\mathfrak {g}\rightarrow \mathfrak{g}\) are such that, for g=τ(ξ)∈G and \(\eta\in \mathfrak{g}\), the following holds:

Using these definitions, variations δξ and δg are constrained by

$$\delta\xi_k=\mathrm{d}\tau^{-1}_{h\xi_k}(- \eta_k+\mathrm{Ad}_{\tau (h\xi_k)} \eta_{k+1})/h, $$

where \(\eta_{k}=g_{k}^{-1}\delta g_{k}\), which is obtained by straightforward differentiation of \(\xi_{k}=\tau^{-1}(g_{k}^{-1}\,g_{k+1})/h\).

The retraction map τ choices are the following:

(a) The exponential map \(\mbox{exp}:\mathfrak{g}\rightarrow G\), defined by exp(ξ)=γ(1), with γ:ℝ→G in the integral curve through the identity of the vector field associated with \(\xi\in\mathfrak{g}\) (hence, with \(\dot{\gamma}(0)=\xi\)). The right trivialized derivative and its inverse are defined by

where B j are the Bernoulli numbers (see Hairer et al. 2002). Typically, these expressions are truncated in order to achieve a desired order of accuracy.

(b) The Cayley map \(\mathrm{cay}:\mathfrak{g}\rightarrow G\) is defined by \(\mathrm{cay}(\xi)=(e-\frac{\xi }{2})^{-1}(e+\frac{\xi}{2})\) and is valid for a general class of quadratic groups (see Hairer et al. 2002) that include the groups of interest in this paper (e.g., SO(3), SE(2), and SE(3)). Its right trivialized derivative and inverse are defined by

Next, the discrete forces and cost function are defined through a trapezoidal approximation, i.e.,

$$f^{\pm}_{k}\bigl(\xi_k, u_k^{\pm} \bigr)=\frac{h}{2}f\bigl(\xi_k,u_k^{\pm} \bigr), $$

and

$$C_{\mathrm{d}}\bigl(u_k^-,\xi_k, u_k^+ \bigr)=\frac{h}{2}C\bigl(\xi_k,u_k^-\bigr)+ \frac{h}{2} C\bigl(\xi_k,u_k^+\bigr), $$

respectively. With the choice of a retraction map and the trapezoidal rule, the equations of motion (13) become

while the momenta defined in (21) take the form

(26)
(27)

Finally, define the Lagrangian \({\ell}_{\mathrm{d}}:\mathfrak {g}^{*}\times\mathfrak{g}\times\mathfrak{g}^{*}\to\mathbb{R} \) such that

$$\ell_{\mathrm{d}}\bigl(\nu,\xi,\nu'\bigr) = \mathcal{L}_{\mathrm{d}} \bigl(\nu, \tau(h\xi), \nu'\bigr). $$

Note that the Lagrangian is well defined only on \(\mathfrak{g}^{*}\times \mathfrak{U} \times\mathfrak{g}^{*}\), where \(\mathfrak{U}\subset\mathfrak{g}\) is an open neighborhood around the identity for which τ is a diffeomorphism. To make the notation as simple as possible, we retain the Lagrangian definition to the full space \(\mathfrak{g}^{*}\times \mathfrak{g} \times\mathfrak{g}^{*}\).

The optimality conditions corresponding to (22) become

(28)
(29)

for k=0,…,N−1. Here, ℓ d|(ξ)(ν,ν′)=ℓ d|(ν,ν′)(ξ)=ℓ d(ν,ξ,ν′). Equations (28) and (29) can also be obtained from (22), employing Lemma 9.2 and Lemma 9.3 in Appendix.

In the underactuated case we define

(30)

and from (25) obtain the equations

$$ \begin{array}{@{}l} \bigl(\mathrm{d} \tau^{-1}_{-h\xi_{k-1}}\bigr)^{*}\,\mathrm{d} \tilde{ \ell}_{\mathrm {d}} |_{(\nu _{k-1},\nu_{k},\lambda_{k-1}^\pm)}(\xi_{k-1})-\bigl(\mathrm{d} \tau^{-1}_{h\xi _{k}}\bigr)^{*}\,\mathrm{d}\tilde{ \ell}_{\mathrm{d}} |_{(\nu_{k},\nu_{k+1},\lambda _k^{\pm })}(\xi_{k}) = 0, \\[2mm] D_{2}\mathcal{L}_{\mathrm{d}} |_{\tau(h\xi_{k-1})}(\nu_{k-1}, \nu_k) + D_{1} \mathcal{L}_{\mathrm{d}} |_{\tau(h\xi_k)} (\nu_{k},\nu_{k+1}) +\lambda_{k-1}^{+} - \lambda_{k}^- = 0, \\[2mm] \varPhi^{-}_{\sigma}\bigl(\nu_k, \tau(h \xi_k) , \nu_{k+1}\bigr)=0, \\[2mm] \varPhi^{+}_{\sigma}\bigl(\nu_k, \tau(h \xi_k) , \nu_{k+1}\bigr)=0, \end{array} $$
(31)

where we employed the notation λ ±:=(λ ±)σ e σ .

Boundary Conditions

Establishing the exact relationship between the discrete and continuous momenta, μ k and μ(t)=∂ ξ l(ξ(t)), respectively, is particularly important for properly enforcing boundary conditions that are given in terms of continuous quantities. The following equations relate the momenta at the initial and final times t=0 and t=T and are used to transform between the continuous and discrete representations:

which also corresponds to the relations ν 0=∂ ξ l(ξ(0)) and ν N =∂ ξ l(ξ(T)). These equations can also be regarded as structure-preserving velocity boundary conditions, i.e., for given fixed velocities ξ(0) and ξ(T).

The exact form of the previous equations depends on the choice of τ. This choice will also influence the computational efficiency of the optimization framework when the above equalities are enforced as constraints. The numerical procedure to compute the trajectory is summarized as follows.

Algorithm 5.2

(Optimal Control)

Data: group G; mechanical Lagrangian l; control functions a, b; cost function C; final time T; number of segments N.

  1. (1)

    Input: boundary conditions (g(0),ξ(0)) and (g(T),ξ(T)).

  2. (2)

    Set momenta ν 0=∂ ξ l(ξ(0)) and ν N =∂ ξ l(ξ(T))

  3. (3)

    Solve for \((\xi_{0},\ldots,\xi_{N-1},\nu_{1},\ldots,\nu_{N-1},\lambda_{1}^{\pm },\ldots,\lambda _{N-1}^{\pm})\) the relations:

    $$\left\{ \begin{array}{@{}l} \mathit{Equations}~(31)\ \mathit{for all}\ k=1,\ldots,N-1,\\[1.5mm] \tau^{-1}(\tau(h\xi_{N-1})^{-1}\ldots\tau(h\xi_{0})^{-1}\, g(0)^{-1}g(T))=0 \end{array} \right. $$
  4. (4)

    Output: optimal sequence of velocities ξ 0,…,ξ N−1.

  5. (5)

    Reconstruct path g 0,…,g N by g k+1=g k τ(hξ k ) for k=0,…,N−1.

The solution is computed using a root-finding procedure such as Newton’s method. If the initial guess does not satisfy the dynamics, we recommend using a Levenberg–Marquardt algorithm, which has slower but more robust convergence.

5.1 Example: Optimal Control Effort

Consider a Lagrangian consisting of the kinetic energy only,

$$l(\xi)=\frac{1}{2}\bigl\langle\mathbb{I}(\xi),\xi\bigr\rangle, $$

full unconstrained actuation, no potential or external forces, and no velocity constraint. The map \(\mathbb{I}:\mathfrak{g}\rightarrow \mathfrak{g}^{*}\) is called the inertia tensor and is assumed full rank.

In the fully actuated case we have \(f(\xi_{k},u^{\pm}_{k})\equiv u^{\pm}_{k}\). We consider a minimum effort control problem, i.e.,

$$C(\xi,u) = \frac{1}{2}\|u\|^2. $$

The optimal control problem for fixed initial and final states (g(0),ξ(0)) and (g(T),ξ(T)) can now be summarized as follows.

The optimality conditions for this problem are derived as follows. The Lagrangian becomes

$$\ell_{\mathrm{d}}(\nu_{k},\xi_{k},\nu_{k+1})= \frac{1}{4h}\sum_{k=0}^{N-1}\bigl( \bigl\Vert \nu_{k}-\bigl(\mathrm{d}\tau^{-1}_{h\xi_{k}} \bigr)^{*}\mathbb {I}(\xi_{k})\bigr\Vert^{2}+ \bigl\Vert \nu_{k+1}-\bigl(\mathrm{d}\tau^{-1}_{-h\xi _{k}} \bigr)^{*}\mathbb{I}(\xi_{k})\bigr\Vert^{2}\bigr), $$

where the momentum has been computed according to

$$ \nu_{k}=\frac{1}{2}\bigl(\bigl(\mathrm{d} \tau^{-1}_{h\xi_{k}}\bigr)^{*}\mathbb {I}( \xi_{k})+\bigl(\mathrm{d}\tau^{-1}_{-h\xi_{k-1}} \bigr)^{*}\mathbb{I}(\xi_{k-1})\bigr). $$
(32)

Thus the optimality conditions become

It is important to note that these last two equations define N  n equations in the N  n unknowns ξ 0:N−1. A solution can be found using nonlinear root finding. Once ξ 0:N have been computed, it is possible to obtain the final configuration g N by reconstructing the curve by these velocities. Also, the boundary condition g(T) is enforced through the relation \(\tau^{-1}(g_{N}^{-1}g(T))=0\) without the need to optimize over any of the configurations g k .

5.2 Extension: The Configuration-Dependent Case

The developed framework can be extended to a configuration-dependent Lagrangian \(L:G\times\mathfrak{g}\rightarrow\mathbb{R}\), for instance, defined in terms of a kinetic energy \(K:\mathfrak{g}\rightarrow\mathbb{R}\) and a potential energy V:G→ℝ according to

$$L(g, \xi)=K(\xi)-V(g), $$

where g∈G and \(\xi\in\mathfrak{g}\). The controlled Euler–Poincaré equations are, in this case,

where the external forces are defined as \(f:G\times\mathfrak{g}\times U\rightarrow\mathfrak{g}^{*}\). Our discretization choice L d:G×G→ℝ will be (recall that \(\xi_{k}=\tau^{-1}(g_{k}^{-1}g_{k+1})/h\))

while the G-dependent discrete forces now become

$$f_k^{-}\bigl(g_k,\xi_k,u_k^- \bigr)=\frac{h}{2}f\bigl(g_k,\xi_k,u_k^- \bigr),\qquad f_k^{+}\bigl(g_{k+1}, \xi_k,u_k^+\bigr)=\frac{h}{2}\,f \bigl(g_{k+1},\xi_k,u_k^+\bigr). $$

This leads to the discrete equations

The momenta become

In consequence, we can define a discrete Lagrangian

$$\mathfrak{L}_{\mathrm{d}}:\mathfrak{g}^{*}\times G\times \mathfrak{g} \times\mathfrak{g}^{*}\to\mathbb{R}, $$

depending on the variables (ν k ,g k ,ξ k ,ν k+1), whose discrete equations of motion will be a mixture between (22) and (28), (29), namely,

6 Applications

6.1 Underwater Vehicle

We illustrate the developed algorithm with an application to a simulated unmanned underwater vehicle. Figure 1 shows the model equipped with five thrusters which produce forces and torques in all directions but the body-fixed “y” axis. Since the input directions span only a five-dimensional subspace, the problem is solved through the underactuated framework.

Fig. 1
figure 1

An underwater vehicle model (a) and various computed optimal trajectories between chosen states (b). Only a few frames along the path are shown for clarity

Full size image

The vehicle configuration space is G=SE(3). We make the identification SE(3)∼SO(3)×ℝ3 using elements R∈SO(3) and x∈ℝ3 through

$$g=\left( \begin{array}{@{}c@{\quad}c@{}} R&x\\ 0_{1\times3}&1 \end{array} \right),\qquad g^{-1}=\left( \begin{array}{@{}c@{\quad}c@{}} R^{T}&-R^{T}x\\ 0_{1\times3}&1 \end{array} \right), $$

where g∈SE(3). Elements of the Lie algebra \(\xi\in \mathfrak{se}(3)\) are identified with body-fixed angular and linear velocities denoted ω∈ℝ3 and v∈ℝ3, respectively, through

$$\xi=\left( \begin{array}{@{}c@{\quad}c@{}} \hat{\omega}&v\\ 0_{1\times3}&0 \end{array} \right), $$

where the map \(\hat{\cdot}:\mathbb{R}^{3}\rightarrow\mathfrak {so}(3)\) is defined by

$$ \hat{\omega}=\left( \begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0&-\omega_{3}&\omega_{2}\\ \omega_{3}&0&-\omega_{1}\\ -\omega_{2}&\omega_{1}&0 \end{array} \right). $$
(33)

The algorithm is thus implemented in terms of vectors in ℝ6 rather than matrices in \(\mathfrak{se} (3)\).

The map \(\tau=\mathrm{cay}:\mathfrak{se} (3)\rightarrow\mathit {SE}(3)\) is chosen, instead of the exponential, since it results in more computationally efficient implementation. It is defined by

$$\mathrm{cay}(\xi)=\left( \begin{array}{@{}c@{\quad}c@{}} \mathrm{cay}(\hat{\omega})&\mathrm{d}\mathrm{cay}_{\omega}v\\ 0&1 \end{array} \right), $$

where \(\mathrm{cay}:\mathfrak{so}(3)\rightarrow\mathit{SO}(3)\) is givenFootnote 1 by

$$ \mathrm{cay}(\hat{\omega})=\mathbf{I}_{3}+\frac{4}{4+\|\omega \|^{2}} \biggl(\hat{\omega}+\frac{\hat{\omega}^{2}}{2}\biggr), $$
(34)

where I n is the n×n identity matrix and dcay:ℝ3→ℝ3 is defined by

$$ \mathrm{d}\mathrm{cay}_{\omega}=\frac{2}{4+\|\omega\|^{2}}(2 \mathbf{I}_3+\hat{\omega}). $$
(35)

The matrix representation of the right trivialized tangent inverse \(\operatorname{d\tau}^{-1}_{(\omega,v)}:\mathbb{R}^{3}\times\mathbb {R}^{3}\rightarrow \mathbb{R}^{3}\times\mathbb{R}^{3}\) becomes

$$ \bigl[\operatorname{dcay}^{-1}_{(\omega,v)}\bigr] = \left[ \begin{array}{@{}c@{\quad}c@{}} \mathbf{I}_3 - \frac{1}{2}\widehat{\omega}+ \frac{1}{4}\omega\omega^T & \mathbf{0}_3 \\[2mm] -\frac{1}{2}(\mathbf{I}_3 - \frac{1}{2}\widehat{\omega})\widehat{v} & \mathbf{I}_3 - \frac{1}{2}\widehat{\omega} \end{array} \right]. $$
(36)

The vehicle inertia tensor \(\mathbb{I}\) is computed assuming cylindrical mass distribution with mass m=3 kg. The control basis vectors are \(\{e_{s}\}_{s=1}^{5}=\{\mathbf{e}_{1},\mathbf{e}_{2}, \mathbf{e}_{3}, \mathbf{e}_{4}, \mathbf{e}_{6}\}\), while the non-actuated direction is e σ =e 5, where e i is the i-th standard basis vector of ℝ6. The control functions take the form

where H is a negative definite viscous drag matrix and the constants c,d are the lengths of the thrusting torque moment arms (see Fig. 1).

We are interested in computing a minimum control effort trajectory between two given boundary states, i.e., conditions on both the configurations and velocities. Such a cost function is defined in Sect. 5.1. The optimal control problem is solved using (31). The computation is performed using Algorithm 5.2. Figure 2 shows the computed velocities and controls for the “reconfiguration” trajectory shown in Fig. 1. The algorithm requires between 10–20 iterations depending on the boundary conditions and when applied to N=32 segments.

Fig. 2
figure 2

Details of the computed optimal path for the reconfiguration maneuver given in Fig. 1

Full size image

6.2 Discontinuous Control

One of the advantages of employing the discrete variational framework is the treatment of discontinuous control inputs as illustrated in Sect. 3. The nature of the control curve depends on the cost function. In the standard squared control effort case (i.e., the L 2 control curve norm employed in Sect. 6.1), the resulting control is smooth. Another cost function of interest is \(\int_{0}^{T} \|u(t)\|\,\mathrm{d}t\), which is typically imposed along with the constraints u min≤u(t)≤u max. This case results in a discontinuous optimal control curve. Our formulation can handle such problems easily, since the terms \(u_{k-1}^{+}\) and \(u_{k}^{-}\) are regarded as the forces before and after time t k , respectively. A computed scenario of a rigid body actuated with two control torques around its principal axes of inertia (Fig. 3) illustrates the discontinuous case.

Fig. 3
figure 3

An optimal trajectory of an underactuated rigid body on SO(3) (a). The body is controlled using two force inputs around the body-fixed x and y axes. A discontinuous optimal trajectory (b) which our algorithm can handle

Full size image

7 Extensions

The methods developed in the previous sections are easily adapted to other cases which are of interest in practical applications. In particular, this section will be devoted to the discussion of two important extensions: the case of optimal control problems for Lagrangians of the type \(l: TM\times{\mathfrak{g}}\to\mathbb{R}\) (that is, reduction by symmetries on a trivial principal fiber bundle) and the case of nonholonomic systems. Here, M denotes a smooth manifold. Observe that the phase space \(TM\times{\mathfrak{g}}\) unifies the previously studied cases of a tangent bundle and a Lie algebra.

The notion of a principal fiber bundle is present in many locomotion and robotic systems (Bullo and Lewis 2005; Bloch et al. 1996; Marsden and Ostrowski 1998). When the configuration manifold is Q=M×G, there exists a canonical splitting between variables describing the position and variables describing the orientation of the mechanical system. Then, we distinguish the pose coordinates g∈G (the elements in the Lie algebra will be denoted by \(\xi\in\mathfrak{g}\)), and the variables describing the internal shape of the system, that is, x∈M (in consequence \((x,\dot{x})\in TM\)). Observe that the Lagrangians of the type \(l: TM\times{\mathfrak{g}}\rightarrow\mathbb{R}\) mainly appear as reductions of Lagrangians of the type L:T(M×G)→ℝ, which are invariant under the action of the Lie group G. Under the identification \(T(M\times G)/G\equiv TM\times{\mathfrak{g}}\) we obtain the reduced Lagrangian l. We first develop the discrete optimal control problem for systems in an unconstrained principal bundle setting in Sect. 42. Nonholonomic constraints are then added to treat the more general case of locomotion systems in Sect. 7.2.

7.1 Discrete Optimal Control on Principal Bundles

The discrete case is modeled by a Lagrangian l d:M×M×G→ℝ which is an approximation of the action integral in one time step:

$$l_{\mathrm{d}}(x_{k},x_{k+1},W_{k})\simeq\int _{hk}^{h(k+1)}l\bigl(x(t), \dot {x}(t), \xi(t)\bigr)\, \mathrm{d}t, $$

where (x k ,x k+1)∈M×M and W k ∈G. Again, we define the discrete control forces according to \(f^{\pm}_{k}: M\times M\times G \times U\rightarrow T^{*}M\times\mathfrak{g}^{*}\), where U⊂ℝm:

Here \(f_{k}^{-}\in T_{x_{k}}^{*}M\times\mathfrak{g}^{*}\) and \(f_{k}^{+}\in T_{x_{k+1}}^{*}M\times\mathfrak{g}^{*}\) (more concretely \(\bar {f}_{k}^{-}\in T_{x_{k}}^{*}M\), \(\bar{f}_{k}^{+}\in T_{x_{k+1}}^{*}M\), \(\hat{f}_{k}^{-}\in\mathfrak{g}^{*}\), \(\hat{f}_{k}^{+}\in\mathfrak {g}^{*}\)).

Similarly to the developments in Sects. 3 and 4.1, we can formulate the discrete Lagrange–D’Alembert principle:

which can be rewritten as

for all variations \(\{\delta x_{k}\}_{k=0}^{N}\) with \(\delta x_{k}\in T_{x_{k}} M\) and δx 0=δx N =0. Also, \(\{\delta W_{k}\} _{k=0}^{N}\) with \(\delta W_{k}\in T_{g_{k}}G\), such that δW k =−η k W k +W k η k+1, \(\{\eta_{k}\}_{k=0}^{N}\) being a sequence of independent elements of \(\mathfrak{g}\) such that η 0=η N =0.

Applying variations in the last expression and rearranging the sum, we finally obtain the complete set of forced discrete Euler–Lagrange equations:

(37)
(38)

with k=1,…,N−1. Since we are dealing with an optimal control problem, we introduce a discrete cost function C d:M×G×M×U×U→ℝ. As in previous cases, our objective is to extremize the following sum:

$$\sum_{k=0}^{N-1}C_{\mathrm{d}} \bigl(x_k, W_{k}, x_{k+1}, u_k^-, u_k^+\bigr), $$

subjected to (37) and (38). Let us initially restrict our attention to the case of fully actuated systems.

Definition 7.1

(Fully Actuated Discrete System)

We say that the discrete mechanical control system is fully actuated if the mappings

are both diffeomorphisms.

According to (37) and (38), we can introduce the momenta by means of the following discrete Legendre transforms:

In the fully actuated case, is possible to find the value of all control forces in terms of x k ,x k+1,W k ,p k ,p k+1,μ k ,μ k+1, that is,

(39)
(40)

Replacing (39) and (40) in C d, we finally obtain the discrete Lagrangian that completely describes our system:

$$\mathcal{L}_{\mathrm{d}}: T^*M\times\mathfrak{g}^{*}\times G\times \mathfrak{g}^{*}\times T^*M\longrightarrow\mathbb{R}. $$

The associated discrete cost functional is

$$ \mathcal{J}_{\mathrm{d}}=\sum_{k=0}^{N-1} \mathcal{L}_{\mathrm {d}}(x_{k},p_{k},\mu_{k},W_{k}, \mu_{k+1}, x_{k+1},p_{k+1}). $$
(41)

As usual, we now take variations in (41) in order to obtain the discrete Euler–Lagrange equations for our optimal control problem (with some abuse of notation we denote \(\hat{Q}_{k}=(x_{k},p_{k},\mu _{k},W_{k},\mu_{k+1}, x_{k+1},p_{k+1})\) the whole set of coordinates in the new phase space):

together with the forced discrete Euler–Lagrange equations (37) and (38).

Typically, actuation is achieved by controlling only a subset of the shape variables. In our setting this can be regarded as underactuation—the mappings in Definition 7.1 become embeddings. If this is the case, it is necessary to introduce constraints and apply constrained variational calculus as in Sects. 3.2 and 4.1.

7.2 Discrete Optimal Control of Nonholonomic Systems

Optimal control subject to nonholonomic constraints such as that in robotic vehicles is considered next. In the following we will expose the theoretical framework, leaving for future research the application to concrete examples.

A controlled discrete nonholonomic system on M×M×G is given by the following quadruple (see Iglesias et al. 2008; Kobilarov et al. 2010 and Ferraro et al. 2008; Jay 2009 for alternative approaches):

  1. (i)

    A regular discrete Lagrangian l d:M×M×G→ℝ.

  2. (ii)

    A discrete constraint embedded submanifold \({\mathcal{M}}_{\mathrm{c}}\) of M×M×G.

  3. (iii)

    A constraint distribution, \({\mathcal{D}}_{\mathrm{c}}\), which is a vector subbundle of the vector bundle \(\tau_{_{TM\times\mathfrak{g}}}:TM\times{\mathfrak{g}}\rightarrow M\), such that \(\dim {\mathcal{M}}_{\mathrm{c}} = \dim{\mathcal{D}}_{\mathrm{c}}\). Typically, there is a relation between the constraint distribution and the discrete constraint, since from \({\mathcal{M}}_{\mathrm{c}}\) we induce for every x∈M, the subspace \({\mathcal{D}}_{\mathrm{c}}(x)\) of \(T_{x} M\times{\mathfrak{g}}\) given by

    $${\mathcal{D}}_{\mathrm{c}}(x)=T_{(x,x,e)}{\mathcal{M}}_{\mathrm{c}}\cap(T_x M\times {\mathfrak{g}}), $$

    where we are identifying \(T_{x} M\times{\mathfrak{g}}\equiv0_{x}\times T_{x}M\times T_{e}G\), with e being the identity element of the Lie group G.

  4. (iv)

    The discrete control forces \(f^{\pm}_{k}: {\mathcal{M}}_{\mathrm{c}} \times U\rightarrow T^{*}M\times{\mathcal{g}}^{*}\) where U⊂ℝm (again, forces \(f_{k}^{\pm}\) split into \(\bar{f}_{k}^{\pm}\) and \(\hat{f}_{k}^{\pm}\) as in the previous section).

We have the following discrete version of the Lagrange–D’Alembert principle for controlled nonholonomic systems:

for all variations \(\{\delta x_{k}\}_{k=0}^{N}\), with δx 0=δx N =0; and \(\{\delta W_{k}\}_{k=0}^{N}\), such that δW k =−η k W k +W k η k+1, with \(\{\eta_{k}\} _{k=0}^{N}\), verifying \((\delta x_{k}, \eta_{k})\in{\mathcal{D}}_{\mathrm{c}}(x_{k})\subseteq T_{x_{k}}M\times{\mathfrak{g}}\) such that η 0=η N =0. Moreover, \((x_{k}, x_{k+1}, W_{k})\in{\mathcal{M}}_{\mathrm{c}}\), k=0,…,N−1 (see Iglesias et al. 2008).

Take a basis of sections \(\{(X^{a}, \tilde{\eta}^{a})\}\) of the vector bundle \(\tau_{{\mathcal{D}}_{\mathrm{c}}}: {\mathcal{D}}_{\mathrm{c}}\longrightarrow M\), where \(X^{a}\in\mathfrak{X}(M)\) and \(\tilde{\eta}^{a}\in\mathfrak{g}\) for \(a=1,\ldots,\mathrm{rank}({\mathcal{D}}_{\mathrm{c}})\). Hence, the equations of motion derived from the discrete Lagrange–D’Alembert principle for controlled nonholonomic systems are:

(42)
(43)

where Ψ α(x k ,x k+1,W k )=0 are the constraints which locally determine \({\mathcal{M}}_{\mathrm{d}}\).

In a more geometric way, we can write (42) and (43) as follows:

where \((x_{k}, x_{k+1}, W_{k})\in{\mathcal{M}}_{\mathrm{c}}\) and \(i_{{\mathcal{D}}_{\mathrm{c}}}: {\mathcal{D}}_{\mathrm{c}}\hookrightarrow TM\times{\mathfrak{g}}\) is the canonical inclusion.

Given a discrete cost function \(C_{\mathrm{d}}: U\times{\mathcal{M}}_{\mathrm{c}}\times U\longrightarrow\mathbb{R}\), the optimal control problem is to minimize the action sum

$$\sum_{k=0}^{N-1} C_{\mathrm{d}} \bigl(u_k^-, x_k, W_{k}, x_{k+1}, u_k^+\bigr), $$

subject to (42) and (43) and to some given boundary conditions. We next distinguish between the fully and underactuated case using the following definition.

Definition 7.2

(Fully Actuated Nonholonomic Discrete System)

We say that the discrete nonholonomic mechanical control system is fully actuated if the mappings

are both diffeomorphisms for all \((x_{0}, x_{1}, W_{1})\in{\mathcal{M}}_{\mathrm{c}}\).

Regarding (42) and its geometric redefinition just below, let us introduce the following momenta:

where both π k and π k+1 belong to \(\mathcal{D}_{\mathrm {c}}^{*}\). In the fully actuated case, the value of all control forces can be completely determined in terms of x k ,x k+1,W k ,π k ,π k+1, where the coordinates (x k ,x k+1,W k ) always belong to \({\mathcal{M}}_{\mathrm{c}}\). Therefore, we can re-express the cost function in terms of these variables and, consequently, derive the discrete Lagrangian

$${\mathcal{L}}_{\mathrm{d}}: \bigl({\mathcal{D}}_{\mathrm{c}}^*\bigr) {}_{\tau_{{\mathcal{D}}_{\mathrm{c}}^*}}{\times}_{{pr_1}} ({\mathcal{M}}_{\mathrm{c}}) {}_{pr_2}{\times}_{\tau_{{\mathcal{D}}_{\mathrm{c}}}^*} \bigl({\mathcal{D}}_{\mathrm{c}}^*\bigr) \rightarrow\mathbb{R}, $$

where \(pr_{i}: {\mathcal{M}}_{\mathrm{d}}\subseteq M\times M\times G\rightarrow M\) are the projections onto the first and second arguments and \(\tau_{{\mathcal{D}}_{\mathrm{c}}^{*}}: {\mathcal{D}}_{\mathrm{c}}^{*}\rightarrow M\) the canonical projection.

Observe that we can consider this case as a constrained discrete variational problem taking an extension

$$\widetilde{{\mathcal{L}}_{\mathrm{d}}}: {\mathcal{D}}_{\mathrm{c}}^*\times G \times{\mathcal{D}}_{\mathrm{c}}^*\rightarrow\mathbb{R} $$

of \({\mathcal{L}}_{\mathrm{d}}\) subjected to the constraints Ψ α(x k ,x k+1,W k )=0.

Therefore, denoting \(\hat{Q}_{k}=(x_{k},\pi_{k},W_{k},x_{k+1},\pi_{k+1})\) as the whole set of coordinates of the new phase space \({\mathcal{D}}_{\mathrm{c}}^{*}\times G \times{\mathcal{D}}_{\mathrm{c}}^{*}\), we deduce that the equations of motion are

where \(\lambda_{\alpha}^{k}\) are the Lagrange multipliers of the new constrained problem. The underactuated case can be handled by adding new constraints and applying discrete constrained variational calculus similarly to Sect. 4.

Finally, note that these constructions can be simplified by expressing the optimal control problems more compactly through the Lie groupoid framework (Marrero et al. 2006), which naturally generalizes the systems studied in this paper such as vector spaces, Lie groups, and principal bundles. In particular, the examples studied in this paper can be equivalently modeled using Lie groupoid techniques (Jiménez and Martín de Diego 2010) adapted to our proposed formalism. Future work will explore these connections.

8 Conclusions

This paper develops numerical methods for optimal control of Lagrangian mechanical systems defined on tangent bundles, Lie groups, trivial principal bundles, and nonholonomic systems. The proposed approach preserves the geometry and variational structure of mechanics through the discretization of the variational principles on manifolds. The key point is to solve the optimal control through discrete mechanics, i.e., by formulating the optimization as the solution of an action principle of a higher dimensional system in a new Lagrangian phase space: T ∗ Q×T ∗ Q in the general case and \(\mathfrak{g}^{*}\times G\times\mathfrak{g}^{*}\) in the Lie group case. The optimal control algorithm is then derived as a variational integrator subject to boundary conditions. We thus expect that both the dynamics and optimal control solutions will have accurate and stable numerical behavior (due to symplectic-momentum preservation), even at large time steps (which allows for improved run-time efficiency).

Simulations of an underactuated underwater vehicle illustrate an application of the method. Yet, further numerical studies and comparisons are necessary to exactly quantify the advantages and the limitations of the proposed algorithm. An important future direction is thus to study the convergence properties of the optimal control system. Convergence for general nonlinear systems is a complex issue. In this respect, it is interesting to note that the discrete mechanics and optimal control on Lie groups such as those used in the example in Sect. 6 using the Cayley map result in a polynomial form without further approximation or Taylor series truncation. A useful future direction is then to study the regions of attraction of the numerical continuation using tools from algebraic geometry.

More generally, the theoretical framework introduced in Sect. 7 can serve as a basis for deriving algorithms for control systems such as multi-body locomotion systems or robotic vehicles with nonholonomic constraints. Furthermore, the developed classes of systems can be unified through the recently developed groupoid framework (Weinstein 1996; Iglesias et al. 2008; Martínez 2007). Each of the considered product spaces (e.g., Q×Q) can be regarded as a single groupoid space with equations of motion resulting from a single generalized discrete variational principle. This will enable the automatic solution of optimal control problems for various complex systems and a convenient unified framework for implementing practical optimization schemes such as (Ober-Blöbaum et al. 2011; Bloch et al. 2009; Lee et al. 2006; Kobilarov and Marsden 2011). More importantly, this viewpoint can be used to apply standard discrete Lagrangian regularity conditions (e.g., Marsden and West 2001) to optimal control problems evolving on the groupoid space. This would provide a deeper insight into the solvability of the resulting optimization schemes.