Optimizing case-pack sizes in the bricks-and-mortar retail trade

Abstract

Before reaching the store, products generally flow through the retail distribution system as larger bundles, the so-called case packs (CP). In several studies these case packs have been identified as having a significant impact on distribution logistics efficiency. In this paper we develop a quantitative model and solution approach determining optimal case-pack sizes for non-perishable products in grocery retailing. The model captures the relevant operative cost drivers along the internal supply chain of a large bricks-and-mortar retailer. It explicitly represents each day of the retailer’s business week, where the replenishment doctrine considered generalizes the well-known periodic review reorder point (r, s, nq) policy as a stationary cyclic version. Exact and approximate methods are developed to evaluate the costs of a model instance. In addition, an optimization procedure is outlined that uses either exact or approximate methods to identify optimal and near-optimal CP sizes for a single store as well as for a network of multiple stores to be operated with one common CP. Applied to real-world examples of a large European retail chain, the methods reveal average cost improvement potential of more than 20% by adjusting the CP sizes that are currently in use. The approach presented is thus shown to be a valuable addition to any integrative retail supply chain planning system. Its results are directly applicable to retail practice.

1 Introduction

European bricks-and-mortar grocery retail companies are operating in an ever more competitive environment. This is mainly the result of two market trends. First, consumers are increasingly expecting higher standards. Second, persistent market consolidation can be observed in the grocery sector. This leads to better purchasing conditions for retailers, resulting in lower retail sales prices, which again intensifies competition (McCarthy-Byrne and Mentzer 2011; Kuhn and Sternbeck 2013). In such a market environment, retail operations efficiency plays an important role in surviving and operating profitably in a market with traditionally low margins. The topic of this study, i.e., the optimization of case-pack sizes, is one of the promising options for further increasing operational efficiency in grocery retailing.

Products offered by a grocery retailer generally flow through the associated supply chain in larger product bundles, i.e., shipping units or case packs (CP). These case packs are then unpacked in the stores, and the consumer units (CU) inside are stacked onto the shelf.

A well-designed case pack facilitates the handling of multiple consumer units in the supply chain and protects the products during picking and transportation (Broekmeulen et al. 2017). The case-pack size, i.e., the number of consumer units bundled in one case, also determines the minimum order quantity of a stock keeping unit (SKU) ordered by a store at the distribution center (DC) and consequently defines the frequency with which an SKU is part of a store order. Furthermore, case-pack size affects the instore inventory level. Defining case-pack sizes thus becomes a highly relevant planning problem in modern grocery retailing that impacts warehouse operations and especially instore logistics (Ketzenberg et al. 2002; Wen et al. 2012; Kuhn and Sternbeck 2013). Decisions on case-pack sizes should therefore be considered on a strategic level, or at least on a tactical decision level (Hübner et al. 2013).

The aim of the present study is to create an analytical framework that captures the relevant cost drivers along the internal supply chain of a large grocery retailer and to provide quantitative decision support for identifying case-pack sizes that maximize the overall efficiency of operational processes. This study considers the relevant subsystems of a grocery retail chain, i.e., distribution center (DC), transportation system and instore logistics system. The main focus is on analyzing instore processes, which are generally recognized to be most affected by the case-pack size in use. The optimization approach identifies the optimal case-pack size of a product offered by the retailer. This is done both from the perspective of a single store and from the perspective of all stores of the retail chain. In grocery retailing the most common strategy applied is “one case-pack size for all stores” (Sternbeck 2015).

The paper is organized as follows. In Sect. 2 we refer to the empirical literature and studies to outline the main cost drivers of logistics processes and describe the kind of system that we examine. In Sect. 3 we present the literature that relates to the decision problem considered and outline the contribution of the paper. The insights of Sect. 2 are then organized and contextualized into an analytical model in Sect. 4. We elaborate an exact and an approximate method to solve the analytical evaluation problem (Sects. 5.1,  5.2), and develop an efficient procedure to identify case-pack sizes that minimize logistics costs (Sect. 5.3). The developed approaches are applied in an empirical study on a real-world data set. The results are presented in Sect. 6. Finally, Sect. 7 concludes our study and gives an outlook on further avenues of research.

2 Problem description

Modern grocery retailers distribute the majority of their product volumes to their stores via distribution centers. In some cases, cross-docking and direct-to-store delivery are also used, but these concepts play a subordinate role in grocery retailing (Fernie et al. 2010; Kuhn and Sternbeck 2013). In general, European grocery retailers—including discounters and full-line supermarkets—operate their own distribution networks consisting of central and/or regional DCs from which stores are supplied with their complete assortment. We therefore concentrate our analysis on this distribution structure, which is a widespread network model, even applied by other retail branches in Europe (Fleischmann 2016). Product distribution via DC consists of three relevant subsystems: DC operations, transportation and store operations. Figure 1 illustrates the main associated processes (Sternbeck and Kuhn 2014). These subsystems are analyzed in the following to identify relevant cost drivers affected by the size of a case pack.

Fig. 1

Subsystems of grocery retail networks

2.1 DC operations

The subsystem DC comprises all processes that are carried out in the DC, i.e., receipt of goods, storing products, order picking, and shipping (de Koster et al. 2007). In terms of operational DC costs these subsystems account for roughly a quarter of the entire grocery retailers’ operational logistics costs (van Zelst et al. 2009; Kuhn and Sternbeck 2013). The picking and packing processes are highly affected by case-pack sizes. Here, case packs and individual products are picked onto roll cages, pallets or into reusable boxes according to store orders. Picking generally is considered the most costly activity in a DC, accounting for approximately 55% of operational DC expenses (Rouwenhorst et al. 2000; de Koster et al. 2007). Depending on the size of the picking unit, two main picking systems are of particular relevance for retail practice:

• (a) Larger cartons and boxes are generally stored on pallets in racks, from which they are brought to dedicated picking places and manually picked according to the worker-to-parts principle. The picking and packing processes are nowadays partly supported by automatic tray building, automatic palletizing (parts-to-robots), and foil shrinking. However, manual systems are still very dominant in retail practice, and are assumed in our study.

• (b) Small product units and single consumer units are stored on flow racks or in highly automated storage-and-retrieval systems. The latter system in particular enables the picking process to follow the parts-to-worker principle with a dynamic product provision at the picking places. Single and small product units are usually packed into reusable boxes that circulate between the DC and the stores.

Typically, we find that case packs supplied by manufacturers are cartons and boxes containing several consumer units and stored on pallets. However, a case pack may also consist of only one single consumer unit. Under these circumstances, it could be considered whether several units of the specific product should be bundled at the DC due to efficiency reasons.

In our study we focus on a manual picking system as described in (a). DC picking costs for case packs can be distinguished by a fixed portion per store order and variable portion per individual pick. Assuming a given delivery schedule, i.e., a specific frequency with which a store receives deliveries from the warehouse (Sternbeck and Kuhn 2014; Holzapfel et al. 2016), the fixed picking costs are unaffected by the size of a case pack, but the variable portion is affected. Given a constant product demand volume, the case-pack size influences the number of cases that have to be picked from the product’s picking place in the warehouse. The number of case packs demanded per period therefore influences the picking costs incurred at the DC.

2.2 Transportation

The transportation subsystem summarizes all the processes that are necessary for bridging the geographical distance between DCs and stores. In grocery retailing, internal transportation networks are characterized by a few origins (DCs) and numerous destinations (stores). Generally, transportation between DCs and stores accounts for roughly 25% of grocery retail logistics costs (van Zelst et al. 2009; Kuhn and Sternbeck 2013).

Transportation costs are mainly driven by fixed costs resulting from the delivery schedule chosen and the possibility of bundling store deliveries into one delivery tour (Sternbeck and Kuhn 2014; Holzapfel et al. 2016). The size of a case pack, however, may possibly influence the packaging density of an outbound pallet or roll cage, which influences the freight space and number of delivery tours required to fulfill all store orders. External carriers are usually paid per tour and/or per pallet or roll cage.

Varying its size will change the volume of an individual case pack. The question thus arises whether the packaging density, i.e., the utilization of a transport pallet, is influenced by the volume size of different case packs stacked up on a pallet. In an accompanying unpublished study we therefore analyzed the dependence of the packaging density of pallets on case-pack size for a sample of 398 mixed pallets containing 6227 different SKUs packed in cases of 3921 different volumes. The sample set originates from the case company of the present study and contains pallets loaded to the maximum and delivered from the DC to three different stores during the time horizon of December 2015 to April 2016. We formulated a linear regression model with case-pack size and case-pack volume as exogenous variables and pallet utilization as an endogenous variable. The regression analysis on the given sample set shows a weak correlation between case-pack volume and pallet utilization. The utilization of a pallet can be increased by 0.0043% if the case-pack volume is increased by 1 l. However, this result is barely significant (significance level: 1% $\le p\le$ 5%). In the present study we therefore assume that transportation costs are unaffected by modifying the case-pack size of a single product.

2.3 Instore operations

Nearly 50% of the entire logistics costs in grocery retailing occur in the outlets of a retail company (Simons et al. 2005; van Zelst et al. 2009; Kuhn and Sternbeck 2013). This is due to the high manual handling effort when placing the associated roll cages or pallets in front of a shelf, opening case packs, stacking consumer units onto the shelf, and restocking the shelf with products from the backroom that do not fit onto the shelf during the initial shelf-filling process. Convinced of their high impact, researchers have increasingly investigated instore operations in the recent past (see Reiner et al. 2012; Eroglu et al. 2013; Atan and Erkip 2015, for example), and this is often considered the operational subsystem with the largest cost savings potential within retail networks nowadays. Figure 2 illustrates the relevant instore process chain.

Fig. 2

Instore operations process chain

The first activity in the store is filling the shelf with the products delivered from retail DCs. Each case pack on the loading carrier results in efforts related to identifying, searching for and handling products. Store employees grab the case from a pallet or a roll cage and identify the SKU. After that, the right slot on the shelf has to be found and the slot is filled either until the space is exhausted or all units of the case are stocked.

When the new deliveries do not fit onto the shelves, the so-called overflow inventory (Eroglu et al. 2013) has to be brought into the store’s backroom and stored temporarily until more shelf space becomes available due to consumer purchases.

The case-pack size impacts restocking from the backroom in two ways. First, the number of overflow events at the time of initially stacking products on the shelf, which were just received from the DC, is affected as the case-pack size impacts product delivery frequency. Second, the number of items that do not fit onto the shelf during this initial shelf stacking process are of course also dependent on the case-pack-size and determine the number of consumer units that take the way via the backroom onto the shelf.

Overflow products are considered the source of several problems. First, there are costs for the handling processes that have to be carried out, mainly internal instore transportation, sorting and searching, backroom management, and restocking activities (Eroglu et al. 2013). Second, backroom inventory and handling increase the operational complexity, which may result in inventory inaccuracy leading to decreasing store order quality (Raman et al. 2001a, b; DeHoratius and Raman 2008; DeHoratius and Ton 2015). That is why, third, backroom usage may also lead to higher out-of-shelf rates (Ehrenthal and Stölzle 2013; Gruen et al. 2002). The process of restocking the shelf from the backroom is typically organized in two different ways:

• (a) Restocking from the backroom is only carried out outside store hours, e.g., at the end of a sales day or in the morning before the shop opens (van den Berg et al. 1998; Broekmeulen et al. 2017). We denote this restocking process “offline instore replenishment.” A retailer may prefer restocking shelves from the backroom outside store hours to avoid the disruption for customers and regular staff. If special shelf-stackers are employed for stacking the delivery from the DC, another advantage of this mode is that they can also attend to the backroom restocking activities and relieve the regular staff of those. However, the disadvantage is that backroom inventories are out of reach during store hours, which has to be accounted for when dimensioning the shelf space allocated to a product in order to guarantee a sufficient service rate.

• (b) Restocking from the backroom is carried out during store opening hours, i.e., at any time before the stock on the shelf is depleted. This restocking process is denoted “online instore replenishment.” In this case the regular staff frequently transfer backroom stock to the shelf during opening hours, avoiding the situation where a product is in the store but not on the shelf, i.e., “phantom products” (DeHoratius and Ton 2015). This approach creates more effort than the “offline instore replenishment” approach, but a higher service level can be achieved with lower overall stock.

The case company practices the “online instore replenishment” approach. We therefore assume this instore restocking policy in the current study and additionally assume that “phantom products” can always be avoided.

Regarding the general store replenishment policy applied, we consider the case that time and dimensioning of replenishments is decided on by an automated system applying a replenishment policy on forecasts based on historic data. For ambient products, such systems typically use a generalized version of the well-known (r, s, nq) policy tailored for the special requirements of retail distribution (Kuhn and Sternbeck 2013). The original policy is discussed in textbooks such as Hadley and Whitin (1963), Zipkin (2000), Axsäter (2006) and more recently Tempelmeier (2011). In the retail environment, the original policy is generalized with regard to considering subperiods, e.g., days of the week, which may exhibit varying customer demand and serve as an underlying demand pattern for the replenishment process (Broekmeulen and Donselaar 2009; van Donselaar and Broekmeulen 2008). In particular, retail systems may be replenished at unequal intervals, i.e., on certain days of a week, e.g., on Monday and Friday. Typically, these delivery patterns are externally predetermined (Sternbeck and Kuhn 2014; Holzapfel et al. 2016).

We consider a cyclic version of the (r, s, nq) policy that works as follows. Replenishment orders may be placed to the DC on a subset of weekdays or even on all of them if it is a large store. At the end of each reorder period, the system checks whether the relevant inventory has dropped to or below the reorder point s, which can differ from subperiod to subperiod in our setting. If so, the system will order n case packs of size q so as to raise the relevant inventory above s, but strictly below $s+q+1$.

From the instore perspective two more relevant aspects can be derived from the application of this replenishment policy described with regard to the case-pack size applied. First, overall instore inventory, i.e., on the shelves and in the backroom, is dependent on the case-pack size. This is relevant as capital tied in inventories and the necessary space induce costs. Second, the case-pack size impacts the supply frequency of a product within the predetermined store delivery pattern. Assuming an online instore replenishment process this in turn impacts the number of periods in which instore inventory is close to a minimum stock level or has even undershot it. It is desirable to always have this minimum stock level on the shelves, even just before new deliveries arrive. We denote this “display stock” that is intended to ensure a nice optical impression of the shelf for the customers. The extent to which insufficient display stock is available is dependent on the case-pack size.

3 Literature

In this section, we first review the literature that explicitly focuses on the retail problem of selecting appropriate case-pack sizes. Second, we review the methodological literature to examine whether theoretical models can help us with the design of a solution approach.

Zheng and Chen (1992) are one of the rare publications considering the optimal base order quantity, i.e., case-pack size q, of an $(r=1,s,nq)$ policy. They assume that s and q are decision variables and develop an efficient algorithm that minimizes inventory holding, backorder and ordering costs. However, they assume unlimited backlogging and stationary demands which contradicts the relevant circumstances in our case. In addition, certain logistics cost drivers, e.g., backroom activities, are not reflected.

Optimal ship pack sizes from the perspective of the entire internal retail supply network—consisting of DCs, transportation and stores—have been studied by Wen et al. (2012). The authors develop a cost minimization model for the discrete selection of packaging units within the packaging hierarchy offered by suppliers, i.e., the selection between cases (supplier shipping box), inners (subpackaging, when applicable) or customer units. Seven cost components are included in the model derived: fixed store order costs, DC costs of replenishing the picking area, DC picking costs, store receiving costs, store extra handling costs of overflow inventory, and store and DC inventory costs. With regard to our approach, instore operations are only reflected in very general terms.

Considering the instore perspective, Sternbeck (2015) develops an approximate model to determine appropriate case-pack sizes based on a cost model that integrates fixed and variable initial stacking costs, restocking costs from the backroom and inventory holding costs. The approach is based on classical approaches to the analysis of the (r, s, nq) inventory policy without taking into account the subperiod structure of the problem that we examine. In its context, the paper generates relevant insights into how case-pack sizes affect instore operations and how retailers could set case-pack sizes appropriately.

Broekmeulen et al. (2017) develop a planning approach that considers the question of where to unpack case packs: at the stores or at the DC. They assume stationary (r, s, nq) and (r, s, S) replenishment policies when unpacking at the stores or at the DC, respectively. In the case of an (r, s, nq) policy, they also include an approximate method for optimizing parameter q, which corresponds to the case-pack size considered in the present study. Since their main focus is on determining the optimal unpacking location, they assume a classical stationary inventory policy that disregards weekly seasonal effects.

Regarding the literature on general inventory theory, the periodic review reorder point (r, s, nq) policy was first studied by Hadley and Whitin (1963), who also connect it to the more elementary policies of the periodic review order-up-to and continuous review reorder point policy. While many works since then have considered the latter two policies, less attention has been paid to the (r, s, nq) policy in spite of its wide application in retail replenishment systems. Customer waiting times as an important performance indicator are analyzed by Kiesmüller and de Kok (2006) and also by Tempelmeier and Fischer (2010) for (r, s, nq) systems with different specific assumptions. Regarding costs, Larsen and Kiesmüller (2007) determine optimal s levels when r and q are given, and Shang and Zhou (2010) suggest heuristic and optimal procedures to configure all three policy parameters.

Our contribution to the existing literature is as follows. We present what is to our knowledge the first coherent framework to systematically quantify the impact of case-pack sizes on the most important cost drivers along the internal supply chain of a grocery retailer. The problem we discuss is most closely related to the problem of finding optimal case packs that Broekmeulen et al. (2017) solve as a subproblem within the larger context of identifying optimal unpacking locations. Our approach differs in three ways. Firstly, we focus on the problem itself and model the related cost factors in greater detail. Secondly, we consider weekly delivery schedules instead of static replenishment frequencies. To our knowledge, no theoretical study has so far considered a replenishment policy that distinguishes subperiods within a planning cycle. Finally, we develop exact analytical formulae and a nonlinear optimization procedure that ensures that the optimal case-pack size for an individual product for a single store and the optimal common case-pack size for a network of multiple stores can be found, reflecting a “one case-pack size for all stores” strategy.

4 Analytical model

In Sect. 2 we described logistics processes and identified general cost drivers influenced by the case-pack size of a product along the internal supply chain of a retailer. We identified the picking effort at the DC, explained why transport costs can be considered independently from case packs, and finally concluded that the main effort—backroom activity, overall inventory (sales and backroom), shelf stocking and restocking as well as undershoot of display stock—occurs within the stores. In this section we develop a formal model that covers these cost drivers in order to quantify the logistics costs of operating a particular case-pack size. From the perspective of decision making, all these cost drivers are affected by the store’s replenishment system. We have therefore put our focus on the stores and particularly on the inventory system that triggers replenishment orders to the DC, and determine all relevant costs from that. Sections. 4.1, 4.2 and 4.3 thus describe the physical instore inventory system and the general replenishment process, the sequence of events and decisions and finally the replenishment policy. This defines the inventory model of the real system. The decision-relevant cost drivers are specified from that model in Sect. 4.4. This allows us to define the entire logistics cost function.

As mentioned above, many products and also entire stores exhibit significant weekly demand seasonality. Furthermore, stores are typically replenished according to weekly reorder patterns that may differ from equidistant intervals. These reorder patterns result from a compromise between DC and store wishes for less frequent or very frequent deliveries while balancing the workload at the DC. We assume that they are externally predetermined (Sternbeck and Kuhn 2014; Holzapfel et al. 2016). To properly cover this kind of delivery process, we analyze our system as a stationary cyclic model where we explicitly address each period of the week $p \in P$.

The upcoming model development uses the notation as listed in Table 1.

Table 1 Notation

4.1 Inventory system outline

The physical outline of the store inventory system is as follows. Products are presented to the customers on a shelf with limited shelf space sp. Supply that does not fit onto the shelf is taken to the backroom.

We assume that the backroom’s storage capacity is not limited in the sense that the store would be forced to send back excess CUs to the DC. We consider that it is always possible to accommodate the whole delivery in the store, either on the shelf of the sales room or in the backroom area. Scarce backroom capacity is reflected by high backroom inventory cost factors in our approach to encourage more frequent replenishment of a store with smaller quantities. In addition, we assume that the staff will frequently transfer backroom stock to the shelf during opening hours, preventing a product from being in the store but not on the shelf. The service goal is to fulfill a specific shelf availability of a product. Shelf availability $\alpha$ is quantified as the minimum probability that the inventory level I of a product is equal to or above a certain display stock, ds, on the shelf at the end of any period, $\alpha = \min \{\alpha _\mathrm{p}| p \in P: \max \{\alpha ^{\star }_\mathrm{p} | \alpha ^{\star }_\mathrm{p} \le {\text {Pr}}(I_\mathrm{p} \ge ds)\}\}$. The display stock is regularly set for presentation purposes, but it also has an effect as (additional) safety stock since it is of course also used to satisfy customer demand. If even the display stock is exhausted, we assume that customer demand will be lost (lost-sales assumption).

4.2 Sequence of events

Figure 3 depicts the sequence of relevant events in each period. Firstly, outstanding replenishment orders arrive. Secondly, customer demand occurs and eventually existing backroom inventory is used to restock the shelf. Finally, replenishment orders are issued. Note that arrivals and issues of orders may not occur in each period.

Fig. 3

Sequence of events within a period

4.3 Replenishment policy

4.3.1 Process

The underlying replenishment process can be modeled as a generalized (r, s, nq) policy. In the original version, an order may be issued every r periods, where the basic order quantity q is ordered n times to increase the current inventory position ip above s, where $n = \min \{n^{*}| ip + n^{*}\cdot q > s\}$, i.e., the smallest available amount is ordered in each order issue period that will raise ip to at least the level $s+1$. The inventory position ip is yielded by the physical inventory plus the volume of outstanding orders. While r and s are integer or real numbers in the original version, they are replaced in our model by an order issue period indication vector $R=(r_1, r_2,\ldots , r_{|P|}), r_\mathrm{p} \in \{0,1\}$ and a reorder point vector $S=(s_1, s_2,\ldots , s_{|P|}), s_\mathrm{p} \in {\mathbb {Z}}^{+}$ to allow for specific order patterns during the weekly cycle. For example, if the store can issue replenishments on Monday, Wednesday and Saturday, this leads to $R=(1,0,1,0,0,1)$ in a 6-day week starting with a Monday with corresponding order levels S that are individually calculated, as described in Sect. 4.3.2. Parameter q corresponds to the case-pack size and lead times also take on the form of a vector $L=(l_1, l_2, \ldots , l_{|P|})$. Finally, we also track the demand $D=(D_1, D_2, \ldots , D_{|P|})$ down to a pattern level, where we assume that the demand distribution of each period $D_\mathrm{p}$ is independent of the others. The inventory position in period $p, \mathrm{IP}_\mathrm{p}$ in our case is defined by the sum of the physical inventory $I_\mathrm{p}$ plus the volume of outstanding orders $O_\mathrm{p}$, i.e., $\mathrm{IP}_\mathrm{p}=I_\mathrm{p}+O_\mathrm{p}, p \in P$.

4.3.2 Parameter setting

We assume that the replenishment vector R is an external input that will be specified in a superordinate planning step. Parameter q will be a subject of our analysis. The parameter vector S is set such that the predefined service level $\alpha$ will at least be reached at the end of an order cycle. We neglect the influence of q on the service level realized and configure the system so as to meet a ready-rate criterion based on the display stock for the special case of $q=1$. We do so for the following reasons. Firstly, it leads to a clearer presentation and allows us to focus on the influence of q with an entirely predefined replenishment policy. Secondly, this approximation is common practice within contemporary inventory management software systems and allows transparent extension of the factors that should be considered in the safety stock determination. Finally, it is also used within the system underlying the empirical study presented in Sect. 6.

Let $p^\mathrm{c}$ be the replenishment period for which we want to configure $s_{\mathrm{p}^\mathrm{c}}$. Let $p^\mathrm{i}$ be the next replenishment period and $p^{\mathrm{a}} = p^\mathrm{i} + l_{\mathrm{p}^\mathrm{i}}$ be the period when an order issued in $p^\mathrm{i}$ will arrive. Ordering in $p^\mathrm{c}$ will raise the inventory position to $s_{\mathrm{p}^\mathrm{c}}+1$ according to the above definition of the replenishment policy. The display stock in period $(p^{\mathrm{a}}-1)$ is undershot if the demand from $p^\mathrm{c}$ to $p^{\mathrm{a}}-1 (D_{[\mathrm{p}^\mathrm{c}, \mathrm{p}^{\mathrm{a}}-1]})$ exceeds $s_{\mathrm{p}^\mathrm{c}}+1-ds$. Since replenishment orders arrive before demand may occur, period $p^{\mathrm{a}}$ belongs to the next order cycle and is not considered here. We therefore set $s_{\mathrm{p}^\mathrm{c}}$ according to $s_{\mathrm{p}^\mathrm{c}} := \min \{s^{*}| {\text {Pr}}( D_{[\mathrm{p}^\mathrm{c}, \mathrm{p}^{\mathrm{a}}-1]} \le s^{*}+1-ds ) = \alpha \}$.

4.4 Logistics cost drivers

Following the studies summarized in Sect. 2, we consider the following five cost factors to quantify the logistics impact of a case-pack size, where a single product within a specific store underlies our definition. All five cost drivers are vectors of random variables in our analytical model, which can significantly deviate between different periods of the week.

• Physical inventory (I) in the store at the end of a period

• Undershoot of display stock (U) in the store at the end of a period

• Backroom inventory (B) in the store at the end of a period

• Backroom activity (A) in the store at the beginning of a period

• Number of case packs (H) that arrive at the store at the end of the lead time and that have left the DC at the beginning of the lead time

We associate the cost drivers with the following cost factors.

• Physical inventory holding costs ($c_\mathrm{i}$) per period that a consumer unit is held in the store, i.e., the cost of capital that is tied up in products and the proportional costs for storage space.

• Undershoot costs ($c_\mathrm{u}$) per period if one consumer unit is missing on the shelf to ensure an attractive appearance in the salesroom that generates a favorable shopping atmosphere (see Abbott and Palekar 2008).

• Backroom inventory handling costs ($c_\mathrm{b}$) for variable backroom handling efforts per period and consumer unit, especially the positioning and sorting of items, and taking them to the sales room when needed. It is assumed that the inventory is refilled whenever free space is detected on a shelf and products are still available in the backroom (see Sect. 2.3). The costs thus account for repeatedly removing consumer units from the backroom to restock the shelves.

• Backroom activity costs ($c_\mathrm{a}$) per event for intermediate storage of consumer units in the backroom area, i.e., conveying excess supply to the backroom (event driven).

• Handling costs ($c_\mathrm{d}$) per case pack at the DC for searching, taking it from storage and safely packing it on the transportation pallet.

• Handling costs ($c_\mathrm{s}$) per case pack in the store for searching, picking and putting it on the shelf, either as a whole or a fraction of the case pack.

A decision maker will typically want to focus on an aggregated total logistics cost figure that is to be expected when a certain configuration is used. We therefore define the expected logistics costs (C) as the sum of expectations over all periods of the week weighted with their cost factors, where we set $c_\mathrm{h}:=c_\mathrm{d}+c_\mathrm{s}$ as the combined handling cost factor:

$$\begin{aligned} C = \sum _{p \in P} [ c_\mathrm{i} \cdot {\text {E}}\{I_\mathrm{p}\} + c_\mathrm{u} \cdot {\text {E}}\{U_\mathrm{p}\} + c_\mathrm{b} \cdot {\text {E}}\{B_\mathrm{p}\} + c_\mathrm{a} \cdot {\text {E}}\{A_\mathrm{p}\} + c_\mathrm{h} \cdot {\text {E}}\{H_\mathrm{p}\} ] \end{aligned}$$

(1)

Note that although we assume the lost-sales case, Eq. (1) does not explicitly contain lost-sales costs. We consider these costs included in the costs of having insufficient display stock, where we assume that effects similar to those associated with the occurrence of lost sales are already induced by the lack of display stock.

In addition, note that the cost function only involves the decision-relevant costs. It does not reflect the entire logistics costs. The costs of stacking individual CUs onto the shelf, for example, are not included since these costs occur independently of the size of a case pack chosen.

5 Solution approach

Within this section we develop a solution approach to determine the optimal case-pack size that minimizes the expected logistics costs as defined in Eq. (1). The optimization approach requires an evaluation of the individual cost drivers and then quantification of the entire expected costs given a certain case-pack quantity. With this in mind, two approaches are developed: first a Markov chain approach providing exact results (see Sect. 5.1) and second a fast approximation approach based on principles of inventory theory (see Sect. 5.2).

Section 5.3 then describes the optimization routine that applies the alternative evaluation approaches developed.

5.1 Exact Markov chain approach

5.1.1 States

To evaluate the cost drivers for a particular system configuration, i.e., the size of a case pack, the shelf space and the replenishment policy assumed, we need to know the current period of the week (p), the physical inventory ($I_\mathrm{p}$) at the end of a period, and the number of product units ($O^{1}_\mathrm{p}, O^{2}_\mathrm{p},\ldots$) that will arrive in 1, 2, ...periods. These three elements completely describe the state of the inventory system for our purposes, since we can derive the relevant cost drivers as follows:

• Physical inventory $I_\mathrm{p}$ is one of the three variables for describing a system state.

• Amount of stock that undershoots the display stock is designated by $U_\mathrm{p} := \max \{0, ds-I_\mathrm{p}\}$.

• Backroom inventory is designated by $B_\mathrm{p} := \max \{0,I_\mathrm{p}-sp\}$.

• Backroom activity $A_\mathrm{p}$ is 1 (i.e., occurring) in an order arrival period if $I_{p-1}+O^{1}_{p-1}>sp$ in the previous period, and 0 otherwise. For reasons of simplicity we identify the backroom activity in the period right before it takes place, since the event is predetermined at the end of the previous period.

• Case packs $H_\mathrm{p}$ arriving in an order arrival period is quantified by $\frac{O^{1}_{p-1}}{q}$.

Thus, the relevant states of the discrete Markov chain are denoted by all possible tuples $(p,i,o^{1}, o^{2},\ldots )$, with p representing the current period of the week, i the physical inventory level, and $o^{1}, o^{2},\ldots$ the amount of outstanding orders that will arrive in the next periods. Knowing the probability distribution of the state space means the cost drivers defined above can be quantified.

5.1.2 Transitions

As time shifts from one period to the next, three types of event change the state of our system: (A) replenishment orders arrive, (B) customer demand materializes (this is the only probabilistic event, where its effect can also be neutral if demand is zero in a period), and (C) a replenishment order is issued. While demand may occur in every period, the other two events only occur at specific periods, depending on the predefined replenishment vector, R, and the given lead time vector L. Four types of transition therefore result, where $p_2$ denotes the next period after $p_1$ either in the same or the next week:

• Nothing but demand can occur [-,B,-]: State $(p_1,i,0, o^{2},\ldots )$ will change to $(p_2,\max \{0,i-d\},o^{2},\ldots )$ with probability ${\text {Pr}}(D_2=d)$.

• Replenishment orders arrive and demand can occur [A,B,-]: State $(p_1,i,o^{1}, o^{2},\ldots )$ will change to $(p_2,\max \{0,i+o^{1}-d\},o^{2},\ldots )$ with probability ${\text {Pr}}(D_2=d)$.

• An order with lead time l is issued and demand can occur [-,B,C]: State $(p_1,i, 0, o^{2},\ldots , o^{l},\ldots )$ will change to $(p_2,\max \{0,i-d\},o^{2},\ldots , o^{l}+o^{*},\ldots )$ with probability ${\text {Pr}}(D_2=d)$, where $o^{*} = n\cdot q, \; n = \min \{n^{*}| i_2 + n^{*}\cdot q \ge s_{p_2}\}$ with $i_2=\max \{0,i+o-d\}, o$ the total amount on order without $o^{*}$.

• An order is issued, replenishment orders arrive and demand can occur [A,B,C]: State $(p_1,i, 0, o^{2},\ldots , o^{l},\ldots )$ will change to $(p_2,\max \{0,i+o^{1}-d\},o^{2},\ldots , o^{l}+o^{*},\ldots )$ with probability ${\text {Pr}}(D_2=d)$, where $o^{n} = n\cdot q, \; n = \min \{n^{*}| i_2 + n^{*}\cdot q \ge s_{p_2}\}$ with $i_2=\max \{0,i+o-d\}, o$ the total amount on order without $o^{*}$.

5.1.3 State space

An upper bound of the number of relevant states can be estimated as follows. Clearly, we have |P| periods, which will in general be six or seven, i.e., store opening days during a week. Inventory levels in an (r, s, nq) system cannot exceed $s+q$, which is the maximum for the inventory position. In our system, we need to consider $s_{\text {max}} = \{\min s^{*}|s^{*} \ge s_\mathrm{p} \; \forall \; p \in P\}$. This also quantifies the maximum order size $(n\cdot q)$, since we consider the lost-sales case that implies a maximum of $\lfloor \frac{s_{\text {max}}+q}{q} \rfloor$ case packs that can be reordered via a single replenishment. It is required to track replenishment orders along their lead time, i.e., up to for $l_{\text {max}}:=\max \{l_\mathrm{p} \in L\}$ periods. Considering inventory levels as well as order amounts may also be zero, we can state $UB = |P| \cdot (s_{\text {max}}+q+1) (\lfloor \frac{s_{\text {max}}+q+1}{q} \rfloor )^{(l_{\text {max}})} \le |P| \cdot \frac{(s_{\text {max}}+q+1)^{(l_{\text {max}}+1)}}{q}$ as an upper bound to the number of states that we have to consider.

5.1.4 Example

Figure 4 illustrates the relevant Markov chain for the following small example. We consider a short (artificial) week of only three periods, $P = (1,2,3)$. In each period demand occurs for either zero or one product unit with equal probability. Orders will be issued in period 2 if the inventory position is smaller or equal to 1 $(s_2=1)$, and they will arrive in the next period (period 3). The product is shipped in bundles of two $(q=2)$. As motivated above, our example system has $3 \cdot 4 \cdot 2 = 24$ states that may be relevant. There are three periods; the inventory level can range between 0 and 3 units, and no more than one case pack can be outstanding because ordering two product units will always raise the inventory position above 1. Figure 4 depicts these 24 states. States drawn in gray are inaccessible from any other state. In periods 1 and 3 no orders can be outstanding, so the corresponding states are disregarded. Furthermore, it is not possible to be out of stock in period 3. In period 2, we cannot have less than 2 units of inventory and no order outstanding at the same time. Similarly, no order will be issued if 2 or 3 units are already at hand. Solid arrows indicate a transition probability of 0.5, while the one dashed arrow implies a definite transition.

Fig. 4

Markov chain with 24 theoretical and 11 reachable states

5.2 Approximation approach

The exact approach developed in Sect. 5.1 may involve the evaluation of large state spaces, leading to long runtimes particularly if the approach is applied multiple times within an optimization routine. This section therefore develops a fast approximate approach based on methods of inventory management.

The key idea is to first analyze the inventory position and then derive all relevant cost drivers from it in a second step. The approach is an approximation in the sense that we consider the backorder case instead of the lost-sales case when determining the inventory position. Furthermore, we disregard certain effects resulting from the cyclic structure of the problem at hand which will be outlined in the following.

For a clearer presentation we distinguish the inventory position before $(\mathrm{IP}^{-}_\mathrm{p})$ and after an order is placed $(\mathrm{IP}^{+}_\mathrm{p})$, where p denotes the period of the order cycle.

5.2.1 Inventory position

It is shown by Hadley and Whitin (1963) for the stationary (r, s, nq) policy with backordering that the inventory position follows a uniform distribution over the interval $[s_\mathrm{p}+1,s_\mathrm{p}+q]$, just after the moment that a new order is issued. However, this property does not hold without limitation for our system due to its cyclic structure. Here, values greater than $s_\mathrm{p}+q$ can also exhibit a positive probability of occurrence if another period uses a reorder point larger than $s_\mathrm{p}$. We therefore suggest recursively determining $\mathrm{IP}^{+}_\mathrm{p}$ in our system, where we define a base case for one particular cycle period and derive the characteristics of all other periods from the last respective order period.

Base case

We suggest the following base case for the recursive procedure. Let $\hat{p}$ be the order issue period that exhibits the largest reorder point, $\hat{p} = \arg \mathop {\max }\nolimits _{p \in P} \{s_\mathrm{p}\}$ and $s_{\hat{p}} = \mathop {\max }\nolimits _{p \in P} \{s_\mathrm{p}\}$. We define $\mathrm{IP}^{+}_{\hat{p}}$ as base case following the observation of Hadley and Whitin (1963) in that period:

$$\begin{aligned}&\mathrm{Pr}\left\{ \mathrm{IP}^{+}_{\hat{p}}<s_{\hat{p}}+1\right\} = 0 \end{aligned}$$

(2)

$$\begin{aligned}&\mathrm{Pr}\left\{ \mathrm{IP}^{+}_{\hat{p}}=s_{\hat{p}}+k\right\} \approx \dfrac{1}{q} \quad \forall \; k \in [1, q] \end{aligned}$$

(3)

$$\begin{aligned}&\mathrm{Pr}\left\{ \mathrm{IP}^{+}_{\hat{p}}>s_{\hat{p}}+q\right\} = 0 \end{aligned}$$

(4)

Recursion

With the base case defined for period $\hat{p}$, we suggest to determine $\mathrm{IP}^{-}_\mathrm{p}$ for all periods $p \ne \hat{p}$ on basis of the inventory position of the previous period, $\mathrm{IP}^{+}_{p-1}$:

$$\begin{aligned} \mathrm{Pr}\left\{ \mathrm{IP}^{-}_\mathrm{p} = i\right\} = \sum _{d = 0}^{\infty } \mathrm{Pr}\left\{ \mathrm{IP}^{+}_{p-1} = i+d\right\} \cdot \mathrm{Pr}\{D_\mathrm{p}=d\} \quad \forall \; i \end{aligned}$$

(5)

If p is not an order issue period, then obviously $\mathrm{IP}^{-}_\mathrm{p} = \mathrm{IP}^{+}_\mathrm{p}$ holds. Otherwise, we derive $\mathrm{IP}^{+}_\mathrm{p}$ as follows:

$$\begin{aligned}&\mathrm{Pr}\{\mathrm{IP}^{+}_\mathrm{p} < s_\mathrm{p} +1 \} = 0 \end{aligned}$$

(6)

$$\begin{aligned}&\mathrm{Pr}\{\mathrm{IP}^{+}_\mathrm{p} = i \} = \sum _{k=0}^{\infty } \mathrm{Pr}\left\{ \mathrm{IP}^{-}_\mathrm{p} = i-k\cdot q\right\} \quad \forall \; i > s_\mathrm{p} \end{aligned}$$

(7)

5.2.2 Derivation of cost drivers

Knowing the distributions of $\mathrm{IP}^{-}_\mathrm{p}$ and $\mathrm{IP}^{+}_\mathrm{p}$, the relevant cost drivers can be derived as follows. To determine the distribution of physical inventory, we first consider the order arrival periods. Within these, we find that the physical inventory is equal to $\mathrm{IP}^{+}_\mathrm{p}$ in the corresponding order period minus the demand consumption since the order has been placed. Let $p^{\mathrm{a}}$ be an order arrival period, $p^\mathrm{c}$ the corresponding issue period and $D_{[\mathrm{p}^\mathrm{c}+1, \mathrm{p}^{\mathrm{a}}]}$ the cumulative demand incurred in $p^{\mathrm{a}}$ after the order in $p^\mathrm{c}$ has been issued. The distribution of $I_{\mathrm{p}^{\mathrm{a}}}$ can then be calculated as follows:

$$\begin{aligned} \mathrm{Pr}\{I_{\mathrm{p}^{\mathrm{a}}} = i\}= & {} \sum _{d = 0}^{\infty } \mathrm{Pr}\left\{ \mathrm{IP}^{+}_{\mathrm{p}^\mathrm{c}} = i+d\right\} \cdot \mathrm{Pr}\{D_{[\mathrm{p}^\mathrm{c}+1, \mathrm{p}^{\mathrm{a}}]} = d\} \quad \forall \; i>0 \end{aligned}$$

(8)

$$\begin{aligned} \mathrm{Pr}\{I_{\mathrm{p}^{\mathrm{a}}} = 0\}= & {} \sum _{d = 0}^{\infty } \mathrm{Pr}\left\{ \mathrm{IP}^{+}_{\mathrm{p}^\mathrm{c}} = d\right\} \cdot \mathrm{Pr}\{D_{[\mathrm{p}^\mathrm{c}+1, \mathrm{p}^{\mathrm{a}}]} \ge d\} \end{aligned}$$

(9)

For non-arrival periods the physical inventory can be derived from the arrival period’s physical inventories. If $p^{\overline{\mathrm{a}}}$ is a non-arrival period and $p^{\overline{\mathrm{a}}}-1$ is its preceding arrival or non-arrival period, then the distribution of $I_{\mathrm{p}^{\overline{\mathrm{a}}}}$ is determined as follows.

$$\begin{aligned} \mathrm{Pr}\left\{ I_{\mathrm{p}^{\overline{\mathrm{a}}}} = i\right\}= & {} \sum _{d = 0}^{\infty } \mathrm{Pr}\left\{ I_{\mathrm{p}^{\overline{\mathrm{a}}}-1} = i+d\right\} \cdot \mathrm{Pr}\{D_{\mathrm{p}^{\overline{\mathrm{a}}}}=d\} \quad \forall \; i>0 \end{aligned}$$

(10)

$$\begin{aligned} \mathrm{Pr}\left\{ I_{\mathrm{p}^{\overline{\mathrm{a}}}} = 0\right\}= & {} \sum _{d = 0}^{\infty } \mathrm{Pr}\left\{ I_{\mathrm{p}^{\overline{\mathrm{a}}}-1} = d \right\} \cdot \mathrm{Pr}\{D_{\mathrm{p}^{\overline{\mathrm{a}}}} \ge d\} \end{aligned}$$

(11)

Given the distribution of $I_\mathrm{p}$, i.e., the overall physical inventory in a period, the distribution of the backroom inventory $B_\mathrm{p}$ and the distribution of the amount of stock that undershoots display stock requirements, $U_\mathrm{p}$ can easily be derived:

$$\begin{aligned} \mathrm{Pr}\{B_\mathrm{p} \le b\}= & {} \mathrm{Pr}\{sp < I_\mathrm{p} \le sp+b\} \quad \forall \; b > 0 \end{aligned}$$

(12)

$$\begin{aligned} \mathrm{Pr}\{B_\mathrm{p} = 0\}= & {} \mathrm{Pr}\{I_\mathrm{p} \le sp\} \end{aligned}$$

(13)

$$\begin{aligned} \mathrm{Pr}\{U_\mathrm{p} \le u\}= & {} \mathrm{Pr}\{ds-u \le I_\mathrm{p}< ds\} \quad \forall \; 0 < u \le ds \end{aligned}$$

(14)

$$\begin{aligned} \mathrm{Pr}\{U_\mathrm{p} = 0 \}= & {} \mathrm{Pr}\{I_\mathrm{p} \ge ds\} \end{aligned}$$

(15)

In our model, we only account for backroom activity in the order arrival periods. This extra effort occurs if the physical inventory exceeds the shelf space just after a new replenishment has arrived. This is the case if (1) an order has been placed in the corresponding order issue period and (2) the inventory position after ordering exceeds the shelf space enlarged by the demand that will be incurred before the replenishment order arrives. Let $p^{\mathrm{a}}$ and $p^\mathrm{c}$ be defined as above and $D_{[\mathrm{p}^\mathrm{c}+1, \mathrm{p}^{\mathrm{a}}-1]}$ be the cumulative demand consumption from issue to arrival of the replenishment order. The distribution of the backroom activity $A_{\mathrm{p}^{\mathrm{a}}}$ can then be derived as follows:

$$\begin{aligned} \mathrm{Pr}\{A_{\mathrm{p}^{\mathrm{a}}} = 0\}= & {} 1-\mathrm{Pr}\{A_{\mathrm{p}^{\mathrm{a}}} = 1\} \end{aligned}$$

(16)

$$\begin{aligned} \mathrm{Pr}\{A_{\mathrm{p}^{\mathrm{a}}} = 1\}= & {} \sum _{d = 0}^{\infty } \mathrm{Pr}\{D_{[\mathrm{p}^\mathrm{c}+1, \mathrm{p}^{\mathrm{a}}-1]}=d\} \cdot \mathrm{Pr}\left\{ \mathrm{IP}^{+}_{\mathrm{p}^\mathrm{c}} > sp+d | \mathrm{IP}^{-}_{\mathrm{p}^\mathrm{c}}\le s_{\mathrm{p}^\mathrm{c}}\right\} \end{aligned}$$

(17)

In the store, case-pack handling—analogous to backroom activity—occurs in order arrival periods only. Since we use unified cost factors for all periods, we can also associate the corresponding handling efforts in the DC with the order arrival period even if they in fact occur in a different period. The number of case packs arriving in an order arrival period $p^{\mathrm{a}}$ is directly determined by the inventory position in the corresponding order issue period before an order is placed. Following the replenishment policy the number of reordered case packs will just suffice to raise the inventory position above s:

$$\begin{aligned} \mathrm{Pr}\{H_{\mathrm{p}^{\mathrm{a}}} \le h\} = \mathrm{Pr}\left\{ \mathrm{IP}^{-}_{\mathrm{p}^\mathrm{c}}> s_{\mathrm{p}^\mathrm{c}} - h \cdot q\right\} \quad \forall \; h>0 \end{aligned}$$

(18)

There is an even simpler way of calculating the overall expected value $E\{H\}$ of 1 week. Since the replenishment arrivals are equal to the demand consumption in the long term, this value can be directly derived from the expected demand per week.

$$\begin{aligned} {\text {E}}\{H\} = \frac{{\text {E}}\{D_{[1, |P|]}\}}{q}. \end{aligned}$$

(19)

5.3 Optimization

In the preceding section we have developed an exact and an approximate approach for evaluating the resulting costs of particular system configurations assuming a predetermined case-pack size.

This section shows how to determine optimal case-pack sizes $(q_{\mathrm{opt}})$ using these two alternative evaluation approaches. We will first address the single-store case (Sect. 5.3.1) and then come to the case of multiple stores (Sect. 5.3.2) that should be replenished with one common case pack. Both problems can be solved with the same optimization framework.

The current case-pack options may be restricted by what the consumer goods industry is willing to provide and what is technically possible in terms of stability and reasonable in terms of package efficiency. Restrictions like this are neglected here, and we recommend considering the realizable case pack that is either next larger or next smaller to the theoretical optimum, depending on which has lower costs.

5.3.1 Single store

Let us first rewrite Eq. (1) according to (20), i.e., as a function of q composed of five subfunctions, $C^I(q) = \sum _{p \in P} c_\mathrm{i} \cdot {\text {E}}\{I_\mathrm{p}(q)\}, C^H(q) = \sum _{p \in P} c_\mathrm{h} \cdot {\text {E}}\{H_\mathrm{p}(q)\}$, etc...

$$\begin{aligned} C(q) = C^I(q) + C^U(q) + C^B(q) + C^A(q) + C^H(q) \end{aligned}$$

(20)

The objective (20) contains two functions decreasing in q, i.e., $C^H(q)$ and $C^U(q)$, and two functions increasing in q, i.e., $C^I(q)$ and $C^B(q)$. Function $C^A(q)$ contains increasing and decreasing segments when q is increased.

The expected handling costs $C^H(q)$ clearly decline when q rises, see Eq. (19). In contrast, the expected physical inventory costs $C^I(q)$ and the expected backroom inventory costs $C^B(q)$ go up as case-pack size q rises due to increasing lot-sizing stock. Since the undershooting of display stock will decrease with increased inventory levels, $C^U(q)$ will be decreased by larger case-pack sizes. Two opposing effects, however, influence how much backroom activity costs $C^A(q)$ are to be expected. While larger case packs and thus higher lot-sizing stock increase the probability of excess inventory, orders will be placed less often so that new products will arrive less frequently.

Based on these observations, we define two functions, $C_{\mathrm {dec}}(q)$ (declining) and $C_{\mathrm {inc}}(q)$ (increasing) that are used as termination criteria during the optimization procedure.

$$\begin{aligned} C_{\mathrm {dec}}(q)= & {} C^H(q) + C^U(q) \end{aligned}$$

(21)

$$\begin{aligned} C_{\mathrm {inc}}(q)= & {} C^I(q) + C^B(q) \end{aligned}$$

(22)

The outline of the procedure is then as follows: During an initial phase (Step 1: Initialization) we define an appropriate initial case-pack size, $q_{\mathrm {start}}$. A possible starting value could be: $q_{\mathrm {start}} = \lceil {\text {E}}[D_{[1,|P|]}] \rceil$. However, the procedure could be started with any positive integer value, i.e., $q_{\mathrm {start}}>0$. $q=q_{\mathrm {start}}$ is the case-pack size in the first iteration. In addition, we evaluate the associated expected total costs and set $C_{\mathrm {UB}}=C(q)$. We then know that any $q^{-}<q$ will exhibit higher costs for the declining cost function, i.e., $C_{\mathrm {dec}}(q^{-})>C_{\mathrm {dec}}(q)$ and any greater $q^{+}>q$ will exhibit higher costs for the increasing cost function, i.e., $C_{\mathrm {inc}}(q^{+})>C_{\mathrm {inc}}(q)$.

Proceeding from the initial start value, the algorithmic idea is to evaluate $C(q), C_{\mathrm {dec}}(q)$ and $C_{\mathrm {inc}}(q)$ for smaller and larger case packs to finally arrive at lower and upper bounds ($q_{\mathrm {min}}$ and $q_{\mathrm {max}}$) beyond which $q_{\mathrm {opt}}$ cannot be found. The best q in $[q_{\mathrm {min}},q_{\mathrm {max}}]$ is then shown to be identical with the overall optimum $q_{\mathrm{opt}}$.

During “Step 2: Iteration left” we evaluate all smaller case packs until a $q_{\mathrm {min}}$ is found for which $C_{\mathrm {UB}}<C_{\mathrm {dec}}(q_{\mathrm {min}})$, i.e., $q_{\mathrm {min}}=\max [q|C_{\mathrm {UB}}<C_{\mathrm {dec}}(q)]$. Similarly, we evaluate in “Step 3: Iteration right” all greater case packs $(q>q_{\mathrm {start}})$ until a $q_{\mathrm {max}}$ is found for which $C_{\mathrm {UB}}<C_{\mathrm {inc}}(q_{\mathrm {max}})$, i.e., $q_{\mathrm {max}}=\min [q|C_{\mathrm {UB}}<C_{\mathrm {inc}}(q)]$. During the evaluation process we update the minimal cost value in each iteration, i.e., $C_{\mathrm {UB}}=C(q)$, and store the associated case-pack size, $q_{\mathrm {opt}}=q$, if a case pack reveals a new smallest objective value so far. Figure 5 depicts the entire optimization procedure.

Fig. 5

Procedure for determining the optimal case-pack size

Figure 6 illustrates the interplay of the defined cost functions based on the example [1 / A] introduced in the next section. (Please note, for a better visualization of the procedure we multiplied the inventory holding cost factor in this example by ten.) Assuming the procedure starts with $q_{\mathrm {start}}=27$, the first and initial upper bound cost value accounts for $C_{\mathrm {UB}}=2.275$, which is symbolized by Point P1 in Fig. 6. Afterwards “Step 2: Iteration left” starts and case-pack sizes are decreased by one in each iteration. During this process $C_{\mathrm {UB}}$ is updated in each iteration until $C_{\mathrm {dec}}(q)$ intersects the latest $C_{\mathrm {UB}}$ between $q=17$ and $q=18$. Step 2 then terminates at $q_{\mathrm {min}}=17$, which is symbolized by Point P3 in Fig. 6. The lowest cost value achieved so far, i.e., $C_{\mathrm {UB}}=1.755$ (Point P2) is found at $q=21$, not knowing yet that this is the optimal solution. Then, “Step 3: Iteration right” starts, and the case-pack sizes are increased by one in each iteration, starting with $q=28$. Analogous to Step 2, this step terminates at $q_{\mathrm {max}} = 33$ (Point P4) because $C_{\mathrm {inc}}(q)$ intersects with the latest $C_{\mathrm {UB}}$ between $q=32$ and $q=33$. The algorithm thus evaluates all case-pack sizes $q \in [17,33]$ and terminates with $q_{\mathrm {opt}}=21$. However, any other initially positive integer value for $q_{\mathrm {start}}$, i.e., $q_{\mathrm {start}} \ge 1$ would also terminate with $q_{\mathrm {opt}}=21$.

Fig. 6

Illustration of the optimization procedure

The cost evaluation within the optimization procedure could be realized by the exact evaluation approach (Markov chain, see Sect. 5.1) or the approximation approach (see Sect. 5.2). When applied to the real-world case studied in Sect. 6 the approximation delivers accurate results. In 38 of 48 cases it suggests the optimal case pack, where in all other 10 cases the resulting case pack is one unit larger than optimal. The approximate solution is 1.73% more expensive in the worst case and only 0.05% on average. On an Intel(R) Core(TM) i7-6820HQ 2.7 GHz CPU, the optimization procedure took 8 s for all 48 cases when the approximation method is used and 374 s when the exact formulae are applied.

5.3.2 Multiple stores

Retailers will hardly consider to customize case packs for the distinctive needs of individual stores since this will significantly increase the logistics’ complexity particularly at the DC. Instead they use the widespread “one case-pack size for all stores” strategy or at most offer some few case packs to choose from. The single-store perspective therefore is of limited value for practical decision support. Nonetheless, it provides us with a lower bound on the total decision-relevant costs achievable and reveals the spread of case-pack sizes that individual stores would be operated most efficiently.

Furthermore, the framework developed above for the single-store case can also be used to solve the highly relevant decision problem of determining the common optimal case-pack size for multiple stores. Instead of the distribution costs of a single store, we need to consider the total costs of all subsystems involved ($f \in F$), leading to the adjusted objective function (23).

$$\begin{aligned} \begin{aligned} C'(q)&= \sum _{f \in F} \left[ C_f^I(q) + C_f^U(q) + C_f^B(q) + C_f^A(q) + C_f^H(q) \right] \\&:= C^{I'}(q) + C^{U'}(q) + C^{B'}(q) + C^{A'}(q) + C^{H'}(q) \end{aligned} \end{aligned}$$

(23)

Since the summation of multiple declining (or increasing) functions forms a declining (or increasing) function in total, the rationales of the single-store case also apply to the multiple store case. We can thus use the procedure outlined in Fig. 5 for the multiple store case, where $C^{I'}(q)$ replaces $C^{I}(q)$ and so on.

6 Empirical study and insights

The evaluation and optimization approach developed is applied in the present section in a real case study of a retail chain that operates almost 3000 stores in Europe. The key data of the case study and an overview of the results for the single-store cases are presented in Sect. 6.1. More detailed results including insights on the shape of the cost drivers and costs relevant to the decision problem are then discussed in Sect. 6.2. In Sect. 6.3 we examine two parameters of our model in greater detail, shelf space and backroom inventory costs, since their impact on the optimal case pack seems to be very strong. Section 6.4 is dedicated to the multiple store case, where common case-pack sizes are also compared with those that would be optimal for the individual stores.

6.1 General view on stores and products

To illustrate the use of our approach, we apply it to a real-world test set involving six products (1, 2, ..., 6; see Table 2) at eight grocery stores (A, B, ..., H; see Table 3).

Table 2 Characterization of products included in the empirical study

Table 3 Characterization of stores included in the empirical study

We consider the complete 2013 sales data for each product and store, and interpret the observed relative demand frequencies as discrete empirical distributions to use in our analytical approach. Delivery patterns, display stock, shelf space and also the present case-pack size are contained in the data. Finally, the reorder points $s_\mathrm{p}, p\in P$ are set such as to ensure that the display stock will not be undershot in $\alpha = 70\%$ of order cycles.

Table 4 Cost parameters for products 1–6

Cost data are assumed as displayed in Table 4. We analyzed and quantified the decision-relevant cost parameters together with supply chain managers of the case company. Afterwards these cost parameters were proportionally scaled at arbitrary levels since we were not allowed to disclose the actual cost data of the case company. The relationships between these cost parameters are congruent with those of comparable retail studies (van Zelst et al. 2009; Broekmeulen et al. 2017).

Let us first look at the overall results for the store and product combinations. Figure 7 depicts the changes between the optimal case-pack sizes and those that are currently in use. We observe that the optimal case-pack sizes differ between stores for the same products, with only a few exceptions. For some products the difference between the stores’ preferences is marginal, whereas for Product 6, for example, store B would be best operated with a case-pack size of $q=13$ that is more than four times the size of what would be best for store C, i.e., $q=3$. The changes recommended, however, point in the same direction in most cases: it appears to be beneficial for all stores to either increase or decrease the case pack currently in use. For the first product, we find the most ambiguous situation: there is little need to adjust the case-pack size at three stores, while it may be beneficial for the other five stores to reduce it by 5–21 units. The sales volume of Product 1 is relatively low in general, while its current case-pack size is quite high (32 CUs). There is therefore a general tendency to reduce the size of this case pack, especially where those stores with scarce shelf space, e.g., Store H, would benefit from the reduction. (See Sect. 6.2 for more insights into this case.)

Fig. 7

Change in current case-pack sizes when optimal case-pack sizes are applied

Figure 8 shows the cost savings potential when switching to the optimal case-pack size. The case-pack size seems relatively appropriate for all stores considered only for Product 6, whereas we note significant cost savings potentials for the other products including the ambiguous case of Product 1.

Fig. 8

Cost improvement in the optimal case-pack size compared to the current status

6.2 Individual product–store combinations

In this section we take a closer look at the effects that lead to the cost savings discussed above. In particular, we analyze one specific product–store combination [1/H] in greater detail. Store H is of medium size and achieves moderate revenues and is replenished three times a week, i.e., Monday, Wednesday, and Friday, so that the relevant order pattern can be described as $R=(1,0,1,0,1,0)$. Product 1 belongs to the low-demand volume category and is nonetheless distributed from the DCs in a relatively large case-pack size of 32 units. Display stock, shelf space, and order levels are given as follows: ${ ds}=3, { sp}=23, S=(13,0,13,0,12,0)$.

We analyze the considered example in three different ways. First we track the influence of different case-pack sizes on the five cost drivers, physical inventory (I), backroom inventory (B), undershooting of the display stock (U), case-pack handling (H), and backroom activity (A). Second, the resulting costs for each of these drivers are presented along with total costs. Third, the stores’ performance using both the original and the optimal case-pack size is simulated using the corresponding real-world data from the first 150 periods in 2013.

When comparing the relatively large case-pack size, $q=32$, with the store’s shelf capacity, ${ sp}=23$, one can already assume that the current case-pack size does not fit to the store’s needs well. However, it is not as readily identifiable to what extent the case-pack size should be reduced, and what operational cost savings that would imply. Figure 9 displays the five cost drivers depending on the case-pack size relative to their respective maximum values for example [1/H]. In each case the associated maximum value is selected from the results of the considered range of case-pack sizes, i.e., $q \in [1,30]$.

Fig. 9

Cost factors depending on the case-pack size relative to their respective maximum values, example [1/H]

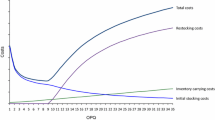
As expected, when case-pack sizes become larger, physical inventory, backroom inventory and backroom activities increase. On the other hand, the undershooting of display stock and case-pack handling decreases. Physical inventory increases linearly when q increases. Backroom inventory, however, does not occur at all until a case pack reaches a certain size, i.e., $q=11$: it then increases overproportionally. This initiating event can be explained as follows: the shelf space and reorder levels of Product 1 at Store H are $sp = 23$ and $S = (13, 0, 13, 0, 12, 0)$, respectively. As soon as inventory levels drop to or below the reorder point, the product is therefore reordered at a minimum order size of one case pack. Since Product 1 is a low volume product, it is possible that on delivery the same quantity of 13 products that originally triggered the replenishment may still be available on the shelf. Assuming a case-pack size of 11 and a shelf space of 23, one item of Product 1 would therefore be taken to the backroom in this case. Accordingly, backroom activities start as soon as the case-pack size reaches 11. The curve is then mainly influenced by two factors. First, it becomes more likely that the shelf space will be exhausted by an arriving replenishment order, resulting in backroom activities. Second, the arrival frequency will drop since larger case packs need longer to be consumed by demand. The amount of case-pack handlings can of course be significantly reduced in the range of $1 \le q \le 5$, from 100% for $q=1$ to 20% for $q=5$.

Fig. 10

Cost curves depending on case-pack size, example [1/H]

Since case-pack handling and backroom inventory are the primary cost drivers, an optimal case-pack size of $q=11$ results. This becomes particularly apparent in Fig. 10, which illustrates the shapes of the cost functions of all factors, including the total cost function. We observe a distinctive cost minimum for a case-pack size of $q=11$. The total costs are mainly influenced by activities and situations that result from case-pack handling, backroom inventory, and undershooting of display stock, respectively. As soon as backroom inventory occurs, the total cost function increases sharply. The inventory holding costs are less important since the product value is relatively low. In case of [1/H] this means, decision makers should maximize case packs as long as backroom inventory getsavoided.

Figures 11 and 12 depict the inventory level process over a time span of 200 periods assuming a case-pack size of 32 (original value) and 11 (optimized value), respectively. In addition, the customer demand (downward bars) and arriving orders (upward bars) are shown for each period. The dark (i.e., red) areas below and above the horizontal lines 3 and 23 indicate (unwanted) phases in which insufficient display stock and backroom inventory occurs, respectively.

Fig. 11

Performance of Product 1 in Store H with an original case-pack size of 32

Comparing these charts it becomes apparent that a reduced case-pack size of 11 will certainly increase case-pack handling efforts as more case packs arrive. Note that each (green) upward bar represents an order arrival. However, this is more than compensated by a substantially improved backroom situation. Summarizing, since the actual case-pack size is far too large, example [1/H] exhibits the largest total cost reduction between the original and the optimal case-pack size of all cases considered in the entire case study, i.e., approx. 81%.

Fig. 12

Performance of Product 1 in Store H with an optimal case-pack size of 11

6.3 Sensitivity analysis

A strong cost driver of our model appears to be the shelf space that the store has allocated for a particular product. In connection with the high costs of bringing product units to the backroom and maintaining them there, the optimal case pack seems to be the largest one that still fits onto the shelf in most cases. A sensitivity analysis confirms this observation. Figure 13 shows the optimal case pack for different amounts of shelf space, for example configuration [1/A], where the original backroom inventory costs $(c_\mathrm{b}=2)$ are also varied to illustrate their impact.

It is interesting to see that parameter $c_\mathrm{b}$ makes a particular difference when shelf space is small. Once a critical space is reached—at around 30 units in the example—the optimal case packs are very similar or even the same for the different values of $c_\mathrm{b}$. At this point, any further enlargement of the shelf space results in a proportional enlargement of the optimal case pack. Since the general inventory holding costs, $c_\mathrm{i}$, are relatively low in the context of our study, the backroom inventory and activity costs impose the only strong limiting factor on the optimal case-pack size. Ever larger case packs are therefore optimal when the shelf space gets less scarce. Figure 14 depicts the analogous observation for case [3/C]. Here, the critical space is reached at around 40 units, beyond which the optimal case pack is also incremented in proportion to the shelf space.

Fig. 13

Optimal case packs of Product 1 in Store A for varying shelf spaces and backroom inventory costs

Fig. 14

Optimal case packs of Product 3 in Store C for varying shelf spaces and backroom inventory costs

6.4 One case pack for all stores

The case company currently applies a “one case-pack size for all stores” strategy. We therefore applied the optimization method outlined in Sect. 5.3.2 to determine the best common case pack for all stores. Figure 15 shows the results of our example test set.

Fig. 15

Optimal case-pack sizes (one for all stores) and cost effects

Based on the status quo currently applied, store-tailored optimal case-pack sizes lead to an instore cost reduction of 24.8% on the average of all product–store combinations. However, by choosing the optimal one-for-all-stores case pack, total costs could already be reduced by 21.4%. Thus, the one-for-all-stores strategy apparently leads to operational instore costs that are close to the theoretical cost minimum, assuming case-pack sizes tailored to each store. For our case company it therefore seems rather unpromising to increase the logistics complexity by offering multiple case-pack sizes to meet the specific needs of individual stores.

These results are consistent with the results of Sect. 6.1 since the individual optimal case-pack sizes are at similar levels for the majority of stores (see Fig. 7). The “one case-pack size for all stores” strategy induces reasonable additional operational costs but also saves the effort of designing, managing and handling different case packs for identical products. The studies of Gámez Albán et al. (2015) and Broekmeulen et al. (2017) confirm these results.

7 Summary and future areas of research

The following research steps form the main content of the paper. First, an operational cost model is developed that quantifies the operational logistics costs along the internal supply chain of a grocery retailer depending on the case-pack size chosen. In a second step, a new inventory model is developed quantifying the decision-relevant drivers of the cost model. Building on that, an exact discrete Markov chain (MC) model and a fast heuristic solution approach are developed evaluating the inventory model for certain instances of the model. A nonlinear optimization approach then makes use of these evaluation approaches specifying the optimal case-pack size of an individual product for a single store and the optimal common case-pack size for a larger group of stores—possibly for all stores of the retail chain.

The inventory model developed comprises multiple periods within a stationary cyclic model in order to cover demand distributions that vary within the store’s business week. The model therefore generalizes the well-known periodic review reorder point (r, s, nq) policy to a cyclic version. The modeling approach reflects store-specific delivery patterns and a replenishment system that is common for non-perishable products in retail chains. In addition, the model takes into account limited shelf space on the sales floor and additional storage space in the backroom of an outlet and considers the corresponding shelf-filling and refilling processes in detail. The model quantifies all the decision-relevant logistics processes, i.e., case-pack handling at the DC, physical inventory on the shelf, dissatisfied service level when the amount of products on the shelf is insufficient (undershooting of display stock), case-pack handling when filling the shelf, and activities involved in bringing excess supply to the backroom and repeatedly removing it from there to restock the shelf. It has been shown that the impact of varying case-pack sizes on transportation costs is negligible.

The modeling and solution approaches are applied to the real-world data set of a leading European grocery retail chain. Cost-optimal case-pack sizes for several distinctive product–store combinations are determined. The case company may realize substantial cost improvements when changing the current case-pack sizes accordingly. The recommended adjustments lead in both directions: some of the case packs currently applied should be enlarged, while others should be reduced. The single-store analysis revealed that most stores would be operated most efficiently with an individually tailored case-pack that deviates slightly or even significantly in some cases from the best case-pack size of other stores. Moreover, it could be shown that a large fraction of the cost reduction potential can already be realized by switching case-pack sizes to the best choice of a “one case-pack size for all stores” strategy, while avoiding the extra effort for maintaining multiple case packs per product.

In some cases, as for Product 5 of the examples in Sect. 6, it seems obvious that the current case-pack sizes are not optimal, so the store managers are most probably aware of the problem and may easily detect possible benefits of an increased or a decreased case-pack size. However, in the majority of instances these benefits are much harder to identify, and most probably require the assistance of an analytical model. The modeling and solution approach suggested can be applied in this sense. The approach contributes to further improving operational efficiency in the future by supporting case-pack-related decisions in retail practice.

The modeling and solution approach suggested here could be extended in several directions, leading to new challenges for further research:

• (a) Case-pack sizes do not just affect operational costs along the internal supply chain but also logistics costs emerging further upstream from the retail supply chain considered. In general, case packs are delivered from the manufacturer in given sizes. Modifying them, e.g., at the DC, creates additional expenses for the retailer. Sometimes manufacturers offer retailers different case-pack sizes or customized case packs on request. These possibilities lead to case-pack-size-dependent manufacturing costs or purchasing prices, respectively. The model presented could therefore be extended with respect to one or more of these aspects.

• (b) In general, product demand, shelf space assigned and listing decisions change over time, e.g., along the product life cycle, especially for seasonal products. In such an environment it may be appropriate to modify case-pack sizes accordingly in the course of time. This would result in a dynamic optimization problem asking when and to what extent a case-pack size should be modified. Costs for resizing case packs would have to be quantified and considered in this enhanced modeling approach.

• (c) Related to (b) it is conceivable that several case-pack sizes could be defined for one product and operated in parallel. Stores could then be served with their individual, (perhaps) optimal case-pack sizes. Under these circumstances the decision problem that arises is how many different sizes per product should be defined, and which of the resulting case-pack sizes should be assigned to which store. This leads to a clustering and assignment problem.

• (d) The Markov model suggested assumes that shelf inventory is continuously replenished from the backroom as long as inventory is available. We denote this policy “online instore replenishment.” However, some stores may also follow the “offline instore replenishment” policy, i.e., restocking from the backroom is only carried out at certain instants of time. An adaptation of the Markov model reflecting this policy may be worthwhile.

• (e) The planning problem considered is highly correlated with the area of category and assortment planning, including listing, facing and pricing decisions. For example, a trade-off exists between the number of products listed and the shelf capacity assigned to each of the products. Having more shelf capacity available reduces the amount of backroom activities and backroom inventory and therefore allows for larger case-pack sizes.