1 Introduction

In online retailing, attended home delivery (AHD) services have gained increasing popularity in recent years. Busy lifestyles, the incapability of leaving the house owing to physical disability or the need for childcare necessitate home delivery services (Hays et al. 2005). In AHD, every delivery needs to take place in a service time window upon which service provider and the customer have agreed in advance. For instance, the delivery of perishable or bulky goods and/or safety reasons require customers to be at home during service execution (Agatz et al. 2008). In this paper, we focus on the e-grocery sector, in which groceries are delivered to customers. The growth potential of the e-grocery sector can be illustrated by a Kantar Worldpanel investigation that reports sales of groceries via e-commerce of $48 billion in the 12 months to June 2016. It also predicts an increase in sales to $150 billion in 2025—an annual growth rate of 20% between 2016 and 2025 (Kantar Worldpanel 2016).

The e-grocers’ business process typically works as follows: first, a customer who is willing to place an order must log on to an e-grocer’s website. Therefore, some basic information (e.g. the customer’s address) is revealed to the system. Second, the customer selects groceries, from which the capacity requirement (in a delivery vehicle) and the order value can be derived. Third, the customer sees a delivery time slot list, offering alternative slots regarding one or several potential delivery days in the near future. For the delivery service, a delivery fee is charged, which can be a fixed or a variable fee, depending on, for instance, the delivery time slot, the customer’s location and/or the order value. As an alternative to a delivery fee, discounts are used in practice to ensure a positive shopping experience for the customer (e.g. Freshdirect, Safeway and Peapod in the USA). Finally, the customer can choose one of the offered delivery time slots along with the corresponding fee/discount or leave the website without booking. Internally, each potential delivery day is connected with a specific cut-off time (quite commonly on its eve), i.e. delivery time slots on that day can only be made available for customers’ order placement before that point in time. Once all orders for a specific day are known, the e-grocer plans its delivery schedule (Agatz et al. 2013). Note that the order of the steps within the business process can be different, i.e. selecting groceries might also take place after selecting the delivery time slot.

While AHD is a convenient service for customers, particularly the “last-mile” problem poses a logistical and economic challenge to retailers (Agatz et al. 2008). Service providers face in particular the trade-off between substantial delivery cost and customers’ high expectations regarding delivery reliability and service quality (Yang et al. 2016). To successfully meet the challenges in the e-grocery sector, cost-efficient operations must be maintained. Customers’ delivery time slot choices strongly impact the delivery cost, since their choices directly influence delivery routes. Thus, e-grocers seek to actively manage their customers’ choices while anticipating the operative delivery costs in order to maximise total profits.

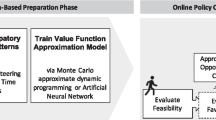
For this purpose, one of the most prominent demand management concepts in practice is dynamic time slot pricing (in the following: dynamic pricing), on which we also focus in this paper. This concept allows an e-grocer to dynamically adjust its delivery time slot prices for every incoming request, based on current information on already accepted requests, a requesting customer’s location, future expected customer requests in the remaining time until cut-off, the anticipated delivery cost and so on. The underlying mathematical price optimisation problem has been formulated as stochastic dynamic programming model in the academic literature (Yang et al. 2016). This represents the most advanced and thus the current de facto standard dynamic pricing framework for AHD. However, even in settings of moderate size, the model cannot be solved to optimality owing to the curse of dimensionality. Therefore, for practical purposes, some heuristic is needed. One meaningful possibility is to apply approximate dynamic programming and so to remove the recursiveness of the stochastic dynamic program. Specifically, when calculating the optimal prices of each possible delivery time slot for an incoming request, the “consequences” concerning potential future requests and the resulting routing cost (monetarily expressed in terms of opportunity cost) are no longer calculated exactly in a recursive fashion; instead, some kind of approximation is used.

In this context, Yang et al. (2016) propose approximating the opportunity cost by calculating the insertion cost of an incoming customer request in a potential delivery schedule based on a classical insertion heuristic that draws on Solomon (1987). Their approach has two parts: the first component approximates insertion cost by alternatively inserting the current incoming request in different potential schedules of the already accepted customers and taking the cheapest one (Hindsight Policy). For the second component, in order to incorporate expectations about future demand, a pool of the most recent historical final schedules for the same delivery weekday is considered as a forecast of future schedules, and insertion cost is approximated by taking the average over all potential insertions in the pool. A linear combination of these two components, weighted depending on the progress of the booking horizon, then serves as an opportunity cost approximation (Foresight Policy).

The approach by Yang et al. (2016) exhibits the following decisive downsides. First, expected future demand and the customers’ time slot choice behaviour are solely taken into account in a very simplifying way, i.e. by using historical final schedules as forecasted schedules. Yang et al. (2016) themselves have pointed out as a future research direction, “if past final delivery schedules are not a good approximation of future schedules, the Foresight Policy could instead be based on final schedule predictions derived from the demand model”. Second, for delivery cost approximation, a very simple approach is used. Third, the already accepted orders and the forecasted schedules are not directly linked, but only jointly considered by the aforementioned linear combination of the insertion cost. In particular, the forecasted data are not updated by incorporating the already accepted customers. Consequently, Yang et al. (2016) have stated that their “model currently approximates the opportunity cost of accepting a customer order in a time slot only with regard to delivery cost, but not with regard to lost profit resulting from reduced capacity for future orders”.

In this paper, we tackle these shortcomings and contribute to the existing literature as follows: we present a novel mixed-integer linear programming (MILP)-based approach to approximate opportunity cost for dynamic pricing in AHD. The approach tightly links the most current information regarding the already accepted customers with a forecast adapted to the progress of the booking horizon. This forecast is based on expected future demand for each delivery area from the current point in time until the end of the booking horizon. Delivery cost of expected customers is approximated by a seed-based scheme that builds on Fisher and Jaikumar (1981). To make this cost approximation more accurate, we dynamise the parameters of the seed-based scheme (i.e. the potential seeds’ locations as well as related distance approximations) under consideration of the locations of already accepted customers. By integrating adequate decision variables, the MILP also incorporates the anticipation of future customer requests demand management. Concerning the delivery cost of already accepted customers, we integrate the result from an appropriate construction heuristic into the MILP, using customers’ exact residence information. A key advantage of our approach is that it allows considering lost profit owing to reduced (physical or timely) capacity for future customer requests when accepting the incoming one, also known as displacement cost.

The paper on hand represents the first work which explicitly includes an approximation of the demand management of expected future customers. Besides, the approaches for delivery cost approximation and displacement cost determination are among the most sophisticated ones in the AHD literature to date. Our model-based approach is the first which jointly considers the aforementioned, interdependent aspects of anticipation of future customer requests demand management, delivery cost approximation and displacement cost when making time slot pricing decisions for the current customer request. In a computational study, we evaluate our novel opportunity cost approximation. In line with Yang et al.’s (2016) investigation, we introduce benchmark pricing approaches in which prices are set in a simple—yet widely applied in practice—way without considering future customer requests and hence opportunity cost (e.g. fixed prices). Further, we benchmark our approach to the state-of-the-art dynamic pricing policy of Yang et al. (2016). We show that our approach always yields the highest profit, specifically given a tight capacity level on the part of the service provider. We also provide insights how to ensure real-time applicability through parallel computing and periodic recalculation of opportunity cost.

The remainder of the paper is organised as follows: in Sect. 2, we provide an overview of the related literature and the underlying dynamic pricing framework we base our work on. In Sect. 3, we introduce our new approach of opportunity cost approximation and state the corresponding mathematical model (MILP). In Sect. 4, we present the computational study, in which we compare our approach to different existing approaches. In Sect. 5, we provide a summary and managerial implications.

2 Related literature and the dynamic pricing framework

We will first briefly review the literature on attended home delivery that is closely connected to our work and will explain how our work fits in (Sect. 2.1). Based on this, we restate the de facto standard dynamic pricing framework for AHD, as proposed by Yang et al. (2016), along with the required notation (Sect. 2.2).

2.1 Related literature

Since the dynamic pricing problem we consider is well defined in the literature, in our review, we focus on publications that are very closely related to our work. For a more general review, including more information on other decision problems that occur in attended home delivery, we refer the reader to Agatz et al. (2013).

Table 1 Classification of demand management concepts
Full size table

In the scientific literature on AHD, four demand management concepts are distinguished (see Table 1). On the one hand, differentiated slotting and differentiated pricing are static approaches at a tactical level, which are based only on forecast data. Hence, decisions are static and thus permanent and are not dynamically adjusted in the progress of the booking horizon. In differentiated slotting approaches, optimisation seeks to decide for each delivery area in a delivery region which time windows to offer. For this purpose, Agatz et al. (2011) propose a continuous approach as well as a nonlinear, mixed-integer optimisation model, relying on a seed-based scheme. They assume that decisions about time windows offered in an area are subject to pre-defined service levels that must be satisfied. Hernandez et al. (2017) formulate the problem as a generalisation of the periodic vehicle routing problem and propose two heuristics for its solution. Analogously, the problem of differentiated pricing aims at a static, optimal price selection for each delivery time slot in each delivery area. Klein et al. (2017) are among the first to study this problem and propose a mixed-integer linear programming formulation of the problem, using a seed-based cost approximation. They incorporate customer choice behaviour via a general nonparametric rank-based choice model.

On the other hand, dynamic slotting and dynamic pricing represent dynamic approaches on an operational level in which real-time information is incorporated. For every incoming customer request, dynamic approaches include the request’s opportunity cost as the basis for the service provider’s decisions. Simply stated, regarding dynamic slotting, for every incoming request, an e-grocer must decide if it wants to accept the request or save the capacity in hope for a more profitable request in the future and hence reject it. Campbell and Savelsbergh (2005) are among the first to dynamically manage customer requests via dynamic slotting—in detail, by adjusting the offered time windows for every incoming customer request. Ehmke and Campbell (2014) extend this concept and propose acceptance mechanisms for customer requests living in metropolitan areas where travel time is time dependent, i.e. dependent on the time of the day owing to traffic, for instance. Cleophas and Ehmke (2014) propose value-based order acceptance by applying Belobaba’s (1987) expected marginal seat revenue heuristic. Campbell and Savelsbergh (2006) as well as Yang et al. (2016) discuss the concept of dynamic pricing for every incoming request. While Campbell and Savelsbergh (2006)—who base their model on Campbell and Savelsbergh (2005)—only include a simple customer choice model, Yang et al. (2016) extend and improve this approach. They model customer choice with a multinomial logit (MNL) model and incorporate (albeit quite simplistic) expectations of future customer requests on the basis of past delivery schedules. Their framework can be seen as the most advanced and thus the de facto standard of dynamic pricing in AHD. We restate it in Sect. 2.2.

Concerning the approximation of routing cost of future expected requests, Agatz et al. (2011) and Klein et al. (2017) apply a seed-based scheme in their static demand management approaches, drawing on Fisher and Jaikumar (1981). Both approximate routing cost based on an aggregation of customers of the same area of origin. While Klein et al. (2017) target the maximisation of expected total profits in their differentiated pricing framework, Agatz et al. (2011) seek to minimise travel cost while deciding about the time windows on offer for customers in a delivery area. In the same work, Agatz et al. (2011) present an alternative approach that builds on continuous approximation models proposed by Daganzo (1987), where total travel costs are derived by aggregating over “local” cost estimates. The most prominent heuristic applied in dynamic settings in AHD is the insertion heuristic that draws on Solomon (1987). Campbell and Savelsbergh (2004) propose efficient variants of this heuristic enabling fast and high-quality solutions of the vehicle routing problem with time windows (VRPTW). Thus, many researchers—e.g. Yang et al. (2016), Campbell and Savelsbergh (2005), Campbell and Savelsbergh (2006), and Cleophas and Ehmke (2014)—build on this heuristic in their dynamic demand management approaches in AHD.

Our work relates to the existing literature as follows: we build on the abovementioned dynamic pricing framework proposed by Yang et al. (2016), that is, we also model customer choice behaviour by the MNL, which allows for continuous price optimisation for each incoming customer. However, in this optimisation problem, we replace the calculation of opportunity cost, which turns out to be the most important element, with a different approximation. The purpose of this approximation is to obtain better results concerning the overall profit performance, while the related computational effort should still allow real-world large-scale implementations. Note that in a very recent working paper, subsequently to the first version of our paper, Yang and Strauss (2017) themselves proposed an alternative way to approximate opportunity cost by approximate dynamic programming, enabling large-scale applications, and potentially better incorporating displacement cost. While their approach turns out to be computationally efficient concerning large-scale implementations, it has the drawback that its profit performance is not as good as their original approach Yang et al. (2016) in most cases.

In our opportunity cost approximation, we calculate delivery cost with a variant of the insertion heuristic (see above) for already accepted customers and tightly link this to a seed-based scheme for delivery cost anticipation of expected customers. Given the dynamic, real-time nature of the problem, our approach differs significantly from existing seed-based approaches in the sense that we dynamically adapt the scheme’s parameters—such as the potential seeds’ locations and distance approximations—during the booking horizon by considering information on the locations of already accepted customers. Further, in contrast to existing works, we do not aggregate expected customers based on their area of origin, and we incorporate the anticipation of their demand management.

2.2 Dynamic pricing framework and basic notation

Our paper is based on the stochastic dynamic program by Yang et al. (2016), which is the de facto standard framework for dynamic pricing in AHD; we will now restate it.

We start by giving a detailed description of the underlying problem definition, introducing the relevant notation we use. An e-grocer plans its operations for a fixed delivery day in a delivery region which is segmented in delivery areas \(a\in {{\mathcal {A}}}=\left\{ {1,\ldots , A} \right\} \). These areas do not overlap, and they cover the whole delivery region. For delivery, the e-grocer operates with a fixed and homogenous delivery vehicle fleet \(v\in {{\mathcal {V}}}=\left\{ {1,\ldots ,V} \right\} \) with known capacity Q per vehicle \(v\in {{\mathcal {V}}}\). The delivery tour of a vehicle v starts and ends at a depot \(a=0\in {{\mathcal {A}}}\cup \left\{ 0 \right\} \). The delivery day is divided into (potentially overlapping) time slots \(s\in {{\mathcal {S}}}=\left\{ {1,\ldots ,S} \right\} \) with length \(l_s \). The booking horizon consists of T periods and ends at a cut-off time (just) before the delivery starts. Customers arriving during that booking horizon are assumed to have chosen the specific delivery day in advance, meaning that potential influences that other delivery day time slot options might have are not explicitly modelled. However, customers who “leave” in the model may actually be re-captured in another delivery day. After period T, no further orders are accepted. In each period, \(t\in \left[ {1,\ldots ,T} \right] \) at most one customer request from a certain delivery area a can occur. For ease of explanation, the order size e in terms of totes is assumed to be equal for all orders and the (estimated) profit of an order before distribution r is known (e.g. from historical data). Note that for a customer request occurring in period t, it would be possible to use the specific customer’s profit \({\dot{r}}\) in Eq. (4) (instead of r), in case this value is exactly known before time slot pricing decisions are made. Alternatively, one could use an estimated profit based on historical data for a delivery area or for the individual customer if he or she has already ordered in the past (Yang et al. 2016). The occurrence probability of a request from area a is expressed by \(\lambda m_a \), with \(\lambda \) denoting the arrival probability of a request in each period and \(m_a \) the probability that this request originates from area a. The components \(x_{tas} \) of the state vector \(\mathbf{x}_t =\left[ {x_{tas} } \right] _{a,s} \) denote the number of accepted customer orders from area a in time slot s until period t in the booking horizon. Since the state vector’s time index t will be obvious from the embedding dynamic program, we will omit it in the following. For every incoming customer request, the e-grocer must check which time slots are still available. All time slots in which the incoming customer request from area a can be served, given the already scheduled orders \(\mathbf{x}\), are contained in the set \(F_a (\mathbf{x} )\subseteq {{\mathcal {S}}}\). If a customer request from area a cannot feasibly be inserted into a time slot owing to vehicle capacity or time constraints, this time slot is not offered.

The e-grocer manages demand via a dynamic pricing policy, i.e. by dynamically (re)calculating the delivery price \(g_{as} \) in each period t of the booking horizon for each delivery area a and for each time slot s. Negative prices represent discounts. The price vector \(\mathbf{g}_a =\left[ {g_{a1} ,\ldots ,g_{aS} } \right] \) is then exposed to an incoming customer from area a who either chooses a slot s at price \(g_{as} \) or leaves the website without ordering. The probability that a customer from area a chooses delivery time slot \(s\in F_a (\mathbf{x})\) if he or she is offered prices \(\mathbf{g}_a \) is given by \(P_{s,F_a (\mathbf{x})} ({\mathbf{g}_a })\). These probabilities are derived from a standard MNL model, i.e.

$$\begin{aligned} P_{s,F_a (\mathbf{x})} ({\mathbf{g}_a } )=\frac{e^{u_{as} }}{e^{u_{a0} }+\mathop \sum \nolimits _{w \in F_a (\mathbf{x})} e^{u_{aw} }}, \end{aligned}$$
(1)

with the parameter \(u_{as} \) denoting the customer’s utility perception for time slot \(s\in {{\mathcal {S}}}\) (\(u_{a0} \) for the no purchase option, respectively), which is a linear function of the price \(g_{as} \) and thus can be influenced by \(g_{as} \).

Further, the choice probability that a slot \(s \notin F_a (\mathbf{x})\) is chosen is defined as 0. The e-grocer’s objective is the maximisation of its total profits.

The resulting dynamic program is given by

$$\begin{aligned} V_t (\mathbf{x})= & {} \mathop {\hbox {max}}\limits _\mathbf{g} \left\{ \mathop \sum \limits _{a\in {{\mathcal {A}}}} \lambda m_a \mathop \sum \limits _{s\in F_a (\mathbf{x})} P_{s,F_a (\mathbf{x} )} ({\mathbf{g}_a })\left[ {r+g_{as} +V_{t+1} ({\mathbf{x}+\mathbf{1}_{\mathrm{as}} })} \right] \right. \nonumber \\&\left. +\left[ 1-\mathop \sum \limits _{a\in {{\mathcal {A}}}} \lambda m_a \mathop \sum \limits _{s\in F_a (\mathbf{x})} P_{s,F_a (\mathbf{x} )} ({\mathbf{g}_a })\right] V_{t+1} (\mathbf{x})\right\} \nonumber \\= & {} \mathop {\hbox {max}}\limits _\mathbf{g} \Bigg \{\mathop \sum \limits _{a\in {{\mathcal {A}}}} \lambda m_a \mathop \sum \limits _{s\in F_a (\mathbf{x} )} P_{s,F_a (\mathbf{x})} ({\mathbf{g}_a } )\Big [r+g_{as} -(V_{t+1} (\mathbf{x})\nonumber \\&-V_{t+1} ({\mathbf{x}+\mathbf{1}_{as} }))\Big ]+V_{t+1} (\mathbf{x})\Bigg \},\quad \hbox {for }{} \mathbf{x}\in {{\mathcal {X}}}, \quad t\in \left[ {1,\ldots ,T} \right] \end{aligned}$$
(2)

with the boundary conditions

$$\begin{aligned} V_{T+1} (\mathbf{x})=-C(\mathbf{x} )\quad \hbox {for }{} \mathbf{x}\in {{\mathcal {X}}}. \end{aligned}$$
(3)

\(C(\mathbf{x})\) represents the minimum delivery cost at a given state \(\mathbf{x}\in {{\mathcal {X}}}:=\left\{ {0,1,\ldots ,T} \right\} ^{\left| A \right| \times \left| S \right| }\). If state \(\mathbf{x}\) does not lead to a feasible delivery schedule, \(C(\mathbf{x} ):=\infty \).

Given a customer arrival from area a, the optimal pricing policy which solves the dynamic program (Eq. 2) is given by

$$\begin{aligned} \mathbf{g}_a^*=\hbox {arg}\mathop {\hbox {max}}\limits _{\mathbf{g}_a } \mathop \sum \limits _{s\in F_a (\mathbf{x})} P_{s,F_a (\mathbf{x})} ({\mathbf{g}_a })\left[ {r+g_{as} -{{\mathcal {O}}}_{xtas} } \right] , \end{aligned}$$
(4)

with \({{\mathcal {O}}}_{xtas} :=V_{t+1} (\mathbf{x})-V_{t+1} ({\mathbf{x}+\mathbf{1}_{as} })\) being the opportunity cost of a customer request from area a for time slot s in period t. It can be shown that since the customers’ utilities are linear functions of the price, Eq. (4) is concave in the purchase probabilities and can easily be solved to optimality, given fixed values of \({{\mathcal {O}}}_{xtas} \) (Dong et al. 2009). However, owing to the large state space of the underlying dynamic program, \({{\mathcal {O}}}_{xtas} \) cannot recursively be determined exactly, even for moderate problem sizes. Also, the sole exact solution of the boundary condition (3) for each terminal state \(\mathbf{x}\in {{\mathcal {X}}}\) would necessitate the solution of \(\left| {{\mathcal {X}}} \right| \) VRPTWs. Since the VRPTW is known to be NP-complete (Savelsbergh 1985), this task is computationally intractable. Hence, to enable real-time pricing decisions for an incoming customer request via the pricing policy given in Eq. (4), an approximation of the value function \({\tilde{V}}_{t+1} (\mathbf{x})\) leading to an approximation of the opportunity cost \({\tilde{{\mathcal {O}}}}_{xtas} :={\tilde{V}}_{t+1} (\mathbf{x})-{\tilde{V}}_{t+1} ({\mathbf{x}+\mathbf{1}_{as} })\) is required.

3 A new model-based approximation of opportunity cost

The approximation of an incoming customer request’s opportunity cost \({\tilde{{\mathcal {O}}}}_{xtas} \) is the basis for a promising pricing decision (see Eq. 4). Given a current customer request from area a at period t of the booking horizon, we use a model-based approach (MILP-based approach) to approximate the opportunity cost \({\tilde{{\mathcal {O}}}}_{xtas} :={\tilde{V}} _{t+1} (\mathbf{x})-{\tilde{V}}_{t+1} ({\mathbf{x}+\mathbf{1}_{as} })\) separately for each time slot the customer may choose. In detail, for each potential time slot, we approximate the value function \(({\tilde{V}} _{t+1} ({\mathbf{x}+\mathbf{1}_{as} }))\) by an adequate MILP as well as for the case that the customer leaves the website without ordering \(({\tilde{V}}_{t+1} (\mathbf{x}))\). The resulting approximations \({\tilde{{\mathcal {O}}}}_{xtas} \) for each slot s can then be plugged into Eq. (4) in order to calculate the prices for the current customer.

We sought to incorporate all available information for the opportunity cost approximation as accurately as possible while keeping the related computational effort on a low level so as to enable real-world large-scale implementations. The available information’s quality improves with each incoming customer request during the booking horizon, since more information is known with certainty and the forecast can be updated, such that the parameters of the MILP to solve are adapted accordingly. In this context, we distinguish between two components in our model, i.e. the set of already accepted customers and the expectations of future customer requests:

  • Concerning already accepted customers, information such as customers’ exact residences, their time slot choices and profits before fulfilment/delivery cost is fully revealed when calculating the opportunity cost approximation. Thus, the fulfilment/delivery cost can be calculated exactly via a variant of the insertion heuristic and can then be adequately plugged into the MILP. We provide details in Sect. 3.1.

  • Concerning expected requests, only expectations regarding the residential areas and the profits are known; even more, demand will depend on future pricing decisions. Thus, we model delivery costs via a seed-based approach that also endogenously anticipates optimal future demand management and requires only expectations about expected customers’ residential areas. Details are given in Sect 3.2.

Based on the description of both components, we provide the MILP formulation in Sect. 3.3.

3.1 Accepted customers

This section deals with the incorporation of the latest information of accepted customers in our approximation approach. Regarding already accepted customers, in period t, information until period \(t-1\) is fully revealed, i.e. the accepted customers’ exact residences and hence Euclidian distances between each other, their time slot choices and profits before fulfilment/delivery cost are known. In line with the current literature on dynamic problems in AHD (cf. Sect. 2.1), we apply a variant of the insertion heuristic commonly used in vehicle routing, which efficiently yields—even for real-world instances—reasonable solutions to the problem at hand. Note that also other construction heuristics for the VRPTW, for instance, the nearest neighbour heuristic or the savings heuristic, could have been alternatively used. Our adaption of the insertion heuristic is inspired by the work of Yang et al. (2016) and Campbell and Savelsbergh (2004). As insertion criterion, we choose the customer’s cheapest insertion position. The insertion heuristic determines a delivery schedule for already accepted customers, i.e. delivery tours of the delivery vehicles \(v\in {{\mathcal {V}}}=\left\{ {1,\ldots ,V} \right\} \) in the fleet. We define the length of the tour which vehicle \(v\in {{\mathcal {V}}}\) drives in time slot \(s\in {{\mathcal {S}}}\) as \(d_s^v \). We determine the corresponding delivery cost via a cost factor c (cost per travel distance unit). Note, the delivery tours determined by the insertion heuristic are only tentative in each period \(1,\ldots ,T\). The final operational delivery schedule can be obtained by solving the insertion heuristic in period \(T+1\).

3.2 Expected customers

In this section, we elaborate on the incorporation of expectations regarding future customer requests in the approximation approach and on the linkage of these expectations to already accepted customers (see Sect. 3.1). In Sect. 3.2.1, we describe the anticipation of expected customer requests demand management, i.e. the anticipation of expected customers’ reactions to the service provider’s future pricing decisions. In Sect. 3.2.2, we introduce our approach for the delivery cost approximation of expected customer requests, which explicitly takes already accepted customer requests under consideration.

3.2.1 Demand management of expected customers

We consider expectations about future customer requests from period \(t+1\) until the end of the booking horizon T for the opportunity cost approximation. A forecast about expected customers, for instance, their expected order size e, generated average profit r and time slot preferences is assumed to be known from the past. The expected number of incoming requests is adapted to the progress of the booking horizon and can consistently be calculated from the parameters introduced in Sect. 2.2 as \({\bar{W}} :=\lambda ({T-t})\). Given the probabilities \(m_a \), the expected number of requests originating from area \(a\in {{\mathcal {A}}}\) is then equal to \({\bar{W}} m_a \).

Now, to endogenously incorporate the pricing of expected future customer requests and thus to anticipate future customers demand management, we use a deterministic demand approximation that is consistent with the (MNL-based) choice probabilities from Eq. (1) and which is inspired by the well-known choice-based, deterministic linear program (CDLP) for network revenue management (Liu and Ryzin 2008),(Gallego et al. 2004). To technically transfer the idea of the CDLP, future customers demand management is limited to a discrete number of potential price lists that contain one price for every time slot. For this purpose, we define a set of N potential price lists \({{\mathcal {G}}}=\left\{ {1,\ldots ,N} \right\} \). Each price list \(n\in {{\mathcal {G}}}\) contains one price \({\hat{g}}_{ns} \in {\mathbb {R}}\) for each time slot \(s\in {{\mathcal {S}}}\), i.e. \(n=\left[ {{\hat{g}}_{n1} ,\ldots ,{\hat{g}}_{nS} } \right] \). An algorithm for determining the discrete price points of the price lists is given in “Appendix A”. Note that a combination of time slot and price corresponds to a product of the CDLP and, hence, each price list \(n\in {{\mathcal {G}}}\) to an offer set. Analogously to the CDLP—which seeks to optimise the proportion of time a set of products is offered to a customer segment—we aim to determine optimal numbers \(\pi _{na} \) of expected customers from area \(a\in {{\mathcal {A}}}\) to which price list \(n\in {{\mathcal {G}}}\) is offered. Depending on the offered price list, the expected future customers select time slots with different probabilities. These probabilities can be pre-calculated. The probability that an expected customer from area \(a\in {{\mathcal {A}}}\) to which price list \(n\in {{\mathcal {G}}}\) is offered selects time slot \(s\in {{\mathcal {S}}}\) is denoted by \(q_{nas} \).

3.2.2 Dynamic seed approximation of the delivery cost

Regarding future expected customer requests from period \(t+1\) until period T, the customers’ exact residences as well as their time slot choices are not known, precluding the application of the insertion heuristic from Sect. 3.1. Since a customer request’s opportunity cost is strongly dependent on its influence on the delivery schedule and hence delivery cost, expectations about the delivery schedule for serving expected customers need to be incorporated. Therefore, we construct a seed-based scheme in order to approximate the resulting delivery distances and finally delivery cost. Seed-based cost approximations have a long tradition in the vehicle routing literature (cf. Sect. 2.1). Figuratively speaking, a seed forms a “virtual” basis for a vehicle from which future expected customers, which are assigned to the specific seed, are served. To obtain a reasonable overall cost approximation, at each period t, we dynamically adjust potential seeds’ locations and related distance approximations under consideration of the locations of already accepted customers, i.e. of the insertion heuristic’s outcomes from Sect. 3.1.

Let the tuple (a, s) denote the area–time slot combination (ATC) for each area \(a\in {{\mathcal {A}}}\) and each time slot \(s\in {{\mathcal {S}}}\). Now, to calculate the delivery cost for expected customer requests located in an ATC, we need to define a corresponding seed for each vehicle \(v\in {{\mathcal {V}}}\). Given this seed, we define the seed-to-customer distance \({\check{d}}_{as}^v \) that must be travelled in an ATC (a, s) by vehicle \(v\in {{\mathcal {V}}}\) to serve each expected customer. Since we do not know the locations of expected customers, we take one or several past schedule(s) of the delivery day under consideration containing information regarding the exact locations of the served customers. Hence, the distance \({\check{d}}_{as}^v \) represents an average distance between the seed in ATC (a, s) and the historical customers from area a and serves as an approximation for the expected distance a vehicle \(v\in {{\mathcal {V}}}\) has to travel to serve a customer in ATC (a, s). Further, as a vehicle needs to drive to an area before customers in this area can be served, we additionally define the to-seed distance \({\hat{d}}_{as}^v \) which vehicle \(v\in {{\mathcal {V}}}\) has to travel once to serve (any number of) expected customers in an ATC (a, s).

The idea underpinning our approach is to make the approximation more accurate by dynamically adjusting the seeds’ locations, the seed-to-customer distances and the to-seed distances according to the already accepted customers in each period \(t\in T\). In this context, given an ATC (a, s) for which we want to approximate the cost, we distinguish three cases, which we illustrate in Fig. 1. For clarity, in the illustration, we only consider a single vehicle \((V=1)\) and a delivery region divided into four areas \((A=4)\).

  • Case 1 No scheduled customers in the delivery tour of vehicle \(v\in {{\mathcal {V}}}\) at all

    Case 1 applies at the beginning of the booking horizon, when no customers have yet been accepted, i.e. no customers have yet been scheduled by the insertion heuristic from Sect. 3.1. In this case, each seed’s location is calculated as the centroid of all historical customers in the corresponding ATC (a, s), with resulting expected average seed-to-customer distances. We calculate the to-seed distances as the distance between the depot and the seed.

  • Case 2 Already scheduled customers in slot s in the delivery tour of vehicle \(v\in {{\mathcal {V}}}\)

    Case 2 represents the “standard case” that occurs most frequently during the booking horizon. In the given time slot s, customers (at least one) have already been accepted to be served in certain areas \({\hat{{\mathcal {A}}}}_v \subseteq {{\mathcal {A}}}\) by the vehicle \(v\in {{\mathcal {V}}}\) under consideration (Areas 1 and 3 in Fig. 1), while eventually in other areas \({{\mathcal {A}}}\backslash {\hat{{\mathcal {A}}}}_v \) no customers have been accepted yet (Areas 2 and 4 in Fig. 1). Now, in case that \(a\in {\hat{{\mathcal {A}}}}_v \), i.e. a refers to an area with accepted customers, each seed’s location is calculated as the centroid of all accepted customers in the corresponding ATC (a, s), with resulting expected average seed-to-customer distances. Further, we define \({\hat{d}}_{as}^v :=0\), since the vehicle is present in ATC (a, s) anyway, owing to the accepted requests. In case that \(a\in {{\mathcal {A}}}\backslash {\hat{{\mathcal {A}}}}_v \), i.e. a refers to an area without accepted customers, we calculate each seed’s location as the centroid of all historical customers in the corresponding ATC (a, s), with resulting expected average seed-to-customer distances. To calculate \({\hat{d}}_{as}^v \), we take the distance between the centroid of all historical customers from area \(a\in {{\mathcal {A}}}\backslash {\hat{{\mathcal {A}}}}_v \) and the seed in ATC \(({~{\hat{a}} ,s})\) for each \({\hat{a}} \in {\hat{{\mathcal {A}}}}_v \), denoted by \({\hat{d}}_{{\hat{a}} as}^v \). Then, we define the to-seed distance to be the minimum of all these distances, i.e. \({\hat{d}}_{as}^v =\mathop {\min }\limits _{{\hat{a}} \in {\hat{{\mathcal {A}}}}_v } {\hat{d}}_{{\hat{a}} as}^v \), reflecting that ATC (a, s) should be “connected” to the existing delivery tour at minimal cost. In Fig. 1, for instance, to travel to the seed of Area 2, we start from Area 1 (and not from Area 3).

  • Case 3 Already scheduled customers in the delivery tour of vehicle \(v\in {{\mathcal {V}}}\), but not (yet) in slot s

    Regarding case 3, customers have been accepted in one or several areas in at least one time slot, but not in time slot s. In this case, each seed’s location is again calculated as the centroid of all historical customers in the corresponding ATC (a, s), with resulting expected average seed-to-customer distances. The to-seed distance is defined as the distance between the centroid of all customers accepted in the closest time slots to time slot s, for instance, in time slots \(s-1\) and \(s+1\) in Fig. 1, and the seed.

The number of future expected customer requests from each area \(a\in {{\mathcal {A}}}\) is updated in each period of the booking horizon (see Sect. 3.2.1). In combination with the anticipation of these future expected customers demand management, this yields an expectation on the number of future customers who need to be served in ATC (a, s). Specifically, the number \(\pi _{na} \) of customers to which price list \(n\in {{\mathcal {G}}}\) is offered is multiplied by the probability \(q_{nas} \) (the probability that an expected customer from area \(a\in {{\mathcal {A}}}\) facing price list \(n\in {{\mathcal {G}}}\) selects time slot \(s\in {{\mathcal {S}}})\). By multiplying these expected numbers of customers by the seed-to-customer distances and by adding the corresponding to-seed distances, we get the expected delivery distances. Finally, these delivery distances need to be multiplied by cost factor c to calculate the expected delivery cost.

Fig. 1
figure 1

Approximation of expected delivery distances via the dynamic seed-based approach

Full size image

3.3 Mathematical model

In this section, we present a mixed-integer linear programming formulation to approximate the value function \({\tilde{V}} _{t+1} (\mathbf{x})\) for a customer request in period \(t\in T\). Recall, in order to obtain a request’s opportunity cost values \({\tilde{{\mathcal {O}}}}_{xtas} :={\tilde{V}} _{t+1} (\mathbf{x})-{\tilde{V}}_{t+1} ({\mathbf{x}+\mathbf{1}_{as} })\), we have to approximate \({\tilde{V}} _{t+1} (\mathbf{x})\) separately for each time slot the current customer may choose and for the case that the customer leaves without ordering. Hence, \(S+1\) instances of the MILP need to be solved. The state (i.e. \(\mathbf{x}\) or \(\mathbf{x}+\mathbf{1}_{as})\), for which the value function is approximated, is indicated by the parameter \(i_{as} \) in the MILP formulation. If the MILP approximates the value function for the state vector \(\mathbf{x}+\mathbf{1}_{as} \) (the current customer request from area \(a\in {{\mathcal {A}}}\) is served in time slot \(s\in {{\mathcal {S}}})\), \(i_{as} \) is set to 1. In contrast, if the MILP approximates the value function for the state vector \(\mathbf{x}\) (the current customer request leaves without ordering), \(i_{as} \) is set to 0 for all \(a\in {{\mathcal {A}}}\) and \(s\in {{\mathcal {S}}}.\)

The model (5)–(17) combines the anticipation of expected customer requests demand management (cf. Sect. 3.2.1) with the approximation of the delivery cost (cf. Sect. 3.2.2). For the anticipation of expected customer requests demand management, \(\pi _{na} \) represent the decision variables taking as value the number of expected customers originating from area \(a\in {{\mathcal {A}}}\) offered price list \(n\in {{\mathcal {G}}}\). To assign the resulting number of expected customers from area \(a\in {{\mathcal {A}}}\) choosing time slot \(s\in {{\mathcal {S}}}\) to the vehicles \(v\in {{\mathcal {V}}}\), we define the variables \(\psi _{as}^v \). The decision variables \(\theta _{as}^v \) are set to 1 if vehicle \(v\in {{\mathcal {V}}}\) travels to ATC (a, s), and 0 otherwise. In case the current customer request is served by vehicle \(v\in {{\mathcal {V}}}\), \(\delta ^{v}\) is equal to 1, and 0 otherwise. For delivery cost approximation, we define the decision variables \({\varDelta }_s^v \ge 0\) to track the total distance of the expected delivery tour in time slot \(s\in {{\mathcal {S}}}\) for vehicle \(v\in {{\mathcal {V}}}\). Regarding the input parameters, \(z_c \) is the (common) service time per customer, and \(z_d \) denotes the time needed to travel one unit of distance. The input parameters \({\dot{e}}_{as}^{v}\) and \(h_{as}^v \) represent the order size and the amount of accepted and scheduled customers in ATC (a, s) served by vehicle \(v\in {{\mathcal {V}}}\). The order size of the current customer request is given by \({\dot{e}}\) and the expected order size is denoted by e.

The mixed-integer linear program is given by

$$\begin{aligned} {\tilde{V}}_t (\mathbf{x})=\mathop {\max }\limits _{{{\varvec{\varDelta }} },{ {\varvec{\uppi }} },{{\varvec{\updelta }} },{{\varvec{\uptheta }} },{{\varvec{\uppsi }} }} \left\{ {\mathop \sum \limits _{n\in {{\mathcal {G}}}} \mathop \sum \limits _{a\in {{\mathcal {A}}}} \mathop \sum \limits _{s\in {{\mathcal {S}}}~} \pi _{na} q_{nas} ({{\hat{g}}_{ns} +r} )-\mathop \sum \limits _{s\in {{\mathcal {S}}}} \mathop \sum \limits _{v\in {{\mathcal {V}}}~} {\varDelta }_s^v c} \right\} \end{aligned}$$
(5)

subject to the constraints

$$\begin{aligned}&\mathop \sum \limits _{n\in {{\mathcal {G}}}} \pi _{na} \le {\bar{W}} m_a \quad \hbox {for all }a\in {{\mathcal {A}}} \end{aligned}$$
(6)
$$\begin{aligned}&\mathop \sum \limits _{n\in {{\mathcal {G}}}} \pi _{na} q_{nas} =\mathop \sum \limits _{v\in {{\mathcal {V}}}} \psi _{as}^v \quad \hbox {for all }s\in {{\mathcal {S}}},\,\, a\in {{\mathcal {A}}} \end{aligned}$$
(7)
$$\begin{aligned}&\mathop \sum \limits _{v\in {{\mathcal {V}}}} \delta ^{v}=1 \end{aligned}$$
(8)
$$\begin{aligned}&\psi _{as}^v +\delta ^{v}i_{as} \le \theta _{as}^v ~M_{as} \quad \hbox {for all }s\in {{\mathcal {S}}},\quad a\in {{\mathcal {A}}},\quad v\in {{\mathcal {V}}} \end{aligned}$$
(9)
$$\begin{aligned}&d_s^v +\mathop \sum \limits _{a\in {{\mathcal {A}}}} {\hat{d}}_{as}^v \theta _{as}^v +\mathop \sum \limits _{a\in {{\mathcal {A}}}} {\check{d}}_{as}^v \left( \psi _{as}^v +\delta ^{v}i_{as} \right) \le {\varDelta }_s^v \quad \hbox {for all }s\in {{\mathcal {S}}},\quad v\in {{\mathcal {V}}} \qquad \end{aligned}$$
(10)
$$\begin{aligned}&\mathop \sum \limits _{a\in {{\mathcal {A}}}} \mathop \sum \limits _{s\in {{\mathcal {S}}}} \left( {\dot{e}}_{as}^{v}+\delta ^{v}i_{as} {\dot{e}} +\psi _{as}^{v}e\right) \le Q \quad \hbox {for all}~v\in {{\mathcal {V}}} \end{aligned}$$
(11)
$$\begin{aligned}&z_d {\varDelta }_s^v +z_c \mathop \sum \limits _{a\in {{\mathcal {A}}}} (h_{as}^v +\delta ^{v}i_{as} +\psi _{as}^v)\le l_s \quad \hbox {for all }s\in {{\mathcal {S}}},\quad v\in {{\mathcal {V}}} \end{aligned}$$
(12)
$$\begin{aligned}&\theta _{as}^v \in \left\{ {0,1} \right\} \quad \hbox {for all }s\in {{\mathcal {S}}},\quad a\in {{\mathcal {A}}},\quad v\in {{\mathcal {V}}} \end{aligned}$$
(13)
$$\begin{aligned}&\delta ^{v}\in \left\{ {0,1} \right\} \quad \hbox {for all }v\in {{\mathcal {V}}} \end{aligned}$$
(14)
$$\begin{aligned}&{\varDelta }_s^v \ge 0\quad \hbox {for all }s\in {{\mathcal {S}}},\quad v\in {{\mathcal {V}}} \end{aligned}$$
(15)
$$\begin{aligned}&\psi _{as}^v \ge 0 \quad \hbox {for all }s\in {{\mathcal {S}}},\quad a\in {{\mathcal {A}}},\quad v\in {{\mathcal {V}}} \end{aligned}$$
(16)
$$\begin{aligned}&\pi _{na} \ge 0 \quad \hbox {for all }n\in {{\mathcal {G}}},\quad a\in {{\mathcal {A}}} \end{aligned}$$
(17)

In the objective function (5), the expected total profit from periods \(t+1\) to T is maximised, i.e. expected total generated profits (before delivery) minus expected total delivery cost. The first term accounts for expected total generated profits by multiplying the number of expected customers from area a that are served in time slot \(s\,(\pi _{na} q_{nas})\) by the price \(({\hat{g}}_{ns})\) and the expected profit per customer (r). Recall that \(\pi _{na} \) in conjunction with the following constraints incorporate the anticipation of future customer requests demand management (cf. Sect. 3.2.1). The last term depicts the expected total delivery cost by summarising delivery cost for each vehicle \(v\in {{\mathcal {V}}}\) in each time slot \(s\in {{\mathcal {S}}}\).

Constraints (6) prevent that more price offers in terms of price lists \(n\in {{\mathcal {G}}}\) are made than the number of future customers expected to arrive from area \(a\in {{\mathcal {A}}}\) during the booking horizon \(({\bar{W}} m_a)\). Depending on the offered price for a time slot \(s\in {{\mathcal {S}}}\), customers choose slot \(s\in {{\mathcal {S}}}\) with a certain probability \(({q_{nas} })\). Thus, the left-hand side of constraints (7) provides the number of expected customers in an ATC (a, s) who choose time slot \(s\in {{\mathcal {S}}}\). These expected customers must be served by the vehicle fleet, which is ensured by the right-hand side of constraints (7). The current customer request must be served by exactly one vehicle [see constraint (8)]. To incorporate the to-seed distance \({\hat{d}}_{as}^v \), constraints (9) force the decision variable \(\theta _{as}^v \) to take the value 1 if vehicle v visits ATC (a, s)—to serve expected customers and/or the current customer request. We define the parameter \(M_{as} :={\bar{W}} m_a \mathop {\hbox {max}}\limits _{n\in {{\mathcal {G}}}} \left\{ {q_{nas} } \right\} +i_{as} \) for all areas \(a\in {{\mathcal {A}}}~\)and time slots \(s\in {{\mathcal {S}}}\) to set the bound as tight as possible. Constraints (10) control the distances \({\varDelta }_s^v \) that contain the distances \(d_s^v \) of the delivery tour of already scheduled customers (first term on the left-hand side) as well as the to-seed distances \({\hat{d}}_{as}^v \) (second term) and the seed-to-customer distances \({\check{d}}_{as}^v \) (third term). Note that first, the to-seed distances \({\hat{d}}_{as}^v\) are only included if \(\theta _{as}^v \) equals 1, i.e. if vehicle \(v\in {{\mathcal {V}}}\) travels to ATC (a, s). Second, the seed-to-customer distances \({\check{d}}_{as}^v \) include the incoming customer request if \(\delta ^{v}\) equals 1. Constraints (11) guarantee that each vehicle’s capacity is respected by adding up the order size of the accepted customers, the incoming customer request and the expected customers. Constraints (12) ensure that the time windows are not exceeded for any delivery time slot \(s\in {{\mathcal {S}}}\) and any vehicle \(v\in {{\mathcal {V}}}\) (note that in the case of nonoverlapping time windows, Constraints (12) need to be slightly adapted). The first term represents the total expected travel time and the last three terms subsume the time for serving the accepted and expected customers. Finally, (13)–(14) are binary constraints and (15)–(17) are nonnegativity constraints for the continuous decision variables.

The MILP’s solutions for the approximated value function \({\tilde{V}}_{t+1} (\mathbf{x})\) as well as the set of available time slots \(F_a (\mathbf{x})\) the current request can possibly be served in are used in conjunction with Eq. (4). This enables an easy determination of the optimal price policy for an incoming customer request. Note that \(F_a (\mathbf{x})\) is determined by inserting the incoming customer request in each time slot and solving the insertion heuristic—independently of the approximation of the value function. Thus, a feasible operational delivery tour is always guaranteed owing to the fact that the current request is offered prices only for delivery slots it can possibly be served in.

Remark

At the cost of approximation accuracy, the computational effort of model (5)–(17) can be significantly reduced by aggregating all vehicles. Thus, the constraints (10), (11) and (12) are adequately adjusted, and the set \({{\mathcal {V}}}\) is re-defined to \({{\mathcal {V}}}=\left\{ 1 \right\} \).

4 Computational study

We will now evaluate the proposed approximation of opportunity cost. In Sect. 4.1, we describe the data informed by practical settings we identified in the related literature. In Sect. 4.2, we introduce simple yet industry standard pricing policies in AHD and the state-of-the-art dynamic pricing policy we use to benchmark our novel approach. In Sect. 4.3, we present and discuss the computational results concerning the introduced benchmarks as well as for practical, large-scale and real-time implementation.

4.1 Description of the data

We conduct the computational experiments for a delivery region that is segmented into 12 equally large delivery areas served by one central depot. Inspired by Campbell and Savelsbergh (2005) and Campbell and Savelsbergh (2006), we generate the delivery region as a grid with a width and length of 10 km. We randomly generate 1000 potential customers on the grid with a minimum distance of 20 metres. Distances between customers are assumed to be equal to the Euclidean distance between them multiplied by the factor 1.5, which approximates the distances on a road network (Ehmke and Campbell 2014). In line with Yang et al. (2016), we divide the finite booking horizon for the delivery day under consideration in sufficiently small periods assuming at most one customer arrival per period. In every period \(t\in \left[ {1,\ldots ,700} \right] \), a customer arrival which is randomly drawn from the set of 1000 potential customers is assumed in accordance with Yang et al. (2016) and Yang and Strauss (2017) with probability \(\lambda =0.814\). The probability \({{m}}_{{a}}\) that a customer request originates from a certain area \({{a}}\in {{\mathcal {A}}}\) is derived on the basis of the location of the 1000 randomly generated customers. We define the average customers’ order sizes and order values in line with Yang et al. (2016) and Yang and Strauss (2017) in terms of number of totes. Hence, the revenue per tote is assumed to be €30. The average profit before delivery cost is assumed to be 30% of the revenue.

In line with Campbell and Savelsbergh (2005) and Campbell and Savelsbergh (2006), we consider a time slot schedule that consists of four nonoverlapping time slots with length \(l_s =2\) h for every time slot \(s\in {{\mathcal {S}}}\), representing a regular shift. In line with Yang et al. (2016), we restrict the optimal prices \(g_{as}^*\in \mathbf{g}_a^*\) for an incoming request to the interval \(\left[ -10,10 \right] \), that is, if a price is outside this interval, we project it onto the interval’s boundary. This is a commonly used interval for delivery time slot pricing in practice (Yang et al. 2016). We consistently derive the choice probabilities \(P_{s,F_a (\mathbf{x})} ({\mathbf{g}_a } )\) of the current customer from area \(a\in {{\mathcal {A}}}\) facing price vector \(\mathbf{g}_a^*\) as well as the choice probabilities of expected future customers \(q_{nas} \) facing price list \(n\in {{\mathcal {G}}}\) in the opportunity cost approximation by means of a MNL model. We adjust the MNL model’s parameters to our setting based on parameters from Yang et al. (2016), who have approximated them on the basis of real-world data. The applied beta factors are \({{\beta }}_{0} ={-\,2.6}\) as the base utility across all options, \({{\beta }}_{{d}} ={-0.088}\) representing the price sensitivity and \({{\beta }}_{{{s}}=1} ={ 1.6},~{{\beta }} _{{{s}}=2} ={ 1.696},~{{\beta }}_{{{s}}=3} ={ 1.70816},~{{\beta }}_{{{s}}=4} ={1.7304}\) denoting the utility for the respective time slot. In line with Yang et al. (2016), we assume that all customers follow the same choice behaviour.

The time (in minutes) needed for one unit of travel (1 km) is based on an official speed statistic and set to \(z_d =2\), i.e. 30 km per hour (Statista 2013). The customer’s service time \(z_c \) equals 8 min (Campbell and Savelsbergh 2006; Punakivi and Saranen 2001). The cost per kilometre of travel distance c is set to €0.30. The e-grocer’s fleet size is varied and is assumed to be 7, 8, 9 and 15 vehicles, respectively. For every fleet size, we simulate 100 customer streams (i.e. booking horizons). The vehicle capacity is assumed to be 120 totes. The order size of a customer follows a normal distribution with mean 3 totes and standard deviation 2 totes. Note that, usually in AHD, time slot length rather than physical vehicle capacity is the constraining factor (Campbell and Savelsbergh 2005; Ehmke and Campbell 2014).

We performed all computations on an Intel(R) Xeon(R) processor with 16 cores, 3.4 GHz and 192 GB RAM. We implemented the approach in MATLAB 2016a. We used MATLAB Parallel Computing Toolbox and CPLEX 12.6 for MATLAB Toolbox from IBM to approximate the value function for the state vectors \(\mathbf{x}\) and \(\mathbf{x}+\mathbf{1}_{as} \) for all time slots \(s\in {{\mathcal {S}}}\) parallel on different cores to enable real-time dynamic pricing. Additionally, we applied the aggregation described in the Remark presented in Sect. 3.3.

4.2 Pricing policies and opportunity cost approximation

To evaluate our novel approach, we compare it to several benchmark pricing policies. First, simple yet widespread static pricing policies in AHD are defined as benchmarks, which do not necessitate price optimisation at all:

  • Fixed pricing (FP): For every incoming customer request—independent of his or her order value and area—a single price is charged for every feasible time slot \(s\in F_a (\mathbf{x})\). This price is fixed before the booking horizon begins. In line with Yang et al. (2016), we examine this policy by fixing the price at a level of €3 \((\hbox {FP}_{3})\) and €5 \((\hbox {FP}_{5})\).

  • Order value-based pricing (OVP): This is a commonly applied policy in practice, where the e-grocer charges a price depending on the customer’s order value. According to practical settings, €5 is charged if a customer’s order value is below €40, and €3 otherwise.

Second, a different dynamic pricing policy in the AHD literature is used as benchmark; it optimises prices for every incoming customer request:

  • Insertion cost-based pricing (ICP): This is based on the work of Yang et al. (2016), who refer to it as the so-called Foresight Policy. Opportunity cost of an incoming request is assumed to be equal to a linear combination of the request’s insertion cost in a schedule for already accepted customers and average insertion cost in past delivery schedules, taken as expectations about the future (cf. Sect. 1). To benchmark our approach to ICP, we have to generate these schedules (for details on the schedule generation, see “Appendix B”).

We use the aforementioned policies to benchmark our pricing decisions based on the novel and model-based opportunity cost approximation:

  • Opportunity cost-based pricing (OCP): For the anticipation of future customer requests demand management, we define a set of prices \({\bar{{\mathcal {G}}}} \) from which we derive the set \({{\mathcal {G}}}\) of price lists (cf. Sect. 3.2.1). The algorithm to define \({\bar{{\mathcal {G}}}} \) dependent on the capacity level is presented in “Appendix A”. For the computational study, this procedure results in the following price sets from which we derive the price lists for the different capacity levels: \({\bar{{\mathcal {G}}}}_{7vans} =\left\{ {4.5,5.5,6.5,7.5,10} \right\} ,~~{\bar{{\mathcal {G}}}}_{8vans} =\left\{ {1.5,2.5,3.5,4.5,9} \right\} ,~{\bar{{\mathcal {G}}}}_{9vans} =\left\{ {-2,-1,0,1,6} \right\} \) and \({\bar{{\mathcal {G}}}}_{15vans} =\left\{ -10,-9,-8,-7,0 \right\} \).

4.3 Results

In this section, we compare the pricing approaches presented in Sect. 4.2 against each other. We conduct all computational experiments for different levels of available capacity. Thus, we assume a fleet size of 7, 8 and 9 vehicles, representing different capacity tightness levels, and 15 vehicles representing no capacity limitation. In Sect. 4.3.1, we compare OCP to \(\hbox {FP}_{3}\), \(\hbox {FP}_{5}\) and OVP. In Sect. 4.3.2, we benchmark OCP to the state-of-the-art dynamic pricing approach ICP. In Sect. 4.3.3, we provide insights how to practically apply our approach when customers arrive almost simultaneously. Thus, we simulate the solution time delay by recalculating opportunity cost used for pricing decisions not for every customer request, but only for every 10th, 15th and 30th customer.

4.3.1 Comparison to fixed-price policies

In this section, we compare OCP against \(\hbox {FP}_{3}\), \(\hbox {FP}_{5}\) and OVP. In particular, OVP with two different delivery price levels depending on the generated revenue is still widespread in industry and thus a very relevant benchmark (Yang et al. 2016).

Table 2 shows the average results of all simulated customer streams at the different capacity levels for the different policies. The policy acronym appears in column 1, the number of available delivery vans and thus the capacity level in column 2, and the average number of scheduled customers at the end of the simulated booking horizons in column 3. The average value of a scheduled customer in terms of profit before distribution (i.e. the revenue multiplied by the profit margin, plus delivery fee) and the average total profit after distribution are shown in columns 4 and 5, respectively. The 95% confidence interval in column 6 refers to the average total profit provided in column 5. Delivery cost in column 7 is the average delivery cost resulting from the schedules to serve all accepted customers. The last column shows the gap between the average total profit obtained by the application of the respective policy and OCP (in line with column 5).

Table 2 Comparison of OCP to fixed-price policies
Full size table

The results show that OCP outperforms both FP and OVP at all capacity levels. FP does not favour big orders over small ones, but rather charges every incoming request the same delivery cost. Although OVP with two-tier pricing does distinguish between orders of different size, it does not link pricing decisions with capacity availability. First, this can be seen in case of very tight capacity (7 vans) when \(\hbox {FP}_{5 }\) outperforms OVP. Apparently, it is better to always charge a price of €5 than to sell some customers the spare capacity at €3. Hence, either the price points of OVP or the threshold revenue value is chosen too low in conjunction with the available capacity. Second, when there is sufficient capacity (15 vans) and the number of customers ordering at a price level of €3 can be served, \(\hbox {FP}_{3}\) also outperforms OVP. This is because even if a customer’s order value is below the threshold, it is on average more profitable to sell some of the plenty capacity for €3 than offering it for €5 and thus decreasing the probability that the customer chooses a time slot. In case capacity availability is neither very tight nor oversupplied (8 vans), OVP outperforms both variants of FP. In summary, we can conclude that the success of OVP and FP strongly depends on how well delivery prices are chosen in accordance with the available capacity level, because none of the policies can determine prices in dependence of capacity availability.

In contrast to these policies, OCP jointly considers the available capacity (and displacement cost) and the order value of every incoming customer request when deciding on the delivery price. This is why OCP constantly outperforms both FP and OVP by at least 3%, independent of the capacity level.

4.3.2 Comparison to the state-of-the-art dynamic pricing policy

In this section, we compare OCP to the state-of-the-art dynamic pricing policy ICP. Table 3 shows the same structure as Table 2 (cf. Sect. 4.3.1).

OCP constantly outperforms ICP, especially when capacity is tight. When there is no lack of capacity (15 vans), there is almost no difference in the average total profit, because there are no displacement costs, and thus, the difference in the opportunity cost of a customer request determined with ICP and OCP can be reduced to the difference of the insertion cost resulting from ICP and OCP. Since these differences are small, pricing decisions that depend on opportunity cost are nearly the same for ICP and OCP and thus are also the average total profits.

Table 3 Comparison of OCP to the state-of-the-art dynamic pricing policy ICP
Full size table

Figure 2 shows the average prices over time of the booking horizon for the different capacity levels when managing customer demand with OCP (grey price path) and ICP (black price path). For all capacity levels, the OCP price path fluctuates relatively accurately around a certain price level over the major part of the booking horizon, while the ICP price path continuously drops in the course of the booking horizon when capacity is limited to a certain extent (7, 8, 9 vans). This is due to the nature of ICP: opportunity cost is assumed to be equal to the linear combination of insertion cost of a customer request in expected delivery schedules (assumed to be equal to past delivery schedules) and a delivery schedule for already accepted customers. The insertion cost of a current request in expected delivery schedules is highly weighted at the start of the booking horizon. If a request cannot feasibly be inserted in expected schedules, insertion cost is set to a “big value” (Yang et al. 2016) to “punish” the infeasibility. Especially when capacity is tight (7, 8 vans), this happens very often. The weight of insertion cost in schedules for already accepted customers increases with increasing t (i.e. the weight of insertion cost in expected schedules decreases with increasing t).

Fig. 2
figure 2

Average delivery prices over time in the booking horizon at different capacity levels

Full size image

When a customer request can be inserted in the schedule for accepted customers, insertion cost is normally considerably lower than the “big value” to punish the infeasibility of inserting that request in an expected schedule. This is why the overall insertion cost (assumed to be equal to the opportunity cost in ICP) and thus the price path naturally decrease for tight capacity levels. The declining price path is further intensified by the fact that displacement cost is not included, which may lead to an increasing underestimation of the true opportunity cost and thus lower prices. This leads to the fact that capacity (especially for popular time slots) is exhausted early in the booking horizon. The following two consequences can be derived: first, even early in the booking horizon, customers need to be rejected, i.e. no more price offers can be made which guarantee feasibility. For instance, in case of 7 vehicles, after (on average) 89% of the booking horizon has passed (in comparison to 98% in OCP), the first customer is rejected, i.e. (on average) about the last 65 customer requests cannot receive a price offer. Second, for customers who can still feasibly be served, high discounts have to be given at the end of the booking horizon to steer them to less popular delivery slots, which again leads to a remarkable decrease in the price path.

Through the anticipation of expected customer requests demand management and the consideration of displacement cost, pricing decisions in OCP are not dependent on the progress of the booking horizon; thus, the price path decreases only slightly. Further, the price level for a certain capacity level is automatically influenced by the considered displacement cost. If, for instance, a customer request occurs when capacity is tight, prices for this request would generally be higher than in an unrestricted capacity scenario (cf. Fig. 2). Thus, capacity availability is significantly better reflected in pricing decisions of OCP than of ICP. Only in the very last periods, when some popular time slots are already closed, OCP’s price path also decreases.

4.3.3 Practical application

To apply OCP in an online environment, we have to ensure that pricing decisions are real-time ones. Thus, we use parallel computing in order to approximate the value function for the state vectors \(\mathbf{x}\) and \(\mathbf{x}+\mathbf{1}_{as} \) for all time slots \(s\in {{\mathcal {S}}}\) parallel on different cores. To approximate opportunity cost in our computational study, this leads to an average solution time of 0.141 s and a maximum solution time over all approximations of 0.647 s. In practice, it may occur that the time span between consecutive customer requests is even smaller than these solution times. To further accelerate pricing decisions, one can apply a periodic re-optimisation of the MILP and thus a periodic re-determination of opportunity cost. This means customers do not have to wait before they receive their price offer. The idea is as follows: already calculated opportunity cost for a customer request originating from area \(a\in {{\mathcal {A}}}\) and for time slot \(s\in {{\mathcal {S}}}\) is used for pricing decisions as long as the recalculation of opportunity cost for an area and time slot lasts. As soon as the recalculation is finished, one uses the “updated” opportunity cost and starts a new recalculation based on the most current information.

Fig. 3
figure 3

Periodic recalculation of opportunity cost for practical applicability

Full size image

Figure 3 illustrates this procedure and shows an excerpt of a booking horizon. Before the booking horizon starts in period \(t=1\), opportunity cost \({\tilde{{\mathcal {O}}}}_{1xas} \) is pre-calculated for customer requests from every area \(a\in {{\mathcal {A}}}\) and for every time slot \(s\in {{\mathcal {S}}}\) based on expectations only. At first, we use \({\tilde{{\mathcal {O}}}}_{1xas} \) for pricing decisions. In period \(t=2\), we start the recalculation of opportunity cost based on the information revealed by the first customer. All customer requests that occur while calculating \({\tilde{{\mathcal {O}}}}_{2xas} \) are offered delivery prices determined based on \({\tilde{{\mathcal {O}}}}_{1xas} \) depending on their delivery area and with the aid of the pricing policy (4). \(\varDelta {\tilde{t}}_j \) represents the solution time necessary to recalculate \({\tilde{{\mathcal {O}}}}_{{\tilde{t}}_j xas} \) where \({\tilde{t}}_j \) represents period t in which the \(j^{th}\) recalculation is started. As soon as the calculation of \({\tilde{{\mathcal {O}}}}_{2xas} \) for a delivery area a and time slot s is finished, we use it to make pricing decisions for customer requests from area a, and the calculation of \({\tilde{{\mathcal {O}}}}_{{\tilde{t}}_3 xas} \) based on the most current information in period \({\tilde{t}}_3 \) (i.e. information about already scheduled customers) begins. This procedure is repeated until the end of the booking horizon. Note that we still execute the insertion heuristic for every customer request in order to determine the set of all time slots \(F_a (\mathbf{x})\) the customer can feasibly be served in.

Table 4 Results for practical applicability
Full size table

While in real-time application, the recalculation time \(\varDelta {\tilde{t}}_j \) varies throughout the booking horizon, we fix \(\varDelta {\tilde{t}}_j \) to 10, 15 and 30 time periods in the following computations, which allows us to systematically examine the influence of different recalculation frequency levels on expected total profits. In practice, the updated opportunity cost can be applied as soon as they are available. Table 4 reports the results for the different capacity levels; it has the same structure as the tables in the previous sections (cf. Sect. 4.3.1).

The results show that the longer the time span between the updates of opportunity cost is, the greater the loss in profit when applying \(\hbox {OCP}^{10}\), \(\hbox {OCP}^{15}\) or \(\hbox {OCP}^{30}\), which confirms intuition. This may result from the approximation and hence demand management error which increases the longer the recalculation time \(\varDelta {\tilde{t}}_j \) lasts. This error also leads to a worse capacity utilisation, which becomes clear from looking at different capacity levels. The tighter and thus the more valuable the capacity is, the greater the loss in profit for the same recalculation time \(\varDelta {\tilde{t}}_j \).

However, note that even if capacity is tight (7, 8, 9 vans), all results are still at least 0.17% better than the application of ICP for the same capacity level. Especially when capacity is very tight (7 vans), the difference of 3.84% between \(\hbox {OCP}^{30 }\) and ICP is remarkable. When there is no lack in capacity (15 vans), opportunity cost can again be reduced to insertion cost only due to the fact that there is no displacement cost (cf. Sect. 4.3.2). Besides displacement cost, in most cases, the profit of a customer rather than insertion cost is the major factor that drives pricing decisions. Hence, \(\hbox {OCP}^{10}\), \(\hbox {OCP}^{15}\), \(\hbox {OCP}^{30}\), ICP and OCP yield almost the same profit after distribution in the 15-vans scenario.

5 Managerial implications and future research

In this paper, we proposed a novel model-based approach to approximate the opportunity cost of a customer request as a basis for dynamic time slot pricing decisions in AHD. In a computational study, we evaluated the dynamic pricing policy obtained from the original dynamic program in combination with the proposed opportunity cost approximation for different levels of available delivery capacity of the service provider. Therefore, we benchmarked our approach to different and widely applied industry standard pricing policies and to the state-of-the-art dynamic pricing approach. Further, we examined our approach’s practical applicability.

The managerial implications of the computational study are as follows: first, the dynamic pricing policy in combination with our novel opportunity cost approximation approach constantly yielded the highest expected average profit for all delivery capacity levels of the service provider in our study. Specifically, over all examined scenarios (different capacity levels), the average profit obtained with our approach is 2.3% higher than the average of the state-of-the-art dynamic pricing policy and 5.5% higher than the average of the fixed-price policies. Specifically given a tight service provider capacity level, i.e. a small fleet that faces high customer demand, our approach performs better than all other pricing approaches. Owing to the fact that we considered displacement cost, prices determined with our pricing approach did not systematically decrease in the booking horizon’s progress. This reflects adequate saving of capacity for the future and more valuable customer requests, and inhibits negative effects of decreasing price paths on total profit. Second, assuming that the worst-case solution time of 0.647 s to make a pricing decision is too long, we used periodic recalculation of opportunity cost. This means that the same opportunity cost is used for pricing decisions for customer requests occurring in quick succession until a new opportunity cost approximation is determined. In the worst case of our computational study, this procedure ended up with 1.66% less profit than updating opportunity cost for every incoming customer request. Even though we chose the recalculation time very pessimistically (in practice, it would probably be faster than in the worst case of our study), our novel approach still outperforms the state-of-the-art dynamic pricing approach and thus also the fixed-price policies, such that it qualifies for practical application.

Several interesting future research directions remain. First, instead of using a CDLP-based approach to anticipate future demand management, one could adapt other linearisation techniques of choice-based approaches from revenue management [e.g. see Talluri (2014) for the segment-based deterministic concave program and Gallego et al. (2015) for the sales-based linear program]. Second, in addition to our periodic re-optimisation, to increase the scalability regarding the number of time slots, promising approaches might be an analytical procedure to reduce the number of price points and/or decomposition approaches. Third, one could also develop other approximations in which the discrete price lists we use to anticipate the future customer requests demand management can be replaced by continuous prices, or pricing decisions for incoming customer requests can be made based on a discrete set of prices only. Since this would allow for an anticipation of future customers demand management to be aligned even better with the real pricing possibilities concerning an incoming customer request, the quality of the opportunity cost approximation should increase. Finally, there might be further possibilities to approximate delivery cost—still including lost profits as well as sophisticated final schedule predictions—for instance, by the use of descriptive approaches (e.g. Agatz et al. 2011; Daganzo 1987) or mixed-integer linear programs that anticipate the final delivery routes at a more detailed level.